Optimal Design of a Miniaturized Cruciform Specimen for Biaxial Testing of TA2 Alloys
Abstract
:1. Introduction
2. Optimal Design of the Cruciform Specimen via FEM
2.1. Design Requirements for the Biaxial Testing of Cruciform Specimens
- It is of great importance to confine the majority of deformation in the center region of the specimen; that is to say, the initial yielding, necking, or rupture should occur in the central gauge area of the specimen.
- The stress-strain distributions in the gauge area of the specimen should be as homogeneous as possible.
- Stress concentration should be avoided in the regions outside the central gauge area of the specimen.
- Once the above requirements are satisfied, the economics of the processing of the test piece should be considered.
2.2. FEM
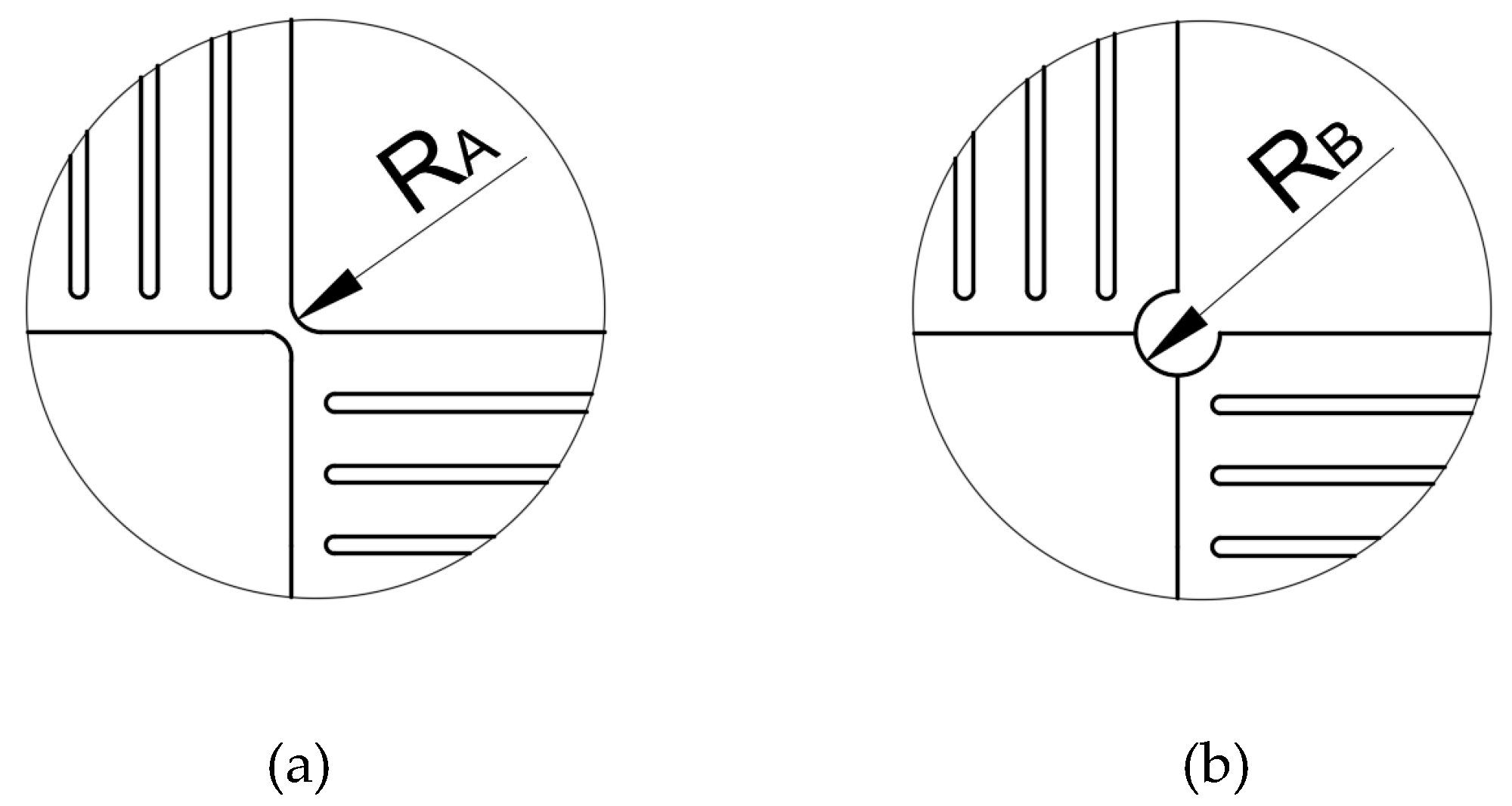
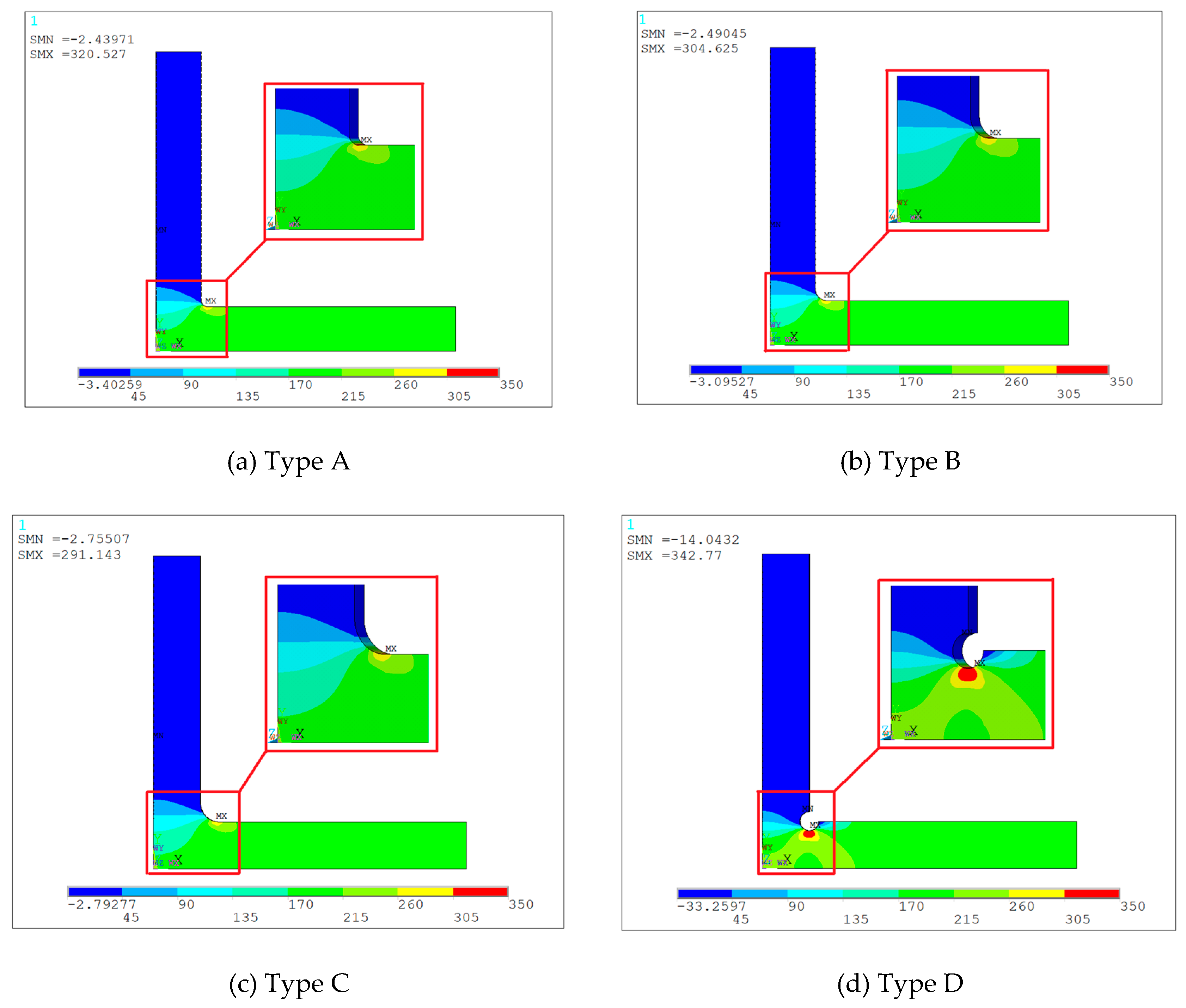
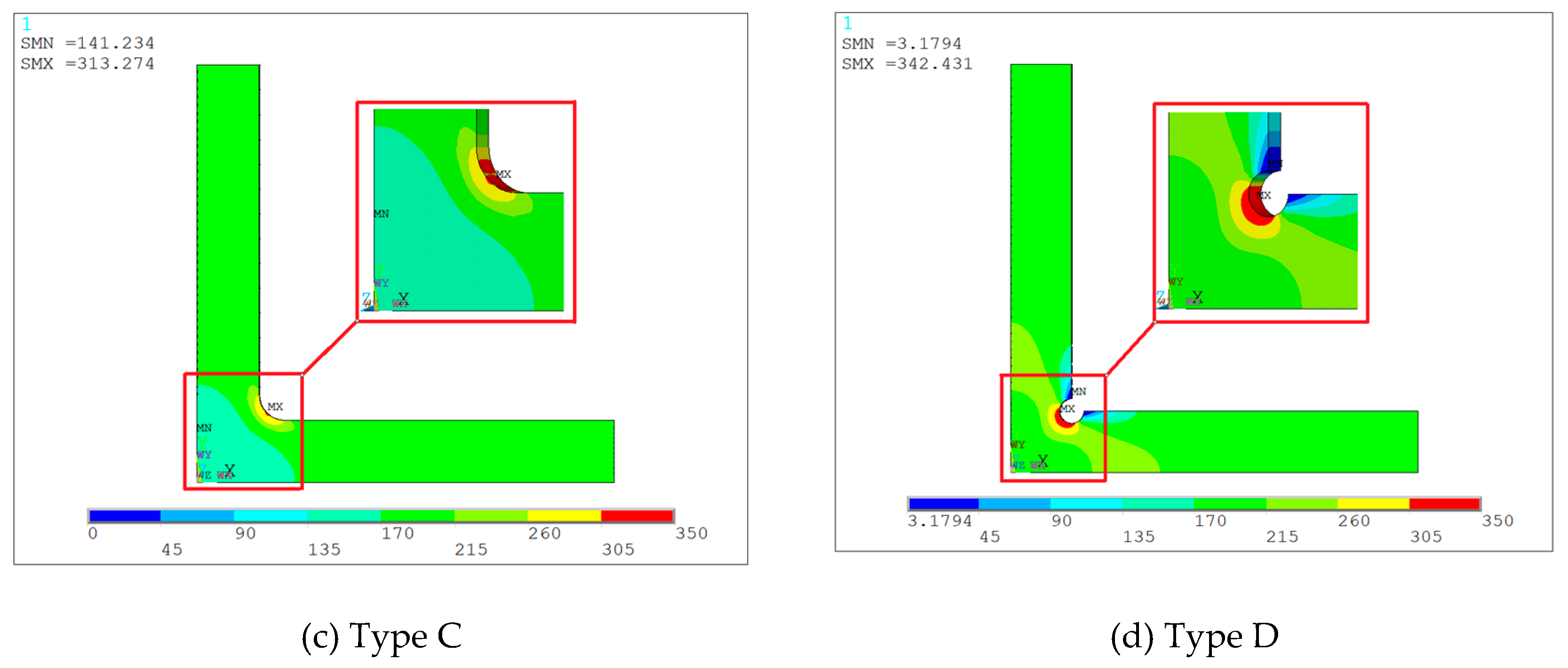
2.3. The Influence of the Geometric Shape of the Transition Section
- —
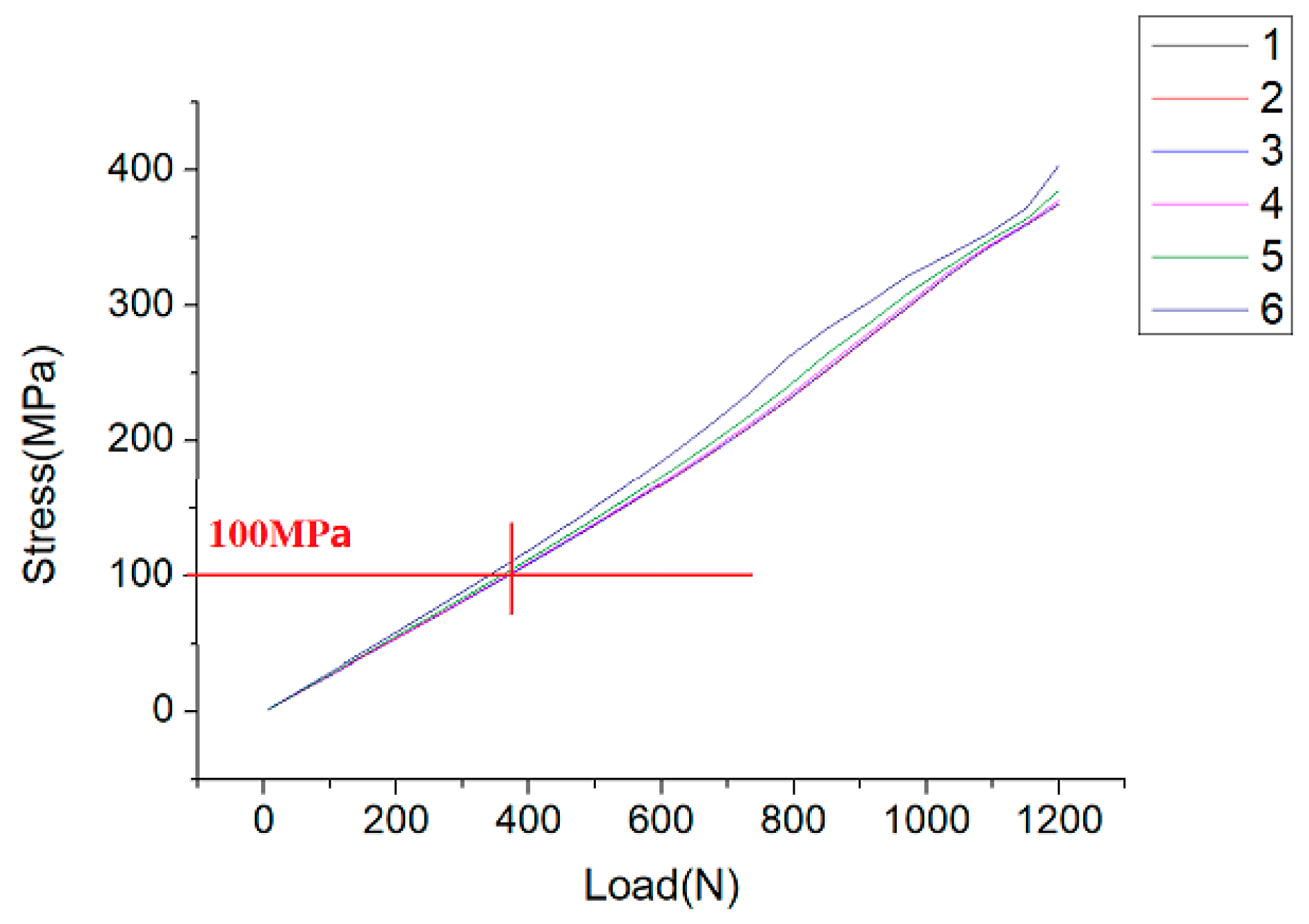
- The of the test piece is almost constant with an increase in the applied stress in the Y direction.
- —
- With an increasing applied stress in the Y axis direction, the overall distribution of Mises stress in the specimen tends to be symmetrical, implying a more homogeneous stress in the central gauge area.
- —
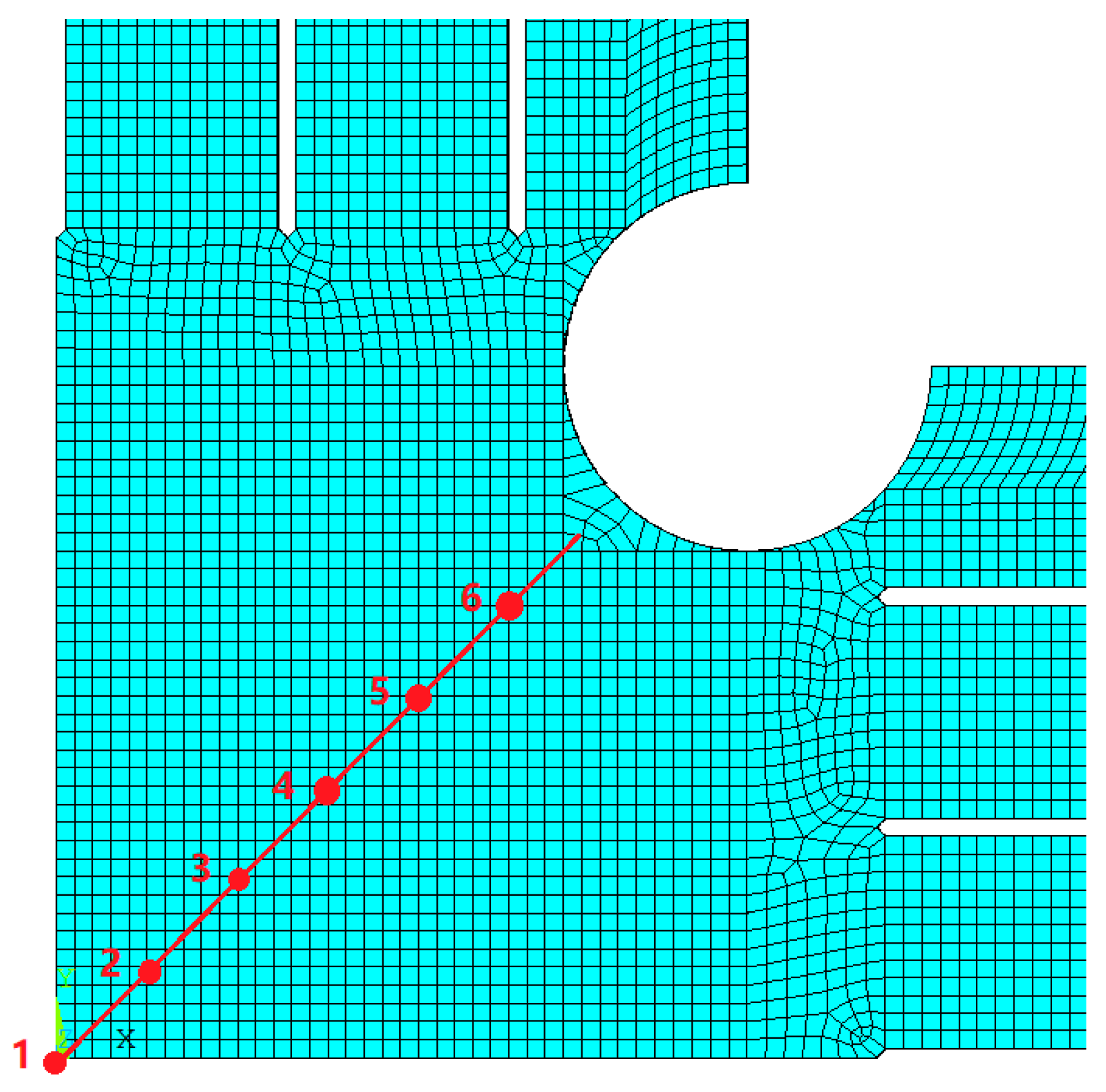
- When n = 1, the Mises stress of the specimen is symmetrical with respect to a 45° diagonal line.
2.4. Effect of the Thickness of the Central Gauge
2.5. Orthogonal Design of Cruciform Specimens
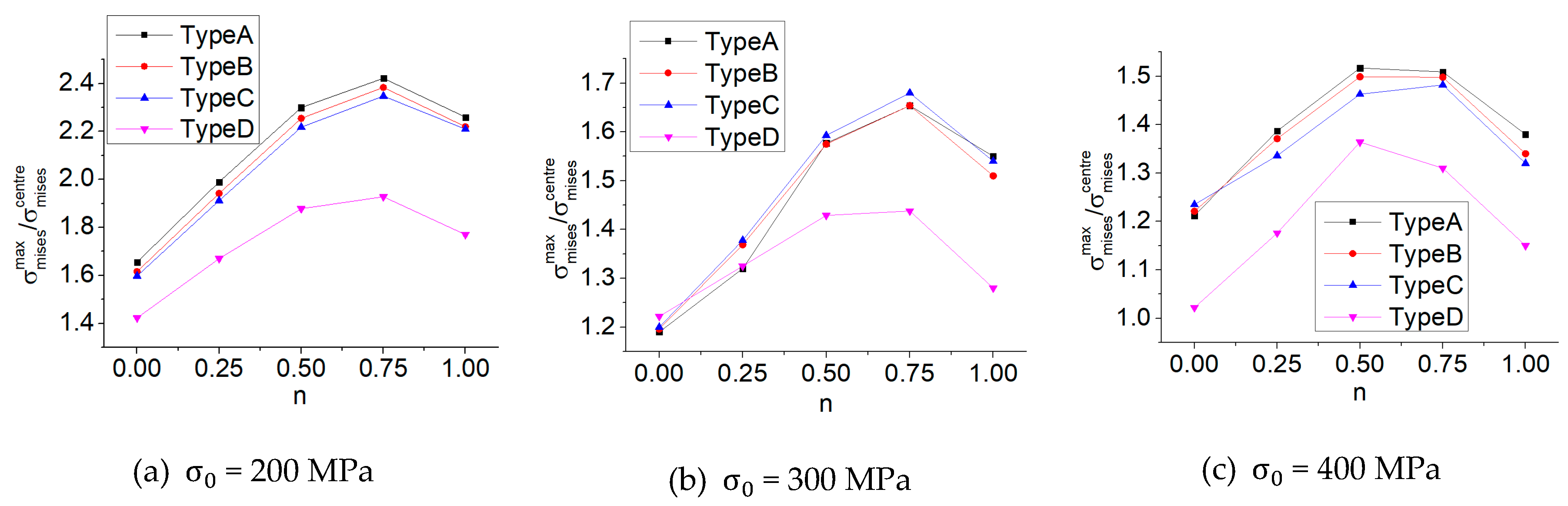
2.5.1. Stress Uniformity in the Central Gauge Region
2.5.2. Orthogonal Design Scheme
3. Experiment
4. Conclusions
- (1)
- An inner chamfer is introduced to the design of the cruciform specimen, which is effective in contributing to a reduced degree of stress concentration and a more homogeneous stress distribution in the center region, resulting in a decreased of 1.77.
- (2)
- The plastic flow can be effectively restricted in the center region of the cruciform specimen via the thinning process. As the thicknesses of the center gauge and the arm are 0.4 and 1.6 mm, respectively, the is less than 1, avoiding the preferential rupture of the arm during the biaxial tensile testing.
- (3)
- According to the results of orthogonal design, with the attendant comprehensive analysis, an optimal geometric design has been successfully attained for the cruciform specimen, in which the thickness of the central gauge region, the width, the length and the number of slits, and the radius of the inner chamfer are 0.4 mm, 0.8 mm, 20 mm, five, and 0.5 mm, respectively.
- (4)
- The full-field strain distribution of the center region for the cruciform specimen has been measured using the advanced DIC technique and is well in line with the results computed by FEM. The validity of the design method of this paper is verified.
- (5)
- This work reports a promising methodology for optimizing the geometry of a miniaturized cruciform specimen of sheet TA2 that shows great potential in the design of specimens for biaxial tensile testing of other sheet metals.
Author Contributions
Funding
Conflicts of Interest
References
- Banerjee, D.; Williams, J.C. Perspectives on Titanium Science and Technology. Acta Mater. 2013, 61, 844–879. [Google Scholar] [CrossRef]
- Ye, H.D. Some Considerations on Tensile Testing Standard of Metallic Materials. Phys. Test. Chem. Anal. 2014, 50, 394–395. [Google Scholar]
- Xiao, R.; Li, X.X.; Li, R.F.; Chen, Y.K.; Ge, Y.L.; Yang, Y.F. Biaxial Tensile Testing of Cruciform Specimens. Phys. Test. Chem. Anal. 2017, 5308, 538–543. [Google Scholar]
- Shiratori, E.; Ikegami, K. A new biaxial tensile testing machine with flat specimen. Bull. Tokyo Inst. Technol. 1967, 82, 105–118. [Google Scholar]
- Shiratori, E.; Ikegami, K. Experimental study of the subsequent yield surface by using cross-shaped specimens. J. Mech. Phys. Solids 1968, 16, 373–394. [Google Scholar] [CrossRef]
- Lebedev, A.A.; Boiko, A.V.; Muzyka, N.R. Method of testing materials in uniform biaxial tension. Strength Mater. 1982, 14, 252–254. [Google Scholar]
- Lebedev, A.A.; Muzyka, N.R. Design of cruciform specimens for fracture toughness tests in biaxial tension (Review). Strength Mater. 1998, 30, 243–254. [Google Scholar] [CrossRef]
- Makinde, A.; Thibodeau, L.; Neale, K.W. Development of an apparatus for biaxial testing using cruciform specimens. Exp. Mech. 1992, 32, 138–144. [Google Scholar] [CrossRef]
- ISO/CD 16842. Metallic Materials—Sheet and Strip—Biaxial Tensile Testing Method Using Cruciform Specimen; ISO: Geneva, Switzerland, 2014. [Google Scholar]
- Smits, A.; Van Hemelrijck, D.; Philippidis, T.; Cardon, A. Design of a cruciform specimen for biaxial testing of fibre reinforced composite laminates. Compos. Sci. Technol. 2006, 66, 964–975. [Google Scholar] [CrossRef]
- Teaca, M.; Charpentier, I.; Martiny, M.; Ferron, G. Identification of sheet metal plastic anisotropy using heterogeneous biaxial tensile tests. Int. J. Mech. Sci. 2010, 52, 572–580. [Google Scholar] [CrossRef]
- Hu, J.J.; Chen, G.W.; Liu, Y.C.; Hsu, S.S. Influence of Specimen Geometry on the Estimation of the Planar Biaxial Mechanical Properties of Cruciform Specimens. Exp. Mech. 2014, 54, 615–631. [Google Scholar] [CrossRef]
- Tiernan, P.; Hannon, A. Design optimisation of biaxial tensile test specimen using finite element analysis. Int. J. Mater. Form. 2014, 7, 117–123. [Google Scholar] [CrossRef]
- Deng, N.; Kuwabara, T.; Korkolis, Y.P. Cruciform Specimen Design and Verification for Constitutive Identification of Anisotropic Sheets. Exp. Mech. 2015, 55, 1005–1022. [Google Scholar] [CrossRef]
- Xiao, R.; Li, X.X.; Lang, L.H.; Chen, Y.K.; Yang, Y.F. Biaxial tensile testing of cruciform slim superalloy at elevated temperatures. Mater. Des. 2016, 94, 286–294. [Google Scholar] [CrossRef]
- Xiao, R.; Li, X.X.; Lang, L.H.; Song, Q.; Liu, K.N. Forming limit in thermal cruciform biaxial tensile testing of titanium alloy. J. Mater. Process. Technol. 2017, 240, 354–361. [Google Scholar] [CrossRef]
- Wu, X.D.; Wan, M.; Zhou, X.B.; Chen, G.P. Biaxial tensile experimental study on the yield loci of steel sheet BH220. J. Plast. Eng. 2004, 1, 39–42. [Google Scholar]
- Wan, M.; Hong, Q.; Wu, X.D.; Zhou, X.B. Establishment and Loading Accuracy Analysis of Bidirectional Deep Drawing Test System for Cruciform Specimens. Chin. J. Mech. Eng. 2001, 1, 57–62. [Google Scholar] [CrossRef]
- Wu, X.D.; Wan, M.; Zhou, X.B. Finite element simulation and analysis of cross biaxial tension test. Chin. J. Plast. Eng. 2001, 2, 57–59. [Google Scholar]
- Han, F.; Wan, M.; Wu, X.D.; Wang, H.B. Design of Cross Bi-directional Tensile Specimens Based on Ultimate Stress Analysis. J. Beijing Univ. Aeronaut. Astronaut. 2007, 5, 600–604. [Google Scholar]
- Han, F.; Wan, M.; Wu, X.D.; Wang, H.B. Study on Tensile Properties of Cruciform Specimens with Thinned Center Area. J. Plast. Eng. 2007, 6, 55–58. [Google Scholar]
- Hong, Q. The Optimal Design of Biaxial Tensile Cruciform Specimens Using Finite Element Method. Unpublished MA dissertation, Beihang University, Beijing, China, 2000. [Google Scholar]
- Peters, W.H.; Ranson, W.F. Digital Imaging Techniques in Experimental Stress Analysis. Opt. Eng. 1982, 21, 213427. [Google Scholar] [CrossRef]
- Sun, P.Y.; Zhu, Z.K.; Su, C.Y.; Lu, L.; Zhou, C.Y.; He, X.H. Experimental characterisation of mechanical behaviour for a TA2 welded joint using digital image correlation. Opt. Lasers Eng. 2019, 115, 161–171. [Google Scholar] [CrossRef]














| Specimens | |||
|---|---|---|---|
| Type A | 320.5 | 152.8 | 2.10 |
| Type B | 304.6 | 147.2 | 2.07 |
| Type C | 291.1 | 141.8 | 2.05 |
| Type D | 342.8 | 193.9 | 1.76 |
| Specimens | |||
|---|---|---|---|
| Type A | 345.6 | 152.9 | 2.26 |
| Type B | 327.2 | 147.2 | 2.22 |
| Type C | 313.3 | 141.8 | 2.21 |
| Type D | 342.4 | 193.9 | 1.77 |
| Specimens | ||||
|---|---|---|---|---|
| H = 1.6 mm | 421.8 | 284.8 | 1.48 | −211.3178.3 |
| H = 1.2 mm | 422.1 | 385.4 | 1.10 | −225.8222.7 |
| H = 0.8 mm | 335.3 | 454.8 | 0.70 | −251.1169.0 |
| H = 0.4 mm | 170.6 | 451.1 | 0.40 | −226.689.5 |
| Levels | A | B | C | D | E |
|---|---|---|---|---|---|
| Central Gauge Region Thickness H (mm) | (mm) | Slit Length L (mm) | Number of Slit M | Radius of the Inner Chamfer R (mm) | |
| Level 1 | 0.8 | 0.2 | 5 | 1 | 0.5 |
| Level 2 | 0.6 | 0.4 | 10 | 3 | 1 |
| Level 3 | 0.4 | 0.6 | 15 | 5 | 1.5 |
| Level 4 | 0.2 | 0.8 | 20 | 7 | 2 |
| Node Number n | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Mises stress(MPa) | 100.0 | 100.0 | 100.2 | 100.9 | 103.1 | 109.2 |
| 1.046 | ||||||
| Test Numbers | Factors | Experimental Scheme | |||||
|---|---|---|---|---|---|---|---|
| A | B | C | D | E | |||
| 1 | 1 | 1 | 1 | 1 | 1 | 1.046 | A1B1C1D1E1 |
| 2 | 1 | 2 | 2 | 2 | 2 | 1.067 | A1B2C2D2E2 |
| 3 | 1 | 3 | 3 | 3 | 3 | 1.091 | A1B3C3D3E3 |
| 4 | 1 | 4 | 4 | 4 | 4 | 1.097 | A1B4C4D4E4 |
| 5 | 2 | 1 | 2 | 3 | 4 | 1.127 | A2B1C2D3E4 |
| 6 | 2 | 2 | 1 | 4 | 3 | 1.096 | A2B2C1D4E3 |
| 7 | 2 | 3 | 4 | 1 | 2 | 1.064 | A2B3C4D1E2 |
| 8 | 2 | 4 | 3 | 2 | 1 | 1.048 | A2B4C3D2E1 |
| 9 | 3 | 1 | 3 | 4 | 2 | 1.083 | A3B1C3D4E2 |
| 10 | 3 | 2 | 1 | 3 | 1 | 1.051 | A3B2C1D3E1 |
| 11 | 3 | 3 | 4 | 2 | 4 | 1.141 | A3B3C4D2E4 |
| 12 | 3 | 4 | 2 | 1 | 3 | 1.120 | A3B4C2D1E3 |
| 13 | 4 | 1 | 4 | 2 | 3 | 1.104 | A4B1C4D2E3 |
| 14 | 4 | 2 | 3 | 1 | 4 | 1.145 | A4B2C3D1E4 |
| 15 | 4 | 3 | 2 | 4 | 1 | 1.073 | A4B3C2D4E1 |
| 16 | 4 | 4 | 1 | 3 | 2 | 1.075 | A4B4C1D3E2 |
| Test Numbers | Factors | Experimental Scheme | |||||
|---|---|---|---|---|---|---|---|
| A | B | C | D | E | |||
| 1 | 1 | 1 | 1 | 1 | 1 | 1.035 | A1B1C1D1E1 |
| 2 | 1 | 2 | 2 | 2 | 2 | 1.044 | A1B2C2D2E2 |
| 3 | 1 | 3 | 3 | 3 | 3 | 1.044 | A1B3C3D3E3 |
| 4 | 1 | 4 | 4 | 4 | 4 | 1.035 | A1B4C4D4E4 |
| 5 | 2 | 1 | 2 | 3 | 4 | 1.040 | A2B1C2D3E4 |
| 6 | 2 | 2 | 1 | 4 | 3 | 1.044 | A2B2C1D4E3 |
| 7 | 2 | 3 | 4 | 1 | 2 | 1.037 | A2B3C4D1E2 |
| 8 | 2 | 4 | 3 | 2 | 1 | 1.044 | A2B4C3D2E1 |
| 9 | 3 | 1 | 3 | 4 | 2 | 1.043 | A3B1C3D4E2 |
| 10 | 3 | 2 | 1 | 3 | 1 | 1.037 | A3B2C1D3E1 |
| 11 | 3 | 3 | 4 | 2 | 4 | 1.035 | A3B3C4D2E4 |
| 12 | 3 | 4 | 2 | 1 | 3 | 1.046 | A3B4C2D1E3 |
| 13 | 4 | 1 | 4 | 2 | 3 | 1.044 | A4B1C4D2E3 |
| 14 | 4 | 2 | 3 | 1 | 4 | 1.064 | A4B2C3D1E4 |
| 15 | 4 | 3 | 2 | 4 | 1 | 1.039 | A4B3C2D4E1 |
| 16 | 4 | 4 | 1 | 3 | 2 | 1.034 | A4B4C1D3E2 |
| Specimen | A1B4C4D3E1 | A3B4C4D3E1 |
|---|---|---|
| 1.035 | 1.040 |
| Fe | C | N | H | O | Al | V | Ti |
|---|---|---|---|---|---|---|---|
| 0.061 | 0.028 | 0.006 | 0.002 | 0.087 | - | - | 99.816 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Z.; Lu, Z.; Zhang, P.; Fu, W.; Zhou, C.; He, X. Optimal Design of a Miniaturized Cruciform Specimen for Biaxial Testing of TA2 Alloys. Metals 2019, 9, 823. https://doi.org/10.3390/met9080823
Zhu Z, Lu Z, Zhang P, Fu W, Zhou C, He X. Optimal Design of a Miniaturized Cruciform Specimen for Biaxial Testing of TA2 Alloys. Metals. 2019; 9(8):823. https://doi.org/10.3390/met9080823
Chicago/Turabian StyleZhu, Zhikang, Zheng Lu, Peng Zhang, Wei Fu, Changyu Zhou, and Xiaohua He. 2019. "Optimal Design of a Miniaturized Cruciform Specimen for Biaxial Testing of TA2 Alloys" Metals 9, no. 8: 823. https://doi.org/10.3390/met9080823
APA StyleZhu, Z., Lu, Z., Zhang, P., Fu, W., Zhou, C., & He, X. (2019). Optimal Design of a Miniaturized Cruciform Specimen for Biaxial Testing of TA2 Alloys. Metals, 9(8), 823. https://doi.org/10.3390/met9080823




