A Modified Constitutive Model for the Description of the Flow Behavior of the Ti-10V-2Fe-3Al Alloy during Hot Plastic Deformation
Abstract
:1. Introduction
2. Experiments
3. Theories
4. Results
4.1. Modelling the Flow Behavior in the Prior-Peak Stage
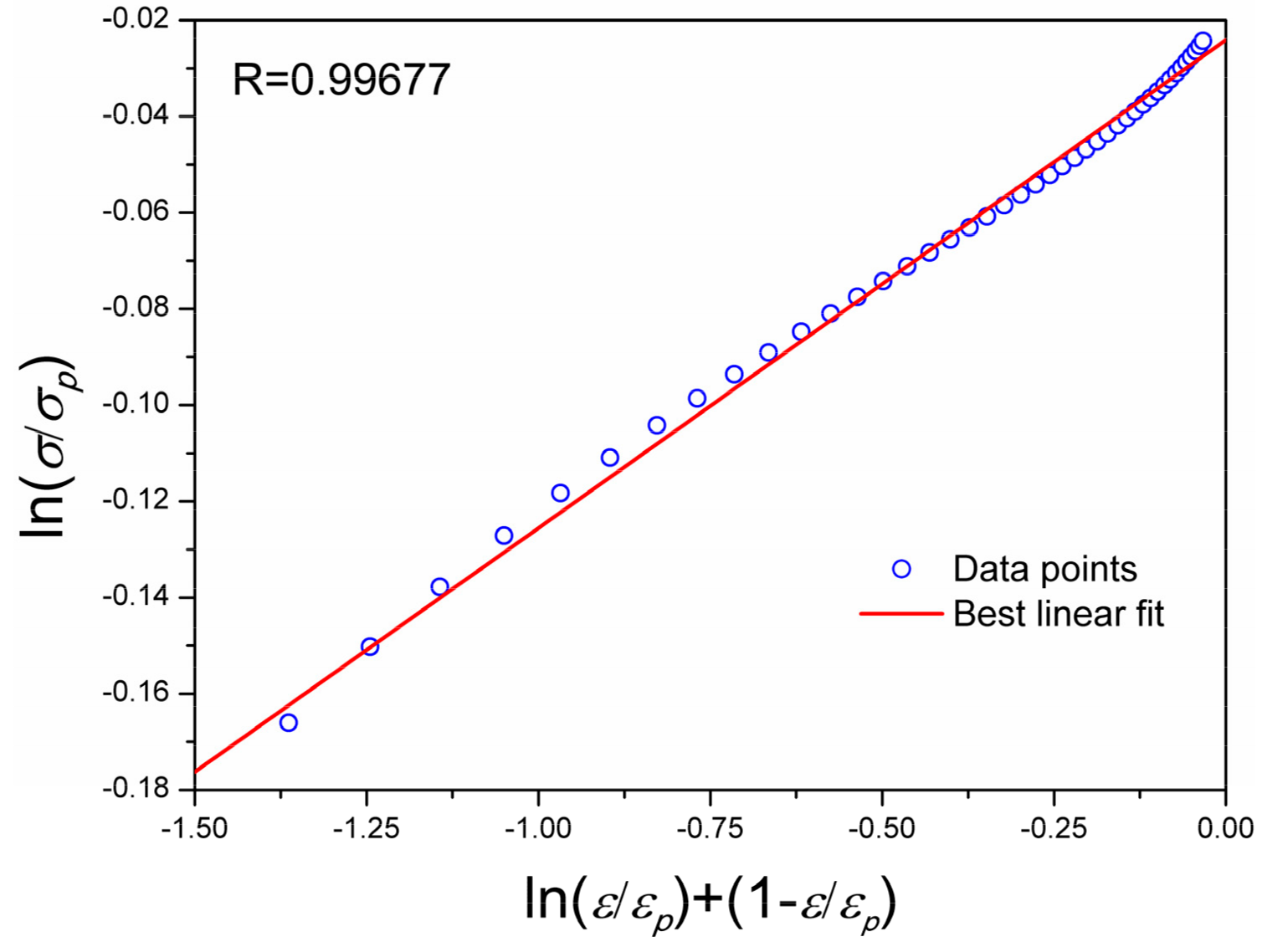
4.2. Modelling the Flow Behavior in the Post-Peak Stage
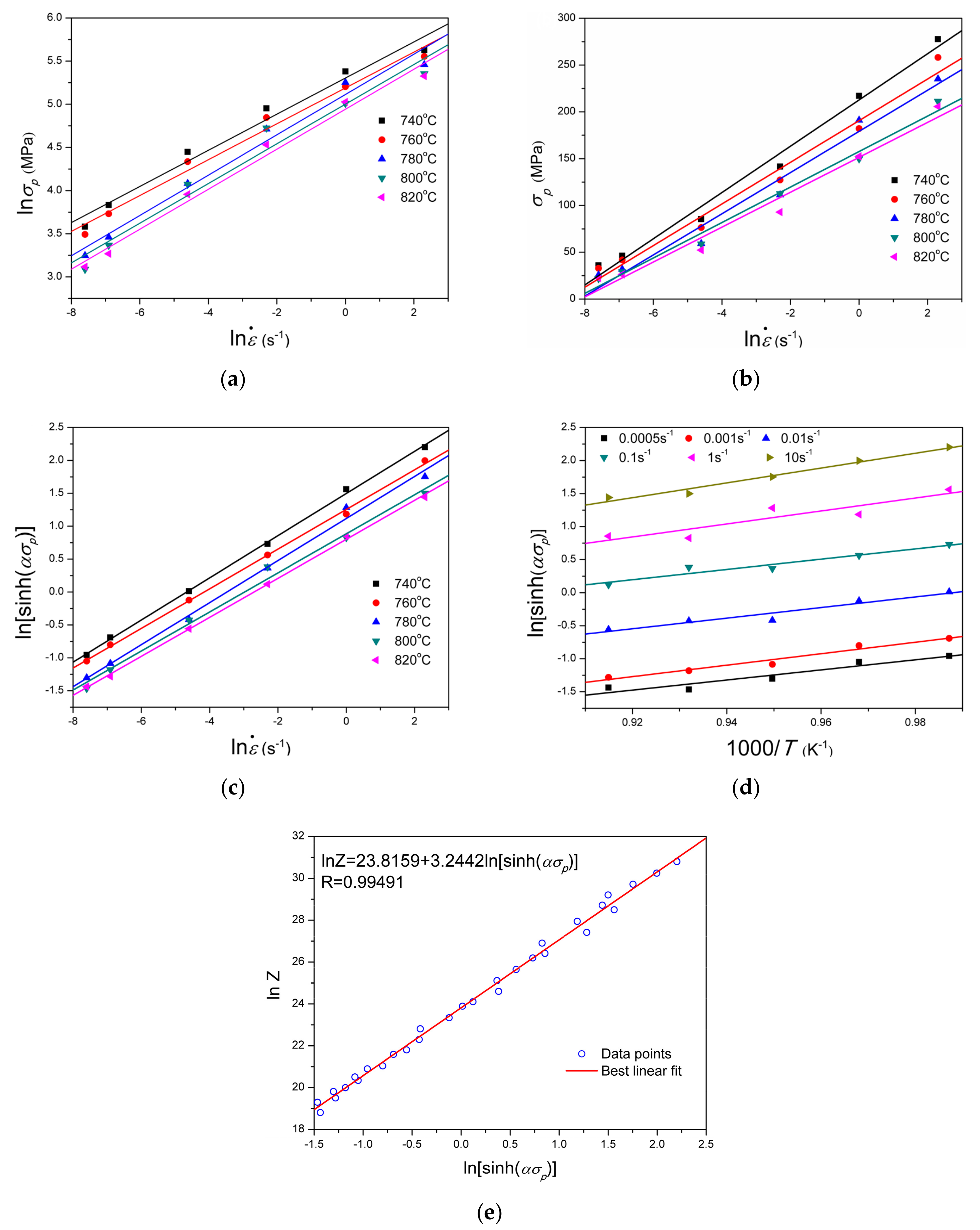
4.3. Application of the Original Constitutive Model
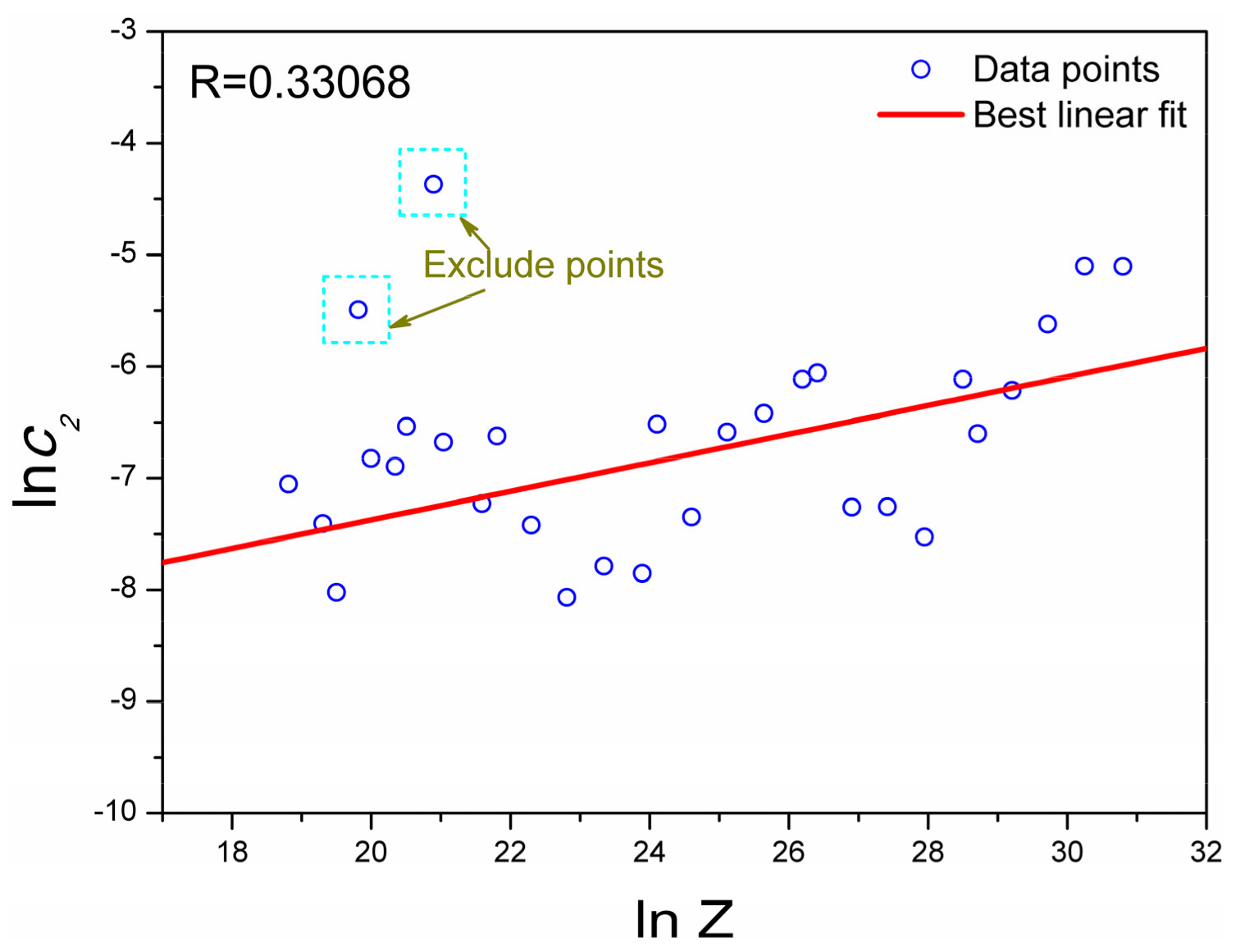
4.4. Development of a Modified Constitutive Model
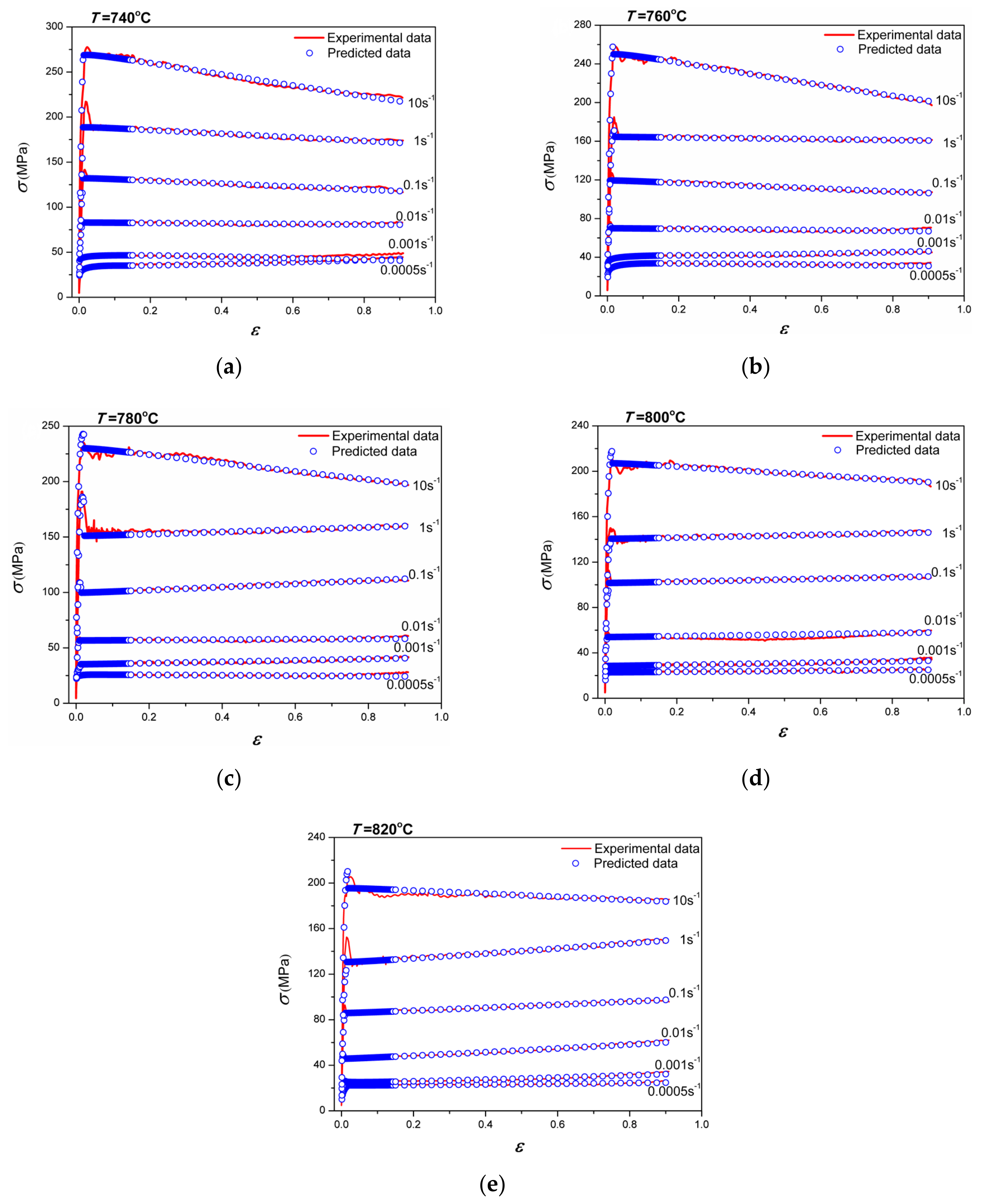
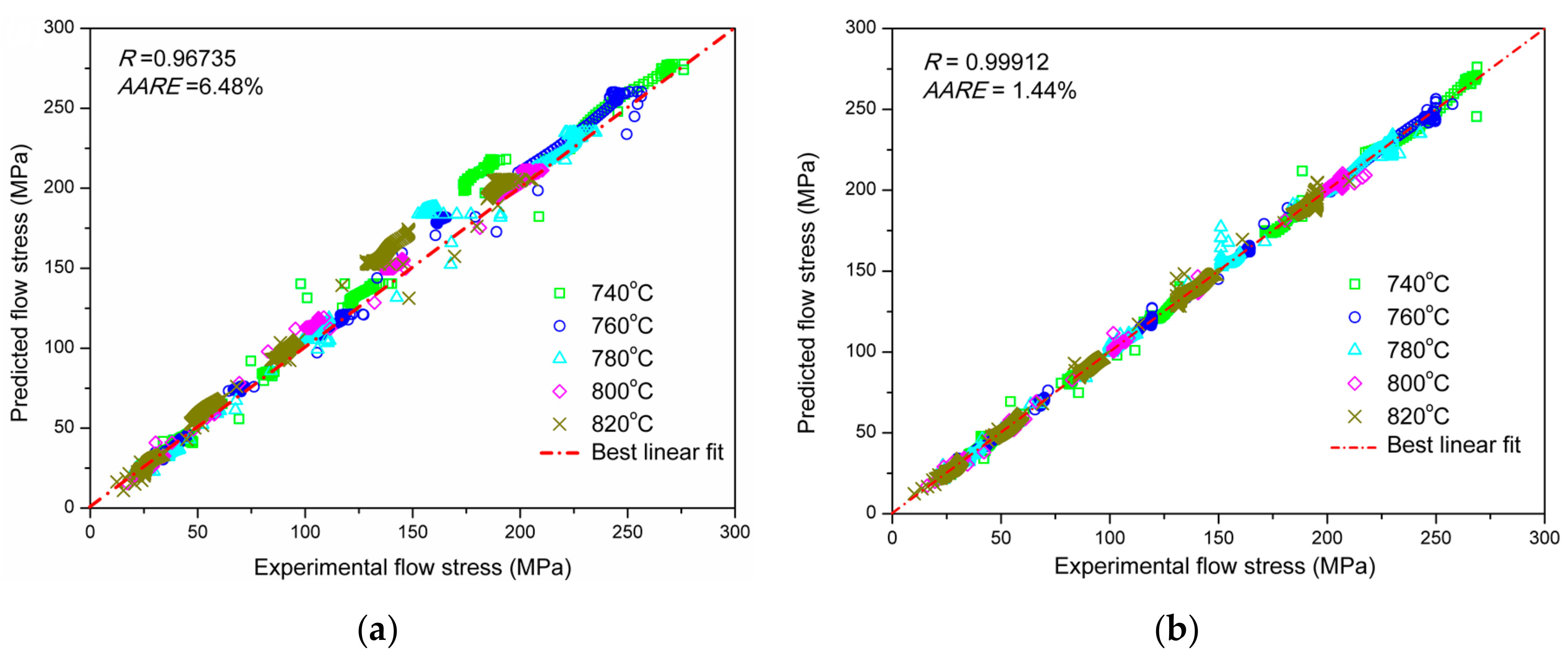
4.5. Verification of the Modified Constitutive Model
4.6. Comparison of the Original and the Modified Constitutive Models
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Utama, M.I.; Park, N.; Baek, E.R. Microstructure and mechanical features of electron beam welded dissimilar titanium alloys: Ti-10V-2Fe-3Al and Ti-6Al-4V. Met. Mater. Int. 2019, 25, 439–448. [Google Scholar] [CrossRef]
- Ren, L.; Xiao, W.L.; Ma, C.L.; Zheng, R.X.; Zhou, L. Development of a high strength and high ductility near β-Ti alloy with twinning induced plasticity effect. Scripta. Metall. 2018, 156, 47–50. [Google Scholar] [CrossRef]
- Qi, L.C.; Qiao, X.L.; Huang, L.J.; Huang, X.; Zhao, X.Q. Effect of structural stability on the stress induced martensitic transformation in Ti-10V-2Fe-3Al alloy. Mater. Sci. Eng. A. 2019, 756, 381–388. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Y.; Zan, X.; Wang, Y. The constitutive responses of Ti-6.6Al-3.3Mo-1.8Zr-0.29Si alloy at high strain rates and elevated temperatures. J. Alloys Compd. 2015, 647, 97–104. [Google Scholar] [CrossRef]
- Haj, M.; Mansouri, H.; Vafaei, R.; Ebrahimi, G.R.; Kanani, A. Hot compression deformation behavior of AISI 321 austenitic stainless steel. Int. J. Min. Met. Mater. 2013, 20, 529–534. [Google Scholar] [CrossRef]
- Liang, H.Q.; Guo, H.Z.; Nan, Y.; Qin, C.; Peng, X.N.; Zhang, J.L. The construction of constitutive model and identification of dynamic softening mechanism of high-temperature deformation of Ti-5Al-5Mo-5V-1Cr-1Fe alloy. Mater. Sci. Eng. A 2014, 615, 42–50. [Google Scholar] [CrossRef]
- Bobbili, R.; Madhu, V. Dynamic behavior and constitutive modeling of Ti-10-2-3 alloy. J. Alloys. Compd. 2019, 786, 588–593. [Google Scholar] [CrossRef]
- Lin, Y.C.; Chen, X.M. A critical review of experimental results and constitutive descriptions for metals and alloys in hot working. Mater. Des. 2011, 32, 1733–1759. [Google Scholar] [CrossRef]
- Sellars, C.M.; McTegart, W.J. On the mechanism of hot deformation. Acta Metall. 1966, 14, 1136–1138. [Google Scholar] [CrossRef]
- Lin, Y.C.; Chen, M.S.; Zhong, J. Constitutive modeling for elevated temperature flow behavior of 42CrMo steel. Comput. Mater. Sci. 2008, 42, 470–477. [Google Scholar] [CrossRef]
- He, A.; Xie, G.L.; Zhang, H.L.; Wang, X.T. A comparative study on Johnson-Cook, modified Johnson-Cook and Arrhenius-type constitutive models to predict the high temperature flow stress in 20CrMo alloy steel. Mater. Des. 2013, 52, 677–685. [Google Scholar] [CrossRef]
- Cai, J.; Wang, K.S.; Zhai, P.; Li, F.G.; Yang, J. A modified Johnson-Cook constitutive equation to predict hot deformation behavior of Ti-6Al-4V alloy. J. Mater. Eng. Perform. 2015, 24, 32–44. [Google Scholar] [CrossRef]
- Zhan, H.Y.; Wang, G.; Kent, D.; Dargusch, M. Constitutive modelling of the flow behavior of a β titanium alloy at high strain rates and elevated temperatures using the Johnson-Cook and modified Zerilli-Armstrong models. Mater. Sci. Eng. A 2014, 612, 71–79. [Google Scholar] [CrossRef]
- Cheng, Y.Q.; Zhang, H.; Chen, Z.H.; Xian, K.F. Flow stress equation of AZ31 magnesium alloy sheet during warm tensile deformation. J. Mater. Process. Technol. 2008, 208, 29–34. [Google Scholar] [CrossRef]
- Jia, W.T.; Xu, S.; Le, Q.C.; Fu, L.; Ma, L.F.; Tang, Y. Modified Fields-Backofen model for constitutive behavior of as-cast AZ31B magnesium alloy during hot deformation. Mater. Des. 2016, 106, 120–132. [Google Scholar] [CrossRef]
- Zhang, H.M.; Chen, G.; Chen, Q.; Han, F.; Zhao, Z.D. A physically-based constitutive modelling of a high strength aluminum alloy at hot working conditions. J. Alloys. Compd. 2018, 743, 283–293. [Google Scholar] [CrossRef]
- Bammann, D.J. An internal variable model of viscoplasticity. Int. J. Eng. Sci. 1984, 22, 1041–1053. [Google Scholar] [CrossRef]
- Holmedal, B. On the formulation of the mechanical threshold stress model. Acta Mater. 2007, 55, 2739–2746. [Google Scholar] [CrossRef]
- Wang, X.D.; Pan, Q.L.; Xiong, S.W.; Liu, L.L. Prediction on hot deformation behavior of spray formed ultra-high strength aluminum alloy-A comparative study using constitutive models. J. Alloys. Compd. 2018, 735, 1931–1942. [Google Scholar] [CrossRef]
- Han, Y.; Yan, S.; Sun, Y.; Chen, H.; Yan, S.; Sun, Y.; Chen, H. Modeling the constitutive relationship of Al-0.62Mg-0.73Si alloy based on artificial neural network. Metals 2017, 7, 114. [Google Scholar] [CrossRef]
- Sabokpa, O.; Zarei-Hanzaki, A.; Abedi, H.R.; Haghdadi, N. Artificial neural network modeling to predict the high temperature flow behavior of an AZ81 magnesium alloy. Mater. Des. 2012, 39, 390–396. [Google Scholar] [CrossRef]
- Li, C.L.; Narayana, P.L.; Reddy, N.S.; Choi, S.W.; Yeom, J.T.; Hong, J.K.; Park, C.H. Modeling hot deformation behavior of low-cost Ti-2Al-9.2Mo-2Fe beta titanium alloy using a deep neural network. J. Mater. Sci. Technol 2019, 35, 907–915. [Google Scholar] [CrossRef]
- Cingara, A.; McQueen, H.J. New formula for calculating flow curves from high temperature constitutive data for 300 austenitic steels. J. Mater. Process. Technol. 1992, 36, 31–42. [Google Scholar] [CrossRef]
- McQueen, H.J.; Bailon, J.P.; Dickson, J.I. Strength of Metals and Alloys (ICSMA 7); Pergamon Press: Oxford, UK, 1986; Volume 2, pp. 935–940. [Google Scholar]
- McQueen, H.J.; Ryan, N.D.; Evangelista, E. Dynamic recovery and strain hardening in the hot deformation of type 317 stainless steel. Mater. Sci. Eng. 1986, 81, 259–272. [Google Scholar]
- Ryan, N.D.; McQueen, H.J. Comparison of dynamic softening in 301, 304, 316 and 317 stainless steels. High Temp. Technol. 1990, 8, 185–200. [Google Scholar] [CrossRef]
- Lin, Y.C.; Wen, D.X.; Deng, J.; Liu, G.; Chen, J. Constitutive models for high-temperature flow behaviors of a Ni-based superalloy. Mater. Des. 2014, 59, 115–123. [Google Scholar] [CrossRef]
- Hajari, A.; Morakabati, M.; Abbasi, S.M.; Badri, H. Constitutive modeling for high-temperature flow behavior of Ti-6242S alloy. Mater. Sci. Eng. A. 2017, 681, 103–113. [Google Scholar] [CrossRef]
- Zener, C.; Hollomon, J.H. Effect of strain rate upon plastic flow of steel. J. Appl. Phys. 1944, 15, 22–32. [Google Scholar] [CrossRef]
- Lin, Y.C.; Chen, M.S.; Zhong, J. Modeling of flow stress of 42CrMo steel under hot compression. Mater. Sci. Eng. A. 2009, 499, 88–92. [Google Scholar] [CrossRef]
- Robertson, D.G.; McShane, H.B. Isothermal hot deformation behavior of (α + β) titanium alloy Ti-4Al-4Mo-2Sn-0.5Si (IMI 550). Mater. Sci. Technol. 1997, 13, 459–468. [Google Scholar] [CrossRef]
- Zhou, M.; Clode, M.P. Constitutive equations for modelling flow softening due to dynamic recovery and heat generation during plastic deformation. Mech. Mater. 1998, 27, 63–76. [Google Scholar] [CrossRef]
- Ji, G.L.; Li, F.G.; Li, Q.H.; Li, H.Q.; Li, Z. A comparative study on Arrhenius-type constitutive model and artificial neural network model to predict high-temperature deformation behavior in Aermet100 steel. Mater. Sci. Eng. A. 2011, 528, 4774–4782. [Google Scholar] [CrossRef]







| Strain Rate (s−1) | Deformation Temperature (°C) | ||||
|---|---|---|---|---|---|
| 740 | 760 | 780 | 800 | 820 | |
| 0.0005 | 0.10143 | 0.10143 | 0.55065 | 0.34829 | 0.31172 |
| 0.001 | 0.42785 | 0.35682 | 0.25596 | 0.35636 | 0.29254 |
| 0.01 | 0.72538 | 0.71803 | 0.62142 | 0.58776 | 0.75455 |
| 0.1 | 0.89752 | 0.80238 | 1.08625 | 0.72074 | 1.04578 |
| 1 | 0.86542 | 1.09427 | 1.09299 | 0.98385 | 0.96104 |
| 10 | 0.86736 | 0.85978 | 0.56476 | 0.81574 | 0.80480 |
| Strain Rate (s−1) | Deformation Temperature (°C) | ||||
|---|---|---|---|---|---|
| 740 | 760 | 780 | 800 | 820 | |
| 0.0005 | 0.01268 | 0.00102 | 0.00412 | 6.08 × 10−4 | 8.65 × 10−4 |
| 0.001 | 7.27 × 10−4 | 0.00126 | 0.00145 | 0.00109 | 3.28 × 10−4 |
| 0.01 | 3.89 × 10−4 | 4.15 × 10−4 | 3.14 × 10−4 | 5.99 × 10−4 | 0.00133 |
| 0.1 | 0.00221 | 0.00163 | 0.00138 | 6.45 × 10−4 | 0.00148 |
| 1 | 0.00221 | 5.39 × 10−4 | 7.07 × 10−4 | 7.04 × 10−4 | 0.00234 |
| 10 | 0.00608 | 0.00609 | 0.00362 | 0.002 | 0.00136 |
| Strain Rate (s−1) | Deformation Temperature (°C) | ||||
|---|---|---|---|---|---|
| 740 | 760 | 780 | 800 | 820 | |
| 0.0005 | 0.97618 | 0.99719 | 1.00238 | 1.02063 | 1.07884 |
| 0.001 | 1.00773 | 1.00260 | 0.97923 | 0.99909 | 1.23495 |
| 0.01 | 0.97764 | 0.94452 | 0.96002 | 0.91924 | 0.93990 |
| 0.1 | 0.93117 | 0.89593 | 1.03672 | 0.97166 | 0.90613 |
| 1 | 0.91977 | 0.93934 | 0.97871 | 0.91032 | 0.99239 |
| 10 | 1.13818 | 1.05228 | 1.03347 | 1.02899 | 1.02356 |
| Strain Rate (s−1) | Deformation Temperature (°C) | ||||
|---|---|---|---|---|---|
| 740 | 760 | 780 | 800 | 820 | |
| 0.0005 | 0.99305 | 0.99204 | 0.99627 | 1.05767 | 0.98968 |
| 0.001 | 0.99713 | 0.98427 | 1.10590 | 1.01442 | 0.95979 |
| 0.01 | 0.97144 | 0.91887 | 0.95548 | 0.88622 | 0.91143 |
| 0.1 | 0.94142 | 0.98570 | 0.94737 | 0.90197 | 0.92483 |
| 1 | 0.86421 | 0.90325 | 0.82194 | 0.93762 | 0.85737 |
| 10 | 0.96838 | 0.96015 | 0.97821 | 0.98048 | 0.95020 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, F.; Shen, J.; Zhang, Y.; Ning, Y. A Modified Constitutive Model for the Description of the Flow Behavior of the Ti-10V-2Fe-3Al Alloy during Hot Plastic Deformation. Metals 2019, 9, 844. https://doi.org/10.3390/met9080844
Wang F, Shen J, Zhang Y, Ning Y. A Modified Constitutive Model for the Description of the Flow Behavior of the Ti-10V-2Fe-3Al Alloy during Hot Plastic Deformation. Metals. 2019; 9(8):844. https://doi.org/10.3390/met9080844
Chicago/Turabian StyleWang, Fukang, Jingyuan Shen, Yong Zhang, and Yongquan Ning. 2019. "A Modified Constitutive Model for the Description of the Flow Behavior of the Ti-10V-2Fe-3Al Alloy during Hot Plastic Deformation" Metals 9, no. 8: 844. https://doi.org/10.3390/met9080844
APA StyleWang, F., Shen, J., Zhang, Y., & Ning, Y. (2019). A Modified Constitutive Model for the Description of the Flow Behavior of the Ti-10V-2Fe-3Al Alloy during Hot Plastic Deformation. Metals, 9(8), 844. https://doi.org/10.3390/met9080844





