Reducing Statistical Uncertainty in Elastic Settlement Analysis of Shallow Foundations Relying on Targeted Field Investigation: A Random Field Approach
Abstract
:1. Introduction
2. Two-Dimensional Probabilistic Elastic Settlement Analysis Based on the Random Finite Element Method (RFEM)
- Virtually sample elastic modulus values from the random field generated in each RFEM realization,
- Calculate the footing settlement (again in each RFEM realization) considerring that the soil is homogenous, having E equal to the mean of the values sampled (this settlement is calculated in addition to the settlement of footing lying on spatially random soil) and,
- Estimate the failure probability of the footing.
3. Parametric Study for Determining the Optimal Sampling Strategy
3.1. Sampling from a Single Point
3.1.1. Effect of Scale of Fluctuation
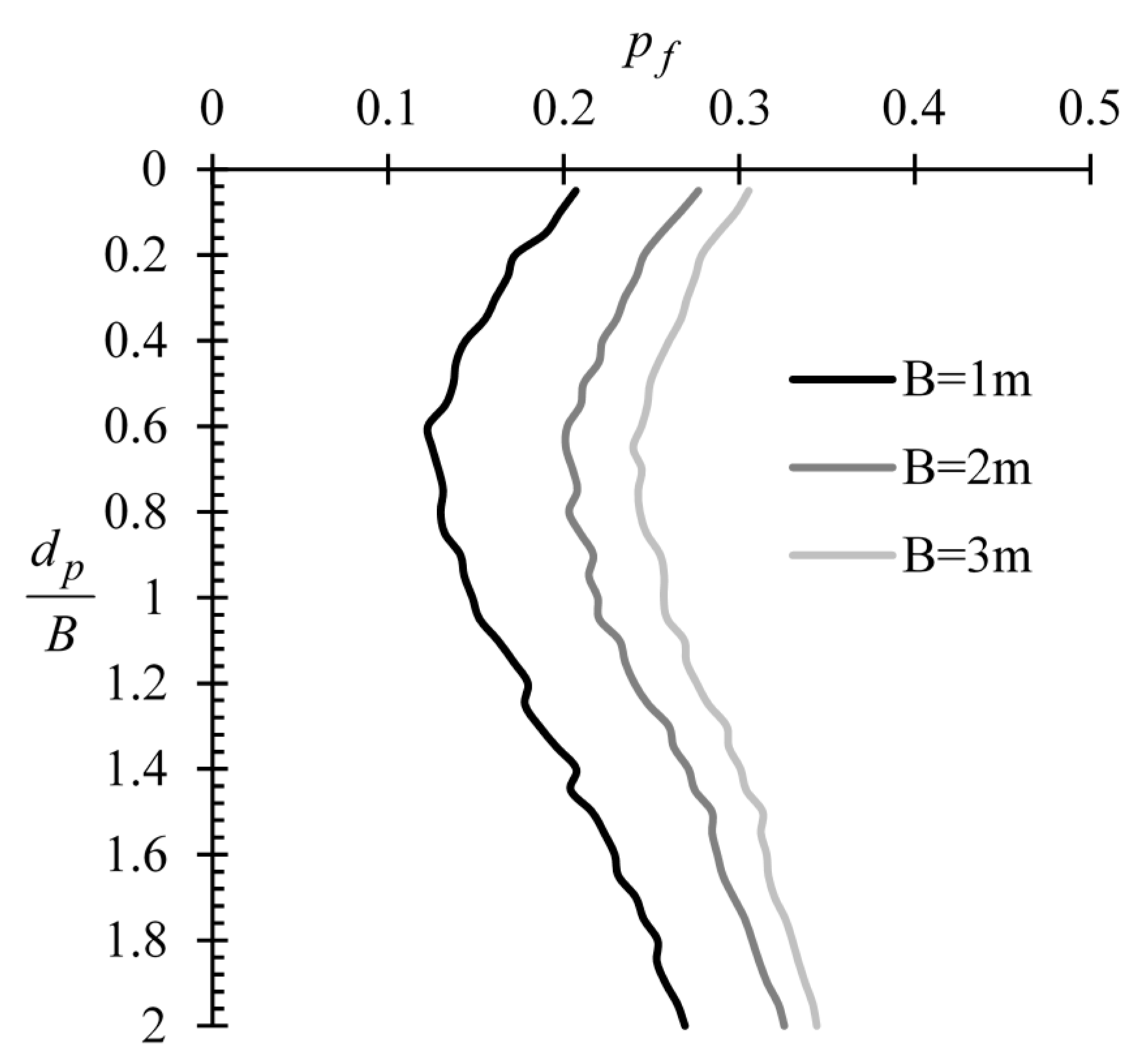
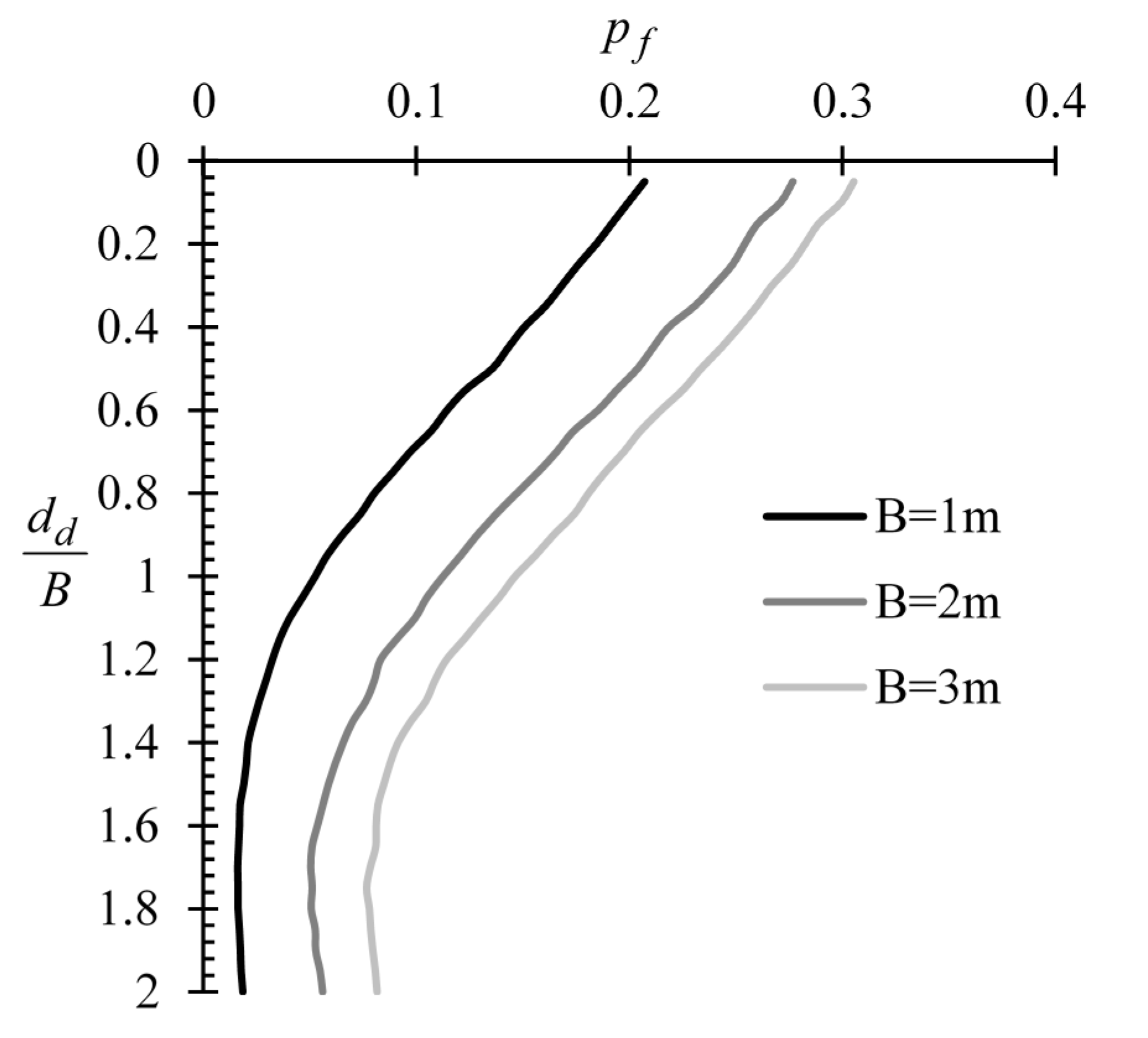
3.1.2. Effect of Footing Width (B)
3.1.3. Effect of COV of the Elastic Constants of Soil
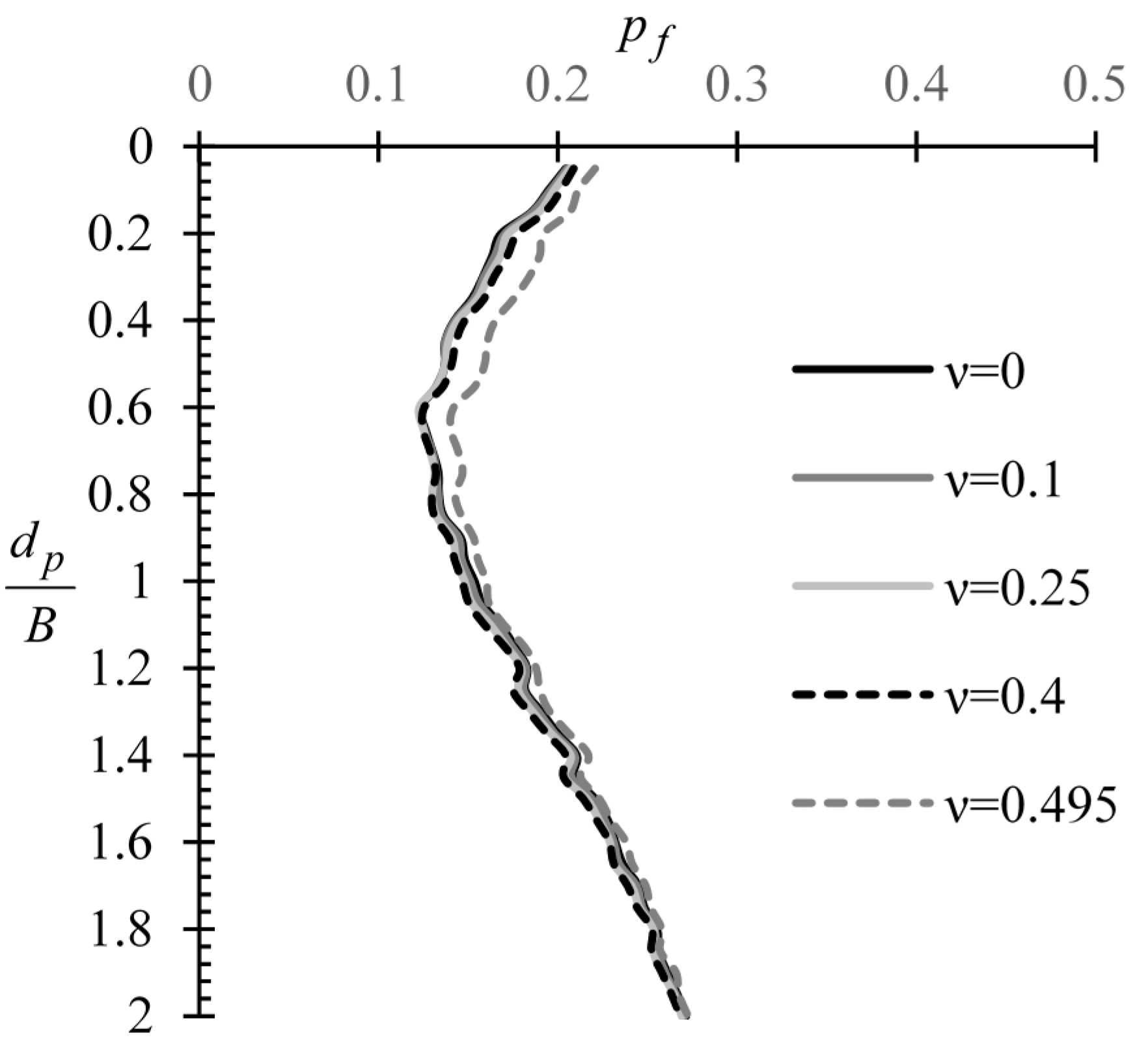
3.1.4. Effect of the Elastic Constant Values of Soil
3.2. Sampling from an Entire Domain
3.2.1. Effect of Scale of Fluctuation
3.2.2. Effect of Footing Width
3.2.3. Effect of COV of the Elastic Constants of Soil
3.2.4. Effect of the Elastic Constant Values of Soil
4. Discussion
4.1. The Importance of Targeted Field Investigation in Practice
4.2. Designing with Load and Resistance Factor Design (LRFD) Codes
5. Summary and Conclusions
- In the case of a single footing (no interference with adjacent footings), the geometric center on its plan-view is the optimal sampling location.
- The sampling strategy is not affected by the elastic constants (E, ν) of soil. The same also stands for the COV of E in the case of sampling from a single point. Regarding the case of sampling an entire domain, the COV of E was found to affect the optimal sampling domain length in a manner suggesting that a more variable soil calls for greater domain length.
- Soil anisotropy also plays no role in the magnitude of the statistical error if the sampling from a single point strategy is chosen. However, it does affect the statistical error in the case of sampling an entire domain, where, an anisotropic medium with θv much smaller than θh requires a smaller sampling length than in the respective isotropic case.
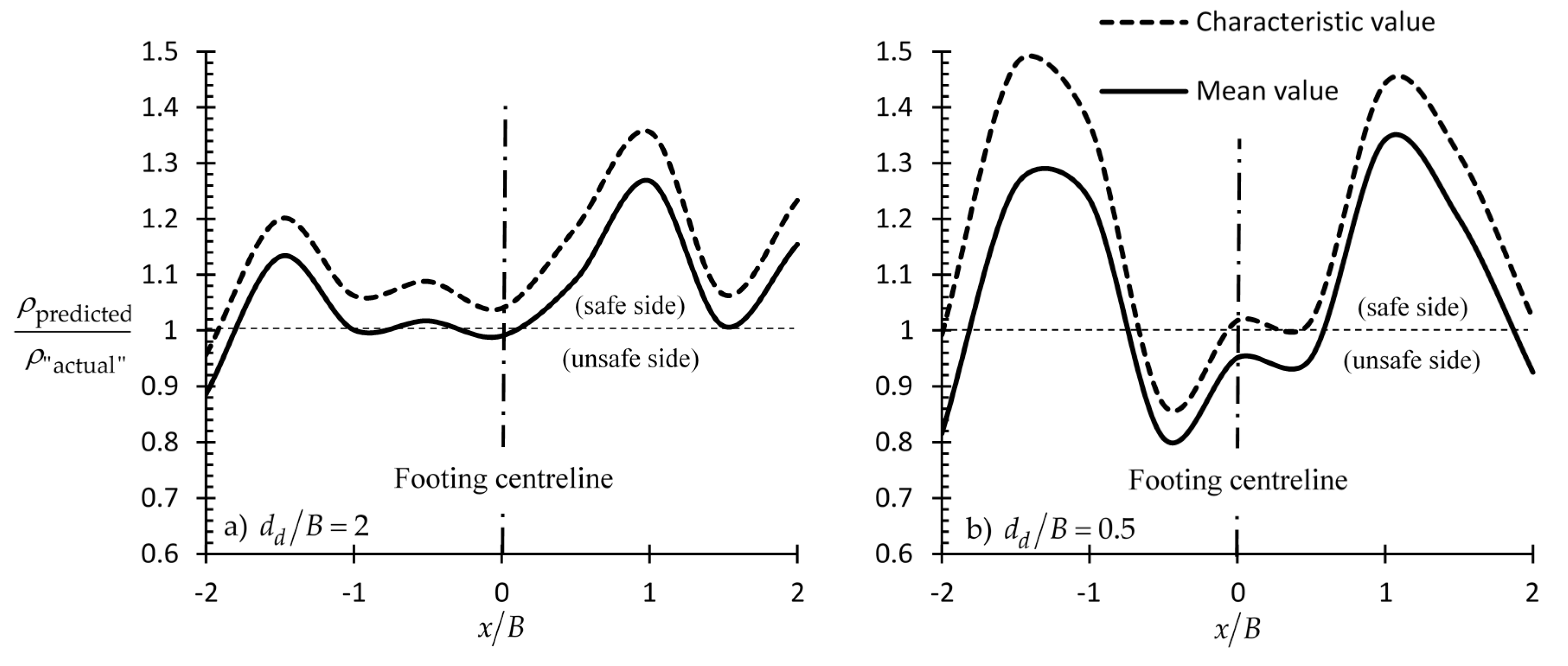
- In addition, it was observed that the sampling domain length strategy usually leads to significantly lower statistical uncertainty than the sampling from a single point strategy, given that an adequate sampling length will be considered. Generally, it is advisable that a domain length of at least 2B should be taken into account in the analysis.
- Finally, it is concluded that the benefit from a targeted field investigation is much greater as compared to the benefit gained using characteristic soil property values. Moreover, despite the conservatism that is inserted into the analysis by using the characteristic value concept, the characteristic values alone, as shown, cannot guarantee a conservative enough engineering study.
Author Contributions
Funding
Conflicts of Interest
Notation List
| footing width | |
| smaller side of footing | |
| smaller side of raft foundation | |
| sampling domain length measured always from the uppermost point of the soil | |
| depth of sampling point | |
| elastic modulus | |
| number of realizations | |
| number of samples | |
| vertical applied force | |
| probability of failure | |
| sample standard deviation | |
| Student t factor for a confidence level of α% in the case of degrees of freedom | |
| horizontal sampling location (measured from the center of the footing) | |
| design values of geotechnical parameters | |
| characteristic value | |
| sample mean | |
| investigation depth below the ground level | |
| partial material factor | |
| model factor | |
| scale of fluctuation (also, it replaces the symbols ); also known as “spatial correlation length” | |
| horizontal scale of fluctuation | |
| vertical scale of fluctuation | |
| mean elastic modulus | |
| Poisson’s ratio | |
| Settlement | |
| σ1 | Major principal stress |
| Absolute distance between two measurements |
Appendix A. Subsurface Exploration by Various Design Codes
Appendix B. Stability of Numerical Results (Distance of Lateral Boundaries and Number of Realizations Considered in the RFEM Models)

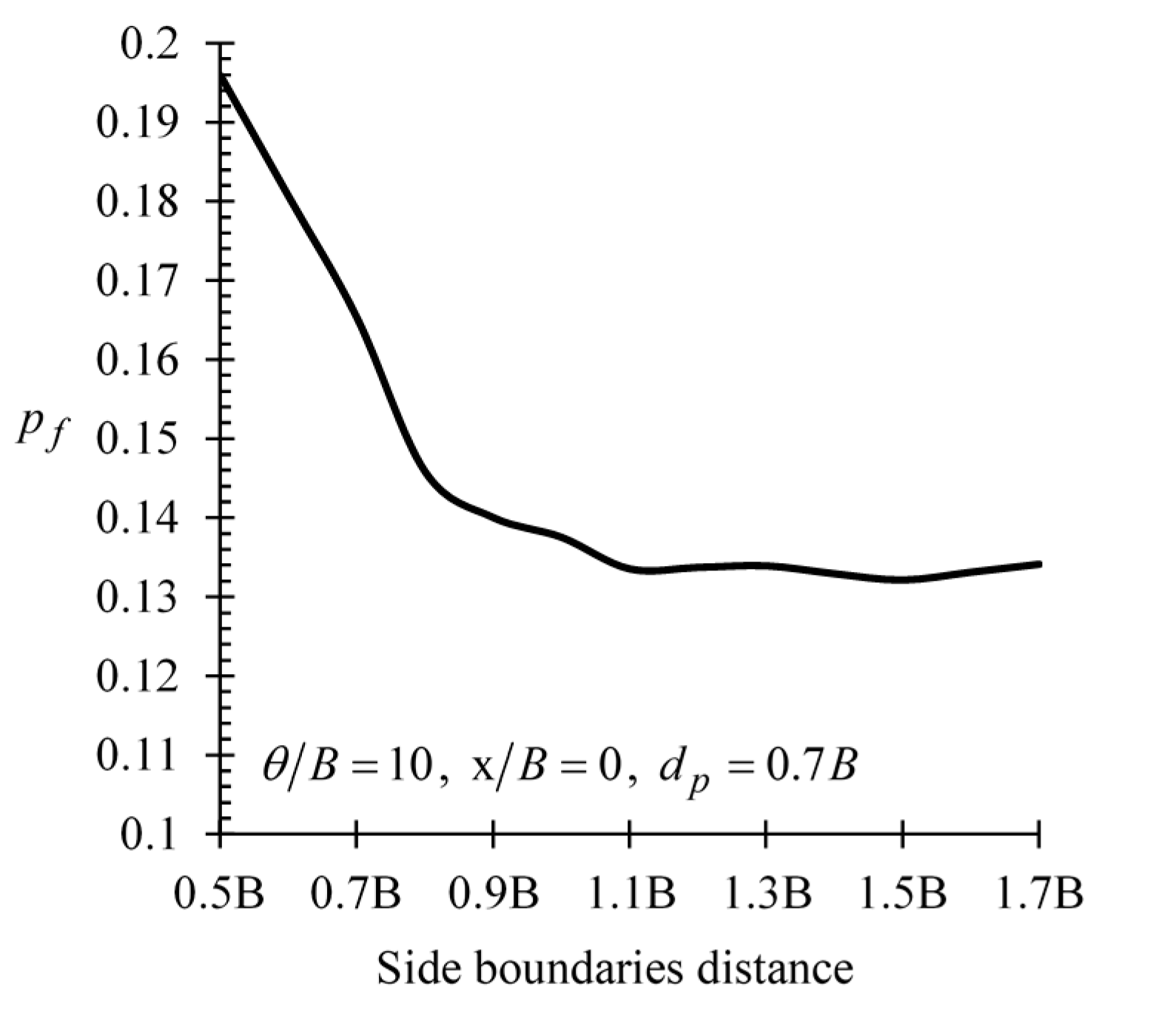
References
- Phoon, K.-K.; Kulhawy, F.H.; Grigoriu, M.D. Reliability-based design for transmission line structure foundations. Comput. Geotech. 2000, 26, 169–185. [Google Scholar] [CrossRef]
- Duzgun, H.S.B.; Yucemen, M.S.; Karpuz, C. A probabilistic model for the assessment of uncertainties in the shear strength of rock discontinuities. Int. J. Rock Mech. Min. Sci. 2002, 39, 743–754. [Google Scholar] [CrossRef]
- Tang, W.H.; Zhang, L. Quality assurance and risk reduction in foundation engineering. In Frontier Technologies Infrastructures Engineering: Structures and Infrastructures Book Series; Chen, S.-S., Ang, H.-S.A., Eds.; CRC Press: Florida, FL, USA, 2009; pp. 123–142. [Google Scholar]
- Jaksa, M.B.; Goldsworthy, J.S.; Fenton, G.A.; Kaggwa, W.S.; Griffiths, D.V.; Kuo, Y.L.; Poulos, H.G. Towards reliable and effective site investigations. Géotechnique 2005, 55, 109–121. [Google Scholar] [CrossRef]
- Griffiths, D.V.; Fenton, G.A.; Ziemann, H.R. Reliability of passive earth pressure. Georisk 2008, 2, 113–121. [Google Scholar] [CrossRef]
- Yang, R.; Huang, J.; Griffiths, D.V.; Sheng, D. Probabilistic stability analysis of slopes by conditional random fields. Geo-Risk 2017, 2017, 450–459. [Google Scholar]
- Ching, J.; Phoon, K.-K. Characterizing uncertain site-specific trend function by sparse Bayesian learning. J. Eng. Mech. 2017, 143, 4017028. [Google Scholar] [CrossRef]
- Yang, R.; Huang, J.; Griffiths, D.V.; Li, J.; Sheng, D. Importance of soil property sampling location in slope stability assessment. Can. Geotech. J. 2019, 56, 335–346. [Google Scholar] [CrossRef]
- Fenton, G.A.; Naghibi, F.; Hicks, M.A. Effect of sampling plan and trend removal on residual uncertainty. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2018, 12, 253–264. [Google Scholar] [CrossRef]
- Li, Y.J.J.; Hicks, M.A.A.; Vardon, P.J.J. Uncertainty reduction and sampling efficiency in slope designs using 3D conditional random fields. Comput. Geotech. 2016, 79, 159–172. [Google Scholar] [CrossRef] [Green Version]
- Yang, R.; Huang, J.; Griffiths, D.V.; Meng, J.; Fenton, G.A. Optimal geotechnical site investigations for slope design. Comput. Geotech. 2019, 114, 103–111. [Google Scholar] [CrossRef]
- Christodoulou, P.; Pantelidis, L.; Gravanis, E. The effect of targeted field investigation on the reliability of earth-retaining structures in active state. Appl. Sci. 2019, 9, 4953. [Google Scholar] [CrossRef] [Green Version]
- EN 1997-2. Eurocode 7-Geotechnical design-Part 2: Ground investigation and testing; CEN (European Committee for Standardization): Brussels, Belgium, 2007. [Google Scholar]
- AASHTO. AASHTO Lrfd Bridge Design Specifications; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2010; ISBN 9781560514510. [Google Scholar]
- Fenton, G.; Griffiths, D.V. Risk Assessment in Geotechnical Engineering; Wiley: Hoboken, NJ, USA, 2008; ISBN 9780470178201. [Google Scholar]
- Orr, T.L.L. Managing Risk and Achieving Reliable Geotechnical Designs Using Eurocode 7. In Risk and Reliability in Geotechnical Engineering; Phoon, K.K., Ching, J., Eds.; CRC Press: Boca Raton, FL, USA, 2014; pp. 395–433. [Google Scholar]
- Ching, J.; Phoon, K.-K. Constructing multivariate distributions for soil parameters. Risk Reliab. Geotech. Eng. 2015, 1, 3–76. [Google Scholar]
- Huang, X.C.; Zhou, X.P.; Ma, W.; Niu, Y.W.; Wang, Y.T. Two-dimensional stability assessment of rock slopes based on random field. Int. J. Geomech. 2016, 17, 4016155. [Google Scholar] [CrossRef]
- Imanzadeh, S.; Denis, A.; Marache, A. Settlement uncertainty analysis for continuous spread footing on elastic soil. Geotech. Geol. Eng. 2015, 33, 105–122. [Google Scholar] [CrossRef]
- Rocscience Inc. RS2 Version 9.0-Finite Element Analysis for Excavations and Slopes 2019. Available online: https://www.rocscience.com/software/rs2 (accessed on 13 August 2018).
- Fenton, G.A.; Vanmarcke, E.H. Simulation of random fields via local average subdivision. J. Eng. Mech. 1990, 116, 1733–1749. [Google Scholar] [CrossRef] [Green Version]
- Vanmarcke, E.H. Probabilistic modeling of soil profiles. J. Geotech. Eng. Div. 1977, 103, 1227–1246. [Google Scholar]
- Paice, G.M.; Griffiths, D.V.; Fenton, G.A. Finite element modeling of settlements on spatially random soil. J. Geotech. Eng. 1996, 122, 777–779. [Google Scholar] [CrossRef]
- Fenton, G.A.; Griffiths, D.V. Probabilistic foundation settlement on spatially random soil. J. Geotech. Geoenviron. Eng. 2002, 128, 381–390. [Google Scholar] [CrossRef] [Green Version]
- Fenton, G.; Griffiths, D.V. Bearing-capacity prediction of spatially random c-ϕ soils. Can. Geotech. J. 2003, 40, 54–65. [Google Scholar] [CrossRef]
- Griffiths, D.V.; Huang, J.; Fenton, G.A. Influence of spatial variability on slope reliability using 2-D random fields. J. Geotech. Geoenviron. Eng. 2009, 135, 1367–1378. [Google Scholar] [CrossRef] [Green Version]
- Vanmarcke, E.H. Reliability of earth slopes. J. Geotech. Eng. Div. 1977, 103, 1247–1265. [Google Scholar]
- Soulie, M.; Montes, P.; Silvestri, V. Modelling spatial variability of soil parameters. Can. Geotech. J. 1990, 27, 617–630. [Google Scholar] [CrossRef]
- Cherubini, C. Data and Considerations on the Variability of Geotechnical properties of Soils. In Proceedings of the International Conference on Safety and Reliability, ESREL, Hannover, Germany, 22–26 September 1997; pp. 1583–1591. [Google Scholar]
- Popescu, R.; Prévost, J.H.; Deodatis, G. Effects of spatial variability on soil liquefaction: Some design recommendations. Geotechnique 1997, 47, 1019–1036. [Google Scholar] [CrossRef]
- Phoon, K.; Kulhawy, F. Characterization of geotechnical variability. Can. Geotech. J. 1999, 36, 612–624. [Google Scholar] [CrossRef]
- Schmertmann, J.H. Static cone to compute static settlement over sand. J. Soil Mech. Found. Div. 1970, 96, 1011–1043. [Google Scholar]
- Schmertmann, J.H.; Hartman, J.P.; Brown, P.R. Improved strain influence factor diagrams. J. Geotech. Geoenviron. Eng. 1978, 104, 1131–1135. [Google Scholar]
- Bergdahl, U.; Malmborg, B.S.; Ottosson, E. Plattgrundläggning; Svensk Byggtjänst: Stockholm, Sweden, 1993; ISBN 9173326623. [Google Scholar]
- EN 1997-1. Eurocode 7 Geotechnical Design—Part 1: General Rules; CEN (European Committee for Standardization): Brussels, Belgium, 2004. [Google Scholar]
- Canadian Standards Association. Canadian Highway Bridge Design Code. CAN/CSA-S6-14; Canadian Standards Association: Mississauga, ON, Canada, 2014. [Google Scholar]
- Kok-Kwang, P.; Kulhawy, F.H.; Grigoriu, M.D. Development of a reliability-based design framework for transmission line structure foundations. J. Geotech. Geoenviron. Eng. 2003, 129, 798–806. [Google Scholar]
- Fenton, G.A.; Naghibi, F.; Dundas, D.; Bathurst, R.J.; Griffiths, D.V. Reliability-based geotechnical design in 2014 canadian highway bridge design code. Can. Geotech. J. 2015, 53, 236–251. [Google Scholar] [CrossRef]
- JGS. Principles for Foundation Design Grounded on a Performance-Based Design Concept (GeoGuide); Japanese Geotechnical Society: Tokyo, Japan, 2004. [Google Scholar]
- Orr, T.L.L. Defining and selecting characteristic values of geotechnical parameters for designs to Eurocode 7. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2016, 11, 103–115. [Google Scholar] [CrossRef]
- White, J.; Yeats, A.; Skipworth, G. Tables for Statisticians, 3rd ed.; Nelson Thornes: Cheltenham, UK, 1979; ISBN 085950462X. [Google Scholar]
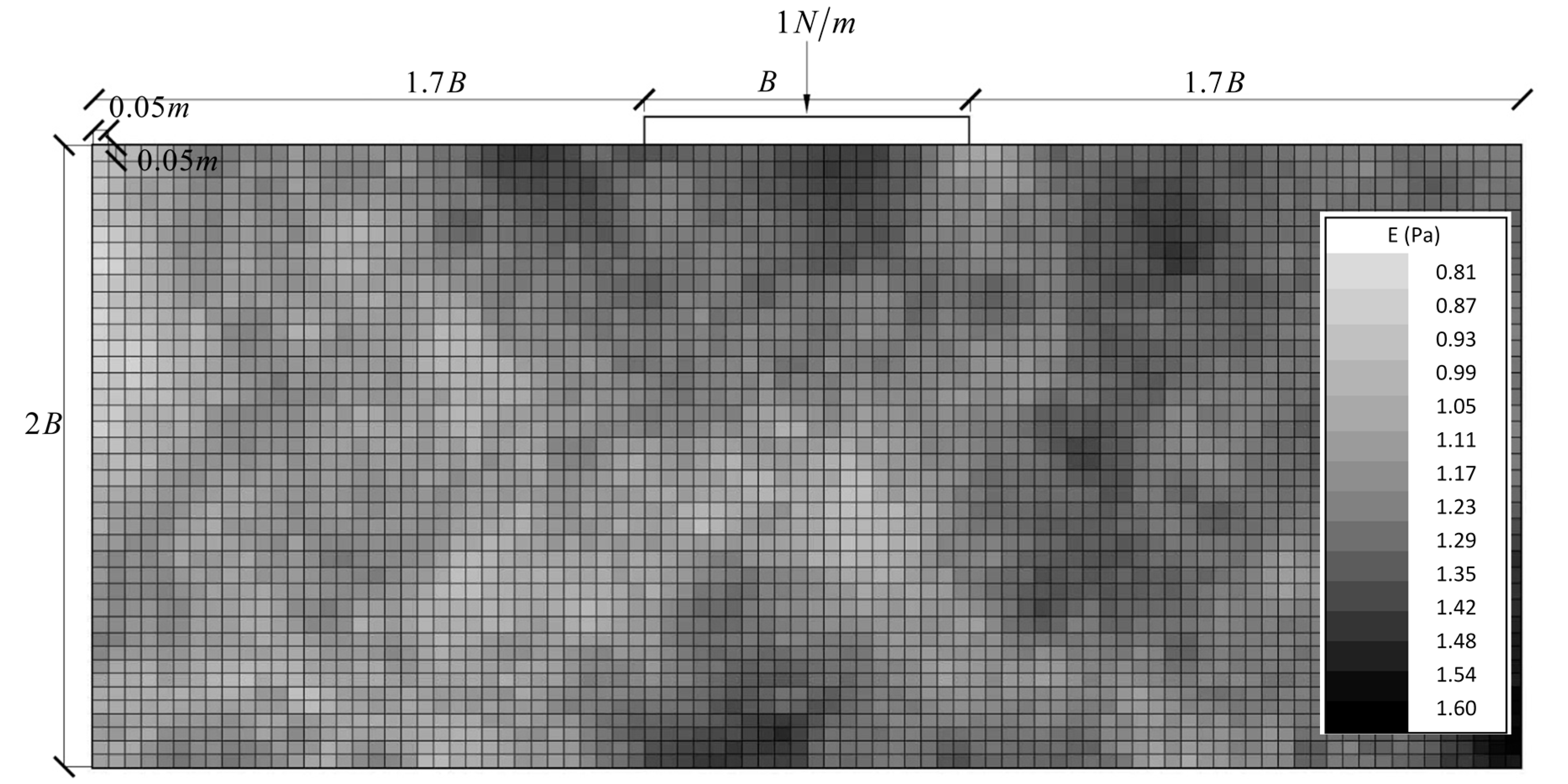
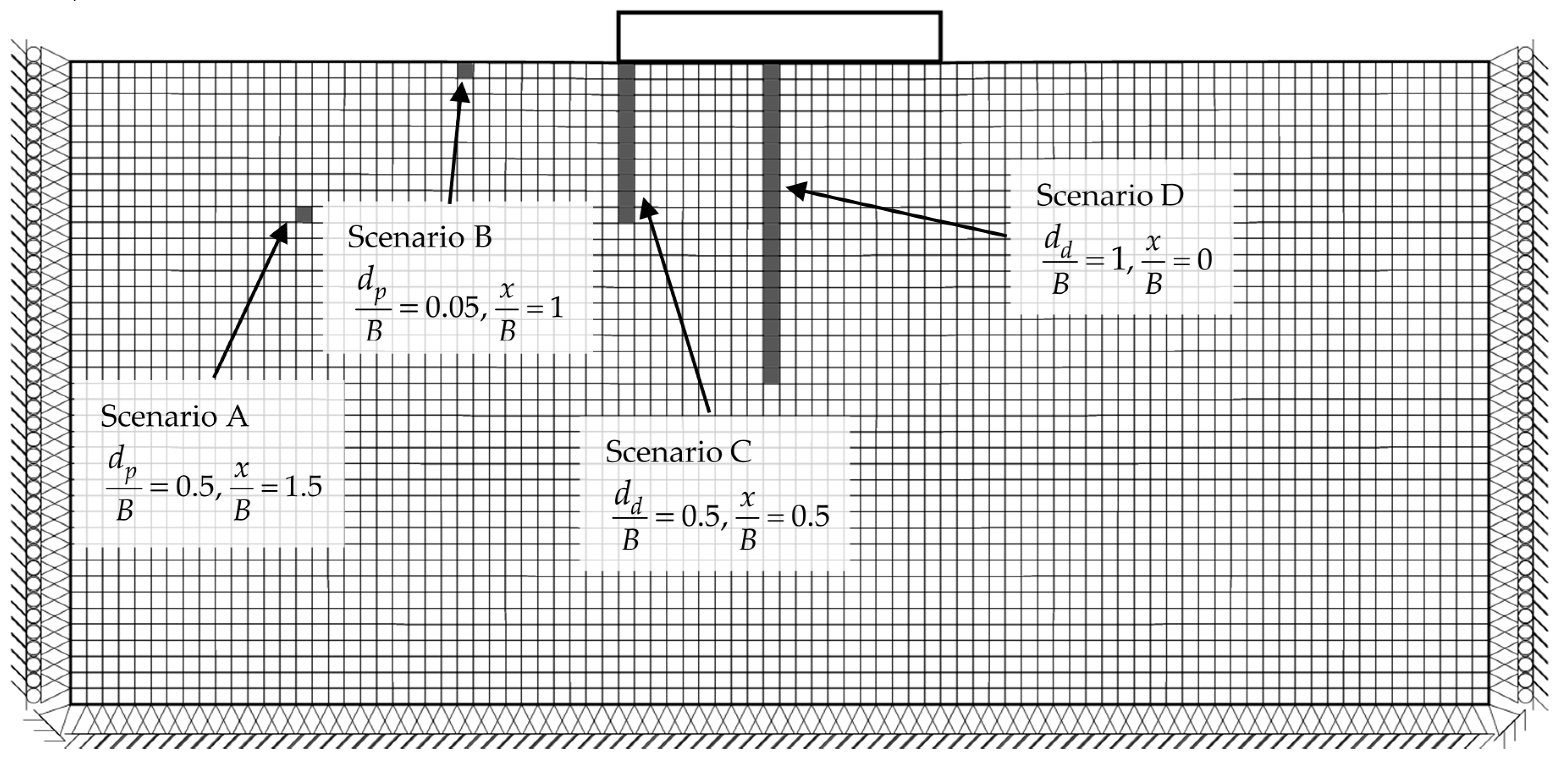








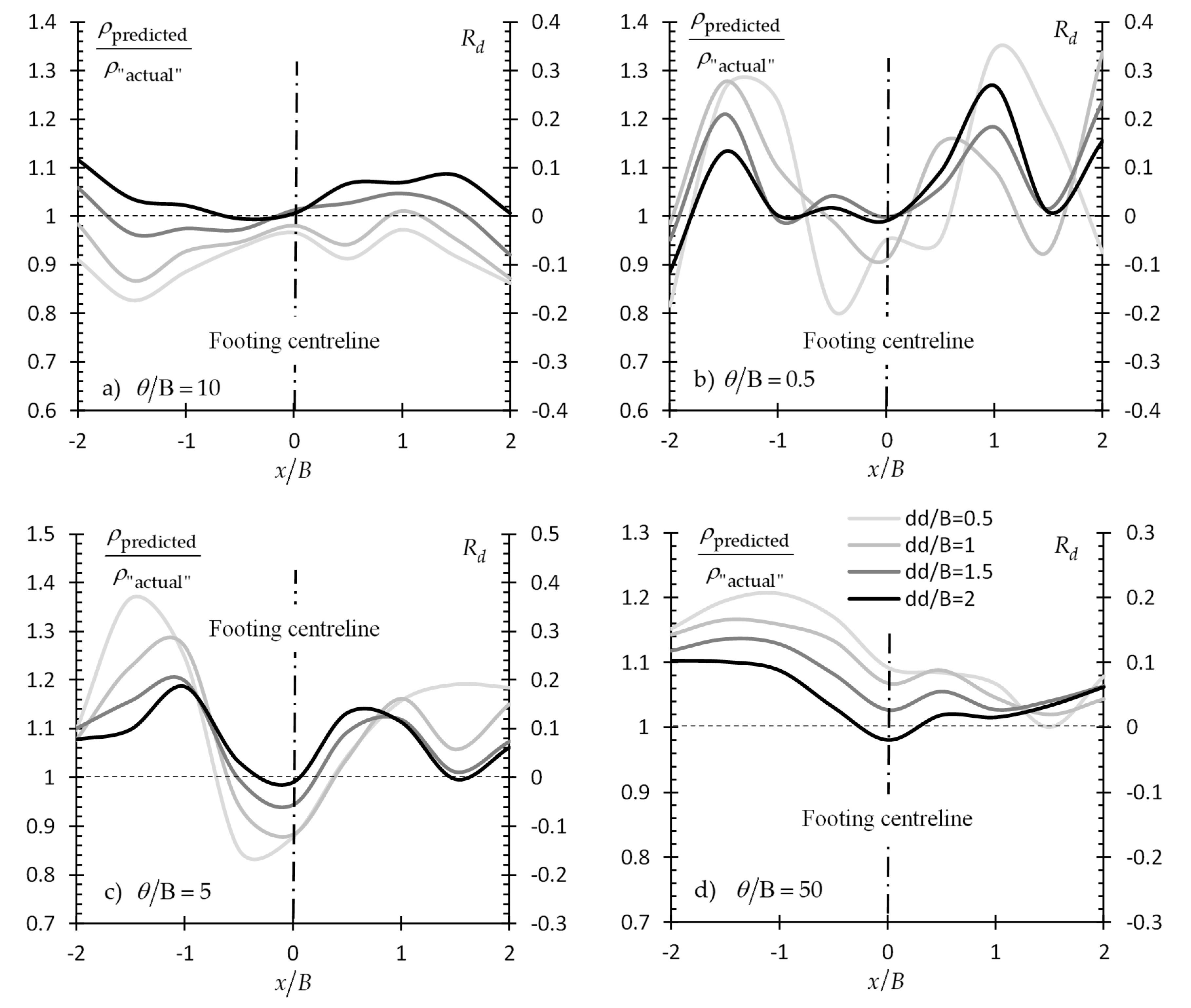
| Example | Random Field (s) | Distribution | ν | COV | Figure (1) | ||
|---|---|---|---|---|---|---|---|
| #1 | E | Log-normal | 1 | 0.25 | 0.3 | 10 | 1 |
| #2 | E | Log-normal | 1 | 0.25 | 0.3 | 0.5 | 11 |
| #3 | E | Log-normal | 1 | 0.25 | 0.3 | 5 | 12 |
| #4 | E | Log-normal | 1 | 0.25 | 0.3 | 50 | 13 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Christodoulou, P.; Pantelidis, L. Reducing Statistical Uncertainty in Elastic Settlement Analysis of Shallow Foundations Relying on Targeted Field Investigation: A Random Field Approach. Geosciences 2020, 10, 20. https://doi.org/10.3390/geosciences10010020
Christodoulou P, Pantelidis L. Reducing Statistical Uncertainty in Elastic Settlement Analysis of Shallow Foundations Relying on Targeted Field Investigation: A Random Field Approach. Geosciences. 2020; 10(1):20. https://doi.org/10.3390/geosciences10010020
Chicago/Turabian StyleChristodoulou, Panagiotis, and Lysandros Pantelidis. 2020. "Reducing Statistical Uncertainty in Elastic Settlement Analysis of Shallow Foundations Relying on Targeted Field Investigation: A Random Field Approach" Geosciences 10, no. 1: 20. https://doi.org/10.3390/geosciences10010020
APA StyleChristodoulou, P., & Pantelidis, L. (2020). Reducing Statistical Uncertainty in Elastic Settlement Analysis of Shallow Foundations Relying on Targeted Field Investigation: A Random Field Approach. Geosciences, 10(1), 20. https://doi.org/10.3390/geosciences10010020





