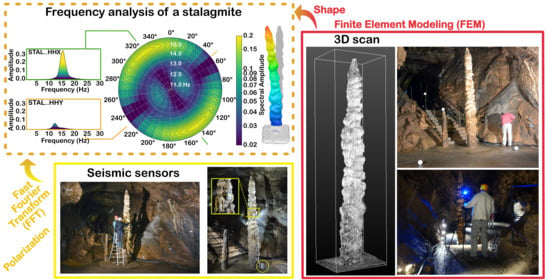
Characterizing Stalagmites’ Eigenfrequencies by Combining In Situ Vibration Measurements and Finite Element Modeling Based on 3D Scans
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Site—Karst System of Han-Sur-Lesse
2.2. Non-Destructive Characterization of the Stalagmite
2.2.1. Shape: 3D Laser Scan of the Minaret Stalagmite
- Elevation (vertical distance between the base and the head)
- Major (a) and minor (b) axes of each ellipse
- Coordinates (X, Y, Z) of the center of each ellipse
- Orientation of each ellipse (major axes (a) with respect to the north)
- Geodesic distance (sum of the distances between two centers of consecutive ellipses)
- Project distance—horizontal displacement (center of the base ellipse to the center of the head ellipse)
- Angle of the horizontal displacement (with respect to the north)
2.2.2. Natural Frequency: Seismic Measurements
2.2.3. Mechanical Properties
2.3. Modeling of the Natural Frequencies
2.3.1. Analytical Method
- A, the area of the cross-section of the cylinder
- I, the moment of inertia of the cross-section
- , the angular frequency
- , a correction parameter that corresponds to each mode of frequency (i = 1,2,3 …)
2.3.2. Finite Element Model (FEM)
- The average element size that specifies the element size relative to the model size.
- The minimum element size relative to the average size. This setting allows automatic refinement in small areas.
- Maximum turn angle, which affects the number of elements on curved surfaces. The smaller the angle, the greater the number of meshes on a curve.
- The adjacent mesh size ratio, which parameterizes the transitions between fine and coarse meshes.
- The aspect ratio (ratio of longest to shortest dimension).
3. Results
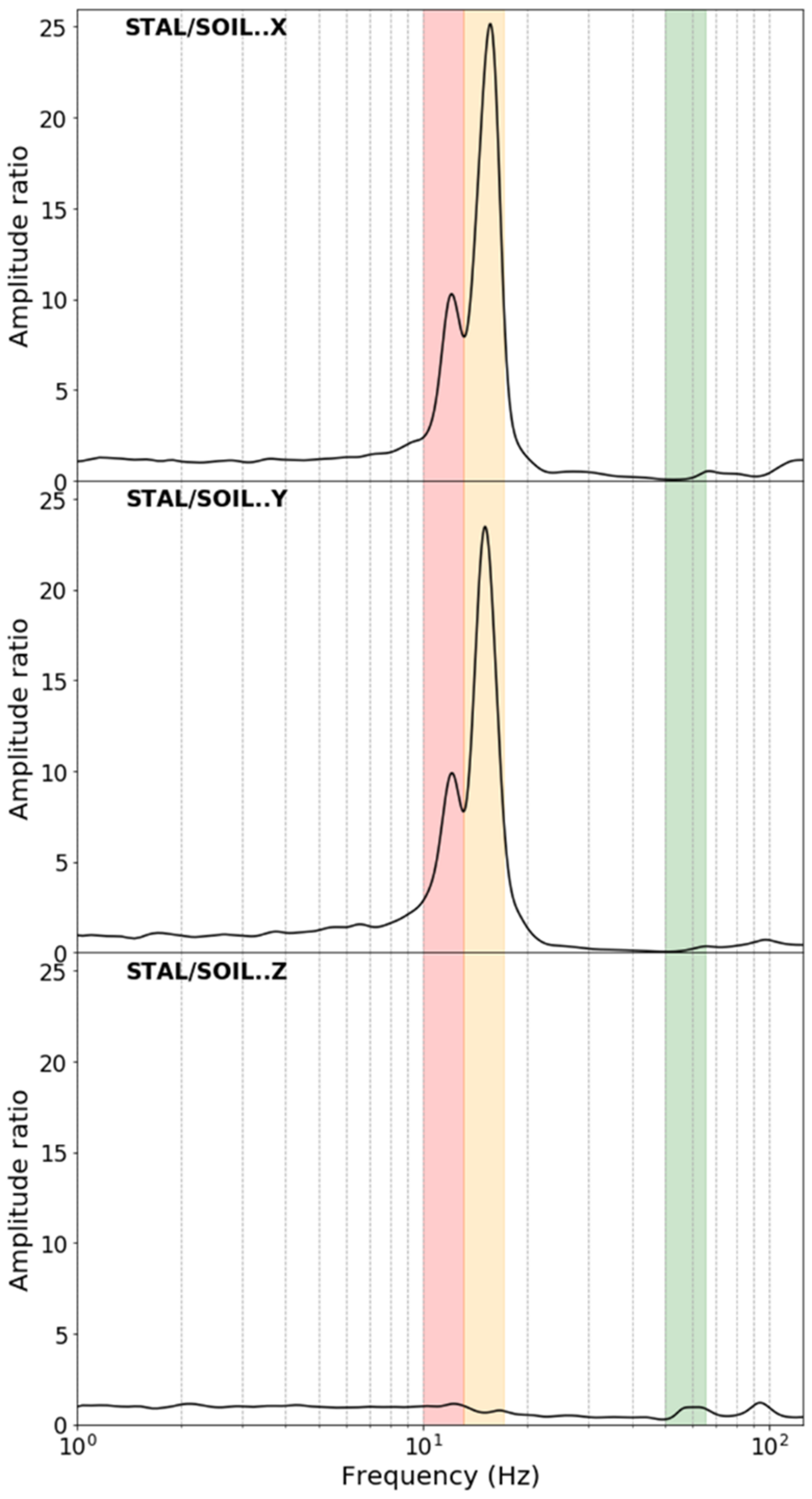
3.1. Seismic Measurement
3.2. 3D Laser Scan
3.2.1. Shape of the Stalagmite
3.2.2. Modal Calculation of the Natural Frequencies
4. Discussion
4.1. Natural Frequencies from Ambient Seismic Noise Measurement
4.2. Using an Elliptical Section to Explain the Split Eigenfrequencies
4.3. Convergence between Observed and Modeling Frequencies Due to a Better Geometric Resolution
4.4. Perspectives of Quantifying the Limit Ground Movements before Rupture
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Forti, P. Seismotectonic and paleoseismic studies from speleothems: The state of the art. Geol. Belg. 2001, 4, 175–185. [Google Scholar]
- Becker, A.; Davenport, C.A.; Eichenberger, U.; Gilli, E.; Jeannin, P.-Y.; Lacave, C. Speleoseismology: A critical perspective. J. Seismol. 2006, 10, 371–388. [Google Scholar] [CrossRef]
- António Crispim, J. Seismotectonic versus man-induced morphological changes in a cave on the Arrábida chain (Portugal). Geodin. Acta 1999, 12, 135–142. [Google Scholar] [CrossRef]
- Gilli, E. Rupture de spéléothèmes par fluage d’un remplissage endokarstique. L’exemple de la grotte de Ribière (Bouches-du-Rhône). Comptes Rendus de l’Académie des Sciences-Series IIA-Earth and Planetary Science 1999, 329, 807–813. [Google Scholar] [CrossRef]
- Kempe, S. Natural Speleothem Damage in Postojnska Jama, Slovenia, Caused by Glacial Cave Ice? A First Assessment. Acta Carsologica 2004, 33. [Google Scholar] [CrossRef]
- Gilli, E. Glacial causes of damage and difficulties to use speleothems as palaeoseismic indicators. Geodin. Acta-GEODIN ACTA 2004, 17, 229–240. [Google Scholar] [CrossRef]
- Gilli, É. Review on the use of natural cave speleothems as palaeoseismic or neotectonics indicators. Comptes Rendus Geosci. 2005, 337, 1208–1215. [Google Scholar] [CrossRef]
- Šebela, S. Broken Speleothems as Indicators of Tectonic Movements. Acta Carsologica 2008, 37, 51–62. [Google Scholar] [CrossRef] [Green Version]
- Cadorin, J.F.; Jongmans, D.; Plumier, A.; Camelbeeck, T.; Delaby, S.; Quinif, Y. Modelling of speleothems failure in the Hotton cave (Belgium). Is the failure earthquake induced? Geol. Mijnb. 2001, 80, 315–321. [Google Scholar] [CrossRef] [Green Version]
- Lacave, C.; Koller, M.G.; Egozcue, J.J. What can be concluded about seismic history from broken and unbroken speleothems? J.Earthq. Eng. 2004, 8, 431–455. [Google Scholar] [CrossRef]
- Camelbeeck, T.; Quinif, Y.; Verheyden, S.; Vanneste, K.; Knuts, E. Earthquakes as collapse precursors at the Han-sur-Lesse Cave in the Belgian Ardennes. Geomorphology 2018, 308, 13–24. [Google Scholar] [CrossRef]
- Paskaleva, I.; Szeidovitz, G.; Kostov, K.; Koleva, G.; Nikolov, G.; Gribovzsky, K. Calculation the peak ground horizontal acceleration generated by paleoearthquake from failure tensile stress of speleotherm. In Proceedings of the International Conference on Civil Engineering Design and Construction, Varna, Bulgaria, 14–16 September 2006. [Google Scholar]
- Szeidovitz, G.; Surányi, G.; Gribovszki, K.; Bus, Z.; Leél-Őssy, S.; Varga, Z. Estimation of an upper limit on prehistoric peak ground acceleration using the parameters of intact speleothems in Hungarian caves. J. Seismol. 2008, 12, 21–33. [Google Scholar] [CrossRef]
- Szeidovitz, G.; Paskaleva, I.; Gribovszki, K.; Kostov, K.; Surány, G.; Varga, P.; Nikolov, G. Estimation of an upper limit on prehistoric peak ground acceleration using the parameters of intact speleothems in caves situated at the western part of Balkan Mountain Range, North-West Bulgaria. Acta Geod. Geoph. Hung. 2008, 43, 249–266. [Google Scholar] [CrossRef]
- Gribovszki, K.; Paskaleva, I.; Kostov, K.; Varga, P.; Nikolov, G. Estimating An Upper Limit On Prehistoric Peak Ground Acceleration Using The Parameters Of Intact Speleothems In Caves In Southwestern Bulgaria. In Proceedings of the Harmonization of Seismic Hazard in Vrancea Zone; Zaicenco, A., Craifaleanu, I., Paskaleva, I., Eds.; Springer: Dordrecht, The Netherlands, 2008; pp. 287–308. [Google Scholar]
- Gribovszki, K.; Bokelmann, G.; Szeidovitz, G.; Paskaleva, I.D.; Brimich, L.; Kovács, K.; Mónus, P. Comprehensive investigation of intact, vulnerable stalagmites to estimate an upper limit on prehistoric horizontal ground acceleration. In Proceedings of the Vienna Congress on Recent Advances in Earthquake Engineering and Structural Dynamics 2013 (VEESD 2013), Vienna, Austria, 28–30 August 2013. [Google Scholar]
- Gribovszki, K.; Kovács, K.; Mónus, P.; Shen, C.; Török, Á.; Brimich, L. Estimation of an upper limit on prehistoric horizontal peak ground acceleration using the parameters of intact stalagmites and the mechanical properties of broken stalagmites in Domica cave, Slovakia. Slov. Kras. 2013, 51, 5–14. [Google Scholar]
- Bokelmann, G.; Gribovszki, K. Constraints on Long-Term Seismic Hazard From Vulnerable Stalagmites. In Proceedings of the CSNI Workshop on “Testing PSHA Results and Benefit of Bayesian Techniques for Seismic Hazard Assessment”, Pavia, Italy, 4–6 February 2015. [Google Scholar]
- Gribovszki, K.; Kovács, K.; Mónus, P.; Bokelmann, G.; Konecny, P.; Lednická, M.; Moseley, G.; Spötl, C.; Edwards, R.L.; Bednárik, M.; et al. Estimating the upper limit of prehistoric peak ground acceleration using an in situ, intact and vulnerable stalagmite from Plavecká priepast cave (Detrekői-zsomboly), Little Carpathians, Slovakia—first results. J. Seismol. 2017, 21, 1111–1130. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gribovszki, K.; Esterhazy, S.; Bokelmann, G. Numerical Modeling of Stalagmite Vibrations. Pure and Appl. Geophys. 2018, 175. [Google Scholar] [CrossRef] [Green Version]
- Brune, J.N. Precariously balanced rocks and ground-motion maps for Southern California. Bull. Seismol. Soc. Am. 1996, 86, 43–54. [Google Scholar]
- Schweppe, G.; Hinzen, K.-G.; Reamer, S.K.; Fischer, M.; Marco, S. The Ruin of the Roman Temple of Kedesh, Israel; Example of a Precariously Balanced Archaeological Structure Used as a Seismoscope. Ann. Geophys. 2017, 60, 0444. [Google Scholar] [CrossRef] [Green Version]
- Lacave, C.; Levret, A.; Koller, M. Measurement of natural frequencies and damping of speleothems. In Proceedings of the 12th World Conference on Earthquake Engineering, Auckland, NewZealand, 30 January–4 February 2000. [Google Scholar]
- Bottelin, P.; Baillet, L.; Mathy, A.; Garnier, L.; Cadet, H.; Brenguier, O. Seismic study of soda straws exposed to nearby blasting vibrations. J. Seismol. 2020. [Google Scholar] [CrossRef]
- Hajri, S.; Sadier, B.; Jaillet, S.; Ployon, E.; Boche, E.; Chakroun, A.; Saulnier, G.-M.; Delannoy, J.-J. Analyse spatiale et morphologique d’une forêt de stalagmites par modélisation 3D dans le réseau d’Orgnac (Ardèche, France). Karstologia 2009, 53, 1–14. [Google Scholar] [CrossRef]
- Jaillet, S.; Sadier, B.; Hajri, S.; Ployon, E.; Delannoy, J.-J. Une analyse 3D de l’endokarst: Applicationslasergrammétriques sur l’aven d’Orgnac (Ardèche, France). Geomorphol. Relief Process. Environ. 2011, 379–394. [Google Scholar] [CrossRef] [Green Version]
- Lacave, C.; Sadier, B.; Delannoy, J.J.; Nehme, C.; Egozcue, J.J. The use of speleothems to better constrain long return period seismic hazard in Lebanon. In Proceedings of the 15th World Conference on Earthquake Engineering, Lisbonne, Portugal, 24–28 September 2012; pp. 1–7. [Google Scholar]
- Havron, C.; Quinif, Y.; Vandycke, S. Tectonique et karstification: Le cas de la région de Han-sur-Lesse (Belgique). Karstologia 2004, 43, 19–26. [Google Scholar] [CrossRef]
- Quinif, Y. La fantômisation-Une nouvelle manière de concevoir la formation des cavernes. Regards 2014, 79, 42–72. [Google Scholar]
- Quinif, Y. Le système karstique de Han-sur-Lesse. In Atlas du Karst Wallon: Bassin de la Lesse Calestienne; CWEPSS/Service Public de Wallonie: Ixelles, Belgium, 2015; pp. 31–38. [Google Scholar]
- Quinif, Y. Le complexe sédimentaire de la Galerie des Verviétois (Grotte de Han-sur-Lesse, Belgique). Geol. Belg. 2017. [Google Scholar] [CrossRef] [Green Version]
- Dubois, C.; Quinif, Y.; Baele, J.-M.; Barriquand, L.; Bini, A.; Bruxelles, L.; Dandurand, G.; Havron, C.; Kaufmann, O.; Lans, B.; et al. The process of ghost-rock karstification and its role in the formation of cave systems. Earth-Sci. Rev. 2014, 131, 116–148. [Google Scholar] [CrossRef]
- Quinif, Y.; Baele, J.-M.; Dubois, C.; Havron, C.; Kaufmann, O.; Vergari, A. Fantômisation: Un nouveau paradigme entre la théorie des deux phases de Davis et la théorie de la biorhexistasie d’Erhart. Geol. Belg. 2014, 17, 66–74. [Google Scholar]
- Camelbeeck, T.; Vanneste, K.; Alexandre, P.; Verbeeck, K.; Petermans, T.; Rosset, P.; Everaerts, M.; Warnant, R.; Van Camp, M. Relevance of active faulting and seismicity studies to assessments of long-term earthquake activity and maximum magnitude in intraplate northwest Europe, between the Lower Rhine Embayment and the North Sea. In Continental Intraplate Earthquakes: Science, Hazard, and Policy Issues; Geological Society of America: Boulder, CO, USA, 2007; ISBN 978-0-8137-2425-6. [Google Scholar]
- Alexandre, P.; Kusman, D.; Petermans, T.; Camelbeeck, T. The 18 September 1692 Earthquake in the Belgian Ardenne and Its Aftershocks. In Historical Seismology: Interdisciplinary Studies of Past and Recent Earthquakes; Fréchet, J., Meghraoui, M., Stucchi, M., Eds.; Modern Approaches in Solid Earth Sciences; Springer Netherlands: Dordrecht, The Netherlands, 2008; pp. 209–230. ISBN 978-1-4020-8222-1. [Google Scholar]
- Delaere, C.; Warmenbol, E. Les nouvelles fouilles subaquatiques aux grottes de Han (Rochefort, prov. de Namur, Belgique). Etude d’une fibule de La Tène B 1 et de son contexte. Lunula. Archaeol. Protohist. 2018, XXVI, 159–165. [Google Scholar]
- Bonniver, I. Etude Hydrogéologique et Dimensionnement par Modélisation du Système-Traçage du Réseau Karstique de Han-sur-Lesse (Massif de Boine-Belgique). Ph.D. Thesis, Universite de Namur, Namur, Belgium, September 2011. [Google Scholar]
- Poulain, A. Flow and Transport Characterization in Vadose and Phreatic Zones of Karst Aquifers-Experimental Approaches in the Givetian limestones of South Belgium. Ph.D. Thesis, Universite de Namur, Namur, Belgium, September 2017. [Google Scholar]
- Blockmans, S.; Dumoulin, V. Houyet–Han-sur-Lesse 59/1-2. Carte Géologique de Wallonie. Submitted.
- Cloud Compare (v2.10.2) [GPL software]. Available online: http://www.cloudcompare.org/ (accessed on 18 October 2020).
- Van der Walt, S.; Schönberger, J.L.; Nunez-Iglesias, J.; Boulogne, F.; Warner, J.D.; Yager, N.; Gouillart, E.; Yu, T. scikit-image: Image processing in Python. PeerJ 2014, 2, e453. [Google Scholar] [CrossRef]
- Halır, R.; Flusser, J. Numerically stable direct least squares fitting of ellipses. In Proceedings of the Proc. 6th International Conference in Central Europe on Computer Graphics and Visualization, Plzen, Czech Republic, 9–13 February 1998; pp. 125–132. [Google Scholar]
- Cooley, J.W.; Tukey, J.W. An algorithm for the machine calculation of complex Fourier series. Math. Comp. 1965, 19, 297–301. [Google Scholar] [CrossRef]
- Konno, K.; Ohmachi, T. Ground-Motion Characteristics Estimated from Spectral Ratio between Horizontal and Vertical Components of Microtremor. Bull. Seismol. Soc. Am. 1998, 18, 228–241. [Google Scholar]
- Van Noten, K.; Devleeschouwer, X.; Goffin, C.; Meyvis, C.; Molron, J.; Debacker, T.N.; Lecocq, T. Bedrock morphology modelling using geologically-dependent empirical equations between resonance frequency and bedrock depth. J. Seismol. under revision.
- Rao, S.S. Vibration of Continuous Systems; Wiley: Hoboken, NJ, USA, 2007; ISBN 978-0-471-77171-5. [Google Scholar]
- Bońkowski, P.; Zembaty, Z.; Bobra, P.; Gribovszki, K. Modeling seismic capacity of stalagmites. In Proceedings of the EGU General Assembly 2020, Online, 4–8 May 2020. [Google Scholar]
- Autodesk Inc. Fusion 360 Help | Getting Started with Fusion 360. Available online: https://help.autodesk.com/view/fusion360/ENU/?guid=GUID-1C665B4D-7BF7-4FDF-98B0-AA7EE12B5AC2 (accessed on 1 October 2020).
- Lecocq, T.; Hicks, S.P.; Noten, K.V.; van Wijk, K.; Koelemeijer, P.; Plaen, R.S.M.D.; Massin, F.; Hillers, G.; Anthony, R.E.; Apoloner, M.-T.; et al. Global quieting of high-frequency seismic noise due to COVID-19 pandemic lockdown measures. Science 2020. [Google Scholar] [CrossRef] [PubMed]
- Lecocq, T.; Massin, F.; Satriano, C.; Vanstone, M.; Megies, T. SeismoRMS-A Simple Python/Jupyter Notebook Package for Studying Seismic Noise Changes; Zenodo, 2020; Available online: https://zenodo.org/record/3820046#.X4u9f3IRVPY (accessed on 18 October 2020).
- Bottelin, P.; Lévy, C.; Baillet, L.; Jongmans, D.; Guéguen, P. Modal and thermal analysis of Les Arches unstable rock column (Vercors massif, French Alps). Geophys. J. Int. 2013, 194, 849–858. [Google Scholar] [CrossRef]
- Mikael, A.; Gueguen, P.; Bard, P.-Y.; Roux, P.; Langlais, M. The Analysis of Long-Term Frequency and Damping Wandering in Buildings Using the Random Decrement Technique. Bull. Seismol. Soc. Am. 2013, 103, 236–246. [Google Scholar] [CrossRef] [Green Version]
- Hinzen, K.-G.; Hinojosa-Prieto, H.R.; Kalytta, T. Site Effects in Archaeoseismic Studies at Mycenaean Tiryns and Midea. Seismol. Res. Lett. 2016, 87, 1060–1074. [Google Scholar] [CrossRef]
- Geimer, P.R.; Finnegan, R.; Moore, J.R. Sparse Ambient Resonance Measurements Reveal Dynamic Properties of Freestanding Rock Arches. Geophys. Res. Lett. 2020, 47, e2020GL087239. [Google Scholar] [CrossRef]
- Aki, K.; Richards, P.G. Quantitative Seismology, 2nd ed.; University Science Books: Mill Valley, CA, USA, 2002; ISBN 0-935702-96-2. [Google Scholar]
- Bethmann, F.; Deichmann, N.; Mai, P.M. Seismic wave attenuation from borehole and surface records in the top 2.5km beneath the city of Basel, Switzerland. Geophys. J. Int. 2012, 190, 1257–1270. [Google Scholar] [CrossRef] [Green Version]
- Hinzen, K.-G.; Fleischer, C.; Schock-Werner, B.; Schweppe, G. Seismic Surveillance of Cologne Cathedral. Seismol. Res. Lett. 2012, 83, 9–22. [Google Scholar] [CrossRef]
- Oliphant, T. Guide to Numpy; 2006; Available online: https://www.researchgate.net/publication/213877900_Guide_to_NumPy (accessed on 18 October 2020).
- Beyreuther, M.; Barsch, R.; Krischer, L.; Megies, T.; Behr, Y.; Wassermann, J. ObsPy: A Python Toolbox for Seismology. Seismol. Res. Lett. 2010, 81, 530–533. [Google Scholar] [CrossRef] [Green Version]
- Krischer, L.; Megies, T.; Barsch, R.; Beyreuther, M.; Lecocq, T.; Caudron, C.; Wassermann, J. ObsPy: A bridge for seismology into the scientific Python ecosystem. Comput. Sci. Disc. 2015, 8, 014003. [Google Scholar] [CrossRef]
- Megies, T.; Beyreuther, M.; Barsch, R.; Krischer, L.; Wassermann, J. ObsPy–What can it do for data centers and observatories? Ann.Geophys. 2011, 54, 47–58. [Google Scholar] [CrossRef]
- Wathelet, M.; Chatelain, J.-L.; Cornou, C.; Di Giulio, G.; Guillier, B.; Ohrnberger, M.; Savvaidis, A. Geopsy: A User-Friendly Open-Source Tool Set for Ambient Vibration Processing. Seismol. Res. Lett. 2020, 91. [Google Scholar] [CrossRef]
- Hunter, J.D. Matplotlib: A 2D Graphics Environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]








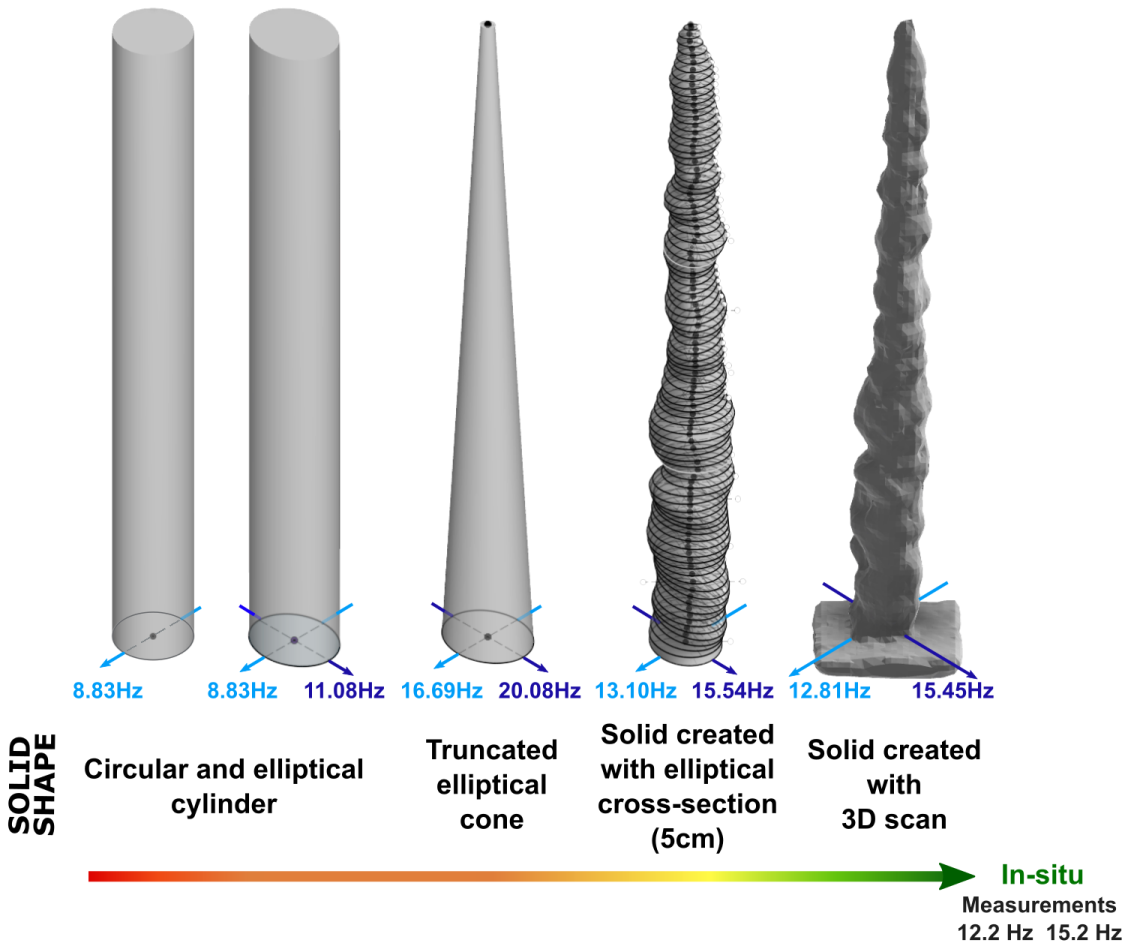
| Circular Cylinder | Elliptical Cylinder | Truncated Elliptical Cone | Solid Based on Elliptical Sections | Solid Based on 3D Scan | ||
|---|---|---|---|---|---|---|
| Mesh parameters | Average element size | 0.03 | 0.03 | 0.03 | 0.03. | 0.08 |
| Minimum element size | 0.05 | 0.05 | 0.05 | 0.05 | 0.2 | |
| Maximum turn angle | 15° | 15° | 15° | 15° | 60° | |
| Adjacent mesh size ratio | 1 | 1 | 1 | 1 | 1.5 | |
| Aspect ratio | 6. | 6. | 6. | 6. | 10 | |
| Size | Nodes | 108,581 | 61,590 | 92,276 | 218,040 | 423,094 |
| Tetrahedra elements | 73,601 | 40,289 | 60,170 | 148,143 | 269,449 | |
| Dynamic degrees of freedom | 650,628 | 368,850 | 552,966 | 1,307,550 | ≈2,500,000 |
| Height Level (m) | Angle Range | Mean Angle (°) | Median Angle (°) | a/b (Median) |
|---|---|---|---|---|
| [0–1.15] | 0–45° | 25 | 26 | 1.33 |
| 1.15 | 130–180° | 161 | 161 | 1.17 |
| [1.2–1.8] | 70–130° | 106 | 108 | 1.11 |
| [1.8–3.65] | 30% (0–45°) | 120 | 159 | 1.18 |
| 70% (130–180°) | ||||
| >3.6 | 56% (70–130°) | 124 | 128 | 1.11 |
| 44% (130–180°) |
| Mode | Type of Mode Shape (Figure 9) | Eigenfrequency (Hz) | X | Y | Z |
|---|---|---|---|---|---|
| Mode 1 x | Type I | 12.81 (12.85 1) | 32% | 5% | 0.001% |
| Mode 1 y | 15.45 (15.51 1) | 4% | 29% | 0.02% | |
| Mode 2 x | Type II | 50.56 (50.72 1) | 15% | 0.1% | 0.01% |
| Mode 2 y | 59.76 (59.95 1) | 0.2% | 17% | 0.2% | |
| Mode 3 x | Type III | 125.1 (125.3 1) | 7% | 0.1% | 0.1% |
| Mode 3 y | 132.8 (132.9 1) | 0.04% | 7% | 0.4% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martin, A.; Lecocq, T.; Hinzen, K.-G.; Camelbeeck, T.; Quinif, Y.; Fagel, N. Characterizing Stalagmites’ Eigenfrequencies by Combining In Situ Vibration Measurements and Finite Element Modeling Based on 3D Scans. Geosciences 2020, 10, 418. https://doi.org/10.3390/geosciences10100418
Martin A, Lecocq T, Hinzen K-G, Camelbeeck T, Quinif Y, Fagel N. Characterizing Stalagmites’ Eigenfrequencies by Combining In Situ Vibration Measurements and Finite Element Modeling Based on 3D Scans. Geosciences. 2020; 10(10):418. https://doi.org/10.3390/geosciences10100418
Chicago/Turabian StyleMartin, Aurélie, Thomas Lecocq, Klaus-G. Hinzen, Thierry Camelbeeck, Yves Quinif, and Nathalie Fagel. 2020. "Characterizing Stalagmites’ Eigenfrequencies by Combining In Situ Vibration Measurements and Finite Element Modeling Based on 3D Scans" Geosciences 10, no. 10: 418. https://doi.org/10.3390/geosciences10100418
APA StyleMartin, A., Lecocq, T., Hinzen, K.-G., Camelbeeck, T., Quinif, Y., & Fagel, N. (2020). Characterizing Stalagmites’ Eigenfrequencies by Combining In Situ Vibration Measurements and Finite Element Modeling Based on 3D Scans. Geosciences, 10(10), 418. https://doi.org/10.3390/geosciences10100418