Next Article in Journal
Constraints on Martian Chronology from Meteorites
Next Article in Special Issue
Complex Shear Partitioning Involving the 6 February 2012 MW 6.7 Negros Earthquake Ground Rupture in Central Philippines
Previous Article in Journal
Chinyero Volcanic Landscape Trail (Canary Islands, Spain): A Geotourism Proposal to Identify Natural and Cultural Heritage in Volcanic Areas
Previous Article in Special Issue
The New Seismotectonic Atlas of Greece (v1.0) and Its Implementation
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Geosciences
Volume 10
Issue 11
10.3390/geosciences10110454
geosciences-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

The Mw = 5.6 Kanallaki Earthquake of 21 March 2020 in West Epirus, Greece: Reverse Fault Model from InSAR Data and Seismotectonic Implications for Apulia-Eurasia Collision

by
Sotiris Valkaniotis
1,*,
Pierre Briole
2,
Athanassios Ganas
3,
Panagiotis Elias
4,
Vassilis Kapetanidis
5,
Varvara Tsironi
3,6,
Anna Fokaefs
3,
Helena Partheniou
3,5 and
Panagiotis Paschos
7
1
Koronidos Str., 42131 Trikala, Greece
2
Ecole Normale Supérieure, PSL Research University, Laboratoire de Géologie—UMR CNRS, 8538 Paris, France
3
National Observatory of Athens, Institute of Geodynamics, Lofos Nymfon, Thission, 11810 Athens, Greece
4
National Observatory of Athens, Institute of Astronomy, Astrophysics, Space Applications and Remote Sensing, Vas. Pavlou & I. Metaxa, GR-15 236 Penteli, Greece
5
Department of Geology, National and Kapodistrian University of Athens, 15784 Athens, Greece
6
Department of Geology, University of Patras, 26504 Rio, Greece
7
Hellenic Survey of Geology and Mineral Exploration, Unit of Epirus, 48100 Eleonas, Preveza, Greece
*
Author to whom correspondence should be addressed.
Geosciences 2020, 10(11), 454; https://doi.org/10.3390/geosciences10110454
Submission received: 20 October 2020 / Revised: 4 November 2020 / Accepted: 5 November 2020 / Published: 11 November 2020
(This article belongs to the Special Issue Seismotectonics, Active Deformation, and Structure of the Crust)
Browse Figures
Review Reports Versions Notes

Abstract

:
We identify the source of the Mw = 5.6 earthquake that hit west-central Epirus on 21 March 2020 00:49:52 UTC. We use Sentinel-1 synthetic aperture radar interferograms tied to one permanent Global Navigation Satellite System (GNSS) station (GARD). We model the source by inverting the INSAR displacement data. The inversion model suggests a shallow source on a low-angle fault (39°) dipping towards east with a centroid depth of 8.5 km. The seismic moment deduced from our model agrees with those of the published seismic moment tensors. This geometry is compatible with reverse-slip motion along the west-verging Margariti thrust fault that accommodates part of the convergence within the collision zone between Apulia and Eurasia. We also processed new GNSS data and estimate a total convergence rate between Apulia and Eurasia of 8.9 mm yr−1, of which the shortening of the crust between the Epirus coastal GNSS stations and station PAXO in the Ionian Sea (across the Ionian Thrust) is equivalent to ~50% of it or 4.6 mm yr−1. By back-slip modelling we found that a 60-km wide deformation zone takes up nearly most of the convergence between Apulia-Eurasia, trending N318°E. Its central axis runs along the southwest coast of Corfu, along the northeast coast of Paxoi, heading toward the northern extremity of the Lefkada island. The island of Paxoi appears kinematically as part of the Apulian plate.

Graphical Abstract

1. Introduction

The tectonics of Epirus is characterised by on-going compression due to the active collision between the Apulian continental block [1,2,3,4] and Eurasian (Aegean) plate. The Apulian continental lithosphere subducts beneath Epirus and was imaged at 70–80 km depth by [5]. Both seismological and geodetic data show that active deformation is occurring by crustal shortening directed in a NNE–SSW to NE–SW orientation [6,7,8,9,10,11] (Figure 1). The overall tectonic strain rate was estimated at 40–50 ns yr−1 of contraction by [11] for west-central Epirus. At least 50 km of horizontal shortening has been suggested for Epirus by geological data [12,13,14,15] accompanied by large scale clockwise rotations [12].
Geological data (field mapping and borehole loggings) indicate that the region between Corfu and Ioannina (Figure 1) is the site of Neogene thrusting and folding [2,3,12] involving mainly thin-skinned thrusting onto the Apulian margin along Triassic evaporite décollements [13]. The rock formations in most of Epirus consist of Mesozoic and Cenozoic carbonate and clastic strata of the Ionian basin of the external Hellenides belt, which have been thrusted westwards onto the Apulian foreland. The inferred trace of the main basal thrust of Eurasia over Apulia, that is part of the Dinaric–Hellenic orogen, passes offshore Corfu–Paxoi islands with a general NNW–SSE orientation (Figure 1A). In the region of Parga–Kanallaki (Figure 1), there are two onshore thrusts of the Ionian zone running N-S and are west-directed (i.e., the Margariti and Paramithia thrusts, [14]). Offshore Parga, two west-verging reverse faults are reported by [15] (mapped on an E–W oriented geological cross-section in that paper, see section B in their Figure 3) to offset Pliocene–Miocene sediments, the western one representing the contact of the overthrusted Ionian zone onto the pre-Apulian zone of the Hellenides (i.e., the Ionian Thrust, see Figure 1A). The Ionian zone is a well-known petroliferous area of Greece [3,13], yet public data on the details of the geological structure (including the detailed pattern of crustal shortening) are lacking. On the other hand, open data on the active tectonics of Epirus can be provided by Space Geodesy (InSAR and GNSS, [10,11]), which can be combined with published data from crustal seismicity surveys [6,9].
Herein we use Sentinel-1 synthetic aperture radar interferograms, tied at the offsets measured at a nearby permanent Global Navigation Satellite System (GNSS) station (located at Gardiki, station GARD, see Figure 1A), to map the co-seismic displacement field of the 21 March 2020 Mw = 5.6 earthquake that occurred near Kanallaki, southwest Epirus (Figure 1C). We relocated seismicity data to constrain the hypocentre of the mainshock and its moment tensor solution (Section 2). InSAR displacement data was used to invert for fault parameters (Section 3). Our inversion approach has resulted in the best-fitting fault model, providing its geometry and kinematics (strike/dip-angle/rake and concluding on its dip-direction). The geodetic observations and the seismicity data allow to discriminate the seismic fault between the two nodal fault planes of the double-couple focal mechanism of the mainshock. We then discuss our findings in terms of the geological structure (Section 4) and in particular the depth of the geodetic centroid in relation to the west-verging thrusts of the Ionian zone in that area. In this interpretation we rely on published geological data [1,2,3,4] as there are no new data (cross-sections or drilling data) investigating the subsurface of Epirus. We also analysed tectonic strain data from the GNSS velocities in Epirus aimed at estimating the rate of convergence and width of the deformation zone between Apulia and Eurasia. Our findings contribute to the understanding of the present tectonic processes in the Apulia–Eurasia collision zone.

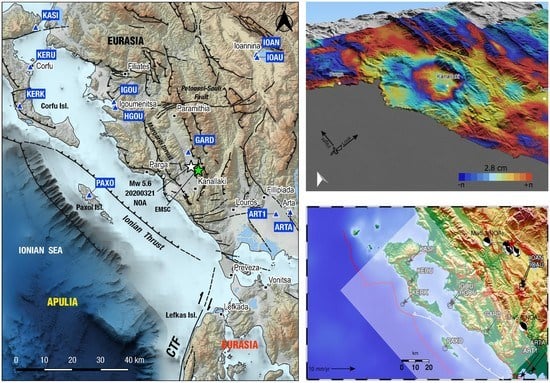
2. Seismicity

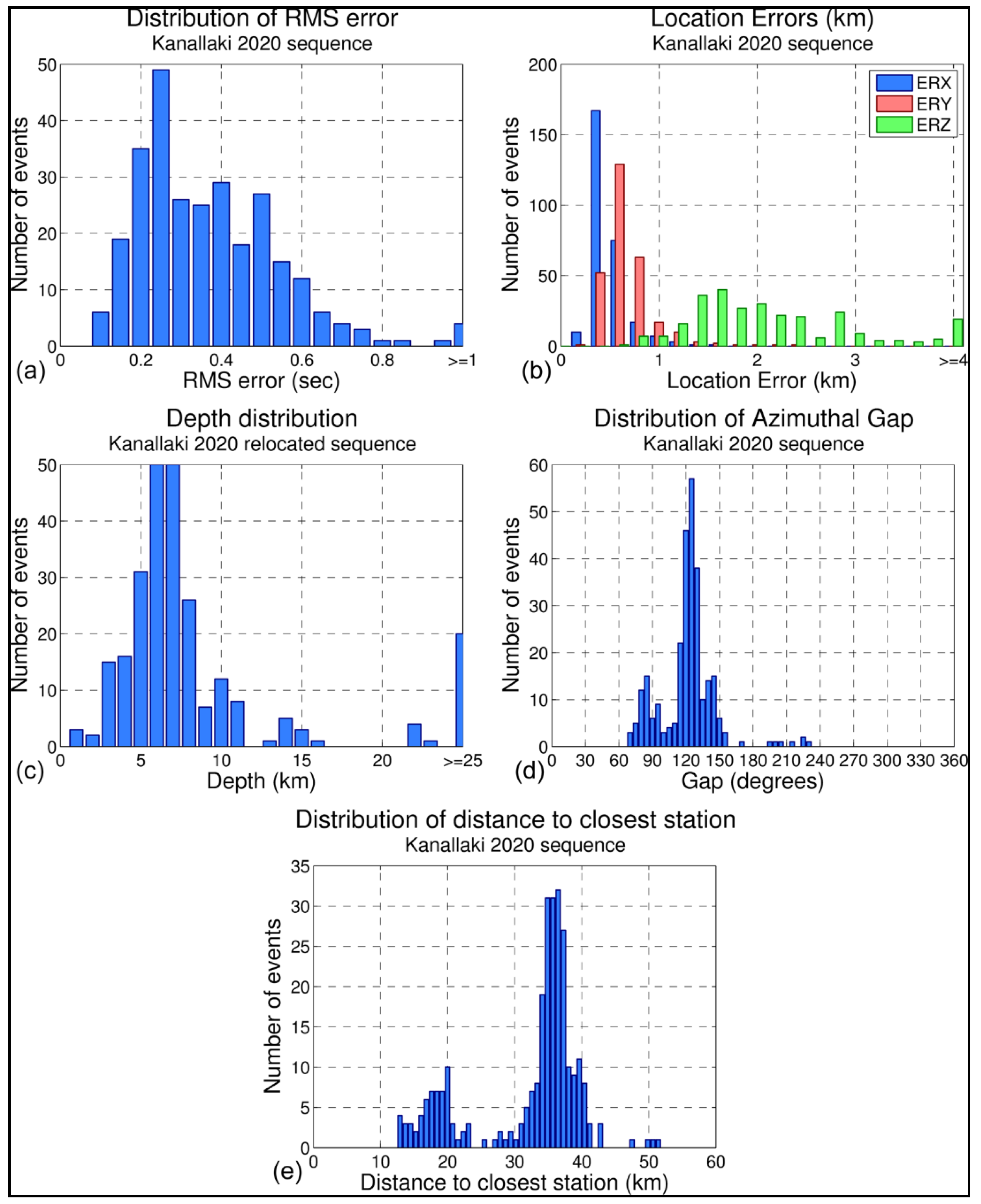
2.1. The 21 March 2020 Earthquake—Relocation of Seismicity

On 21 March 2020 a Mw = 5.6 earthquake occurred at 00:49:52 UTC near the village of Kanallaki in Epirus (Figure 1C), 15 km east of Parga, in north-western Greece [18]. The earthquake caused damage to old houses in Kanallaki and surrounding villages (Figure 1) but no major injuries. The mainshock was preceded by an earthquake with a magnitude of Mw = 4.2 on 20 March 2020, 21:38 UTC (see Table 1 for moment tensor details). Until 23 May, 2020 more than 280 aftershocks (with 1.0 ≤ ML ≤ 4.0) were recorded by the Institute of Geodynamics, National Observatory of Athens (NOAGI) of which 270 events were relocated for the purposes of this study, with horizontal location uncertainties below 1 km (see Figure 1C and Figure 2). The mainshock was followed by two small-size aftershocks, one on 23 March 2020 04:41 UTC and one on 25 March 2020 09:49 UTC with magnitudes of Mw = 3.8 and Mw = 3.9, respectively (Table 1). The moment tensor solutions of all four events indicate NW-SE reverse faulting in agreement with the regional, compressional tectonics (Table 1). For the mainshock, two moment tensor calculations are included in Table 1. The first one is based on the rapid manual solution (Figure 3a) provided by NOA a few minutes after the occurrence of the earthquake. The second one is based on the relocated determination of its hypocentre for the needs of the present study (Figure 3b). The calculation of the focal mechanism solutions is based on a waveform inversion methodology employing ISOLA point source inversion software ([19], see Figure S1 for details on the quality of waveform fit). The crustal velocity model used for the relocated focal mechanism solution calculation was published by [20].
For seismicity relocation we collected catalogue and arrival-time data for the 2020 Kanallaki sequence from the online public databases of the Geodynamics Institute of the National Observatory of Athens (NOA) and the Seismological Laboratory of the National and Kapodistrian University of Athens (SL-NKUA). We merged the two databases by complementing arrival-time data for events that are common in the two catalogues, also including unique events only available on one of the two catalogues. In total, a database of 281 events was constructed for the period between 1 March and 1 May, 2020 in the study area. After several tests with different velocity models (e.g., [20]), we adopted the 1-D P-wave velocity model of [21] for the region of northwest Greece (Table 2), which produced adequate results in terms of travel-time residuals and focal depth distribution. We determined a constant ratio of Vp/Vs = 1.74 using the [22] method, considering also the root mean square (RMS) deviation curve with variable Vp/Vs, which presents a wide minimum for Vp/Vs between 1.71 and 1.75. The mean RMS error is 0.367 s (Figure 2a) while the average location errors are ERX = 0.54 km, ERY = 0.73 km, and ERZ = 2.7 km (Figure 2b). Although the azimuthal gap is relatively small for most events (mean gap = 121°, see Figure 2d), the epicentral distances from the recording stations are, in general, larger than 30 km (Figure 2e), which is why focal depths cannot be well constrained.
To improve the hypocentral distribution, the double-difference relocation method was applied using the algorithm HypoDD [23]. This method works by assuming that when the distance between two neighbouring events is much smaller than their hypocentral distance from a station, then their travel-time differences can be attributed to their inter-event distance. Relative relocation between hypocentres is achieved by minimising the double-difference between observed and calculated travel-times for pairs of neighbouring events at common stations, reducing errors caused by an unmodeled velocity structure. To further enhance the relocation procedure, differential P and S travel-times from waveform cross-correlation was also incorporated. This creates links between strongly correlated events and reduces errors due to arrival-time reading inconsistencies. We acquired waveform data from stations of the Hellenic Unified Seismological Network from the National EIDA node (http://eida.gein.noa.gr/), hosted at the Institute of Geodynamics (NOA). The relocation procedure was performed using two sets of iterations, the first with stronger a priori weights on catalogue data and the second with higher weights on the cross-correlation data. A total of 270 events were successfully relocated (Figure 3). The relocated focal depths are mainly distributed between 3 and 11 km. The Mw = 5.6 mainshock’s relocated focal depth is estimated at 6.4 km however, it should be noted that there are significant uncertainties in the absolute focal depths due to the unavailability of data from near-field stations that cannot be corrected by double-difference relocation. Soon after the Mw = 5.6 mainshock, the aftershock activity spread to a larger region further south and to the east (Figure 3). Cross-sections of seismicity are presented in supplementary Figure S2.
The focal mechanism solutions produced by various agencies for the Kanallaki mainshock are reported in Table 3. The local agencies (NOA, AUTH) report centroid depths significantly lower than other agencies. Our revised moment tensor solution provided a centroid depth of 8 km. We favour the east-dipping nodal plane because it fits the regional geological data (west-verging thrusts, see Figure 1C and Figure 4, [3,13,15]). We further justify our choice for a low-angle fault plane as the auxiliary nodal plane of our revised Moment Tensor solution indicates a steep dip-angle of 59° (see Supplementary Figure S1 and Table 3, columns NP2), which is mechanically unfavourable (based on our InSAR data). In addition, there are no mapped backthrusts (i.e., high-angle, west-dipping fault planes) in our study area (see Figure 4 for a map of active faults). Concerning the fault’s strike, there are two clusters of solutions, one with NOA (initial), USGS, and GFZ around N317° E and the others (GCMT, IPGP, AUTH, and INGV) around N336° E. The average dip angle is 39° towards east-northeast while the average rake angle is 103°, i.e., almost pure reverse-slip.

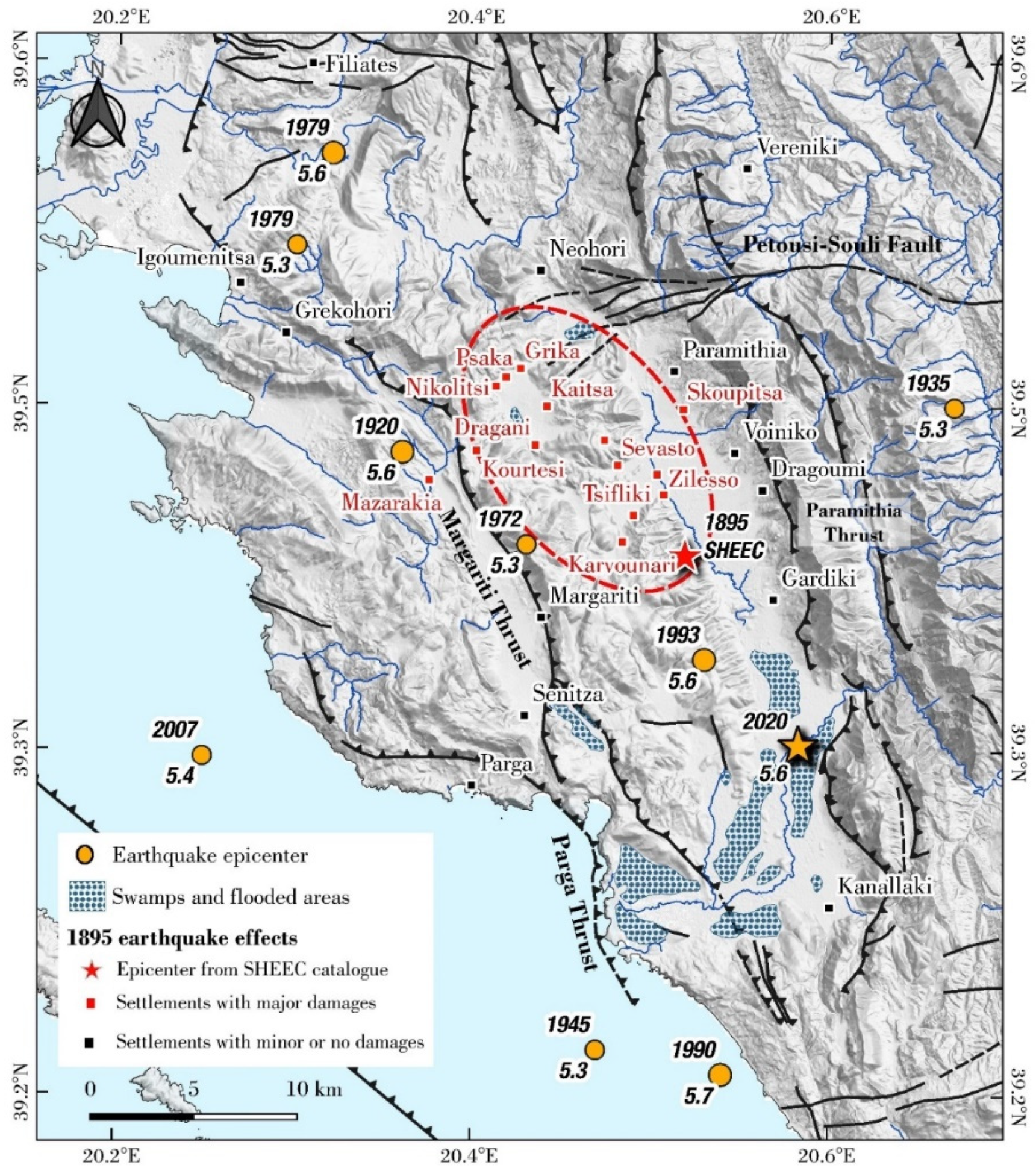
2.2. Historical Seismicity and the 1895 Event

The Kanallaki region is an area of Greece where damaging earthquakes are rare during the last century and occurred with magnitudes M < 6.0 (Figure 4, see Table S1 for the record 1915–2019) however, a disastrous earthquake took place in the 19th century. Both [24] and [25] report information on the occurrence of a major M = 6.3 earthquake on 14 May, 1895 at 20.61°E, 39.42°N near the village Dragani ([25], Figure 4), 15 km north of the Kanallaki. The village Dragoumi (mod. Zervohori), [24] reports, was the location of the heaviest damage, however contemporary sources (Greek newspaper “Voice of Epirus”, 19 May, 1895, accessed on July 2020 through the digital archives of the Greek Parliament) and [25] mention the village Dragani (mod. Ampelia) as the meizoseismal area. According to the sources, the earthquake also destroyed the village Karvounari (Figure 4) and damaged several others, killing in total almost 100 people. We identified all settlements mentioned in the original sources with reported damages and plot them on a map (Figure 4), and an approximate location of the 1895 rupture can be inferred by the damage distribution (dotted red ellipse in Figure 4). Both the approximate location of the rupture and damage distribution are compatible with a M = 5.8 ± 0.3 magnitude reverse rupture along the Margariti thrust (east-dipping), as the 1895 damage zone is located on the hanging wall of this active fault. We document this finding by proper macroseismic intensity data analysis that can be found in Section 4.2 of this paper. The main shock was preceded by a strong foreshock on the previous day (see the catalogue of the Aristotle University of Thessaloniki at http://geophysics.geo.auth.gr/ss/CATALOGS/seiscat.dat).
Moreover, on 16 June, 1990 02:16 UTC an offshore M = 5.5 event occurred, which was studied by [8] who determined a reverse focal mechanism. That earthquake was localised at 20.54°E, 39.16°N (see Figure 4), thus ~15 km to the southwest of the 2020 event with a centroid depth of 8.5 ± 4 km, and strike, dip, and rake angles of 352° ± 20°, 37° ± 9°, and 110° ± 15° respectively, and a seismic moment of 2.49 × 1017 N m. The focal mechanism and magnitude of the 1990 event are thus comparable with those of the 2020 earthquake.

3. Geodesy

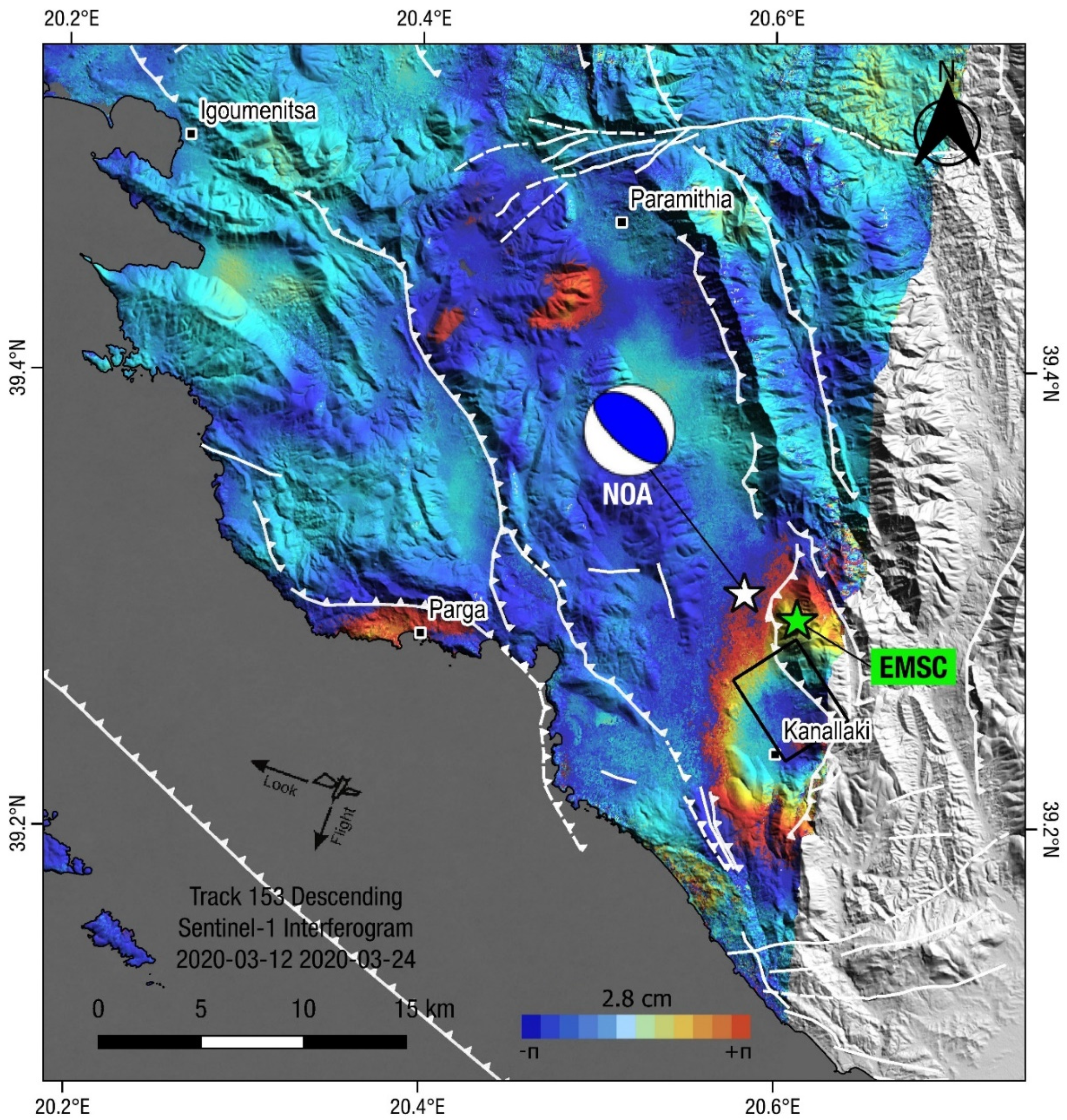
3.1. Interferograms

We used synthetic aperture radar interferometry (InSAR) to capture the deformation produced by the earthquake (Figure 5 and Figure 6). In the broader Aegean area, InSAR is systematically used to map the ground deformation produced by large earthquakes after removing the signal from the topography [27,28,29,30,31,32,33] and minimising the effect of decorrelation factors such as tropospheric noise [30,31].
We use the Sentinel-1 descending interferogram made with the 12 March and 24 March 2020 scenes acquired on track 153 (Figure 5), and the ascending interferogram made with the 19 March and 31 March 2020 scenes acquired on track 175 (Figure 6). The quality of the descending interferogram (track 153) is exceptional as it exhibits particularly high coherence and low tropospheric disturbances. The quality of the ascending interferogram is also good (in terms of coherence and tropospheric noise). Several interferograms of overlapping tracks were also processed (see Figure S3 for ground coverage) however, the extracted information was of a lower quality (see Figure S4 for results of unused interferograms). The unit vectors from the ground to the satellites are [−0.098, 0.504, 0.858] and [−0.105, −0.569, 0.816] in the east, north, and up components for the descending and ascending views, respectively. The interferograms were produced on the Geohazards Exploitation Platform (https://geohazards-tep.eu) using the DIAPASON module developed by TRE-ALTAMIRA.
The two interferograms capture the ground motion along two nearly-opposite lines of sight (l.o.s., see Look arrows in Figure 5 and Figure 6). It is these measurements of l.o.s. that we are going to model to retrieve the parameters of the seismic fault. The digital elevation model (DEM) used for processing is the Shuttle Radar Topography Mission (SRTM) 1 Arc-Second Global (Digital Object Identifier number: /10.5066/F7PR7TFT). We enhanced the signal to noise ratio of the interferograms by applying the adaptive power spectrum filter of [34] with a coherence threshold of 0.3.
The two small aftershocks that occurred, one on 23 March with magnitude Mw(NOA) = 3.8, the other on 25 March with magnitude Mw(NOA) = 3.9 (see Table 1 and https://bbnet.gein.noa.gr/HL/) were not expected to affect the deformation signal of the mainshock. There was also a significant foreshock of magnitude Mw(NOA) = 4.2 on 20 March 21:38 UTC (Table 1) that was also not expected to have produced any measurable surface deformation.

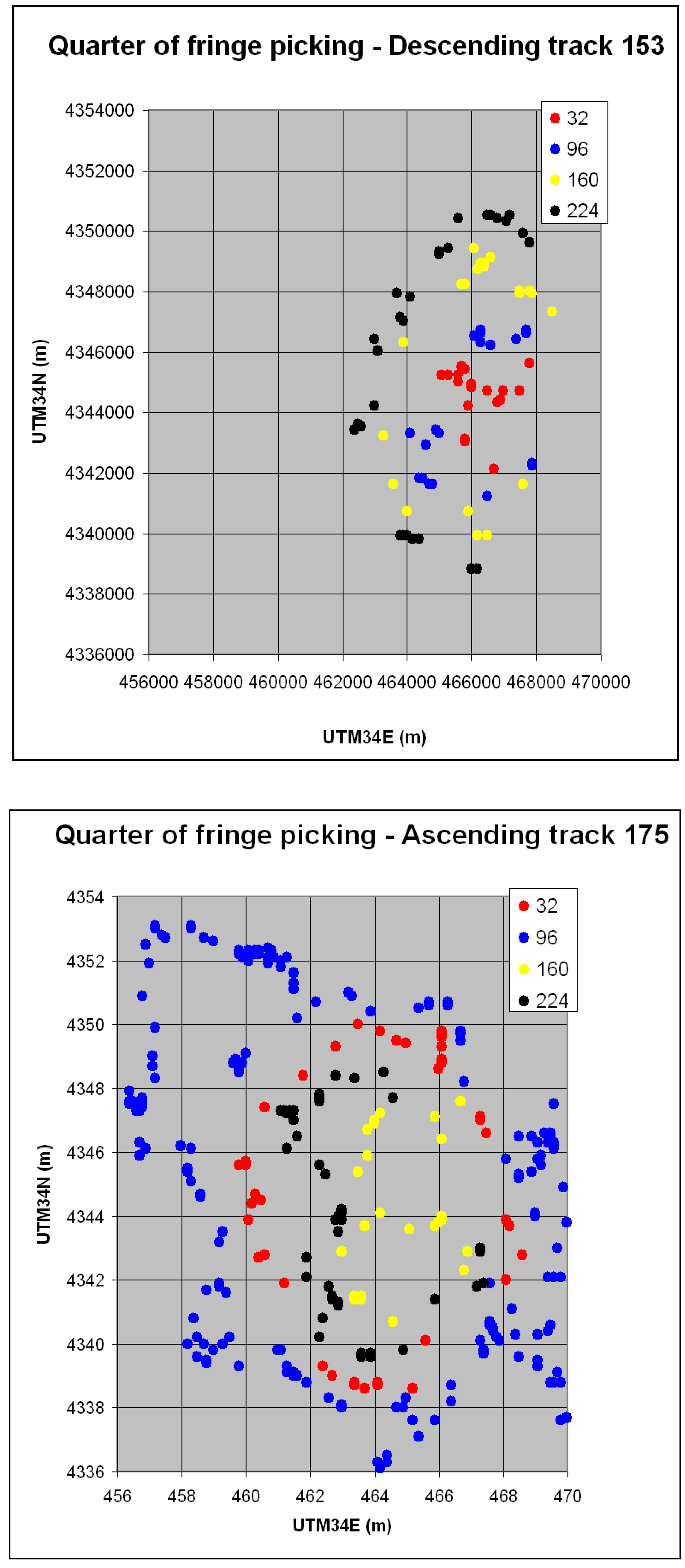
3.2. Geodetic Data Inversion: Picking Quarter of Fringes

On the two above interferograms we extracted numerically by manual picking the pixels constituting the fringe with values 32, 96, 160, and 224. On the descending interferogram (see Table 4) we selected 86 values among 247, and on the ascending interferogram (see Table 5) 86 among 289. As expected, there are less pixels for the larger displacements as this corresponds (by definition) to smaller areas. On the descending interferogram (Figure 5), the zero value of the interferogram is very well constrained due to the high coherence of the interferogram. We assume that the zero value is the average zero counted in the triangle Parga–Igoumenitsa–Paramithia (see Figure 4 for locations). This assumption is justified by the small offset in the position time-series of the GNSS station GARD (Gardiki) which is located at the SE side of the triangle (see Supplementary Figure S5 for time series of this station and see Figure 1 and Figure 6 for its location). We measured a −3.2 ± 0.2 mm static offset on the E-W component of station GARD (minus sign indicates displacement towards the west) which is compatible with the assumed co-seismic motion along a low-angle thrust towards west, as indicated by nodal plane 1 of the moment tensor of the mainshock (Table 3). The InSAR uncertainty is around 1/8 of a fringe, i.e., 3.5 mm in the l.o.s. Regarding InSAR data uncertainty, there are two contributions, the first being linked to the picking of the fringes, but in our case, as we extracted only pixels with a pre-defined value this uncertainty is zero. The second is related to the tropospheric noise that is present in the scene. In our case, especially for the ascending interferogram, this noise is very low. It can be assessed visually and this was confirmed by our group. Table 6 shows how the output of our modelling changes when changing by 1/8 of a fringe the zero of our fringes which is equivalent to changing of the same amount the maximum l.o.s. displacement, here 28 to 31.5 mm. This test is made for a descending interferogram case and with strike, dip, and rake angles of 329°, 39°, and 103° (i.e., the average values for NP1, see Table 3). The test shows that changing the zero of the interferogram by 1/8 of a fringe (3.5 mm) results in the change of the moment tensor by 32%, here completely absorbed by the increase of the fault length as this is the only free geometric parameter, the other free parameters being the three coordinates of the fault-top centre. As our first models predicted a geodetic moment slightly lower that the seismic moment (see Table S4), we use for the zero of the fringes the value that maximises the interferogram, thus the case of maximum line of sight change is 31.5 mm.
Table
Table 4. Picked values of the descending interferogram. See Figure 7 for locations.
Table 4. Picked values of the descending interferogram. See Figure 7 for locations.
Pixel ValueNumber of Available PixelsNumber of Selected PixelsDisplacement in the Line of Sight (mm)
321611831.5
96251924.4
160242117.5
224372810.5
Total24786
The ascending interferogram (Figure 6) is noisier and therefore its zero more difficult to establish. We therefore used a different method and performed the fringe tuning by aligning the geodetic moment predicted for the descending interferogram with the one predicted for the ascending one. The best fit is obtained when using 34 mm for the displacement on the top quarter of fringe of the ascending interferogram. The fault model is now made with joint inversion of the l.o.s ground motions measured with descending and ascending Sentinel-1 interferograms. Our geodetic data provided us with a robust model and in particular on (a) the 3D location of the fault-top centre, (b) fault length and width, and (c) amount of slip.

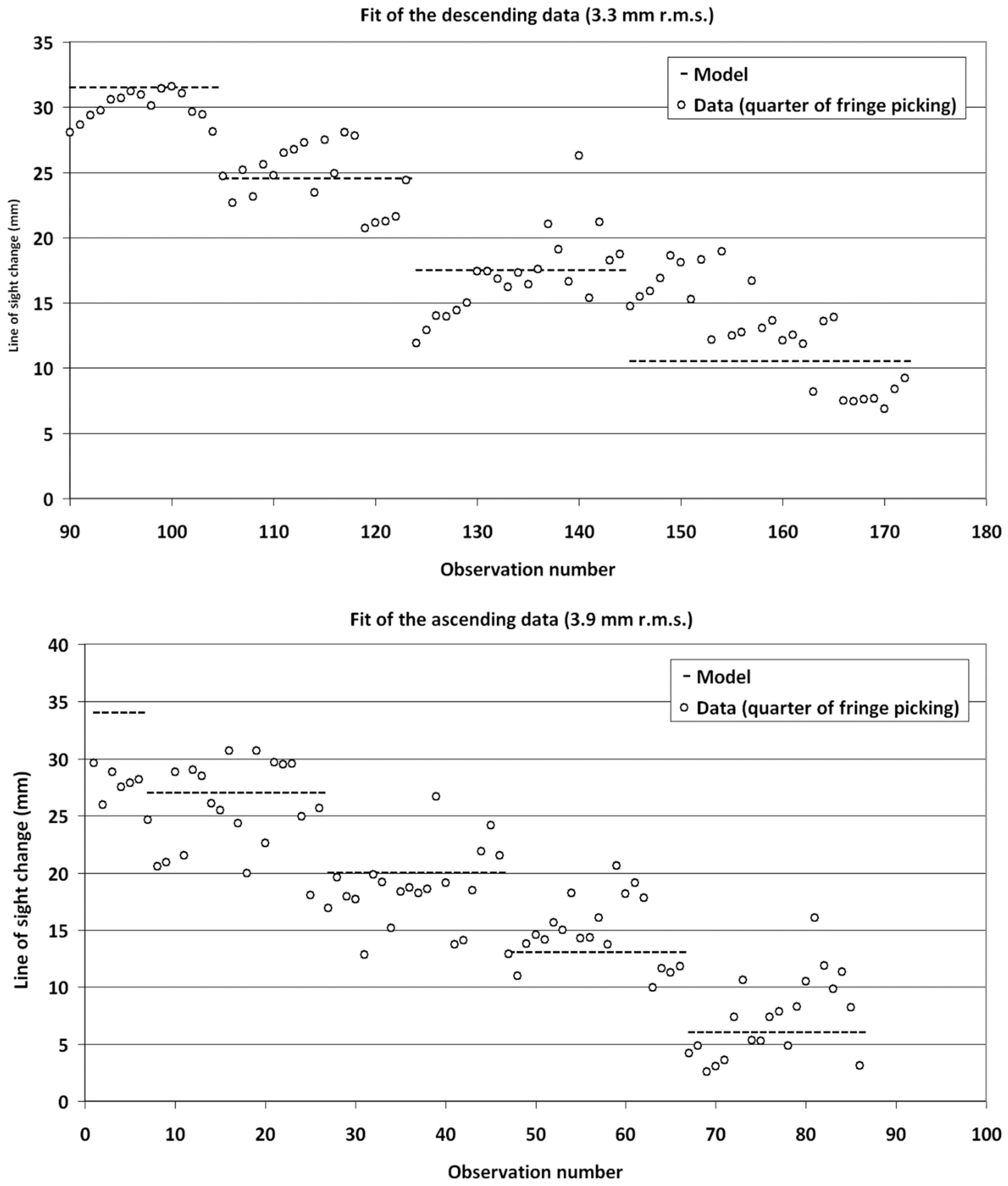
3.3. Results of Inversion Modelling

Assuming a half-space elastic model with uniform slip along a rectangular fault surface, the source of the ground deformation was inverted using the InSAR data and the code inverse6 [35]. For the modelling of the interferograms, the same weight to the ascending and descending data was given and the same zero value for the fringes. The question of the tuning of the zero values has already been explained in the previous section. The equal weight is obtained by using the same number of ascending and descending observations (fringe pickings), here 86 for both, thus 172 observations in total (all 172 data points are compared against the model in Table S2). The mean scatter between data and model is 3.3 mm for the 86-descending data (Figure 8 top) and 3.9 mm for the 86-ascending data (Figure 8 bottom). We assume that the seismic fault plane is the one with low-angle reverse fault dipping towards ENE. This is the most consistent with the geomorphology and tectonic context of the area. Concerning the hypothesis of the antithetic plane, in our paper this hypothesis is not rejected primarily on the basis of the interferograms but on the basis of geological and seismological considerations [2,3,7,8,12,13,15]. As the fault is not very shallow, the magnitude is only Mw = 5.6 and the dip angle is not very different from 45°, the two conjugate planes produce modelled interferograms that are very similar to each other, therefore InSAR does not have the capability to discriminate.
The 3D coordinates of the fault-top centre and for the fault length are inverted. We do not invert for the strike, dip, and rake angles, assuming 329°, 39°, and 103° respectively, i.e., using the average values of the various determinations of the focal mechanism parameters (see Table 3). The dip angle is, among the three angles, the one that is less constrained. For the two other angles there is a trade-off between strike and rake. We tested models with the strike and/or the rake free but we could not constrain well those parameters. This was expected given the almost circular shape of the interferograms, especially the ascending one (Figure 6). Indeed, the near-circular shape of the InSAR deformation pattern does not favour any angle in the azimuth and poorly constrains the dip angle as well. We may have tried to constrain the rake, but we know that in the modelling of InSAR (and also GNSS), there is a strong trade-off between rake and azimuth angles. Therefore we considered that it was more rigorous to rely on the angles provided by seismology through the focal mechanisms. Moreover, there is a strong compatibility between the azimuth angle and orientation of the tectonic structures (see active faults in Figure 5 and Figure 6).
In a first series of inversions we find that the width of the fault tends to become large, between 4.5 and 6 km and the length small, between 4 and 5 km, with the surface (rupture) area remaining almost constant. As the width is not well constrained, it was fixed at 4.7 km, a value the leads to an equal length of 4.7 km, thus a square fault. The amplitude of slip and rake was also released and it was found that the amplitude had the tendency to grow (i.e., from an initial 0.3 m to 0.6 m or more) and the rake to remain steady. In the second set of inversions, we constrained the slip to be 0.5 m, as the standard scaling laws (i.e., [36]) do not suggest a higher value for this earthquake, given also the size of the fault. The best fitting values for the four free parameters are reported in Table 7. Concerning the location of the fault, the horizontal coordinates are well constrained by InSAR (centre of top-fault edge) and the vertical coordinates are also well constrained by the slope of the interferograms. The three parameters that remain unknown are the fault length, width, and amount of slip. The fault length is well constrained by the spatial extension of the interferogram. This leaves two parameters remaining: The width of the fault and amount of slip. Like for azimuth and rake, there is also a strong trade-off between these two parameters, therefore it is a bit difficult to estimate a best fitting solution. We used the estimates on the centroid depth from seismology (6.4–8 km) to estimate approximately the width and it was assumed that the fault could not have a width significantly larger than its length. Under those assumptions two remaining parameters were fixed. The variable slip was not tested because the earthquake size (Mw = 5.6) is too small for that and its deformation is almost similar to the one of a point source. Non-planar fault solutions were not tested for the same reason.

4. Discussion

4.1. Characteristics of the Kanallaki Seismic Fault

Figure 9a shows the surface projection of the seismic fault and Figure 9b a cross section, oriented NE-SW. The upper edge of the fault is located at a depth of 7.0 km, beneath the village of Kanallaki. The mid-point of the top-fault is located at 20.59° E, 39.25° N and the geodetic centroid is at a depth of 8.5 km. The fault length is 4.7 km (Table 7). The geodetic seismic moment, assuming a rigidity of 3 × 1010 Pa for the upper crust is 3.31 × 1017 N m. This is within the range of values found from seismology (Table 3) and close to the NOA-revised (2.86 × 1017 N m; Table 3) so it is consistent. The slip inferred from our model (0.5 m) is twice larger than the theoretical slip predicted by the scaling relationships of [37] (0.24 m). Those scaling laws predict a fault length of 5.5 km and a fault width of 5.8 km, respectively. In this case, the length is very well constrained by the fringes and cannot grow above a maximum of 5 km (4.7 km in our best fitting model) while the width, which is not very well constrained, could grow up to 6–6.5 km. Accepting such an unusual elongated (along-dip) shape for the fault would allow reducing the amplitude of the slip. For example a fault of 4.5 × 6.5 km and slip of 0.38 m would fit the interferogram equally well with better consistency with scaling laws. We prefer to retain a square geometry for the seismic source primarily because (a) it fits rupture-size data [37] for sources with M~5.5, (b) it comprises a continental thrust with a dip-angle of ~39° which is compatible with regional geological data. And (c) the map view of aftershocks (Figure 3b, Supplementary Figure S2) does not indicate a NE-SW distribution which would be in favour of an increased fault-width.
Figure 9b presents, with the same horizontal and vertical scale, a 19-km-long cross section of the Kanallaki area running from the shore towards the interior, perpendicular to the strike of the fault (passing through the geodetic centroid). In this section we show the topography in blue and the predicted vertical deformation (surface uplift) in red, as deduced from our fault model (Table 7). The maximum value of the vertical displacement is +4 cm at the abscissa 9.71 km, i.e., almost on top of the location of the upper tip of the fault (abscissa 8.9 km), that is on its hanging wall side. A similar surface displacement maximum (uplift) was mapped by InSAR for the 2019 Durres earthquake, as well [33].
Figure 10 shows a simplified geological map and a simplified structural section of the crust beneath Kanallaki. The 21 March 2020 earthquake has presumably occurred on one of the two main reverse-slip structures of Margariti or Parga, outcropping in the area. The thrust fault of Margariti (code GR0695 on the NOAFault database, [38], https://arcg.is/04Haer) continues south towards Loutsa (Figure 9a, following [39]) and possibly offshore. It may root into the basal decollement of the Ionian zone over the crystalline basement. There are also Triassic evaporitic outcrops near Margariti (Figure 10a) and Loutsa that imply the existence of a major thrust there. As the Margariti thrust fault (see Figure 10a) is more than 12 km long its down-dip extension is comparable to its length so it could reach beneath the Kanallaki area (Figure 10b). Indeed, Kanallaki is located ~10 km to the east of the trace of the Margariti thrust and such an east-dipping fault geometry also complies with a geodetic centroid depth of 8.5 km that we obtained for the 2020 seismic fault.
To the northwest of Kanallaki and west of village Gliki (Figure 10a), the Lippa mountain forms a ~400 m high N-S anticline composed of hard carbonate rocks of the Ionian zone. The Kokitos and Acherontas rivers reach the sea southwest of this anticline (Figure 9a, see Figure S6 for an aerial view, other sub-parallel anticlines also exist). Whether the Lippa mountain structure is part of the active thrust system that roots at the decollement of 7–8 km depth requires further investigations (seismic profiles and drilling). In such a case, the lateral growth of the anticline would be balanced by erosion removed by the two rivers. On-going tectonic activity is also evidenced by the uplift of the Epirus coastline due to the Late Tertiary convergence between the Apulian continental block and Eurasia [12].

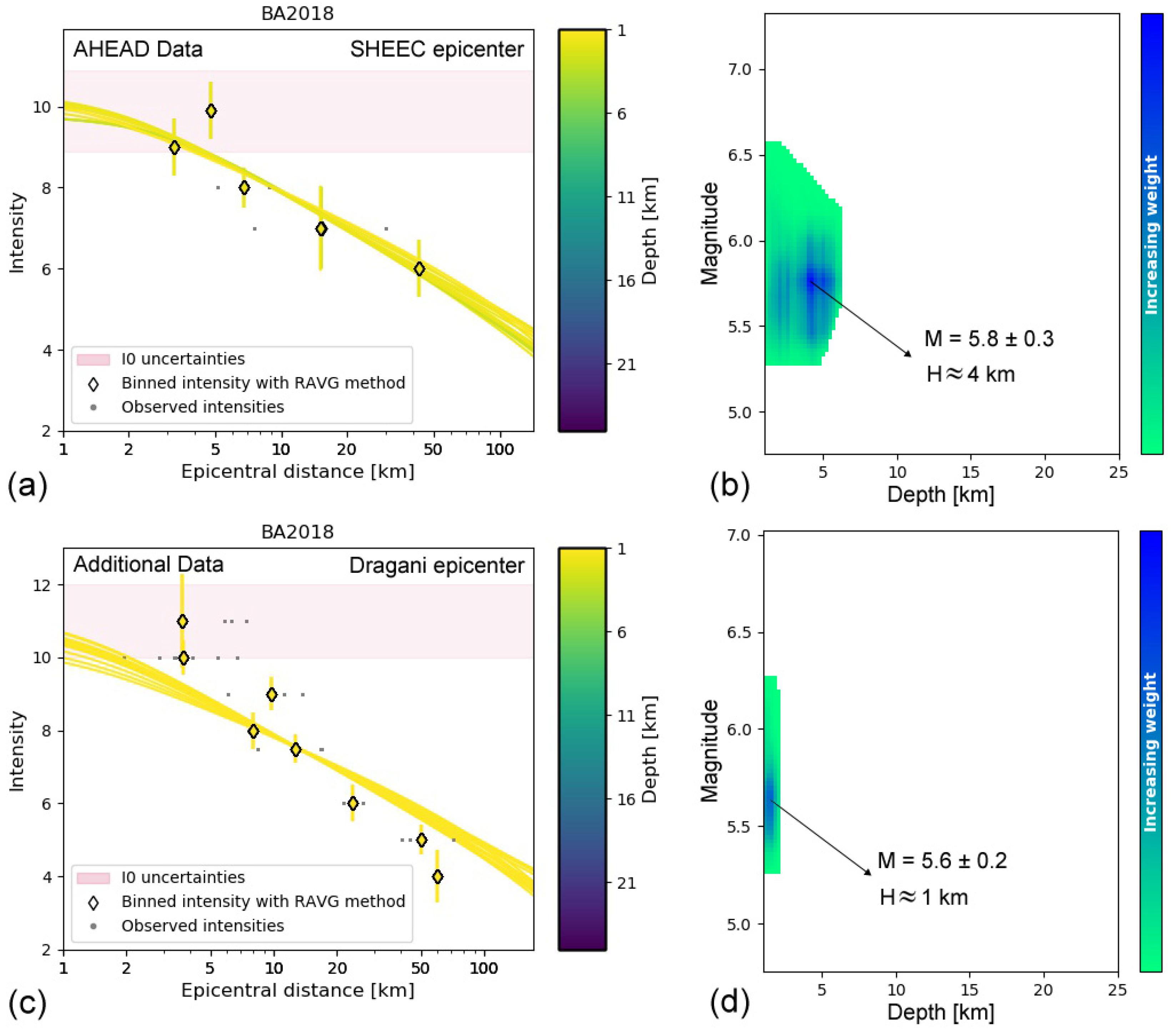
4.2. Revision of the Magnitude and Location of the 1895 Earthquake in West Epirus

In order to assess the magnitude and depth of the 1895 event in Dragani, we employed the QUake-MD open-source code [41]. This algorithm inverts intensity data points for a fixed macroseismic epicentre with a set of different Intensity Prediction Equations (IPE) and determines a plausible range of magnitudes and focal depths that better match the observations. We first acquired macroseismic data from the AHEAD database [42] (https://www.emidius.eu/AHEAD/event/18950514_0000_000, accessed on 14 September, 2020) and the macroseismic epicentre from the SHEEC catalogue [43]. Then, using new intensity sites from the aforementioned sources and also revising some of the intensity values reported by [24,25], we provide a new list of macroseismic intensities in Supplementary Table S3. A detailed map of the updated macroseismic intensities is presented in Supplementary Figure S7. In this work we used the default IPEs from [44], for southern France, and [45], for metropolitan France and high-attenuation area that came along with the Quake-MD code [41]. With an intensity threshold of Ic = 6 and maximum intensity Io = 10, we determined a range of magnitudes M = 5.8 ± 0.3 for shallow focal depths H~4 km (Figure 11a,b). Other macroseismic epicentres reported in the AHEAD database were tried out, producing similar results concerning M and H, but not a better fit than with the SHEEC epicentral solution.
The calculations with intensity observations (see Table S3) and an intensity threshold of Ic = 4, with maximum intensity Io = 11 were repeated considering several different cases for a macroseismic epicentre, including the ones reported in the AHEAD database and SHEEC, but also took into account the four sites for which a maximum intensity of Io = 11 was reported. The fit of the IPEs to the data was generally inadequate with the theoretical curves underestimating the intensity at short epicentral distances (<10 km) and overestimating larger ones. This may be due to the uncertain quality of intensity data points at intermediate and farther distances, while some high intensity observation could be attributed to local site conditions, amplifying the peak ground motion. In Figure 11c,d we used the site of Dragani, in the meizoseismal area (Io = 11) as a macroseismic epicentre. In that case, the plausible magnitude range was found at M = 5.6 ± 0.2 but the resulting focal depth, derived from the inversions, was very shallow (H~1 km, Figure 11c,d). Please note that Dragani and Karvounari, which were both completely destroyed (Io = 11) by the 1895 event, are located near the trace of a west-verging thrust, parallel to the Margariti active fault (Figure 4). To summarise this discussion, due to lack of data (such as geo-environmental effects) on this historical event we find it more reasonable to attribute the 1895 event to the Margariti fault as well.
The occurrence of two M5.6 + events (1895 and 2020) along the 38 km long Margariti fault is exceptional for Epirus and for the seismic behaviour of the active thrusts of the Ionian zone of the Hellenides. The two earthquakes likely ruptured different asperities along strike and this behaviour may indicate some sort of systematic rupture pattern of this fault and possibly of similar thrust faults in Epirus. The near 100 year earthquake record in this area (see Figure 4) is far from complete, however it is notable that no events with M > 6.1 have been recorded.

4.3. Tectonic Strain and the Determination of the Deformation Zone across the Apulia—Eurasia Plate Boundary

New GNSS data of the Greek permanent stations in Epirus and north Ionian Sea (Corfu and Paxoi islands, Table 8) were analysed. The GNSS stations belong to the NOANET geodetic network [46,47], the Hexagon SmartNet and Uranus commercial network (see Figure 1 for locations). The processing was made with the Precise Point Positioning (PPP) strategy [48] by means of the GIPSY/OASIS II software (ver. 6.4) developed by the Jet Propulsion Laboratory (JPL; http://gipsy-oasis.jpl.nasa.gov, [49]). The JPL final orbits (flinnR) and clocks, absolute antenna calibrations, random walk troposphere estimation, and the FES2004 ocean loading model were used. An in-depth description of similar GPS data processing can be found in [31,32,33]. The tectonic velocities and uncertainties retrieved from the analysis of the time series are given in Table 8 and were used to calculate plate convergence (Figure 12).
The long-term N-S velocities, in the reference frame ITRF2014, are increasing from south (ARTA; 10.8 ± 0.3 mm yr−1) to north (KASI; 14.0 ± 0.3 mm yr−1; KASI is located in northern Corfu) while the E-W velocities show a “plateau” at 20.3-22.1 mm yr−1 (the two ARTA stations show lower rates). The station velocities near Arta (Figure 1) also reflect the ongoing N-S extension of the Amvrakikos graben [11,50,51], so they will be left out in further analysis. Another notable exception in this kinematic field is the Hexagon-SmartNet station PAXO (Figure 1) whose E–W velocity is 24.3 ± 0.4 mm yr−1 (N-S velocity is 16.4 ± 0.4 mm yr−1) and was also considered in the strain analysis made by [11].
Using the velocities of Table 8 we calculate the convergence towards Apulia in the azimuth N228°Ε which is the azimuth that fit best the vectors of the stations located close to the coast (thus excluding the two stations of Ioannina). Note that the orientation of the coast of Epirus is globally perpendicular to this azimuth. The adopted Apulian plate velocity (vE:25.1 mm/yr–vN:18.4 mm/yr) is derived from [11] by averaging the velocities of 10 GPS points located, with no ambiguity, on the Apulian platform in SE Italy. The values of convergence and their uncertainties are presented in Table 9. The convergence of PAXO towards Apulia is of 1.9 ± 0.4 mm yr−1. For the three stations of Corfu (KASI, KERK, and KERU, Figure 1) the average convergence towards Apulia is 5.6 ± 0.4 mm yr−1 (in the azimuth N228°E). For the two stations of Igoumenitsa (IGOU and HGOU) the average convergence is 5.8 ± 0.4 mm yr−1, close to the value of Corfu. For GARD, the rate is 6.5 ± 0.45 mm yr−1. For the two stations of Ioannina (IOAN and IOAU) the average convergence is 7.6 ± 0.4 mm yr−1. As the net rate of convergence between Apulia and stable Europe is only 5.2 mm yr−1 (considering stations across the Adriatic Sea), we see that the convergence is amplified in northwest Greece by a factor of ~1.5. This is due to the compression and clockwise rotation imposed by the westward component of movement of the Anatolian micro-plate towards Apulia together with dextral motion along the Cephalonia Transform Fault (Figure 1), a process that can be perceived until the north of Albania [11,12,52]. It is noteworthy that the shortening rate of the crust between the Epirus coastal GNSS stations and station PAXO in the Ionian Sea (i.e., across the Ionian Thrust; see Figure 13) is equivalent to 4.6 mm yr−1 or ~50% of the overall convergence.
By modelling this convergence data with a simple back-slip model in elastic half-space (Figure 12) we find the best fit for a total convergence rate of 8.9 mm yr−1, thus an extra compression of 3.7 mm yr−1 is recovered in the regions located to the east and north of Ioannina. For back-slip modelling, we used the programme described (and distributed) in [35], simulating the locked interface like in [29], except that in this case the movement is reverse instead of strike slip. The modelled central axis of the convergence band, with azimuth N318°E, passes along the southwest coast of Corfu, along the northeast coast of Paxoi, heading toward the northern extremity of the Lefkada island (Figure 13). The 21 March 2020 earthquake occurred inside this band (Figure 12 and Figure 13). The extent of the deforming area (box in Figure 12), when defined as the band that accommodates 80% of the total convergence is 60 km with a best fitting locking depth of 11 km. Unfortunately, the limited surface displacement data were not dense enough to allow for a formal inversion so as to recover the slip deficit patterns along the deformation front.
Therefore, PAXO appears to be located on the Apulian side of the deforming zone, while it is exactly the opposite for the stations onshore Corfu (KASI, KERK, and KERU), with the axis of the plate boundary zone with Africa passing close to both islands and continuing along the coast of Albania. Between Corfu and Epirus (the Igoumenitsa stations IGOU–HGOU) the data and model (Figure 12) show that there is no significant shortening within the velocity uncertainties of ± 0.2 mm yr−1, confirming the conclusions of [47].
In terms of strain, it is noteworthy that there is a 120 ns yr−1 active shortening of the crust between the two GNSS stations PAXO and GARD, located 38 km apart, and roughly in the ENE-WSW direction (N246°E). This 1D estimate of tectonic strain is about 2.4 times larger than the 2D estimates from regional studies, e.g., the 50 ns yr−1 found by [11] possibly because of the strong smoothing effect of the regional strain calculations of [11]. In addition, both Ioannina GNSS stations (IOAN and IOAU) exhibit a long-term shortening of 41 and 51 ns yr−1 with respect to GARD, respectively (Figure 14), indicating ongoing compression onshore Epirus and to the east-northeast of the Kanallaki area, yet decreasing significantly when moving away from the collision front.

4.4. On the Regional Extent of On-Going Compression in Epirus and the Significance of the Ioannina 2016 Compressional Event

Unlike the shallow depth of the Kanallaki event, the MNOA = 5.3 15 October 2016 20:14 UTC Ioannina thrust earthquake [53,54,55] (Figure 13) had a depth of 14 km, while maintaining similar kinematics. The earthquake occurred 20 km to the NW of Ioannina, Epirus, NW Greece, at an area where microseismicity had already been detected by [6]. The main shock was followed by a few hundreds of aftershocks in the period up to 25 October 2016. The hypocentre (14 km depth) is located at the bottom of the pile of deformed carbonates of the Ionian zone of the Hellenides and close to the crystalline basement as did the Durres earthquake in 2019 [33]. Due to concern for Ioannina, Sentinel differential interferograms were made immediately after that event but no deformation could be seen. This is because the moderate-size event was too deep. In addition, GPS data processing showed no displacement at the two stations of Ioannina (Figure 1). Analysis of the moment tensor solution of the earthquake and its stronger aftershocks (Figure 13) and map distribution of aftershocks revealed seismic slip along a shallow, east-dipping (27°) reverse fault, striking NNW-SSE [55], thus confirming the shortening regime suggested by the GNSS data. Moreover, the 2016 reverse-slip earthquake signifies the change in the stress-field near the meridian 20.9° E from ~N-S extension (Pindos mountains) to ~E-W shortening near Ioannina [11]. The deep setting of the thrust fault inside the Ionian fold-and-thrust belt of the external Hellenides denotes the ongoing accommodation of brittle deformation about 80 km to the east of the collision front with Apulia (Figure 14). We therefore suggest that deep crustal seismicity near Ioannina is of a compressional type and it is due to ongoing crustal shortening between Apulia and Eurasia, as documented by the GNSS data (Figure 12).

5. Conclusions

  • The main source of the Mw = 5.6 earthquake that hit western-central Epirus on 21 March 2020 was identified to be located on the Margariti thrust fault, within the frontal area of the Ionian fold and thrust belt of the Hellenic orogen;
  • The seismic fault was modelled by combining the ascending and descending Sentinel-1 observations. It was found that we could model the overall fringe pattern by reverse slip on an east-dipping fault. The fault plane is a low-angle thrust fault (~5 by 5 km) that dips 39° towards east;
  • The inversion of geodetic data suggests that the upper edge of the fault is at a depth of 7 km, well constrained by the modelling of the interferograms;
  • The geodetic centroid of the slip plane is located at 8.5 km depth which is in agreement with our revised moment tensor solution that provided a centroid depth of 8 km;
  • InSAR showed ground motion towards the southwest and surface uplift in agreement with moment tensor solutions from seismology;
  • The damage distribution of the 14 May, 1895 M5.8 ± 0.3 damaging earthquake was found to be compatible with a reverse-slip rupture along the Margariti thrust;
  • Deep crustal seismicity near Ioannina is of a compressional type and is due to ongoing crustal shortening between Apulia and Eurasia;
  • GNSS data indicate that the extent of the deforming crustal area between Apulia–Epirus (from offshore Paxoi until Kanallaki), accommodating 80% of the total convergence, is 60 km, with a best fitting locking depth of 11 km;
  • The shortening rate of the crust between the Epirus coastal GNSS stations and station PAXO in the Ionian Sea (i.e., across the Ionian Thrust) is equivalent to 4.6 mm yr−1 or ~50% of the overall convergence;
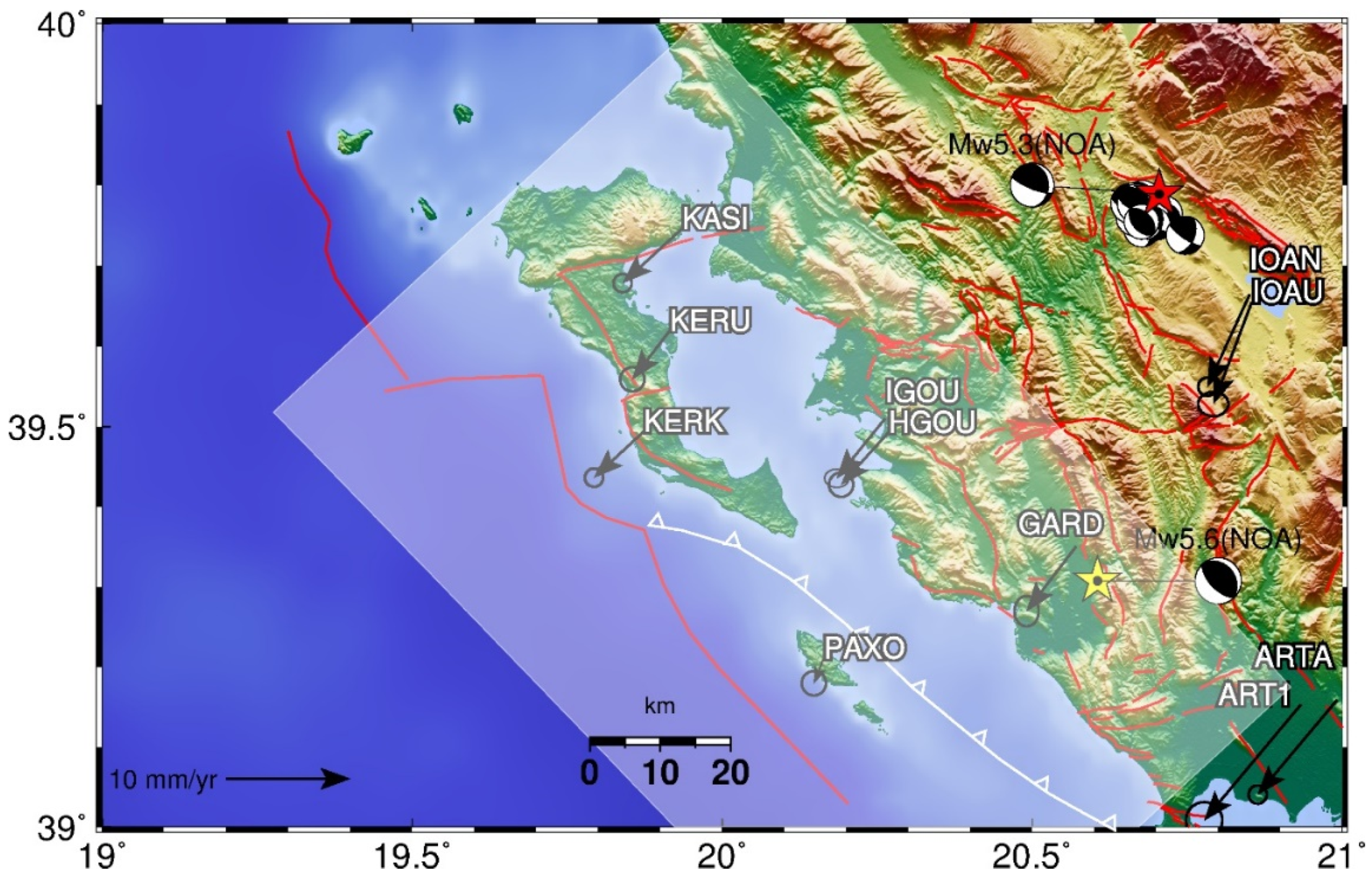
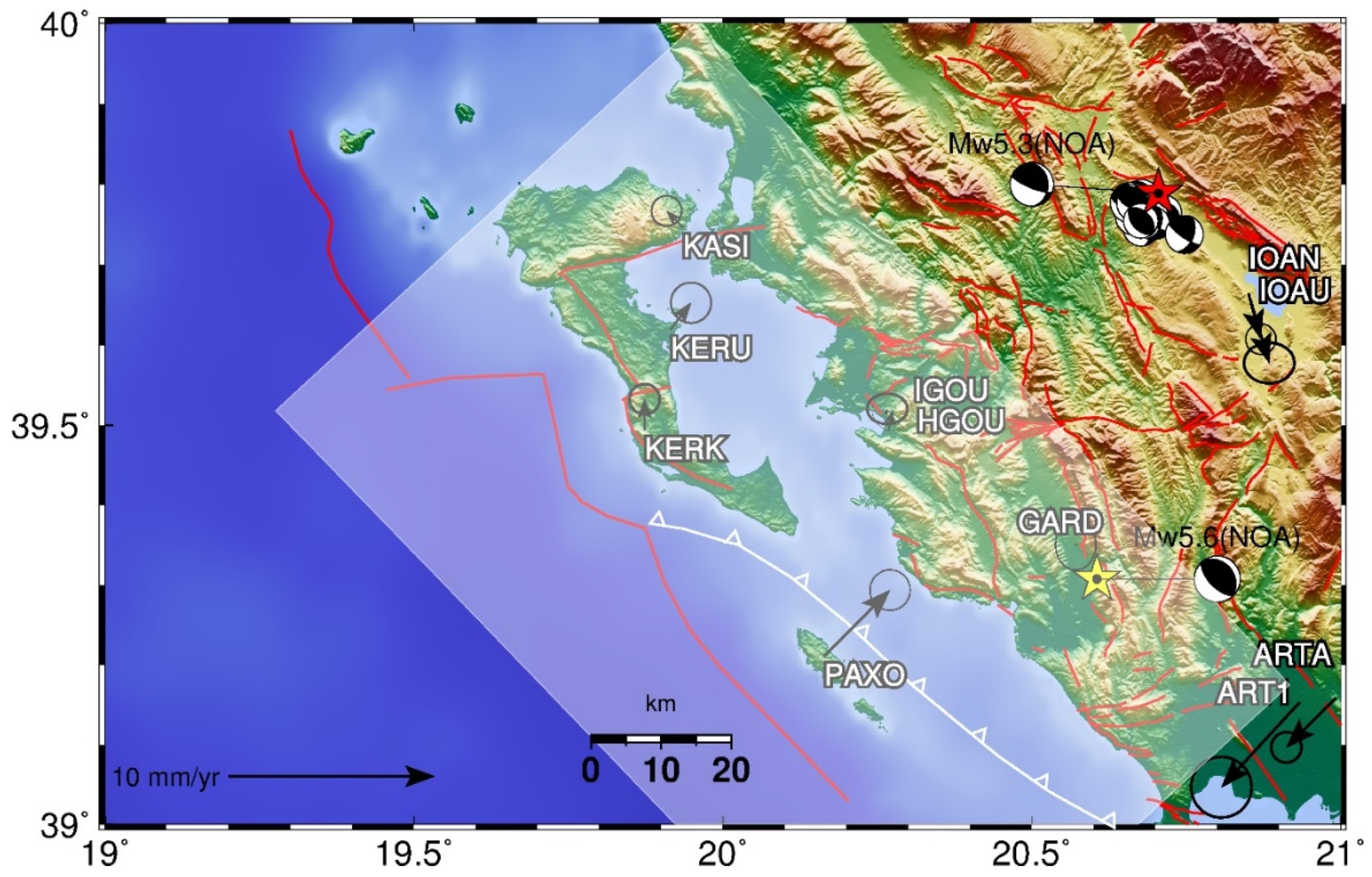
  • The island of Paxoi appeared to already be on the Apulian side of the deforming zone, while it is exactly the opposite for the GNSS stations onshore Corfu (KASI, KERK, and KERU, Figure 13), with the axis of the plate boundary zone between Africa passing close to both islands and continuing along the coast of Albania.

Supplementary Materials

The following are available online at https://www.mdpi.com/2076-3263/10/11/454/s1, Figure S1: Results of the ISOLA modelling of the mainshock, Figure S2: Map and cross-sections of the relocated 2020 Kanallaki earthquake sequence, Figure S3: Map showing the Sentinel-1 frames with data used in this paper, Figure S4: Coseismic interferograms for the Kanallaki earthquake that were not used in the inversion due to low quality and noise, Figure S5: Graph of the GNSS time series of station GARD Figure S6: Aerial overview of the earthquake epicentre area, Figure S7: Detailed macroseismic intensity distribution for the 1895 earthquake, Table S1: Catalogue of strong events for the study area, 1915–2019, Table S2: Observed values (fringe picking) and modelled values, Table S3: Intensity observations for the 1895 earthquake near Dragani Table S4: Variability of the solution as a function of the focal mechanism parameters, Table S5: Location of co-seismic landslides identified using Sentinel-2 images for the Mw 5.6 21 March 2020 earthquake.

Author Contributions

Conceptualization, S.V., A.G. and P.B.; methodology, P.B. and P.E.; software, S.V., P.E., V.K. and V.T.; validation, S.V., P.P. and A.G.; formal analysis, P.B., V.K. and P.E.; investigation, A.G., S.V., V.T., A.F. and H.P.; resources, S.V., P.P. and A.G.; data curation, P.B., A.G., V.T., A.F. and H.P.; writing—original draft preparation, S.V., P.B. and A.G.; writing—review and editing, all authors.; visualization, S.V., V.K. and P.E.; supervision, A.G. and P.B.; funding acquisition, A.G. All authors have read and agreed to the published version of the manuscript.

Funding

A.G. thanks “HELPOS—Hellenic Plate Observing System” (MIS 5002697) which is funded by the Operational Programme “Competitiveness, Entrepreneurship and Innovation” (NSRF 2014-2020) and co-financed by Greece and the European Union (European Regional Development Fund).

Acknowledgments

We thank three anonymous reviewers for their constructive reviews and Efthimios Lekkas, Efthimios Sokos, Hélène Lyon-Caen, Nicolas Chamot-Rooke, Ioannis Kassaras, Ioannis Karamitros, and Christos Papaioannou for discussions. We thank ESA, Geohazards Lab, and Terradue for providing access to Geohazards Exploitation Platform (GEP) for InSAR cloud processing. GNSS data were provided by NOANET, Hexagon SmartNET and Uranus (Tree) networks of Greece. Seismic Waveform data were sourced from the corresponding ORFEUS EIDA node operated by the National Observatory of Athens (eida.gein.noa.gr). We thank the NOA analysis team for their phase data. We used data from the HL (Institute of Geodynamics, National Observatory of Athens, doi:10.7914/SN/HL), HP (University of Patras, doi:10.7914/SN/HP), which is cooperating certain stations jointly with the Charles University in Prague, HT (Aristotle University of Thessaloniki, doi:10.7914/SN/HT), HA (National and Kapodistrian University of Athens, doi:10.7914/SN/ HA), and HI (Institute of Engineering Seismology and Earthquake Engineering, doi: 10.7914/SN/HI) networks. The ALOS Global Digital Surface Model–30 m is available from https://www.eorc.jaxa.jp/ALOS/en/aw3d30/index.htm. We thank the QGIS Development Team–Open Source Geospatial Foundation Project http://qgis.osgeo.org.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Underhill, J.R. Late Cenozoic deformation of the Hellenide foreland, western Greece. Geol. Soc. Am. Bull. 1989, 101, 613–634. [Google Scholar] [CrossRef]
  2. King, G.; Sturdy, D.; Whitney, J. The landscape geometry and active tectonics of northwest Greece. Geol. Soc. Am. Bull. 1993, 105, 137–161. [Google Scholar] [CrossRef]
  3. Karakitsios, V. Western Greece and Ionian Sea petroleum systems. AAPG Bull. 2013, 97, 1567–1595. [Google Scholar] [CrossRef] [Green Version]
  4. Handy, M.R.; Giese, J.; Schmid, S.M.; Pleuger, J.; Spakman, W.; Onuzi, K.; Ustaszewski, K. Coupled crust-mantle response to slab tearing, bending, and rollback along the Dinaride-Hellenide orogen. Tectonics 2019, 38, 2803–2828. [Google Scholar] [CrossRef]
  5. Olive, J.-A.; Pearce, F.; Rondenay, S.; Behn, M.D. Pronounced zonation of seismic anisotropy in the Western Hellenic subduction zone and its geodynamic significance. Earth Planet. Sci. Lett. 2014, 391, 100–109. [Google Scholar] [CrossRef]
  6. Hatzfeld, D.; Kassaras, I.; Panagiotopoulos, D.; Amorese, D.; Makropoulos, K.; Karakaisis, G.; Coutant, O. Microseimicity and strain pattern in northwestern Greece. Tectonics 1995, 14, 773–785. [Google Scholar] [CrossRef]
  7. Baker, C.; Hatzfeld, D.; Lyon-Caen, H.; Papadirnitriou, E.; Rigo, A. Earthquake mechanisms of the Adriatic Sea and Western Greece: Implications for the oceanic subduction-continental collision transition. Geophys. J. Int. 1997, 131, 559–594. [Google Scholar] [CrossRef] [Green Version]
  8. Louvari, E.; Kiratzi, A.; Papazachos, B.; Hatzidimitriou, P. Fault-plane solutions determined by waveform modeling confirm tectonic collision in the eastern Adriatic. Pure Appl. Geophys. 2001, 158, 1613–1637. [Google Scholar] [CrossRef]
  9. Tselentis, G.A.; Sokos, E.; Martakis, N.; Serpetsidaki, A. Seismicity and seismotectonics in Epirus, western Greece: Results from a microearthquake survey. Bull. Seismol. Soc. Am. 2006, 96, 1706–1717. [Google Scholar] [CrossRef] [Green Version]
  10. Pérouse, E.; Chamot-Rooke, N.; Rabaute, A.; Briole, P.; Jouanne, F.; Georgiev, I.; Dimitrov, D. Bridging onshore and offshore present-day kinematics of central and eastern Mediterranean: Implications for crustal dynamics and mantle flow. Geochem. Geophys. Geosyst. 2012, 13. [Google Scholar] [CrossRef] [Green Version]
  11. D’Agostino, N.; Métois, M.; Koci, R.; Duni, L.; Kuka, N.; Ganas, A.; Georgiev, I.; Jouanne, F.; Kaludjerovic, N.; Kandić, R. Active crustal deformation and rotations in the southwestern Balkans from continuous GPS measurements. Earth Planet. Sci. Lett. 2020, 539, 116246. [Google Scholar] [CrossRef]
  12. Van Hinsbergen, D.J.J.; van der Meer, D.G.; Zachariasse, W.J.; Meulenkap, J.E. Deformation of western Greece during Neogene clockwise rotation and collision with Apulia. Int. J. Earth Sci. 2005, 95, 463. [Google Scholar] [CrossRef]
  13. Zelilidis, A.; Piper, D.J.W.; Vakalas, I.; Avramidis, P.; Getsos, K. Oil and gas plays in Albania: Do equivalent plays exist in Greece? J. Pet. Geol. 2006, 26, 29–48. [Google Scholar] [CrossRef]
  14. IGRS-IFP. Etude Géologique de l’Εpire (Grèce Nord-occidentale); Editions Technip: Paris, France, 1966; p. 306. [Google Scholar]
  15. Monopolis, D.; Bruneton, A. Ionian Sea (western Greece): Its structural outline deduced from drilling and geophysical data. Tectonophysics 1982, 83, 227–242. [Google Scholar] [CrossRef]
  16. Paschos, P.; Rondoyianni, T.; Mettos, A. Neotectonic Map of Greece in Scale 1:100000, Map Sheet Arta; Institute of Geology and Mineral Exploration: Athens, Greece, 2011. [Google Scholar]
  17. Ntokos, D. Neotectonic study of Northwestern Greece. J. Maps 2018, 14, 178–188. [Google Scholar] [CrossRef] [Green Version]
  18. Lekkas, E.; Mavroulis, S.; Carydis, P.; Skourtsos, E.; Kaviris, G.; Paschos, P.; Ganas, A.; Kazantzidou-Firtinidou, D.; Parcharidis, I.; Gatsios, T.; et al. The March 21, 2020, Mw 5.7 Epirus (Greece) Earthquake; Newsletter of Environmental, Disaster and Crises Management Strategies; Department of Geology and Geoenvironment, National and Kapodistrian University of Athens: Athens, Greece, 2020; ISSN 2653-9454. [Google Scholar]
  19. Sokos, E.N.; Zahradnik, J. ISOLA a Fortran code and a Matlab GUI to perform multiple-point source inversion of seismic data. Comput. Geosci. 2008, 34, 967–977. [Google Scholar] [CrossRef]
  20. Haslinger, F.; Kissling, E.; Ansorge, J.; Hatzfeld, D.; Papadimitriou, E.; Karakostas, V.; Makropoulos, K.; Kahle, H.-G.; Peter, Y. 3D crustal structure from local earthquake tomography around the Gulf of Arta (Ionian region, NW Greece). Tectonophysics 1999, 304, 201–218. [Google Scholar] [CrossRef]
  21. Karakonstantis, A. 3-D Simulation of Crust and Upper Mantle Structure in the Broader Hellenic Area Through Seismic Tomography. Ph.D. Thesis, Department of Geophysics-Geothermics, Faculty of Geology, University of Athens, Athens, Greece, March 2017. [Google Scholar]
  22. Wadati, K. On the travel time of earthquake waves. Part. II. Geophys. Mag. 1933, 7, 101–111. [Google Scholar]
  23. Waldhauser, F. hypoDD-A Program to Compute Double-Difference Hypocenter Locations. US Geol. Surv. Open File Rep. 2001, 1, 113. [Google Scholar]
  24. Papazachos, B.; Papazachou, C. The Earthquakes of Greece; Editions Ziti: Thessaloniki, Greece, 1997. [Google Scholar]
  25. Ambraseys, N. Earthquakes in the Mediterranean and Middle East: A Multidisciplinary Study of Seismicity up to 1900; Cambridge University Press: Cambridge, UK, 2009; p. 970. [Google Scholar]
  26. Makropoulos, K.; Kaviris, G.; Kouskouna, V. An updated and extended earthquake catalogue for Greece and adjacent areas since 1900. Nat. Hazards Earth Syst. Sci. 2012, 12, 1425–1430. [Google Scholar] [CrossRef] [Green Version]
  27. Kontoes, C.; Elias, P.; Sykioti, O.; Briole, P.; Remy, D.; Sachpazi, M.; Veis, G.; Kotsis, I. Displacement field and fault model for the September 7, 1999 Athens Earthquake inferred from ERS2 Satellite radar interferometry. Geophys. Res. Lett. 2000, 27, 3989–3992. [Google Scholar] [CrossRef] [Green Version]
  28. Atzori, S.; Manunta, M.; Fornaro, G.; Ganas, A.; Salvi, S. Postseismic displacement of the 1999 Athens earthquake retrieved by the Differential Interferometry by Synthetic Aperture Radar time series. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
  29. Briole, P.; Elias, P.; Parcharidis, O.; Bignami, C.; Benekos, G.; Samsonov, S.; Kyriakopoulos, C.; Stramondo, S.; Chamot-Rooke, N.; Drakatou, M.L.; et al. The seismic sequence of January–February 2014 at Cephalonia Island (Greece): Constraints from SAR interferometry and GPS. Geophys. J. Int. 2015, 203, 1528–1540. [Google Scholar] [CrossRef] [Green Version]
  30. Ilieva, M.; Briole, P.; Ganas, A.; Dimitrov, D.; Elias, P.; Mouratidis, A.; Charara, R. Fault plane modelling of the 2003 August 14 Lefkada Island (Greece) earthquake based on the analysis of ENVISAT SAR interferograms. Tectonophysics 2016, 693, 47–65. [Google Scholar] [CrossRef]
  31. Ganas, A.; Elias, P.; Bozionelos, G.; Papathanassiou, G.; Avallone, A.; Papastergios, A.; Valkaniotis, S.; Parcharidis, I.; Briole, P. Coseismic deformation, field observations and seismic fault of the 17 November 2015 M = 6.5, Lefkada Island, Greece earthquake. Tectonophysics 2016, 687, 210–222. [Google Scholar] [CrossRef]
  32. Ganas, A.; Elias, P.; Kapetanidis, V.; Valkaniotis, S.; Briole, P.; Kassaras, I.; Argyrakis, P.; Barberopoulou, A.; Moshou, A. The July 20, 2017 M6.6 Kos Earthquake: Seismic and Geodetic Evidence for an Active North-Dipping Normal Fault at the Western End of the Gulf of Gökova (SE Aegean Sea). Pure Appl. Geophys. 2019, 176, 4177–4211. [Google Scholar] [CrossRef]
  33. Ganas, A.; Elias, P.; Briole, P.; Cannavo, F.; Valkaniotis, S.; Tsironi, V.; Partheniou, E.I. Ground Deformation and Seismic Fault Model of the M6.4 Durres (Albania) Nov. 26, 2019 Earthquake, Based on GNSS/INSAR Observations. Geosciences 2020, 10, 210. [Google Scholar] [CrossRef]
  34. Goldstein, R.M.; Werner, C.L. Radar interferogram filtering for geophysical applications. Geophys. Res. Lett. 1998, 25, 4035–4038. [Google Scholar] [CrossRef] [Green Version]
  35. Briole, P. Modelling of earthquake slip by inversion of GNSS and InSAR data assuming homogenous elastic medium. Zenodo 2017, 1. [Google Scholar] [CrossRef]
  36. Wells, D.L.; Coppersmith, K.L. New Empirical Relationships among Magnitude, Rupture Length, Rupture Width, Rupture Area and Surface Displacement. Bull. Seismol. Soc. Am. 1994, 84, 974–1002. [Google Scholar]
  37. Thingbaijam, K.K.S.; Martin Mai, P.; Goda, K. New empirical earthquake source-scaling laws. Bull. Seismol. Soc. Am. 2017, 107, 2225–2246. [Google Scholar] [CrossRef] [Green Version]
  38. Ganas, A. NOAFAULTS KMZ layer. Zenodo 2019, 2. [Google Scholar] [CrossRef]
  39. Bacopoulos, I. Lithostratigraphy of the Ionian Basin in the Southern Part of Epirus Related to the Migration and Entrapment of its Hydrocarbons. Ph.D. Thesis, University of Athens, Athens, Greece, 2006. [Google Scholar]
  40. Perrier, R.; Koukouzas, C. Geological Map of Greece in Scale 1:50000, Map Sheet Parga; Institute of Geology and Mineral Exploration: Athens, Greece, 1969. [Google Scholar]
  41. Provost, L.; Scotti, O. QUake-MD: Open-Source Code to Quantify Uncertainties in Magnitude–Depth Estimates of Earthquakes from Macroseismic Intensities. Seismol. Res. Lett. 2020, 91, 2520–2530. [Google Scholar] [CrossRef]
  42. Locati, M.; Rovida, A.; Albini, P.; Stucchi, M. The AHEAD Portal: A Gateway to European Historical Earthquake Data. Seismol. Res. Lett. 2014, 85, 727–734. [Google Scholar] [CrossRef] [Green Version]
  43. Stucchi, M.; Rovida, A.; Gomez Capera, A.A.; Alexandre, P.; Camelbeeck, T.; Demircioglu, M.B.; Gasperini, P.; Kouskouna, V.; Musson, R.M.W.; Radulian, M.; et al. The SHARE European Earthquake Catalogue (SHEEC) 1000–1899. J. Seismol. 2013, 17, 523–544. [Google Scholar] [CrossRef] [Green Version]
  44. Bakun, W.H.; Scotti, O. Regional intensity attenuation models for France and the estimation of magnitude and location of historical earthquakes. Geophys. J. Int. 2006, 164, 596–610. [Google Scholar] [CrossRef] [Green Version]
  45. Baumont, D.; Manchuel, K.; Traversa, P.; Durouchoux, C.; Nayman, E.; Ameri, G. Intensity predictive attenuation models calibrated in Mw for metropolitan France. Bull. Earthq. Eng. 2018, 16, 2285–2310. [Google Scholar] [CrossRef]
  46. Ganas, A.; Drakatos, G.; Rontogianni, S.; Tsimi, C.; Petrou, P.; Papanikolaou, M.; Argyrakis, P.; Boukouras, K.; Melis, N.; Stavrakakis, G. NOANET: The new permanent GPS network for Geodynamics in Greece. Eur. Geophys. Union Geophys. Res. Abstr. 2008, 10, 43–80. [Google Scholar]
  47. Ganas, A.; Marinou, A.; Anastasiou, D.; Paradissis, D.; Papazissi, K.; Tzavaras, P.; Drakatos, G. GPS-derived estimates of crustal deformation in the central and north Ionian Sea, Greece: 3-yr results from NOANET continuous network data. J. Geodyn. 2013, 67, 62–71. [Google Scholar] [CrossRef]
  48. Zumberge, J.F.; Heflin, M.B.; Jefferson, D.C.; Watkins, M.M.; Webb, F.H. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. Space Phys. 1997, 102, 5005–5017. [Google Scholar] [CrossRef] [Green Version]
  49. Bertiger, W.; Desai, S.D.; Haines, B.; Harvey, N.; Moore, A.W.; Owen, S.; Weiss, J.P. Single receiver phase ambiguity resolution with GPS data. J. Geod. 2010, 84, 327–337. [Google Scholar] [CrossRef]
  50. Métois, M.; D’Agostino, N.; Avallone, A.; Chamot-Rooke, N.; Rabaute, A.; Duni, L.; Kuka, K.; Koci, R.; Georgiev, I. Insights on continental collisional processes from GPS data: Dynamics of the peri-Adriatic belts. J. Geophys. Res. Solid Earth 2015, 120, 8701–8719. [Google Scholar] [CrossRef] [Green Version]
  51. Ntokos, D.; Lykoudi, E.; Rondoyanni, T. Geomorphic analysis in areas of low-rate neotectonic deformation: South Epirus (Greece) as a case study. Geomorphology 2016, 263, 156–169. [Google Scholar] [CrossRef]
  52. Van Hinsbergen, D.J.J.; Langereis, C.G.; Meulenkamp, J.E. Revision of the timing, magnitude and distribution of Neogene rotations in the western Aegean region. Tectonophysics 2005, 396, 1–34. [Google Scholar] [CrossRef]
  53. The Institute of Engineering Seismology and Earthquake Engineering. Preliminary Report on the 15/10/2016 Ioannina M5.5 Earthquake; Institute of Engineering Seismology and Earthquake Engineering: Thessaloniki, Greece, 2016; p. 13. (In Greek) [Google Scholar]
  54. Pavlides, S.; Ganas, A.; Papathanasiou, G.; Valkaniotis, S.; Thomaidou, E.; Georgiadis, G.; Sboras, S.; Chatzipetros, A. Geological-seismotectonic study of the wider area of Ioannina. In Proceedings of the Tectonics & Structural Geology Committee of the G.S.G. 1st TSG Meeting, Athens, Greece, 6 December 2016. [Google Scholar]
  55. Pavlides, S.; Ganas, A.; Chatzipetros, A.; Sboras, S.; Valkaniotis, S.; Papathanassiou, G.; Thomaidou, E.; Georgiadis, G. Geological and seismotectonic characteristics of the broader area of the 15 October 2016, earthquake (Ioannina, Greece). Eur. Geophys. Union Geophys. Res. Abstracts 2017, 19, 18135. [Google Scholar]
Geosciences 10 00454 g001 550
Figure 1. Map of Epirus (A) showing active fault traces (black lines with ticks on the overriding side), Global Navigation Satellite System (GNSS) stations (blue triangles) and epicentres determined for the 21 March 2020 Mw = 5.6 earthquake. Panel (B) shows the study area in the NW corner of Greece. Panel (C) shows the relocated epicentre of the mainshock (this study; white star) and its aftershocks (red circles; period 20 March 2020–23 May 2020). Fault traces modified after [16,17]. The black line between the Paxoi and Corfu islands indicates the trace of the Ionian thrust (ticks on the overriding side).
Figure 1. Map of Epirus (A) showing active fault traces (black lines with ticks on the overriding side), Global Navigation Satellite System (GNSS) stations (blue triangles) and epicentres determined for the 21 March 2020 Mw = 5.6 earthquake. Panel (B) shows the study area in the NW corner of Greece. Panel (C) shows the relocated epicentre of the mainshock (this study; white star) and its aftershocks (red circles; period 20 March 2020–23 May 2020). Fault traces modified after [16,17]. The black line between the Paxoi and Corfu islands indicates the trace of the Ionian thrust (ticks on the overriding side).
Geosciences 10 00454 g001
Geosciences 10 00454 g002 550
Figure 2. Distributions of location uncertainties and other statistics for the 2020 earthquake sequence in Kanallaki: (a) Travel-time root mean square (RMS) error, (b) horizontal (ERX, ERY) and vertical (ERZ) location errors, (c) relocated focal depths, (d) azimuthal gap, and (e) epicentral distance to the closest station with available arrival-time data.
Figure 2. Distributions of location uncertainties and other statistics for the 2020 earthquake sequence in Kanallaki: (a) Travel-time root mean square (RMS) error, (b) horizontal (ERX, ERY) and vertical (ERZ) location errors, (c) relocated focal depths, (d) azimuthal gap, and (e) epicentral distance to the closest station with available arrival-time data.
Geosciences 10 00454 g002
Geosciences 10 00454 g003 550
Figure 3. Relief map showing locations of epicentres (solid circles) of the 2020 Kanallaki earthquake sequence (a) before and (b) after relocation with HypoDD. Colours correspond to the focal depths. The star represents the epicentre of the Mw = 5.6 mainshock of 21 March 2020.
Figure 3. Relief map showing locations of epicentres (solid circles) of the 2020 Kanallaki earthquake sequence (a) before and (b) after relocation with HypoDD. Colours correspond to the focal depths. The star represents the epicentre of the Mw = 5.6 mainshock of 21 March 2020.
Geosciences 10 00454 g003
Geosciences 10 00454 g004 550
Figure 4. Map of west Epirus showing active fault traces (black lines with ticks on the overriding side (modified after [16,17]) and the epicentral area of the 1895 event (red ellipse). The instrumental seismicity data for Mw > 5.2 [26] is shown as solid circles. Dotted blue areas mark swamps and flooded fluvial areas during the early 20th century, while the used settlement names are the original ones mentioned in the 1895 earthquake reports.
Figure 4. Map of west Epirus showing active fault traces (black lines with ticks on the overriding side (modified after [16,17]) and the epicentral area of the 1895 event (red ellipse). The instrumental seismicity data for Mw > 5.2 [26] is shown as solid circles. Dotted blue areas mark swamps and flooded fluvial areas during the early 20th century, while the used settlement names are the original ones mentioned in the 1895 earthquake reports.
Geosciences 10 00454 g004
Geosciences 10 00454 g005 550
Figure 5. Descending interferogram using DIAPASON. Solid stars indicate earthquake epicentres (green for EMSC, white for NOA relocated). Black rectangle is the preferred fault model from the geodetic inversion. Beachball indicates the NOA focal mechanism (moment tensor solution; compressional quadrant is shown in blue). White lines are active faults (ticks on the upthrown side). Colour scale (2π) shows one cycle of phase difference between a pair of images relative to the satellite (line-of-sight). A displacement fringe of at least 2.8 cm along the satellite line of sight is observed in the wider Kanallaki area.
Figure 5. Descending interferogram using DIAPASON. Solid stars indicate earthquake epicentres (green for EMSC, white for NOA relocated). Black rectangle is the preferred fault model from the geodetic inversion. Beachball indicates the NOA focal mechanism (moment tensor solution; compressional quadrant is shown in blue). White lines are active faults (ticks on the upthrown side). Colour scale (2π) shows one cycle of phase difference between a pair of images relative to the satellite (line-of-sight). A displacement fringe of at least 2.8 cm along the satellite line of sight is observed in the wider Kanallaki area.
Geosciences 10 00454 g005
Geosciences 10 00454 g006 550
Figure 6. Ascending interferogram. Solid stars indicate earthquake epicentres (green for EMSC, white for NOA relocated). The black rectangle is the preferred fault model from the geodetic inversion. Beachball indicates the NOA focal mechanism (moment tensor solution; compressional quadrant is shown in blue). White lines are active faults (ticks on the upthrown side).
Figure 6. Ascending interferogram. Solid stars indicate earthquake epicentres (green for EMSC, white for NOA relocated). The black rectangle is the preferred fault model from the geodetic inversion. Beachball indicates the NOA focal mechanism (moment tensor solution; compressional quadrant is shown in blue). White lines are active faults (ticks on the upthrown side).
Geosciences 10 00454 g006
Geosciences 10 00454 g007 550
Figure 7. Location (UTM zone 34 coordinates in km) of the picked fringes on the descending (top) and ascending (bottom) interferogram. Ground deformation extends to approximately 14 km (E-W) and 17 km (N-S) for the ascending interferogram and it is much more localised for the ascending one.
Figure 7. Location (UTM zone 34 coordinates in km) of the picked fringes on the descending (top) and ascending (bottom) interferogram. Ground deformation extends to approximately 14 km (E-W) and 17 km (N-S) for the ascending interferogram and it is much more localised for the ascending one.
Geosciences 10 00454 g007
Geosciences 10 00454 g008 550
Figure 8. Scatterplots showing fit of the data to the reverse fault model (open circles). The mean scatter between data and model is 3.3 mm for the 86-descending data (top) and 3.9 mm for the 86-ascending data (bottom). The numerical values are in the Supplementary Table S2.
Figure 8. Scatterplots showing fit of the data to the reverse fault model (open circles). The mean scatter between data and model is 3.3 mm for the 86-descending data (top) and 3.9 mm for the 86-ascending data (bottom). The numerical values are in the Supplementary Table S2.
Geosciences 10 00454 g008
Geosciences 10 00454 g009 550
Figure 9. Map (a) showing surface projection of the fault plane (yellow rectangle; length 4.7 km, width 4.7 km), (b) cross-section along the yellow line of (a). Subsurface location of the fault (black line with arrows indicating the relative motion of the two blocks) inferred from the modelling of the descending interferogram. The scale is the same in both horizontal and vertical axes and the topography is not exaggerated.
Figure 9. Map (a) showing surface projection of the fault plane (yellow rectangle; length 4.7 km, width 4.7 km), (b) cross-section along the yellow line of (a). Subsurface location of the fault (black line with arrows indicating the relative motion of the two blocks) inferred from the modelling of the descending interferogram. The scale is the same in both horizontal and vertical axes and the topography is not exaggerated.
Geosciences 10 00454 g009
Geosciences 10 00454 g010 550
Figure 10. (a) Simplified geological map, modified after [14,16,40]. Red diamonds mark the locations of co-seismic landslides for the 21 March 2020 earthquake, identified using Sentinel-2 optical imagery (see Table S5 for coordinates). (b) Simplified section (not to scale) of the crustal structure beneath the Parga–Kanallaki area (azimuth of the section N245° E). Red line (with arrow on the overthrusting side) indicates the seismic fault.
Figure 10. (a) Simplified geological map, modified after [14,16,40]. Red diamonds mark the locations of co-seismic landslides for the 21 March 2020 earthquake, identified using Sentinel-2 optical imagery (see Table S5 for coordinates). (b) Simplified section (not to scale) of the crustal structure beneath the Parga–Kanallaki area (azimuth of the section N245° E). Red line (with arrow on the overthrusting side) indicates the seismic fault.
Geosciences 10 00454 g010
Geosciences 10 00454 g011 550
Figure 11. (Left; a,c) Intensity Prediction Equations (IPE) [45] fit on intensity observations (a) from the AHEAD database [42] (accessed on 14 September, 2020) and (c) from other sources, after the applied inversion using the QUake-MD code [41], considering as a fixed macroseismic epicentre (a,b) the SHEEC [43] solution (39.385° N, 20.519° E), or (c,d) the location of Dragani village, with Io = 11 (39.4333° N, 20.4345° E). (Right; b,d) Magnitude (M) and focal depth (H) solution space for the combined inversion results using the IPEs of [44,45] for the intensity data presented in the panels (a) and (c) for diagrams (b) and (d), respectively. Values with increased weight indicate M = 5.8 ± 0.3 and M = 5.6 ± 0.2 for each case, with a shallow focal depth H~4 km and H~1 km, respectively.
Figure 11. (Left; a,c) Intensity Prediction Equations (IPE) [45] fit on intensity observations (a) from the AHEAD database [42] (accessed on 14 September, 2020) and (c) from other sources, after the applied inversion using the QUake-MD code [41], considering as a fixed macroseismic epicentre (a,b) the SHEEC [43] solution (39.385° N, 20.519° E), or (c,d) the location of Dragani village, with Io = 11 (39.4333° N, 20.4345° E). (Right; b,d) Magnitude (M) and focal depth (H) solution space for the combined inversion results using the IPEs of [44,45] for the intensity data presented in the panels (a) and (c) for diagrams (b) and (d), respectively. Values with increased weight indicate M = 5.8 ± 0.3 and M = 5.6 ± 0.2 for each case, with a shallow focal depth H~4 km and H~1 km, respectively.
Geosciences 10 00454 g011
Geosciences 10 00454 g012 550
Figure 12. Graph showing convergence rate (in mm/yr) with respect to the Apulian block along a profile oriented N228° E. The reference of the convergence (zero value in Y axis) is the Apulian block. The sign reversal declares the two sides across the Apulian front (see red line in Figure 13). Red star indicates the projection of the 21 March 2020 earthquake on this profile.
Figure 12. Graph showing convergence rate (in mm/yr) with respect to the Apulian block along a profile oriented N228° E. The reference of the convergence (zero value in Y axis) is the Apulian block. The sign reversal declares the two sides across the Apulian front (see red line in Figure 13). Red star indicates the projection of the 21 March 2020 earthquake on this profile.
Geosciences 10 00454 g012
Geosciences 10 00454 g013 550
Figure 13. GNSS station velocities with respect to the Apulian block, assuming an ITRF2014 velocity of 25.1 mm yr−1 (Veast) and 18.4 mm yr−1 (Vnorth) for this Apulian block at the coordinate 20.0° E, 39.0° N (error ellipses are at 95% confidence interval). The shaded rectangle denotes the wide deformation zone along the Apulia–Eurasia collision front, determined at this study. Beachballs indicate focal mechanisms referring to the 2016 Ioannina event (red star) and the 2020 Kanallaki event (yellow star; NOA database (https://bbnet.gein.noa.gr/HL/index.php). White line between Paxoi island and Corfu indicates the trace of the Ionian thrust (ticks on the overriding side). Offshore red line indicates the plate boundary Apulia–Eurasia.
Figure 13. GNSS station velocities with respect to the Apulian block, assuming an ITRF2014 velocity of 25.1 mm yr−1 (Veast) and 18.4 mm yr−1 (Vnorth) for this Apulian block at the coordinate 20.0° E, 39.0° N (error ellipses are at 95% confidence interval). The shaded rectangle denotes the wide deformation zone along the Apulia–Eurasia collision front, determined at this study. Beachballs indicate focal mechanisms referring to the 2016 Ioannina event (red star) and the 2020 Kanallaki event (yellow star; NOA database (https://bbnet.gein.noa.gr/HL/index.php). White line between Paxoi island and Corfu indicates the trace of the Ionian thrust (ticks on the overriding side). Offshore red line indicates the plate boundary Apulia–Eurasia.
Geosciences 10 00454 g013
Geosciences 10 00454 g014 550
Figure 14. Velocity vectors of the GPS stations around Kanallaki, assigning zero motion to GARD. The shaded rectangle denotes the wide deformation zone along the Apulia–Eurasia collisional front, determined at this study. Beachballs indicate focal mechanisms referring to the 2016 Ioannina event (red star) and the 2020 Kanallaki event (yellow star; NOA database (https://bbnet.gein.noa.gr/HL/index.php). White line between Paxoi island and Corfu indicates the trace of the Ionian thrust (ticks on the overriding side). The offshore red line is the plate boundary Apulia–Eurasia.
Figure 14. Velocity vectors of the GPS stations around Kanallaki, assigning zero motion to GARD. The shaded rectangle denotes the wide deformation zone along the Apulia–Eurasia collisional front, determined at this study. Beachballs indicate focal mechanisms referring to the 2016 Ioannina event (red star) and the 2020 Kanallaki event (yellow star; NOA database (https://bbnet.gein.noa.gr/HL/index.php). White line between Paxoi island and Corfu indicates the trace of the Ionian thrust (ticks on the overriding side). The offshore red line is the plate boundary Apulia–Eurasia.
Geosciences 10 00454 g014
Table
Table 1. Parameters and focal mechanisms of the most important events of the 2020 Kanallaki earthquake sequence (by using ISOLA software). All angles are in degrees.
Table 1. Parameters and focal mechanisms of the most important events of the 2020 Kanallaki earthquake sequence (by using ISOLA software). All angles are in degrees.
dd/mm/yyyy
HH:MM		EpicentreHypocentral Depth (km)MwStrike/Dip/Rake 1Strike/Dip/Rake 2P-axis Azimuth/PlungeT-axis Azimuth/Plunge
20 March 2020 21:3839.3123N 20.5650E14.74.2133/56/82328/35/102229/1014/77
21 March 2020 00:4939.3265N 20.5215E7.95.5315/33/92132/57/89223/1238/78
21 March 2020 00:4939.3025N 20.5829E
(re-located)		6.45.6129/59/72341/36/117232/12358/71
23 March 2020 04:4139.3027N 20.5966E14.13.8293/60/9199/82/149250/15152/27
25 March 2020 09:4939.2757N 20.6218E13.43.9141/63/74353/31/118242/1721/68
Table
Table 2. 1-D P-wave velocity model for this region [21].
Table 2. 1-D P-wave velocity model for this region [21].
LayerVP (km/s)Ceiling Depth (km)
14.60.0
25.77.0
36.111.0
46.311.5
56.516.5
67.335.0
78.080.0
Table
Table 3. Focal mechanisms of the 21 March 2020 mainshock calculated by various agencies (GCMT: Global Centroid Moment Tensor; GFZ: GeoForschungsZentrum; IPGP: Institut de Physique du Globe de Paris; USGS United States Geological Survey; NOA: National Observatory of Athens; AUTH: Aristotle University of Thessaloniki; INGV: Instituto Nazionale di Geofisica e Vulcanologia. NP stands for nodal plane.
Table 3. Focal mechanisms of the 21 March 2020 mainshock calculated by various agencies (GCMT: Global Centroid Moment Tensor; GFZ: GeoForschungsZentrum; IPGP: Institut de Physique du Globe de Paris; USGS United States Geological Survey; NOA: National Observatory of Athens; AUTH: Aristotle University of Thessaloniki; INGV: Instituto Nazionale di Geofisica e Vulcanologia. NP stands for nodal plane.
AgencyStrike
NP1		Dip
NP1		Rake
NP1		Strike
NP2		Dip
NP2		Rake
NP2		Centroid DepthMoment
°°°°°°km× 1017 N m
GCMT33838122120596813.64.93
GFZ31837901375289204.10
IPGP331351001395683106.61
USGS3175287142399313.54.04
NOA3153392132578982.38
NOA revised (this study)34136117129597282.86
AUTH33638105137537873.82
INGV33342107131507514.24.80
average32939103133538112
standard deviation106126684
Table
Table 5. Picked values on the ascending interferogram. See Figure 7 for locations.
Table 5. Picked values on the ascending interferogram. See Figure 7 for locations.
Pixel ValueNumber of Available PixelsNumber of Selected PixelsDisplacement in the Line of Sight (mm)
966634
160242027
224422020
32402013
96177206
Total28986
Table
Table 6. Range of variation of the 3D location of fault-top centre, geodetic moment tensor, and fault length when changing the zero value of the interferogram. Easting and Northing refer to UTM coordinates (zone 34).
Table 6. Range of variation of the 3D location of fault-top centre, geodetic moment tensor, and fault length when changing the zero value of the interferogram. Easting and Northing refer to UTM coordinates (zone 34).
Max. l.o.s. Change Fault LengthGeodetic Moment Tensor
EastingNorthingDepth× 1017 N m
kmkmkmkm
28 mm465.454344.387.294.322.27
31.5 mm465.444344.417.995.72.99
Table
Table 7. Parameters of the best fitting fault model assuming fixed values for strike = 329°, dip = 39°, rake = 103°, and fault width = 4.7 km. The fault tip is located at a 7 km depth.
Table 7. Parameters of the best fitting fault model assuming fixed values for strike = 329°, dip = 39°, rake = 103°, and fault width = 4.7 km. The fault tip is located at a 7 km depth.
Centre of Upper Edge of the FaultFault Length
EastNorthVertical
UTM34 (km)UTM34 (km)kmkm
464.764344.287.04.7
Table
Table 8. Velocities of several permanent GPS stations located in north-western Greece (Figure 1b) with longitude between 19°–21° and latitude between 39°–40°. The velocities are plotted in Figure 13 (with respect to rigid Apulia) and Figure 14 (w.r.t. station GARD). See Figure 1 for locations.
Table 8. Velocities of several permanent GPS stations located in north-western Greece (Figure 1b) with longitude between 19°–21° and latitude between 39°–40°. The velocities are plotted in Figure 13 (with respect to rigid Apulia) and Figure 14 (w.r.t. station GARD). See Figure 1 for locations.
SiteNetworkLongLatvEvNvE_ApuliavN_Apulia
°°mm yr−1mm yr−1mm yr−1mm yr−1
KERKHxSmart19.873439.493721.1 ± 0.314.7 ± 0.3−4.0−3.7
KERUTree19.915239.619122.1 ± 0.414.5 ± 0.4−3.0−3.9
KASINOA19.935539.746420.3 ± 0.314.0 ± 0.3−4.8−4.4
PAXOHxSmart20.163939.210824.3 ± 0.416.4 ± 0.4−0.8−2.0
IGOUHxSmart20.262739.510021.2 ± 0.413.6 ± 0.3−3.9−4.8
HGOUTree20.267939.492721.3 ± 0.414.2 ± 0.4−3.8−4.2
GARDTree20.571039.350621.1 ± 0.413.2 ± 0.5−4.0−5.2
IOANHxSmart20.850539.664121.7 ± 0.311.0 ± 0.3−3.4−7.4
IOAUTree20.854139.654922.0 ± 0.510.2 ± 0.4−3.1−8.2
ART1HxSmart20.933339.152917.3 ± 0.69.1 ± 0.6−7.8−9.3
ARTAHxSmart20.991739.158818.7 ± 0.310.8 ± 0.3−6.4−7.6
Table
Table 9. Values of the convergence rate of the stations of Epirus with Apulia using the azimuth N228°E for the convergence axis.
Table 9. Values of the convergence rate of the stations of Epirus with Apulia using the azimuth N228°E for the convergence axis.
StationConvergence towards ApuliaUncertainty
mm yr−1mm yr−1
KERK5.40.3
KERU4.80.4
KASI6.50.3
PAXO1.90.4
IGOU6.10.4
HGOU5.60.4
GARD6.50.5
IOAN7.50.3
IOAU7.80.5
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Valkaniotis, S.; Briole, P.; Ganas, A.; Elias, P.; Kapetanidis, V.; Tsironi, V.; Fokaefs, A.; Partheniou, H.; Paschos, P. The Mw = 5.6 Kanallaki Earthquake of 21 March 2020 in West Epirus, Greece: Reverse Fault Model from InSAR Data and Seismotectonic Implications for Apulia-Eurasia Collision. Geosciences 2020, 10, 454. https://doi.org/10.3390/geosciences10110454

AMA Style

Valkaniotis S, Briole P, Ganas A, Elias P, Kapetanidis V, Tsironi V, Fokaefs A, Partheniou H, Paschos P. The Mw = 5.6 Kanallaki Earthquake of 21 March 2020 in West Epirus, Greece: Reverse Fault Model from InSAR Data and Seismotectonic Implications for Apulia-Eurasia Collision. Geosciences. 2020; 10(11):454. https://doi.org/10.3390/geosciences10110454

Chicago/Turabian Style

Valkaniotis, Sotiris, Pierre Briole, Athanassios Ganas, Panagiotis Elias, Vassilis Kapetanidis, Varvara Tsironi, Anna Fokaefs, Helena Partheniou, and Panagiotis Paschos. 2020. "The Mw = 5.6 Kanallaki Earthquake of 21 March 2020 in West Epirus, Greece: Reverse Fault Model from InSAR Data and Seismotectonic Implications for Apulia-Eurasia Collision" Geosciences 10, no. 11: 454. https://doi.org/10.3390/geosciences10110454

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop