Factors Affecting the Formation and Evolution of Permafrost and Stability Zone of Gas Hydrates: Case Study of the Laptev Sea

Abstract

The key factors controlling the formation and dynamics of relicpermafrost and the conditions for the stability of associated gas hydrates have been investigated using numerical modeling in this work. A comparison was made between two scenarios that differed in the length of freezing periods and corresponding temperature shifts to assess the impact on the evolution of the permafrost–hydrate system and to predict its distribution and geometry. The simulation setup included the specific heat of gas hydrate formation and ice melting. Significantly, it was shown that the paleoscenario and heat flows affect the formation of permafrost and the conditions for gas hydrate stability. In the Laptev Sea, the minimum and maximum predicted preservation times for permafrost are 9 and 36.6 kyr, respectively, whereas the presence of conditions consistent with methane hydrate stability at the maximum permafrost thickness is possible for another 25.9 kyr. The main factors influencing the rate of permafrost degradation are the heat flow and porosity of frozen sediments. The rates of permafrost thawing are estimated to be between 1 and 3 cm/yr. It is revealed that the presence of gas hydrates slows the thawing of the permafrost and feeds back to prolong the conditions under which gas hydrates are stable.

1. Introduction

Gas hydrates, an ice-like form of water and concentrated gas that is stable at low temperatures and moderate pressures, often occur within and beneath permafrost. Thus, the study of subsea permafrost is closely related to the problem of associated cryogenic submarine gas hydrates. In turn, cryogenic gas hydrates are nearly always associated with permafrost, since they formed many millennia ago when the bottom of the shallow Arctic seas was subaerially exposed and frozen. Here, we refer to relic subsea permafrost (RSP) as representing ice-bearing sediments formed during the glacial intervals of the Quaternary, when lower sea levels exposed the shelves and mean winter temperatures were well below contemporary values [1,2,3,4]. As sea levels rose during the Holocene, the uppermost ice-rich rocks were thermally abraded and partially washed-out [1,5,6].

Both the low temperatures and the presence of RSP have created opportunities for gas hydrate formation. In deep water, gas hydrate formation requires high pressure, but the unique combination of permafrost and low temperatures beneath the shallow Arctic seas also permits the formation of gas hydrates. The RSP on the Eastern Siberian Arctic Shelf (ESAS) is poorly studied due to a lack of evidence about its distribution and thickness as well as the related physical parameters of the subsoil. The geothermal field of the ESAS, for the instance, is underexplored (direct measurements are sporadic). Thus, gas hydrates within the ESAS are assumed based on geomorphological, climatic and thermo-baric prerequisites and by analogy with gas hydrates found in permafrost studied in the seas of the Canadian and American Arctic [7,8,9]. To date, the only direct evidence of gas hydrate presence in the Eurasian Arctic is that recently discovered in the seeps of the East Siberian Sea [10].

Difficulties in identifying hydrate-bearing sediments in permafrost are due to the similarity of the physical properties of methane hydrate and ordinary hexagonal ice. The large amount of high-resolution seismic activity acquired within the Arctic shows that, due to the presence of ice-bonded permafrost, cryogenic factors often mask both real geological structures and hydrate-induced anomalies. The recognition of hydrate-bearing sediments within the RSP by remote methods and the lack of boreholes are among the pressing problems of studying ESAS. For these reasons, mathematical modeling in most cases is the only way to determine the distribution and evolution of RSP and the associated gas hydrate stability zone (GHSZ). Past permafrost maps (mainly based on the results of numerical models) provide important information about the seaward extent of subsea permafrost and possible relic gas hydrates beneath the ESAS [1,2,11,12,13,14,15]. These maps have advanced our understanding of the state and distribution of permafrost and related GHSZ on a broad scale. More recent numerical models of subsea permafrost vary significantly depending on the physical assumptions regarding the paleogeographic scenarios, geological structure, sediment thermal and physical properties, initial temperature distribution and heat flow (HF) in the past [16,17,18,19]. Scarce field observations show that still not all models adequately reproduce the diversity of RSP. Another issue is that when mathematically evaluating relic permafrost, it is essential to consider the possible presence of gas hydrates that may influence the occurrence and persistence of permafrost. The mutual influences of permafrost and hydrates on one another, as well as the consequences of the impact of warming on the permafrost–hydrate system, are currently considered only in general terms. However, the forecast of hydrate destabilization as a result of melting permafrost requires a more detailed study.

The formation and dissociation of cryogenic gas hydrates, in turn, are among the most discussed issues in Quaternary geology, initiated by the development of offshore gas fields and the necessity for related infrastructure. Indeed, the presence of unstable underwater permafrost and associated gas hydrates in the upper part of the sediment column can lead to engineering risks. The degradation of submarine ice-bonded layers also has implications for the potential release of methane from the seafloor (permafrost thawing and gas hydrate destabilization are possibly associated with increased methane flux into the atmosphere) [20,21]. As for the high potential of gas hydrates as a fuel for the future, it has been (and remains) the subject of continued interest for several decades. Thus, the relevance of studying RSP and hydrate spatial distribution on the Arctic shelves is due to both resource and environmental issues.

Our study aims to consider the factors that control the propagation of submarine relic permafrost and permafrost-associated GHSZ over the area and to predict their evolution over time using a numerical simulation. We tried to assess the impact of such factors as (1) a paleogeographic scenario, involving the duration of subaerial freezing and the jump in temperatures of the subaquatic and subaerial periods; (2) heat flow, preventing freezing and contributing to the degradation of RSP and GHSZ at the base of both zones; and (3) gas hydrate content.

1.1. Geological Settings

The Laptev Sea is bound by the Taimyr Peninsula to the west and the Novosibirsk Islands to the east. The Laptev Sea shelf has a flat bottom and is shallow. Its water depth does not exceed 100 m even in rifts, which are considered to be centers of tectonic activity and manifestations of modern volcanism [22]. The reason is that Late Mesozoic–Cenozoic and present-day river run-off has caused large masses of sedimentary material, filling rift valleys and forming large sediment fans. The latest tectonic movements in the region were mostly descending and were accompanied by compensatory sediment accumulation.

Within the greater part of the Laptev Sea, ice sheets in cryochrones were absent. The geological structure of the region is extremely complex; the ensemble of tectonic structures of different ages includes the Siberian platform, the Laptev Sea rift system and the system of banks and shoals [22,23,24]. It is believed that the Gakkel Ridge, which represents a boundary between the North America and Eurasia Plates in the Eurasia Basin, propagates under the Laptev Sea and has resulted in the development of geomorphological structures that comprise the Laptev Rift System, characterized by a high heat flow [25].

The Laptev Sea shelf has been studied by seismic methods, which suggest the sea to be the most promising area for hydrocarbon prospecting in the northern part of East Siberia [26,27,28,29]. This is evident from the significant thickness of its sedimentary cover (up to 15 km) [30] and the presence of large troughs, swells, and rift structures [27,30,31,32]. Using seismic data, a number of large offshore sedimentary basins with significant estimated hydrocarbon potential were revealed on the Laptev shelf. Unfortunately, no offshore exploration wells have been drilled there so far; thus, all the information on the geological settings is based on the marine seismic profiles and knowledge of the adjoining near-coastal areas. Seismoacoustic studies show the presence of so-called ‘permafrost tables’—acoustic signs of the top of the underwater permafrost [33].

1.2. Permafrost Occurrence and Distribution

Available data on the distribution of subsea permafrost within the Laptev Sea are derived mostly from thermal modeling [1,2,11,14,16,18,19,20], geophysical data [27,33] and some geological onshore data [1,34,35]. Some recent near-shore drilling results [20,36,37,38] are available as well. There are minimal data regarding the top of the RSP observed during drilling, coring and seismic survey. However, there are no actual data on the RSP base.

The thickness of the permafrost and the associated temperature field are strongly influenced by the ground surface temperature history during the past. Important considerations include sea level regressions and transgressions, whose durations vary considerably depending on which paleogeographic model is used. The duration of freezing during regressions and thawing during the transgressions, as well as the magnitude of the temperature jump (the temperature difference between the temperature of the sediment surface in the subaquatic and subaerial conditions), determines the strength of the subaerial freezing of sediments and, as a consequence, the duration of RSP and GHSZ. Besides sea-level fluctuations, the air and bottom water temperatures, the geothermal heat flow and interstitial water salinity are the next most important factors influencing the distribution of submarine permafrost [39,40,41]. At present, the thermal state of subsea permafrost is controlled by seawater temperature, sediment salinity and by the HF from the Earth’s interior. The temperature of seawater and shallow sediments at the Laptev Sea is mostly negative and varies from −0.5 to −2.0 °C [42], which favors RSP preservation. Due to these negative water temperatures, either the RSP does not thaw or its degradation happens rather slowly.

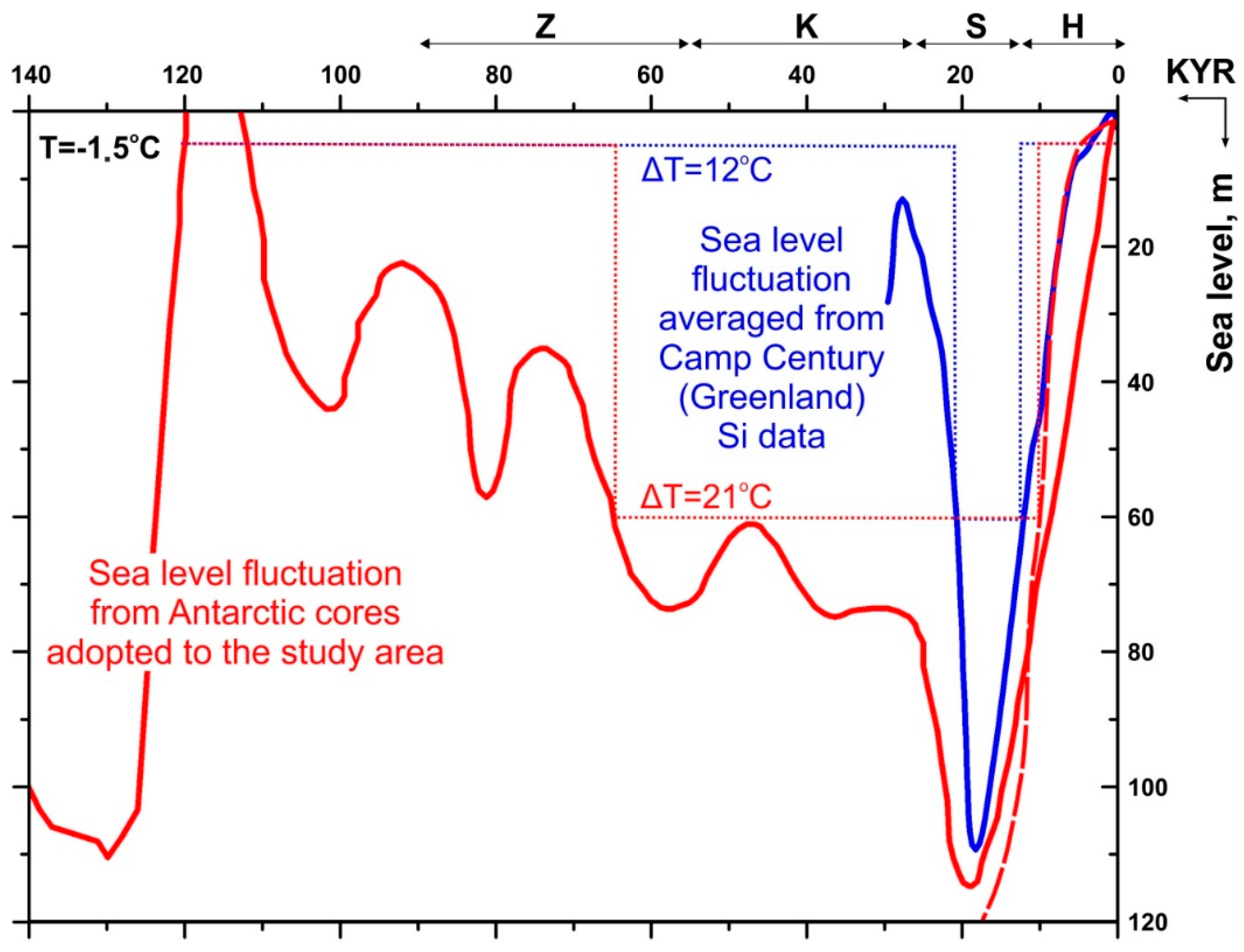
1.3. ESAS Paleoenvironment

The leading role in the formation of the paleogeographic setting is played by sea-level fluctuations. The result of these fluctuations is the repetitive change of regressive and transgressive cycles [1,2,3,43,44,45]. Fluctuations of the sea level on geological timescales determine the processes associated with changes in the mass and volume of water in the ocean, which, in turn, are caused by changes in the volume of the oceanic depressions due to tectonic movements. Thus, the main contribution is attributed to neotectonic and isostatic movements of the Earth’s crust, as well as climatically-caused changes of oceanic water. In [46], the authors reconstructed sea-level variation and shoreline migration in the Laptev Sea, taking into account the processes of isostatic adjustment, and revealed that the application of the eustatic sea-level curve is a valid first-order approximation for reconstructing the shoreline position from the last glacial maximum to the present, whereas sea-level heights away from the shoreline inferred from the eustatic sea-level curve differ markedly from glacial isostatic adjustment predictions based on simulations.

Some studies based on seismic data have concluded that the influence of tectonics—in particular, the Gakkel Ridge—on Laptev Sea seismicity is insignificant [24,32], and thus this factor can be neglected. However, there is evidence that the features of the permafrost deposits within the Laptev Sea are due to the structure of the Earth’s crust. The composition of perennially frozen deposits holds information about the paleo-environment during and following deposition. For instance, the well-studied terraces along the coastline of the Laptev Sea and the deposits of the ice complex represented in them are manifestations of both tectonic movements and eustatic sea-level fluctuations [1,34,35,47]. This ice complex that formed in non-glaciated Beringia between approximately 60 and 12 kyr before present (BP) was later stratigraphically named Yedoma [48,49]. It should be noted that the consideration of the influence of tectonics on sea-level fluctuations using numerical modeling is carried out by differentiating the HF values by the age of tectonic structures. However, the contribution of vertical tectonic movements and thermal abrasion to the formation of the RSP has previously been taken into account [1].

These arguments and the absence of ice-sheets in the Laptev Sea region are the reasons why paleoclimate reconstructions are based mainly on eustatic changes in sea level. For example, Bauch et al. [50] and Nicolsky et al. [51] used the eustatic sea-level curves of Fairbanks [45] and Fleming et al. [43], respectively, to simulate sea-level changes in the Laptev Sea region.

Any permafrost map of the ESAS is simply a geothermal-based forecast that considers general cryogenic patterns, geological settings and paleogeographic scenarios of the Quaternary based on the calculations of the possible RSP distribution. The goal of the calculations is to obtain the time-dependence for the thickness of permafrost and the GHSZ by solving the non-steady-state Stefan problem. Usually, the models are based on the same climate reconstruction for the entire period or different ones for the corresponding epoch.

We took this approach further by comparing, according to the results of our modeling, two scenarios that differed in the duration of freezing periods (when paleoenvironments were subaerial) and temperature jumps (the maximum temperature shift required to preserve the ice complex), which had a large impact on the formation of permafrost in the Laptev Sea in the past.

In the history of permafrost formation on the Eurasian Arctic shelf and paleo shelf, three main stages can be distinguished: the Pleistocene transgression, the late Pleistocene regression (up to the Holocene) and the late Pleistocene–Holocene transgression. The first stage, covering the period from the Eopleistocene to the second half of the Late Pleistocene, was characterized mainly by unfavorable conditions for the formation of submarine permafrost due to extensive transgressions. However, while seawater in the western part of the Arctic penetrated far to the south, in the ESAS, there were large areas of paleoland, where a thick sequence of frozen rocks was formed [1].

The second stage was optimal for the deep freezing of almost the entire Eurasian Arctic shelf. Moreover, in the ESAS, over a large area adjacent to the Novosibirsk Islands, the southern coast of the Laptev Sea and the southwestern coast of the East Siberian Sea, freezing proceeded simultaneously with the accumulation of sediments and the formation of thick syngenetic veins of polygonal wedge ice. The overwhelming majority of frozen rocks existing outside the littoral zone are relics of this period [1]. This stage had the greatest impact on the formation of underwater permafrost in the Laptev Sea. During this time, the area of sea glaciation exceeded the area of continental glaciation nearly two-fold [52,53].

The third (and final) stage, which began about 19–18 thousand years ago, was characterized by a gradual change from subaerial to subaquatic conditions. The thermal abrasion and degradation of the frozen zone were the most important processes accompanying this transgression. These events also determined the peculiarities of Holocene sedimentation on the shelf. During the Holocene transgression, associated with the rapid eustatic rise of the sea level at an average rate of about 0.6 cm/year between 19–18 to 7–5 ka before present, thick sediment sequences that were different in origin and age were abraded and thermoabraded. The frozen strata, formed during subaerial freezing, were exposed to submergence [1]. These processes substantially affected the ESAS. After the subaerial submergence, frozen sediments underwent thawing from the bottom due to the influence of deep HF.

2. Materials and Methods

2.1. Considered Paleoenvironments

We adopted the second stage (Sartanian cooling) as the paleoscenario for the simulation since it was assumed that the influence of this particular period would dominate all previous climatic changes. This paleoscenario is referred to hereafter as Scenario 1. A curve of eustatic sea-level fluctuations during the last Sartanian glaciation in the Late Pleistocene from the Kemp Century (Greenland) from [1] (Figure 1) was used in Scenario 1.

A sea-level curve similar to that from [1] was used in [54,55] to simulate the freezing of the Laptev Sea shelf after the Kargan transgression; i.e., 25 kyr BP. The curve of eustatic sea-level variations for the last 140 kyr reconstructed from the Antarctic Vostok ice-core representing paleo records over the last 420 kyr [44] adjusted by the authors of the work presented in [45] was taken for Scenario 2 from the work presented in [2] (see Figure 1).

These two scenarios were chosen because of their large differences in regression periods and temperature shifts, providing extreme values to model the paleogeographic parameters used in our simulation.

The periods of drainage and flooding (i.e., freezing and thawing) for water depths from 10 to 90 m with a 10 m step were taken according to sea-level fluctuation patterns (see Figure 1), which differed greatly in the duration of subaerial freezing and the magnitude of the temperature change.

When reconstructing the paleoenvironment in the Laptev Sea, it was assumed that long-term temperature fluctuations would be synchronous. Therefore, it was accepted that the regionally-adjusted paleotemperature [45] described the dynamics of the soil temperature on the shelf of the Laptev Sea.

The bottom water temperature during sea transgressions was taken as −1.5 °C [42]. The temperatures of −13.5 and −22.5 °C were used as threshold quantities during marine regressions according to Scenarios 1 and 2, respectively. For Scenario 1, the value of −12 °C was derived from the difference between the actual temperatures at the bottom of the layer of annual fluctuations (up to −14 to −15 °C on the Novosibirsk Islands) and the actual values of the bottom water layer (up to −1.9 °C) [1]. For Scenario 2, the value of −21 °C was derived from the difference between the mean ground annual temperatures during the longest regression period of the Late Pleistocene, including the Zyrianian, Kargan and Sartanian cooling, and the actual values of the bottom water layer (up to −2 °C) [2]. Examples of the bottom temperature change over time for both scenarios for a water depth of 60 m are shown in Figure 1. In Scenario 1, freezing begun 20.7 kyr BP and occurred for 8.7 kyr, whereas the beginning of glaciation in Scenario 2 occurred 64.8 kyr BP and continued for 54.8 kyr.

For each scenario, the start and end of the regression, as well as the duration of freezing for the present-day sea depths of 10, 20, 30, 40, 50, 60, 70, 80 and 90 m, were calculated (

Table 1. Frost duration (kyr) for series of the model run depths.

Water Depth, m	Freezing (Scenario 1)			Freezing (Scenario 2)
	Start	Completion	Duration	Start	Completion	Duration
10	27.7	6.2	21.5	111.0	5.9	105.1
20	25.7	7.7	18.0	109.8	7.5	102.3
30	23.9	8.7	15.2	91.0	8.5	77.5
40	22.2	9.5	12.7	86.0	9.0	60.0
50	21.4	11.0	10.4	67.5	9.5	58.0
60	20.7	12.0	8.7	64.8	10.0	54.8
70	20.5	13.1	7.4	40.5	11.1	29.4
80	19.9	14.1	5.8	25.0	11.8	13.2
90	19.6	15.2	4.4	23.5	12.0	11.5

). These data were used to set up the upper boundary condition in the form of piecewise constant functions (see Figure 1).

2.2. Heat Flow

Information about the temperature field of the Laptev Sea is scarce and unevenly distributed (Figure 2).

The forecasting of HF and the distribution of the geothermal gradient has been carried out using long-distance extrapolation and shallow-depth temperature measurements, as well as indirect data on thermal conditions and known correlations between the HF and the age of geologic structures [1,59].

According to the work presented in [59], the deep HF of the Arctic shelf as a whole varies in the range of 40–60 mW/m², and in the Laptev Sea, this increases to 60 mW/m². This value was determined by using techniques established in [60] indicating that the density of deep HF is associated with the age of tectonogenesis. This contrasts with [41,61], where the permafrost thickness in the Laptev Sea was calculated with HF values varying from 40 to 100 and even up to 250 mW/m². Due to the lack of HF data, these values were chosen by analogy with rift blocks on the continent, tectonic structures on the shelf and from wells on the coast and islands. In [2], for the eastern part of the Laptev shelf, permafrost was simulated using HF values of 50 mW/m² (within tectonic blocks) and 100 mW/m² (within rifts). In [51], the main structural elements of the Laptev Sea rift system were assigned HF values of 45, 50 and 60 mW/m².

After analyzing past studies devoted to permafrost and HF, as well as the available measured HF data of the Laptev Sea, we have adopted HF values of 60 and 100 mW/m² for our calculations. These values were used to set the lower boundary condition of our model and to determine the degree of the influence of HF on the formation and evolution of permafrost and the associated hydrate reservoir. The HF value of 60 mW/m² is considered to be typical for the Arctic shelf (according to [25,59]). The value of 100 mW/m² from [61] was set as the minimum elevated value for the rifts.

2.3. Mapping

The actual top and bottom of the GHSZ—i.e., its thickness—can only be established by drilling frozen ground or predicted by modeling. For the forecast mapping, a grid of points from 10 to 90 m water depths with a resolution of 0.1 degrees in latitude and 0.5 degrees in longitude was created, corresponding to a 10 × 10 km grid (with a total of around 3000 points). Each point was assigned a water depth by bathymetry (International Bathymetric Chart of the Arctic Ocean (IBCAO))) and associated HF. The grid was assigned the value of the GHSZ thickness calculated at an HF value of 60 mW/m² for both Scenarios 1 and 2 (see below). The calculated RSP and GHSZ thicknesses for each point with a unique depth were obtained by interpolating the calculated data from the nearest depth (i.e., for a water depth of 15 m, the interpolated GHSZ and RSP thicknesses were taken from the calculated data for depths of 10 and 20 m). Mapping the RSP and GHSZ and their differentiation in terms of thickness was carried out in Surfer^® in 100 m increments using Kriging interpolation, which was selected as a method for constructing the grid function. Thus, the resulting maps represent 3D models of the RSP and GHSZ.

2.4. Model Setup

The method we used implemented a simplified numerical solution of the heat transfer equation accounting for the step-function of the upper boundary conditions consistent with the temperature change at the sediment–water or air–water interfaces during terrestrial and submarine periods on the Arctic shelf in the Pleistocene. To calculate the thicknesses of the RSP and GHSZ, the sediment temperature graph was compared with the water freezing curve and the equilibrium curve of the formation/decomposition of gas hydrates for each point of the grid (Figure 3).

In the calculations, we used the methane hydrate equilibrium curve at a salinity of 35‰ according to [62]. When calculating the equilibrium temperature for hydrate formation, the effect of sea-level fluctuation on the hydrostatic pressure was not considered.

Contemporary average annual salinity values in the Laptev Sea range from 10 to 35‰, which corresponds to freezing temperatures from −0.5 to −1.9 °C. We accepted the minimum freezing temperature (−1.8 °C) of seawater, corresponding to a salinity of about 34‰. This value matches the maximum salinity within the studied area of the Laptev Sea according to [42]. The choice of a constant value is suggested by a slight change in salinity with depth in Quaternary sediments.

Sediment temperature profiles were obtained by solving a non-stationary 1D heat conduction equation (the Stefan problem) through the ANSYS Fluent student software package:

$$\rho C\frac{\partial T}{\partial t}=\frac{\partial }{\partial z}\left({\lambda }_e\frac{\partial T}{\partial z}\right),$$

(1)

where $\rho$ is the sediment density, $C$ is the sediment heat capacity and ${\lambda }_e$ is the effective thermal conductivity coefficient of the sediment.

Our modeling domain reached the maximum sediment thickness of the Laptev Sea, which according to [30] reaches 15 km. The following assumptions were made: porosity decreases with depth exponentially according to Athi’s Law [63]—φ (z) = φ₀⋅exp(−φ_a·z), where φ₀ is the surface sediment porosity and φ_a is the compaction factor; and the modeled sediments are represented by three components—the mineral matrix, water, ice or gas hydrate. Key model parameters for each component are given in

Table 2. Key model parameters of the relic subsea permafrost (RSP) and GHSZ simulations.

Symbol	Parameter	Unit	Value	References
λsk	Sediment thermal conductivity	W/(m∙K)	2.5	[64]
λw	Water thermal conductivity	W/(m∙K)	0.58	[62]
λi	Ice thermal conductivity	W/(m∙K)	2.23	[62]
λgh	Methane hydrate thermal conductivity	W/(m∙K)	0.49	[62]
Csk	Sediment heat capacity	J/(kg∙K)	1000	[64]
Cw	Water heat capacity	J/(kg∙K)	4187	[64]
Ci	Ice heat capacity	J/(kg∙K)	2050	[64]
Cgh	Methane hydrate heat capacity	J/(kg∙K)	2080	[64]
Lwi	Latent heat of ice formation	kJ/kg	334	[65]
Lgh	Latent heat of methane hydrate crystallization	kJ/kg	430	[65]
Psk	Sediment density	kg/m3	2700	[66,67]
Pw	Sediment pore water density	kg/m3	1035	[64]
Pi	Ice density	kg/m3	917	[62]
Pgh	Methane hydrate density	kg/m3	913	[62]
φ	Porosity at the seafloor	–	0.6	[67,68]
K	Sediment compaction factor	–	0.00045	[64]

.

The main equation variables are the effective thermal conductivity and effective heat capacity. The heat equation for a two-component medium was derived from [64]:

$$\frac{1}{{\lambda }_e}=3{{\displaystyle \sum }}_{k=1}^n\frac{{\sigma }_k}{2{\lambda }_e+{\lambda }_k},$$

(2)

where ${\lambda }_e$ is the effective thermal conductivity, $k$ is the parameter of the multicomponent medium represented either by a mineral matrix (sk), water (w), ice (i) or gas hydrate (gh), n is the total number of components and ${\sigma }_k$ is the relative volume (fraction) of the k component in a unit volume of the medium, which is determined as follows: sediment (rock) matrix ${\sigma }_{sk}=1-\varphi$; water ${\sigma }_w=\varphi \left(1-H_c\right) \mathrm{or} \varphi$; ice ${\sigma }_i= \varphi \left(1-H_c\right) \mathrm{or} \varphi$; hydrate ${\sigma }_{gh}=\varphi H_c$, where Hc is the gas hydrate content.

It should be noted that the gas saturation of the sediments was not taken into account, and the thermal conductivity of thawed gas-saturated sediments, as in similar studies, was set to be equal to its value in thawed sediments saturated with water.

For wet, frozen and hydrate-containing sediments, we used the equation for the heat capacity of sediments modified from Equation (2) from A. Golmstock [64] by adding ice and hydrate components to the formula and taking into account the latent heat of ice and hydrate formation:

$$\rho C={\rho }_{sk}{C}_{sk}\left(1-\varphi \right)+{\rho }_k{C}_k\varphi \left(1-H_c\right)+{\rho }_{gh}{C}_{gh}\varphi H_c+C_{latent\left(i\right)}+C_{latent\left(gh\right)},$$

(3)

where $\varphi$ is porosity, $\rho$ is density, $C$ is heat capacity, $sk$ is the sediment (rock) matrix, $k$ refers to the interstitial pore components—water (w) or ice (i)—Hc is the gas hydrate content (0, 5, 25, 50 or 100%) at T > Tp (the equilibrium temperature of hydrate formation), where Hc = 0. C_latent(i) is a U-shaped function equal to the latent heat of ice formation in the “freezing point of water ± 0.5 °C”, temperature range, which is equal to 0 outside this interval; C_latent(gh) is a U-shaped function equal to the latent heat of hydrate formation, multiplied by the hydrate content, within the “Tp ± 0.5 °C” interval and equal to 0 outside that interval.

Thus, the presence of ice and hydrate in sediment is strictly regulated by temperature. As a result, in our simulation, the thermal–physical properties of sediment changed continuously across different depths with the same phase composition and changed abruptly during the phase transitions. The thicknesses of the GHSZ and RSP were determined for each of the selected scenarios and HF values assuming 0%, 5%, 25%, 50% and 100% hydrate contents.

An absence of ice-bound permafrost on the Laptev shelf 120 kyr BP and a gradient temperature distribution in the sediment were taken as the initial conditions of the model.

Initial conditions were as follows:

$\mathrm{T}{|}_{\mathrm{t}=0}={\mathrm{T}}_0\left(\mathrm{z}\right)$, meaning that

$$\frac{\partial }{\partial \mathrm{z}}\left({\mathsf{\lambda }}_{\mathrm{e}}\frac{\partial {\mathrm{T}}_0\left(\mathrm{z}\right)}{\partial \mathrm{z}}\right)=0$$

(4)

A time-constant HF at the base of the modeling domain and a variable piecewise-constant function of temperature (with constant temperatures for the regression and transgression periods and instantaneous temperature change during the transition) at the top of the modeling domain were taken as the boundary conditions.

Upper boundary conditions were as follows:

$$\mathrm{T}{|}_{\mathrm{z}=0}={\mathrm{T}}_{{\mathrm{z}}_0}\left(\mathrm{t}\right)$$

(5)

During the sea regression (tr):

• ${\mathrm{T}}_{{\mathrm{z}}_0}$ = −13.5 $℃$ (Scenario 1)
• ${\mathrm{T}}_{{\mathrm{z}}_0}$ = −22.5 $℃$ (Scenario 2)

During the sea transgression (tt):

• ${\mathrm{T}}_{{\mathrm{z}}_0}$ = −1.5 $℃$

Lower boundary conditions were as follows:

$${\mathsf{\lambda }}_{\mathrm{e}}\frac{\partial \mathrm{T}\left(\mathrm{z}\right)}{\partial \mathrm{z}}{|}_{\mathrm{z}={\mathrm{z}}_{\max }}=60\left(100\right)\frac{\mathrm{mW}}{{\mathrm{m}}^2}$$

(6)

A one-dimensional calculation was obtained for each set of parameters. Particularly, two scenarios, two values of HF and five values of hydrate content were calculated for each depth interval. In total, 24 computations were launched for sea depths from 10 to 90 m (Table 1). A total of 216 1D calculation runs were performed.

2.5. Modeling Assumptions

The latitudinal temperature distribution in the past was considered to correspond to that today. The seafloor topography of the Laptev shelf in the past matched that of today, and thermal abrasion was not considered.

3. Results and Discussions

3.1. RSP and GHSZ Distribution Forecast

3.1.1. Forecast for Present-Day Lateral Extension

The results of the simulated present-day RSP distribution in the Laptev Sea are shown in Figure 4 and Figure 5. In Scenario 1, even with an average HF of 60 mW/m² and a relatively short duration of marine regression (30–19 kyr), during which the subaerial temperature dropped to −13.5 °C, the RSP still reached a 50 m thickness (Figure 4a and Figure 5a). The largest permafrost thickness (140–170 m) was observed in the coastal zone, within the wide shallow water around Novosibirsk and Lyakhovsky islands, as well as in the area of the Semenovskoe shoal (Figure 4a). Remarkably, the simulated paleoenvironment of Scenario 1 appears to have been insufficient to maintain the GHSZ until today.

A more favorable GHSZ forecast was obtained for Scenario 2. Under this scenario, RSP propagated to 100 m isobaths, and the coverage area of the GHSZ generally coincided with that of RSP (Figure 4b,c). An increase in the duration of the freezing and a larger temperature difference between warm and cold periods led to a doubling of the area of RSP distribution and created a thick GHSZ. In particular, longer (2.3–6.2-fold, depending on the sea depth) freezing and a 1.75-fold greater temperature jump at the same HF allowed both the RSP and GHSZ to extend to depths of little more than 90 and 70 m, where they reached thicknesses of about 120 m (Figure 4c and Figure 5b). The RSP thickness at a water depth of 70 m was 253 m (Figure 4c and Figure 5b). The maximum thicknesses of RSP and GHSZ (occurring at the 10 m isobath) reached 473 and 453 m, respectively (Figure 4b,c and Figure 5b).

Comparing the results from the two scenarios, we note that the thicknesses of ice-containing deposits differed by about 300 m. Assuming that the scenarios represented the minimum and maximum estimates, we came to the following conclusions. At the present day, permafrost is widespread but is unlikely to be deeper than 50 m to 100 m (minimum-to-maximum estimate) of water depth. The greatest thicknesses of the RSP may occur in the coastal zone and reach 473 m, whereas the minimum thickness at the same water depth is about 170 m. In contrast, the GHSZ at present is either completely absent (Scenario 1) or propagates no deeper than the 80 m isobath (Scenario 2). The greatest thicknesses of the GHSZ (543 m, Scenario 2) naturally occurs in the coastal zone. Thus, the duration of freezing and its magnitude significantly affects the distribution of the RSP but controls its thickness to a greater extent. The lesser influence of the paleoscenario on the distribution of the RSP can be explained by the insignificant difference in the duration of freezing and thawing that occurred in deep waters.

3.1.2. Forecast of Present-Day Geometry

Towards the ocean, both zones become thinner from above and below and pinch out until they disappear completely. The specifics of the geometry of the RSP and the GHSZ—i.e., “wedging-out” toward the ocean—and the predicted changes in the position of the permafrost tables are presented in Figure 5.

The limit of RSP water depth increases from 50 to 90 m and from 10 to 70 at HFs of 60 and 100 mW/m², respectively (Scenarios 1 and 2). The RSP is forecasted to occur at sub-bottom depths from 15 to 200 m (according to Scenario 2, with an HF of 100 mW/m², and Scenario 1, with both calculation HF values) and from 15 to 500 m (Scenario 1, with an HF of 60 mW/m²). The GHSZ extends up to the 70 m isobath in the sub-bottom depth interval of 240–700 m. The permafrost tables, according to our calculations, occur at sub-bottom depths of 19–46 m and 15–29 m and gradually deepen from sea depths of 10 to 50 m and 10 to 90 m for Scenarios 1 and 2, respectively (Figure 5c,d). The subsidence of the permafrost table sharpens from a water depth of 60 m (Figure 5d).

We suggest that these changes in geometry are the result of different durations of drainage (and, consequently, freezing) of areas that are now located near the coastline and those located seaward. The closer to the shelf break, the longer the subaqueous period. Therefore, at different rates of thawing, determined by the magnitude of the HF, the difference in the thickness of the permafrost will be greater.

3.2. Evolution of RSP and GHSZ

3.2.1. Geometry Changes over Time

The RSP and the GHSZ do not completely coincide and overlap; the GHSZ is located both within and under permafrost (Figure 6). Because of the constant temperature at the upper boundary condition, the increase in the thicknesses of both zones in the subaerial period and decrease in the subaquatic zone occurred smoothly. Initially, permafrost was formed, and at the moment when it reached a certain thickness, conditions favorable for the preservation of hydrates were created. For Scenario 1, this time gap was about 20 kyr (Figure 6a), while for Scenario 2, the gap was between 7 and 20 kyr (Figure 6b,c). The establishment of the stability conditions lagged behind the formation of permafrost, most likely due to the duration of freezing; i.e., the duration of the subaerial period. After the beginning of the transgression, the GHSZ disappeared more quickly, and it is interesting that the deeper the water, the faster the GHSZ disappeared, in contrast with permafrost (Figure 6c,d).

The reason that GHSZ degrades first followed by permafrost is because the model assumes a constant HF value from below. Indeed, in our simulation, the deep HF is constant, and heating from above took place only at the very beginning of the subaquatic period. Moreover, both zones thawed faster at greater sub-bottom depths, since the porosity there was noticeably reduced (since we used Athi’s law to determine porosity). In contrast, at shallower sub-bottom depths, the thawing was reduced since gas hydrate decomposition and ice melting requires a great deal of energy. Therefore, the amount of hydrate or ice in the sediment (depending on the porosity) determined the rate thawing.

During the first hundred years after the transgression, the temperature inside the RSP leveled off, approaching the melting point of ice. This was due to the specific heat capacity of ice, which made an insignificant contribution to the heat balance of sediments relative to the latent heat of ice formation (i.e., ice melts for a much longer time than it warms up). Therefore, the thawing of permafrost from above was smoother.

Rapid temperature equalization within the permafrost led to a sharp change in the top of the GHSZ (Figure 6e) at the beginning of the marine transgression. After the temperature jump, the position of the top of the GHSZ did not change as long as the conditions were stable.

3.2.2. Influence of Paleoscenario and Heat Flow

The influences of the chosen paleoscenario and HF on the geometry are shown in Figure 6, showing changes in the shape of permafrost and GHSZ over time (both past and future) versus the water depths for both scenarios and different HFs.

In Scenario 1, the calculated thickness of permafrost and its propagation were generally lower, while the GHSZ was practically absent throughout the entire sea. Thus, Figure 6a shows the minimum thickness of the RSP required to establish hydrate stability at an average HF value (that is, outside the zones of tectono-magmatic activation) with a minimum freezing time and temperature jump.

Considering the dynamics of changes in the RSP and GHSZ for both paleoscenarios, it can be suggested that longer freezing and a lower subaerial temperature (as in Scenario 2) increased the permafrost thickness between 1.6 (at 100 mW/m²) to 2.2 (at 60 mW/m²) times (see Figure 6c,d,

Table 3. Simulation results.

Sea Depth, m	HF = 60 mW/m2				HF = 100 mW/m2
	Scenario 1		Scenario 2		Scenario 1		Scenario 2
	RSP 1	Duration 2	RSP	Duration	RSP	Duration	RSP	Duration
10	250	15.0	535	42.0	182	6.5	288	15.0
20	240	14.0	531	41.5	178	7.3	287	15.0
30	229	13.0	505	38.3	174	7.0	282	14.3
40	217	12.0	477	35.1	169	6.8	275	13.6
50	204	11.0	473	34.6	163	6.3	274	13.6
60	192	10.0	465	34.0	156	5.8	273	13.5
70	182	9.3	394	26.8	150	5.5	254	11.8
80	165	8.3	305	18.8	139	4.8	224	9.8
90	151	7.0	281	17.4	129	4.3	214	9.3

¹ RSP—permafrost thickness at the end of regression (m). ² Duration—duration of degradation from the moment of transgression (kyr).

). Moreover, the influence of the paleoscenarios on the evolution of permafrost and its geometry at a HF of 60 mW/m² was more significant at shallow sea depths, and at a HF of 100 mW/m² was more significant at greater depths. An increase in HF by 66% reduced the thickness of the frozen zone between 1.3-fold (for Scenario 1) and 1.7-fold (for Scenario 2). Naturally, a greater HF had a greater influence on permafrost thawing, but on the other hand, this shows that the effect will be greater the larger the permafrost thickness.

The maximum thickness of the RSP and the GHSZ was reached by the beginning of the transgression. In particular, at a water depth of 10 m, the time of the inundation (that is, the beginning of RSP degradation) was about 6 kyr BP. At this point, according to the first scenario, the maximum RSP (GHSZ) thicknesses at an HF of 60 mW/m² reached 250 m (20 m), and at an HF of 100 mW/m² reached 182 m (0 m). Our simulation suggests that, according to Scenario 1, the conditions for the stability of methane hydrates in the Laptev Sea are absent. At the same moment in the past, in the second scenario, the maximum RSP (GHSZ) thicknesses at an HF of 60 mW/m² were 535 m (560 m), and at an HF of 100 mW/m², the thicknesses were 288 m and 150 m, respectively.

We analyzed the influence of HF and paleoscenarios on the thickness and the duration of RSP degradation on the geometry of the studied zones. These effects on the RSP are visible from the simulation results shown in Table 3 for different sea depths, HF values and paleoscenarios.

The data obtained allow us to summarize the following: if freezing occurs over more than 100 kyr, the thickness of the RSP by the end of the transgression (i.e., its maximum thickness) is directly proportional to the temperature jump but depends less on the freezing time. An increase in the temperature jump by 1 °C leads to an increase in the maximum thickness of the RSP by 20–40 m. In contrast, when the duration of freezing is less than 100 kyr, the effect of the temperature jump is not as strong, and in this case, the maximum thickness of the RSP depends mainly on the duration of freezing.

The shorter the freezing period and the temperature jump, the less the thermal energy affects the maximum thickness of the RSP. An increase in HF by 10% reduces the thickness of the RSP by 10% for Scenario 2 and by 5% for Scenario 1.

The dependence of the continuation of degradation on the maximum RSP thickness is close to proportional. Increasing the maximum thickness by 10 m increases the degradation time by 500–1000 years at an HF of 60 mW/m² and for 350–700 years with an HF of 100 mW/m².

The dependence of the duration of degradation on the HF is close to inversely proportional. An increase in HF by 10% reduces the period of degradation by 6–8%.

Thus, studying the evolution of the studied zones make it possible to (1) trace changes in the geometry of the GHSZ with changes of the paleogeographic setting; (2) assess the beginning of permafrost and GHSZ formation; (3) estimate the maximum thickness of both zones when changing climatic regimes over different water depths; and to (4) predict the existence of permafrost and GHSZ today and in the future.

3.2.3. RSP as a Factor Controlling GHSZ

Our calculations suggest that methane hydrates become stable at RSP thickness larger than 240 m, which allows us to explore the relationship between the RSP and GHSZ thicknesses (Figure 7). Under subaerial conditions, the thickness of the GHSZ increased almost linearly with an increase in the thickness of the RSP (Figure 7a). Under subaqueous conditions, the nature of the dependence changed, and the thickness of the GHSZ became, on average, higher than in subaerial conditions (Figure 7b). This relationship allows us to estimate the GHSZ thickness based on that of the RSP.

3.2.4. Forecast for the Future

To predict the thermal state and the evolution of the RSP and the GHSZ, we performed calculations up to 40 kyr into the future with a temperature of −1.5 °C at the upper boundary. During thawing, the rate of the rise of the base of the RSP was directly proportional to the magnitude of the HF. During freezing, an increase in HF, in contrast, reduced the rate of subsidence of the base of the RSP. However, the RSP thawing rates at the beginning of the transgression, calculated for both scenarios at both HF values, were the same (1 cm/yr) before complete permafrost thawing.

We also predict an increase in the rate of permafrost degradation up to 3 cm/year during the last 1000 years of its existence. The reason why the rates are approximately the same is that, at an HF of 100mW/m², freezing occurs at a shallow depth, where the porosity and as a consequence the ice content is higher, and therefore more energy is required for melting. Therefore, besides HF and the paleoscenario, another factor affecting the rate of permafrost thawing is the porosity.

According to our forecast, the existence of the RSP in Scenario 1 (at ab HF of 60 mW/m²) is possible for a maximum of another 9 kyr (see Figure 6).

The same calculation with an HF of 100 mW/m² assumes the existence of permafrost only up to the 10 m isobath and only for about 1000 years from present. According to Scenario 2 (at an HF of 60 mW/m²), the RSP may exist for another 36.6 kyr. For an HF of 100 mW/m², the predicted time of the existence of RSP decreases to 9.6 kyr. The maximum duration of the conditions under which gas hydrate stability is predicted to be another 25.9 kyr (Scenario 2). For an HF of 100 mW/m² (Scenario 2) and both HF values (Scenario 1), the GHSZ is already absent today.

3.2.5. Influence of Hydrate Content

Most studies devoted to the predictions of relic permafrost [2,51,69,70] or relict permafrost and the associated GHSZ [1,14,41,61,71,72,73,74] do not take into account any contribution of gas hydrates to the heat balance of the system. However, the specific heat of hydrate formation has a noticeable effect on the dynamics of temperature changes in hydrate-containing sediments, even with a small percentage of hydrates. For instance, a 5% hydrate content reduces the thickness of the GHSZ to several tens of meters but increases the duration of its existence by several thousand years.

We have not only included hydrate content in our model calculations but also traced how its presence in sediments affects the permafrost and considered the contribution of different hydrate contents to the dynamics of changes in the RSP (Figure 8). Our model suggests that, with an initially high content of hydrates (50%), the thickness of the GHSZ by the end of the regression could decrease by 70 m (1.2 times). This is due to the fact that (1) the presence of hydrates prevents freezing at depth due to the specific heat of hydrate formation, and (2) the thermal conductivity of hydrate-bearing sediments is lowered. On the other hand, during the warming period, the presence of gas hydrates slows down the thawing process (i.e., GHSZ base has a gentler slope during the subaquatic period), which contributes to the maintenance of hydrate stability conditions for a longer time (up to 7.7 Ka). These effects are most noticeable at an HF value of 60 mW/m² and a water depth of 10 m (see Figure 8). During thawing, the top of the GHSZ is unchanged as long as the permafrost exists. As soon as the permafrost base displaces above the top of the GHSZ, the stability zone, in turn, will begin to shift downward. We established that the shift rate of the GHSZ top is affected by the hydrate content. At low (5%) hydrate contents, the top of the GHSZ shifts sharply downward, approaching its base, and the thermobaric conditions of hydrate stability disappear. If the concentration of hydrates is significant (50% and higher), then the top of the GHSZ drops gradually. The more hydrates in the sediment, the flatter the angle of the upper boundary of the GHSZ. Thus, the lifetime of the GHSZ during the subaquatic period is influenced by two parameters: the depth of freezing and the rate of thawing. The concentration of hydrates has a negative effect on the freezing depth but has a positive effect on the thawing rate. This multidirectional effect of the hydrate content on the GHSZ lifetime leads to the existence of an optimal hydrate concentration at which the GHSZ is maintained for the longest time (50% hydrate content, see Figure 8). At the same time, the thickness of GHSZ is large at 5% GH content.

4. Conclusions

Using numerical simulations, we have carried out a parametric study of the mutual influence of the RSP and the GHSZ in which we evaluated the impact on the RSP and the GHSZ of such factors as (1) the duration of subaerial freezing and the temperature jump between the subaquatic and subaerial periods, which determine how strongly both zones freeze when in a subaerial environment and how long the RSP then thaws and degrades the GHSZ when in an underwater environment; (2) the heat flow that prevents freezing and contributes to the maximal reduction in RSP and GHSZ from the bottom; and (3) the content of gas hydrates, which appeared to have a multidirectional influence. The influence of the hydrate content on the permafrost–hydrate system was estimated for the first time.

The impact of these factors on the relict permafrost and stability of gas hydrates in the Laptev Sea has been assessed from three angles: (1) the spatial distribution of the RSP and the GHSZ; (2) the lifetime of both the RSP and the GHSZ (the state in the past, the present and the forecast for the future (i.e., evolution)); (3) changes in the geometry of the RSP and the GHSZ.

A feature of our model is that the latent heat of ice and hydrate formation is considered. The model accounts for the heat-insulating properties of gas hydrates and their influence on the geometry of the RSP and the GHSZ. In our simulation, the thermophysical properties of the sediments are continuously changing for different depths with the same phase composition and abruptly during phase transitions. In previous studies, the thermophysical properties of sediments changed piecewise or were constant.

The use of a small step in water depth for the simulation and a dense grid for mapping allowed us to predict the change in the geometry of both zones under various climatic and geological conditions and to assess the contribution of the main factors that control the changes in permafrost and the conditions of hydrate stability in time and space.

Our parametric study shows that the choice of an adequate paleogeographic scenario and heat flow is significant for modeling the RSP and, therefore, the stability of cryogenic hydrates. We assessed how these factors affected the evolution of both zones over time (Figure 6) and their current geometry (Figure 5). It is evident that the temperature in general and, in particular, the paleoscenario and heat flow most significantly affect the permafrost and the conditions for the stability of cryogenic gas hydrates.

According to the considered paleoscenarios, an increase in the duration of transgressive–regressive cycles four times and a temperature jump during the transition from a subaquatic to a subaerial position by a factor of 1.75 occurred in Scenario 2, in contrast to Scenario 1. From these differences, it is possible to estimate the influence of these factors on the dynamics of the relict permafrost and the associated hydrate stability zone at the same HF (60 or 100 mW/m²).

Assuming these scenarios as minimum and maximum estimates, we can summarize the following:

• Longer freezing and a lower subaerial temperature doubles the thickness of the RSP and makes the pressure-and-temperature conditions favorable for the existence of methane hydrate;
• All other things being equal, an increase in HF by 66% reduces the thickness of the RSP by 1.5 times (average value for both scenarios);
• With prolonged freezing and a higher temperature jump, the limiting water depths at which RSP is still present increase;
• Present-day relic submarine permafrost in the Laptev Sea is forecasted to propagate to the 50–100 m isobaths with a maximal thickness in the range of 170–473 m;
• The conditions for the stability of cryogenic hydrates in the Laptev Sea are either currently completely absent (Scenario 1) or exist up to a sea depth of 70 m—the maximum thickness of the GHSZ is forecasted to be as thick as 453 m;
• The thickness of the GHSZ is less (by 1.2 times at the end of the regression) in scenarios where there is initially a high hydrate content;
• The minimum and maximum predicted preservation times for the RSP are 9 and 36.6 kyr, whereas the presence of conditions for the stability of methane hydrates in the Laptev Sea at the maximum permafrost thickness is possible for another 25.9 kyr;
• During the warming period, the presence of gas hydrates slows down the thawing of the RSP, and the stability persists up to 7.7 kyr longer—i.e., an increase from 25.9 to 33.6 kyr.

It is important to note in both scenarios that the rate of permafrost thawing at the beginning of the transgression was estimated to be 1 cm/year, increasing to 3 cm/year during the last thousand years of the existence of permafrost.

The main factors influencing the rate of degradation are heat flow and the porosity of frozen sediments. The reason why we calculated approximately the same degradation rates at HFs of 60 mW/m² and 100 mW/m² is that, at 100 mW/m², freezing occurs at a shallower depth, where the porosity and ice content are higher, and therefore more energy is needed for the thawing.

The approach presented in our work made it possible to carry out extreme assessments, which, given the current level of knowledge about the permafrost zone and the geothermal environment of the Arctic seas, allowed us to explore the range of possible outcomes. The minimum and maximum temperatures in the subaerial period (in both scenarios) were chosen as extreme endmembers. However, since the temperature parameters provide the basis for the extreme estimates, it is assumed that the natural environment corresponds to conditions that are somewhere between these values.