Sea Level Trend and Fronts in the South Atlantic Ocean

Abstract

The understanding of the physical drivers of sea level trend is crucial on global and regional scales. In particular, little is known about the sea level trend in the South Atlantic Ocean in comparison with other parts of the world. In this work, we computed the South Atlantic mean sea level (SAMSL) trend from 25 years of satellite altimetry data, and we analyzed the contributions of steric height (thermosteric and halosteric components) and ocean mass changes for the period 2005–2016 when all the source data used (Argo, GRACE and satellite altimetry) overlap. The SAMSL trend is 2.65 ± 0.24 mm/yr and is mostly explained by ocean mass trend, which is 2.22 ± 0.21 mm/yr. However, between 50° S–33° S, the steric height component constitutes the main contribution in comparison with the ocean mass component. Within that latitudinal band, three regions with trend values higher than the SAMSL trend are observed when considering 25 years of satellite SLA. In the three regions, a southward displacement of the Subtropical, Subantarctic, and Polar Fronts is observed. The southward shift of the fronts is associated with the strengthening and polar shift of westerly winds and contributes to a clear thermosteric trend that translates to the SLA trend observed in those regions.

1. Introduction

1.1. Untangling Sea Level Trend

In the context of climate change, the understanding of the physical drivers of sea level variability is crucial, not only on a global scale, but also on a regional scale. This work aims to contribute to such understanding, focusing in the South Atlantic Ocean (Figure 1).

Sea level rise has been estimated for the past, present and future. Long records of sea surface height (SSH) from different sources indicate that the global mean sea level (GMSL) increased 1.7 mm/yr from 1901 to 2010 [1]. From 1993 to 2015, satellite altimetry measurements showed a trend of 3.1 mm/yr [2]. The sea level variability in the tropical and Southern Ocean explains the acceleration rate in the global sea level prior to the period 1990 to 2007 [3]. The good agreement between models and historical in situ data [4] gives confidence to the future scenarios of climate change. The projections from IPCC models indicate that SSH will increase between 0.52 m and 0.98 m for the year 2100, in the worst-case scenarios (RPC8.5, [4]). To improve the accuracy of climate models, it is necessary to apprehend the physical mechanisms that drive GMSL. Several studies demonstrated that the main drivers of the GMSL rise are due to changes in density and in ocean mass (e.g., [2,5]).

Changes in the density of sea water, called steric effects, are due to the ocean’s exchange of heat and fresh water with the atmosphere. Over the last 50 years, the ocean has absorbed 93% of the heat energy excess of the Earth [6]. This impacted on global temperature, providing an increment of 0.015 °C/decade in the upper 700 m between 1971 and 2010 [7]. In fact, the warming is larger in the near-surface (0–75 m) layer, with a rate of 0.11 °C/decade [8]. One of the consequences of increasing temperatures is a decrease in density, and hence an increment in SSH. Indeed, density variability is mostly dominated by temperature. Salinity plays a secondary role in the steric height variability [9]. Therefore, several studies focused on the contribution of thermosteric height to the global sea level trend. However, changes in salinity can be significant to sea level variability on a regional scale, such as polar regions [10].

The remaining 7% of Earth’s heat energy excess warms the atmosphere and continents, melting sea and land ice. Thanks to the Gravity Recovery and Climate Experiment (GRACE) space gravity mission, it became possible to monitor changes in the mass of Greenland and Antarctic land ice. For the period 2005–2015, these land ices contributed to a sea level trend of 0.76 ± 0.10 mm/yr (Greenland) and 0.42 ± 0.10 mm/yr (Antarctic) [2], while a sea level rise due to glaciers was 0.74 ± 0.10 mm/yr for the same period. The changes in Greenland, Antarctica and glacier masses are components of the ocean mass variability. Another component is the land water storage associated with climate change (i.e., water stored in rivers, lakes, wetlands) and direct human interventions (i.e., groundwater pumping, impoundment in reservoirs). For the period 2003–2013, human intervention was the main factor that dominated the decrease observed in the total land water storage, which corresponds to a sea level trend of 0.30 ± 0.18 mm/yr [11].

When studying sea level variability, the mass transfer between continental ice and the oceans during the last deglaciation should be considered. This transfer of mass also contributes significantly to the ongoing sea level change due to the viscoelastic deformation of the land, and the corresponding changes on the seafloor and gravity (referred to as Glacial Isostatic Adjustment, GIA) [12,13].

On regional scales, the SSH variability is not only affected by steric effects and ocean mass changes, but also by wind-driven circulation changes, among others [14]. For instance, the cause of sea level rise in the northwest tropical Pacific is associated with a southward migration of the Norequatorial current and Norequatorial countercurrent [15]. The change in the currents could be due to changes in atmospheric circulation [15]. In addition, using numerical models, it has been evidenced that the eddy momentum flux can generate an increase or decrease in the sea level trend in the North Pacific circulation [16]. In the Southern Hemisphere, [17] suggested that large trends in the SSH indicate a strengthening of the subtropical gyres. One of the few studies that focused in the South Atlantic shows that the sea level increased 2.5 mm/year for the period 1993–2013 in the Southwestern Atlantic Continental Shelf [18]. Large positive trends of sea level, of the order of 5 mm/year, were also reported on the shelf-break between 34° S and 37° S [18], an area affected by the Malvinas and Brazil currents [19]. This evidence of a positive trend in the sea level encourages us to explore the sea level variability in the South Atlantic. A better understanding of the origin of the sea level trends will improve the future prediction of climate models. In the following section, we describe the mean circulation in the South Atlantic and the processes that might affect the trend of the sea level on large and local scales.

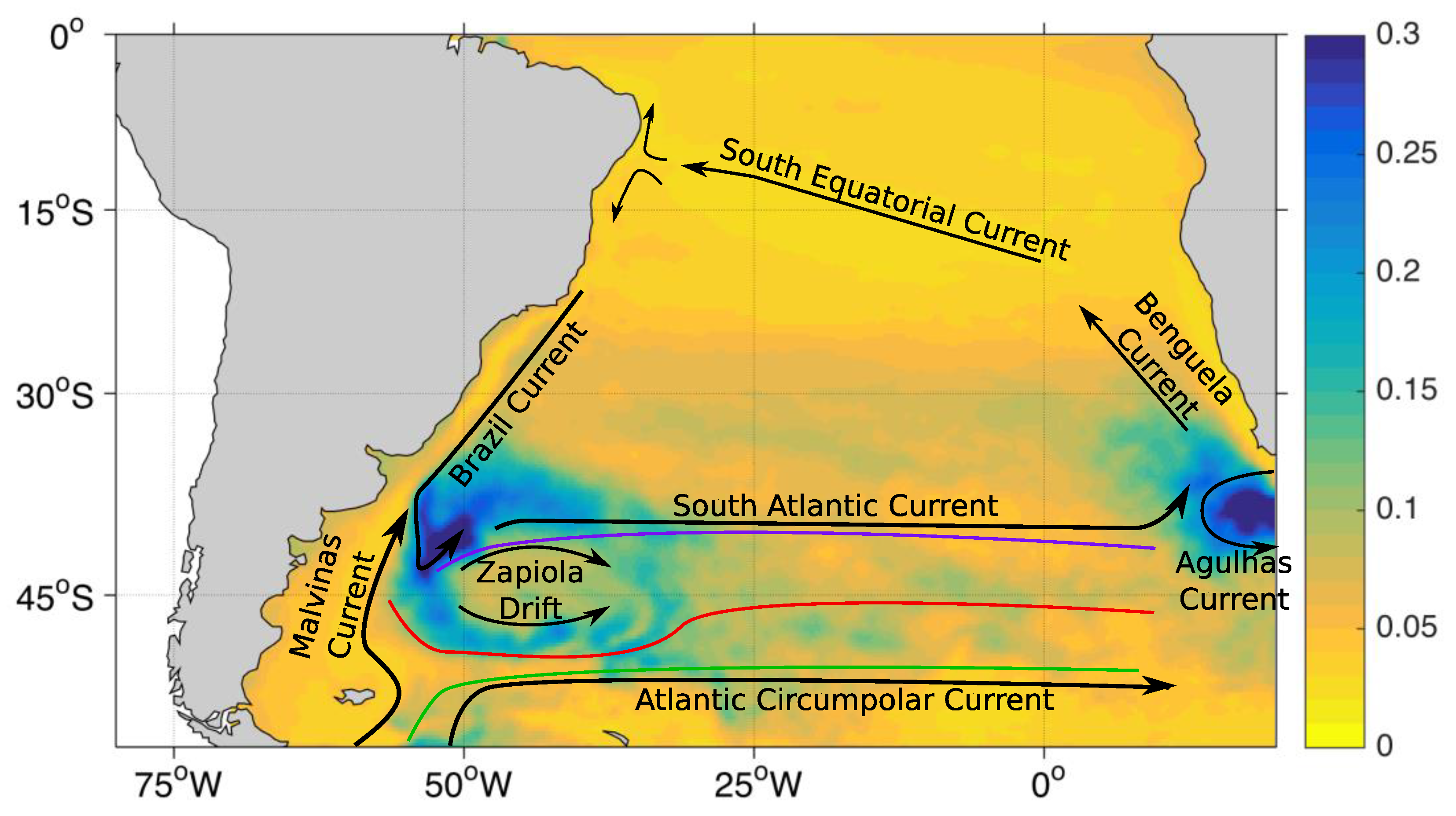
1.2. Processes that Affect Sea Level Trend in the South Atlantic

Ocean circulation in the South Atlantic is very complex. The encounter of two large western boundary currents, the presence of several fronts and eddies are the main processes in which variability can impact on the sea level trend.

The mean surface circulation of the South Atlantic is an anticyclonic gyre formed by the following currents: the eastward South Atlantic Current, the Benguela Current that flows along the coast of Africa towards the Equator, the South Equatorial Current and the southward Brazil Current (BC) (Figure 1). The center of the gyre narrows and moves poleward with increasing depth [17,20]. Using satellite altimetry data, [21] found that the subtropical gyre is composed by a double-cell circulation. They also showed a slow southward migration of the double-cell and the intensification of the South Equatorial Current and Benguela Current. In agreement with the latter observation, [17] observed a positive trend in the South Equatorial Current transport of 1.2 Sv per decade over a 24 years period, based on a numerical model run. On the other hand, [22] documented a positive trend in BC velocities using 25 years of ocean reanalysis data. Both the [17] and [22] observations are compatible with an expansion and southern migration of the anticyclonic gyre of the South Atlantic [23], that, in turn, are due to changes in westerly winds associated with an increasing Southern Annular Mode [17]. The expansion and southern migration of the anticyclonic gyre of the South Atlantic has large consequences in the ocean and in the atmosphere; large positive trends in sea surface temperature (SST) and air–sea fluxes are observed in the Brazil–Malvinas confluence region [23].

In the southern portion of the subtropical gyre there is the only current that flows 360 degrees around the Antarctic continent: the Antarctic Circumpolar Current (ACC). The current is associated with the Southern ACC Front, the Polar Front (PF) and the Subantarctic Front (SAF). The Malvinas Current (MC) detaches from the northernmost branch of the ACC, defined by the SAF, and travels northward along the shelf-break of the Argentine Continental Shelf until it collides with the southward BC at about 38 degrees south (Figure 1). The confluence of these two currents is called the Brazil–Malvinas Confluence (BMC) region and it is characterized for being one of the most energetic regions of the world (e.g., [24]) and for generating a large number of eddies.

The eddies in this region are important for the sea level. For instance, it has been found that the spatial distribution and polarity of eddies are strongly linked to the anticyclonic gyre around the Zapiola Drift, SAF and Subtropical Front (STF) positions [25]. There are more anticyclonic eddies along or south of the STF and more cyclonic eddies north of this front. Furthermore, the anticyclonic circulation around the Zapiola Drift meanders and generates a cyclonic eddy that enters the Zapiola Drift region across the northeastern border, where the potential vorticity gradient is lower [25]. In addition, the eddies in the South West Atlantic are also important for the air–sea interaction; anticyclonic (cyclonic) eddies are associated with positive (negative) sea surface temperature anomalies that cause a positive (negative) heat flux into the atmosphere [26]. In the South Atlantic, there is another region with large mesoscale activity, the Agulhas Retroflection Current, that plays an important role in the climate by transporting heat and salt from the Indian Ocean to the Atlantic through rings and eddies (e.g., [27]). There, an acceleration of eddy propagation, associated with an increment in the eddy activity in the Agulhas system, has been observed since the early 1990s [28,29].

All the processes described above impact the density and, hence, the sea level variability. In particular, changes in the position of the fronts will influence the distribution of the eddies and water masses, which in turn will affect the sea level.

1.3. Scope and Article Organization

The aim of this work is to study the regional sea level trend obtained from 25 years of satellite altimetry in the South Atlantic, between 55° S and 0° S. The South Atlantic mean sea level (SAMSL) trend and its forcing are also investigated. The data and methods needed to carry out the work are presented in Section 2. The results are presented in Section 3. Section 4 presents the discussion and the main conclusions.

2. Materials and Methods

For this study, we used satellite and in situ data for the analysis of sea level anomaly (SLA) trends in the South Atlantic. On a regional scale, SLA can be represented as [2]:

SLA = SH + SM + atmospheric loading + static terms

(1)

where SH is the Steric Height, the sea level variability due to changes in the column density (the sum of thermal expansion and salinity contraction) and SM represents the sea level variability due to ocean mass. The static terms refer to ocean loadings that do not generate dynamic responses to sea level such as the inverted barometer (IB) effect [30] and GIA [31].

Here we focus on SLA, SH and SM trends in the South Atlantic, and we discuss the contribution of GIA. For the matching period, we calculated the linear trend with and without the seasonal cycle. To remove the seasonal cycle from the monthly SLA, SH and SM, we used harmonic analysis as in [18]. This method represents the time series variability as the sum of cosines with different amplitudes and phases; in this work we considered the annual and semiannual cycles only. To compute the SAMSL estimation, we first removed the seasonal cycle, and then we used an area-weighted coefficient as a function of latitude for the spatial averaging. Finally, a low pass filter was applied to remove the variability with periods less than 4 months. The linear trends were calculated using the least square method. We approximated the uncertainty of the linear trends by the standard error of the fitted slope. The standard error of the regression slope represents the average distance between the observed values and the regression line. The significance of the trends was calculated with a Student’s t-test with a level of confidence of 95% [32]. Note that the spatial pattern of sea level trends maps were done simply by removing the seasonal cycle and computing the linear regression at each grid point.

For the datasets described, we estimated the uncertainties as [33]:

$$error=\sqrt{\sum {\sigma }_i^2+{\sigma }_{spread}^2}$$

(2)

where $\sigma$_i is the uncertainty associated with the time series and $\sigma$_spread is the standard deviation of the ensemble mean (e.g., the standard deviation of the two SLA datasets).

2.1. Sea Level Anomaly

For the SLA trends, we used two data sets:

(1)

CMEMS: gridded sea level anomaly maps of ¼ of a degree and daily resolution produced and distributed by the Copernicus Marine and Environment Monitoring Service (CMEMS, https://www.marine.copernicus.eu). The delayed time all-sat (DT all-sat) product is used because it is more precise than near real-time data and has the best possible spatial and temporal sampling. In fact, this product was successfully used to study sea level variability in the South West Atlantic (e.g., [18,19,34,35]). The SLA maps are constructed merging all the available satellite missions (TOPEX/POSEIDON, Jason-1, Geosat Follow-on, Jason-2, Envisat, ERS-1, ERS-2, Cryosat-2, Saral/Altika, Jason-3, Sentinel-3A, HY-2A). There are more than three satellites 70 percent of the time, which increase spatial resolution and improve coverage in high latitudes. An optimal interpolation with realistic correlation functions is applied to produce the high spatial resolution SLA maps [36]. To compare this data with the other data sets (see below), we computed a monthly mean for the January 1993 to December 2017 period. In addition, we used gridded Absolute Dynamic Topography (ADT) to analyze the interannual variability of BMC, Subantarctic Front (SAF) and Polar Front (PF). The ADT product is computed as the SLA plus Mean Dynamic Topography (MDT) [37].

(2)

CSIRO: the sea level products offered by CSIRO Oceans and Atmosphere, Centre for Southern Hemisphere Oceans. The chosen product is based on satellite altimetry data (www.cmar.csiro.au/sealevel/sl_data_cmar.html). CSIRO delivers gridded global monthly maps of SLA, combining TOPEX/Poseidon, Jason-1, Jason-2/OSTM and Jason-3 with one-degree resolution. The advantage of these missions is that they provide the most accurate long-term stability [38]. Within this product, there are different versions depending on the correction applied, such as IB and GIA (the static terms of SLA). The IB removes the effect of atmospheric pressure on sea level, on scales longer than seasonal and GIA correction removes the effect of vertical crustal motions due to post-glacial rebound. For this study, we downloaded the SLA maps corrected (i) only by IB and (ii) by GIA and IB for the period January 1993 to December 2017.

The CMEMS and CSIRO SLA products are corrected for instrumental noise, orbit error, atmospheric attenuation, tidal effects and dynamic atmospheric corrections. All these instrumentals and geophysical corrections add uncertainties to the sea level measurements. The spatial average of individual measurements during orbital cycles and the correction needed to link successive missions are another source of uncertainty [39]. All these uncertainties are decreasing thanks to the efforts of the scientific community [40,41,42]. To account for the uncertainty values associated to the CMEMS and CSIRO products, we considered the along-track SLAs errors ($\sigma$_i) for TOPEX/Poseidon, Jason-1, Jason-2/OSTM and Jason-3, as estimated by [43]. Then, we computed $\sigma$_spread as the standard deviation of the two SLA products. Note that this selection of $\sigma$_i is a lower bound of the actual error, since we are not considering the possible error mapping. In addition, errors might be larger on regional scales [36,44].

2.2. Steric Height

To calculate the steric height and its thermosteric and halosteric components, we vertically integrated the density [18], potential temperature and salinity measurements from Argo buoys as follow:

$$SH=-\frac{1}{{\rho }_0} {{\displaystyle \int }}_{-2000}^0{\rho }^{\prime }\left(z\right)dz={{\displaystyle \int }}_{-2000}^0\alpha T^{\prime }dz-{{\displaystyle \int }}_{-2000}^0\beta S^{\prime }dz$$

(3)

where ρ’ is the time-dependent density anomaly relative to a reference profile (Stammer, 1997) and ρ₀ is a reference water density. α and β are the thermal expansion and haline contraction coefficients, respectively, estimated with Gibbs SeaWater (GSW) Oceanographic Toolbox [45] that considers the Thermodynamic Equation of Seawater 2010 (TEOS-2010).

Argo buoys drift and profile the ocean. The number of floats has increased since the start of the program, and currently there are 4068 operational floats (http://www.argo.ucsd.edu/). The Asia-Pacific Data-Research Center (APDRC) of the International Pacific Research Center (IPRC) generates products based on individual profiles from the US Global Data Assembly Centers (GDACs) available at http://apdrc.soest.hawaii.edu/projects/argo/. In particular, we used two monthly products for the period January 2005 to December 2017: the “horizontal gridding” and the “vertical interpolation”. The first one is based on gridding data from profiles to a regular 1° × 1° grid using an optimal interpolation method. This method interpolates over missing data, filling all the ocean grid points. In the “vertical interpolation” product, the Argo measurements are interpolated into the standard depth levels and it is possible to quantify the number of buoys available at a chosen time.

This Argo product does not provide errors; hence, we assumed a constant uncertainty ($\sigma$_i) of 2.9 mm, following results obtained by [46]. This value is the largest within the error range estimated by [46] for the global thermosteric height. In the case of Argo, $\sigma$_spread is zero since we used only one Argo product.

2.3. Ocean Mass

Thanks to the Gravity Recovery and Climate Experiment (GRACE) mission, it is possible to analyze the sea level variability due to mass change. The mission was launched on 17th March 2002 and ended on 12th October 2017. GRACE consisted of two satellites monitoring the terrestrial water cycle, ice sheet and glacier mass balance, sea level change and ocean bottom pressure variations. Three different data sets are available from http://grace.jpl.nasa.gov: the Center for Space Research of the University of Texas (CSR RL06), the Deutsches Geo Forschungs Zentrum (GFZ RL06) and the Jet Propulsion Laboratory (JPL RL06). They are corrected by GIA based on the model from [47]. In addition, standard corrections for geocenter (degree-1), C20 (degree-20, earth oblateness) and C30 (degree-30) are incorporated. For more detail about GRACE processing, see [48].

Here, we averaged the three data sets to reduce the noise in gravity field solutions [49]. The standard deviation of the three data represents $\sigma$_spread in Equation (2) and we assumed $\sigma$_i is 2 mm, as on global scales [46]. This error estimation represents the lower bound of the real uncertainty. We used 12 complete years, from January 2005 to December 2016, which is the matching period with the Argo and altimetry data.

3. Results

3.1. Sea Level Trends and Fronts

The spatial patterns of the non-seasonal SLA trend for the period 1993–2017 from CMEMS and CSIRO are displayed in Figure 2. CMEMS SLA was corrected by GIA in order to produce a SLA closer to the SLA of CSIRO. Both non-seasonal SLA trend maps, CMEMS and CSIRO, present a similar spatial pattern (Figure 2): the trend values are positive in the entire region, with relatively high values in the latitudinal band between 33° S and ~50° S, in good agreement with the results obtained by [17]. Except in a few regions in the CMEMS data set, the non-seasonal SLA trends are significant with a 95% confidence level. This result did not change significantly when a level of significance of 90% was considered. The SAMSL trends are (2.91 ± 0.46) mm/yr and (2.73 ± 0.12) mm/yr for CMEMS and CSIRO, respectively. These non-seasonal SLA trends are not significantly different from the global value obtained from the ensemble of six altimetry datasets (3.1 ± 0.3 mm/yr [50]).

CMEMS shows finer spatial structures compared to CSIRO (Figure 2). The differences observed are due to different corrections applied and to the different number of satellites considered to produce each product [51]. Indeed, CSIRO has a one-degree spatial resolution, and uses only two satellite missions, while CMEMS has a ¼ of a degree spatial resolution and considers all the available satellite missions. This impacts on the spatial wavelength that the datasets can resolve. [52] analyzed the wavelength spectra of different altimetry products, including CSIRO and CMEMS. Their result showed that the CSIRO SLA trend has less power than the CMEMS SLA trend at a wavelength of less than 10³ km and within the study region mesoscale features with lower spatial scales dominant [25,53].

To analyze the regional sea level trends, we removed the SAMSL value from the SLA (2.91 mm/yr for CMEMS and 2.73 mm/yr for CSIRO). The results are displayed in Figure 3. As in Figure 2, the large spatial patterns of non-seasonal SLA trends derived from CMEMS and CSIRO are similar. Both datasets display a relative maximum between 50° W and 0° E and 33° S and 50° S with trends of the order of 2–3 mm/yr. In the case of CMEMS, there is also a relative maximum trend in the South West Atlantic, in a region marked by a dark green line, with trends higher than 4 mm/yr (Figure 3) that CSIRO does not capture. This region is characterized by variabilities lower than 10³ km associated with a mesoscale [25] that CSIRO cannot resolve [52]. The large positive trends in the region, marked by a dark green line, correspond quite well with the extended BC region, where a positive and significant SST trend was found [23]. The authors argue that the SST increment in that region is associated with a southwest expansion and an intensification of the South Atlantic Subtropical High. The changes in this high-pressure system cause an increase in wind speed, which intensifies the western boundary current, the BC. Thus, the increasing input of warm water from the BC is increasing the SST in the region affected by the BC and, hence, raising the sea level.

The intensification of the BC is not the only factor that can explain the large positive non-seasonal SLA trends observed in Figure 3a in the South West Atlantic. Indeed, the southern shift of the BMC that is due to the southwest expansion of the South Atlantic Subtropical High [23,54] might in turn contribute to the observed trends in the SLA. To confirm our hypothesis, we selected the ADT contour of 30 cm to represent the position of the BMC [55] and we plotted the annual evolution of this contour for the 25-year period (Figure 4). Figure 4b shows a southward displacement of the 30 cm isoline of the order of −0.06 °/yr (

Table 1. The tendency of the latitudinal (°/yr) movement of the ADT contours for four regions along the Atlantic basin. The values presented in this table are significant with a 95% confidence level.

ADT	BMC/45° W	40° W–20° W	20° W–0° E	0° E–15° E
30 cm	−0.06 °/yr/--	−0.05 °/yr	−0.12 °/yr	−0.07 °/yr
5 cm (SAF)	--/−0.16 °/yr	−0.06 °/yr	−0.04 °/yr	−0.04 °/yr
−40 cm (PF)	--/−0.02 °/yr	−0.03 °/yr	−0.04 °/yr	−0.03 °/yr

). Our results are in good agreement with [22], who found a 200 km southward displacement of the STF in 25 years of ocean reanalysis data.

The combination of a stronger (larger transport) BC and a southward displacement of the BMC generates a sizeable impact on the SLA trend in the area previously dominated by cold MC waters (Figure 3a, Figure 4a). At the same time, the evidence of the BC getting warmer at the surface [23] and in the upper 1000 m [22] indicates a possible increase in the thermosteric height.

The southward displacement observed in the BMC region with the 30 cm isoline is also detected across the South Atlantic with different iso-contours that correspond to different fronts (Figure 4a). In fact, superposed to the annual variability, the SAF (ADT contour of 5 cm) and PF (ADT contour of −40 cm) are showing a significant poleward movement (Figure 4a) as well (Table 1). This is consistent with the poleward migration observed in the ACC by [56]. We suggest that the southward shift of the fronts involves the advection of waters that might explain part of the sea level trends in the Zapiola gyre area (between the SAF and STF) and the region between 25° W and 0° E. Our hypothesis is that the advected waters will change the density of the water column and the contribution to the non-seasonal SLA trend will be related to the steric height. A detailed study of the role of advection in the non-seasonal SLA trends could be addressed with a three-dimensional velocity dataset. Unfortunately, there are not enough in situ observations to perform such a study in this region. An analysis based on numerical model outputs should be considered for such a purpose.

The poleward trend observed in the fronts might be related to the wind regime. The intensification and the expansion of the South Atlantic Subtropical High observed by [23] affect the wind pattern. There is evidence that the westerlies have strengthened and moved poleward in the last two decades [17]. As a consequence, the ocean wind-driven circulation—the subtropical gyre—moves poleward together with the fronts.

3.2. What Are the Drivers of SLA Trends in the South Atlantic?

The literature about the GMSL rise has shown that the main contributors to the sea level rise are the changes in mass due to the melting of Arctic and Antarctic ices and the changes in density due to the warming of ocean waters (steric height) (e.g., [2,57]). Most of the studies are based on observations from GRACE to estimate ocean mass and on Argo to compute the thermal component of steric height. Even though the time records available are not long enough to cover the 25 years of altimetry, the results on a global scale show that it is possible to close the SLA budget with small uncertainty (e.g., [2]).

The objective of this section is to analyze the SAMSL rise for the concomitant period of CMEMS, CSIRO, GRACE and Argo, from January 2005 to December 2016. For the spatial mean, we applied the Argo mask to CMEMS, CSIRO and GRACE, removing the South West Atlantic continental shelf.

We first analyzed the SAMSL without removing the seasonal signal (Figure 5). The seasonal signal is clear in the SAMSL time series derived from CMEMS and CSIRO (Figure 5a) and in the steric height time series (Figure 5b). This observation suggests that the seasonal cycle of the SLA is mainly due to the thermal expansion and haline contraction of the water column. The first mode of empirical orthogonal function (EOF) of the detrended SLA is dominated by a seasonal cycle (15.88% for CMEMS and 37.06% for CSIRO) (not shown). The time series of the first mode is highly correlated with steric height (0.89 (95% CL) for CMEMS and 0.81 (95% CL) for CSIRO). The SLA reaches its maximum around March and its minimum in August–September, in concordance with the annual cycle of steric height in the Southern Hemisphere [58]. The ocean mass variability measured by GRACE, on the other hand, presents a weak seasonal cycle with a small amplitude and with an opposite phase (Figure 5b). This indicates that the ocean mass contribution diminishes the amplitude of the steric height.

An interesting feature is that both SAMSL time series show a significant positive trend (

Table 2. South Atlantic mean sea level (SAMSL) trends (mm/yr) derived from CMEMS, CSIRO, GRACE and Argo for the period January 2005 to December 2016. Trend values shown in bold are statistically significant at the 95% significance level.

	SAMSL Trend	Non-seasonal SAMSL Trend
CMEMS	2.38 ± 0.59 mm/yr	2.56 ± 0.36 mm/yr
CSIRO IB	2.02 ± 0.61 mm/yr	2.21 ± 0.29 mm/yr
CSIRO IB GIA	2.28 ± 0.61 mm/yr	2.47 ± 0.29 mm/yr
GRACE	2.32 ± 0.45 mm/yr	2.22 ± 0.21 mm/yr
Steric height	0.50 ± 1.00 mm/yr	0.88 ± 0.23 mm/yr
Thermosteric height	1.02 ± 1.00 mm/yr	1.39 ± 0.32 mm/yr
Halosteric height	−0.26 ± 0.14 mm/yr	−0.26 ± 0.13 mm/yr
GRACE + Steric	2.81 ± 0.80 mm/yr	3.10 ± 0.29 mm/yr

). The discrepancy between CMEMS and CSIRO is small (correlation 0.88, 95% CL). When CSIRO is corrected by GIA, we do observe an increase in the SAMSL trend (2.28 ± 0.61 mm/yr, Table 2). The GIA signal generates a decrease in the sea level trend of 0.26 mm/yr, similar to the value obtained globally (global GIA trend −0.3 mm/yr, [31]). The above results clearly show that the ocean mass is the major contributor to the SAMSL trend (Figure 5b,c, Table 2), while the steric height trend is lower than 1 mm/yr and is not significant (Figure 5b, Table 2). However, when we computed the contribution of thermosteric and halosteric height to the SAMSL trend, we found that both trends are significant (Table 2). What is more, the halosteric height trend compensates for the increment associated with thermosteric height (Table 2). SLA corrected by GIA (ensemble mean of CMEMS and CSIRO) and the sum of the ocean mass and steric height times series are very similar (Figure 5c). Both time series show comparable seasonal variability and trends (Table 2). The trend of the sum of ocean mass and steric height is slightly higher than CMEMS and CSIRO, however, their error bounds overlap.

When the seasonal cycle is removed from the sea level time series, the SAMSL trend increases to 2.56 mm/yr with CMEMS and 2.21 mm/yr with CSIRO, being larger when the GIA correction is applied (Figure 6, Table 2). As we showed in Figure 5, the SAMSL trend is mostly explained by changes in ocean mass estimated by GRACE (2.22 mm/yr). The steric height contribution plays a secondary role (0.88 ± 0.23 mm/yr), observing that the haline component reduces the thermosteric trend (Table 2). These results are similar to GMSL trend studies: the global ocean mass changes (sum of the Antarctic, Arctic and glacier contributions) explain most of the GMSL trend (e.g., [57,59]) and the acceleration rate [2]. It has been shown that the melting ice from Greenland contributes more to the global ocean mass trend than to the Antarctic ice melting [4]. In the case of the South Atlantic, further analysis is needed to estimate the contribution of the different sources to the ocean mass change.

Figure 6c shows the mean of the CMEMS and CSIRO non-seasonal SLA corrected by GIA with the sum of its components, ocean mass and steric height. Both time series display a similar sea level variability. Yet, more discrepancies are observed than in the seasonal variability (Figure 5c). Furthermore, the SAMSL trend is lower than the sum of ocean mass and steric height trends (Figure 7, Table 2) and their intervals slightly overlap. Part of this result might be due to the uncertainties of the datasets. The uncertainty in the sea level trend has been studied through the analysis of the error budget of satellite data (e.g., [38,42,44,60]). Considering a global or a regional approach might also change the results, on a regional scale, [44] found that the uncertainty of the trend is slightly lower than 3 mm/yr; on a global scale the uncertainty is almost one order of magnitude lower (0.3–0.4 mm/yr) [2,60]. In addition to the uncertainties in the datasets, the interannual variability associated with other drivers, such as wind, might contribute to the sea level budget, as well as the steric height at a layer deeper than 2000 m. The latter is not significant on global scales since the sea level budget is almost closed with a small residual [2].

More recently, [52] studied the sea level budget on at the basin scale using the most up-to-date observation products. The budget for an area larger than that considered in this study closes within two standard errors (~0.62 mm/yr). The difference with our result is that they included the abyssal steric height (depth > 2000 m), obtaining a trend of 1 mm/yr. The use of different datasets is also a factor to take into account for the ocean mass trend calculation. We obtained a trend of 2.22 ± 0.21 mm/yr from the mean of CSR RL06, JPL RL06 and GFZ RL06, while [52] estimated a trend of 1.78 ± 0.22 mm/yr derived from RL06 JPL mascon. Indeed, GIA correction is a source of uncertainties [52] and the GIA model changes between GRACE products. On the contrary, the steric height trend estimation in the upper 2000 m (0.88 ± 0.23 mm/yr) shown here is very similar to [52] (0.82 ± 0.11 mm/yr). Despite the importance of obtaining an accurate sea level trend, the sea level budget is mainly explained by ocean mass and steric height on a global (e.g., [2]) and regional scale (e.g., [52]).

It is worth mentioning that, considering error bounds, SAMSL trends are not different; the trend for the 12 years period is 2.65 ± 0.24 mm/yr, and for the 25-year period it is 2.92 ± 0.09 mm/yr (Figure 7). Similar results were obtained on a global scale: for the 12 years period (2005–2016), [59] estimated a trend of 3.75 ± 0.39 mm/yr. For the longer period (1993–2017), [60] obtained a value of 3.35 ± 0.4 mm/yr. Considering their respective error bounds, the values are not significantly different. Therefore, we can observe that despite the smaller trends that were obtained in the South Atlantic, the linear trend computed both on a global level and in the South Atlantic is not dependent on the time period (2005–2016 or 1993–2017) considered.

The spatial pattern of the non-seasonal sea level trends of each component shows that the steric height gives a larger contribution than GRACE to the sea level trend in the BMC, around the Zapiola Drift and in the mid-Atlantic between 33° S and 50° S (Figure 8c,d). The steric height trends have a maximum of 9 mm/yr that CSIRO does not capture. However, there are two spots where the non-seasonal SLA trends are relatively high (<50° W and 55°–50° S, between 25° W and 0° E) that coincide with steric height trends. Even though there are non-seasonal SLA trend values from CMEMS (corrected by GIA) that are not statistically significant (white area in Figure 8a), the hot spot in the southwest (<50° W and 55°–50° S) was observed. The magnitude of these trends is more similar to steric height. A similar situation is identified between 25° W–0° E and 45° S, the relatively high positive non-seasonal SLA trends are also detected by CMEMS.

In general, the spatial pattern of the steric height trends is dominated by the thermosteric component (Figure 8d,f), except for a few areas where the haline component is not negligible. In the case of the two hotspot areas (<50° W and 55°–50° S, between 25° W and 0° E), the halosteric height trends intensify the positive thermosteric trends (Figure 8e,f). As an opposite situation, there is a region in the west, between 30° S and 15° S, where the positive high thermosteric trends are compensated by negative halosteric trends (Figure 8d–f). This region is related to the BC, which carries warm and salty water. The trend maps indicate that the BC is getting warmer and saltier (Figure 8e,f) as it was shown by [22] using 25 years of Mercator ocean reanalysis data in the upper 1000 m. At the same time, the halosteric signal near 15° S coincides with the subtropical salinity maximum. There, the evaporation-dominated region presented an increment in salinity from 1950 to 2008, with a rate of about 0.2 pss/50 years [61]. Assuming that the salinity changes in the water column are dominated by the surface fluxes, a positive trend in salinity would generate a decrease in the SLA.

A peculiar feature is observed in the region located between the Zapiola Drift and the STF, between 43.5° S–39.5° S and 47.5° W–39.5° W. There, negative trend values of steric height are observed. Yet, CMEMS and CSIRO do not observe these negative values in any of the two periods analyzed (Figure 2, Figure 8). This negative trend in steric height is not fully compensated by ocean mass trend. To further analyze this feature, we compared our thermosteric height estimation with thermosteric height produced by NOAA (https://www.nodc.noaa.gov/OC5/3M_HEAT_CONTENT/tsl_global.html) finding a slightly higher trend (not shown). We also used reanalysis data from Mercator (http://marine.copernicus.eu/) to estimate the steric height, thermosteric and halosteric components in this box from the surface to 2000 m for the period 2005–2016. The results showed a positive steric height trend (1.76 ± 1.31 mm/yr) as a combination of temperature and salinity changes (not shown). Even though Argo underestimated the steric height trend, it did capture the importance of the halosteric height in the area (Figure 8d–f). Gridded Argo data is probably underestimating the density changes in the region between the Zapiola Drift and STF due to the poor number of measurements per month to be considered for the interpolation during the first year of the Argo program.

Overall, the map of the steric height trends derived from gridded Argo shows a pattern coherent with the South West Atlantic circulation (Figure 1). There are positive significant trends on the BMC, where the warm BC collides with the cold MC (Figure 8d). This positive signal extends to the southeast following the SAF, and to the northwest, along the STF. As suggested in Section 3.1., the positive trend of the advection of warm waters by the BC [22] to the BMC region is affecting the density and, hence, increasing steric height. Moreover, the BC is a shallow current, and the strongest temperature increment is observed within the upper 600 m [22]. Our results indicate that warming is not only in the upper 1000 m and there is also a small contribution from the layer 1000–2000 m of 1–2 mm/yr. From the analysis of the SAMSL, we also found evidence of warming in deeper layers, since the contribution of steric height is larger when the density change integration is from 0 to 2000 m (0.88 mm/yr) rather than from 0 to 700 m (0.29 ± 0.17 mm/yr). This result is in good agreement with observations on a global scale [2]. Further analysis is needed to fully understand the origin of the positive trend of steric height at deeper layers.

On the other hand, the sea level trend spatial pattern related to ocean mass has a homogeneous distribution in comparison with steric height (Figure 8c). The values oscillate between 1 and 4 mm/yr. Overall, the South Atlantic can be split into two regions: North of 30° S, where the sea level trend varies around 3 mm/yr, similar to GRACE, and south of 30° S. This second region shows a pattern with similarities to the steric height trend map, except on the Agulhas Current region (Figure 8). In that region, the thermosteric height is reduced by the halosteric effect, and the ocean mass trend dominates the non-seasonal SLA trends (Figure 8b–d).

4. Discussion and Conclusions

In this work, we studied the South Atlantic mean sea level (SAMSL) trend derived from two satellite altimetry products (CMEMS and CSIRO) and the role of the main drivers responsible for the global mean sea level rise: ocean mass change and steric height. Results indicate that the SAMSL trend is 2.56 mm/yr using CMEMS data and 2.21 mm/yr using CSIRO data. The trend in ocean mass change (sum of the mass change in the Antarctic, Arctic and glaciers) detected by GRACE in the region is 2.22 mm/yr. We then concluded that the SAMSL trend is dominated by ocean mass changes. The contribution of steric height, estimated with gridded Argo density data for the period of time coincident with the GRACE measurements, is smaller than the mass change contribution. This is in agreement with global mean sea level trend studies (e.g., [57,59]). It was also observed that the halosteric component reduces the thermosteric effect on steric height trends (Table 2).

The analysis of the sea level trend spatial pattern derived from CMEMS, CSIRO, GRACE and Argo revealed that the steric height dominates the sea level trend in the Brazil–Malvinas Confluence (BMC), around the Zapiola Drift and in the mid-Atlantic between 33° S and 50° S (Figure 8c,d). North of 30° S and in the Agulhas retroflection, the ocean mass change contributions are dominant. In addition, the analysis of these maps of non-seasonal SLA trends allowed us to identify the regions where the halosteric signal is important (Figure 8). The results show three areas where the halosteric effect reduces the thermosteric height: between 30° S and 15° S, related to the Brazil Current and subtropical salinity maximum, in the Agulhas Current and between the Zapiola Drift and the Subtropical Front. This corroborates the importance of the salinity variability on regional scales as [10] pointed out.

Furthermore, we estimated the linear trend of the non-seasonal monthly SLA for the entire South Atlantic for the period 1993–2017 (Figure 2). We found some differences with the non-seasonal SLA trends map for the period 2005–2016 (Figure 8a,b). For instance, the hotspot at ~50° W and 55°-50° S disappears, while a marked positive trend appears in the Zapiola Drift (Figure 2a,b and Figure 3). Considering a longer period of non-seasonal SLA, the areas of non-statistically significant trends decreased. The discrepancies between the spatial distribution of linear trends for the period 2005–2016 and the period 1993–2017 might indicate a natural variability (e.g., El Niño Southern Oscillation, North Atlantic Oscillation, Pacific Decadal Oscillation and Antarctic Oscillation) that affects the steric height. To better comprehend the interannual variability of SLA, it is necessary to use long records of temperature and salinity. The use of a reanalysis model will allow future investigation on this subject.

On the other hand, the spatial trend pattern of the 25 years period of sea level showed three regions with tendencies higher than the SAMSL trend. One of those regions is located in the southwest of the extended Brazil region. We associated the presence of this hotspot to the southern shift of the BMC (e.g., [23,54]) and to the intensification of the Brazil current [22]. The interannual evolution of the BMC showed a trend of −0.06 °/yr (Figure 4b, Table 1). What is more, a southward displacement of ADT contours was also observed for the Subantarctic Front (ADT contour of 5 cm) and the Polar Front (ADT contour of −40 cm) across the Atlantic (Table 1). The southward shift of the fronts contributes to a clear thermosteric trend that translates into the SLA trend observed in the Zapiola Drift and between 25° W and 0° W. The poleward shift of the fronts might be related to changes in the wind regime. The southward trend in the westerlies [17], and southwest expansion of the South Atlantic Subtropical High [23] generate a displacement of the wind-driven ocean circulation towards high latitudes.

It is worth mentioning that the relative maximums of non-seasonal SLA trends coincide with the region of high standard deviation of sea level (Figure 1, Figure 2), except in the Zapiola drift. The high variability of sea level in the South Atlantic is related to mesoscale activity (e.g., [25]). This indicates that eddy activity and mean circulation are important in sea level trends. On one hand, the changes in circulation are associated with density changes (steric height), and to wind changes. For instance, a spin-up of the subtropical gyres in the southern oceans has been detected and associated with an increase in the Southern Hemisphere Annular Mode by analyzing sea surface height trends with satellite and Argo data (e.g., [17,62]). On the other hand, the anticyclonic and cyclonic eddies might increase or decrease the sea level locally, and more importantly, the heat transport by eddies would affect the air-sea interaction. The one-degree spatial resolution of CSIRO helps to filter out the mesoscale activity. We thus suggest that part of the differences observed between the CSIRO and CMEMS trends are due to the eddy activity. Our results also show that CMEMS and CSIRO SLA trends are more similar when the longest matching period is considered, suggesting that the influence of mesoscale in the SLA trends decreases when considering long periods. The exception is the Agulhas Retroflection Current where the trends estimated by CMEMS are not significant with the 95% confidence level (Figure 2, Figure 8a).

In summary, our main results indicate that, in the latitudinal band of 50° S–33° S, the role of the advection of warm waters and the associated poleward migration of the currents explain the variability of steric height (both components) observed and thus are the key factors to understand the sea level trend.