Long-Lasting Patterns in 3 kHz Electromagnetic Time Series after the ML = 6.6 Earthquake of 2018-10-25 near Zakynthos, Greece
Abstract
:Research Highlights
- One-month 3 kHz EM disturbances after the 2018/10/25, earthquake near Zakynthos Island and Ilia, Greece.
- Computational recording of common dates with out-of-threshold results from five different chaos analysis techniques.
- All 17 subsequent earthquakes were jointly matched by selected combinations of five, four, three and two chaos analysis methods.
1. Introduction
2. Experimental Aspects
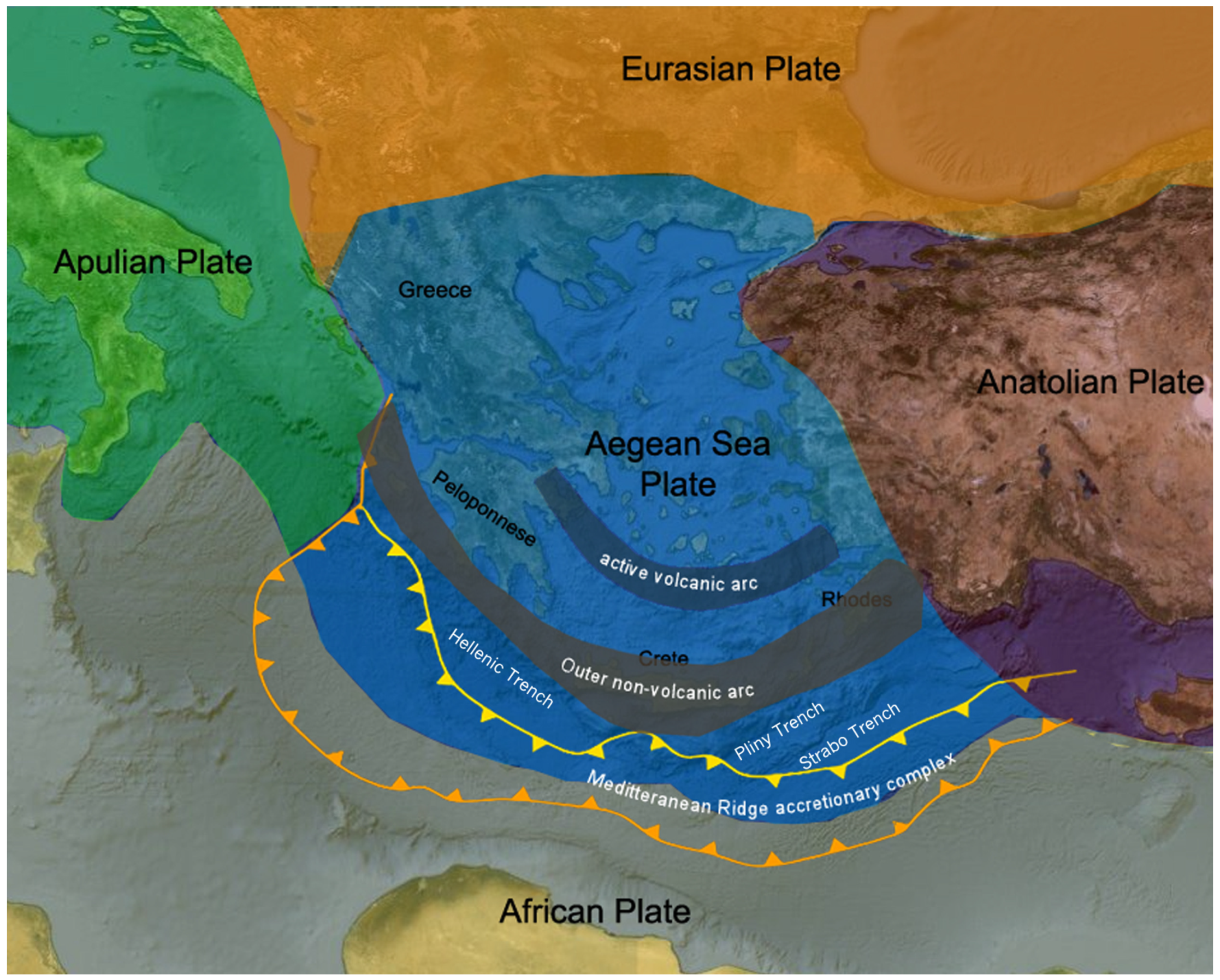
2.1. Geology and Seismic Significance of the Area
- (a)
- Pyrgos, 1993/03/26, and ;
- (b)
- Patra, 1993/07/14, ;
- (c)
- Vartholomio 1998/10/16, ;
- (d)
- Vartholomio, 2002/12/02, ;
- (e)
- Kato Achaia, 2008/06/08, .
2.2. Earthquake Activity and Significance
2.3. Instrumentation
- (i)
- circular magnetic field antennas synchronized properly at 3 kHz;
- (ii)
- Cambel CR-10 data-logger with 2-h buffer;
- (iii)
- telemetry equipment sending continuously the measurements to a personal computer at the rate of 1 Hz.
3. Mathematical Aspects
3.1. Fractal and Long Memory
3.2. Hurst Exponent
- (i)
- If , there is a positive long-range autocorrelation within the series. A high value of the series is followed by a high value and vice versa. High Hurst exponents indicate long-lasting interactions projected to the far future of the series (persistency);
- (ii)
- If , high values of the time series are followed by low values and vice versa. For low H values there is a long-lasting interchange between low and high values which continues in the future of the time series (anti-persistency);
- (iii)
- If the time series completely uncorrelated, i.e., the related processes are random.
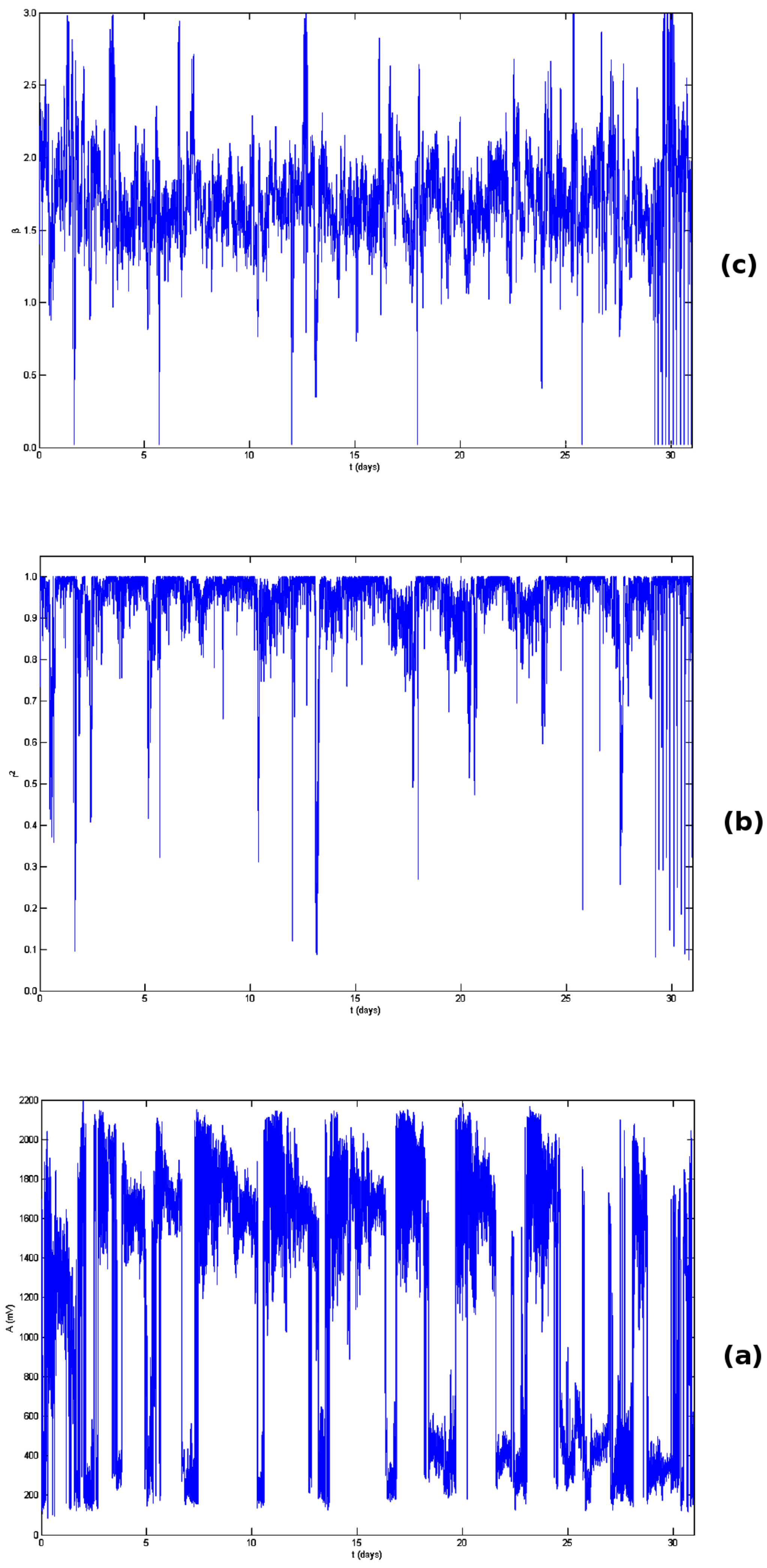
3.3. Detrended Fluctuation Analysis (DFA)
- (i)
- First, the time series is integrated:In Equation (1), the symbol <...> indicates the total average value of the time series and k denotes the various time scales.
- (ii)
- Then, the integrated time series, , is sub-divided into equal bins of length, n without overlapping.
- (iii)
- (iv)
- Then, the integrated time series is detrended. This is iterated in every box of length n, by subtracting the local linear trend, . In this way and for every bin, the detrended time series, , is calculated as:
- (v)
- For every bin of size n, the root-mean-square (rms) of the fluctuations of the integrated and detrended time series is then calculated aswhere are the rms fluctuations of the detrended time series .
- (vi)
- The procedure steps (i)–(v) are iterated for several sizes of the scale boxes. This provides the type of link between and n. If there are long-term associations in the time series, the relationship between and n is exponential:In Equation (4), the scaling exponent (DFA exponent) evaluates the power of the long-term associations of the time series.
- (vii)
- Via a logarithmic transformation of Equation (4), the linear relation between and is determined the slope of which equals . A good linear correlation indicates indicates the related fluctuations are long-lasting and, therefore, associated phenomenon has long memory. In this paper, the goodness of the linear fit is quantified by the square of the Spearman’s () correlation coefficient [3,4,16,17,49,87]. Good linear fits were considered those with 0.95.
- (a)
- The time series were segmented in equal windows of 1024 samples each. This approximated one-month duration of the investigated segment of the time series;
- (b)
- A least-square fit of versus was employed in every window in accordance to Equation (4). Following the approach of a recent paper of members of the team [88] the data were fitted to a straight line without seeking crossovers under the constraint that the slope of the fit exhibited square of Spearman’s correlation coefficient above 0.95;
- (c)
- The window was forwarded one sample and the procedure (a)–(b) was iterated until the end of the signal;
- (d)
- DFA slopes were finally plotted versus time and the corresponding plot data were extracted to ASCII output files for further use.
3.4. Fractal Dimension Analysis
3.4.1. Katz’s Method
3.4.2. Higuchi’s Method
3.4.3. Sevcik’s Method
3.4.4. Computational Methodology of Fractal Dimension
- (i)
- The time series was segmented in windows of 1024 samples each, i.e., of approximately 20 min span).
- (ii)
- In reference to each method, the fractal dimensions were calculated:
- Katz’s method: Equal to D of Equation (8) for n = 1024 and = 1, a value that corresponds to the distance between the points of the series that constitute the parameter L and to the sampling rate of the electromagnetic time series (1 Hz).
- Higuchi’s method: Equal to the slope D of the first order least-square fit of the log–log transformation of Equation (8), namely the relation of versus , for .
- Sevcik’s method: Equal to the Hausdorff dimension of Equation (16) () for N = 1024, namely equal to the number of samples in each window which constitutes parameter L.
- (iii)
- Each window was forwarded one sample (sliding window technique) and the procedure (i)–(ii) was iterated until the end of the time series.
- (iv)
- Time-evolution plots of the fractal dimensions in accordance to the Katz’s, Higuchi’s and Sevcik’s methods were generated, and the partial data were extracted to ASCII files for further use.
3.5. Fractal Analysis
Computational Methodology of Fractal Analysis
- (a)
- The time series was divided in windows of length of 1024 samples;
- (b)
- The power spectrum, and the central frequency, f of the Morlet wavelet were calculated in every window;
- (c)
- A least-square fit was implemented in each window between and . Acceptable fits were considered those exhibiting ;
- (d)
- Each window was slid one sample forward and the steps (A)–(C) were repeated to the end of the time series;
- (e)
- Plots of and with time were produced and the partial results were extracted to ASCII files for further use.
3.6. Further Issues for Chaos Analysis
3.6.1. Segmentation to Chaos Analysis Classes
- (a)
- Class I: This class includes the windows that, on one hand, exhibited DFA least-square log–log fits with Spearman’s coefficient while, on the other hand, the DFA’s scaling exponent was in the interval , namely they can be modelled by the fBm class [4]. It is significant that the Class-I segments:
- (b)
- Class II: this class contains the windows of the time series segments with DFA’s (i.e., they do not follow the prominent fBm class) or with (i.e., they follow the fractional Gaussian noise (fGn) class).It is important that the Class-II segments:
- are the complement of the Class-I ones.
3.7. Chaos Analysis Outcomes Comparisons
- (1)
- From (DFA exponent) () as:
- (2)
- From fractal dimension (D) as:(Berry’s equation)
- (3)
- From power-law as:
3.8. Meta-Analysis
- (a)
- Each ASCII output results file is computationally searched for out-of-thresholds values according to user-defined limits. The ASCII files containing the DFA’s exponents and the spectral power law -values are searched for over-threshold values whereas the ASCII files containing the fractal dimension values are searched for under threshold values. The out-of-thresholds values are written in new ASCII meta-analysis stage 1 files;
- (b)
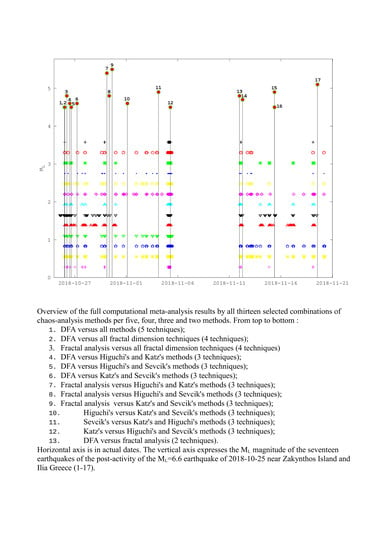
- The meta-analysis ASCII files of (a) are further filtered computationally to identify areas with common dates, under the constraint that each segment’s date is arbitrarily considered to be the date of the first sample of this segment. Taking into account that the analysis of each of the five methods is performed via a sliding window technique of one sample gliding, the above date consideration, finally, yields to full coverage of all dates but the one of the last segment. The computational search is iterated in the results of all possible combinations of:
- DFA versus fractal analysis or versus at least two fractal dimension calculation techniques (6 combinations);
- Fractal analysis versus at least two fractal dimension calculation techniques (4 combinations);
- One fractal dimension calculation technique versus the other two (3 combinations);
4. Results and Discussion
- (1)
- If , the time series constitute a temporal fractal and follow the precursory Class-I category;
- If , the time series are anti-persistent;
- If , the time series are persistent;
- (2)
- If , the time series follow the Class-II category, i.e., they are of low predictability and precursory value;Especially:
- If , the fluctuations of the processes do not grow and the related system is stationary;
- If , the system follows random dynamics of no memory (random-walk);
- (i)
- A total of 22,943 EM segments are persistent with according to the DFA. The robustness of DFA, its fundamental property to locate hidden long-memory trends in time series, together with its extensive use in studies pre-seismic activity from geosystems, e.g., [10,11,16,23,99], provide strong clues on the pre-seismic nature of the related EM segments.
- (ii)
- A significant portion of EM segments are below-threshold and recognized as signs of pre-seismic activity via three different fractal dimension calculation algorithms. A total of 564,082 are identified by the Katz’s method, 142,725 with the Higuchi’s method and 652,603 with the Sevcik’s method. These segments are directly linked through relation (Equations (19) and (20)) to several out-of-threshold EM segments identified from DFA. The out-of-threshold EM segments (common with DFA or not) have low fractal dimensions and high Hurst exponents both indicating high predictability of the related time series and significant precursory value of these segments as regards their pre-seismic nature. In addition, all fractal dimension algorithms have been used with success in radon in soil pre-earthquake disturbances [3].
- (iii)
- A total of 62,294 EM segments are recognized as of high predictability and of significant pre-earthquake fractal nature according to the findings of the fractal analysis technique. The fractal methods are very important in the study of pre-earthquake geosystems, because these exhibit intense fractal activity, both in space and time, according to extensive literature reports, e.g., [8,10,16].
5. Conclusions
- (1)
- This paper focuses on the post-seismic activity of a strong earthquake occurred on 2018/10/25 in Zakynthos Island, Greece. The post-seismic period extends over one month and is based on 3 kHz EM disturbance measurements derived by a ground-station located at Kardamas, Ilia, Greece. Seventeen earthquakes are included in the study with magnitudes between and and depths between 3 km and 17 km with all epicenters near Zakynthos Island and Ilia.
- (2)
- Five different time-evolving chaos analysis methods are employed in the analysis. These methods are the detrended fluctuation analysis, the fractal dimension analysis with the methods of Higuchi, Katz and Sevcik and the power-law spectral fractal analysis. All these methods have been used with success in several pre-earthquake EM and radon signals in Greece.
- (3)
- A novel fully computational methodology (meta-analysis) is applied to the time-evolution ASCII outcomes of all five chaos analysis techniques. Via a two-stage process, all out-of-threshold ASCII data values are computationally searched and the common time instances of 13 possible combinations of five, four, three and two techniques are noted. Through this process combination results of significant value are produced.
- (4)
- Several persistent segments are found through DFA with exponents between . Higuchi’s, Katz’s and Sevcik’s methods identify numerous segments with fractal dimensions . Many segments with are recognized by the fractal analysis method. All these thresholds refer to persistent fBm Class-I segments of high predictability and pre-seismic value.
- (5)
- Numerous combined meta-analysis segments are located with fractal behavior, dynamical complexity and long-memory. All these correspond to persistent fBm Class-I segments and are considered to be pre-earthquake footprints of high reliability.
- (6)
- Six of the 17 post-earthquakes are matched by all 13 selected combinations of five, four, three and two chaos analysis methods. Four earthquakes are matched by all combinations of four, three and two methods from the 13 combinations. The remaining seven earthquakes are matched by at least one combination of three methods. Activity within typical time windows among or after these earthquakes is reported as well.
Author Contributions
Funding
Conflicts of Interest
References
- Nikolopoulos, D.; Petraki, E.; Cantzos, D.; Yannakopoulos, P.H.; Panagiotaras, D.; Nomicos, C. Fractal Analysis of Pre-Seismic Electromagnetic and Radon Precursors: A Systematic Approach. J. Earth Sci. Clim. Chang. 2016, 7, 1–11. [Google Scholar]
- Nikolopoulos, D.; Cantzos, D.; Petraki, E.; Yannakopoulos, P.H.; Nomicos, C. Traces of long-memory in pre-seismic MHz electromagnetic time series-Part1: Investigation through the R/S analysis and time-evolving spectral fractals. J. Earth Sci. Clim. Chang. 2016, 7. [Google Scholar] [CrossRef] [Green Version]
- Nikolopoulos, D.; Matsoukas, C.; Yannakopoulos, P.H.; Petraki, E.; Cantzos, D.; Nomicos, C. Long-Memory and Fractal Trends in Variations of Environmental Radon in Soil: Results from Measurements in Lesvos Island in Greece. J. Earth Sci. Clim. Chang. 2018, 9, 1–11. [Google Scholar]
- Nikolopoulos, D.; Yannakopoulos, P.H.; Petraki, E.; Cantzos, D.; Nomicos, C. Long-Memory and Fractal Traces in kHz-MHz Electromagnetic Time Series Prior to the ML = 6.1, 12/6/2007 Lesvos, Greece Earthquake: Investigation through DFA and Time-Evolving Spectral Fractals. J. Earth Sci. Clim. Chang. 2018, 9, 1–15. [Google Scholar]
- Cicerone, R.; Ebel, J.; Britton, J. A systematic compilation of earthquake precursors. Tectonophysics 2009, 476, 371–396. [Google Scholar] [CrossRef]
- Ghosh, D.; Deb, A.; Sengupta, R. Anomalous radon emission as precursor of earthquake. J. Appl. Geophys. 2009, 187, 245–258. [Google Scholar] [CrossRef]
- Hayakawa, M.; Hobara, Y. Current status of seismo-electromagnetics for short-term earthquake prediction. Geomat. Nat. Hazards Risk 2010, 1, 115–155. [Google Scholar] [CrossRef]
- Uyeda, S.; Nagao, T.; Kamogawa, M. Short-term earthquake prediction: Current status of seismo-electromagnetics. Tectonophysics 2009, 470, 205–213. [Google Scholar] [CrossRef]
- Cantzos, D.; Nikolopoulos, D.; Petraki, E.; Yannakopoulos, P.H.; Nomicos, C. Earthquake precursory signatures in electromagnetic radiation measurements in terms of day-to-day fractal spectral exponent variation: Analysis of the eastern Aegean 13/04/2017–20/07/2017 seismic activity. J. Seismol. 2018, 22, 1499–1513. [Google Scholar] [CrossRef]
- Petraki, E.; Nikolopoulos, D.; Nomicos, C.; Stonham, J.; Cantzos, D.; Yannakopoulos, P.; Kottou, S. Electromagnetic Pre-earthquake Precursors: Mechanisms, Data and Models—A Review. J. Earth Sci. Clim. Chang. 2015, 6, 1–11. [Google Scholar]
- Petraki, E.; Nikolopoulos, D.; Panagiotaras, D.; Cantzos, D.; Yannakopoulos, P.; Nomicos, C.; Stonham, J. Radon-222: A Potential Short-Term Earthquake Precursor. J. Earth Sci. Clim. Chang. 2015, 6, 1–11. [Google Scholar]
- Khan, P.A.; Tripathi, S.C.; Mansoori, A.A.; Bhawre, P.; Purohit, P.K.; Gwal, A. Scientific efforts in the direction of successful Earthquake Prediction. Int. J. Geomat. Geosci. 2011, 1, 669–677. [Google Scholar]
- Nikolopoulos, D.; Petraki, E.; Marousaki, A.; Potirakis, S.; Koulouras, G.; Nomicos, C.; Panagiotaras, D.; Stonhamb, J.; Louizi, A. Environmental monitoring of radon in soil during a very seismically active period occurred in South West Greece. J. Environ. Monit. 2012, 14, 564–578. [Google Scholar] [CrossRef] [PubMed]
- Nikolopoulos, D.; Petraki, E.; Vogiannis, E.; Chaldeos, Y.; Giannakopoulos, P.; Kottou, S.; Nomicos, C.; Stonham, J. Traces of self-organisation and long-range memory in variations of environmental radon in soil: Comparative results from monitoring in Lesvos Island and Ileia (Greece). J. Radioanal. Nucl. Chem. 2014, 299, 203–219. [Google Scholar] [CrossRef]
- Nikolopoulos, D.; Petraki, E.; Nomicos, C.; Koulouras, G.; Kottou, S.; Yannakopoulos, P.H. Long-Memory Trends in Disturbances of Radon in Soil Prior ML = 5.1 Earthquakes of 17 November 2014 Greece. J. Earth Sci. Clim. Chang. 2015, 6, 1–11. [Google Scholar]
- Petraki, E. Electromagnetic Radiation and Radon-222 Gas Emissions as Precursors of Seismic Activity. Ph.D. Thesis, Department of Electronic and Computer Engineering, Brunel University, London, UK, 2016. [Google Scholar]
- Petraki, E.; Nikolopoulos, D.; Fotopoulos, A.; Panagiotaras, D.; Koulouras, G.; Zisos, A.; Nomicos, C.; Louizi, A.; Stonham, J. Self-organised critical features in soil radon and MHz electromagnetic disturbances: Results from environmental monitoring in Greece. Appl. Radiat. Isotop. 2013, 72, 39–53. [Google Scholar] [CrossRef]
- Petraki, E.; Nikolopoulos, D.; Fotopoulos, A.; Panagiotaras, D.; Nomicos, C.; Yannakopoulos, P.; Kottou, S.; Zisos, A.; Louizi, A.; Stonham, J. Long-range memory patterns in variations of environmental radon in soil. Anal. Methods 2013, 5, 4010–4020. [Google Scholar] [CrossRef]
- Balasis, G.; Daglis, I.; Papadimitriou, C.; Kalimeri, M.; Anastasiadis, A.; Eftaxias, K. Dynamical complexity in Dst time series using non-extensive Tsallis entropy. Geophys. Res. Lett. 2008, 35, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Cantzos, D.; Nikolopoulos, D.; Petraki, E.; Nomicos, C.; Yannakopoulos, P.H.; Kottou, S. Identifying Long-Memory Trends in Pre-Seismic MHz Disturbances through Support Vector Machines. J. Earth. Sci. Clim. Chang. 2015, 6, 1–9. [Google Scholar]
- Cantzos, D.; Nikolopoulos, D.; Petraki, E.; Yannakopoulos, P.H.; Nomicos, C. Fractal Analysis, Information-Theoretic Similarities and SVM Classification for Multichannel, Multi-Frequency Pre-Seismic Electromagnetic Measurements. J. Earth. Sci. Clim. Chang. 2016, 7, 1–10. [Google Scholar] [CrossRef]
- Sarlis, N.; Skordas, E.; Varotsos, P.; Nagao, T.; Kamogawa, M.; Tanaka, H.; Uyeda, S. Minimum of the order parameter fluctuations of seismicity before major earthquakes in Japan. Proc. Natl. Acad. Sci. USA 2013, 110, 13734–13738. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Skordas, E.S. On the increase of the “non-uniform” scaling of the magnetic field variations before the M(w)9.0 earthquake in Japan in 2011. Chaos 2014, 24, 023131. [Google Scholar] [CrossRef] [PubMed]
- Smirnova, N.; Hayakawa, M. Fractal characteristics of the ground-observed ULF emissions in relation to geomagnetic and seismic activities. J. Atmos. Sol. Terr. Phys. 2007, 69, 1833–1841. [Google Scholar] [CrossRef]
- Smirnova, N.; Hayakawa, M.; Gotoh, K. Precursory behavior of fractal characteristics of the ULF electromagnetic fields in seismic active zones before strong earthquakes. Phys. Chem. Earth 2004, 29, 445–451. [Google Scholar] [CrossRef]
- Smirnova, N.A.; Kiyashchenko, D.A.T.; Troyan, V.N.; Hayakawa, M. Multifractal Approach to Study the Earthquake Precursory Signatures Using the Ground-Based Observations. Rev. Appl. Phys. 2013, 2, 3. [Google Scholar]
- Varotsos, P.; Sarlis, N.; Skordas, E. Scale-specific order parameter fluctuations of seismicity in natural time before mainshocks. Europhys. Lett. 2011, 96, 59002. [Google Scholar] [CrossRef] [Green Version]
- Varotsos, P.; Sarlis, N.; Skordas, E.S.; Christopoulos, G.; Lazaridou, M.S. Identifying the occurrence time of an impending mainshock: A very recent case. Earthq. Sci. 2015, 8, 215–222. [Google Scholar] [CrossRef] [Green Version]
- Varotsos, P.; Sarlis, N.; Skordas, E. Identifying the occurrence time of an impending major earthquake: A review. Earthq. Sci. 2017, 30, 209–218. [Google Scholar] [CrossRef]
- Parrot, M.; Tramutoli, V.; Liu, J.Y.; Pulinets, S.; Ouzounov, D.; Genzano, N.; Lisi, M.; Hattori, K.; Namgaladze, A. Atmospheric and ionospheric coupling phenomena related to large earthquakes. Nat. Hazards Earth Syst. Sci. Discuss 2016, 172, 1–30. [Google Scholar] [CrossRef] [Green Version]
- Ryu, K.; Parrot, M.; Kim, S.G.; Jeong, K.S.; Chae, J.S.; Pulinets, S.; Oyama, K.I. Suspected Seismo-Ionospheric Coupling Observed by Satellite Measurements and GPS TEC Related to the M7.9 Wenchuan Earthquake of 12 May 2008. J. Geophys. Res. Space Phys. 2014, 119, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Kovachev, S.A. Results of seismological observations in the western Kaliningrad region and in the Baltik Sea water area, Izv. Phys. Solid Earth 2008, 44, 706–716. [Google Scholar] [CrossRef]
- Skarlatoudis, A.A.; Papazachos, C.B.; Margaris, B.N.; Theodulidis, N.; Papaioannou, C.; Kalogeras, I.; Scordilis, E.M.; Karakostas, V. Empirical peak ground-motion predictive relations for shallow earthquakes in Greece. Bull. Seismol. Soc. Am. 2003, 93, 2596–2603. [Google Scholar] [CrossRef]
- Hayakawa, M.; Kawate, R.; Molchanov, O.; Yumoto, K. Results of ultra-low-frequency magnetic field measurements during the Guam earthquake of 8 August 1993. Geophys. Res. Lett. 1996, 23, 241–244. [Google Scholar] [CrossRef]
- Hayakawa, M.; Itoh, T.; Hattori, K.; Yumoto, K. ULF electromagnetic precursors for an earthquake at Biak, Indonesia on February 17, 1996. Geophys. Res. Lett. 2000, 27, 1531–1534. [Google Scholar] [CrossRef]
- Hayakawa, M.; Ida, Y.; Gotoh, K. Multifractal analysis for the ULF geomagnetic data during the Guam earthquake. In Proceedings of the IEEE 6th International Symposium on Electromagnetic Compatibility and Electromagnetic Ecology, Saint Petersburg, Russia, 21–24 June 2005; pp. 239–243. [Google Scholar]
- Hayakawa, M.; Ida, Y.; Gotoh, K. Fractal (mono- and multi-) analysis for the ULF data during the 1993 Guam earthquake for the study of prefracture criticality. Curr. Dev. Theory Appl. Wavelets 2008, 2, 159–174. [Google Scholar]
- Varotsos, P.; Alexopoulos, K. Physical properties of the variations of the electric field of the earth preceding earthquakes, I. Tectonophysics 1984, 110, 73–98. [Google Scholar] [CrossRef]
- Varotsos, P.; Alexopoulos, K. Physical properties of the variations of the electric field of the earth preceding earthquakes, II. Tectonophysics 1984, 110, 99–125. [Google Scholar] [CrossRef]
- Varotsos, P.; Sarlis, N.; Lazaridou, M.B.N. Statistical evaluation of earthquake prediction results. Comments on the success rate and alarm rate. Acta Geophys. Pol. 1996, 44, 329–347. [Google Scholar]
- Varotsos, P.; Sarlis, N.; Eftaxias, K.; Lazaridou, M.B.N.; Makris, J.; Abdulla, A.; Kapiris, P. Prediction of the 6.6 Grevena-Kozani Earthquake of 13 May 1995. Phys. Chem. Earth 1999, 24, 115–121. [Google Scholar] [CrossRef]
- Varotsos, P.; Sarlis, N.; Skordas, E. Magnetic field variations associated with SES. The instrumentation used for investigating their detectability. Proc. Jpn. Acad. Ser. B 2001, 77, 87–92. [Google Scholar] [CrossRef] [Green Version]
- Varotsos, P.; Sarlis, N.; Skordas, E. Long-range correlations in the electric signals that precede rupture: Further investigations. Phys. Rev. E 2003, 67, 021109. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Varotsos, C.; Ondov, J.; Efstathiou, M. Scaling properties of air pollution in Athens, Greece and Baltimore. Md. Atmos. Environ. 2005, 39, 4041–4047. [Google Scholar] [CrossRef]
- Varotsos, C.A.; Ondov, J.M.; Cracknell, A.P.; Efstathiou, M.N.; Assimakopoulos, M.N. Long-range persistence in global aerosol index dynamics. Int. J. Remote Sens. 2006, 27, 3593–3603. [Google Scholar] [CrossRef]
- Varotsos, P.; Sarlis, N.; Skordas, E.; Lazaridou, M. Electric pulses some minutes before earthquake occurrences. Appl. Phys. Lett. 2007, 90, 1–3. [Google Scholar] [CrossRef] [Green Version]
- Varotsos, P.; Sarlis, N.; Skordas, E. Detrended Fluctuation Analysis of the magnetic and electric field variations that precede rupture. Chaos 2009, 19. [Google Scholar] [CrossRef] [Green Version]
- Yonaiguchi, N.; Ida, Y.; Hayakawa, M.; Masuda, S. Fractal analysis for VHF electromagnetic noises and the identification of preseismic signature of an earthquake. J. Atmos. Sol. Ter. Phy. 2007, 69, 1825–1832. [Google Scholar] [CrossRef]
- Nikolopoulos, D.; Moustris, K.; Petraki, E.; Koulougliotis, D.; Cantzos, D. Fractal and long-memory traces in PM10 time series in Athens, Greece. Environmnets 2019, 6, 29. [Google Scholar] [CrossRef] [Green Version]
- gredass. Available online: http://gredass.unife.it (accessed on 23 August 2019).
- INGV. 2007. Available online: http://diss.rm.ingv.it/diss/medtsunami/HTMLSourceZoneMaps/Hellenic_Arc.html (accessed on 23 August 2019).
- Lekas, A.; Fountoulis, I.; Papanikolaou, D. Intensity Distribution and Neotectonic Macrostructure Pyrgos Earthquake Data 26 March 1993, Greece. Nat. Hazards 2000, 21, 19–33. [Google Scholar] [CrossRef]
- NOA. Available online: http://www.gein.noa.gr/services/cat.html (accessed on 23 August 2019).
- USGS. Available online: http://earthquake.usgs.gov/earthquakes/map/ (accessed on 23 August 2019).
- Mandelbrot, B.B.; Ness, J.W.V. Fractional Brownian motions, fractional noises and applications. J. Soc. Ind. Appl. Math 1968, 10, 422–437. [Google Scholar] [CrossRef]
- Morales, I.O.; Landa, O.; Fossion, R.; Frank, A. Scale invariance, self-similarity and critical behaviour in classical and quantum system. J. Phys. Conf. Ser. 2012, 380. [Google Scholar] [CrossRef] [Green Version]
- Musa, M.; Ibrahim, K. Existence of long memory in ozone time series. Sains Malays. 2012, 41, 1367–1376. [Google Scholar]
- May, R.M. Simple mathematical models with very complicated dynamics. Nature 1976, 261, 459–467. [Google Scholar] [CrossRef] [PubMed]
- Sugihara, G.; May, R. Nonlinear forecasting as a way of distinguishing chaos from measurement error in time series. Nature 1990, 344, 734–741. [Google Scholar] [CrossRef] [PubMed]
- Hurst, H. Long term storage capacity of reservoirs. Trans. Am. Soc. Civ. Eng. 1951, 116, 770–808. [Google Scholar]
- Hurst, H.; Black, R.; Simaiki, Y. Long-term Storage: An Experimental Study; Constable: London, UK, 1965. [Google Scholar]
- Lopez, T.; Martınez-Gonzalez, C.; Manjarrez, J.; Plascencia, N.; Balankin, A. Fractal Analysis of EEG Signals in the Brain of Epileptic Rats, with and without Biocompatible Implanted Neuroreservoirs. AMM 2009, 15, 127–136. [Google Scholar] [CrossRef]
- Kilcik, A.; Anderson, C.; Rozelot, J.; Ye, H.; Sugihara, G.; Ozguc, A. Nonlinear Prediction of Solar Cycle 24. Astrophys. J. 2009, 693, 1173–1177. [Google Scholar] [CrossRef] [Green Version]
- Gilmore, M.; Yu, C.; Rhodes, T.; Peebles, W. Investigation of rescaled range analysis, the Hurst exponent, and long-time correlations in plasma turbulence. Phys. Plasmas 2002, 9, 1312–1317. [Google Scholar] [CrossRef] [Green Version]
- Granero, M.S.; Segovia, J.T.; Perez, J.G. Some comments on Hurst exponent and the long memory processes on capital Markets. Phys. A Stat. Mech. Appl. 2008, 387, 5543–5551. [Google Scholar] [CrossRef]
- Dattatreya, G. Hurst Parameter Estimation from Noisy Observations of Data Traffic Traces. In Proceedings of the 4th WSEAS International Conference on Electronics, Control and Signal Processing, Rio de Janeiro, Brazil, 25–27 April 2005; pp. 193–198. [Google Scholar]
- Fujinawa, Y.; Takahashi, K. Electromagnetic radiations associated with major earthquakes. Phys. Earth Planet. Inter. 1998, 105, 249–259. [Google Scholar] [CrossRef]
- Hayakawa, M. VLF/LF radio sounding of ionospheric perturbations associated with earthquakes. Sensors 2007, 7, 1141–1158. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Polygiannakis, J.; Kapiris, P.; Peratzakis, A.; Eftaxias, K.; Yao, X. Fractal spectral analysis of pre-epileptic seizures in terms of criticality. J. Neural Eng. 2005, 2, 11–16. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rehman, S.; Siddiqi, A. Wavelet based Hurst exponent and fractal dimensional analysis of Saudi climatic dynamics. Chaos Solitons Fractals 2009, 39, 1081–1090. [Google Scholar] [CrossRef]
- Stanley, H.E. Powerlaws and universality. Nature 1995, 378, 597–600. [Google Scholar] [CrossRef]
- Stratonovich, R.L. Topics in the Theory of Random Noise; Gordon and Breach: New York, NY, USA, 1981. [Google Scholar]
- Chen, Z.; Ivanov, P.; Hu, K.; Stanley, H. Effect of nonstationarities on detrended fluctuation analysis. Phys. Rev. E 2002, 65, 1–15. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hu, K.; Ivanov, P.C.; Chen, Z.; Hilton, M.F.; Stanley, H.E.; Shea, S. Non-random fluctuations and multi-scale dynamics regulation of human activity. Phys. A Stat. Mech. Appl. 2004, 337, 307–318. [Google Scholar] [CrossRef] [Green Version]
- Peng, C.; Mietus, J.; Havlin, S.; Stanley, H.; Goldberger, A. Long-range anti-correlations and non-Gaussian behavior of the heartbeat. Phys. Rev. Lett. 1993, 70, 1343–1346. [Google Scholar] [CrossRef]
- Peng, C.; Buldyrev, S.; Simons, M.; Havlin, S.; Stanley, H.; Goldberger, A. On the mosaic organization of DNA sequences. Phys. Rev. E 1994, 49, 1685–1689. [Google Scholar] [CrossRef] [Green Version]
- Peng, C.; Havlin, S.; Stanley, H.; Goldberger, A. Quantification of scaling exponents and crossover phenomena in nonstationary heartbeat time series. Chaos 1995, 5, 82–87. [Google Scholar] [CrossRef]
- Peng, C.; Hausdor, J.; Havlin, S.; Mietus, J.; Stanley, H.; Goldberger, A. Multiple-time scales analysis of physiological time series under neural control. Phys. A Stat. Mech. Appl. 1998, 249, 491–500. [Google Scholar] [CrossRef]
- Buldyrev, S.V.; Goldberger, A.L.; Havlin, S.; Mantegna, R.N.; Matsa, M.E.; Peng, C.K.; Simons, M.; Stanley, H.E. Long-range correlation properties of coding and noncoding DNA sequences: GenBank analysis. Phys. Rev. E Stat. Phys. 1995, 51, 5084–5091. [Google Scholar] [CrossRef]
- Ivanov, P.C.; Rosenblum, M.G.; Peng, C.K.; Mietus, J.E.; Havlin, S.; Stanley, H.E.; Goldberger, A.L. Multifractality in human heartbeat dynamics. Nature 1999, 399, 461–465. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hu, K.; Ivanov, P.; Chen, Z.; Carpena, P.; Stanley, H. Effect of trends on Detrended Fluctuation Analysis. Phys. Rev. E 2001, 64, 1–19. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ivanova, K.; Ausloos, M. Application of the detrended fluctuation analysis (DFA) method for describing cloud breaking. Phys. A Stat. Mech. Appl. 1999, 274, 349–354. [Google Scholar] [CrossRef]
- Koscielny-Bunde, E.; Bunde, A.; Havlin, S.; Roman, H.E.; Goldreich, Y.; Schellnhuberet, H. Indication of a Universal Persistence Law Governing Atmospheric Variability. Phys. Rev. Lett. 1998, 81, 729–732. [Google Scholar] [CrossRef]
- Vandewalle, N.; Ausloos, M. Coherent and random sequences in financial fluctuations. Phys. A Stat. Mech. Appl. 1997, 246, 454–459. [Google Scholar] [CrossRef]
- Varotsos, P.; Sarlis, N.; Skordas, E. Natural Time Analysis: The New View of Time. Precursory Seismic Electric Signals, Earthquakes and other Complex Time- Series; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Varotsos, P.; Sarlis, N.; Skordas, E.; Lazaridou, M. Identifying sudden cardiac death risk and specifying its occurrence time by analyzing electrocardiograms in natural time. Appl. Phys. Lett. 2007, 91. [Google Scholar] [CrossRef]
- Nikolopoulos, D.; Valais, I.; Michail, C.; Bakas, A.; Fountzoula, C.; Cantzos, D.; Bhattacharyya, D.; Sianoudis, I.; Fountos, G.; Yannakopoulos, P.H.; et al. Radioluminescence properties of the CdSe/ZnS Quantum Dot nanocrystals with analysis of long-memory trends. Radiat. Meas. 2016, 92, 19–31. [Google Scholar] [CrossRef] [Green Version]
- Alam, A.; Wang, N.; Zhao, G.; Mehmood, T.; Nikolopoulos, D. Long-lasting patterns of radon in groundwater at Panzhihua, China: Results from DFA, fractal dimensions and residual radon concentration. Geochem. J. 2019, 53, 341–358. [Google Scholar] [CrossRef]
- Katz, M. Fractals and the analysis of waveforms. Comput. Biol. Med. 1988, 18, 145–156. [Google Scholar] [CrossRef]
- Raghavendra, B.; Dutt, D.N. Computing Fractal Dimension of Signals using Multiresolution Box-counting Method. Int. J. Electr. Comput. Energetic Electron. Commun. Eng. 2010, 4, 183–198. [Google Scholar]
- de la Torre, F.C.; Ramirez-Rojas, A.; Pavia-Miller, C.; Angulo-Brown, F.; Yepez, E.; Peralta, J. A comparison between spectral and fractal methods in electrotelluric time series. Rev. Mex. Fis. 1999, 45, 298–302. [Google Scholar]
- de la Torre, F.C.; Gonzaalez-Trejo, J.; Real-Ramírez, C.; Hoyos-Reyes, L. Fractal dimension algorithms and their application to time series associated with natural phenomena. J. Phys. Conf. Ser. 2013, 475, 1–10. [Google Scholar] [CrossRef]
- Higuchi, T. Approach to an irregular time series on basis of the fractal theory. Phys. D Nonlinear Phenom. 1988, 31, 277–283. [Google Scholar] [CrossRef]
- Sevcik, C. On fractal dimension of waveforms. Chaos Solit. Fract. 2006, 27, 579–580. [Google Scholar] [CrossRef]
- Gotoh, K.; Hayakawa, M.; Smirnova, N. Fractal analysis of the ULF geomagnetic data obtained at Izu Peninsula, Japan in relation to the nearby earthquake swarm of June-August 2000. Nat. Haz. Earth Sys. 2003, 3, 229–234. [Google Scholar] [CrossRef]
- Gotoh, K.; Hayakawa, M.; Smirnova, N.; Hattori, K. Fractal analysis of seismogenic ULF emissions. Phys. Chem. Earth 2004, 29, 419–424. [Google Scholar] [CrossRef]
- Ida, Y.; Hayakawa, M. Fractal analysis for the ULF data during the 1993 Guam earthquake to study prefracture criticality. Nonlinear Process. Geophys. 2006, 13, 409–412. [Google Scholar] [CrossRef] [Green Version]
- Telesca, L.; Lasaponara, R. Vegetational patterns in burned and unburned areas investigated by using the detrended fluctuation analysis. Phys. A Stat. Mech. Appl. 2006, 368, 531–535. [Google Scholar] [CrossRef]
- Telesca, L.; Lapenna, V.; Vallianatos, F. Monofractal and multifractal approaches in investigating scaling properties in temporal patterns of the 1983–2000 seismicity in the Western Corinth Graben, Greece. Phys. Earth Planet. Int. 2002, 131, 63–79. [Google Scholar] [CrossRef]
- Petraki, E.; Nikolopoulos, D.; Chaldeos, Y.; Koulouras, G.; Nomicos, C.; Yannakopoulos, P.H.; Kottou, S.; Stonham, J. Fractal evolution of MHz electromagnetic signals prior to earthquakes: Results collected in Greece during 2009. Geomat. Nat. Hazards Risk 2016, 7, 550–564. [Google Scholar] [CrossRef] [Green Version]




| i | Symbol | Date | GMT | JD | Lt (°N) | Lg (°E) | Depth (km) | Dist (km) | |
|---|---|---|---|---|---|---|---|---|---|
| 1. | EQ1 | 2018/10/26 | 00:13:39 | 299 | 4.5 | 37.47 | 20.67 | 06 | 67.2 |
| 2 | EQ2 | 2018/10/26 | 01:06:03 | 299 | 4.5 | 37.39 | 20.86 | 06 | 59.0 |
| 3. | EQ3 | 2018/10/26 | 05:48:36 | 299 | 4.8 | 37.36 | 20.51 | 08 | 85.6 |
| 4. | EQ4 | 2018/10/26 | 12:41:13 | 299 | 4.6 | 37.38 | 20.54 | 05 | 82.2 |
| 5. | EQ5 | 2018/10/26 | 16:07:09 | 299 | 4.5 | 37.42 | 20.59 | 07 | 76.1 |
| 6. | EQ6 | 2018/10/27 | 05:28:46 | 300 | 4.6 | 37.47 | 20.64 | 05 | 69.6 |
| 7 | EQ7 | 2018/10/30 | 02:59:59 | 303 | 5.4 | 37.59 | 20.51 | 07 | 75.5 |
| 8. | EQ8 | 2018/10/30 | 08:32:26 | 303 | 4.8 | 37.48 | 20.43 | 11 | 86.0 |
| 9. | EQ9 | 2018/10/30 | 15:12:02 | 303 | 5.5 | 37.46 | 20.45 | 06 | 85.2 |
| 10. | EQ10 | 2018/11/01 | 02:44:48 | 305 | 4.6 | 37.37 | 20.57 | 11 | 80.5 |
| 11. | EQ11 | 2018/11/04 | 03:12:44 | 308 | 4.9 | 37.38 | 20.41 | 05 | 92.2 |
| 12. | EQ12 | 2018/11/05 | 06:46:12 | 309 | 4.5 | 37.63 | 20.49 | 08 | 76.2 |
| 13. | EQ13 | 2018/11/11 | 23:38:35 | 315 | 4.8 | 37.63 | 20.51 | 07 | 74.4 |
| 14. | EQ14 | 2018/11/12 | 06:50:27 | 316 | 4.7 | 37.14 | 20.55 | 10 | 98.1 |
| 15. | EQ15 | 2018/11/15 | 09:02:05 | 319 | 4.9 | 37.52 | 20.68 | 17 | 63.9 |
| 16. | EQ16 | 2018/11/15 | 09:09:26 | 319 | 4.5 | 37.49 | 20.65 | 07 | 67.8 |
| 17. | EQ17 | 2018/11/19 | 13:05:54 | 323 | 5.1 | 37.15 | 20.50 | 10 | 100.5 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nikolopoulos, D.; Petraki, E.; Yannakopoulos, P.H.; Priniotakis, G.; Voyiatzis, I.; Cantzos, D. Long-Lasting Patterns in 3 kHz Electromagnetic Time Series after the ML = 6.6 Earthquake of 2018-10-25 near Zakynthos, Greece. Geosciences 2020, 10, 235. https://doi.org/10.3390/geosciences10060235
Nikolopoulos D, Petraki E, Yannakopoulos PH, Priniotakis G, Voyiatzis I, Cantzos D. Long-Lasting Patterns in 3 kHz Electromagnetic Time Series after the ML = 6.6 Earthquake of 2018-10-25 near Zakynthos, Greece. Geosciences. 2020; 10(6):235. https://doi.org/10.3390/geosciences10060235
Chicago/Turabian StyleNikolopoulos, Dimitrios, Ermioni Petraki, Panayiotis H. Yannakopoulos, Georgios Priniotakis, Ioannis Voyiatzis, and Demetrios Cantzos. 2020. "Long-Lasting Patterns in 3 kHz Electromagnetic Time Series after the ML = 6.6 Earthquake of 2018-10-25 near Zakynthos, Greece" Geosciences 10, no. 6: 235. https://doi.org/10.3390/geosciences10060235
APA StyleNikolopoulos, D., Petraki, E., Yannakopoulos, P. H., Priniotakis, G., Voyiatzis, I., & Cantzos, D. (2020). Long-Lasting Patterns in 3 kHz Electromagnetic Time Series after the ML = 6.6 Earthquake of 2018-10-25 near Zakynthos, Greece. Geosciences, 10(6), 235. https://doi.org/10.3390/geosciences10060235