Overview of Retrogressive Landslide Risk Analysis in Sensitive Clay Slope
Abstract
:1. Introduction
2. Materials and Methods
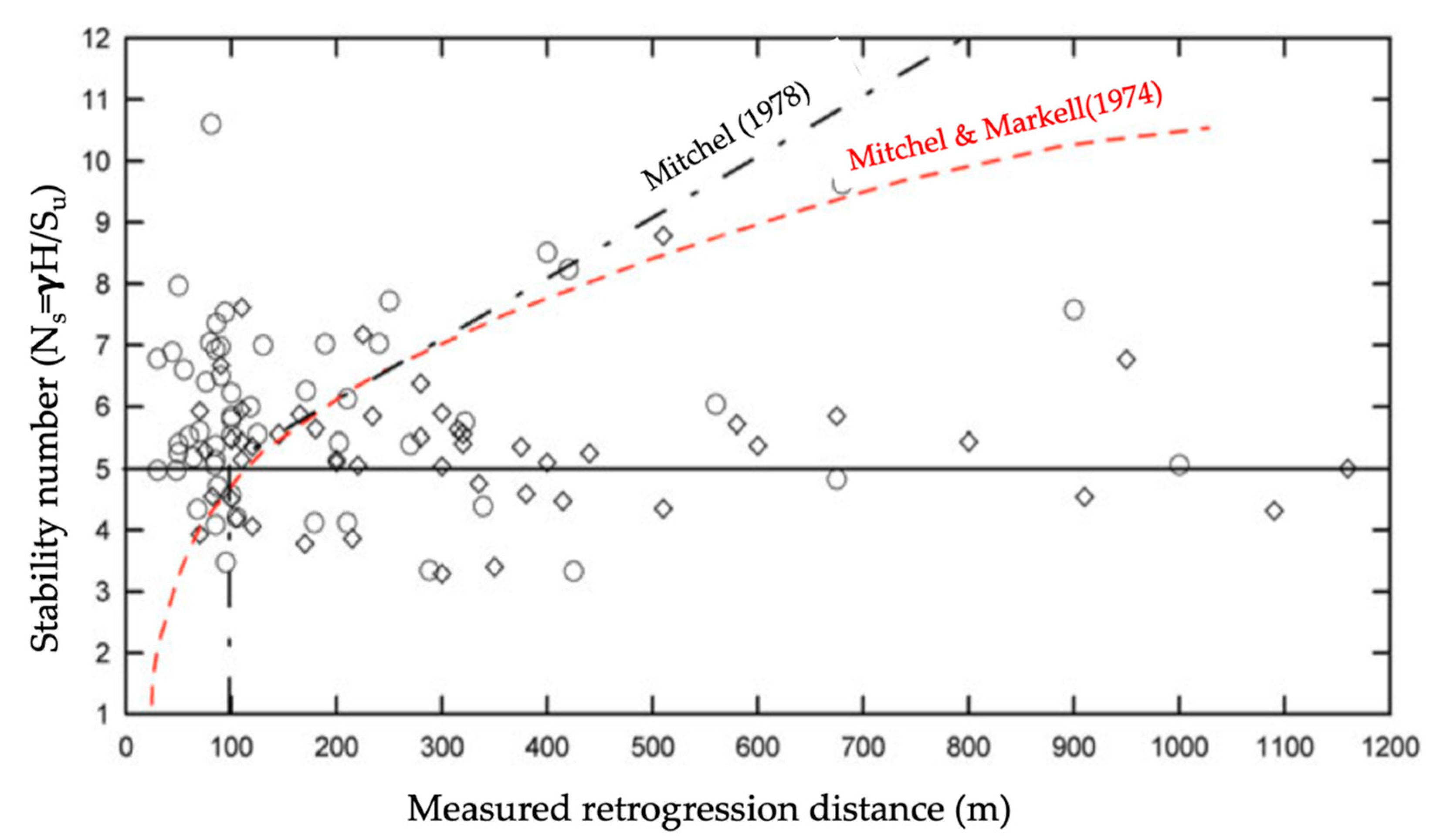
2.1. Retrogression Potential
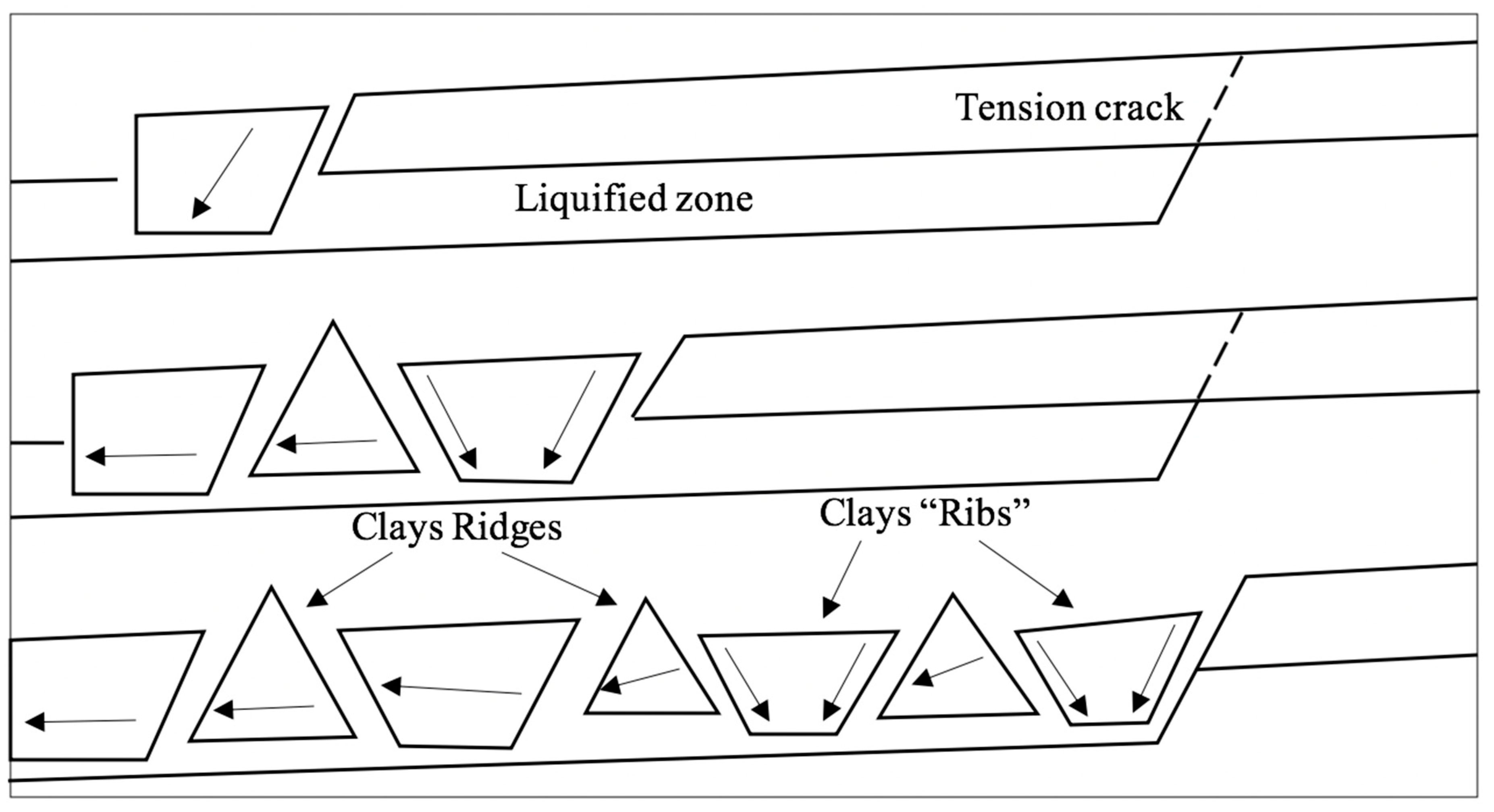
2.2. Zoning of the Slope at Risk
2.3. Stability Analysis: Analytical Methods
2.4. Stability Analysis: Numerical Methods
2.5. Shear Strength Reduction Technique
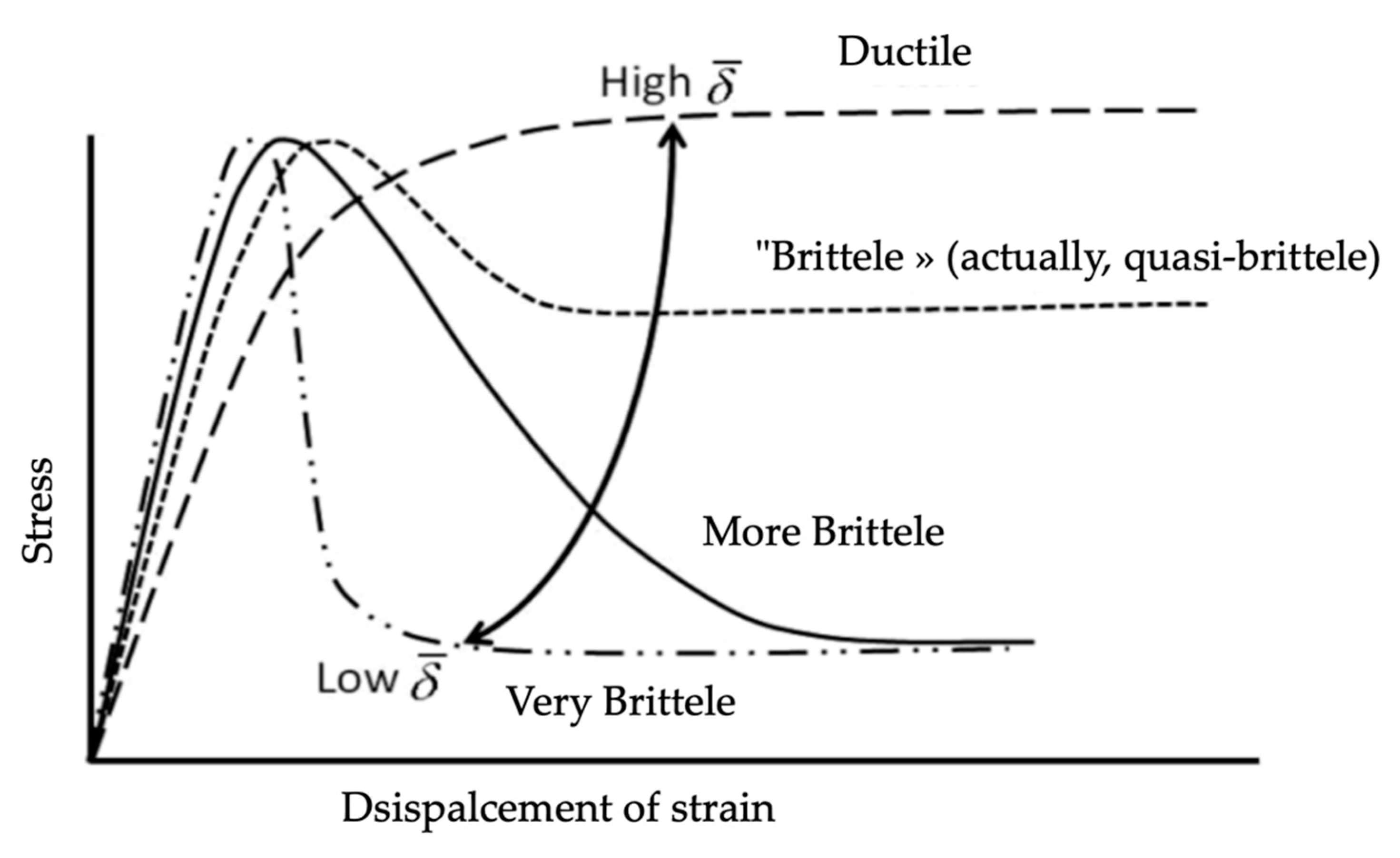
2.6. Modelling of the Progressive Failure Mechanism
3. Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviation
| Symbols | |
| St | Sensitivity |
| Sr | Remoulded shear strength |
| σ | Total stress |
| σ′ | Effective stress |
| u | Pore pressure |
| τ | Shear strength |
| Su | Undrained shear strength |
| Ns | Stability number |
| Ir | Remoulding index |
| IL | Liquidity index |
| Q | Quickness |
| N | Normal force at slice base |
| T | Shear force at slice base |
| H | Interslice normal force |
| V | Interslice shear force |
| y | Location of interslice normal force |
| NVE | Norwegian Water Resources and Energy Directorate |
| NIFS | Natural hazards – infrastructure for floods and slides |
| NGI | Norwegian Geotechnical Institute |
| MTMDET | Ministère des Transports, de la Mobilité durable et de l’Électrification des Transports |
| E | Runout distance |
| R | Retrogressive distance |
| SF | Safety factor |
| FEM | Finite element methods |
| BEM | Boundary element methods |
| FDM | Finite difference methods |
| DEM | Discrete element methods |
| SRF | Strength reduction factor |
| CEL | Coupled Eulerian–Lagrangian |
References
- Holtz, R.D.; Kovacs, W.D. An Introduction to Geotechnical Engineering; Prentice-Hall Inc.: Englewood Cliffs, NJ, USA, 1981. [Google Scholar]
- L’Heureux, J.-S.; Locat, A.; Leroueil, S.; Demers, D.; Locat, J. Landslides in Sensitive Clays—From Geosciences to Risk Management. In Landslides in Sensitive Clays—From Geosciences to Risk Management; Springer: New York, NY, USA, 2014; pp. 1–12. [Google Scholar] [CrossRef]
- Karlsson, R.; Hansbo, S. Soil Classification and Identification: Byggforskningsrådet. Swedish Geotechnical Soc. 1989. Document, D8. [Google Scholar]
- Thakur, V.; Degago, S.A. Quickness of Sensitive Clays. Geotech. Lett. 2012, 2, 87–95. [Google Scholar] [CrossRef]
- Torrance, J.K. Chemistry, Sensitivity and Quick-Clay Landslide Amelioration. In Landslides in Sensitive Clays—From Geosciences to Risk Management; Springer: New York, NY, USA, 2014; pp. 15–24. [Google Scholar] [CrossRef]
- Richard, P.J.H. Chronologie de La Déglaciation: De l’importance Des Années Étalonnées (Calibrées)*. Available online: http://www.aqqua.uqam.ca/articles/ChronoDeglaciation.pdf (accessed on 17 July 2019).
- Varnes, D.J. Slope Movement Types and Processes. Spec. Rep. Natl. Res. Counc. Transp. Res. Board 1978, 176, 11–33. [Google Scholar]
- Hungr, O.; Leroueil, S.; Picarelli, L. The Varnes Classification of Landslide Types, an Update. Landslides 2014, 11, 167–194. [Google Scholar] [CrossRef]
- Mitchell, R.J.; Klugman, M.A. Mass Instabilities in Sensitive Canadian Soils. Eng. Geol. 1979, 14, 109–134. [Google Scholar] [CrossRef]
- Marko, K.; Tiit, H.; Peeter, T.; Volli, K. Analysis of a Retrogressive Landslide in Glaciolacustrine Varved Clay. Eng. Geol. 2010, 116, 109–116. [Google Scholar] [CrossRef]
- Demers, D.; Robitaille, D.; Locat, P.; Potvin, J. Inventory of Large Landslides in Sensitive Clay in the Province of Quebec, Canada: Preliminary Analysis. In Landslides in Sensitive Clays: From Geosciences to Risk Management; Springer: New York, NY, USA, 2014; pp. 77–89. [Google Scholar]
- Quinn, P.E.; Diederichs, M.S.; Hutchinson, D.J.; Rowe, R.K. An Exploration of the Mechanics of Retrogressive Landslides in Sensitive Clay. Ottawa Geotech. 2007, 2007, 721–727. [Google Scholar]
- Quinn, P.E.; Diederichs, M.; Rowe, R.; Hutchinson, D. A New Model for Large Landslides in Sensitive Clay Using a Fracture Mechanics Approach. Can. Geotech. J. 2011, 48, 1151–1162. [Google Scholar] [CrossRef]
- Locat, A.; Leroueil, S.; Jostad, H.P. Failure Mechanism of Spreads in Sensitive Clays. In Landslides in Sensitive Clays: From Geosciences to Risk Management; Springer: New York, NY, USA, 2014; pp. 279–290. [Google Scholar] [CrossRef]
- Quinn, P.E.; Diederichs, M.S.; Rowe, R.K.; Hutchinson, D.J. Development of Progressive Failure in Sensitive Clay Slopes. Can. Geotech. J. 2012, 49, 782–795. [Google Scholar] [CrossRef]
- Locat, A.; Leroueil, S.; Bernander, S.; Demers, D.; Jostad, H.P.; Ouehb, L. Progressive Failures in Eastern Canadian and Scandinavian Sensitive Clays. Can. Geotech. J. 2011, 48, 1696–1712. [Google Scholar] [CrossRef]
- Fellenius, W. Earth Stability Calculations Assuming Friction and Cohesion on Circular Slip Surfaces; W. Ernst: Berlin, Germany, 1927. [Google Scholar]
- Bishop, A.W. The Use of the Slip Circle in the Stability Analysis of Slopes. Géotechnique 1955, 5, 7–17. [Google Scholar] [CrossRef]
- Faure, R.M. The Evolution of Slope Stability Methods Part 1: Failure Methods. Rev. Fran. Géotech. 2000, 92, 3–16. [Google Scholar] [CrossRef] [Green Version]
- Duncan, J.M.; Wright, S.G.; Brandon, T.L. Soil Strength and Slope Stability, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Geertsema, M.; L’Heureux, J.-S. Controls on the Dimensions of Landslides in Sensitive Clays. In Landslides in Sensitive Clays: From Geosciences to Risk Management; Springer: Dordrecht, The Netherlands, 2014; pp. 105–117. [Google Scholar] [CrossRef]
- Geertsema, M.; Clague, J.J.; Schwab, J.W.; Evans, S.G. An Overview of Recent Large Catastrophic Landslides in Northern British Columbia, Canada. Eng. Geol. 2006, 83, 120–143. [Google Scholar] [CrossRef]
- Mitchell, R.J.; Markell, A.R. Flowsliding in Sensitive Soils. Can. Geotech. J. 1974, 11, 11–31. [Google Scholar] [CrossRef]
- Mitchell, R.J. Earthflow Terrain Evaluation in Ontario; Project Q-53, Report 213. Available online: https://books.google.com.ph/books/about/Earthflow_Terrain_Evaluation_in_Ontario.html?id=kovMSgAACAAJ&redir_esc=y (accessed on 20 July 2020).
- Carson, M.A. On the Retrogression of Landslides in Sensitive Muddy Sediments. Can. Geotech. J. 1979, 16, 431–444. [Google Scholar] [CrossRef]
- Turmel, D.; Potvin, J.; Demers, D.; Locat, P.; Locat, J.; Leroueil, S.; De, D.; Laval, U. Empirical Estimation of the Retrogression and the Runout Distance of Sensitive Clay Flowslides. Geohazard 2018, 7, 8. [Google Scholar]
- Lebuis, J.; Robert, J.-M.; Rissmann, P. Regional Mapping of Landslide Hazard in Quebec. In Symposium on Slopes on Soft Clays, Linköping, Sweden; Statens geotekniska Institut: Linköping, Sweden, 1983; pp. 205–262. [Google Scholar]
- Leroueil, S. Compressibility of Clays: Fundamental and Practical Aspects. J. Geotech. Eng. 1996, 122, 534–543. [Google Scholar] [CrossRef]
- Leroueil, S.; Tavenas, F.; Bihan, J.-P.L. Propriétés Caractéristiques Des Argiles de l’est Du Canada. Can. Geotech. J. 1983, 20, 681–705. [Google Scholar] [CrossRef]
- Soderblom, R. A New Approach to the Classification of Quick Clays. Available online: https://trid.trb.org/view/26131 (accessed on 20 July 2020).
- Haugen, E.D.; Tveit, M.; Heyerdahl, H. Mapping Quick Clay Hazard Zones: Comparison of Methods for the Estimation of the Retrogression Distance. In Advances in Natural and Technological Hazards Research; Springer: Dordrecht, The Netherlands, 2017; Volume 46, pp. 311–321. [Google Scholar] [CrossRef]
- Karlsrud, K.; Aas, G.; Gregersen, O. Can We Predict Landslide Hazards in Soft Sensitive Clay? Summary of Norwegian Practice and Experiences. Publ. Norges Geotek. Inst. 1985, 158, 405–429. [Google Scholar] [CrossRef]
- NIFS. Metode for Vurdering Av Løsne—Og Utløpsområder for Områdeskred; NVE: Eden Prairie, MI, USA, 2016. [Google Scholar]
- Strand, S.-A.; Thakur, V.; L’Heureux, J.-S.; Lacasse, S.; Karlsrud, K.; Nyheim, T.; Aunaas, K.; Ottesen, H.B.; Gjelsvik, V.; Fauskerud, O.A.; et al. Runout of Landslides in Sensitive Clays. Adv. Nat. Technol. Hazards Res. 2017, 46, 289–300. [Google Scholar] [CrossRef]
- L’Heureux, J.-S. A Study of the Retrogressive Behavior and Mobility of Norwegian Quick Clay Landslides2013 and Continuation): Integration of Geophysical, Hydrogeological and Geotechnical Methods to Aid Monitoring Landslide in Nordic Countries: A 4D Approach for Landslide. Available online: https://www.researchgate.net/publication/236008671_A_study_of_the_retrogressive_behavior_and_mobility_of_Norwegian_quick_clay_landslides. (accessed on 20 February 2020).
- Coulomb, C.A. Essai Sur Une Application Des Regles Des Maximas et Minmas a Quelques Problemes de Statique Relatifs a l’architecture; Academie Royale des Sciences: Paris, France, 1776; pp. 343–382. [Google Scholar]
- Collin, A. Recherches Experimentales Sur Les Glissements Spontanes Des Terrains Argileux, Accompagnees de Considerations Sur Quelques Principes de La Mecanique Terrestre; Carilian-G.: Paris, France, 1846. [Google Scholar]
- Sivakugan, N.; Das, B.M. Geotechnical Engineering Handbook; J. Ross Pub: Plantation, FL, USA, 2010. [Google Scholar]
- U.S. Corps of Engineers. Slope Stability; U.S. Corps of Engineers: Washington, DC, USA, 2003. [Google Scholar]
- Lowe, J.; Karafiath, L. Effect of Anisotropic Consolidation on the Undrained Shear Strength of Compacted Clays; ASCE: Reston, VA, USA, 1960; pp. 837–858. [Google Scholar]
- Janbu, N. Application of Composite Slip Surface for Stability Analysis. Available online: https://www.semanticscholar.org/paper/Application-of-composite-slip-surfaces-for-analysis-Janbu/2dc458aff6274da8f27780753663dbde4cf26f28. (accessed on 20 July 2020).
- Spencer, E. Embankments Assuming Parallel Inter-Slice Forces. Géotechnique 1967, 17, 11–26. [Google Scholar] [CrossRef]
- Morgenstern, N.R.; Price, V.E. The Analysis of the Stability of General Slip Surfaces. Geotechnique 1965, 15, 79–93. [Google Scholar] [CrossRef]
- Sarma, S.K. Stability Analysis of Embankments and Slopes. Géotechnique 1973, 23, 423–433. [Google Scholar] [CrossRef]
- Skempton, A.W. Long-Term Stability of Clay Slopes. Géotechnique 1964, 14, 77–102. [Google Scholar] [CrossRef] [Green Version]
- Burland, J.B.; Longworth, T.I.; Moore, J.F.A. A Study of Ground Movement and Progressive Failure Caused by a Deep Excavation in Oxford Clay. Geotechnique 1977, 27, 557–591. [Google Scholar] [CrossRef]
- Narasaiah, G.L. Finite Elements Analysis; BS Publications: Telangana, India, 2008. [Google Scholar]
- Lin, J. Basic Geotechnical Analysis; University of Pittsburgh: Pittsburgh, PA, USA; University of Massachusetts: Amherst, MA, USA, 2001. [Google Scholar]
- Zienkiewicz, O.C.; Cormeau, I.C. Visco-Plasticity and Plasticity an Alternative for Finite Element Solution of Material Nonlinearities. In Computing Methods in Applied Sciences and Engineering Part 1; Springer: Berlin/Heidelberg, Germany, 1974; pp. 259–287. [Google Scholar] [CrossRef]
- Donald, I.; Giam, S. Application of the Nodal Displacement Method to Slope Stability Analysis. In Fifth Australia-New Zealand Conference on Geomechanics: Prediction Versus Performance; Preprints of Papers; Institution of Engineers: Barton, Australia, 1988. [Google Scholar]
- Matsui, T.; San, K.-C. Finite Element Slope Stability Analysis by Shear Strength Reduction Technique. Soils Found. 1992, 32, 59–70. [Google Scholar] [CrossRef] [Green Version]
- Griffiths, D.V.; Lane, P.A. Slope Stability Analysis by Finite Elements. Geotechnique 1999, 49, 387–403. [Google Scholar] [CrossRef]
- Chang, Y.; Huang, T. Slope Stability Analysis Using Strength Reduction Technique. J. Chin. Inst. Eng. 2005, 28, 231–240. [Google Scholar] [CrossRef]
- Lawrence, D.E.; Morey, C.R. Sensitive Clay Flows along the South Nation River, Ontario, Canada and Their Impact on Land Use. Landslides 1996, 479–484. [Google Scholar]
- Del Gaudio, V.; Wasowski, J.; Pierri, P.; Mascia, U.; Calcagnile, G. Gravimetric Study of a Retrogressive Landslide in Southern Italy. Surv. Geophys. 2000, 21, 391–406. [Google Scholar] [CrossRef]
- Bjerrum, L. Progressive Failure in Slopes of Overconsilidated Plastic Clay and Clay Shales. J. Soil Mech. Found. Div 1967, 93, 2–49. [Google Scholar]
- Dey, R.; Hawlader, B.; Phillips, R.; Soga, K. Large Deformation Finite-Element Modelling of Progressive Failure Leading to Spread in Sensitive Clay Slopes. Géotechnique 2015, 65, 657–668. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Hawlader, B. Numerical Modeling of Three Types of Sensitive Clay Slope Failures. In Proceedings of the ICSMGE 2017—19th International Conference on Soil Mechanics and Geotechnical Engineering, Seoul, Korea, 17–21 September 201; Volume 2017-Septe, pp. 871–874.
- Bentley Systems Inc. User’s Manual of PLAXIS; Bentley Systems Inc.: Exton, PA, USA, 2014. [Google Scholar]
- Andersen, K.H.; Jostad, H.P. Shear Strength Along Outside Wall of Suction Anchors in Clay after Installation. Proc. Int. Offshore Polar Eng. Conf. 2002, 12, 785–794. [Google Scholar]
- Andersen, K.H.; Jostad, H.P. Shear Strength along inside of Suction Anchor Skirt Wall in Clay. Proc. Annu. Offshore Technol. Conf. 2004, 3, 2142–2154. [Google Scholar] [CrossRef]
- Wang, C.; Hawlader, B.; Islam, N.; Soga, K. Implementation of a Large Deformation Finite Element Modelling Technique for Seismic Slope Stability Analyses. Soil Dyn. Earthq. Eng. 2019, 127, 105824. [Google Scholar] [CrossRef]
- Tran, Q.A.; Sołowski, W. Generalized Interpolation Material Point Method Modelling of Large Deformation Problems Including Strain-Rate Effects—Application to Penetration and Progressive Failure Problems. Comput. Geotech. 2019, 106, 249–265. [Google Scholar] [CrossRef]



| Parameters | Canada | Sweden | Norway |
|---|---|---|---|
| Sensitivity (St) | >16 | ≥50 | ≥30 |
| Remoulded shear strength (Sr) | - | <0.4 kPa | <0.5 kPa |
| Parameters | Proposed by |
|---|---|
| Ns >4, if Ip ~ 10 | Leroueil [28] |
| Ns >8, if Ip ~ 40 | |
| Sr <1 kPa | Mitchell & Markell [23] |
| IL >1.2 (flowslide) | Leroueil et al. [29] |
| Rapidity number >8 | Söderblom [30] |
| Q >15% | Thakur and Degago [4] |
| Procedure | Assumption and Characteristics | Equilibrium Conditions Satisfied | ||
|---|---|---|---|---|
| Ordinary method of slices/Fellenius method [17] | Circular slip surfaces only; interslice forces are zero | No | No | Yes |
| Simplified Bishop [18] method | Circular slip surfaces only; interslice shear forces are zero | No | Yes | Yes |
| Corps of engineers [39] modified Swedish method | Slip surfaces of any shape, interslice force is parallel to the ground or inclined at an angle equal to the slope of a line connecting the crest and the toe (called average embankment slope) | Yes | Yes | No |
| Lowe and Karafiath’s [40] method | Slip surface of any shape; interslice force is inclined at an angle of (1/2 α + β) | Yes | Yes | No |
| Janbu’s [41] simplified method | Slip surface of any shape, interslice shear force is zero | Yes | Yes | No |
| Spencer’s [42] method | Slip surface of any shape; interslice forces are parallel with an unknown inclination | Yes | Yes | Yes |
| Morgenstern-Price [43] method | Slip surface of any shape; interslice shear forces are related to the interslice normal forces by X = λf(x)E, where λ is an unknown scaling factor, and f(x) is an assumed function with prescribed values at slice boundaries | Yes | Yes | Yes |
| Sarma’s [44] method | Slip surface of any shape; interslice shear force is related to the interslice shear strength by X = λf(x)Sy, where λ is an unknown scaling factor, f(x) is an assumed function with prescribed values at slice boundaries, and Sy is the available shear force depending on c′ and φ′ along the slice boundaries | Yes | Yes | Yes |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Richer, B.; Saeidi, A.; Boivin, M.; Rouleau, A. Overview of Retrogressive Landslide Risk Analysis in Sensitive Clay Slope. Geosciences 2020, 10, 279. https://doi.org/10.3390/geosciences10080279
Richer B, Saeidi A, Boivin M, Rouleau A. Overview of Retrogressive Landslide Risk Analysis in Sensitive Clay Slope. Geosciences. 2020; 10(8):279. https://doi.org/10.3390/geosciences10080279
Chicago/Turabian StyleRicher, Blanche, Ali Saeidi, Maxime Boivin, and Alain Rouleau. 2020. "Overview of Retrogressive Landslide Risk Analysis in Sensitive Clay Slope" Geosciences 10, no. 8: 279. https://doi.org/10.3390/geosciences10080279
APA StyleRicher, B., Saeidi, A., Boivin, M., & Rouleau, A. (2020). Overview of Retrogressive Landslide Risk Analysis in Sensitive Clay Slope. Geosciences, 10(8), 279. https://doi.org/10.3390/geosciences10080279







