Ionosonde Data Analysis in Relation to the 2016 Central Italian Earthquakes

Abstract

Ionospheric characteristics and crustal earthquakes that occurred in 2016 next to the town of Amatrice, Italy are studied together with the previous events that took place from 1984 to 2009 in Central Italy. The earthquakes with M larger than 5.5 and epicentral distances from the ionosonde less than 150 km were selected for the analysis. A multiparametric approach was applied using variations of sporadic E-layer parameters (the height and the transparency frequency) together with variations of the F2 layer critical frequency foF2 at the Rome ionospheric observatory. Only ionospheric data under quiet geomagnetic conditions were considered. The inclusion of new 2016 events has allowed us to clarify the earlier-obtained seismo-ionospheric empirical relationships linking the distance in space (km) and time (days) between the ionospheric anomaly and the impending earthquake, with its magnitude. The improved dependencies were shown to be similar to those obtained in previous studies in different parts of the world. The possibility of using the obtained relationships for earthquake predictions is discussed.

1. Introduction

Earthquakes (EQs) constitute one of the most energetic phenomena occurring in the Earth’s crust (e.g., [1]). A possible coupling of large EQs with the atmosphere and ionosphere has to be considered during the long-term process of their preparation (e.g., [2,3,4,5]) and at the moment when the largest part of energy is released due to the main fault rupture [6,7,8,9,10,11]. Different models have been proposed: (a) radon emanation from the lithosphere affecting the electric field in the troposphere–ionosphere electric circuit (e.g., [4]), (b) generation of electric currents in the lithospheric rocks when they are under stress [2,12], and (c) atmospheric processes producing acoustic and/or gravity waves in the seismic preparation region [13].

Pre-EQ ionospheric anomalies are defined as middle-term precursors when they occur up to 1–2 months in advance, while those with lead times from some hours up to 1 day are defined as short-term precursors [14]. Ionospheric parameters like critical frequency of the ionospheric F2-layer (foF2), electron temperature (T_e) at F2-region heights, total electron content (TEC), electron density (N_e) at satellite heights (~460–510 km), as well as magnetic pulsations and low-frequency radio signals are investigated for these purposes [15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31].

In this paper we analyze variations of ionospheric parameters observed with ground-based ionosondes, namely, foF2 and parameters directly related to the sporadic E-layer (Es). Several papers have focused on foF2 variations during seismo-active periods. Hobara and Parrot [20] found a decrease in foF2 recorded by ionosonde stations in the Asian longitudinal sector for the isolated and very powerful 1968 Hachinohe EQ with M = 8.3. Decreases of 25% in foF2 in the 5 days following EQs were observed by Liu et al. [21] in their analysis of the relation between foF2 and 184 EQs with M > 5.0, from 1994 to 1999 in the Taiwan area. The probability of occurrence and semi-transparency coefficient of the Es layer have been considered by Silina et al. [32].

Although the authors attempted to avoid periods with elevated geomagnetic activity in their analyses, foF2 is a very variable parameter, affected both from above (e.g., by solar EUV, magnetospheric and dynamo electric fields, variable thermospheric circulation and neutral composition, travelling atmospheric disturbances (TADs), etc.; [33,34,35]) and from below (e.g., by planetary and gravity waves, neutral gas vertical motion and eddy diffusion changing the thermospheric neutral composition, and tropospheric electric fields not necessarily related to seismic processes; [36,37]). Therefore, besides the geomagnetic activity effects, there are many other sources of foF2 variation. The morphology of the F2-layer perturbations not related to geomagnetic activity (so-called Q-disturbances) can be found in Perrone et al. [38] (see also, e.g., [39,40]).

Any attempt to derive quantitative relationships for the seismo-ionospheric coupling should be considered an important step towards better understanding of the physical mechanisms driving such phenomena. An approach showing remarkable results was proposed by Korsunova and Khegai [41,42] and successively applied by Perrone et al. [43,44], according to which a dense Es layer can be produced over the preparation zone of future EQs at 120–140 km height. The preparation zone is defined by the Dobrovolsky formula [45], ρ ≤ 10^0.43M, where M is the magnitude of the EQ and ρ is the radius (in km) of the supposed circular preparation zone, centered in the epicentral location. A multi-parametric approach considering quasi-simultaneous variations in three parameters of the Es and regular F2 layers is applied [42,43,44,46]. This approach relates the lead time ΔT for a future EQ event, counted from the moment of the observed ionospheric anomaly occurrence, with the magnitude of the EQ and the distance of its epicenter. The aim of the present analysis was to check whether the method applied for central Italian moderate (5.5 ≤ M ≤ 5.8) EQs by Perrone et al. [43] is valid in the case of the stronger 2016 Amatrice EQs.

2. Observations and Methods

The crustal EQs of magnitude M6.0, M5.9, and M6.1 that occurred in Central Italy on 24 August 2016, 10 October 2016, and 30 October 2016 were studied. Those EQs match the criteria applied in our previous analysis [43], namely, their magnitudes were M > 5.5, the hypocentral depths were < 50 km, and the epicentral distances were within 150 km from the ionosonde location. The characteristics of the analyzed EQs provided by the Centro Nazionale Terremoti of the Istituto Nazionale di Geofisica e Vulcanologia (INGV-CNT) (http://cnt.rm.ingv.it/) are given in

Table 1. List of the shallow earthquakes (EQs) with magnitude M ≥ 6.0 registered in Central Italy in 2016. Geographical coordinates of the EQ epicenters from the Centro Nazionale Terremoti of the Istituto Nazionale di Geofisica e Vulcanologia (INGV-CNT) (http://cnt.rm.ingv.it/) and the epicentral distance (R) from the Rome ionosonde are given.

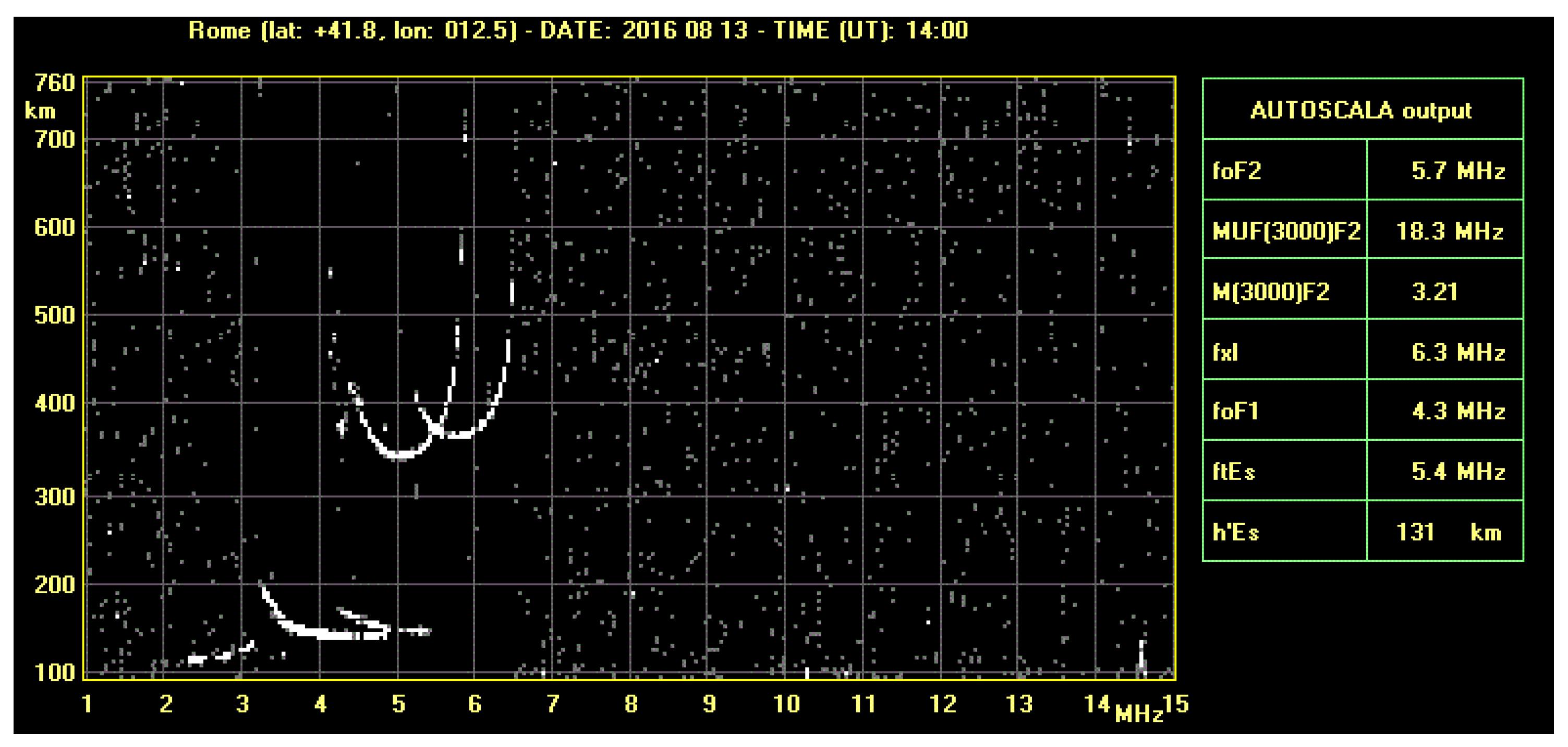
Date EQ	UT (h:min)	M	R (km)	Lat (degree)	Long. (degree)
24 August 2016	01:36	6.0	117	42.7	13.2
26 October 2016	19:18	5.9	133	42.9	13.1
30 October 2016	06:40	6.1	125	42.8	13.1

.

For all the considered EQs, the ionospheric station of Rome is located in their preparation zone according to the formula by Dobrovolsky et al. [45]. Long-living (~2–3 h) Es layers were observed and used in this analysis. The increases in the Es altitude h’Es were accompanied by an increase in the blanketing frequency fbEs of the Es layer and an increase in foF2. In order to define anomalies in the ionospheric parameters, the background values for each parameter should be specified. A 27-day hourly running median centered on a particular hourly value was considered as the background level. Deviations in h’Es, fbEs, and foF2 hourly values with respect to the background were calculated in accordance with the following expressions, and they should correspond to the following criteria:

$$\Delta {\mathrm{h}}^{\prime }\mathrm{Es}={{\mathrm{h}}^{\prime }\mathrm{Es}}_{\left(\mathrm{hourly}\right)}-{{\mathrm{h}}^{\prime }\mathrm{Es}}_{\left(\mathrm{background}\right)}\ge 10\mathrm{km},$$

(1)

$$\mathsf{\delta }\mathrm{fbEs}=\frac{{\mathsf{\delta }\mathrm{fbEs}}_{\left(\mathrm{hourly}\right)}-{\mathsf{\delta }\mathrm{fbEs}}_{\left(\mathrm{background}\right)}}{{\mathsf{\delta }\mathrm{fbEs}}_{\left(\mathrm{background}\right)}}\ge 0.2,$$

(2)

$$\mathsf{\delta }\mathrm{foF}2=\frac{\mathsf{\delta }\mathrm{foF}{2}_{\left(\mathrm{hourly}\right)}-\mathsf{\delta }\mathrm{foF}{2}_{\left(\mathrm{background}\right)}}{\mathsf{\delta }\mathrm{foF}{2}_{\left(\mathrm{background}\right)}}\ge 0.1.$$

(3)

High Es layers were not considered in our analysis, and we have confined ourselves with 10 km ≤ Δh’Es ≤ 40 km deviations as in the previous study [43]. Ionospheric historical data from Rome observatory were used in our analysis. In particular, data from different ionosondes were used for different epochs, i.e., (a) Union Radio Mark II recorded type ionosonde [47] until 1979, (b) Bibl 128P type ionosonde [48] from 1980 to 1995, (c) Barry ionosonde [49] from 1996 to 2004, and (d) Advanced Ionospheric Sounder ionosonde, developed at INGV (AIS-INGV) [50], since 2005. Hourly observations of three parameters, manually scaled from ionograms occurring in geomagnetic quiet conditions (daily A_p < 9 nT and 3-hourly a_p index < 12 nT), were considered. For example, the ionogram recorded on 13 August 2016 at 14:00 UT during the ionospheric anomaly associated with the 30 October 2016 EQ (more information to follow) is reported in Figure 1, along with the outputs of the Autoscala software [51,52], developed at INGV. As can be seen, the automatically scaled value of h’Es is more than 10 km higher than the usual 95–120 km range [53].

3. Results

All available central Italian crustal EQs, including those considered by Perrone et al. [43], were re-analyzed, keeping in mind their correspondence to the above formulated criteria (1–3). For the association of the anomalies to the different EQs, the following rule was used when EQs followed each other with a small time interval: under similar epicenter distances and time, an ionospheric anomaly for an EQ with larger magnitude occurs earlier and exhibits larger deviations in h’Es [40]. This enabled us to identify ionospheric precursors for all the EQs in question. The total number of EQs with M ≥ 5.5 in the period 1979–2016 was 13, of which we selected 6 whose associated ionospheric anomalies occurred during quiet geomagnetic conditions. Their characteristics along with corresponding ionospheric anomalies are given in

Table 2. Identified ionospheric anomalies and corresponding EQs. Daily A_p indices are given as well.

Date of Observed Ionospheric Anomaly	UT Hour	Δh’Es (km)	δfbEs	δfoF2	ΔT (days)	Ap	Date of EQ	Geogr. Coord.	UT Hour	M	R (km)
24 April 1984	01:00–02:00	27	0.82	0.16	17.4	6	11 May 1984	41.7 N; 14.1 E	10:41	5.7	133
2 September 1997	14:00–15:00	28	0.79	0.16	23.8	4	26 September 1997	43.0 N; 12.9 E	09:40	5.8	137
2 October 1997	00:00–01:00	21	0.87	0.22	12.6	5	14 October 1997	43.0 N; 13.0 E	15:23	5.5	140
3 March 2009	06:00–07:00	30	0.24	0.21	33.8	7	6 April 2009	42.3 N; 13.3 E	01:32	5.8	90
13 September 2016	01:00–02:00	26	0.69	0.12	43.8	4	26 October 2016	42.9 N; 13.1 E	19:18	5.9	133
13 August 2016	14:00–15:00	32	0.44	0.28	77.7	4	30 October 2016	42.8 N; 13.1 E	06:40	6.1	125

.

The dependencies relating the lead time ΔT between the ionospheric anomalies and the EQ occurrence with the EQ magnitude M and the epicentral distance R were found in [41,43,44,54]. The logarithmic dependence was taken from the Dobrovolsky formula [45]. The adoption of this kind of relationship between ΔT and M comes from ground observations of various geophysical parameters for a number of EQs with M = 4–8 [54] and resulted in the following dependence: log(ΔT·R) = 0.72M − 0.72. Liu et al. [21] and Korsunova and Khegai [41,42] also use this type of dependence, and a similar dependence is the Rikitake [55] empirical law between precursor time and EQ magnitude, recently confirmed for ionospheric precursors [31]. It should be noted that De Santis et al. [31] also provide a reasonable physical explanation for the Rikitake law [55], which in turn provides the order of magnitude of precursors lead time. These time delays could be attributed to the long-term process of EQ preparation (more information to follow). Our newly found dependences are given in Figure 2 for the EQs reported in Table 2. The upper panel gives the dependence of lead time on the EQ magnitude. The central panel gives the same dependence, but for the product (ΔT·R). The bottom panel gives the dependency for Δh’Es.

The dependencies are statistically significant at the confidence level >95% according to Fisher F-criterion.

Linear regressions for log(ΔT), log(ΔT·R), and log(Δh’Es) from Figure 2 are as follows:

$$\log \left(\Delta \mathrm{T}\right)=\left(1.386\pm 0.335\right)\mathrm{M}-\left(6.573\pm 1.943\right),$$

(4)

$$\log \left(\Delta \mathrm{T}·\mathrm{R}\right)=\left(1.311\pm 0.349\right)\mathrm{M}-\left(4.041\pm 2.026\right),$$

(5)

$$\log \left(\Delta {\mathrm{h}}^{\prime }\mathrm{Es}\right)=\left(0.266\pm 0.166\right)\mathrm{M}-\left(0.113\pm 0.965\right).$$

(6)

The confidence intervals for the regression coefficients were estimated using t-criterion under 95% confidence level. In all cases the regression coefficients are statistically significant, apart from the second coefficient in (6) and this is a serious restriction for any EQ prediction (more information to follow). It should be noted that the effect of R inclusion is small because all the EQs took place practically in the same area with R = 90–140 km from Rome. However, Sidorin [54] has shown that the inclusion of R to the ∆T on M dependence improves the relationship, and Liu et al. [21] also used an expression that depends on the epicentral distance R.

Similar relationships were obtained by analyzing Greek EQs with M ≥ 6 for the period of 2003–2015 [44]:

$$\log \left(\Delta \mathrm{T}\right)=0.81\mathrm{M}-3.53,$$

(7)

$$\log \left(\Delta \mathrm{T}·\mathrm{R}\right)=0.84\mathrm{M}-1.33,$$

(8)

$$\log \left(\Delta {\mathrm{h}}^{\prime }\mathrm{Es}\right)=0.28\mathrm{M}-0.41,$$

(9)

and we also compared these values to Korsunova and Khegai’s [41] results. They analyzed 33 EQs with M ≥ 6 that occurred in the region of Kokubunji station from 1985 to 2000, obtaining the dependence:

$$\log \left(\Delta \mathrm{T}·\mathrm{R}\right)=1.14\mathrm{M}-4.72.$$

(10)

Analyzing the difference between the relationships, one can see that the regressions (6) and (9) are practically the same, while by comparing (4), (5) to (7), (8) we see differences. This could be due to the small number of events considered or to the rate of preparation processes, which may be different in different regions. Indeed, the long-term preparation phase of an EQ can involve different geochemical and seismic processes (such as crustal heterogeneities, infiltration of fluids into the upper crust, and stress changes illuminated by b-value mapping), and can be manifested both in the seismic quiescence and the accelerated seismic energy release [56,57]. This means that it can be characterized by different phases, each one with distinct peculiarities and seismicity rates before the mainshock.

3.1. Ionospheric Anomalies under All Geomagnetic Conditions

It is interesting to note that even some of the ionospheric anomalies that have been previously discarded because they occurred under a_p > 12 may be related to EQs.

Figure 3 gives, together with previously validated ionospheric anomalies, those anomalies with a_p > 12 that could be linked to other three EQs. Details on these discarded cases are given in

Table 3. Revealed ionospheric anomalies during disturbed magnetic conditions and corresponding EQs. Daily A_p indices are given as well.

Date of Observed Ionospheric Anomaly	UT Hour	Δh’Es (km)	δfbEs	δfoF2	ΔT (days)	Ap	Date of EQ	Geogr. Coord.	UT Hour	M	R (km)
4 April 1984	00:00–01:00	37	0.25	0.30	33.8	84	7 May 1984	41.7 N; 14.1 E	17:49	5.9	133
8 September 1997	05:00–06:00	19	0.61	0.16	17.8	12	26 September 1997	43.0 N; 12.9 E	00:33	5.6	137
9 July 2016	03:00–05:00	36	0.71	0.25	46.0	7	24 August 2016	42.7 N; 13.2 E	01:36	6.0	117

. However, it should be stressed that the number of ionospheric anomalies not related to EQs increases during disturbed periods, as already observed for Greek EQs [44]. For instance, in 2016 we found 11 ionospheric anomalies of this type, but only 1 of them could be related to an EQ.

The inclusion of disturbed cases slightly changed the regression coefficients:

$$\log \left(\Delta \mathrm{T}\right)=\left(1.266\pm 0.253\right)\mathrm{M}-\left(5.888\pm 1.471\right),$$

(11)

$$\log \left(\Delta \mathrm{T}·\mathrm{R}\right)=\left(1.174\pm 0.267\right)\mathrm{M}-\left(3.253\pm 1.552\right),$$

(12)

$$\log \left(\Delta {\mathrm{h}}^{\prime }\mathrm{Es}\right)=\left(0.419\pm 0.218\right)\mathrm{M}-\left(0.991\pm 1.270\right).$$

(13)

Similar to the previous case, the dependencies are statistically significant at the confidence level >95% according to Fisher F-criterion. The second coefficient in (13) is also insignificant at this confidence level.

3.2. Forecast Possibilities

An important result of our analysis are quantitative expressions (4–6), which relate the EQ magnitude and the epicentral distance with observed h’Es variations. In principle, such expressions could be used for prediction purposes to determine the magnitude M and lead time ΔT of future EQs. However, this cannot be done for at least two reasons. Firstly, due to a small body of data (only 6 cases are available) the second coefficient in the inverted expression (6),

$$\mathrm{M}=\left(2.670\pm 1.666\right)\log \left(\Delta {\mathrm{h}}^{\prime }\mathrm{Es}\right)+\left(1.975\pm 2.389\right),$$

(14)

is statistically insignificant at the 95% confidence level. Although (14) significantly indicates that the EQ magnitude increases with Δh’Es (according to F-criterion), this expression cannot be formally used for a quantitative prediction of M. Consequently, the lead time ΔT cannot be retrieved, as the reversed expression (4) requires (14), and the uncertainties of the coefficients in (4) would add further inaccuracies. It follows that the approach does not know when the event will occur, so it would be a somewhat inaccurate forecast.

Another aspect is the occurrence of ionospheric anomalies not related to EQs. It is obvious that dependences similar to (4–6) are only practical if the probability of false ionospheric anomalies is not high. We checked the whole 2016 year. The Δh’Es, δfbEs, and δfoF2 deviations were calculated for 24 UT moments of all days and all months of the year. The revealed anomalies are shown in

Table 4. Ionospheric anomalies during 2016 not related to EQs. Daily A_p indices are given as well.

Date of Observed Ionospheric Anomaly	UT Hour	Δh’Es (km)	δfbEs	δfoF2	Ap
12 May	01:00–02:00	27	0.82	0.16	3
15 September	03:00–04:00	15	0.50	0.26	6
6 October	10:00–11:00	18	0.43	0.26	5
19 November	14:00–15:00	13	1.50	0.30	1
12 December	22:00–23:00	22	0.69	0.23	5

and are not numerous, but their number is comparable to the number of EQs (Table 2) and they cannot be distinguished from real cases.

Finally, for possible future practical application of the method, a different background should be used in the anomaly definition, as only past data can be used by a real-time warning system.

4. Discussion

Physical processes proposed to explain the penetration of seismic processes into the ionosphere, are the electrostatic or the atmospheric/acoustic gravity waves (e.g., [13,58,59]). Considering the electromagnetic channel, difficulties are encountered in simulation of the penetrating electric field and current through the atmosphere. Models [60,61,62] show that the field penetrating into the ionosphere is several orders of magnitude smaller than required. The mechanism based on gravity waves [13] cannot be discarded as well.

According to the theory of the EQ preparation based on electromagnetic processes or acoustic gravity waves, the spreading of the preparation zone (i.e., the spreading from the future epicenter to the periphery of the above-mentioned EQ preparation processes [56,57]) is accompanied by the formation of a sporadic E-layer with large electron concentration at the height of 120–140 km above the same area. An increase in h’Es is accompanied by an increase in fbEs and in foF2. However, the h’Es increase is the crucial point of the method as the observed ionospheric anomaly in h’Es is directly related (via expression (6)) to the EQ magnitude.

The undertaken analysis showed that the simultaneous deviations in Δh’Es, δfbEs, and δfoF2 above the corresponding thresholds for 2–3 h following each other within one day can be related by logarithmic dependences with the EQ magnitude and the epicenter distance. Despite having only a few available cases, the obtained dependences (1)–(3) for log(ΔT), log(ΔT·R), and log(Δh’Es) versus the EQ magnitude are statistically significant at the 95% confidence level. Hypothetically, it is supposed that the time of the EQ preparation process is longer with stronger EQs and that the lead time depends on a seismological context. For this reason, ΔT is larger for stronger EQs (Table 2).

Moreover, similar expressions have been obtained in other parts of the world (e.g., Japan), where the number of events is much larger [41]. Similar relationships take place for Greek EQs as well [44]. All this indicates that the working hypothesis used in the present analysis may have real physical value.

Of course, an intriguing point is to use the obtained relationships for EQ predictions. Formally, the expression (14) gives the magnitude M of an EQ, which can be used to find the lead time ΔT and the epicentral distance R. The main obstacle is the insufficient data, which can potentially be enlarged. However, false cases which cannot be separated from the real EQ precursors is a serious limitation. It should be noted that as the electrostatic fields on the ground are produced by metallic aerosols and radon (e.g., [58]); the measure of these phenomena on the ground could improve the effectiveness of the method for prediction purposes. A potential future study could then use ground-based radon measurements along with monitoring ionosphere anomalies.

5. Conclusions

The results of the undertaken analysis may be formulated as follows.

• The crustal EQs that occurred in 2016 next to the town of Amatrice, Italy belong to the same type of events that took place earlier in Central Italy. Similar to the earlier analyzed events, they support the relationship between the observed ionospheric anomalies and the magnitude, lead time, and the epicentral distance of the EQs.
• The obtained relationships (linear regressions) are statistically significant at the confidence level >95% according to F-criterion. They are similar to expressions obtained earlier for Japanese and Greek EQs.
• The inclusion in the analysis of anomalies obtained during magnetically disturbed periods only slightly changes the regression coefficients without changing statistical significance of the regressions as a whole.
• The existence of false ionospheric precursors that cannot be separated from real ones and the statistic insignificance of the second coefficient in (6) are the main obstacles to using the obtained quantitative relationships for EQ predictions. The number of false precursors increases for magnetically disturbed periods. Besides, for possible future practical application of the method, a different background making use of past data only should be used in the anomaly definition.