New Stress Reduction Factor for Evaluating Soil Liquefaction in the Coastal Area of Catania (Italy)
Abstract
:1. Introduction
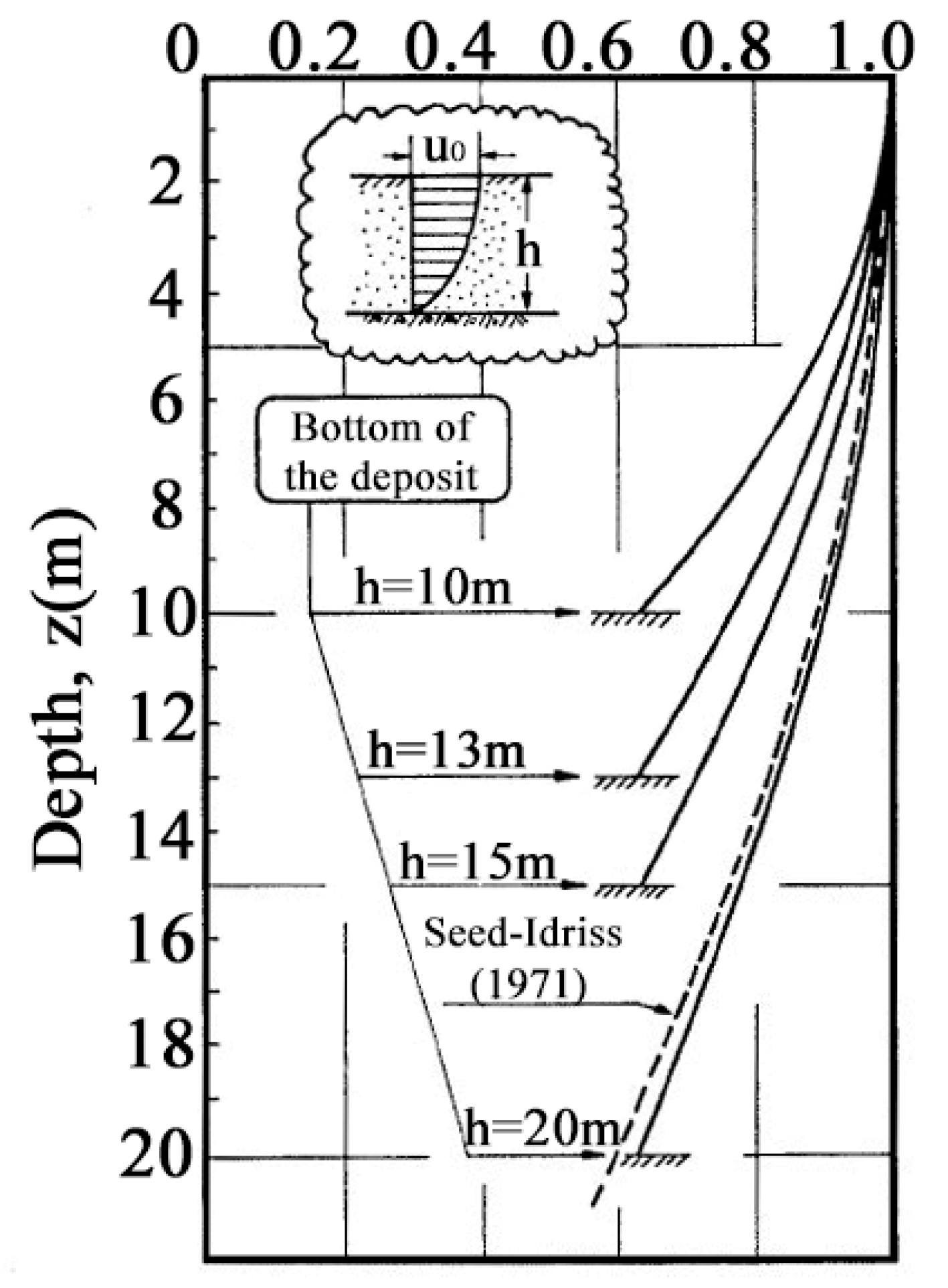
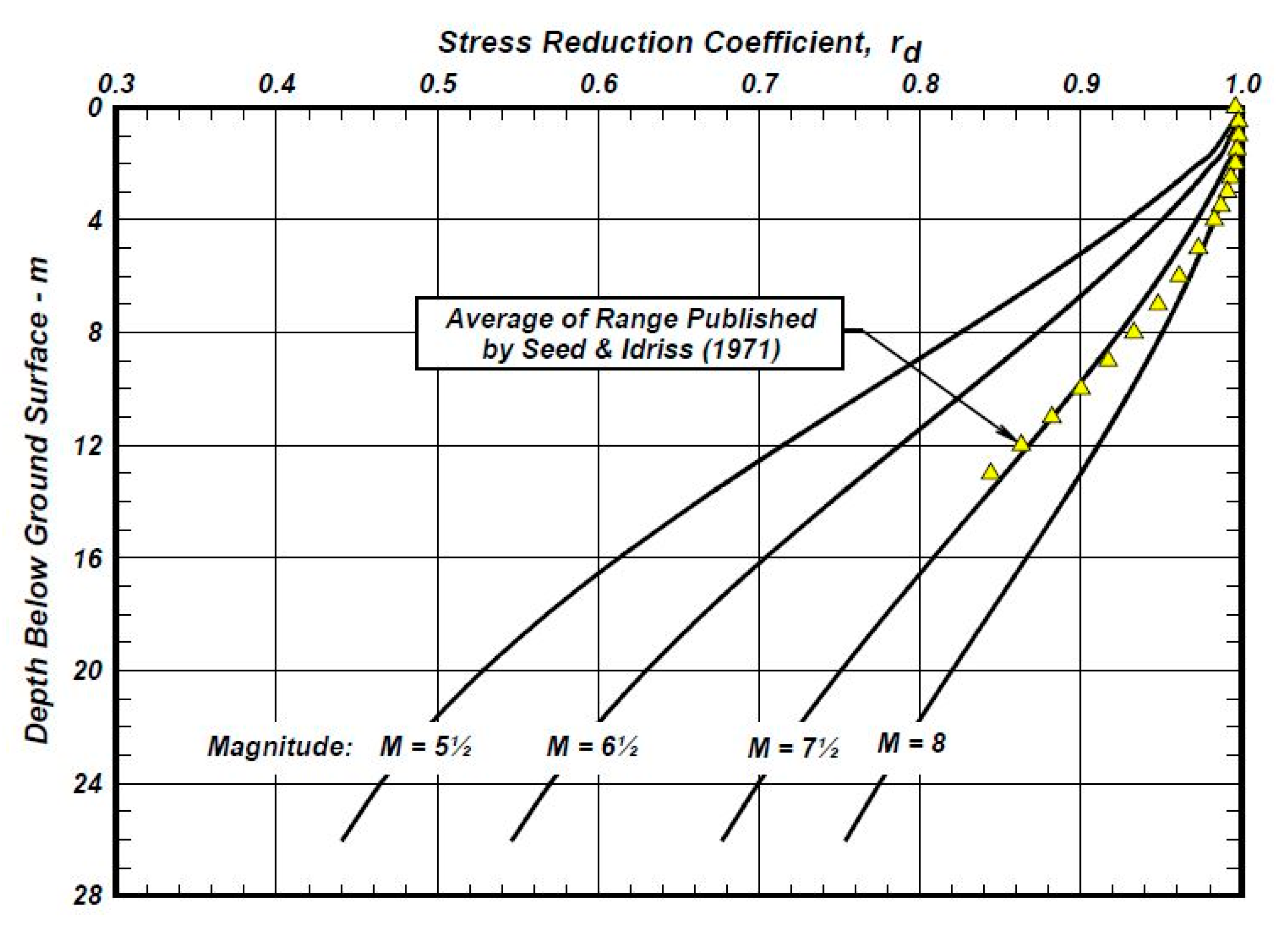
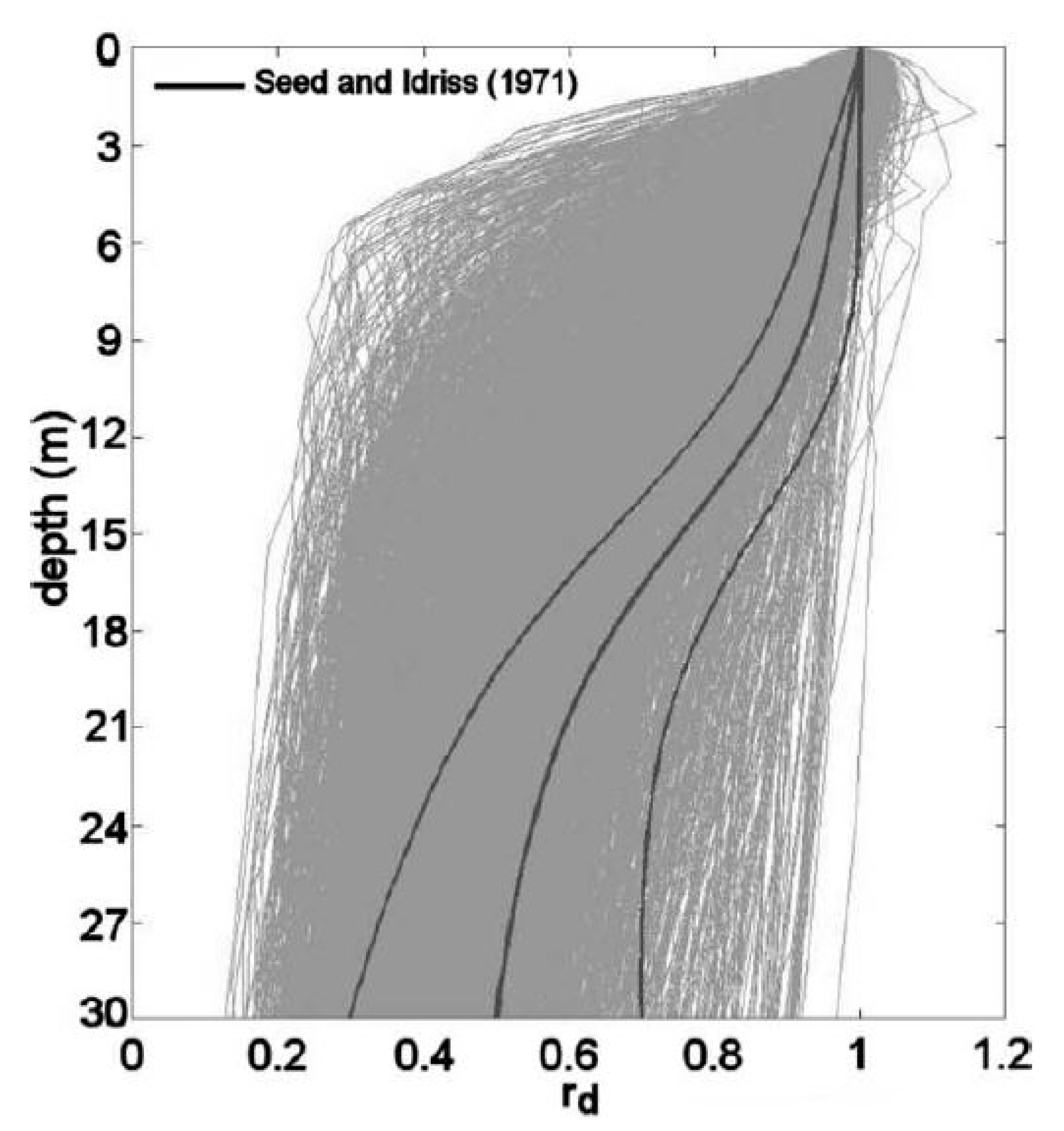
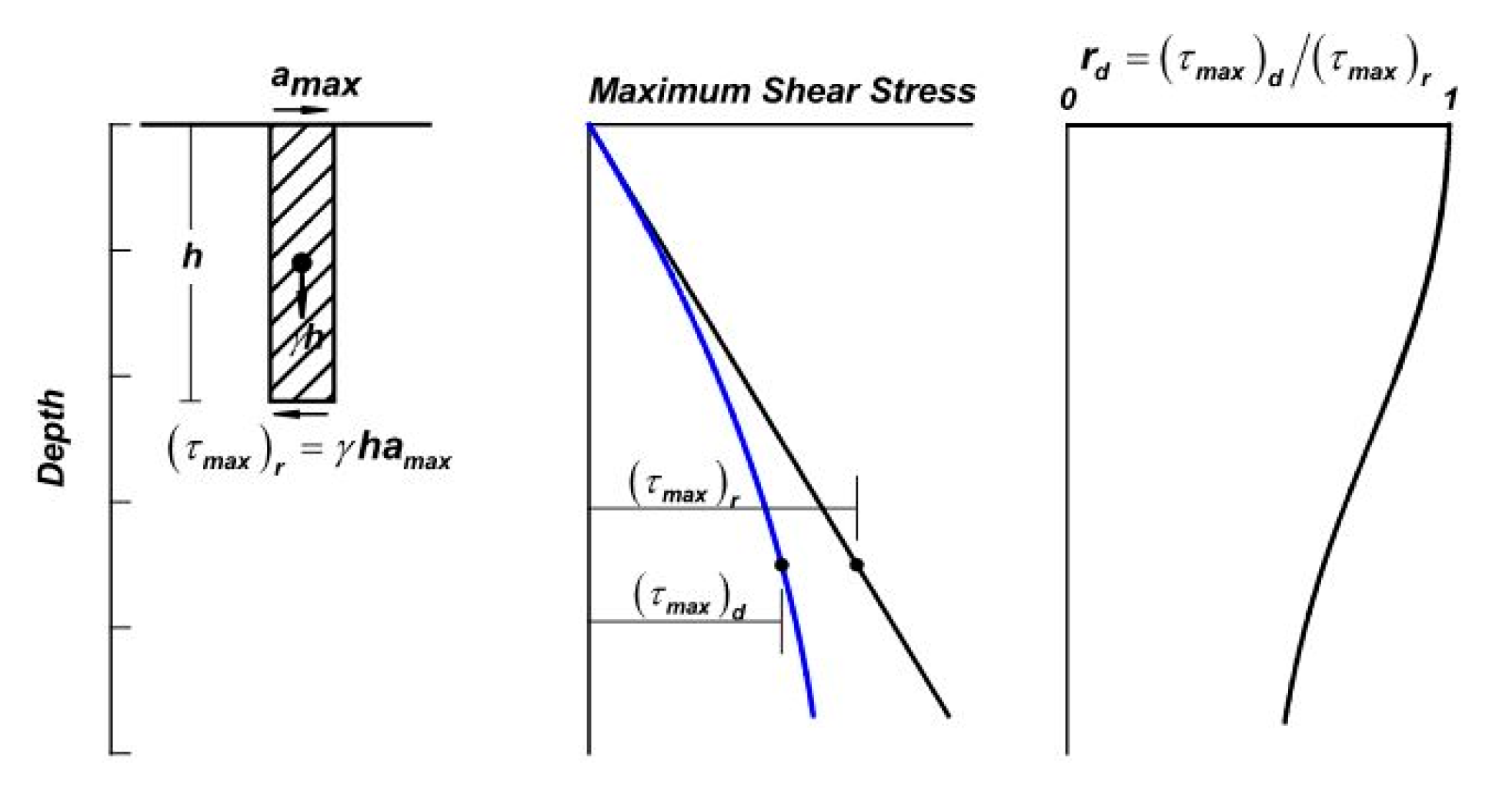
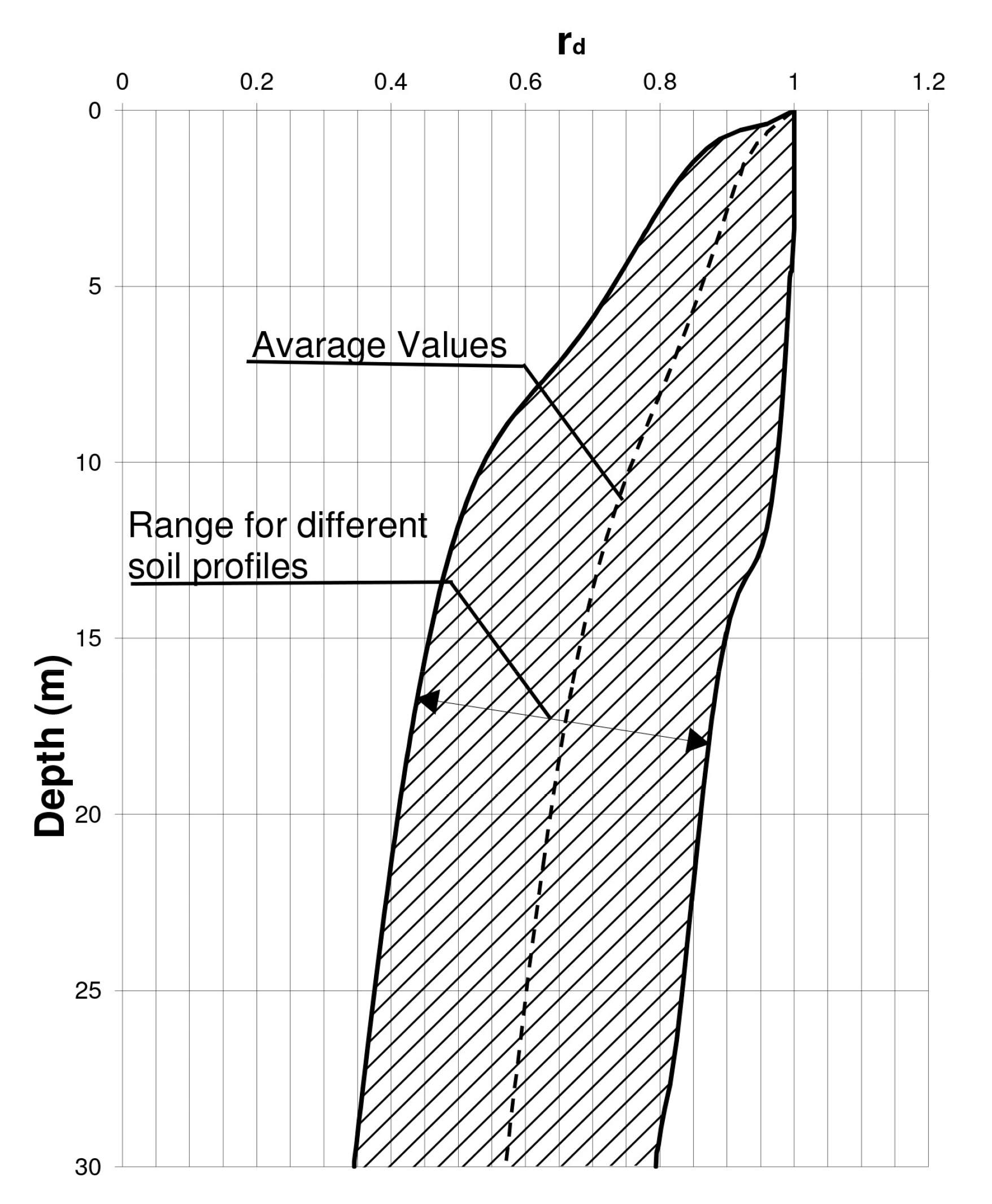
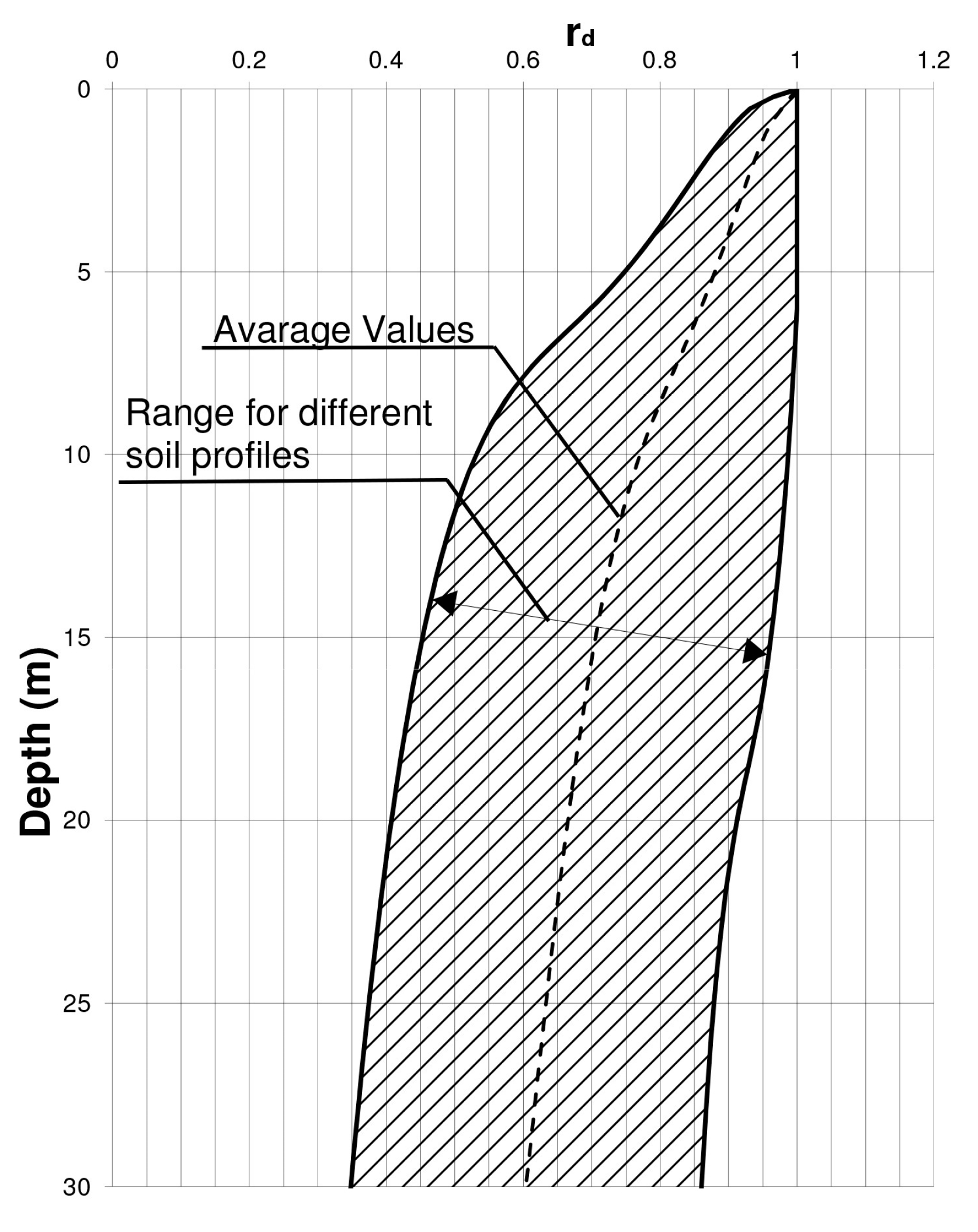
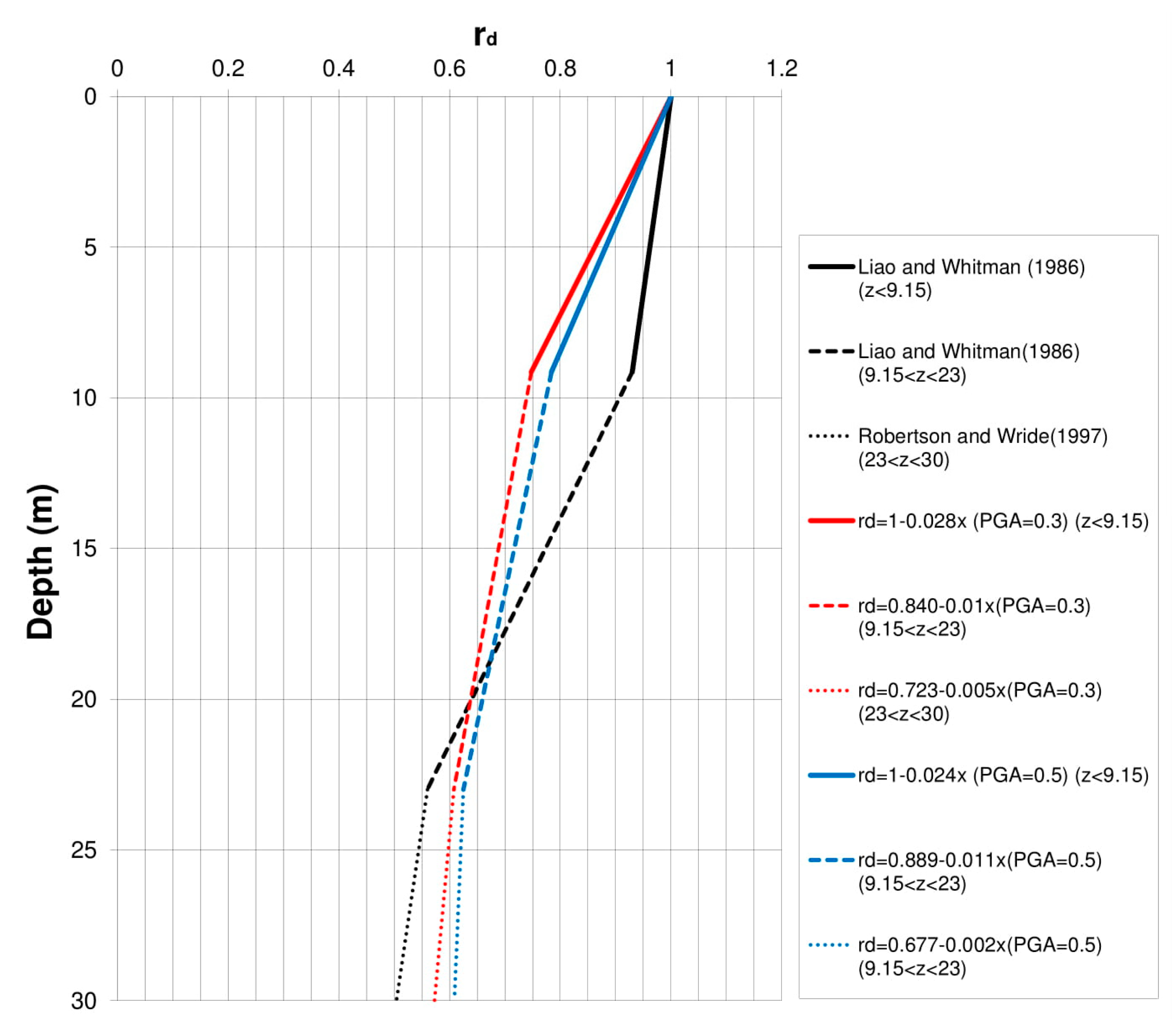
2. Shear Stress Reduction Factor: State-of-Art Review
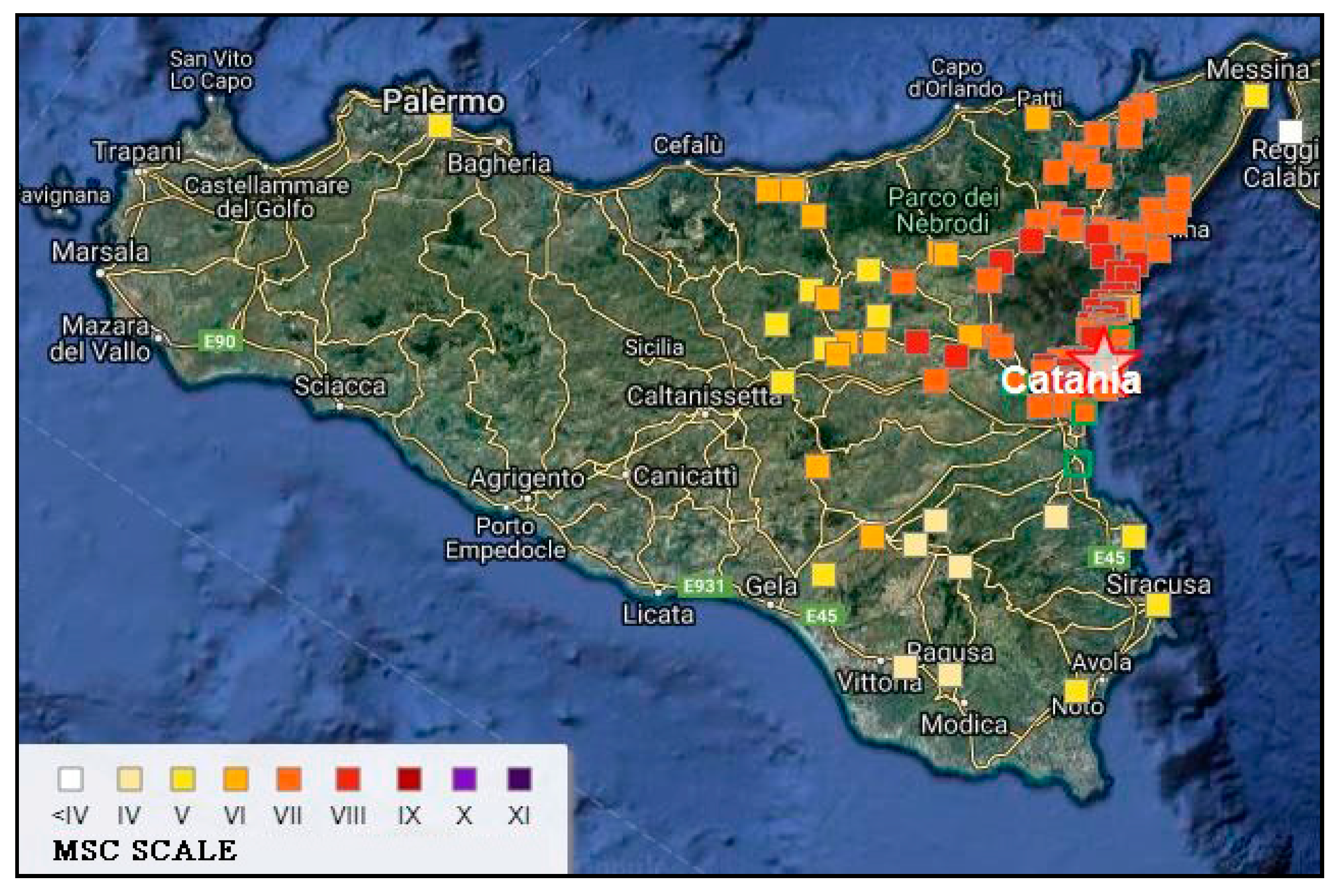
3. Seismicity of the Catania Area
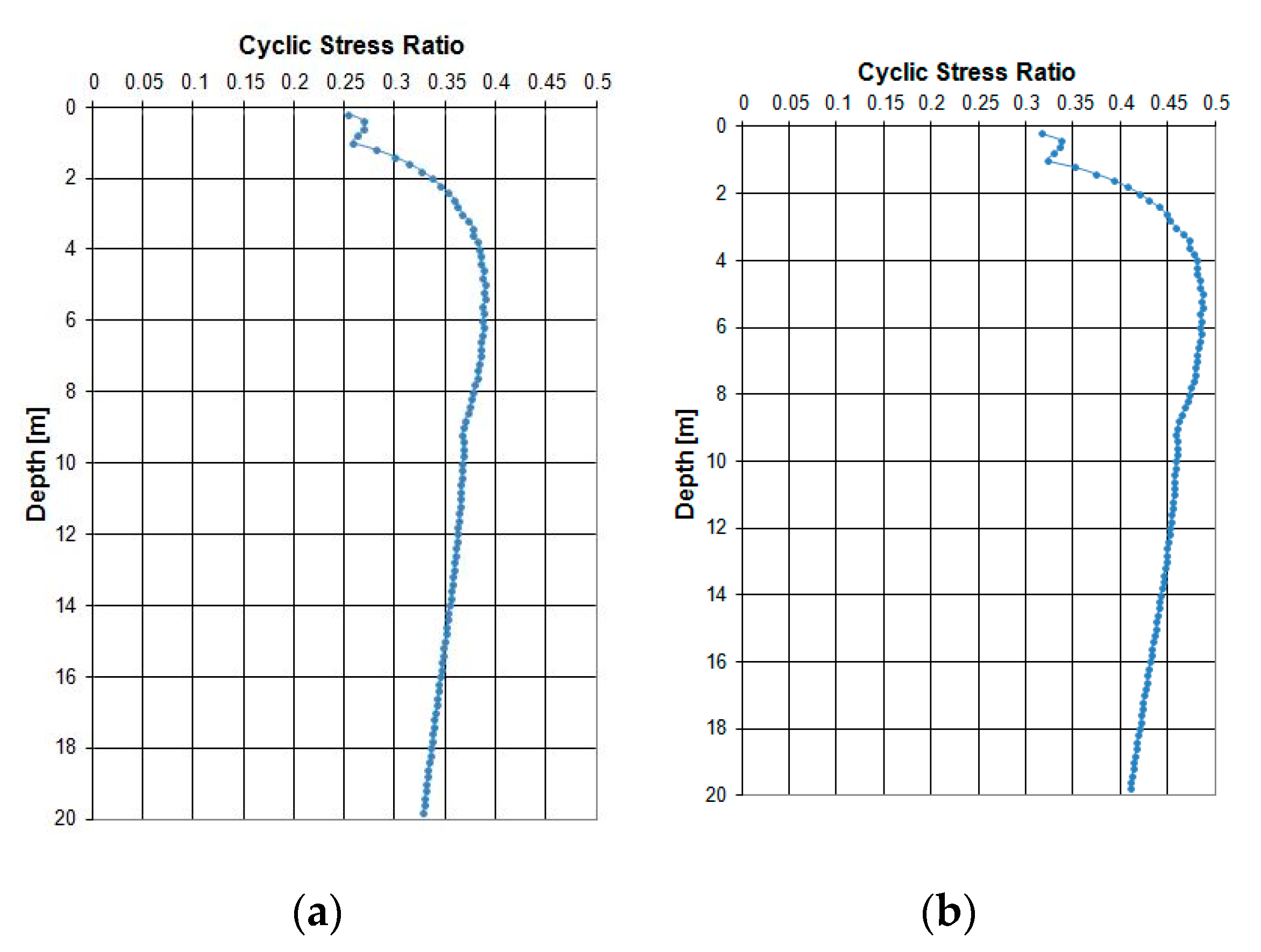
4. Site Response Analysis
- (a)
- Ohta and Goto [45]:where VS = shear wave velocity (m/s), NSPT = number of blows from SPT, z = depth in meters, = age factor (Holocene = 1.000, Pleistocene = 1.303), = geological factor (clays = 1.000, sands = 1.086).
- (b)
- Yoshida and Motonori [46]:where VS = shear wave velocity (m/s), NSPT = number of blows from SPT,geological factor (any soil 55, fine sand 49), σv0’ = effective vertical stress.
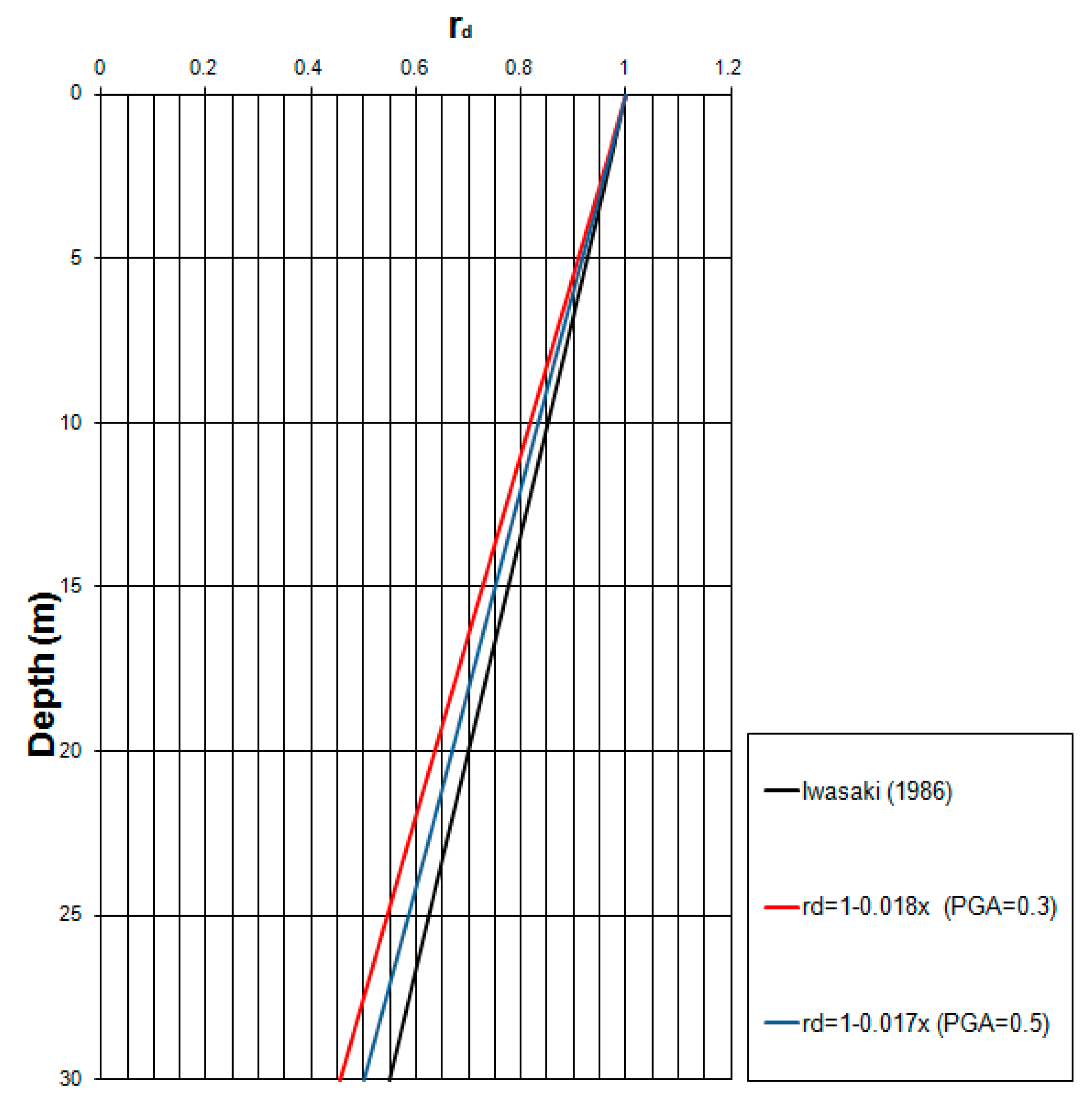
5. Shear Stress Reduction Factor rd in the Catania Area (Italy)
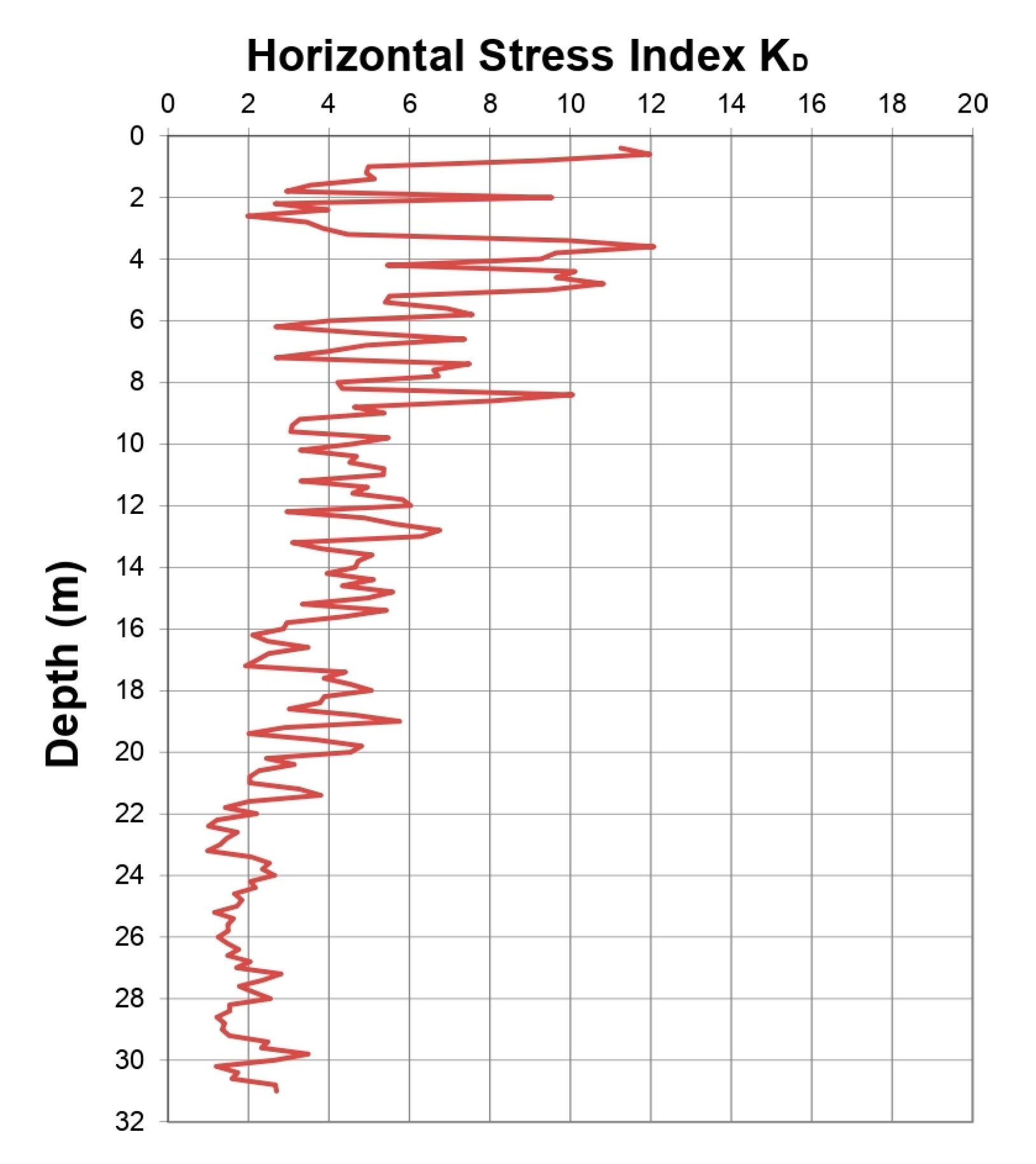
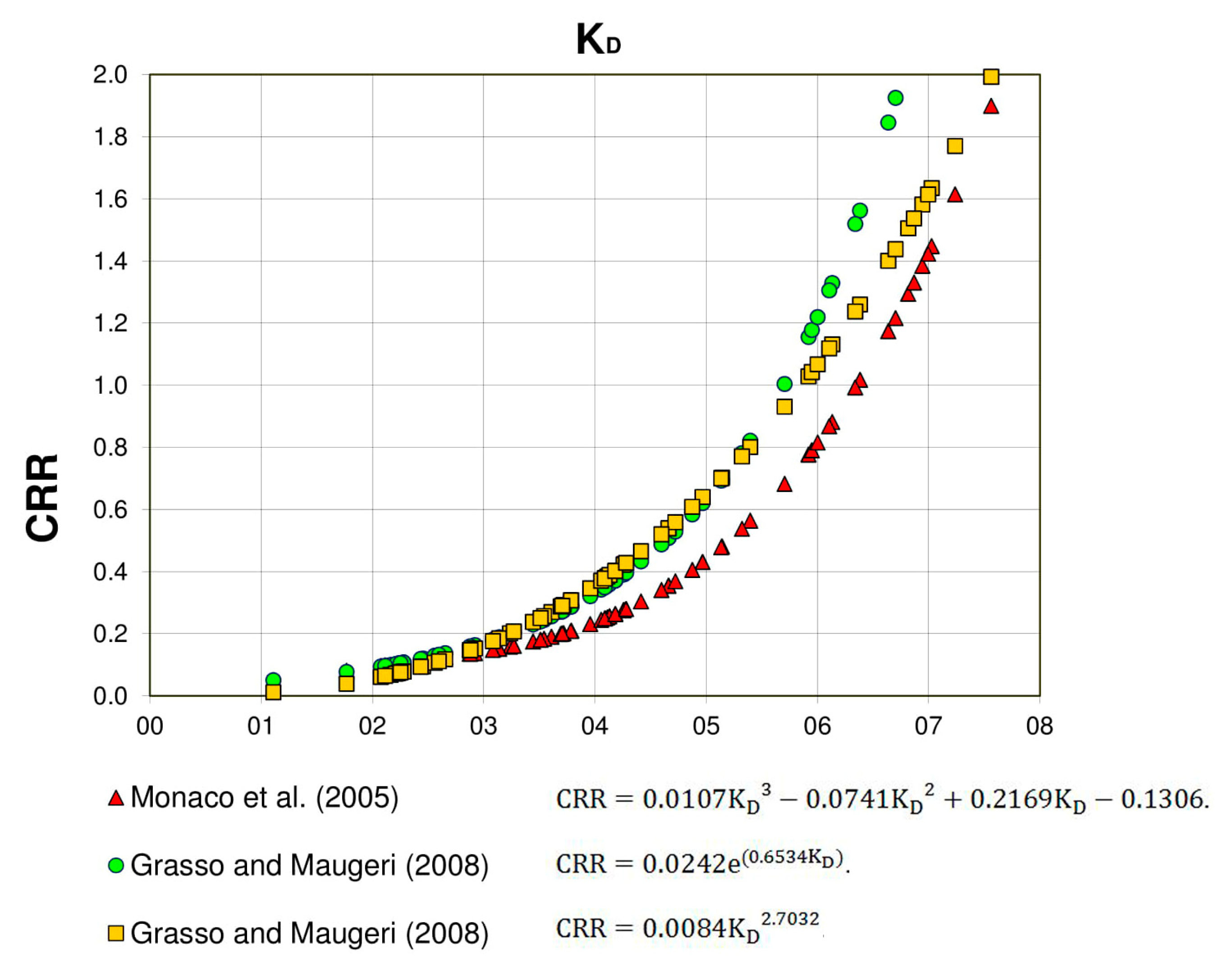
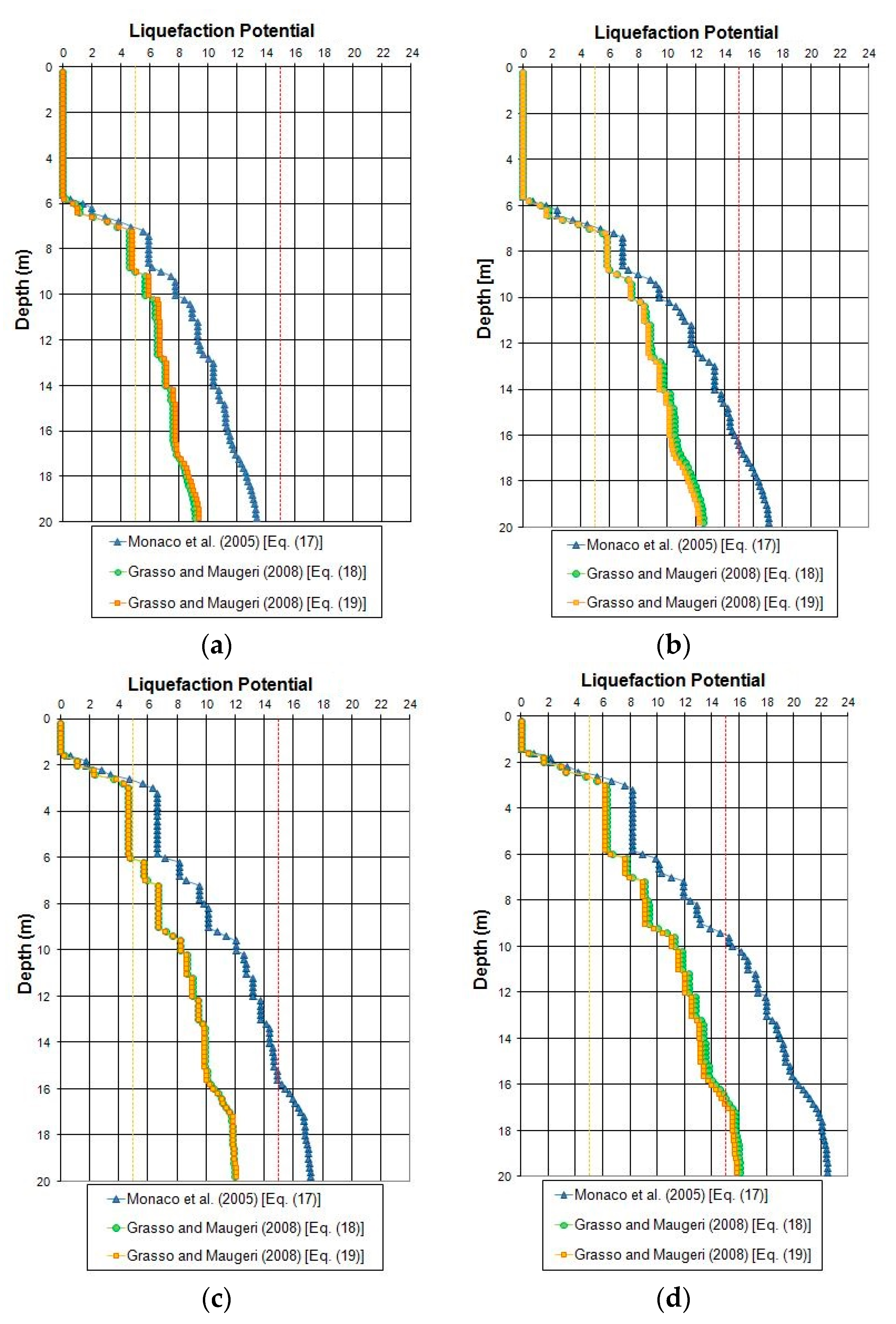
6. Evaluation of Liquefaction Potential Using the Seismic Dilatometer Marchetti Tests (SDMTs) in the Catania Harbour (Italy)
7. Conclusions
- (1)
- The results obtained from the three CRR-KD curves are in good agreement. However, it is possible to observe that the equation developed by Monaco provides LPI values slightly larger than those obtained from the equations proposed by Grasso and Maugeri;
- (2)
- The results show a high liquefaction potential from the depth of about 3–7 m;
- (3)
- Lower values of the liquefaction potential index are obtained from the SDMT4 and higher values from the SDMT3;
- (4)
- Finally, results demonstrate that the peak horizontal acceleration at the ground surface amax is an important parameter in the evaluation of liquefaction potential.
Author Contributions
Funding
Conflicts of Interest
References
- Seed, R.B.; Cetin, K.O.; Moss, R.E.S.; Kammerer, A.M.; Wu, J.; Pestana, J.M.; Reimer, M.F. Recent advances in soil liquefaction engineering and seismic site response evaluation. In Proceedings of the 4th International Conference and Symposium on Recent Advances in Geotechnical Earthquake Engineering and Soil Dynamics, San Diego, CA, USA, 31 March 2001. [Google Scholar]
- Marcuson, W.F. Definition of terms related to liquefaction. J. Geotech. Engrg. Div. 1978, 104, 1197–1200. [Google Scholar]
- Boulanger, R.W.; Idriss, I.M. CPT and SPT Based Liquefaction Triggering Procedures; Report No. UCD/CGM-14/01; Center for Geotechnical Modeling, Department of Civil and Environmental Engineering, College of Engineering, University of California: Davis, CA, USA, 2014. [Google Scholar]
- Boulanger, R.W.; Idriss, I.M. CPT-based liquefaction triggering procedure. J. Geotech. Geoenvir. Eng. 2015, 142, 2. [Google Scholar] [CrossRef]
- Cetin, K.O.; Seed, R.B. Nonlinear shear mass participation factor (rd) for cyclic shear stress ratio evaluation. Soil Dyn. Earthq. Eng. 2004, 24, 103–113. [Google Scholar] [CrossRef]
- Idriss, I.M.; Boulanger, R.W. Semi-empirical procedures for evaluating liquefaction potential during earthquakes. In Proceedings of the 11th IC SDEE/3rd ICEGE Proceedings, Berkeley, CA, USA, 7–9 January 2004; Volume 1, pp. 32–56. [Google Scholar] [CrossRef]
- Youd, T.L.; Idriss, I.M.; Andrus, R.D.; Arango, I.; Castro, G.; Christian, J.T.; Dobry, R.; Finn, W.D.L.; Harder, L.F.; Hynes, M.E.; et al. Liquefaction Resistance of Soils: Summary Report from the 1996 NCEER and 1998 NCEER/NSF Workshops on Evaluation of Liquefaction Resistance of Soils. J. Geotech. Geoenviron. Eng. 2001, 127, 817–833. [Google Scholar] [CrossRef] [Green Version]
- Grasso, S.; Maugeri, M. The Seismic Dilatometer Marchetti Test (SDMT) for Evaluating Liquefaction Potential under Cyclic Loading. In Proceedings of the IV Geotechnical Earthquake Engineering and Soil Dynamic, Sacramento, CA, USA, 18–22 May 2008; ISBN 978-0-7844-0975-6. [Google Scholar]
- Maugeri, M.; Grasso, S. Liquefaction potential evaluation at Catania Harbour (Italy). Wit Trans Built Environ. 2013, 1, 69–81. [Google Scholar] [CrossRef] [Green Version]
- Guidoboni, E.; Ferrari, G.; Mariotti, D.; Comastri, A.; Tarabusi, G.; Sgattoni, G.; Valensise, G. CFTI5Med, Catalogue of Strong Earthquakes in Italy (461 B.C.-1997) and Mediterranean Area (760 B.C.-1500). INGV 2018. [Google Scholar] [CrossRef]
- Guidoboni, E.; Ferrari, G.; Tarabusi, G.; Sgattoni, G.; Comastri, A.; Mariotti, D.; Ciuccarelli, C.; Bianchi, M.G.; Valensise, G. CFTI5Med, The new release of the catalogue of strong earthquakes in Italy and in Mediterranean area. Sci. Data 2019, 6, 80. [Google Scholar] [CrossRef]
- Seed, H.B.; Idriss, I.M. Simplified procedure for evaluating soil liquefaction potential. J. Soil Mech. Found. Div. 1971, 97, 1249–1273. [Google Scholar]
- Liao, S.S.C.; Whitman, R.V. Overburden Correction Factor for SPT in Sands. J. Geotech. Eng. 1986, 112, 373–377. [Google Scholar] [CrossRef]
- Robertson, P.K.; Wride, C.E. Cyclic Liquefaction and its Evaluation Based on the SPT and CPT. In Proceedings of the NCEER Workshop on Evaluation of Liquefaction Resistance of Soils, Salt Lake City, UT, USA, 5–6 January 1996; Technical Report No. NCEER-97-0022. pp. 41–88. [Google Scholar]
- Ishihara, K. Simple method of analysis for liquefaction of sand deposits during earthquakes. Soils Found. 1977, 17, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Iwasaki, T. Soil liquefaction studies in Japan: State-of-the-art. Soil Dyn Earthquake Engng. 1986, 5, 2–68. [Google Scholar] [CrossRef]
- Idriss, I.M. An update to the Seed-Idriss simplified procedure for evaluating liquefaction potential. In Proceedings of the TRB Workshop on New Approaches to Liquefaction, Washington, DC, USA, 10 January 1999. [Google Scholar]
- Golesorkhi, R. Factor Influencing the Computational Determination of Earthquake-Induced Shear Stressed in Sandy Soils. Ph.D. Thesis, University of California, Berkeley, CA, USA, 1989. [Google Scholar]
- Kishida, T.; Boulanger, R.W.; Abrahamson, N.A.; Driller, M.W.; Wehling, T.M. Site effects for the Sacramento-San Joaquin Delta. Earthq. Spectra 2009, 25, 301–322. [Google Scholar] [CrossRef]
- Kishida, T.; Boulanger, R.W.; Abrahamson, N.A.; Driller, M.W.; Wehling, T.M. Seismic response of levees in Sacramento-San Joaquin Delta. Earthq. Spectra 2009, 25, 557–582. [Google Scholar] [CrossRef]
- Lasley, S.J.; Green, R.A.; Rodriguez-Marek, A. New stress reduction coefficient relationship for liquefaction triggering analyses. J. Geotech. Geoenvironmental Eng. 2016, 142, 06016013. [Google Scholar] [CrossRef]
- Bonaccorso, R.; Grasso, S.; Lo Giudice, E.; Maugeri, M. Cavities and hypogeal structures of the historical part of the City of Catania. Adv. Earthq. Eng. 2005, 14, 197–223. [Google Scholar]
- Baratta, M. I Terremoti d’Italia. Saggio di storia, Geografia e Bibliografia Sismica Italiana Con 136 Sismocartogrammi; Arnaldo Forni Editore: Rome, Italy, 1901. [Google Scholar]
- Del Giudice, F. Terremoti avvenuti nel Regno delle due Sicilie nel 1857. Annali Civili del Regno delle due Sicilie nel 1857. 1858. Available online: http://storing.ingv.it/cfti/cfti4/quakes/08443.html (accessed on 28 December 2020).
- Mercalli, G. I Terremoti Storici Italiani. Geologia d’Italia, Part III, Vulcani e Fenomeni Vulcanici in Italia; Vallardi Editore: Milan, Italy, 1883. [Google Scholar]
- Galli, P.; Meloni, F. Nuovo catalogo nazionale dei processi di liquefazione avvenuti in occasione dei terremoti storici in Italia. Quat. Ital. J. Quat. Sci. 1993, 6, 271–292. [Google Scholar]
- Castelli, F.; Grasso, S.; Lentini, V.; Massimino, M.R. In situ measuremnts for evaluating liquefaction potential under cyclic loading. In Proceedings of the 1st 1MEKO TC4 International Workshop on Metrology for Geotechnics, Benevento, Italy, 17–18 March 2016; pp. 79–84. [Google Scholar]
- Cavallaro, A.; Massimino, M.R.; Maugeri, M. Noto Cathedral: Soil and foundation investigation. Constr. Build. Mater. J. 2003, 17, 533–541. [Google Scholar] [CrossRef]
- Grasso, S.; Maugeri, M. Seismic Microzonation Studies for the City of Ragusa (Italy). Soil Dyn. Earthq. Eng. 2014, 56, 86–97. [Google Scholar] [CrossRef]
- Castelli, F.; Cavallaro, A.; Grasso, S. SDMT soil testing for the local site response analysis. In Proceedings of the 1st IMEKO TC4 International Workshop on Metrology for Geotechnics, Benevento, Italy, 17–18 March 2016; pp. 143–148. [Google Scholar]
- Castelli, F.; Cavallaro, A.; Ferraro, A.; Grasso, S. In situ and laboratory tests for site response analysis in the ancient city of Noto (Italy). In Proceedings of the 1st IMEKO TC4 International Workshop on Metrology for Geotechnics, Benevento, Italy, 17–18 March 2016; pp. 85–90, ISBN 978-929900750-1. [Google Scholar]
- Boschi, E.; Guidoboni, E.; Mariotti, D. Seismic effects of the strongest historical earthquakes in the Syracuse area. Ann. Geofis. 1995, 38, 223–253. [Google Scholar]
- Barbano, M.S.; Rigano, R. Earthquake sources and seismic hazard in Southeastern Sicily. Ann. Geofis. 2001, 44, 723–738. [Google Scholar]
- Imposa, S.; Lombardo, G. The Etna earthquake of February 20, 1818. In Atlas of Isoseismal Maps of Italian Earthquakes; Postpischl, D., Ed.; Quaderni de La Ricerca Scientifica: Bologna, Italy, 1985; pp. 80–81. [Google Scholar]
- Abate, G.; Corsico, S.; Massimino, M.R. FEM Modelling of the Seismic Behavior of a Tunnel-soil-Aboveground Building System: A Case History in Catania (Italy). Procedia Eng. 2016, 158, 380–385. [Google Scholar] [CrossRef] [Green Version]
- Abate, G.; Massimino, M.R.; Romano, S. Finite Element Analysis of DSSI Effects for a Building of Strategic Importance in Catania (Italy). Procedia Eng. 2016, 158, 374–379. [Google Scholar] [CrossRef] [Green Version]
- Caruso, S.; Ferraro, A.; Grasso, S.; Massimino, M.R. Site Response Analysis in eastern Sicily based on direct and indirect Vs measurements. In Proceedings of the 1st IMEKO TC4 International Workshop on Metrology for Geotechnics, Benevento, Italy, 17–18 March 2016; pp. 115–120, ISBN 978-929900750-1. [Google Scholar]
- Castelli, F.; Cavallaro, A.; Ferraro, A.; Grasso, S.; Lentini, V.; Massimino, M.R. Static and dynamic properties of soils in Catania (Italy). Ann. Geophys. 2018, 61, SE221. [Google Scholar] [CrossRef]
- Ferraro, A.; Grasso, S.; Massimino, M.R. Site effects evaluation in Catania (Italy) by means of 1-D numerical analysis. Ann. Geophys. 2018, 61, SE224. [Google Scholar] [CrossRef]
- Massimino, M.R.; Abate, G.; Corsico, S.; Louarn, R. Comparison Between Two Approaches for Non-linear FEM Modelling of the Seismic Behaviour of a Coupled Soil–Structure System. Geotech. Geol. Eng. 2019, 37, 1957–1975. [Google Scholar] [CrossRef]
- Maugeri, M. (Ed.) Seismic Prevention of Damage: A Case Study in a Mediterranean City; WIT Press: Southampton, UK, 2005; ISBN 1-84564-004-7. [Google Scholar]
- Grasso, S.; Maugeri, M. The Seismic Microzonation of the City of Catania (Italy) for the Maximum Expected Scenario Earthquake of January 11, 1693. Soil Dyn. Earthq. Eng. 2009, 29, 953–962. [Google Scholar] [CrossRef]
- Grasso, S.; Maugeri, M. The Seismic Microzonation of the City of Catania (Italy) for the Etna Scenario Earthquake (M = 6.2) of February 20, 1818. Earthq. Spectra 2012, 28, 573–594. [Google Scholar] [CrossRef]
- Kokusho, T.; Yoshida, Y. SPT N-value and S-wave velocity for gravely soils with different grain size distribution. Soils Found. 1997, 37, 105–113. [Google Scholar] [CrossRef] [Green Version]
- Ohta, Y.; Goto, N. Empirical Shear Wave Velocity Equations in Terms of Characteristic Soil Indexes. Earthq. Eng. Struct. Dyn. 1978, 6, 167–187. [Google Scholar] [CrossRef]
- Yoshida, Y.; Motonori, I. Empirical Formulas of SPT Blow-Counts for Gravelly Soils. In Proceedings of the ISOPT-1, Orlando, FL, USA, 20–24 March 1988; pp. 381–387. [Google Scholar] [CrossRef]
- Yokota, K.; Imai, T.; Konno, M. Dynamic Deformation Characteristics of Soils Determined by Laboratory Tests. Oyo Tec. Rep. 1981, 3, 13–37. [Google Scholar]
- Ferraro, A.; Grasso, S.; Maugeri, M.; Totani, F. Seismic response analysis in the southern part of the historic centre of the City of L’Aquila (Italy). Soil Dyn. Earthq. Eng. 2016, 88, 256–264. [Google Scholar] [CrossRef]
- Kottke, A.R.; Rathje, E.M. Technical Manual for STRATA; PEER Report 2008/10; University of California: Berkeley, CA, USA, 2008. [Google Scholar]
- NTC [2018] D. M. 17/01/2018. New Technical Standards for Buildings. Official Journal of the Italian Republic. 2018. Available online: https://www.gazzettaufficiale.it/eli/gu/2018/02/20/42/so/8/sg/pdf (accessed on 23 October 2020).
- Grasso, S.; Laurenzano, G.; Maugeri, M.; Priolo, E. Seismic response in Catania by different methodologies. Adv. Earthq. Eng. 2005, 14, 63–79. [Google Scholar]
- Laurenzano, G.; Priolo, E.; Klinc, P.; Vuan, A. Near fault earthquake scenarios for the February 20, 1818 M = 6.2 “Catanese” event. In Proceedings of the Fourth International Conference on Computer Simulation in Risk Analysis and Hazard Mitigation: “Risk Analysis 2004”, Rhodes, Greece, 27–29 September 2004; pp. 81–91. [Google Scholar]
- Meletti, C.; Montaldo, V. Stime di Pericolosità Sismica per Diverse Probabilità di Superamento in 50 Anni: Valori di Ag. Progetto DPC-INGV S1, Deliverable D2. 2007. Available online: http://esse1.mi.ingv.it/d2.html (accessed on 23 October 2020).
- Cavallaro, A.; Capilleri, P.P.; Grasso, S. Site characterization by dynamic in situ and laboratory tests for liquefaction potential evaluation during Emilia Romagna earthquake. Geosciences 2018, 8, 242. [Google Scholar] [CrossRef] [Green Version]
- Rollins, K.M.; Remund, T.K.; Amoroso, S. Evaluation of DMT-based liquefaction triggering curves based on field case histories. In Proceedings of the 5th International Conference on Geotechnical and Geophysical Site Characterisation, Queensland, Australia, 5–9 September 2016. [Google Scholar]
- Marchetti, S. Detection of liquefiable sand layers by means of quasi-static penetration test. In Proceedings of the 2nd European Symp. on Penetration Testing, Amsterdam, The Netherlands, 24–27 May 1982; Volume 2, pp. 689–695. [Google Scholar]
- Monaco, P.; Marchetti, S.; Totani, G.; Calabrese, M. Sand liquefiability assessment by Flat Dilatometer Test (DMT). In Proceedings of the XVI ICSMGE, Osaka, Japan, 12–16 September 2005; Volume 4, pp. 2693–2697. [Google Scholar]
- Iwasaki, T.; Tatsuoka, F.; Tokida, K.; Yasuda, S. A practical method for assessing soil liquefaction potential based on case studies at various sites in Japan. In Proceedings of the 2nd Int Conf on Microzonation for Safer Construction, Research and Application, San Francisco, CA, USA, 26 November–1 December 1978; Volume 1, pp. 885–896. [Google Scholar]
- NASEM-National Academies of Sciences, Engineering, and Medicine. State of the Art and Practice in the Assessment of Earthquake-Induced soil Liquefaction and Its Consequences; The National Academies Press: Washington, DC, USA, 2016. [Google Scholar] [CrossRef]
- Iwasaki, T.; Tokida, K.; Tatsuoka, F.; Watanabe, S.; Yasuda, S.; Sato, H. Microzonation for soil liquefaction potential using simplified methods. In Proceedings of the 3rd International Conference on Microzonation, Seattle, WA, USA, 28 June–1 July 1982; pp. 1319–1330. [Google Scholar]
- Chung, J.; Rogers, J. Simplified method for spatial evaluation of liquefaction potential in the St. Louis area. J. Geotech. Geoenvironmental Eng. 2011, 137, 505–515. [Google Scholar] [CrossRef]
- Dixit, J.; Dewaikar, D.M.; Jangrid, J.S. Assessment of liquefaction potential index for Mumbai City. Nat. Hazards Earth Sci. Syst. 2012, 12, 2759–2768. [Google Scholar] [CrossRef] [Green Version]
- Holzer, T.L.; Bennett, M.J.; Noce, T.E.; Padovani, A.C.; Tinsley, J.C., III. Liquefaction hazard mapping with LPI in the greater Oakland, California, area. Earthq. Spectra 2006, 22, 693–708. [Google Scholar] [CrossRef]
- Holzer, T.L.; Blair, J.L.; Noce, T.E.; Bennett, M.J. Predicted liquefaction of east bay fills during a repeat of the 1906 San Francisco earthquake. Earthq. Spectra 2006, 22, S261–S277. [Google Scholar] [CrossRef]
- Kim, H.S.; Kim, M.; Baise, L.G.; Kim, B. Local and regional evaluation of liquefaction potential index and liquefaction severity number for liquefaction-induced sand boils in Pohang, South Korea. Soil Dyn. Earthq. Eng. 2020, 106459. [Google Scholar] [CrossRef]
- Lenz, A.; Baise, L.G. Spatial variability of liquefaction potential in regional mapping using CPT and SPT data. Soil Dyn. Earthq. Eng. 2007, 27, 690–702. [Google Scholar] [CrossRef]
- Maurer, B.W.; Green, R.A.; Cubrinovski, M.; Brendon, A.; Bradley, B.A. Evaluation of the liquefaction potential index for assessing liquefaction hazard in Christchurch, New Zealand. J. Geotech. Geoenviron. Eng. 2014, 140, 04014032. [Google Scholar] [CrossRef]
- Muley, P.; Maheshwari, B.K.; Paul, D.K. Assessment of Liquefaction Potential Index for Roorkee Region. In Proceedings of the 16th Symposium on Earthquake Engineering, Indian Institute of Technology, Roorkee, India, 20–22 December 2018. [Google Scholar]
- Papathanassiou, G.; Pavlides, S.; Ganas, A. The 2003 Lefkada earthquake: Field observation and preliminary microzonation map based on liquefaction potential index for the town of Lefkada. Eng. Geol. 2005, 82, 12–31. [Google Scholar] [CrossRef]
- Sonmez, H. Modification of the liquefaction potential index and liquefaction susceptibility mapping for a liquefaction-prone area (Inegol, Turkey). Env. Geol. 2003, 44, 862–871. [Google Scholar] [CrossRef]
- Yalcin, A.; Gokceoglu, C.; Sonmez, H. Liquefaction severity map for Aksaray city center. Nat. Hazards Earth Syst. Sci. 2008, 8, 641–649. [Google Scholar] [CrossRef]

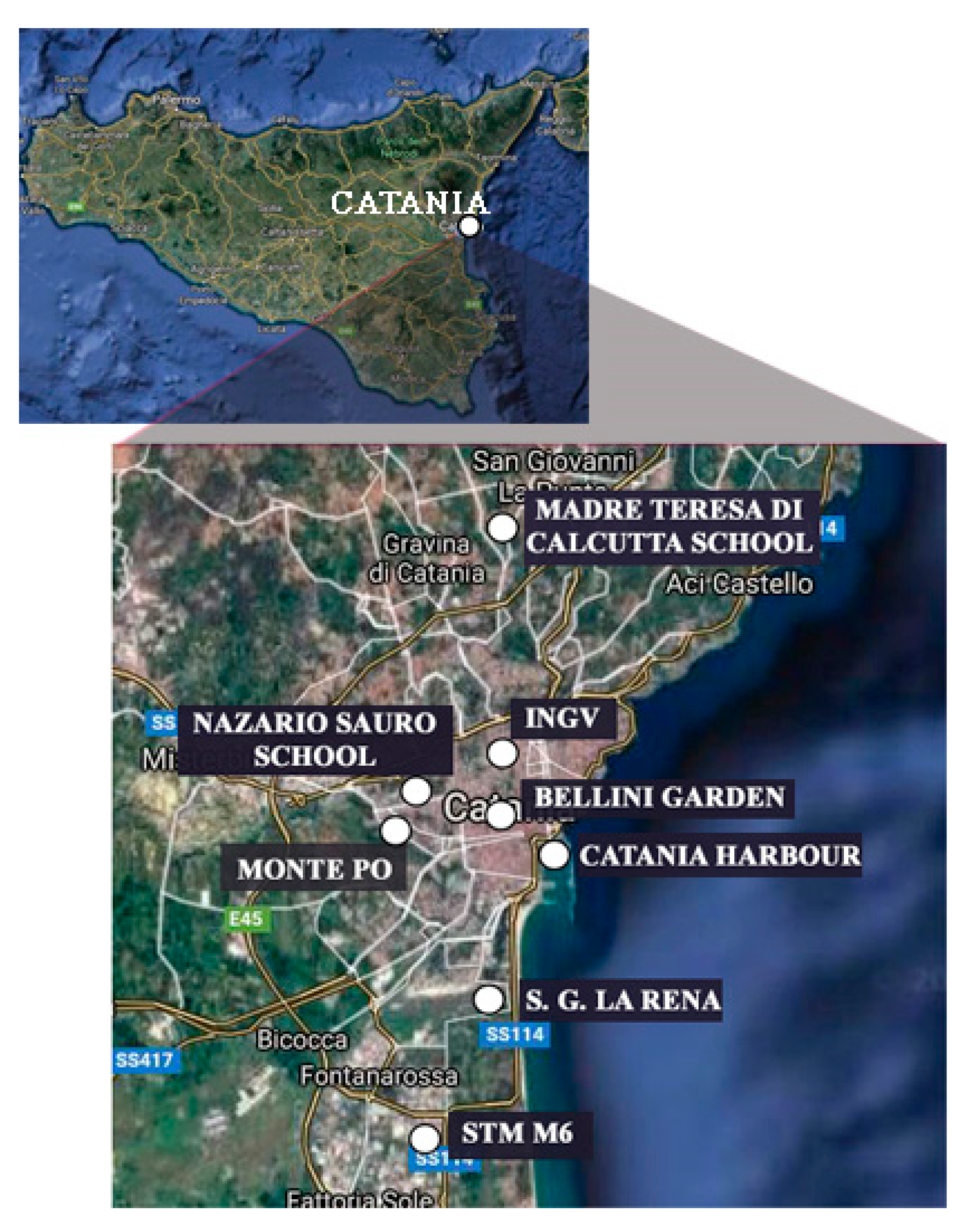
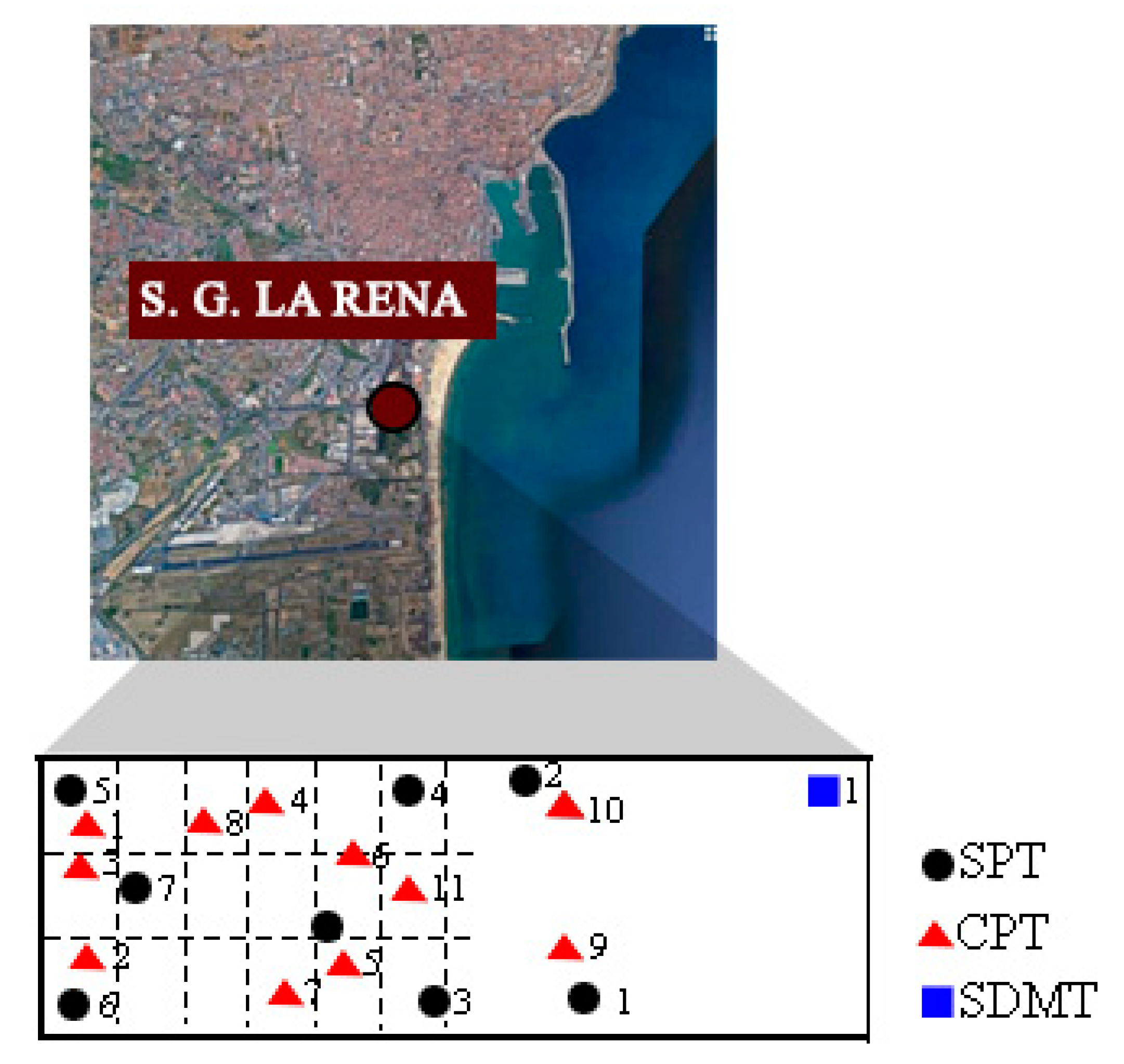



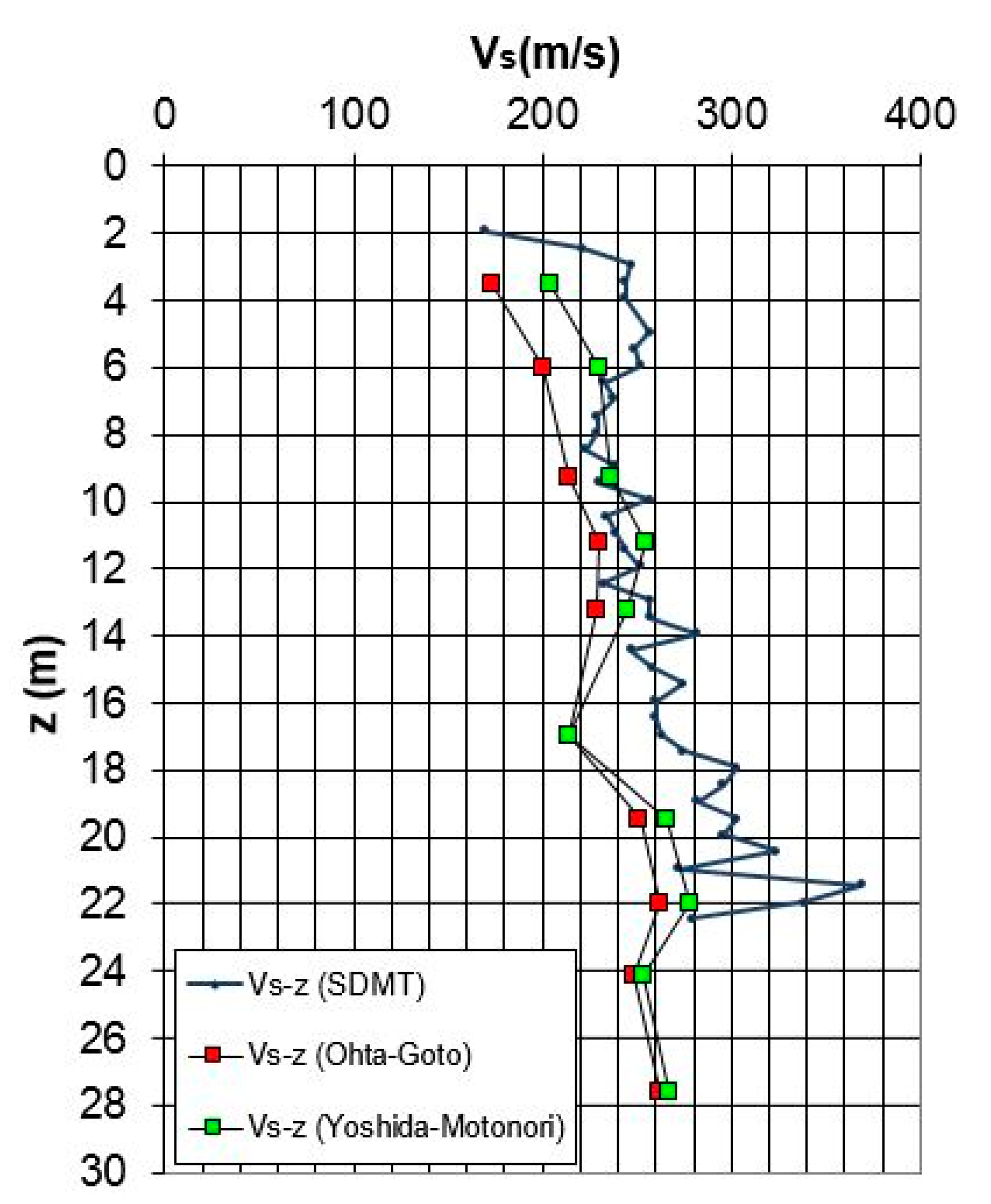
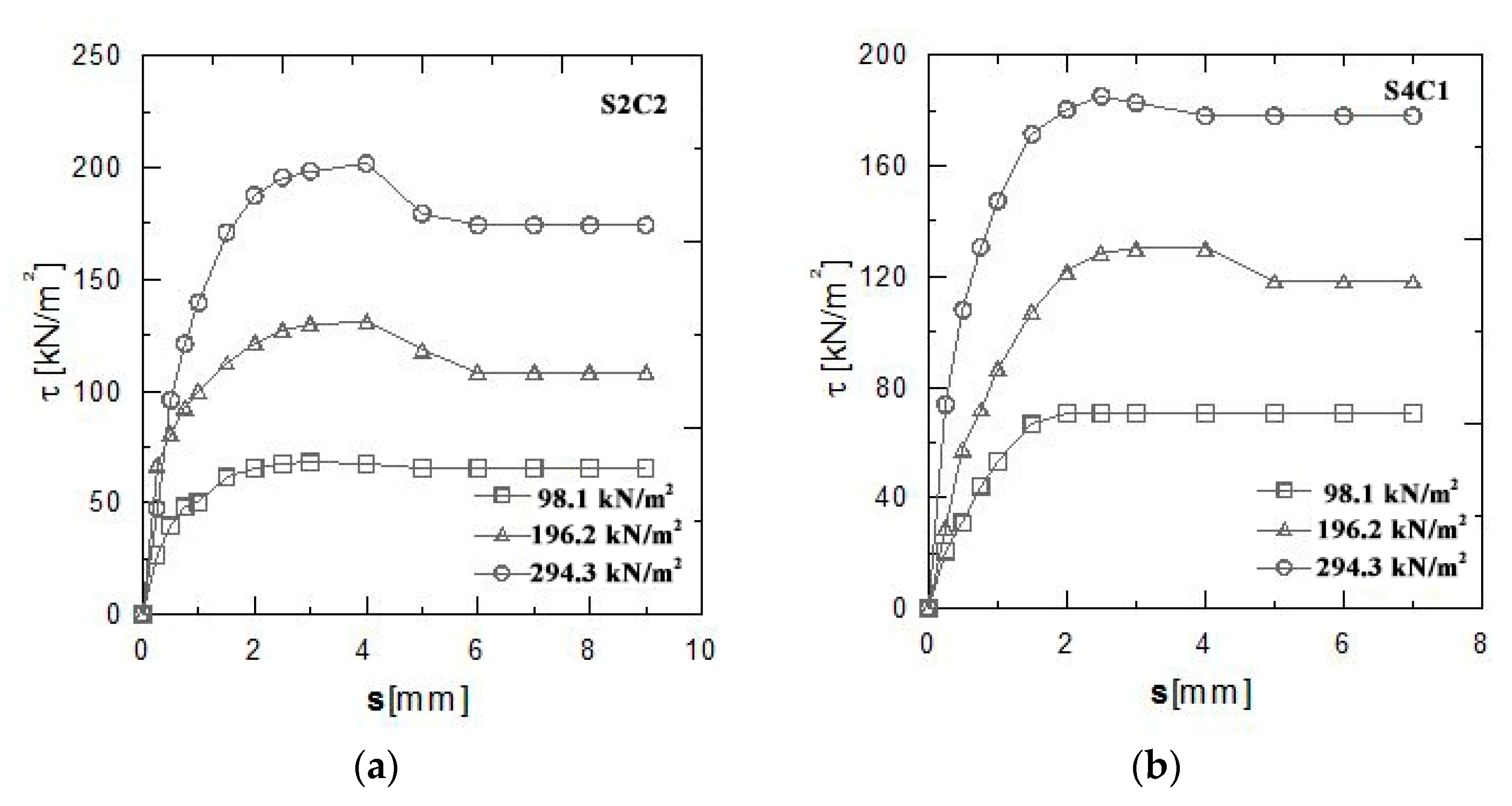
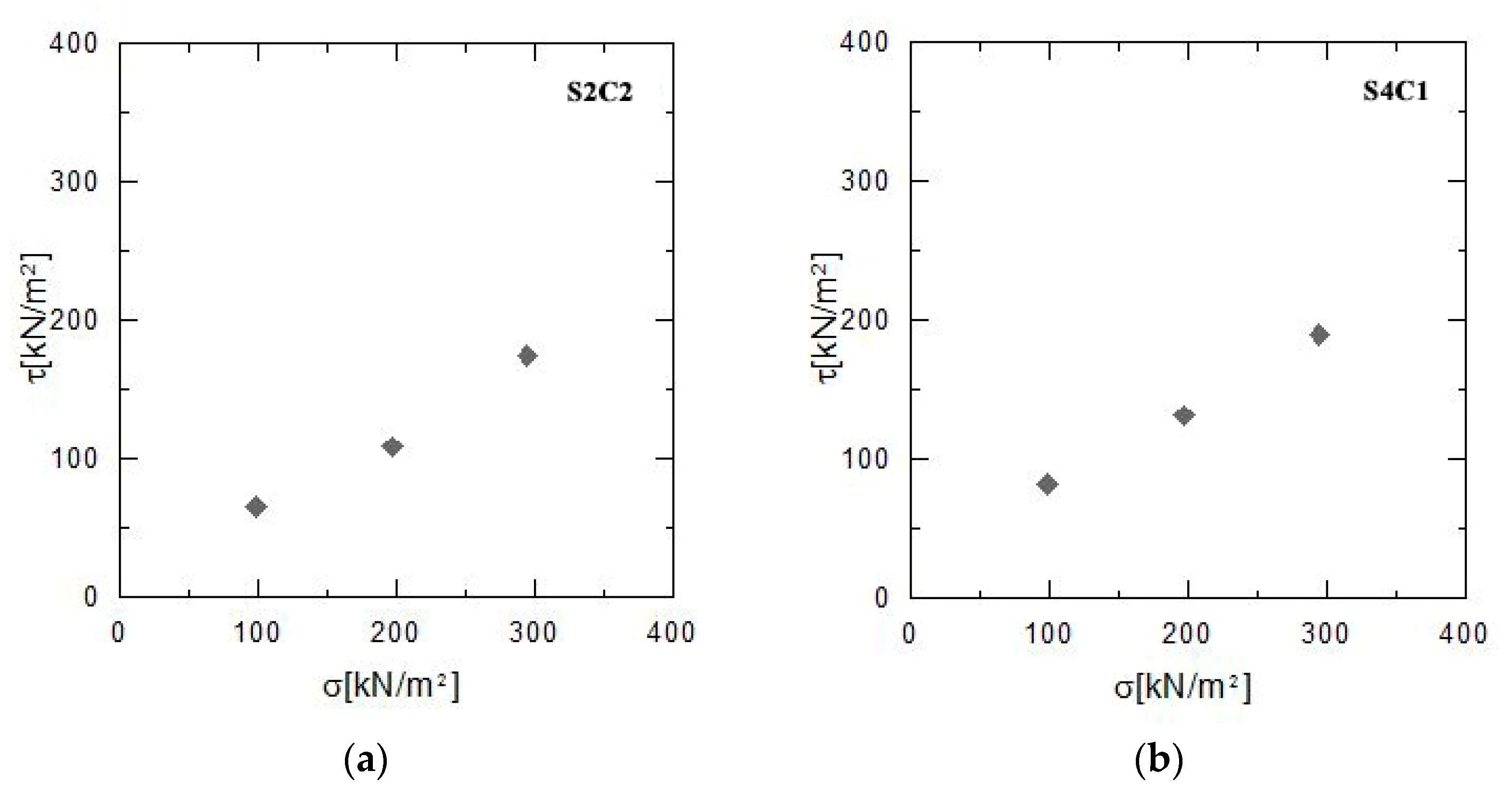
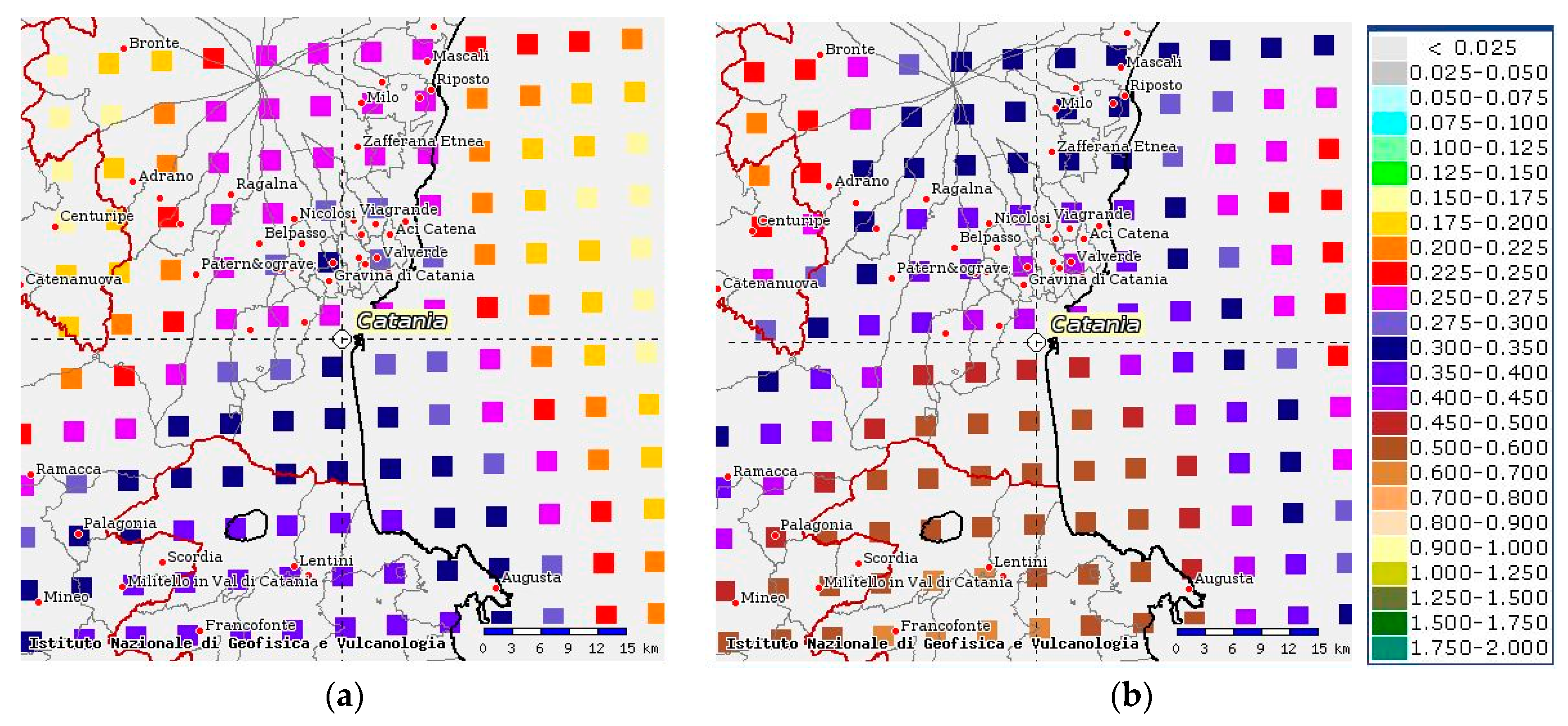

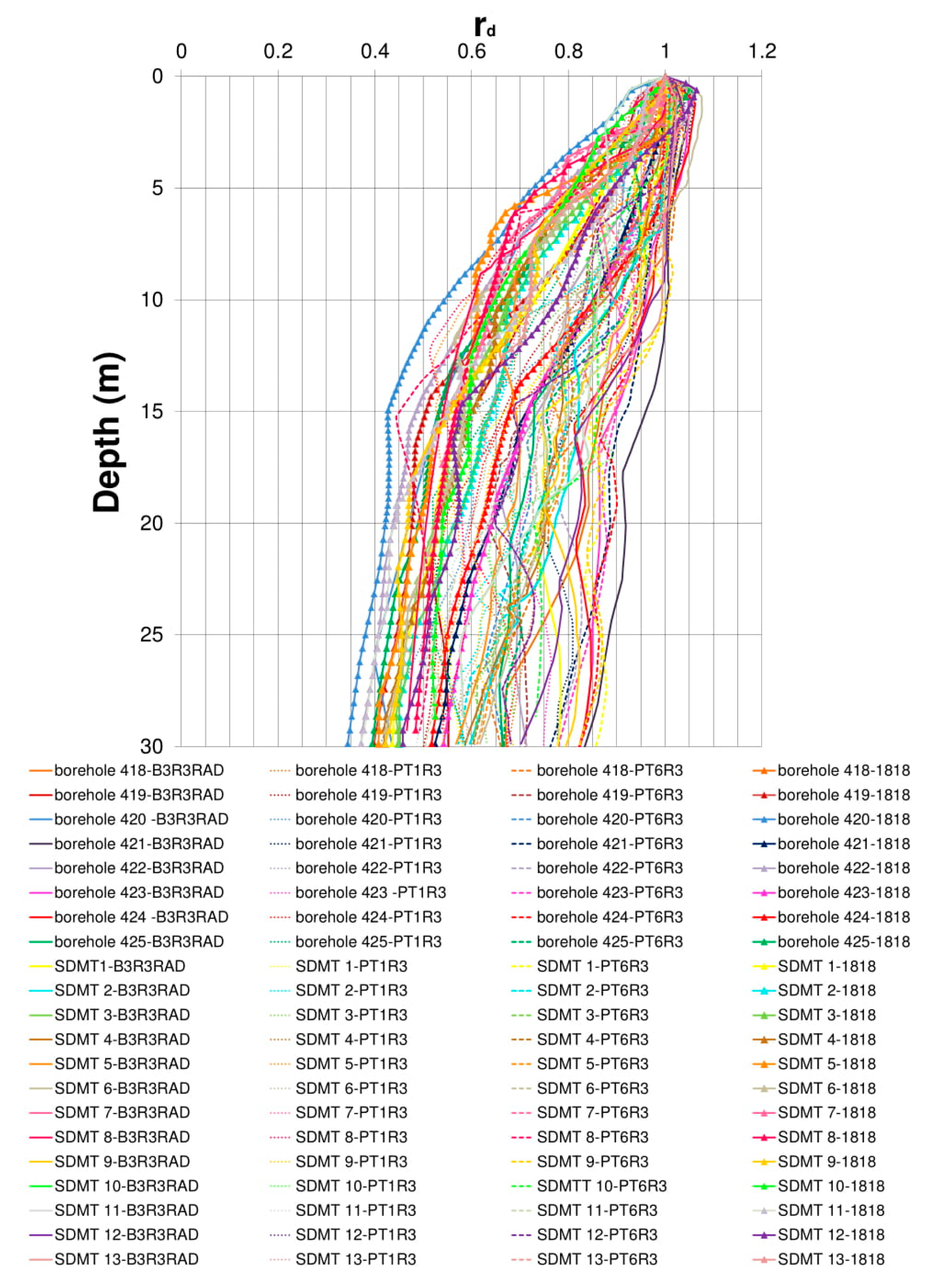
| Experimental Sites | Tests |
|---|---|
| Saint Giuseppe La Rena | SPT 1 (borehole 418) |
| Saint Giuseppe La Rena | SPT 2 (borehole 419) |
| Saint Giuseppe La Rena | SPT 3 (borehole 420) |
| Saint Giuseppe La Rena | SPT 4 (borehole 421) |
| Saint Giuseppe La Rena | SPT 5 (borehole 422) |
| Saint Giuseppe La Rena | SPT 6 (borehole 423) |
| Saint Giuseppe La Rena | SPT 7 (borehole 424) |
| Saint Giuseppe La Rena | SPT 8 (borehole 425) |
| Saint Giuseppe La Rena | SDMT 1 |
| Catania Harbour | SDMT 2 |
| Catania Harbour | SDMT 3 |
| Catania Harbour | SDMT 4 |
| Catania Harbour | SDMT 5 |
| Catania Harbour | SDMT 6 |
| Nazario Sauro school | SDMT 7 |
| Nazario Sauro school | SDMT 8 |
| INGV building | SDMT 9 |
| Madre Teresa di Calcutta School | SDMT 10 |
| STM M6 | SDMT 11 |
| Bellini Garden | SDMT 12 |
| Monte Po | SDMT 13 |
| LPI | Level of Liquefaction Severity |
|---|---|
| 0 | Very low |
| 0 < LPI ≤ 5 | Low |
| 5 < LPI ≤ 15 | High |
| LPI > 15 | Very high |
| Surface Maximum Accelerations | |
|---|---|
| SDMT2 | 0.44g |
| SDMT3 | 0.43g |
| SDMT4 | 0.45g |
| SDMT5 | 0.49g |
| SDMT6 | 0.41g |
| Liquefaction Potential Index | ||||||
|---|---|---|---|---|---|---|
| amax | 0.4 g | 0.5 g | ||||
| CRR-KD curves | 1 | 2 | 3 | 1 | 2 | 3 |
| SDMT2 | 13.30 | 9.12 | 9.37 | 17.04 | 12.52 | 12.22 |
| SDMT3 | 12.44 | 7.48 | 7.80 | 16.47 | 11.06 | 10.59 |
| SDMT4 | 17.13 | 11.97 | 12.01 | 22.50 | 16.06 | 15.78 |
| SDMT5 | 7.50 | 3.36 | 3.53 | 11.13 | 6.02 | 5.41 |
| SDMT6 | 12.51 | 8.99 | 9.44 | 15.83 | 11.86 | 11.74 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grasso, S.; Massimino, M.R.; Sammito, M.S.V. New Stress Reduction Factor for Evaluating Soil Liquefaction in the Coastal Area of Catania (Italy). Geosciences 2021, 11, 12. https://doi.org/10.3390/geosciences11010012
Grasso S, Massimino MR, Sammito MSV. New Stress Reduction Factor for Evaluating Soil Liquefaction in the Coastal Area of Catania (Italy). Geosciences. 2021; 11(1):12. https://doi.org/10.3390/geosciences11010012
Chicago/Turabian StyleGrasso, Salvatore, Maria Rossella Massimino, and Maria Stella Vanessa Sammito. 2021. "New Stress Reduction Factor for Evaluating Soil Liquefaction in the Coastal Area of Catania (Italy)" Geosciences 11, no. 1: 12. https://doi.org/10.3390/geosciences11010012
APA StyleGrasso, S., Massimino, M. R., & Sammito, M. S. V. (2021). New Stress Reduction Factor for Evaluating Soil Liquefaction in the Coastal Area of Catania (Italy). Geosciences, 11(1), 12. https://doi.org/10.3390/geosciences11010012