Evaluating Spatial Regression-Informed Cokriging of Metals in Soils near Abandoned Mines in Bumpus Cove, Tennessee, USA
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Sampling Procedure
2.3. Data Analysis and Kriging
3. Results
3.1. Descriptive Statistics
3.2. Kriging and Cokriging Model Comparison
3.2.1. Manganese
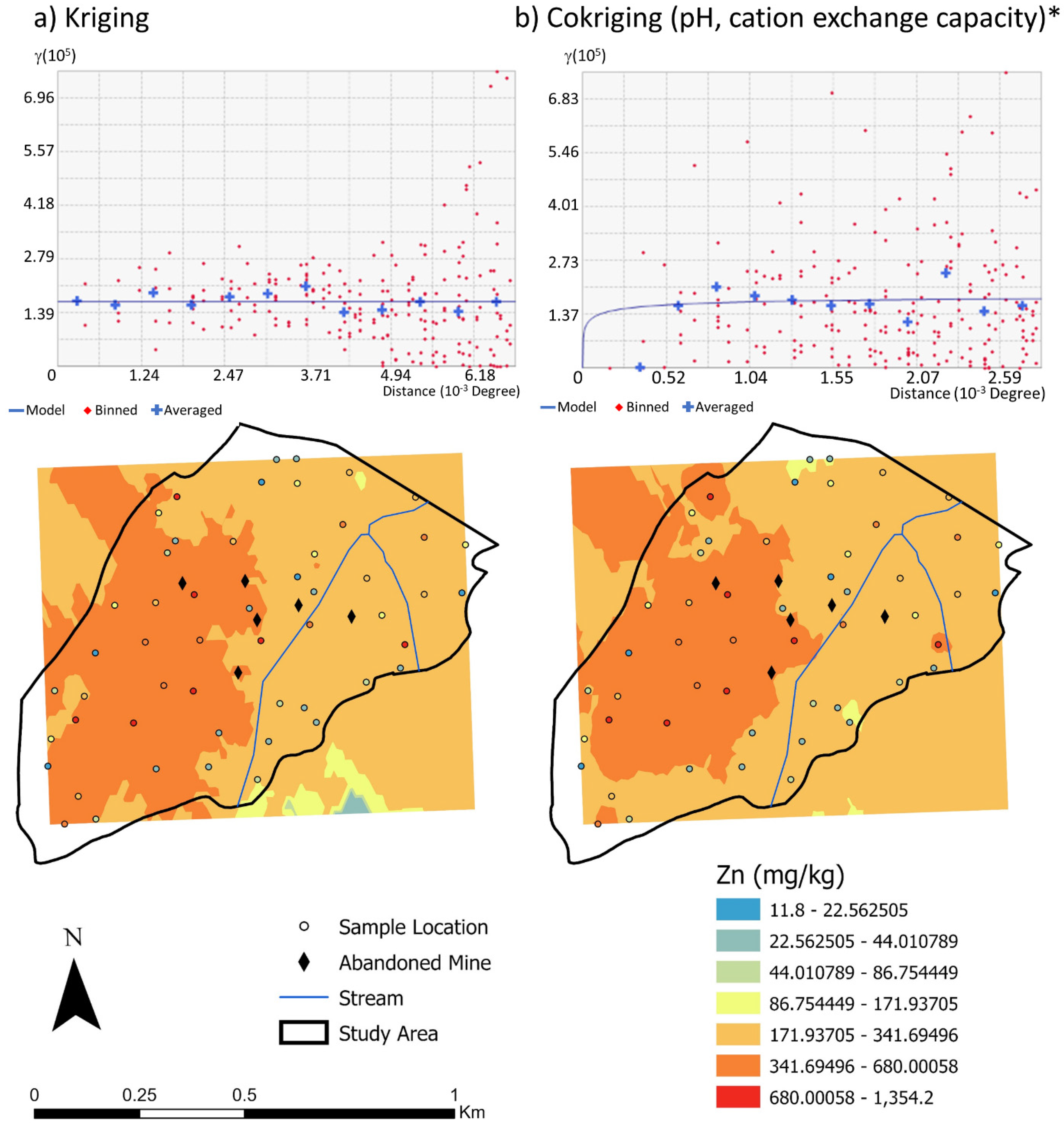
3.2.2. Zinc
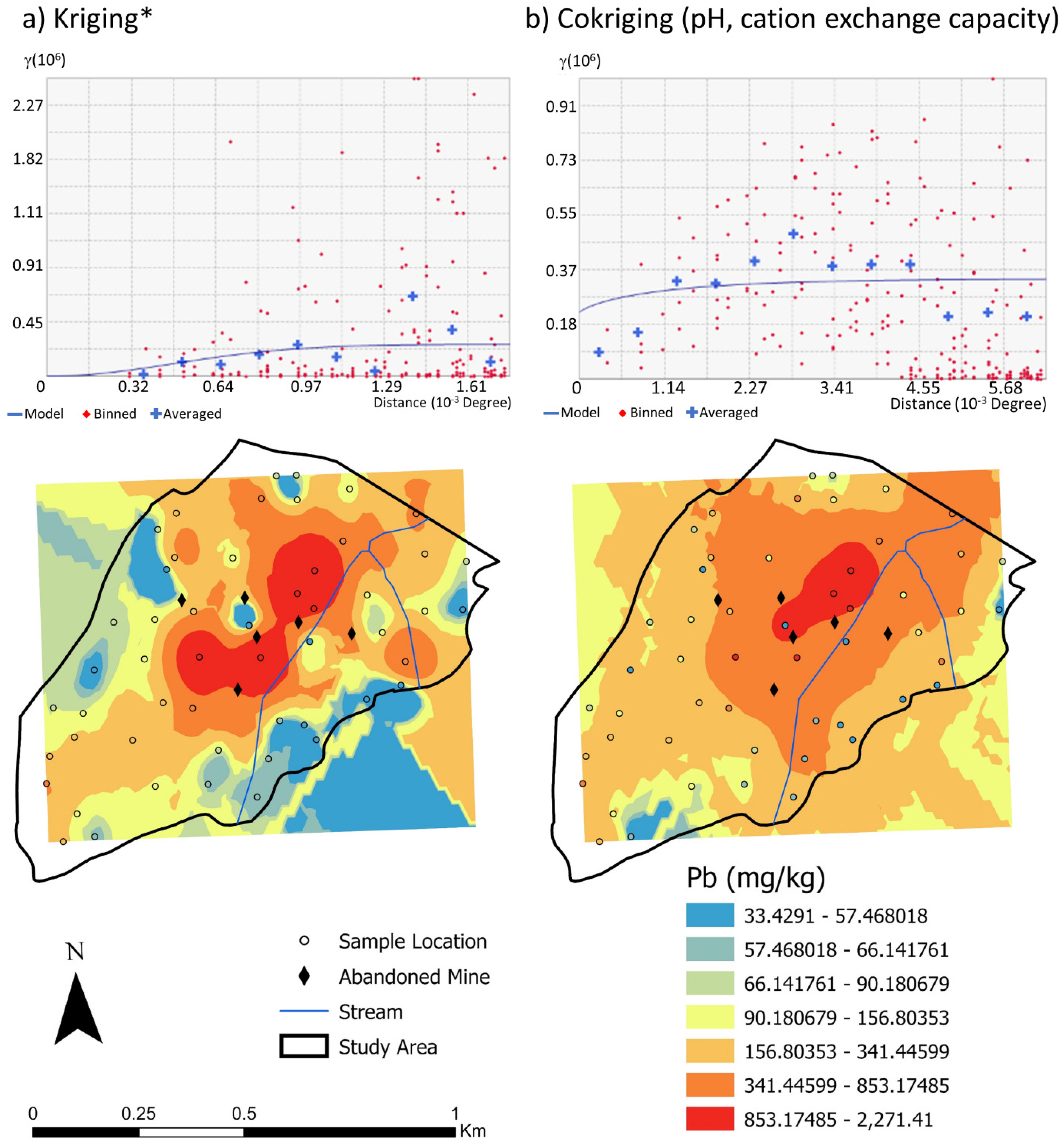
3.2.3. Lead
3.2.4. Copper
3.2.5. Cadmium
4. Discussion
4.1. Manganese
4.2. Zinc
4.3. Lead
4.4. Copper
4.5. Cadmium
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Weiss, F.T.; Leuzinger, M.; Zurbrügg, C.; Eggen, R.I.L. Chemical Pollution in Low and Middle-Income Countries; Eawag: Dubendorf, Switzerland, 2016. [Google Scholar]
- Dowdy, R.H.; Volk, V.V.; Nelson, D.W.; Elrick, D.E.; Tanji, K.K. Movement of heavy metals in soils. In Chemical Mobility and Reactivity in Soil Systems; American Society of Agronomy: Madison, MI, USA, 1983; pp. 227–240. [Google Scholar]
- Reeder, R.J.; Schoonen, M.A.A.; Lanzirotti, A. Metal Speciation and Its Role in Bioaccessibility and Bioavailability. Rev. Miner. Geochem. 2006, 64, 59–113. [Google Scholar] [CrossRef]
- Pierzynski, G.M.; Vance, G.F.; Sims, J.T. Soils and Environmental Quality; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Jain, C. Metal fractionation study on bed sediments of River Yamuna, India. Water Res. 2004, 38, 569–578. [Google Scholar] [CrossRef]
- Förstner, U.; Wittmann, G.T. Metal Pollution in the Aquatic Environment, 2nd ed.; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Alloway, B.J. Heavy Metals in Soils; Springer Science and Business Media: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- He, Z.L.; Yang, X.E.; Stoffella, P.J. Trace elements in agroecosystems and impacts on the environment. J. Trace Elem. Med. Biol. 2005, 19, 125–140. [Google Scholar] [CrossRef]
- Vega, F.; Covelo, E.; Andrade, M. Competitive sorption and desorption of heavy metals in mine soils: Influence of mine soil characteristics. J. Colloid Interface Sci. 2006, 298, 582–592. [Google Scholar] [CrossRef]
- Li, Z.; Schuman, L.M. Heavy metal movement in metal-contaminated soil profiles. Soil Sci. 1996, 161, 656–666. [Google Scholar] [CrossRef]
- Chang, A.C.; Warneke, J.E.; Page, A.L.; Lund, L.J. Accumulation of Heavy Metals in Sewage Sludge-Treated Soils. J. Environ. Qual. 1984, 13, 87–91. [Google Scholar] [CrossRef]
- Ersoy, A.; Yunsel, T.Y.; Cetin, M. Characterization of Land Contaminated by Past Heavy Metal Mining Using Geostatistical Methods. Arch. Environ. Contam. Toxicol. 2004, 46, 162–175. [Google Scholar] [CrossRef]
- Alloway, B.; Davies, B. Trace element content of soils affected by base metal mining in Wales. Geoderma 1971, 5, 197–208. [Google Scholar] [CrossRef]
- Kabala, C.; Singh, B.R. Fractionation and Mobility of Copper, Lead, and Zinc in Soil Profiles in the Vicinity of a Copper Smelter. J. Environ. Qual. 2001, 30, 485–492. [Google Scholar] [CrossRef]
- Qin, F.; Ji, H.; Li, Q.; Guo, X.; Tang, L.; Feng, J. Evaluation of trace elements and identification of pollution sources in particle size fractions of soil from iron ore areas along the Chao River. J. Geochem. Explor. 2014, 138, 33–49. [Google Scholar] [CrossRef]
- Tessier, A.; Campbell, P.G.C.; Bisson, M. Sequential extraction procedure for the speciation of particulate trace metals. Anal. Chem. 1979, 51, 844–851. [Google Scholar] [CrossRef]
- Hernandez, L.; Probst, A.; Probst, J.L.; Ulrich, E. Heavy metal distribution in some French forest soils: Evidence for atmospheric contamination. Sci. Total Environ. 2003, 312, 195–219. [Google Scholar] [CrossRef]
- Yao, Q.; Wang, X.; Jian, H.; Chen, H.; Yu, Z. Characterization of the Particle Size Fraction associated with Heavy Metals in Suspended Sediments of the Yellow River. Int. J. Environ. Res. Public Health 2015, 12, 6725–6744. [Google Scholar] [CrossRef]
- Cabral, A.R.; Lefebvre, G. Use of Sequential Extraction in the Study of Heavy Metal Retention by Silty Soils. Water Air Soil Pollut. 1998, 102, 329–344. [Google Scholar] [CrossRef]
- Rodríguez, L.; Ruiz, E.; Alonso-Azcárate, J.; Rincón, J. Heavy metal distribution and chemical speciation in tailings and soils around a Pb–Zn mine in Spain. J. Environ. Manag. 2009, 90, 1106–1116. [Google Scholar] [CrossRef]
- Santos-Francés, F.; Martínez-Graña, A.; Zarza, C.; Sánchez, A.G.; Rojo, P.A. Spatial Distribution of Heavy Metals and the Environmental Quality of Soil in the Northern Plateau of Spain by Geostatistical Methods. Int. J. Environ. Res. Public Health 2017, 14, 568. [Google Scholar] [CrossRef]
- Magno, M.A.; Nandi, A.; Luffman, I.E. Using Spatial Regression to Model Potentially Toxic Metal (PTM) Mobility Based on Physicochemical Soil Properties. Appl. Environ. Soil Sci. 2019, 2019, 6432571. [Google Scholar] [CrossRef]
- Gu, G.-Q.; Wan, X.-M.; Zeng, W.-B.; Lei, M. Analysis of the Spatial Distribution of Heavy Metals in Soil from a Coking Plant and Its Driving Factors. Huanjing Kexue 2021, 42, 1081–1092. [Google Scholar]
- Mirčovski, V.; Gičevski, B.; Dimov, G. Hydrochemical characteristics of the groundwaters in Prilep’s part of Pelagonia valley–Republic of Macedonia. Rud. Geol. Naft. Zb. 2018, 33, 111–119. [Google Scholar] [CrossRef]
- Šapina, M. A comparison of artificial neural networks and ordinary kriging depth maps of the lower and upper Pannonian stage border in the Bjelovar Subdepression, Northern Croatia. Rud. Geol. Naft. Zb. 2016, 31, 75–85. [Google Scholar] [CrossRef]
- Kiš, I.M. Comparison of ordinary and universal kriging interpolation techniques on a depth variable (a case of linear spatial trend), case study of the Šandrovac Field. Rud. Geol. Naft. Zb. 2016, 31, 41–58. [Google Scholar] [CrossRef]
- Ivšinović, J.; Malvić, T. Application of the Radial Basis Function interpolation method in selected reservoirs of the Croatian part of the Pannonian Basin System. Min. Miner. Depos. 2020, 14, 37–42. [Google Scholar] [CrossRef]
- Huo, X.-N.; Li, H.; Sun, D.-F.; Zhou, L.-D.; Li, B.-G. Combining Geostatistics with Moran’s I Analysis for Mapping Soil Heavy Metals in Beijing, China. Int. J. Environ. Res. Public Health 2012, 9, 995–1017. [Google Scholar] [CrossRef]
- Amini, M.; Afyuni, M.; Fathianpour, N.; Khademi, H.; Flühler, H. Continuous soil pollution mapping using fuzzy logic and spatial interpolation. Geoderma 2005, 124, 223–233. [Google Scholar] [CrossRef]
- Davis, H.T.; Aelion, C.M.; McDermott, S.; Lawson, A.B. Identifying natural and anthropogenic sources of metals in urban and rural soils using GIS-based data, PCA, and spatial interpolation. Environ. Pollut. 2009, 157, 2378–2385. [Google Scholar] [CrossRef]
- Ding, Q.; Cheng, G.; Wang, Y.; Zhuang, D. Effects of natural factors on the spatial distribution of heavy metals in soils surrounding mining regions. Sci. Total Environ. 2017, 578, 577–585. [Google Scholar] [CrossRef]
- Qiao, P.; Lei, M.; Yang, S.; Yang, J.; Guo, G.; Zhou, X. Comparing ordinary kriging and inverse distance weighting for soil as pollution in Beijing. Environ. Sci. Pollut. Res. 2018, 25, 15597–15608. [Google Scholar] [CrossRef]
- Mahmoudabadi, E.; Sarmadian, F.; Savaghebi, G.H.; Alijani, Z. Accuracy assessment of geostatistical methods for zoning of heavy metals in soils of urban-industrial areas. Int. Res. J. Appl. Basic Sci. 2012, 3, 991–999. [Google Scholar]
- Kravchenko, A.N. Influence of Spatial Structure on Accuracy of Interpolation Methods. Soil Sci. Soc. Am. J. 2003, 67, 1564–1571. [Google Scholar] [CrossRef]
- Li, J.; Heap, A.D. A review of comparative studies of spatial interpolation methods in environmental sciences: Performance and impact factors. Ecol. Inform. 2011, 6, 228–241. [Google Scholar] [CrossRef]
- Oliver, M.A.; Webster, R. Kriging: A method of interpolation for geographical information systems. Int. J. Geogr. Inf. Syst. 1990, 4, 313–332. [Google Scholar] [CrossRef]
- Wang, Y.; Duan, X.; Wang, L. Spatial distribution and source analysis of heavy metals in soils influenced by industrial enterprise distribution: Case study in Jiangsu Province. Sci. Total Environ. 2019, 710, 134953. [Google Scholar] [CrossRef]
- Reza, S.K.; Baruah, U.; Singh, S.K.; Das, T.H. Geostatistical and multivariate analysis of soil heavy metal contamination near coal mining area, Northeastern India. Environ. Earth Sci. 2014, 73, 5425–5433. [Google Scholar] [CrossRef]
- Li, X.; Yang, H.; Zhang, C.; Zeng, G.; Liu, Y.; Xu, W.; Wu, Y.; Lan, S. Spatial distribution and transport characteristics of heavy metals around an antimony mine area in central China. Chemosphere 2016, 170, 17–24. [Google Scholar] [CrossRef]
- Chen, T.; Liu, X.; Li, X.; Zhao, K.; Zhang, J.; Xu, J.; Shi, J.; Dahlgren, R. Heavy metal sources identification and sampling uncertainty analysis in a field-scale vegetable soil of Hangzhou, China. Environ. Pollut. 2008, 157, 1003–1010. [Google Scholar] [CrossRef]
- Chen, T.; Chang, Q.; Liu, J.; Clevers, J.; Kooistra, L. Identification of soil heavy metal sources and improvement in spatial mapping based on soil spectral information: A case study in northwest China. Sci. Total Environ. 2016, 565, 155–164. [Google Scholar] [CrossRef]
- Smichowski, P.; Gómez, D.; Frazzoli, C.; Caroli, S. Traffic-Related Elements in Airborne Particulate Matter. Appl. Spectrosc. Rev. 2007, 43, 23–49. [Google Scholar] [CrossRef]
- Liu, D.; Wang, Z.; Zhang, B.; Song, K.; Li, X.; Li, J.; Li, F.; Duan, H. Spatial distribution of soil organic carbon and analysis of related factors in croplands of the black soil region, Northeast China. Agric. Ecosyst. Environ. 2006, 113, 73–81. [Google Scholar] [CrossRef]
- Rodgers, J. Geological and Mineral Deposits of Bumpass Cove, Unicoi and Washington Counties; Bulletin 54; Division of Geology: Nashville, TN, USA, 1948. [Google Scholar]
- National Weather Service National Weather Service Climate. Available online: http://w2.weather/gov/climate/xmacis/php?wfo=mrx (accessed on 10 June 2016).
- ArcGIS Pro 2.7.0 2020; Environmental Systems Research Institute Inc.: West Redlands, CA, USA, 2020.
- United States Department of Agriculture. Natural Resources Conservation Service Heavy Metal Soil Contamination. In Soil Quality—Urban Technical Note No. 3; United States Department of Agriculture: Auburn, AL, USA, 2000. [Google Scholar]
- Oliver, M.; Webster, R. A tutorial guide to geostatistics: Computing and modelling variograms and kriging. Catena 2014, 113, 56–69. [Google Scholar] [CrossRef]
- Interstate Technology Regulatory Council. Geospatial analysis for optimization at Environmental Sites (GRO-1). In Evaluate Geospatial Method Accuracy; ITRC: Washington, DC, USA, 2016. [Google Scholar]
- Vepraskas, M.J.; Sprecher, S.W. Overview of aquic conditions in hydric soils. In Aquic Conditions and Hydric Soils: The Problem Soils; Vepraskas, M.J., Sprecher, S.W., Eds.; Soil Science Society of America: Madison, WI, USA, 1997; pp. 1–22. [Google Scholar]
- Fageria, N.K.; Nascente, A.S. Management of Soil Acidity of South American Soils for Sustainable Crop Production. Adv. Agron. 2014, 128, 221–275. [Google Scholar] [CrossRef]
- Navas, A.; Machín, J. Spatial distribution of heavy metals and arsenic in soils of Aragón (northeast Spain): Controlling factors and environmental implications. Appl. Geochem. 2002, 17, 961–973. [Google Scholar] [CrossRef]
- Orhue, E.R.; Frank, U.O. Fate of some heavy metals in soils: A review. J. Appl. Nat. Sci. 2011, 3, 131–138. [Google Scholar] [CrossRef]
- Ghosh, M.; Singh, S.P. A review of phytoremediation of heavy metals and utilization of its by products. Asian J. Energy Environ. 2005, 6, 214–231. [Google Scholar]
- Imperato, M.; Adamo, P.; Naimo, D.; Arienzo, M.; Stanzione, D.; Violante, P. Spatial distribution of heavy metals in urban soils of Naples city (Italy). Environ. Pollut. 2003, 124, 247–256. [Google Scholar] [CrossRef]
- Yun, S.-W.; Yu, C. Immobilization of Cd, Zn, and Pb from Soil Treated by Limestone with Variation of pH Using a Column Test. J. Chem. 2015, 2015, 641415. [Google Scholar] [CrossRef][Green Version]





| Metal | Covariates | Neighborhood Size | Number of Neighbors |
|---|---|---|---|
| Manganese (Mn) | Moisture content, silt | 300 m | 16–24 |
| Zinc (Zn) | pH, cation exchange capacity | 150 m | 6–8 |
| Lead (Pb) | pH, cation exchange capacity | 150 m | 6–8 |
| Copper (Cu) | Sand, silt, bulk density | 200 m | 8–12 |
| Cadmium (Cd) | pH, sand, silt | 150 m | 6–8 |
| Variables | Min | Max | Mean | Standard Deviation | Skewness | Kurtosis |
|---|---|---|---|---|---|---|
| Soil Properties | ||||||
| moisture content (%) | 8.29 | 75.21 | 24.59 | 13.2 | 1.4 | 3.1 |
| bulk density (g/cm3) | 0.79 | 1.79 | 1.25 | 0.2 | 0.2 | −0.07 |
| cation exchange capacity (meq/100 g) | 1.52 | 16.58 | 4.83 | 3.5 | 1.8 | 2.9 |
| total organic carbon (%) | 3.2 | 31.5 | 8.6 | 4.7 | 2.6 | 10.6 |
| sand (%) | 88 | 99 | 95 | 0.03 | −0.5 | −0.8 |
| silt (%) | 1 | 11 | 4 | 0.03 | 0.6 | −0.8 |
| clay (%) | 0 | 3 | 1 | 0.01 | 0.3 | −0.2 |
| Metal Concentration | ||||||
| Mn (mg/kg) | 6.29 | 2574.93 | 344.49 | 652.2 | 2.4 | 4.9 |
| Zn (mg/kg) | 11.80 | 1354.16 | 302.52 | 402.7 | 1.7 | 1.6 |
| Pb (mg/kg) | 33.43 | 2271.43 | 326.69 | 529.6 | 2.7 | 6.4 |
| Cu (mg/kg) | 1.14 | 64.67 | 13.96 | 13.2 | 2.3 | 5.9 |
| Cd (mg/kg) | 7.14 | 40.00 | 1186 | 5.1 | 3.6 | 17.8 |
| Mn | Zn | Pb | Cu | Cd | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Model | OK | OCK | OK | OCK | OK | OCK | OK | OCK | OK | OCK |
| Cokriging covariates | - | MC, silt | - | pH, CEC | - | pH, CEC | - | sand, silt, BD | - | pH, sand, silt |
| Neighbors | 16–24 | 6–8 | 6–8 | 8–12 | 6–8 | |||||
| ME | −29.315 | −19.714 | 12.814 | 14.316 | 23.280 | 20.734 | 0.086 | −0.193 | 0.237 | 0.0350 |
| RMS | 611.194 | 611.253 | 409.981 | 378.532 | 435.264 | 405.224 | 12.798 | 12.166 | 5.005 | 3.954 |
| MES | −0.0287 | −0.0212 | 0.0292 | 0.0358 | 0.0366 | 0.0412 | −0.0017 | −0.109 | 0.0398 | 0.00857 |
| RMSS | 1.022 | 1.021 | 0.967 | 0.966 | 0.876 | 0.824 | 0.834 | 1.213 | 0.912 | 0.947 |
| ASE | 571.525 | 583.366 | 424.396 | 392.328 | 491.351 | 494.574 | 14.420 | 10.875 | 5.552 | 4.187 |
| ASE−RMS | 39.669 | −27.887 | 14.417 | 13.797 | 56.086 | 89.350 | 1.621 | −1.290 | 0.5465 | 0.2333 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Magno, M.; Luffman, I.; Nandi, A. Evaluating Spatial Regression-Informed Cokriging of Metals in Soils near Abandoned Mines in Bumpus Cove, Tennessee, USA. Geosciences 2021, 11, 434. https://doi.org/10.3390/geosciences11110434
Magno M, Luffman I, Nandi A. Evaluating Spatial Regression-Informed Cokriging of Metals in Soils near Abandoned Mines in Bumpus Cove, Tennessee, USA. Geosciences. 2021; 11(11):434. https://doi.org/10.3390/geosciences11110434
Chicago/Turabian StyleMagno, Melissa, Ingrid Luffman, and Arpita Nandi. 2021. "Evaluating Spatial Regression-Informed Cokriging of Metals in Soils near Abandoned Mines in Bumpus Cove, Tennessee, USA" Geosciences 11, no. 11: 434. https://doi.org/10.3390/geosciences11110434
APA StyleMagno, M., Luffman, I., & Nandi, A. (2021). Evaluating Spatial Regression-Informed Cokriging of Metals in Soils near Abandoned Mines in Bumpus Cove, Tennessee, USA. Geosciences, 11(11), 434. https://doi.org/10.3390/geosciences11110434






