Calcite Twin Formation, Measurement and Use as Stress–Strain Indicators: A Review of Progress over the Last Decade
Abstract
:1. Introduction
2. Formation of Twins
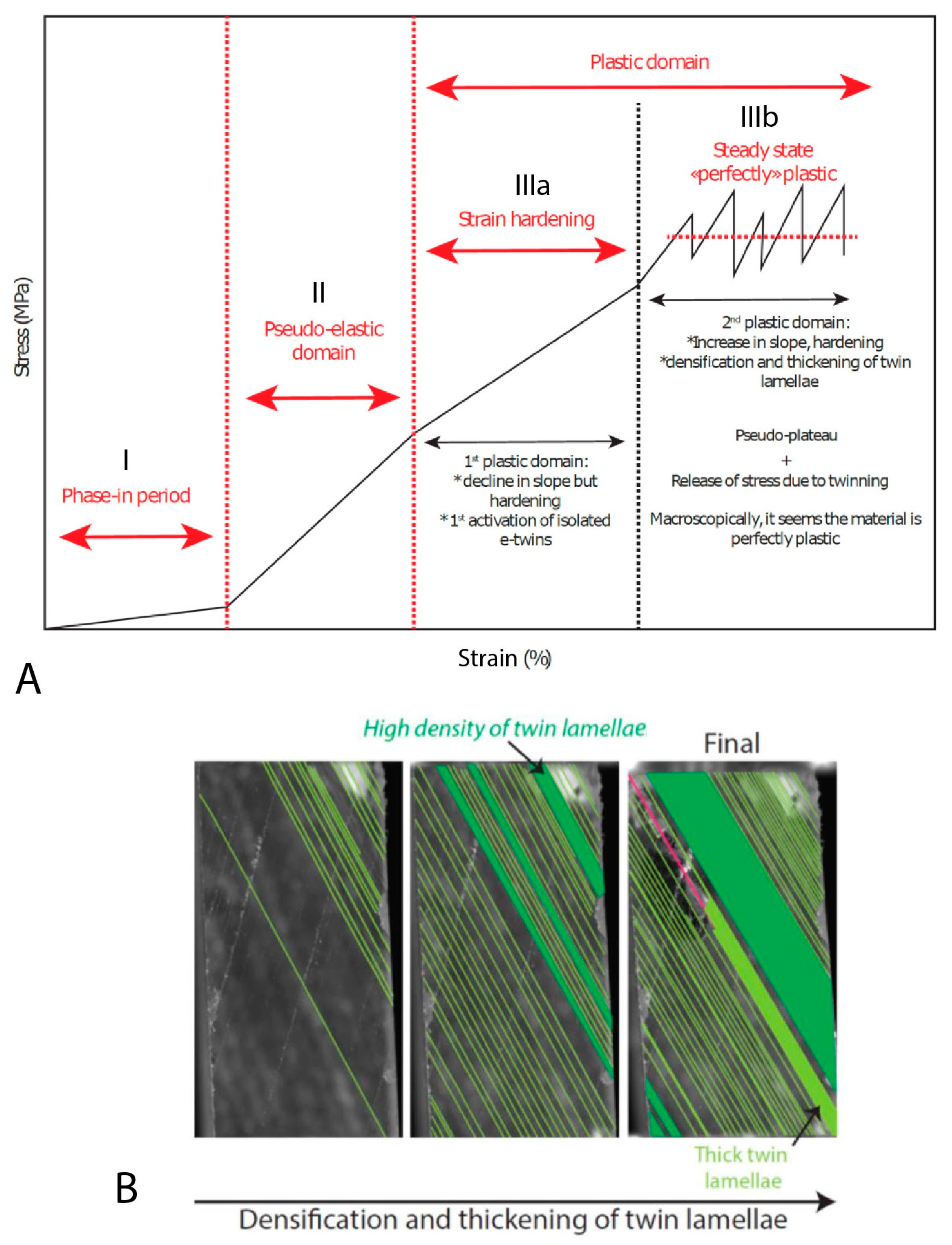
2.1. Nucleation and Growth of Twins
2.2. The Concept of CRSS for Twinning
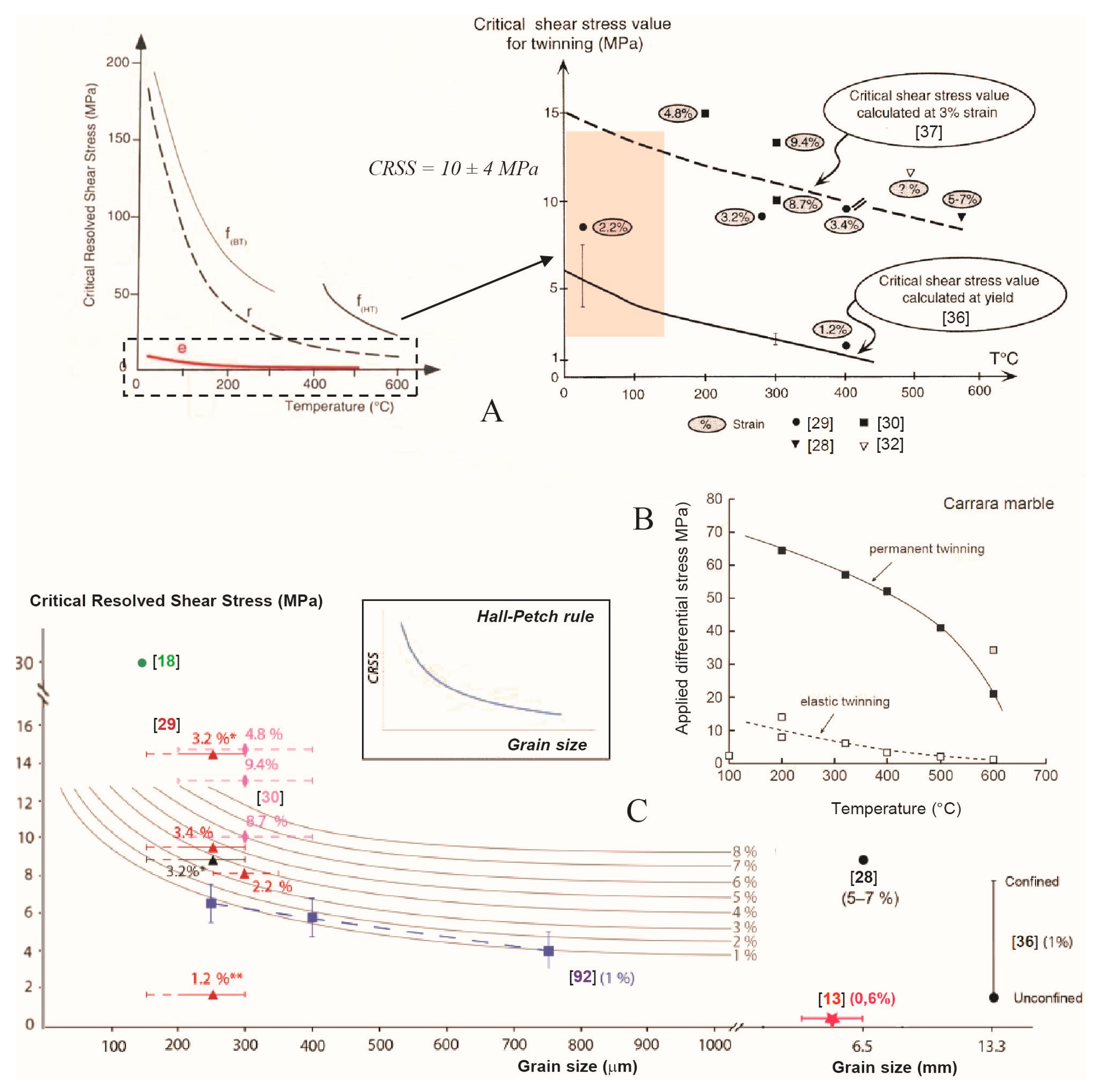
2.2.1. Dependence of CRSS on Temperature and Strain Rate
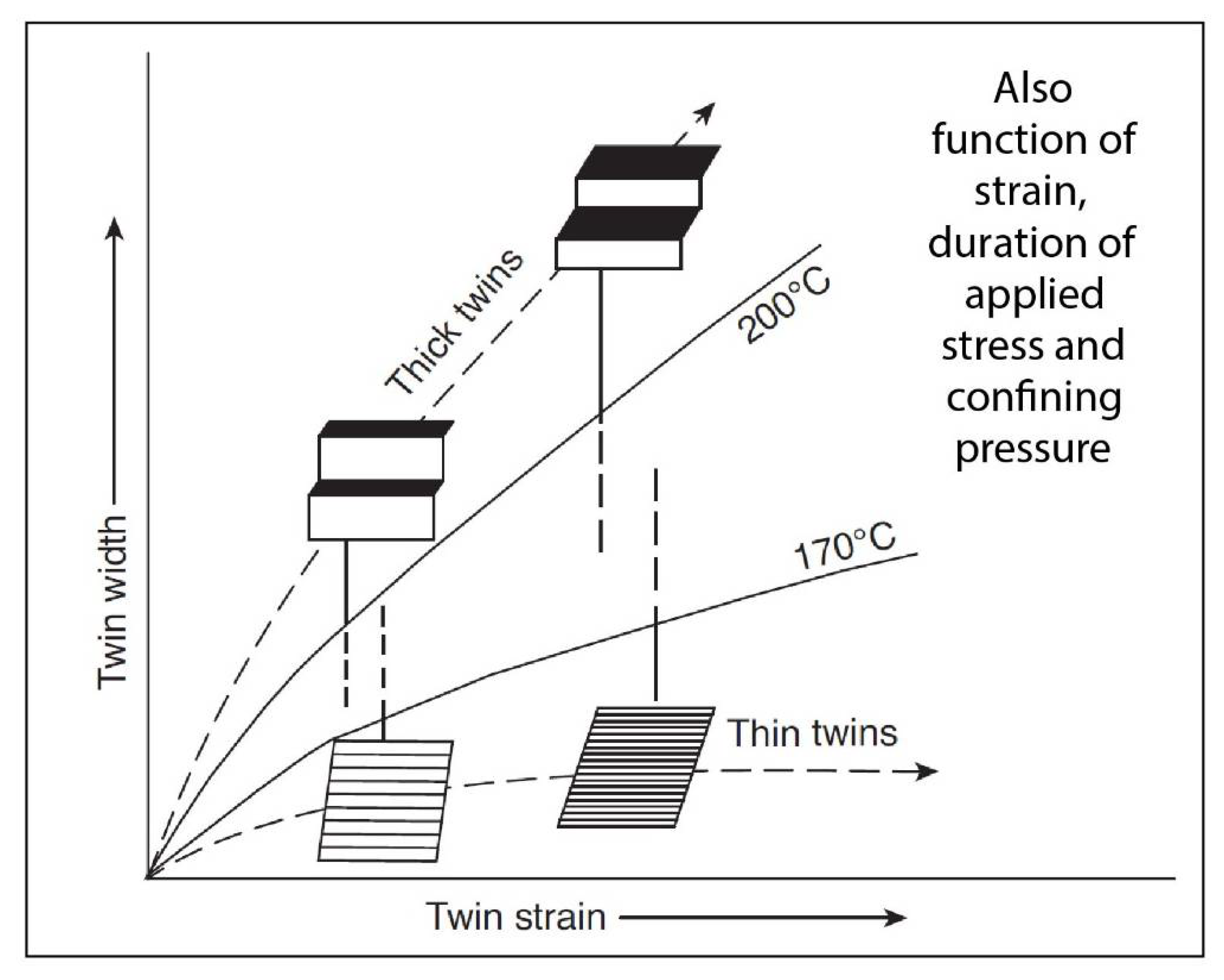
2.2.2. Dependence of CRSS on Strain
2.2.3. Dependence of CRSS on Grain Size
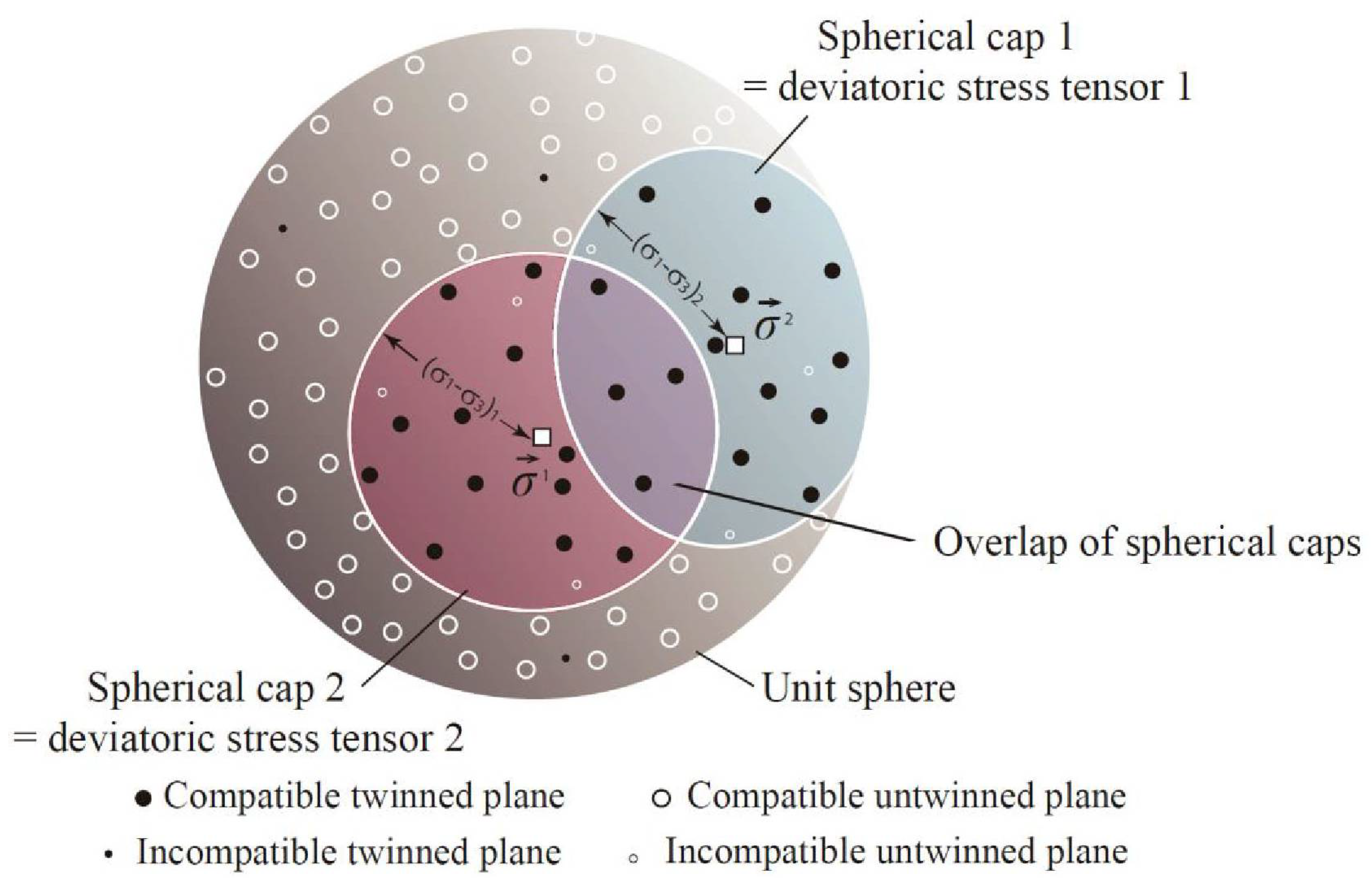
2.3. The Need for Accommodation of the Geometric Incompatibility at Twinned Grain Boundaries
3. Calcite Twins: A Low-Temperature Geothermometer?
4. Calcite Twin Data Measurements for Paleostress/Paleostrain Analyses
4.1. Universal Stage
4.2. Automated Fabric Analyser
4.3. EBSD
5. Calcite Twins: Indicators of Stress, Strain or Both?
6. Use of Calcite Twins as Markers of Stress Regime: Inversion of Calcite Twin Data for Principal Stress Orientations and Stress Ratio
6.1. Brief Review of Recent Methods and Improvements of Calcite Twin Inversion for Stress
6.1.1. Etchecopar Technique: CSIT
6.1.2. Yamaji Technique
6.1.3. Parlangeau et al. Technique: CSIT-2
6.1.4. Shan et al. Technique
6.1.5. Rez Technique: TwinCalc
6.1.6. Common Limitations of Calcite Twin Inversion Techniques for Stress and Ways for Improvement
6.2. Some Regional Studies Using Analysis of Calcite Twins for Paleostress
7. Dating Calcite Twinning Events
8. Use of Calcite Twins as a Strain Gauge
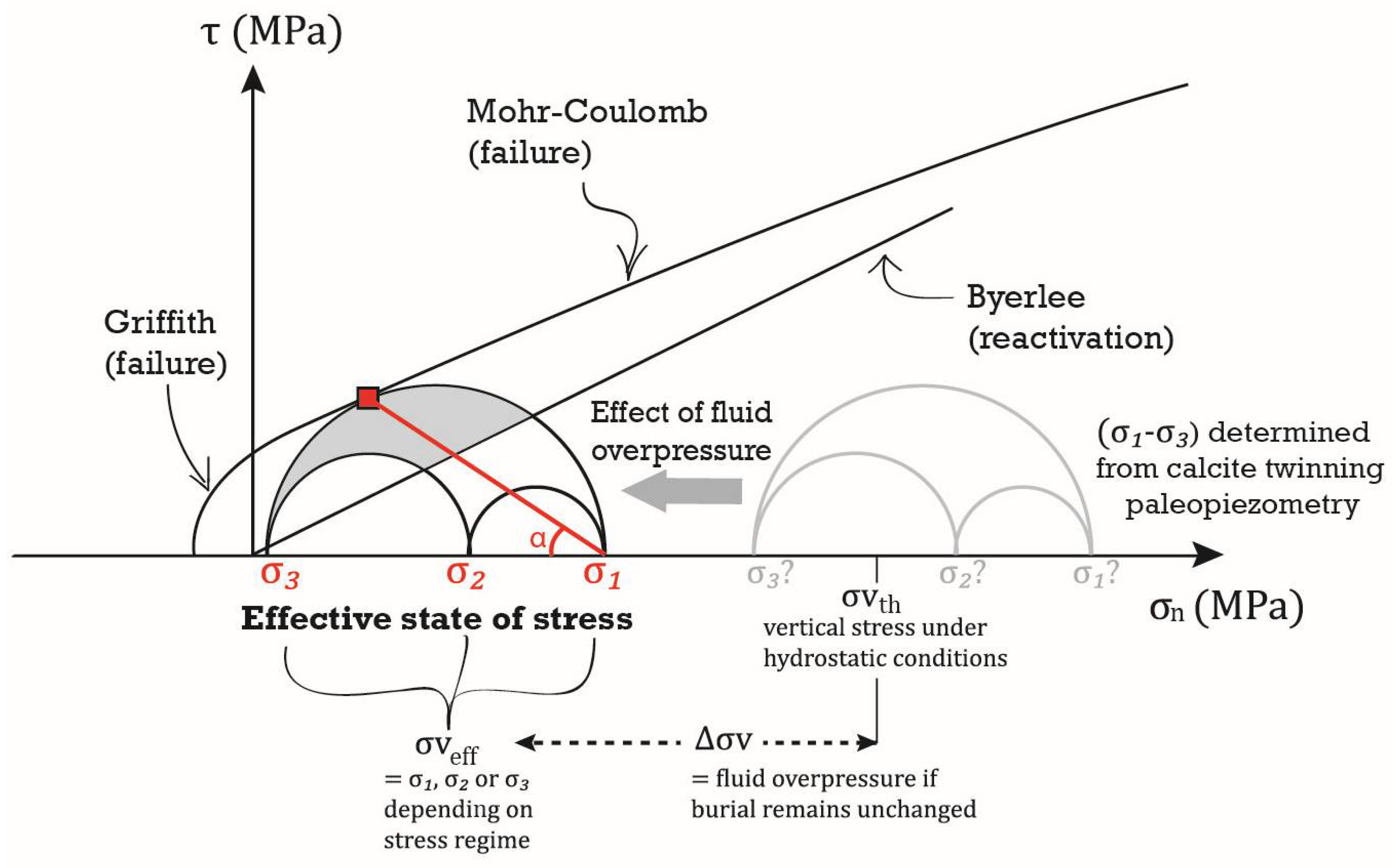
9. Use of Calcite Twins as a Stress Gauge
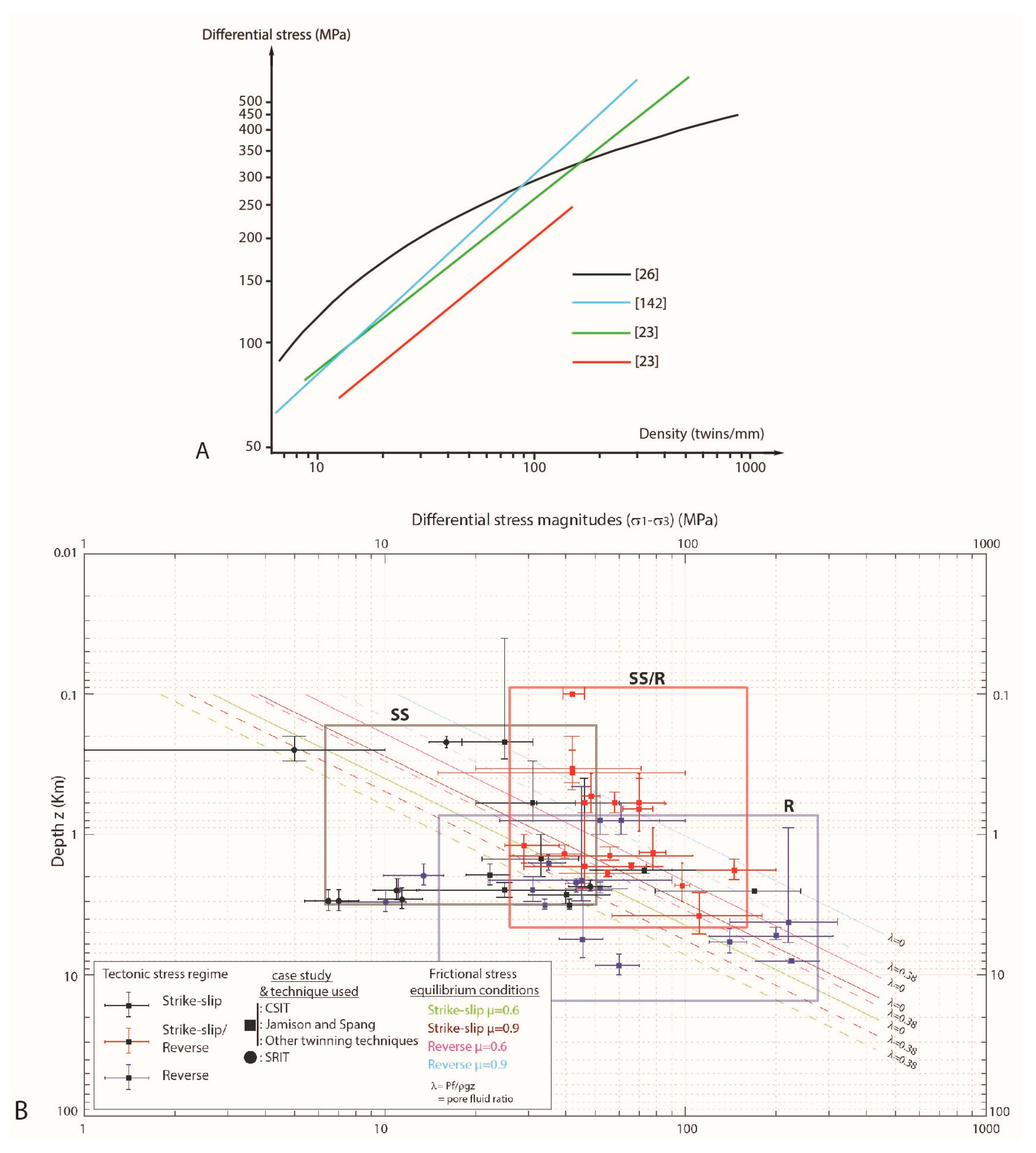
9.1. Low-T °C Paleopiezometers Based on Calcite Twin Density
9.2. Calcite Twinning Paleopiezometry Based on Both Residual Stress and Plastic Strain Determination
9.3. Determination of Differential Stress Magnitudes Using Calcite Twin Inversion Techniques
9.4. Case Studies
10. Combination of Calcite Twins with Rock Mechanics and Other Paleopiezometers
10.1. Combining Calcite Twinning Paleopiezometry with Fractures and Rock Mechanics Data
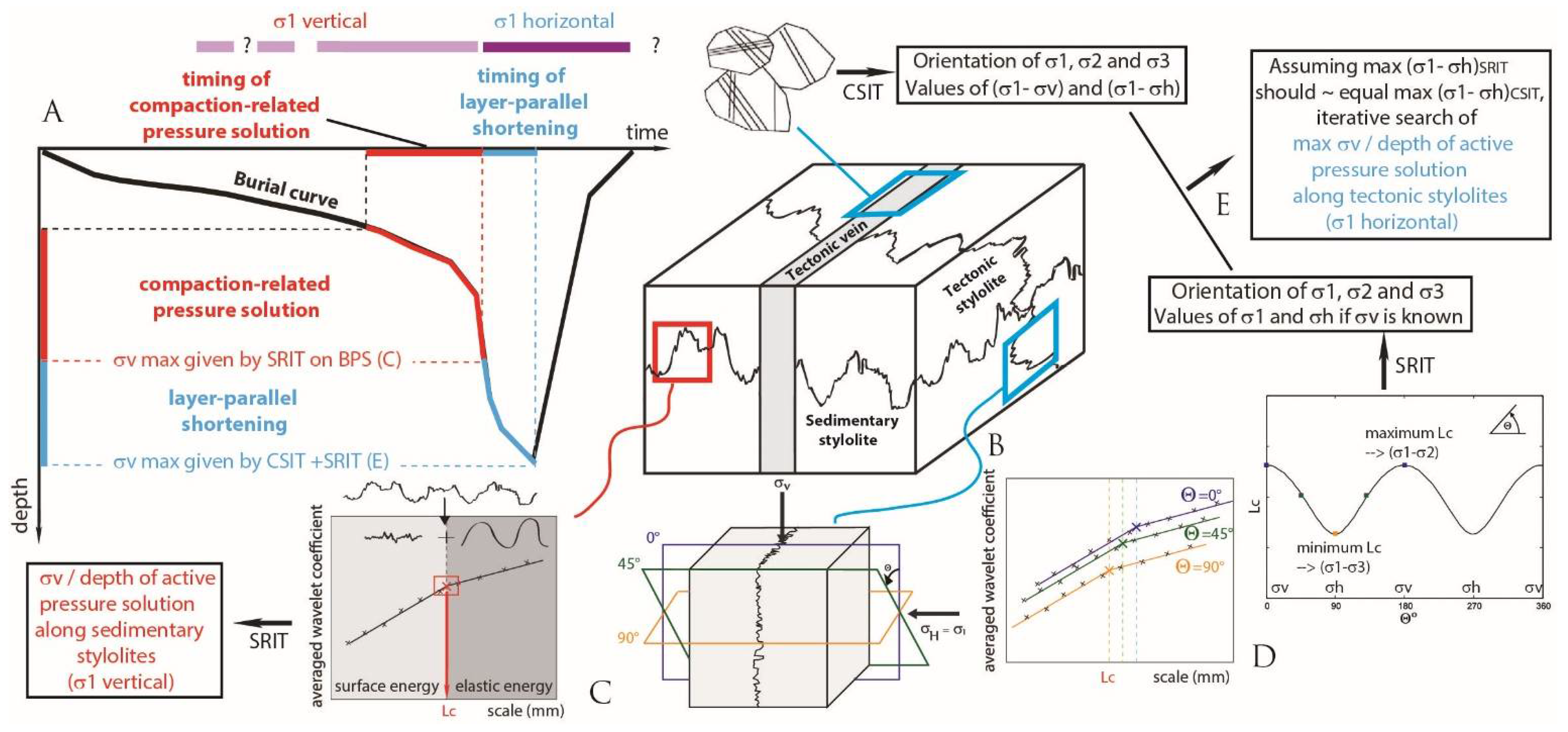
10.2. Combining Calcite Twinning Paleopiezometry with Stylolite Roughness Paleopiezometry
11. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Clayton, J.D. Nonlinear Mechanics of Crystals; Springer Science & Business Media: Berlin, Germany, 2010; Volume 177. [Google Scholar]
- Handin, J.W.; Griggs, D. Deformation of Yule marble part II: Predicted fabric changes. Geol. Soc. Am. Bull. 1951, 62, 863–886. [Google Scholar] [CrossRef]
- Lacombe, O. Comparison of paleostress magnitudes from calcite twins with contemporary stress magnitudes and frictional sliding criteria in the continental crust: Mechanical implications. J. Struct. Geol. 2007, 29, 86–99. [Google Scholar] [CrossRef]
- Burkhard, M. Calcite twins, their geometry, appearance and significance as stress-strain markers and indicators of tectonic regime: A review. J. Struct. Geol. 1993, 15, 351–368. [Google Scholar] [CrossRef] [Green Version]
- Ferrill, D.A.; Morris, P.; Evans, M.A.; Burkhard, M.; Groshong, R.H.; Onasch, C.M. Calcite twin morphology: A low-temperature deformation geothermometer. J. Struct. Geol. 2004, 26, 1521–1529. [Google Scholar] [CrossRef] [Green Version]
- Groshong, R.H., Jr.; Pfiffner, O.A.; Pringle, L.R. Strain partitioning in the Helvetic thrust belt of Eastern Switzerland from the leading edge of the internal zone. J. Struct. Geol. 1984, 6, 5–18. [Google Scholar] [CrossRef]
- Craddock, J.P.; Jackson, M.; Van Der Pluijm, B.; Versical, R.T. Regional shortening fabrics in eastern north America: Far-field stress transmission from the Appalachian-Ouachita orogenic belt. Tectonics 1993, 12, 257–264. [Google Scholar] [CrossRef]
- Lacombe, O. Paleostress magnitudes associated with development of mountain belts: Insights from tectonic analyses of calcite twins in the Taiwan Foothills. Tectonics 2001, 20, 834–849. [Google Scholar] [CrossRef] [Green Version]
- Lacombe, O. Calcite twins, a tool for tectonic studies in thrust belts and stable orogenic forelands. Oil Gas Sci. Technol. 2010, 65, 809–838. [Google Scholar] [CrossRef] [Green Version]
- Duparc, O.H. A review of some elements for the history of mechanical twinning centred on its German origins until Otto Mügge’s K1 and K2 invariant plane notation. J. Mater. Sci. 2017, 52, 4182–4196. [Google Scholar] [CrossRef]
- Christian, J.W.; Mahajan, S. Deformation twinning. Prog. Mater. Sci. 1995, 39, 1–157. [Google Scholar] [CrossRef]
- Hirth, J.P.; Lothe, J. Theory of Dislocations, 2nd ed.; John Wiley & Sons: New York, NY, USA, 1982; p. 857. [Google Scholar]
- Parlangeau, C.; Dimanov, A.; Lacombe, O.; Hallais, S.; Daniel, J.M. Uniaxial compression of calcite single crystals at room temperature: Insights into twinning activation and development. Solid Earth 2019, 10, 307–316. [Google Scholar] [CrossRef] [Green Version]
- Urai, J.L.; Means, W.D.; Lister, G.S. Dynamic recrystallization of minerals. In Mineral and Rock Deformation: Laboratory Studies; AGU: Washington, DC, USA, 1986; Volume 36, pp. 161–199. [Google Scholar]
- Schuster, R.; Habler, G.; Schafler, E.; Abart, R. Intragranular deformation mechanisms in calcite deformed by high-pressure torsion at room temperature. Mineral. Petrol. 2020, 114, 105–118. [Google Scholar] [CrossRef] [Green Version]
- Schuster, R.; Schafler, E.; Schell, N.; Kunz, M.; Abart, R. Microstructure of calcite deformed by high-pressure torsion: An X-ray line profile study. Tectonophysics 2017, 721, 448–461. [Google Scholar] [CrossRef] [Green Version]
- Covey-Crump, S.J.; Schofield, P.F. Neutron diffraction and the mechanical behavior of geological materials. In Neutron Applications in Earth, Energy and Environmental Sciences; Springer: Boston, MA, USA, 2009; pp. 257–282. [Google Scholar]
- Covey-Crump, S.J.; Schofield, P.F.; Oliver, E.C. Using neutron diffraction to examine the onset of mechanical twinning in calcite rocks. J. Struct. Geol. 2017, 100, 77–97. [Google Scholar] [CrossRef] [Green Version]
- Kaga, H.; Gilman, J.J. Twinning and detwinning in calcite. J. Appl. Phys. 1969, 40, 3196–3207. [Google Scholar] [CrossRef]
- Clayton, J.D.; Knap, J. Phase field modeling of twinning in indentation of transparent crystals. Model. Simul. Mater. Sci. Eng. 2011, 19, 085005. [Google Scholar] [CrossRef]
- Cahn, R.W. Twinned crystals. Adv. Phys. Philos. Mag. 1954, 3, 363–445. [Google Scholar] [CrossRef]
- Williams, A.J.; Cahn, R.W. The dynamics of elastic twinning in calcite. In Proceedings of the Conference on Deformation Twinning, Gainesville, FL, USA, 21–22 March 1963; Reed-Hill, R.E., Hirth, J.P., Rogers, H.C., Eds.; Gordon and Breach Science Publishers: New York, NY, USA, 1964; pp. 192–208. [Google Scholar]
- Rybacki, E.; Evans, B.; Janssen, C.; Wirth, R.; Dresen, G. Influence of stress, temperature, and strain on calcite twins constrained by deformation experiments. Tectonophysics 2013, 601, 20–36. [Google Scholar] [CrossRef]
- De Bresser, J.H.P.; Spiers, C.J. Slip systems in calcite single crystals deformed at 300–800 C. J. Geophys. Res. Solid Earth 1993, 98, 6397–6409. [Google Scholar] [CrossRef]
- Bell, R.L.; Cahn, R.W. The dynamics of twinning and the interrelation of slip and twinning in zinc crystals. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1957, 239, 494–521. [Google Scholar]
- Rowe, K.J.; Rutter, E.H. Paleostress estimation using calcite twinning: Experimental calibration and application to nature. J. Struct. Geol. 1990, 12, 1–17. [Google Scholar] [CrossRef]
- Daymond, M. Internal stresses in deformed crystalline aggregates. Rev. Mineral. Geochem. 2006, 63, 427–458. [Google Scholar] [CrossRef]
- De Bresser, J.H.P.; Spiers, C.J. Strength characteristics of the r, f, and c slip systems in calcite. Tectonophysics 1997, 272, 1–23. [Google Scholar] [CrossRef]
- Lacombe, O.; Laurent, P. Determination of deviatoric stress tensors based on inversion of calcite twin data from experimentally deformed monophase samples: Preliminary results. Tectonophysics 1996, 255, 189–202. [Google Scholar] [CrossRef]
- Laurent, P.; Kern, H.; Lacombe, O. Determination of deviatoric stress tensors based on inversion of calcite twin data from experimentally deformed monophase samples. Part II. Axial and triaxial stress experiments. Tectonophysics 2000, 327, 131–148. [Google Scholar] [CrossRef]
- Ferrill, D.A. Critical re-evaluation of differential stress estimates from calcite twins in coarse-grained limestones. Tectonophysics 1998, 285, 77–86. [Google Scholar]
- Spiers, C.J.; Wenk, H.R. Evidence for slip on r and f in the positive sense in deformed calcite single crystals. EOS Trans. AGU 1980, 61, 1128. [Google Scholar]
- Hnat, J.S.; van der Pluijm, B.A. Foreland signature of indenter tectonics: Insights from calcite twinning analysis in the Tennessee salient of the Southern Appalachians, USA. Lithosphere 2011, 3, 317–327. [Google Scholar] [CrossRef] [Green Version]
- Tullis, T.E. The use of mechanical twinning in minerals as a measure of shear stress magnitudes. J. Geophys. Res. Solid Earth 1980, 85, 6263–6268. [Google Scholar]
- Tome, C.N.; Beyerlein, I.J.; Wang, J.; McCabe, R.J. A multi-scale statistical study of twinning in magnesium. J. Miner. Met. Mater. Soc. 2011, 63, 19–23. [Google Scholar] [CrossRef]
- Turner, F.J.; Griggs, D.T.; Heard, H.C. Experimental deformation of calcite crystals. Geol. Soc. Am. Bull. 1954, 65, 883–934. [Google Scholar] [CrossRef]
- Turner, F.J.; Heard, H.C. Deformation in calcite crystals at different strain rates. Univ. Calif. Publ. Geol. Sci. 1965, 46, 103–126. [Google Scholar]
- Rybacki, E.; Janssen, C.; Wirth, R.; Chen, K.; Wenk, H.R.; Stromeyer, D.; Dresen, G. Low-temperature deformation in calcite veins of SAFOD core samples (San Andreas Fault)—Microstructural analysis and implications for fault rheology. Tectonophysics 2011, 509, 107–119. [Google Scholar] [CrossRef] [Green Version]
- Meyers, M.A.; Vohringer, O.; Lubarda, V.A. The onset of twinning in metals: A constitutive description. Acta Mater. 2001, 49, 4025–4039. [Google Scholar] [CrossRef]
- Beyerlein, I.J.; Capolungo, L.; Marshall, P.E.; McCabe, R.J.; Tome, C.N. Statistical analyses of deformation twinning in magnesium. Philos. Mag. 2010, 90, 2161–2190. [Google Scholar] [CrossRef]
- Hosford, W.F. The Mechanics of Crystals and Textured Polycrystals; Oxford University Press: New York, NY, USA, 1993. [Google Scholar]
- Barnett, M.R. A rationale for the strong dependence of mechanical twinning on grain size. Scripta Mater. 2008, 59, 696–698. [Google Scholar] [CrossRef]
- Newmann, J. The influence of grain size and grain size distribution on methods for estimating paleostresses from twinning in carbonates. J. Struct. Geol. 1994, 16, 1589–1601. [Google Scholar] [CrossRef]
- Larsson, A.K.; Christy, A.G. On twinning and microstructures in calcite and dolomite. Am. Mineral. 2008, 93, 103–113. [Google Scholar] [CrossRef]
- Machel, H.G. Cathodoluminescence in calcite and dolomite and its chemical interpretation. Geosci. Can. 1995, 12, 139–147. [Google Scholar]
- Fougerouse, D.; Reddy, S.M.; Seydoux-Guillaume, A.-M.; Kirkland, C.L.; Erickson, T.M.; Saxey, D.W.; Rickard, W.D.A.; Jacob, D.; Leroux, H.; Clark, C. Mechanical twinning of monazite expels radiogenic lead. Geology 2021, 49, 417–421. [Google Scholar] [CrossRef]
- Moore, J.; Beinlich, A.; Porter, J.K.; Talavera, C.; Berndt, J.; Piazolo, S.; Austrheim, H.; Putnis, A. Microstructurally controlledvtrace element (Zr, U–Pb) concentrations in metamorphic rutile: An example from the amphibolites of the Bergen Arcs. J. Metamorph. Geol. 2020, 38, 103–127. [Google Scholar] [CrossRef]
- Ferrill, D.A. Calcite twin widths and intensities as metamorphic indicators in natural low-temperature deformation of limestone. J. Struct. Geol. 1991, 13, 667–675. [Google Scholar] [CrossRef]
- Janssen, C.; Rybacki, E.; Dresen, G. Critical re-evaluation of calcite twins as a low-temperature deformation geothermometer. Geophys. Res. Abstr. 2007, 9, 02228. [Google Scholar]
- Curzi, M.; Aldega, L.; Bernasconi, S.M.; Berra, F.; Billi, A.; Boschi, C.; Franchinia, S.; Van der Lelij, R.; Viola, G.; Carminati, E. Architecture and evolution of an extensionally-inverted thrust (Mt. Tancia Thrust, Central Apennines): Geological, structural, geochemical, and K–Ar geochronological constraints. J. Struct. Geol. 2020, 136, 104059. [Google Scholar] [CrossRef]
- De Bresser, J.H.P. On the mechanism of dislocation creep of calcite at high temperature: Inferences from experimentally measured pressure sensitivity and strain rate sensitivity of flow stress. J. Geophys. Res. Solid Earth 2002, 107, B12. [Google Scholar] [CrossRef]
- Lacombe, O.; Angelier, J.; Laurent, P.; Bergerat, F.; Tourneret, C. Joint analyses of calcite twins and fault slips as a key for deciphering polyphase tectonics: Burgundy as a case study. Tectonophysics 1990, 182, 279–300. [Google Scholar] [CrossRef]
- Groshong, R.H., Jr. Experimental test of least-squares strain calculations using twinned calcite. Geol. Soc. Am. Bull. 1974, 85, 1855–1864. [Google Scholar]
- Turner, F.J. Nature and dynamic interpretation of deformation lamellae in calcite of three marbles. Am. J. Sci. 1953, 251, 276–298. [Google Scholar] [CrossRef]
- Kruhl, J.H.; Peternell, M. The equilibration of high-angle grain boundaries in dynamically recrystallized quartz: The effect of crystallography and temperature. J. Struct. Geol. 2002, 24, 1125–1137. [Google Scholar] [CrossRef]
- Sperner, B.; Ratschbacher, L. A Turbo Pascal program package for graphical presentation and stress analysis of calcite deformation. Z. Dtsch. Geol. Ges. 1994, 145, 414–423. [Google Scholar]
- Tourneret, C.; Laurent, P. A new computer method for rapid and precise determination of calcite crystallographic orientation from u-stage measurements. Comput. Geosci. 1991, 17, 251–269. [Google Scholar] [CrossRef]
- Rez, J. TwinCalc: A multitool for calcite twinning based stress analysis. Appl. Comput. Geosci. 2020, 5, 100020. [Google Scholar] [CrossRef]
- Turner, F.J.; Weiss, L.E. Structural Analysis of Metamorphic Tectonites; McGraw-Hil: New York, NY, USA, 1963. [Google Scholar]
- Parlangeau, C.; Lacombe, O.; Schueller, S.; Daniel, J.M. Inversion of calcite twin data for paleostress orientations and magnitudes: A new technique tested and calibrated on numerically-generated and natural data. Tectonophysics 2018, 722, 462–485. [Google Scholar] [CrossRef] [Green Version]
- Yamaji, A. How tightly does calcite e-twin constrain stress? J. Struct. Geol. 2015, 72, 83–95. [Google Scholar] [CrossRef] [Green Version]
- Saha, D. Universal stage measurements in petrofabric analysis revisited. J. Earth Syst. Sci. 2021, 130, 116. [Google Scholar] [CrossRef]
- Köpping, J.; Peternell, M.; Prelević, D.; Rutte, D. Cretaceous tectonic evolution of the Sava-Klepa Massif, Republic of North Macedonia–Results from calcite twin based automated paleostress analysis. Tectonophysics 2019, 758, 44–54. [Google Scholar] [CrossRef]
- Peternell, M.; Kohlmann, F.; Wilson, C.J.L.; Seiler, C.; Gleadow, A.J.W. A new approach to crystallographic orientation measurement for apatite fission track analysis: Effects of crystal morphology and implications for automation. Chem. Geol. 2009, 265, 527–539. [Google Scholar] [CrossRef]
- Etchecopar, A. Etude des Etats de Contraintes en Tectonique Cassante et Simulation de Déformations Plastiques (Approche Mathématique). Ph.D. Thesis, Université Sciences et Techniques du Languedoc, Montpellier, France, 1984; p. 270. [Google Scholar]
- Yamaji, A. Generalized Hough transform for the stress inversion of calcite twin data. J. Struct. Geol. 2015, 80, 2–15. [Google Scholar] [CrossRef] [Green Version]
- Shan, Y.; Zheng, J.; Liang, X. Inversion of polyphase calcite twin data for deviatoric stress tensors: 1. A novel numerical approach. J. Struct. Geol. 2019, 128, 103873. [Google Scholar] [CrossRef]
- Rez, J.; Melichar, R.; Poelt, P.; Mitsche, S.; Kalvoda, J. Calcite twinning stress inversion using OIM (EBSD) data. Geolines 2005, 19, 100. [Google Scholar]
- Evenson, A. Late Laramide Paleostress in Basement Rocks Determined from Calcite Twins using Electron Backscatter Diffraction, Lead-Deadwood Dome, South Dakota. Master’s Thesis, South Dakota School of Mines and Technology, Rapid City, SD, USA, 2011. [Google Scholar]
- Yan, S.; Zhang, B.; Zhang, J.; Wu, J.; Zhao, Z. Calcite twins as a tool for the estimation of paleostress orientation on the basis of EBSD technique. Geol. Sci. Technol. Inf. 2016, 35, 50–54. [Google Scholar]
- Tielke, J.A. Development and Application of a Method for Determining Paleostress from Calcite Deformation Twins Using Electron Backscatter Diffraction. Master’s Thesis, South Dakota School of Mines, Rapid City, SD, USA, 2010; 124p. [Google Scholar]
- Parlangeau, C.; Lacombe, O.; Brisset, F.; Kohler, E.; Daniel, J.-M.; Schueller, S. Inversion of calcite twin data for paleostress (2): EBSD as a tool for data measurements. In Geophysical Research Abstracts; European Geosciences Union: Vienna, Austria, 2015. [Google Scholar]
- Parlangeau, C. Quantification des Paléocontraintes par l’Analyse des Macles de la Calcite: Nouvelle Approche d’Acquisition et d’Inversion des Données et Mécaniques du Maclage. Ph.D. Thesis, Université Pierre et Marie Curie, Paris, France, 2017; 360p. [Google Scholar]
- McNamara, D.D.; Lister, A.; Prior, D.J. Calcite sealing in a fractured geothermal reservoir: Insights from combined EBSD and chemistry mapping. J. Volcanol. Geotherm. Res. 2016, 323, 38–52. [Google Scholar] [CrossRef] [Green Version]
- Groshong, R.H., Jr. Strain calculated from twinning in calcite. Geol. Soc. Am. Bull. 1972, 83, 2025–2038. [Google Scholar] [CrossRef]
- Groshong, R.H., Jr. Origin and Application of the Twinned Calcite Strain Gauge. Geosciences 2021, 11, 296. [Google Scholar] [CrossRef]
- Pfiffner, O.A.; Burkhard, M. Determination of paleo-stress axes orientations from fault, twin and earthquake data. Ann. Tecton. 1987, 1, 48–57. [Google Scholar]
- Evans, M.A.; Dunne, W.M. Strain factorization and partitioning in the North Mountain thrust sheet, central Appalachians, U.S.A. J. Struct. Geol. 1991, 13, 21–35. [Google Scholar] [CrossRef]
- Lacombe, O.; Angelier, J.; Laurent, P.; Bergerat, F.; Tourneret, C. Contribution de l’analyse des macles de la calcite à la connaissance de l’histoire tectonique d’une région: L’exemple de la plate-forme carbonatée bourguignonne. Comptes Rendus Académie Sci. Paris 1989, 309, 1979–1984. [Google Scholar]
- Lacombe, O.; Angelier, J.; Laurent, P. Determining paleostress orientations from faults and calcite twins: A case study near the Sainte-Victoire Range (southern France). Tectonophysics 1992, 201, 141–156. [Google Scholar] [CrossRef]
- Spiers, C.J. Fabric development in calcite polycrystals deformed at 400 °C. Bull. Minéralogie 1979, 102, 282–289. [Google Scholar] [CrossRef]
- Amrouch, K.; Lacombe, O.; Bellahsen, N.; Daniel, J.M.; Callot, J.P. Stress and strain patterns, kinematics and deformation mechanisms in a basement-cored anticline: Sheep Mountain Anticline, Wyoming. Tectonics 2010, 29, TC1005. [Google Scholar] [CrossRef] [Green Version]
- Wakamori, K.; Yamaji, A. The integrated stress-strain analysis of calcite twins: Consistent stress and strain determined from natural data. In EGU General Assembly Conference Abstracts; European Geosciences Union: Munich, Germany, 2020; p. 12819. [Google Scholar] [CrossRef]
- Conel, J.E. Studies of the Development of Fabrics in Some Naturally Deformed Limestones. Ph.D. Dissertation, California Institute of Technology, Pasadena, CA, USA, 1962. [Google Scholar]
- Craddock, J.P.; Malone, D.H.; Wartman, J.; Kelly, M.J.; Junlai, L.; Bussolotto, M.; Invernizzi, C.; Knott, J.; Porter, R. Calcite twinning strains from syn-faulting calcite gouge: Small-offset strike-slip, normal and thrust faults. Int. J. Earth Sci. 2020, 109, 1–42. [Google Scholar] [CrossRef]
- Shan, Y.; Zheng, J.; Liang, X. Synthetic slip plane, the combination of a pair of twinned and untwinned e-planes in a single calcite crystal: Application in dynamic analysis. J. Struct. Geol. 2019, 119, 81–92. [Google Scholar] [CrossRef]
- Jamison, W.R.; Spang, J. Use of calcite twin lamellae to infer differential stresses. Geol. Soc. Am. Bull. 1976, 87, 868–887. [Google Scholar] [CrossRef]
- Laurent, P.; Bernard, P.; Vasseur, G.; Etchecopar, A. Stress tensor determination from the study of e-twins in calcite: A linear programming method. Tectonophysics 1981, 78, 651–660. [Google Scholar] [CrossRef]
- Laurent, P.; Tourneret, C.; Laborde, O. Determining deviatoric stress tensors from calcite twins: Applications to monophased synthetic and natural polycrystals. Tectonics 1990, 9, 379–389. [Google Scholar] [CrossRef]
- Shelley, D. Calcite twinning and determination of paleostress orientations: Three methods compared. Tectonophysics 1992, 206, 193–201. [Google Scholar] [CrossRef]
- Beaudoin, N.; Lacombe, O. Recent and future trends in paleopiezometry in the diagenetic domain: Insights into the tectonic paleostress and burial depth history of fold-and-thrust belts and sedimentary basins. J. Struct. Geol. 2018, 114, 357–365. [Google Scholar] [CrossRef]
- Gagala, L. Reliability of selected procedures of stress inversion and data separation for inhomogeneous populations of calcite twins and striated faults: Insights from numerical experiments. Int. J. Earth Sci. 2009, 98, 461–479. [Google Scholar] [CrossRef]
- Rez, J.; Melichar, R. Peek inside the black box of calcite twinning paleostress analysis. Trab. Geol. Univ. Oviedo 2010, 30, 163–168. [Google Scholar]
- Rocher, M.; Cushing, M.; Lemeille, F.; Lozac’h, Y.; Angelier, J. Intraplate paleostresses reconstructed with calcite twinning and faulting: Improved method and application to the eastern Paris Basin (Lorraine, France). Tectonophysics 2004, 387, 1–21. [Google Scholar] [CrossRef]
- Lacombe, O.; Laurent, P.; Angelier, J. Calcite twins as a key to paleostresses in sedimentary basins: Preliminary results from drill cores of the Paris basin. In Peri-Tethyan Platforms; Roure, F., Ed.; Technip: Paris, France, 1994; pp. 197–210. [Google Scholar]
- Lacombe, O.; Angelier, J.; Laurent, P. Calcite twins as markers of recent compressional events in an active orogen: The reefal limestones of southern Taiwan as a case study. Comptes Rendus Académie Sci. Paris II 1993, 316, 1805–1813. [Google Scholar]
- Lacombe, O.; Angelier, J.; Rocher, M.; Bergues, J.; Chu, H.-T.; Deffontaines, B.; Hu, J.-C. Stress patterns associated with folding at the front of a collision belt: Example from the Pliocene reef limestones of Yutengping (Taiwan). Bull. Société Géologique Fr. 1996, 167, 361–374. [Google Scholar]
- Lacombe, O.; Amrouch, K.; Mouthereau, F.; Dissez, L. Calcite twinning constraints on late Neogene stress patterns and deformation mechanisms in the active Zagros collision belt. Geology 2007, 35, 263–266. [Google Scholar] [CrossRef]
- Lacombe, O.; Malandain, J.; Vilasi, N.; Amrouch, K.; Roure, F. From paleostresses to paleoburial in fold–thrust belts: Preliminary results from calcite twin analysis in the Outer Albanides. Tectonophysics 2009, 475, 128–141. [Google Scholar] [CrossRef]
- Rocher, M.; Lacombe, O.; Angelier, J. Mechanical twin sets in calcite as markers of recent collisional events in a fold-and-thrust belt: Evidence from the reefal limestones of southwestern Taiwan. Tectonics 1996, 15, 984–996. [Google Scholar] [CrossRef] [Green Version]
- Rocher, M.; Lacombe, O.; Angelier, J.; Deffontaines, B.; Verdier, F. Cenozoic folding and faulting in the south Aquitaine Basin (France): Insights from combined structural and paleostress analyses. J. Struct. Geol. 2000, 22, 627–645. [Google Scholar] [CrossRef]
- Beaudoin, N.; Leprêtre, R.; Bellahsen, N.; Lacombe, O.; Amrouch, K.; Callot, J.P.; Emmanuel, L.; Daniel, J.M. Structural and microstructural evolution of the Rattlesnake Mountain Anticline (Wyoming, USA): New insights into the Sevier and Laramide orogenic stress build-up in the Bighorn Basin. Tectonophysics 2012, 576–577, 20–45. [Google Scholar] [CrossRef]
- Beaudoin, N.; Koehn, D.; Lacombe, O.; Lecouty, A.; Billi, A.; Aharonov, E.; Parlangeau, C. Fingerprinting stress: Stylolite and calcite twinning paleopiezometry revealing the complexity of progressive stress patterns during folding. The case of the Monte Nero anticline in the Apennines, Italy. Tectonics 2016, 35, 1687–1712. [Google Scholar] [CrossRef] [Green Version]
- Arboit, F.; Amrouch, K.; Collins, A.S.; King, R.; Morley, C. Determination of the tectonic evolution from fractures, faults, and calcite twins on the southwestern margin of the Indochina Block. Tectonics 2015, 34, 1576–1599. [Google Scholar] [CrossRef]
- Kulikowski, D.; Amrouch, K. Combining geophysical data and calcite twin stress inversion to refine the tectonic history of subsurface and offshore provinces: A case study on the Cooper-Eromanga Basin, Australia. Tectonics 2017, 36, 515–541. [Google Scholar] [CrossRef]
- Rosenbrock, H.H. An automatic method for finding the greatest or least value of a function. Comput. J. 1960, 3, 175–184. [Google Scholar] [CrossRef] [Green Version]
- Zheng, J.; Shan, Y.; Hu, S. Palaeostress analysis of calcite twins from the Longshan Dome (central Hunan, South China): Mesozoic mega-fold superimposition in the reworked continent. Geosciences 2021. submitted. [Google Scholar]
- Spang, J.H. Numerical method for dynamic analysis of calcite twin lamellae. Geol. Soc. Am. Bull. 1972, 83, 467–472. [Google Scholar] [CrossRef]
- Kernstockova, M.; Melichar, R. Numerical paleostress analysis—Limits of automation. Trab. Geol. 2009, 29, 399–403. [Google Scholar]
- Lacombe, O. Do fault slip data inversions actually yield “paleostresses” that can be compared with contemporary stresses? A critical discussion. Comptes Rendus Geosci. 2012, 344, 159–173. [Google Scholar] [CrossRef]
- Rez, J. Paleostress analysis in the Mokrá quarries (Moravosilezian Zone, Czech Republic): Two methods, one result. Miner. Slovaca 2012, 44, 103. [Google Scholar]
- Shafiei, S.H.; Alavi, S.A.; Mohajjel, M. Calcite twinning constraints on paleostress patterns and tectonic evolution of the Zagros hinterland: The Sargaz complex, Sanandaj–Sirjan zone, SE Iran. Arab. J. Geosci. 2011, 4, 1189–1205. [Google Scholar] [CrossRef]
- Jang, B.A.; Kim, C.B.; Kang, S.S. Paleostress from calcite twins of limestone and its tectonic implication in South Korea. Geosyst. Eng. 2012, 15, 157–170. [Google Scholar] [CrossRef]
- Jang, B.A.; Ko, C.S.; Kim, J.H.; Kim, C.B.; Kang, S.S. Paleostress of the Joseon and Pyeongan Supergroups in South Korea using the New Calcite Strain Gauge (NCSG). J. Eng. Geol. 2014, 24, 311–322. [Google Scholar] [CrossRef] [Green Version]
- Sarkarinejad, K.; Kamali, Z. Mesoscopic and microscopic analyses of paleostress and strain orientation of the Dasht-e-Arjan graben (Southwestern Iran) using calcite e-twin and c-axis of the slickensides and slikenlines. J. Geosci. 2014, 23, 131–140. [Google Scholar]
- Kamali, Z.; Rahnamarad, J.; Sarkarinejhad, K. Structural analyses of fault planes using fault slickenlines and calcite e-twins data from the Dasht-e-Arjan graben, SW Iran. Iran. J. Earth Sci. 2017, 9, 121–136. [Google Scholar]
- Aubourg, C.; Smith, B.; Eshrahi, A.; Lacombe, O.; Authemayou, C.; Amrouch, K.; Bellier, O.; Mouthereau, F. New magnetic fabric data and their comparison with stress/strain markers from the Western Fars arc (Zagros); tectonic implications. In Tectonic and Stratigraphic Evolution of Zagros and Makran during the Meso-Cenozoic; Geological Society of London: London, UK, 2010; Volume 330, pp. 97–120. [Google Scholar]
- Amrouch, K.; Robion, P.; Callot, J.P.; Lacombe, O.; Daniel, J.M.; Bellahsen, N.; Faure, J.L. Constraints on deformation mechanisms during folding provided by rock physical properties: A case study at Sheep Mountain anticline (Wyoming, USA). Geophys. J. Int. 2010, 182, 1105–1123. [Google Scholar] [CrossRef] [Green Version]
- Tripathy, V.; Saha, D. Inversion of calcite twin data, paleostress reconstruction and multiphase weak deformation in cratonic interior–Evidence from the Proterozoic Cuddapah basin, India. J. Struct. Geol. 2015, 77, 62–81. [Google Scholar] [CrossRef]
- Jaya, A.; Nishikawa, O. Paleostress reconstruction from calcite twin and fault–slip data using the multiple inverse method in the East Walanae fault zone: Implications for the Neogene contraction in South Sulawesi, Indonesia. J. Struct. Geol. 2013, 55, 34–49. [Google Scholar] [CrossRef]
- Yamaji, A. The multiple inverse method: A new technique to separate stresses from heterogeneous fault-slip data. J. Struct. Geol. 2000, 22, 441–452. [Google Scholar] [CrossRef] [Green Version]
- Zheng, J.; Shan, Y. Inversion of polyphase calcite-twin data for deviatoric stress tensors: 2. Application to the Huangling Dome, northern South China. J. Struct. Geol. 2020, 138, 104089. [Google Scholar] [CrossRef]
- Amrouch, K.; Beaudoin, N.; Lacombe, O.; Bellahsen, N.; Daniel, J.M. Paleostress magnitudes in folded sedimentary rocks. Geophys. Res. Lett. 2011, 38, L17301. [Google Scholar] [CrossRef] [Green Version]
- Arboit, F.; Amrouch, K.; Morley, C.; Collins, A.S.; King, R. Palaeostress magnitudes in the Khao Khwang fold-thrust belt, new insights into the tectonic evolution of the Indosinian orogeny in central Thailand. Tectonophysics 2017, 710, 266–276. [Google Scholar] [CrossRef]
- Barber, D.J.; Wenk, H.R. Defects in deformed calcite and carbonate rocks. In Electron Microscopy in Mineralogy; Wenk, H.R., Ed.; Springer: Berlin/Heidelberg, Germany, 1976; pp. 428–442. [Google Scholar]
- Roberts, N.M.W.; Walker, R.J. U-Pb geochronology of calcite-mineralized faults: Absolute timing of rift-related fault events on the northeast Atlantic margin. Geology 2016, 44, 531–534. [Google Scholar] [CrossRef]
- Beaudoin, N.; Lacombe, O.; Roberts, N.M.W.; Koehn, D. U-Pb dating of calcite veins reveals complex stress evolution and thrust sequence in the Bighorn Basin, Wyoming, USA. Geology 2018, 46, 1015–1018. [Google Scholar] [CrossRef]
- Roberts, N.M.W.; Drost, K.; Horstwood, M.S.A.; Condon, D.J.; Chew, D.; Drake, H.; Milodowski, A.E.; McLean, N.M.; Smye, A.J.; Walker, R.J.; et al. Laser ablation inductively coupled plasma mass spectrometry (LA-ICP-MS) U–Pb carbonate geochronology: Strategies, progress, and limitations. Geochronology 2020, 2, 33–61. [Google Scholar]
- Nuriel, P.; Weinberger, R.; Kylander-Clark, A.; Hacker, B.; Craddock, J. The onset of the Dead Sea transform based on calcite age-strain analyses. Geology 2017, 45, 587–590. [Google Scholar] [CrossRef] [Green Version]
- Craddock, J.P.; Nuriel, P.; Kylander-Clark, A.R.C.; Hacker, B.R.; Luczaj, J.; Weinberger, R. Long-term (7 Ma) strain fluctuations within the Dead Sea transform system from high-resolution U-Pb dating of a calcite vein. Geol. Soc. Am. Bull. 2021, in press. [Google Scholar] [CrossRef]
- Roberts, N.M.W.; Žák, J.; Vacek, F.; Sláma, J. No more blind dates with calcite: Fluid-flow vs. fault-slip along the Očkov thrust, Prague Basin. Geosci. Front. 2021, 12, 101143. [Google Scholar] [CrossRef]
- Evans, M.A.; Groshong, R.H., Jr. A computer program for the calcite strain-gauge technique. J. Struct. Geol. 1994, 468, 277–281. [Google Scholar] [CrossRef]
- Craddock, J.P.; Malone, D.H.; Porter, R.; MacNamee, A.; Mathisen, M.; Kravitz, K.; Leonard, A. Structure, timing and kinematics of the Early Eocene South Fork Slide, Northwest Wyoming, USA. J. Geol. 2015, 123, 311–335. [Google Scholar] [CrossRef]
- Craddock, J.P.; Liu, J.; Zheng, Y. Twinning strains in synfolding calcite, Proterozoic Sinian System, China. Geosciences 2018, 8, 131. [Google Scholar] [CrossRef] [Green Version]
- Craddock, J.P.; Princen, M.; Wartman, J.; Xia, H.; Liu, J. Calcite twinning in the Ordovician Martinsburg Formation, Delaware Water Gap, New Jersey, USA: Implications for cleavage formation and tectonic shortening in the Appalachian Piedmont Province. Geosciences 2016, 6, 10. [Google Scholar] [CrossRef] [Green Version]
- Klein, T.; Craddock, J.P.; Zulauf, G. Constraints on the geodynamical evolution of Crete: Insights from illite crystallinity, Raman spectroscopy and calcite twinning above and below the ‘Cretan detachment’. Int. J. Earth Sci. 2013, 102, 139–182. [Google Scholar] [CrossRef]
- Craddock, J.P.; Neilson, K.; Petersen, C.; Porter, R.; Malone, D.H. Calcite twinning fabrics along the Middle America trench, Costa Rica and the Motagua sinistral fault, Honduras and Jamaica: Tectonic implications for the Caribbean plate. J. S. Am. Earth Sci. 2020, 104, 102816. [Google Scholar] [CrossRef]
- Craddock, J.P.; Malone, D.H.; Porter, R.; Compton, J.; Luczaj, J.; Konstantinou, A.; Day, J.E.; Johnston, S.T. Paleozoic reactivation structures in the Appalachian-Ouachita-Marathon foreland: Far-field deformation across Pangea. Earth Sci. Rev. 2017, 169, 1–34. [Google Scholar] [CrossRef]
- Craddock, J.P.; Craddock, S.D.; Konstantinou, A.; Kylander-Clark, A.R.; Malone, D.H. Calcite twinning strain variations across the Proterozoic Grenville orogen and Keweenaw-Kapuskasing inverted foreland, USA and Canada. Geosci. Front. 2017, 8, 1357–1384. [Google Scholar] [CrossRef]
- Craddock, J.P.; Malone, D.H.; Schmitz, M.D.; Gifford, J.N. Strain variations across the Proterozoic Penokean orogen, USA and Canada. Precambrian Res. 2018, 318, 25–69. [Google Scholar] [CrossRef]
- Paulsen, T.S.; Wilson, T.J.; Demosthenous, C.; Millan, C.; Jarrard, R.; Läufer, A. Kinematics of the Neogene Terror rift: Constraints from calcite twinning strains in the ANDRILL McMurdo Ice Shelf (AND-1B) core, Victoria Land Basin, Antarctica. Geosphere 2014, 10, 828–841. [Google Scholar] [CrossRef]
- Sakaguchi, A.; Sakaguchi, H.; Nishiura, D.; Nakatani, M.; Yoshida, S. Elastic stress indication in elastically rebounded rock. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Chen, K.; Kunz, M.; Tamura, N.; Wenk, H.R. Deformation twinning and residual stress in calcite studied with synchrotron polychromatic X-ray microdiffraction. Phys. Chem. Miner. 2011, 38, 491–500. [Google Scholar] [CrossRef] [Green Version]
- Brandstätter, J.; Kurz, W.; Rogowitz, A. Microstructural analysis and calcite piezometry on hydrothermal veins: Insights into the deformation history of the Cocos Plate at Site U1414 (IODP Expedition 344). Tectonics 2017, 36, 1562–1579. [Google Scholar] [CrossRef]
- Craddock, J.P.; Farris, D.W.; Roberson, A. Calcite-twinning constraints on stress-strain fields along the Mid-Atlantic Ridge, Iceland. Geology 2004, 32, 49–52. [Google Scholar] [CrossRef]
- Craddock, J.P.; Pearson, A.M. Non-coaxial horizontal shortening strains preserved in twinned amygdule calcite, DSDP Hole 433, Suiko seamount, northwest Pacific plate. J. Struct. Geol. 1994, 16, 719–724. [Google Scholar] [CrossRef]
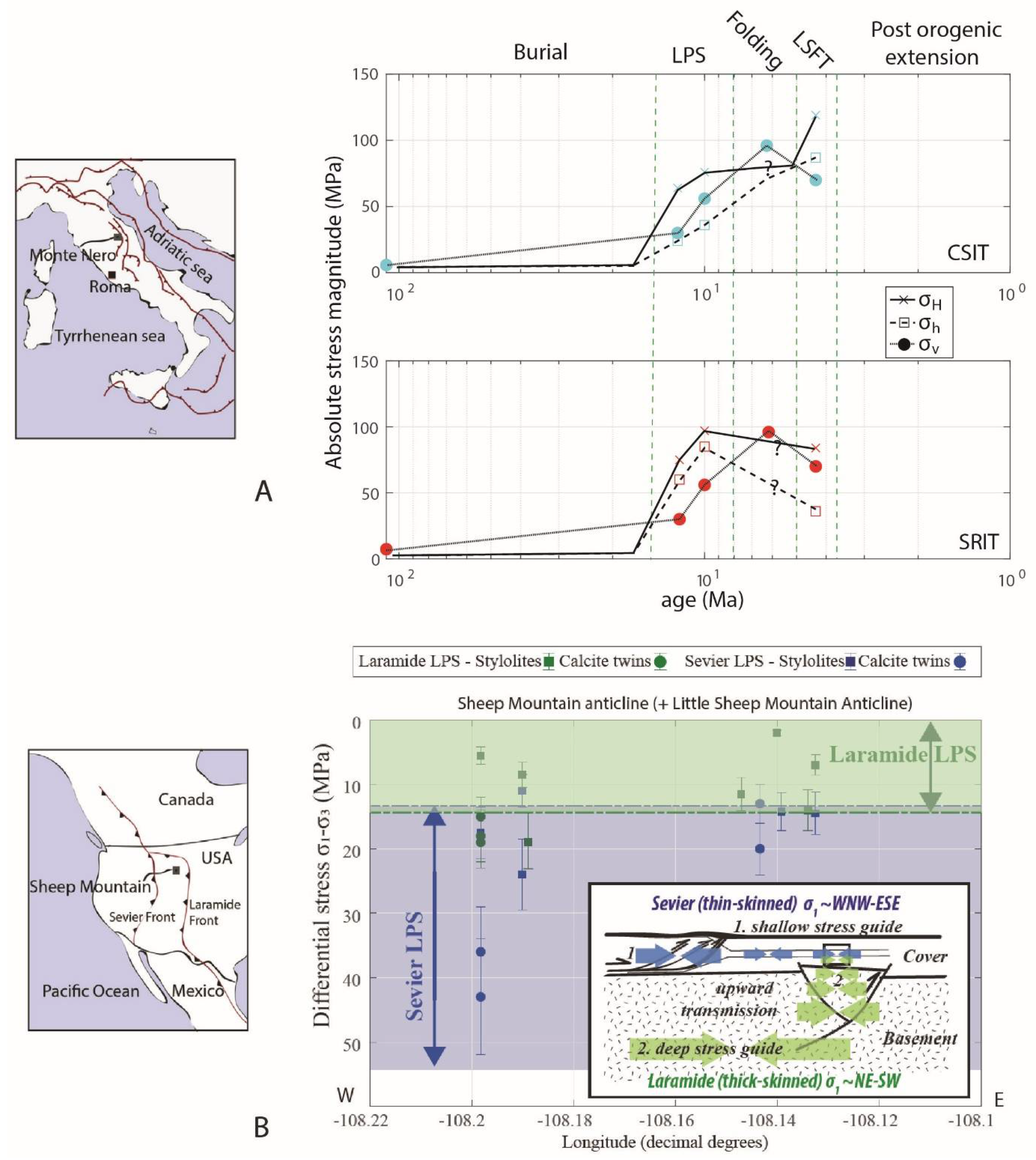
- Beaudoin, N.; Lacombe, O.; David, M.E.; Koehn, D. Does stress transmission in forelands depend on structural style? Distinctive stress magnitudes during Sevier thin-skinned and Laramide thick-skinned layer-parallel shortening in the Bighorn Basin (USA) revealed by stylolite and calcite twinning paleopiezometry. Terra Nova 2020, 32, 225–233. [Google Scholar]
- Kulikowski, D.; Amrouch, K.; Cooke, D. Geomechanical modelling of fault reactivation in the Cooper Basin, Australia. Aust. J. Earth Sci. 2016, 63, 295–314. [Google Scholar] [CrossRef]
- Kulikowski, D.; Amrouch, K. 4D modelling of fault reactivation using complete paleostress tensors from the Cooper–Eromanga Basin, Australia. Aust. J. Earth Sci. 2018, 65, 661–681. [Google Scholar] [CrossRef]
- Roure, F.; Andriessen, P.; Callot, J.P.; Faure, J.L.; Ferket, H.; Gonzales, E.; Guilhaumou, N.; Hardebol, N.; Lacombe, O.; Malandain, J.; et al. The use of palaeo-thermo-barometers and coupled thermal, fluid flow and pore-fluid pressure modelling for hydrocarbon and reservoir prediction in fold and thrust belts. Geol. Soc. Lond. Spec. Publ. 2010, 348, 87–114. [Google Scholar] [CrossRef]
- Lindgren, P.; Price, M.C.; Lee, M.R.; Burchell, M.J. Constraining the pressure threshold of impact induced calcite twinning: Implications for the deformation history of aqueously altered carbonaceous chondrite parent bodies. Earth Planet. Sci. Lett. 2013, 384, 71–80. [Google Scholar] [CrossRef]
- Winkler, R.; Luther, R.; Poelchau, M.H.; Wünnemann, K.; Kenkmann, T. Subsurface deformation of experimental hypervelocity impacts in quartzite and marble targets. Meteorit. Planet. Sci. 2018, 53, 1733–1755. [Google Scholar] [CrossRef]
- Lacombe, O.; Laurent, P. Determination of principal stress magnitudes using calcite twins and rock mechanics data. Tectonophysics 1992, 202, 83–93. [Google Scholar] [CrossRef]
- Pascal, C. Paleostress Inversion Techniques: Methods and Applications for Tectonics, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2021; Chapter 8; 400p. [Google Scholar]
- Beaudoin, N.; Lacombe, O.; Bellahsen, N.; Amrouch, K.; Daniel, J.M. Evolution of pore-fluid pressure during folding and basin contraction in overpressured reservoirs: Insights from the Madison–Phosphoria carbonate formations in the Bighorn Basin (Wyoming, USA). Mar. Pet. Geol. 2014, 55, 214–229. [Google Scholar] [CrossRef]
- Beaudoin, N.; Bellahsen, N.; Lacombe, O.; Emmanuel, L. Fracture-controlled paleohydrogeology in a basement-cored, fault-related fold: Sheep Mountain Anticline, Wyoming, United States. Geochem. Geophys. Geosyst. 2011, 12, Q06011. [Google Scholar] [CrossRef] [Green Version]
- Renard, F.; Schmittbuhl, J.; Gratier, J.P.; Meakin, P.; Merino, E. Three-dimensional roughness of stylolites in limestones. J. Geophys. Res. Solid Earth 2004, 109, B03209. [Google Scholar] [CrossRef] [Green Version]
- Schmittbuhl, J.; Renard, F.; Gratier, J.P.; Toussaint, R. Roughness of stylolites: Implications of 3D high resolution topography measurements. Phys. Rev. Lett. 2004, 93, 238501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ebner, M.; Koehn, D.; Toussaint, R.; Renard, F.; Schmittbuhl, J. Stress sensitivity of stylolite morphology. Earth Planet. Sci. Lett. 2009, 277, 394–398. [Google Scholar] [CrossRef] [Green Version]
- Rolland, A.; Toussaint, R.; Baud, P.; Conil, N.; Landrein, P. Morphological analysis of stylolites for paleostress estimation in limestones. Int. J. Rock Mech. Min. Sci. 2014, 67, 212–225. [Google Scholar] [CrossRef] [Green Version]
- Beaudoin, N.; Gasparrini, M.; David, M.E.; Lacombe, O.; Koehn, D. Bedding-parallel stylolites as a tool to unravel maximum burial depth in sedimentary basins: Application to Middle Jurassic carbonate reservoirs in the Paris basin. Geol. Soc. Am. Bull. 2019, 131, 1239–1254. [Google Scholar] [CrossRef]
- Bertotti, G.; de Graaf, S.; Bisdom, K.; Oskam, B.; Vonhof, H.B.; Bezerra, F.H.R.; Reijmer, J.J.G.; Cazarin, C.L. Fracturing and fluid-flow during post-rift subsidence in carbonates of the Jandaíra Formation, Potiguar Basin, NE Brazil. Basin Res. 2017, 29, 836–853. [Google Scholar] [CrossRef] [Green Version]
- Beaudoin, N.E.; Lacombe, O.; Koehn, D.; David, M.E.; Farrell, N.; Healy, D. Vertical stress history and paleoburial in foreland basins unravelled by stylolite roughness paleopiezometry: Insights from bedding-parallel stylolites in the Bighorn Basin, Wyoming, USA. J. Struct. Geol. 2020, 136, 104061. [Google Scholar] [CrossRef]
- Beaudoin, N.; Labeur, A.; Lacombe, O.; Koehn, D.; Billi, A.; Hoareau, G.; Boyce, A.; John, C.M.; Marchegiano, M.; Roberts, N.M.; et al. Regional-scale paleofluid system across the Tuscan Nappe—Umbria Marche Apennine Ridge (northern Apennines) as revealed by mesostructural and isotopic analyses of stylolite-vein networks. Solid Earth 2020, 11, 1617–1641. [Google Scholar] [CrossRef]
- Labeur, A.; Beaudoin, N.E.; Lacombe, O.; Emmanuel, L.; Petracchini, L.; Daëron, M.; Klimowicz, S.; Callot, J.P. Burial-deformation history of folded rocks unraveled by fracture analysis, stylolite paleopiezometry and vein cement geochemistry: A case ctudy in the Cingoli Anticline (Umbria-Marche, Northern Apennines). Geosciences 2021, 11, 135. [Google Scholar] [CrossRef]
- Ebner, M.; Toussaint, R.; Schmittbuhl, J.; Koehn, D.; Bons, P. Anisotropic scaling of tectonic stylolites: A fossilized signature of the stress field? J. Geophys. Res. Solid Earth 2010, 115, B06403. [Google Scholar] [CrossRef] [Green Version]
- Toussaint, R.; Aharonov, E.; Koehn, D.; Gratier, J.P.; Ebner, M.; Baud, P.; Rolland, A.; Renard, F. Stylolites: A review. J. Struct. Geol. 2018, 114, 163–195. [Google Scholar] [CrossRef] [Green Version]
- Tavani, S.; Storti, F.; Lacombe, O.; Corradetti, A.; Muñoz, J.A.; Mazzoli, S. A review of deformation pattern templates in foreland basin systems and fold-and-thrust belts: Implications for the state of stress in the frontal regions of thrust wedges. Earth Sci. Rev. 2015, 141, 82–104. [Google Scholar] [CrossRef]
- Ferrill, D.A.; Smart, K.J.; Cawood, A.J.; Morris, A.P. The fold-thrust belt stress cycle: Superposition of normal, strike-slip, and thrust faulting deformation regimes. J. Struct. Geol. 2021, 148, 104362. [Google Scholar] [CrossRef]
- Van der Pluijm, B.A.; Craddock, J.P.; Graham, B.R.; Harris, J.H. Paleostress in cratonic North America: Implications for deformation of continental interiors. Science 1997, 277, 794–796. [Google Scholar] [CrossRef] [Green Version]
- Petracchini, L.; Antonellini, M.; Billi, A.; Scrocca, D. Syn-thrusting polygonal normal faults exposed in the hinge of the Cingoli anticline, northern Apennines, Italy. Front. Earth Sci. 2015, 3, 67. [Google Scholar] [CrossRef] [Green Version]
- Engelder, T. Stress Regimes in the Lithosphere; Princeton University Press: Princeton, NJ, USA, 1993; 451p. [Google Scholar]
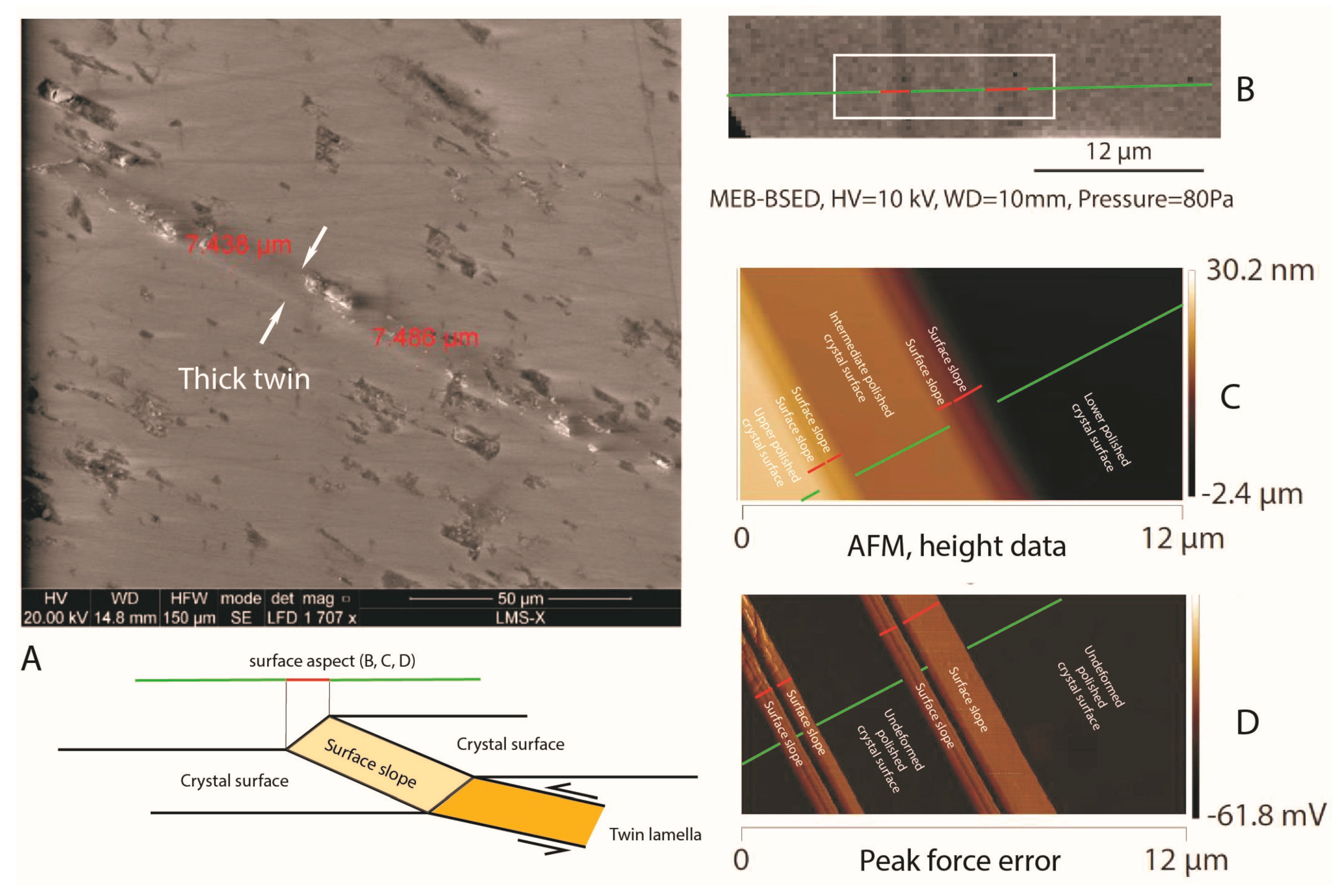


| Twin Morphology | Twin Development/CRSS | |
|---|---|---|
| Differential stress | - | +++ |
| Fluid pressure | - | - |
| Confining pressure | + if very high | -? |
| Temperature | +++ | + |
| Grain size | - | +++ |
| Strain | +++ | ++ (strain hardening) |
| Strain rate | - | - (except for very small grain size) |
| Chemistry | - | -? |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lacombe, O.; Parlangeau, C.; Beaudoin, N.E.; Amrouch, K. Calcite Twin Formation, Measurement and Use as Stress–Strain Indicators: A Review of Progress over the Last Decade. Geosciences 2021, 11, 445. https://doi.org/10.3390/geosciences11110445
Lacombe O, Parlangeau C, Beaudoin NE, Amrouch K. Calcite Twin Formation, Measurement and Use as Stress–Strain Indicators: A Review of Progress over the Last Decade. Geosciences. 2021; 11(11):445. https://doi.org/10.3390/geosciences11110445
Chicago/Turabian StyleLacombe, Olivier, Camille Parlangeau, Nicolas E. Beaudoin, and Khalid Amrouch. 2021. "Calcite Twin Formation, Measurement and Use as Stress–Strain Indicators: A Review of Progress over the Last Decade" Geosciences 11, no. 11: 445. https://doi.org/10.3390/geosciences11110445
APA StyleLacombe, O., Parlangeau, C., Beaudoin, N. E., & Amrouch, K. (2021). Calcite Twin Formation, Measurement and Use as Stress–Strain Indicators: A Review of Progress over the Last Decade. Geosciences, 11(11), 445. https://doi.org/10.3390/geosciences11110445







