Cultural Heritage and Rockfalls: Analysis of Multi-Scale Processes Nearby the Lucus Angitiae Archaeological Site (Central Italy)
Abstract
:1. Introduction
2. Geological and Geomorphological Setting
3. Materials and Methods
3.1. Rock Blocks Inventory
3.2. Rockfall Probabilistic Modeling: Input Data
3.2.1. Slope Geometry
3.2.2. Initial Motion Conditions
- a)
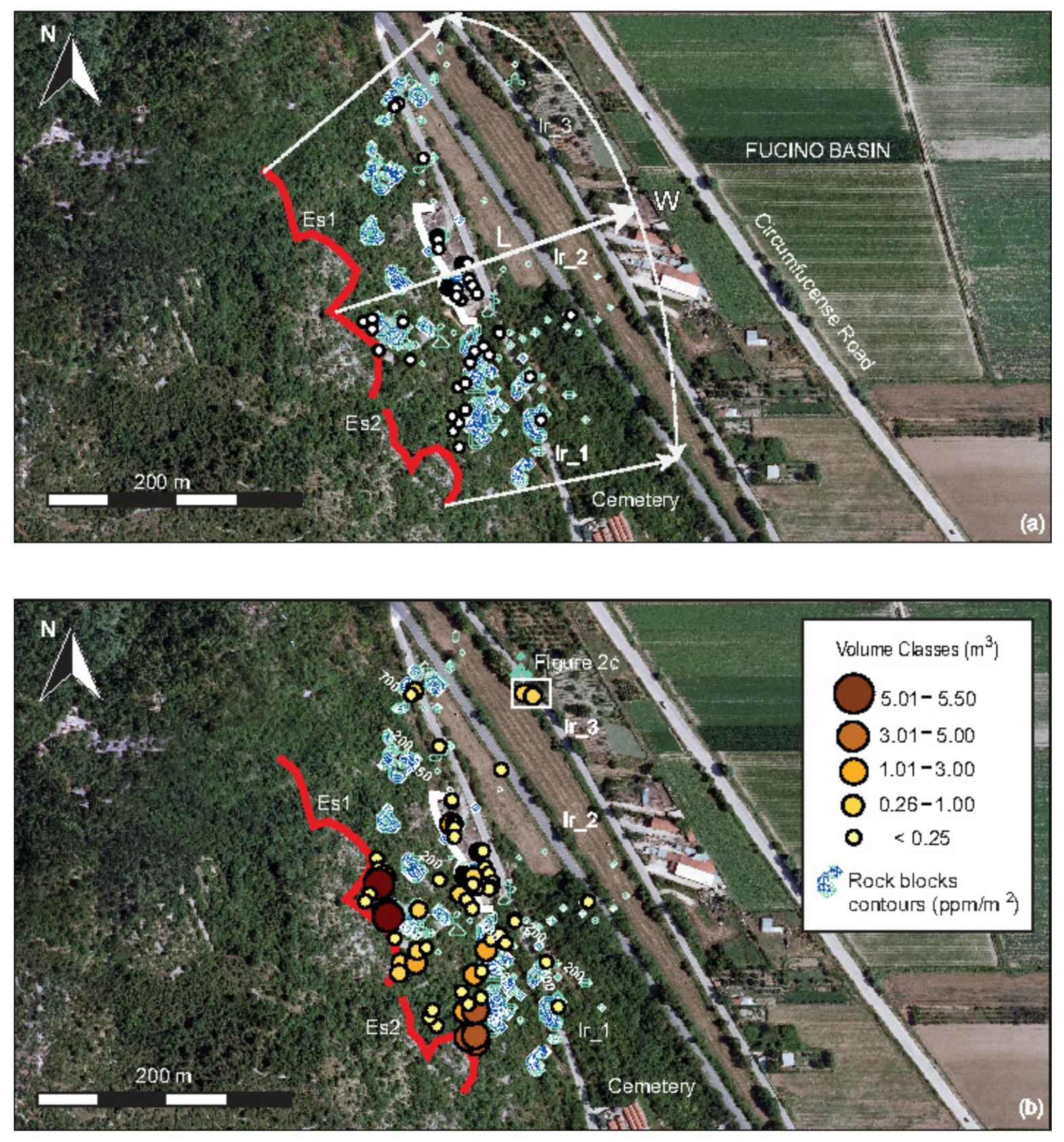
- Number of starting points (nSp): Rotomap® simulates the detachments ì along a starting line corresponding to the base of the cliff, from which the rock blocks move, after the free-fall phase, with an initial velocity V0i ≠ 0. Since any information was available regarding the location of former rockfall source areas (except for the rock scars of the 2005 event shown in Figure 4a), a conservative approach was adopted, and starting points were placed along the entire length of Es1 and Es2 at a regular distance of 5 m and at mid-point positions. Considering the length of Es1 (100 m) and Es2 (80 m), 39 and 33 starting points were identified, respectively;
- b)
- Number of initial velocity (nV0), corresponding to the number of release points on the cliff, on the vertical line of each starting point: uncertainty in initial velocity was accounted for by considering different detachment elevations (Hi). Each V0i was then calculated in correspondence of the starting line according to:
- c)
- Number of angular deviations (nAd) for each detachment point: this number represents the number of allowed initial motion directions out of the maximum slope direction plane. This parameter accounts for the lateral dispersion of the trajectories. Initially, four angular deviations with a maximum angle of 10° for each starting point were assumed, and this choice was confirmed after the model calibration.
3.2.3. Kinematic Parameters
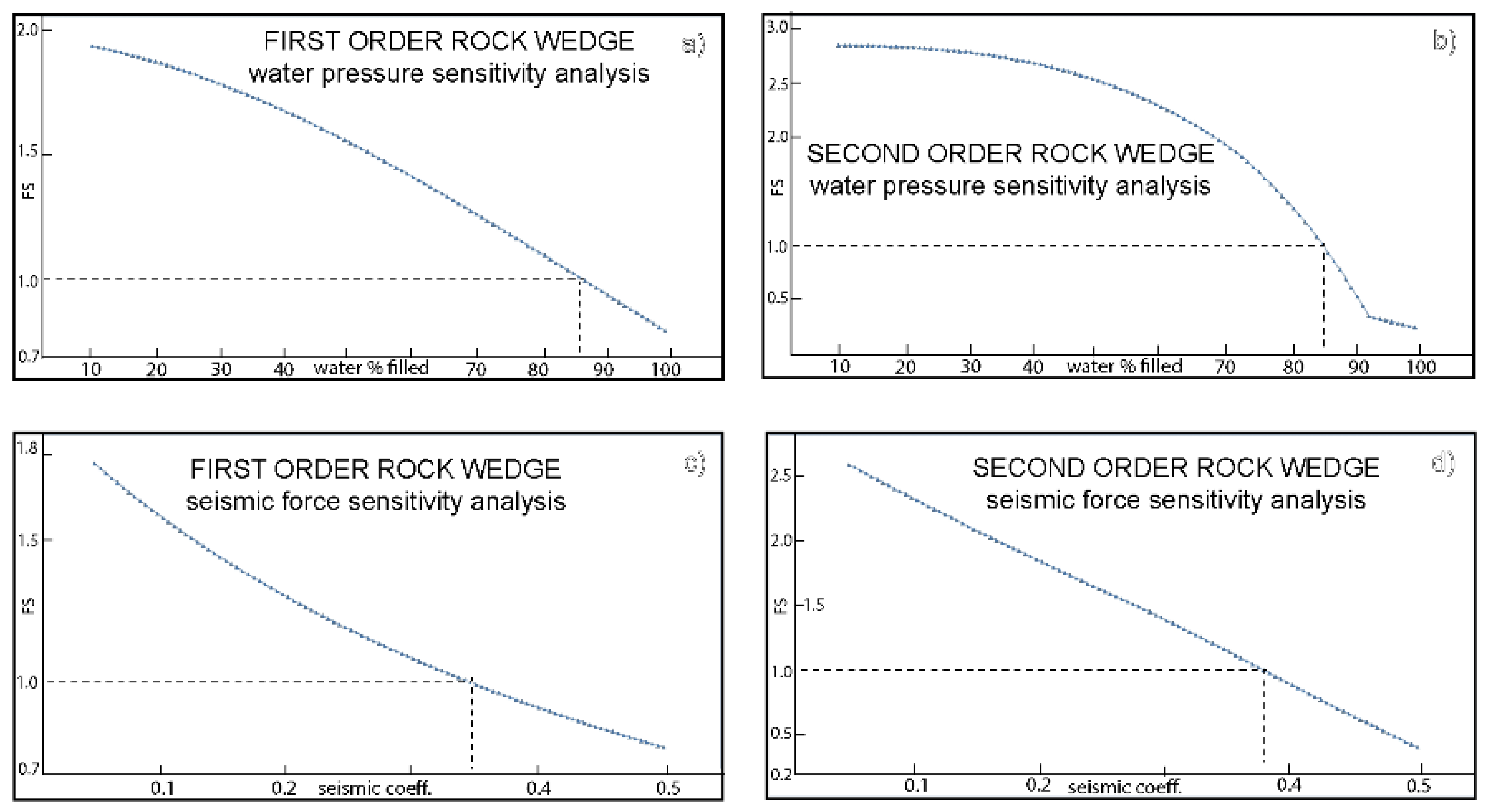
3.3. Geomechanical and Sensitivity Analyses
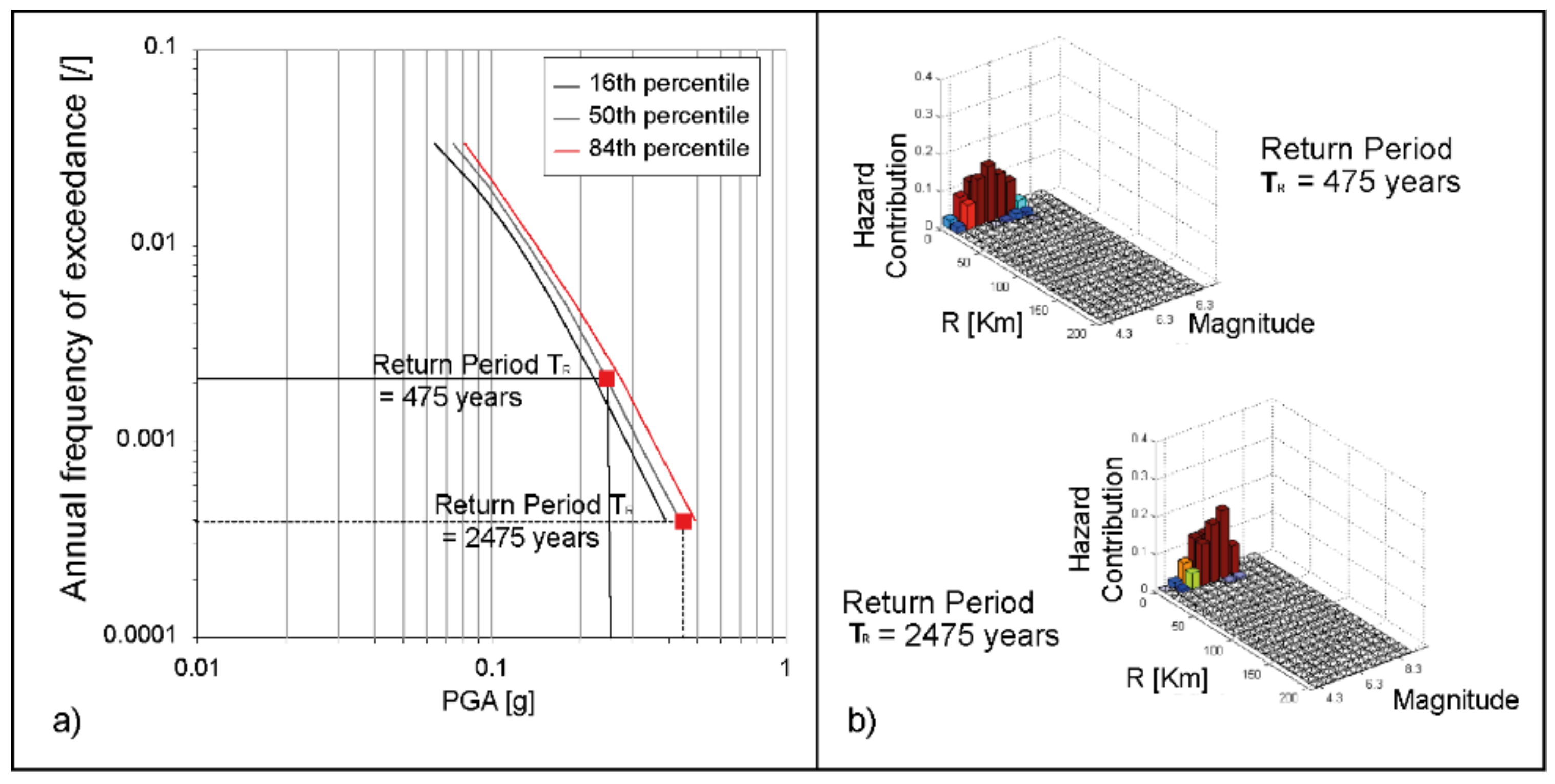
3.4. Seismic Action Assessment DEM
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nicu, I.C. Natural hazards-a threat for immovable cultural heritage, A review. Int. J. Conserv. Sci. 2017, 8, 375–388. [Google Scholar]
- Klimeš, J. Landslide temporal analysis and susceptibility assessment as bases for landslide mitigation, Machu Picchu, Peru. Environ. Earth Sci. 2013, 70, 913–925. [Google Scholar] [CrossRef]
- Schilirò, L.; Cevasco, A.; Esposito, C.; Mugnozza, G.S. Shallow landslide initiation on terraced slopes: Inferences from a physically based approach. Geomat. Nat. Hazards Risk 2018, 9, 295–324. [Google Scholar] [CrossRef] [Green Version]
- Tunusluoglu, M.C.; Zorlu, K. Rockfall hazard assessment in a cultural and natural heritage (Ortahisar Castle, Cappadocia, Turkey). Environ. Geol. 2009, 56, 963–972. [Google Scholar] [CrossRef]
- Marchetti, D.; Avanzi, G.A.; Sciarra, N.; Calista, M.; Mazzanti, G. Numerical Modeling Applied to a Cultural Heritage Site Threatened by Rock Falls in Tuscany (Italy). In Rock Mechanics in Civil and Environmental Engineering; Zhao, L., Dudt, M., Eds.; Taylor & Francis Group: London, UK, 2010; pp. 647–650. [Google Scholar]
- Di Luzio, E.; Fasani, G.B.; Bretschneider, A. Potential rockfalls and analysis of slope dynamics in the Palatine archaeological area. Geol. Acta 2013, 11, 245–264. [Google Scholar] [CrossRef]
- Di Luzio, E.; Colosi, F.; Fidenzi, E.; Malinverni, E.S.; Gaudiosi, I.; Bozzi, C.A.; Orazi, R. Slope analysis and rock fall assessment in the Khinis archaeological area (Kurdistan, northern Iraq). Ital. J. Eng. Geol. Environ. 2019, 19, 13–35. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, L.; Wang, S.; Agliardi, F.; Frattini, P.; Crosta, G.B.; Yang, Z. Field investigation and rockfall hazard zonation at the Shijing Mountains Sutra caves cultural heritage (China). Environ. Earth Sci. 2012, 66, 1897–1908. [Google Scholar] [CrossRef]
- Di Luzio, E.; Mazzanti, P.; Brunetti, A.; Baleani, M. Assessment of tectonic-controlled rock fall processes threatening the ancient Appia route at the Aurunci Mountain pass (central Italy). Nat. Hazards 2020, 102, 909–938. [Google Scholar] [CrossRef]
- Dinçer, I.; Orhan, A.; Frattini, P.; Crosta, G.B. Rockfall at the heritage site of the Tatlarin Underground City (Cappadocia, Turkey). Nat. Hazards 2016, 82, 1075–1098. [Google Scholar] [CrossRef]
- Fanti, R.; Gigli, G.; Lombardi, L.; Tapete, D.; Canuti, P. Terrestrial laser scanning for rock fall stability analysis in the cultural heritage site of Pitigliano (Italy). Landslides 2013, 10, 409–420. [Google Scholar] [CrossRef] [Green Version]
- Margottini, C.; Antidze, N.; Corominas, J.; Crosta, G.B.; Frattini, P.; Gigli, G.; Giordan, D.; Iwasaky, I.; Lollino, G.; Manconi, A.; et al. Landslide hazard, monitoring and conservation strategy for the safeguard of Vardzia Byzantine monastery complex, Georgia. Landslides 2015, 12, 193–204. [Google Scholar] [CrossRef] [Green Version]
- Boldini, D.; Guido, G.L.; Margottini, C.; Spizzichino, D. Stability analysis of a large-volume block in the historical rock-cut city of Vardzia (Georgia). Rock Mech. Rock Eng. 2018, 51, 341–349. [Google Scholar] [CrossRef]
- Frodella, W.; Elashvili, M.; Spizzichino, D.; Gigli, G.; Nadaraia, A.; Kirkitadze, G.; Adikashvili, L.; Margottini, C.; Antidze, N.; Casagli, N. Applying Close Range Non-Destructive Techniques for the Detection of Conservation Problems in Rock-Carved Cultural Heritage Sites. Remote Sens. 2021, 13, 1040. [Google Scholar] [CrossRef]
- Tarragüel, A.A.; Krol, B.; van Westen, C. Analysing the possible impact of landslides and avalanches on cultural heritage in Upper Svaneti, Georgia. J. Cult. Herit. 2012, 13, 453–461. [Google Scholar] [CrossRef]
- Michalski, S.; Pedersoli, J.L., Jr. The ABC Method: A Risk Management Approach to the Preservation of Cultural Heritage. Available online: https://www.iccrom.org/it/publication/abc-method-risk-management-approach-preservation-cultural-heritage (accessed on 15 November 2021).
- Valagussa, A.; Frattini, P.; Crosta, G.; Spizzichino, D.; Leoni, G.; Margottini, C. Multi-risk analysis on European cultural and natural UNESCO heritage sites. Nat. Hazards 2021, 105, 2659–2676. [Google Scholar] [CrossRef]
- Monaghan, P. Encyclopedia of Goddess and Heroines; Greenwood Press: Santa Barbara, CA, USA, 2009; p. 641. [Google Scholar]
- Galadini, F.; Ceccaroni, E.; Falcucci, E.; Gori, S. Natural hazards in the Abruzzi Apennines (Italy) and the risk to archaeological sites. Disaster Adv. 2012, 5, 72–78. [Google Scholar]
- Scioldo, G. Rotomap: Analisi Statistica del Rotolamento dei Massi. In Guida di Informatica Ambientale; Guariso, G., Ed.; Patron: Bologna, Italy, 1991; pp. 81–84. [Google Scholar]
- Geo&Soft International, RotoMap 32. Available online: https://www.geoandsoft.com/italiano/geomeccanica_software_calcolo_caduta_rotolamento_massi.htm (accessed on 10 December 2021). CNR License number T3N2781(16-18-34).
- Del Maschio, L.; Gozza, G.; Piacentini, D.; Pizziolo, M.; Soldati, M. Previsione delle traiettorie dei blocchi mobilizzati da frane di crollo: Applicazione e confronto di modelli. G. Geol. Appl. 2007, 6, 33–44. [Google Scholar]
- Bourrier, F.; Dorren, L.; Nicot, F.; Berger, F.; Darve, F. Toward objective rockfall trajectory simulation using a stochastic impact model. Geomorphology 2009, 110, 68–79. [Google Scholar] [CrossRef] [Green Version]
- Ferrari, F.; Giani, G.P.; Apuani, T. Towards the comprehension of rockfall motion, with the aid of in situ tests. Ital. J. Eng. Geol. Environ. 2013, 6, 163–171. [Google Scholar] [CrossRef]
- Patacca, E.; Scandone, P.; Di Luzio, E.; Cavinato, G.P.; Parotto, M. Structural architecture of the central Apennines: Interpretation of the CROP 11 seismic profile from the Adriatic coast to the orographic divide. Tectonics 2008, 27. [Google Scholar] [CrossRef]
- Cosentino, D.; Cipollari, P.; Marsili, P.; Scrocca, D. Geology of the Central Apennines: A Regional Review, The Geology of Italy: Tectonics and Life along Plate Margins. J. Virtual Explor. 2010, 12. [Google Scholar] [CrossRef]
- Galadini, F.; Messina, P. Plio-Quaternary tectonics of the Fucino basin and surrounding areas (central Italy). G. Geol. 1994, 56, 73–99. [Google Scholar]
- Bosi, C.; Galadini, F.; Messina, P. Stratigrafia plio-pleistocenica della Conca del Fucino. Quaternario 1995, 8, 83–94. [Google Scholar]
- Cavinato, G.P.; Carusi, C.; Dall’Asta, M.; Miccadei, E.; Piacentini, T. Sedimentary and tectonic evolution of Plio-Pleistocene alluvial and lacustrine deposits of Fucino Basin (central Italy). Sediment. Geol. 2002, 148, 29–59. [Google Scholar] [CrossRef]
- Galadini, F.; Messina, P.; Giaccio, B.; Sposato, A. Early uplift history of the Abruzzi Apennines (central Italy): Available geomorphological constraints. Quat. Int. 2003, 101-102, 125–135. [Google Scholar] [CrossRef]
- Michetti, A.M.; Brunamonte, F.; Serva, L.; Vittori, E. Trench investigations of the 1915 Fucino earthquake fault scarps (Abruzzo, Central Italy): Geological evidence of large historical events. J. Geophys. Res. Solid Earth 1996, 101, 5921–5936. [Google Scholar] [CrossRef]
- Galadini, F.; Galli, P. The Holocene paleoearthquakes on the 1915 Avezzano earthquake faults (central Italy): Implications for active tectonics in the central Apennines. Tectonophysics 2000, 308, 143–170. [Google Scholar] [CrossRef]
- Galadini, F.; Galli, P. Active tectonics in the Central Apennines (Italy). Input data for seismic hazard assessment. Nat. Hazards 2000, 22, 225–268. [Google Scholar] [CrossRef]
- Rovida, A.; Locati, M.; Camassi, R.; Lolli, B.; Gasperini, P.; Antonucci, A. Catalogo Parametrico dei Terremoti Italiani (CPTI15), versione 3.0; Istituto Nazionale di Geofisica e Vulcanologia (INGV): Rome, Italy, 2021. [Google Scholar] [CrossRef]
- Agliardi, F.; Crosta, G.B. High resolution three-dimensional numerical modelling of rockfalls. Int. J. Rock Mech. Min. Sci. 2003, 40, 455–471. [Google Scholar] [CrossRef]
- Crosta, G.B.; Agliardi, F. Parametric evaluation of 3D dispersion of rockfall trajectories. Nat. Hazards Earth Syst. Sci. 2004, 4, 583–598. [Google Scholar] [CrossRef] [Green Version]
- Ritchie, A.M. Evaluation of rockfall and its control. Highw. Res. Rec. 1963, 17, 13–28. [Google Scholar]
- Broili, L. In situ tests for the study of rockfall. Geol. Appl. Idrogeol. 1973, 8, 105–111. [Google Scholar]
- Wu, S.S. Rockfall evaluation by computer simulation. Transp. Res. Rec. 1985, 1031, 1–5. [Google Scholar]
- Pfeiffer, T.J.; Higgins, J.D. Rockfall hazard analysis using the Colorado rockfall simulation program. Transp. Res. Rec. 1990, 1288, 117–126. [Google Scholar]
- Evans, S.G.; Hungr, O. The assessment of rockfall hazard at the base of talus slopes. Can. Geotech. J. 1993, 30, 620–636. [Google Scholar] [CrossRef]
- Budetta, P.; Santo, A. Morphostructural evolution and related kinematics of rockfalls in Campania (southern Italy): A case study. Eng. Geol. 1994, 36, 197–210. [Google Scholar] [CrossRef]
- Robotham, E.; Wang, M.; Walton, G. Assessment of risk of rockfall from active and abandoned quarry slopes. Trans. Inst. Min. Metall. Sect. A 1995, 104, 25–33. [Google Scholar]
- Azzoni, A.; De Freitas, M.H. Experimentally gained parameters, decisive for rock fall analysis. Rock Mech. Rock Eng. 1995, 28, 111–124. [Google Scholar] [CrossRef]
- Azzoni, A.; La Barbera, G.; Zaninetti, A. Analysis and prediction of rockfalls using a mathematical model. Int. J. Rock Mech. Min. Sci. 1995, 32, 709–724. [Google Scholar] [CrossRef]
- Giani, G.P.; Giacomini, A.; Migliazza, M.; Segalini, A. Experimental and theoretical studies to improve rock fall analysis and protection work design. Rock Mech. Rock Eng. 2004, 37, 369–389. [Google Scholar] [CrossRef]
- Pfeiffer, T.J.; Bowen, T.D. Computer simulation of rockfalls. Bull. Assoc. Eng. Geol. 1989, 26, 135–146. [Google Scholar] [CrossRef]
- Fornaro, M.; Nebbia, M.; Peila, D. Block Falls on Rock Slopes: Application of a Numerical Simulation Program to Some Real Cases. In Proceedings of the 6th International Congress of the IAEG, Amsterdam, The Netherlands, 6–10 August 1990; Price, D.G., Ed.; Amsterdam Balkema: Rotterdam, The Netherlands, 1990; pp. 2173–2180. [Google Scholar]
- Kobayashi, Y.; Harp, E.L.; Kagawa, T. Simulation of rockfalls triggered by earthquakes. Rock Mech. Rock Eng. 1990, 23, 1–20. [Google Scholar] [CrossRef]
- Guzzetti, F.; Reichenbach, P.; Wieczorek, G.F. Rockfall hazard and risk assessment in the Yosemite Valley, California, USA. Nat. Hazards Earth Syst. Sci. 2003, 3, 491–503. [Google Scholar] [CrossRef] [Green Version]
- Guzzetti, F.; Reichenbach, P.; Ghigi, S. Rockfall hazard and risk assessment along a transportation corridor in the Nera Valley, Central Italy. Environ. Manag. 2004, 34, 191–208. [Google Scholar] [CrossRef]
- Longo, S.; Oreste, P. Ceppo Morelli block-falls probability study to support the decision of excavating a by-pass tunnel. Am. J. Eng. Appl. Sci. 2010, 3, 723–727. [Google Scholar] [CrossRef]
- Wang, X.; Frattini, P.; Crosta, G.B.; Zhang, L.; Agliardi, F.; Lari, S.; Yang, Z. Uncertainty assessment in quantitative rockfall risk assessment. Landslides 2014, 11, 711–722. [Google Scholar] [CrossRef]
- Chau, K.T.; Wong, R.H.C.; Wu, J.J. Coefficient of restitution and rotational motions of rockfall impacts. Int. J. Rock Mech. Min. Sci. 2002, 39, 69–77. [Google Scholar] [CrossRef]
- Piteau, D.R.; Clayton, R. Computer Rockfall Model. In Proceedings of the Meeting on Rockfall Dynamics and Protective Works Effectiveness, Bergamo, Italy, 20—21 May 1976; pp. 123–125. [Google Scholar]
- Hoek, E. Rockfall: A Computer Program for Predicting Rockfall Trajectories; Unpublished internal notes; Golder Associates: Vancouver, BC, Canada, 1986. [Google Scholar]
- Descoeudres, F.; Zimmermann, T. Three-dimensional dynamic calculation of rockfalls. In Proceedings of the 6th International Society for Rock Mechanics Congress, Montreal, QC, Canada, 30 August–3 September 1987; pp. 337–342. [Google Scholar]
- Giani, G.P. Rock Slope Stability Analysis; Balkema: Rotterdam, The Netherlands, 1992; p. 374. [Google Scholar]
- Rocscience. Swedge 6.0. Available online: https://www.rocscience.com/software/swedge (accessed on 10 December 2021). CNR License number 18324-001.
- Barton, N.; Choubey, V. The shear strength of rock joints in theory and practice. Rock Mech. 1977, 10, 1–54. [Google Scholar] [CrossRef]
- Hoek, E.; Bray, J.W. Rock Slope Engineering, Revised, 3rd ed.; The Institution of Mining and Metallurgy: London, UK, 1981; pp. 341–351. [Google Scholar]
- Cruden, D.M.; Hu, X.Q. Basic friction angles of carbonate rocks from Kananaskis country. Can. Bull. Int. Assoc. Eng. Geol. 1988, 38, 55–59. [Google Scholar] [CrossRef]
- Bruce, I.G.; Cruden, D.M.; Eaton, T.M. Use of a tilting table to determine the basic friction angle of hard rock samples. Can. Geotech. J. 1989, 26, 474–479. [Google Scholar] [CrossRef]
- Goodman, R.E. Introduction to Rock Mechanics, 2nd ed.; Wiley J and Sons: New York, NY, USA, 1989; p. 576. [Google Scholar]
- Gonzalez de Vallejo, L.I.; Ferrer, M.; Ortuno, L.; Oteo, C. Geoingegneria; Pearson Education: Milan, Italy, 2005; p. 816. [Google Scholar]
- Waltham, A.C. Foundations of Engineering Geology, 3rd ed.; Spon Press, Taylor and Francis: London, UK, 2009; p. 104. [Google Scholar]
- Barton, N.; Bandis, S. Review of Predictive Capabilities of JRC-JCS Model in Engineering Practice. In Proceedings of the Regional Conference of the International Society for Rock Mechanics, Loen, Norway, 4–6 June 1990; Barton, N., Stephansson, O., Eds.; CRC Press: Boca Raton, FL, USA, 1990; pp. 603–610. [Google Scholar]
- Mazzanti, P.; Schilirò, L.; Martino, S.; Antonielli, B.; Brizi, E.; Brunetti, A.; Margottini, C.; Scarascia Mugnozza, G. The Contribution of Terrestrial Laser Scanning to the Analysis of Cliff Slope Stability in Sugano (Central Italy). Remote Sens. 2018, 10, 1475. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.; Xu, Q.; Peng, D.; Zhu, Z.; Li, W.; Wong, H.; Shen, P. Stability analysis of rock wedge slide subjected to groundwater dynamic evolution. Eng. Geol. 2020, 270, 105528. [Google Scholar] [CrossRef]
- He, K.; Li, Y.; Ma, G.; Hu, X.; Liu, B.; Ma, Z.; Xu, Z. Failure mode analysis of post-seismic rockfall in shattered mountains exemplified by detailed investigation and numerical modelling. Landslides 2021, 18, 425–446. [Google Scholar] [CrossRef]
- Mateos, R.M.; Garcia-Moreno, I.; Azanon, J.M. Freeze-thaw cycles and rainfall as triggering factors of mass movements in a warm Mediterranean region: The case of the Tramuntana Range (Majorca, Spain). Landslides 2012, 9, 417–432. [Google Scholar] [CrossRef]
- Delonca, A.; Gunzburger, Y.; Verdel, T. Statistical correlation between meteorological and rockfall databases. Nat. Hazards Earth Syst. Sci. 2014, 14, 1953–1964. [Google Scholar] [CrossRef] [Green Version]
- D’Amato, J.; Hantz, D.; Guerin, A.; Jaboyedoff, M.; Baillet, L.; Mariscal, A. Influence of meteorological factors on rockfall occurrence in a middle mountain limestone cliff. Nat. Hazards Earth Syst. Sci. 2016, 16, 719–735. [Google Scholar] [CrossRef] [Green Version]
- Jibson, R.W.; Jibson, M.W. Java Programs for Using Newmark’s Method and Simplified Decoupled Analysis to Model Slope Performance During Earthquakes, version 1.1; U.S. Geological Survey: Reston, VA, USA, 2003. [Google Scholar]
- Stucchi, M.; Meletti, C.; Montaldo, V.; Crowley, H.; Calvi, G.M.; Boschi, E. Seismic Hazard Assessment (2003-2009) for the Italian Building Code. Bull. Seismol. Soc. Am. 2011, 101, 1885–1911. [Google Scholar] [CrossRef]
- Iervolino, I.; Galasso, C.; Cosenza, E. REXEL: Computer aided record selection for code-based seismic structural analysis. Bull. Earthq. Eng. 2009, 8, 339–362. [Google Scholar] [CrossRef]
- CEN-Comité Européen de Normalisaton; 2004: Eurocode 8-EN 1998-1; General Rules, Seismic Actions and Rules for Buildings; European Committee for Standardization: Bruxelles, Belgium, 2004.



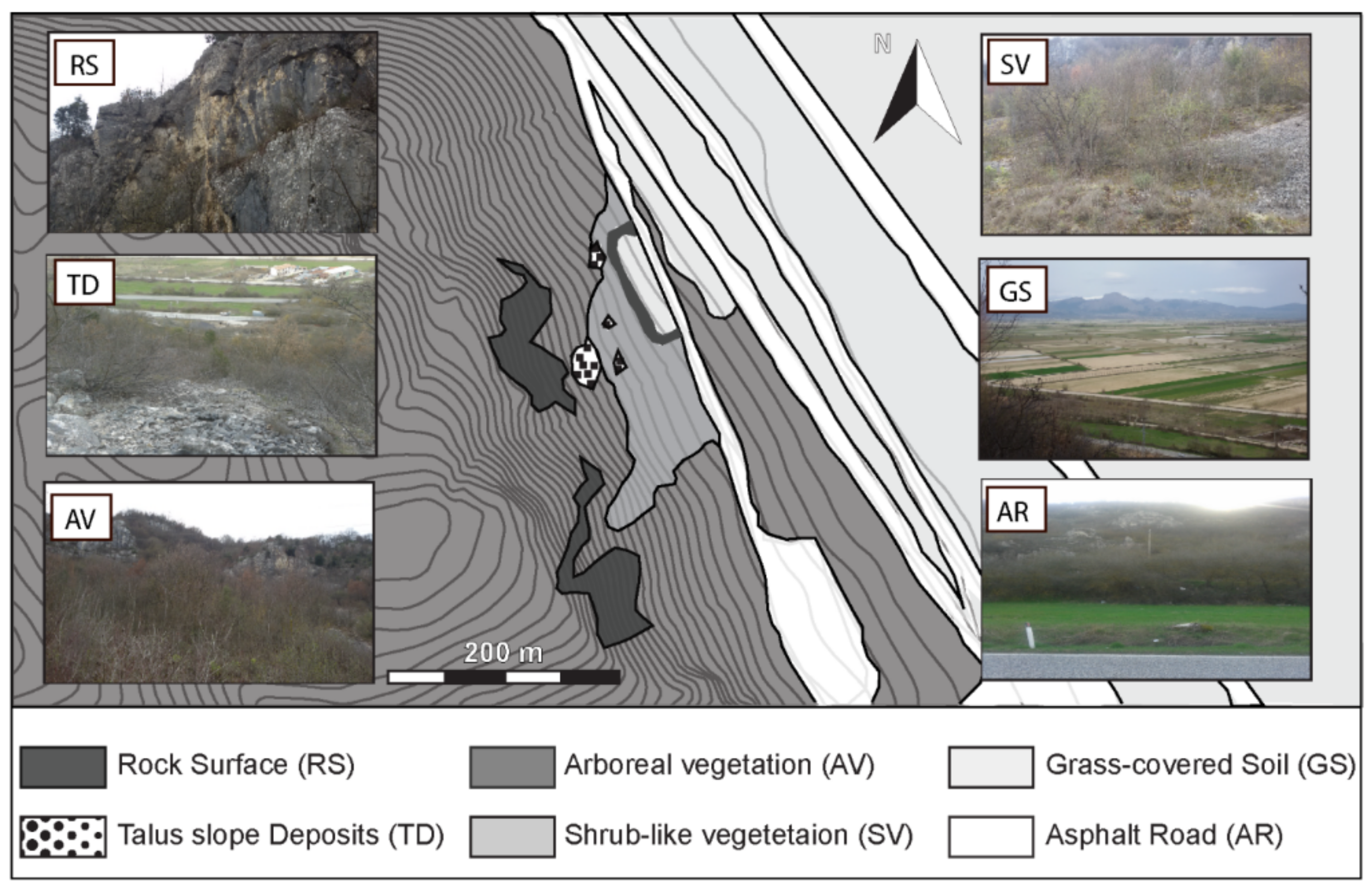




| RS | TD | AV | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Kn | Kt | φμd | Kn | Kt | φμd | Kn | Kt | φμd | |
| [38] | 0.75–0.80 (k) | ||||||||
| [55] | 0.65–0.75 | 0.8–0.9 | 0.45–0.65 | 0.5–0.86 | 0.65 | ||||
| [56] | 0.32 | 0.8 | 0.65 | ||||||
| [57] | 0.8 | 0.8 | |||||||
| [47] | 0.30–0.33 | 0.8–0.83 | |||||||
| [40] | 0.3–0.33 | 0.83–0.87 | |||||||
| [58] | 0.3 | 0.25 | |||||||
| [42] | 0.2 | 0.53 | |||||||
| [44] | 0.51–0.92 (k) | 0.32–0.65(k) | |||||||
| [45] | 0.75–0.90 (k) | 0.40–0.45 | 0.55–0.70 (k) | 0.65–0.80 | |||||
| [43] | 0,3 | 0,61 | |||||||
| [54] | 0.4–0.6 | 0.65–0.9 | |||||||
| [35] | 0.35 | 0.7 | 0.6 | 0.35 | 0.65 | 0.55 | |||
| [50] | 0.65 | 0.8 | 0.3 | 0.35 | 0.55 | 0.7 | |||
| [51] | 0.65 ± 0.0175 | 0.75 ± 0.0275 | 0.25 ± 0.01 | 0.35 ± 0.0175 | 0.55 ± 0.0275 | 0.65 ± 0.03 | |||
| [24] | 0.6 | 0.8 | 0.2 | 0.4 | 0.63–1.4 | 0.65 | 0.2 | 0.4 | 0.7 |
| min/max aver. | 0.594–0.765 | 0.714–0.737 | 0.287–0.24 | 0.362–0.397 | 0.604–0.655 | 0.65–0.582 | 0.275–0.282 | 0.616–0.626 | 0.625 |
| aver. | 0.6795 | 0.7255 | 0.527 | 0.3795 | 0.6295 | 0.616 | 0.278 | 0.621 | 0.625 |
| SV | GS | AR | |||||||
| Kn | Kt | φμd | Kn | Kt | φμd | Kn | Kt | φμd | |
| [38]. | |||||||||
| [55] | 0.2–0.3 | 0.2–0.4 | |||||||
| [56] | 0.3 | 0.8 | 0.4 | 0.9 | 0.45 | ||||
| [57] | |||||||||
| [47] | 0.30–0.33 | 0.83–0.87 | 0.28–0.32 | 0.68–0.72 | 0.37–0.42 | 0.87–0.92 | |||
| [40] | 0.82–0.85 | 0.28–0.33 | 0.37–0.42 | 0.87–0.92 | |||||
| [58] | |||||||||
| [42] | |||||||||
| [44] | |||||||||
| [45] | 0.50–0.60 (k) | 0.45–0.65 | 0.75(k) | 0.40–0.45 | |||||
| [43] | |||||||||
| [54] | |||||||||
| [35] | 0.33 | 0.75 | 0.5 | 0.3 | 0.7 | 0.6 | 0.45 | 0.7 | 0.6 |
| [50] | 0.15 | 0.2 | 0.85 | ||||||
| [51] | 0.15 ± 0.025 | 0.3 ± 0.015 | 0.8 ± 0.04 | ||||||
| [24] | 0.4 | 0.5 | 0.3 | 0.4 | 0.9 | 0.2 | |||
| min/max averages | 0.315–0.33 | 0.8–0.823 | 0.5 | 0.284–0.302 | 0.485–0.491 | 0.6–0.488 | 0.456–0.473 | 0.831–0.848 | 0.413–0.425 |
| averaged | 0.3225 | 0.8115 | 0.5 | 0.293 | 0.488 | 0.544 | 0.4645 | 0.8395 | 0.419 |
| (Averaged Values in Table 1) | Kn | Kt | φμd |
|---|---|---|---|
| RS | 0.6795 | 0.7255 | 0.527 |
| TD | 0.3795 | 0.6295 | 0.616 |
| AV | 0.278 | 0.621 | 0.625 |
| SV | 0.3225 | 0.8115 | 0.5 |
| GS | 0.293 | 0.488 | 0.544 |
| AR | 0.4645 | 0.8395 | 0.419 |
| (values after calibration) | Kn | Kt | φμd |
| RS | 0.6 | 0.7 | 0.45 |
| TD | 0.3 | 0.3 | 0.5 |
| AV | 0.3 | 0.3 | 0.5 |
| SV | 0.5 | 0.6 | 0.8 |
| GS | 0.4 | 0.8 | 0.5 |
| AR | 0.35 | 0.75 | 0.6 |
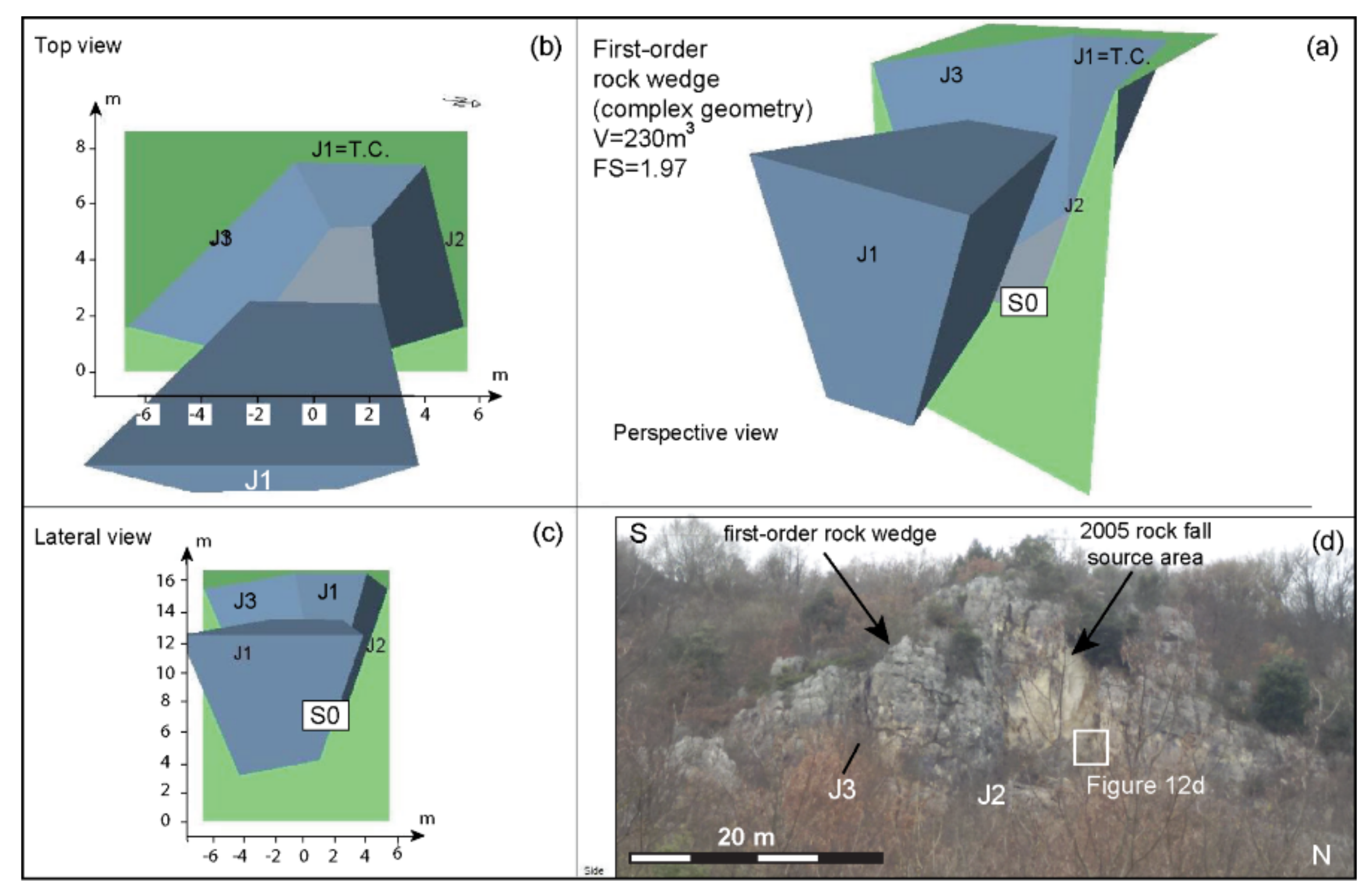
| S_1 | Joint set J1 = TC—Main Plane: 84°;75° | Joint set J2—Main Plane: 170°;77° |
| R | 48,53,52,54,50,36,46,40,42,36,38,49,48,41 | 38,32,48,32,38,44,32,42,44,48,48,42,48 |
| R | 54,51,48,55,46,50,58,50,48,56,52,44, 48,50 | 53,58,44,52,56,40,48,42,56,42,44,50,52 |
| Φr | (35–20) + 20(45.25/50.67)=32.86 | (35–20) + 20(41.45/48.81)=31.98 |
| JRC | 8 | 10 |
| JCS | 80MPa | 80MPa |
| S_1 | Joint set J3—Main Plane: 40°;75° | S0 = 92°;31° |
| R | 44,32,48,38,46,44,34,40,48,42,32,38,44,40 | 32,44,34,32,44,48,36,32,40 |
| R | 48,54,58,46,54,46,44,44,56,58,46,48,50 | 44,50,48,50,44,46,52,48,44 |
| Φr | (35–20) + 20(40.83/50.251) = 31.25 | (35–20) + 20(38.00/47.33) = 31.05 |
| JRC | 10 | 8 |
| JCS | 80 MPa | 80 MPa |
| Potentially Unstable Wedges on Es1, Es2 | Second-Order | Second-Order | First-Order | |
|---|---|---|---|---|
| Volume (m3) | 5 | 2.5 | 230 | |
| Design block (Db) | Db1 | Db2 | Db1 | |
| Design block volume (m3) adopted | 5 | 0.66 + 1.82 = 2.48 | 5 | |
| Fragmentation to 0.25 m3 | 95% | 90.1% | Frag. from 230 to 5 m3 | 97.8% |
| Design block mass (kg) | 12,500 | 6200 | 12,500 | |
| Design block weight (N) | 122,625 | 60,822 | 122,625 | |
| Barriers | ||||
| Specific kinetic energy (m²/s²) | 200 | 200 | 200 | |
| Impact energy (kJ) | 2500 | 1240 | 2500 | |
| Energy absorption capacity (kJ) | 3000 | 2000 | 3000 | |
| Height (m) | 4 | 4 | 4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di Luzio, E.; Schilirò, L.; Gaudiosi, I. Cultural Heritage and Rockfalls: Analysis of Multi-Scale Processes Nearby the Lucus Angitiae Archaeological Site (Central Italy). Geosciences 2021, 11, 521. https://doi.org/10.3390/geosciences11120521
Di Luzio E, Schilirò L, Gaudiosi I. Cultural Heritage and Rockfalls: Analysis of Multi-Scale Processes Nearby the Lucus Angitiae Archaeological Site (Central Italy). Geosciences. 2021; 11(12):521. https://doi.org/10.3390/geosciences11120521
Chicago/Turabian StyleDi Luzio, Emiliano, Luca Schilirò, and Iolanda Gaudiosi. 2021. "Cultural Heritage and Rockfalls: Analysis of Multi-Scale Processes Nearby the Lucus Angitiae Archaeological Site (Central Italy)" Geosciences 11, no. 12: 521. https://doi.org/10.3390/geosciences11120521
APA StyleDi Luzio, E., Schilirò, L., & Gaudiosi, I. (2021). Cultural Heritage and Rockfalls: Analysis of Multi-Scale Processes Nearby the Lucus Angitiae Archaeological Site (Central Italy). Geosciences, 11(12), 521. https://doi.org/10.3390/geosciences11120521






