Modelling of Coupled Hydro-Thermo-Chemical Fluid Flow through Rock Fracture Networks and Its Applications
Abstract
1. Introduction
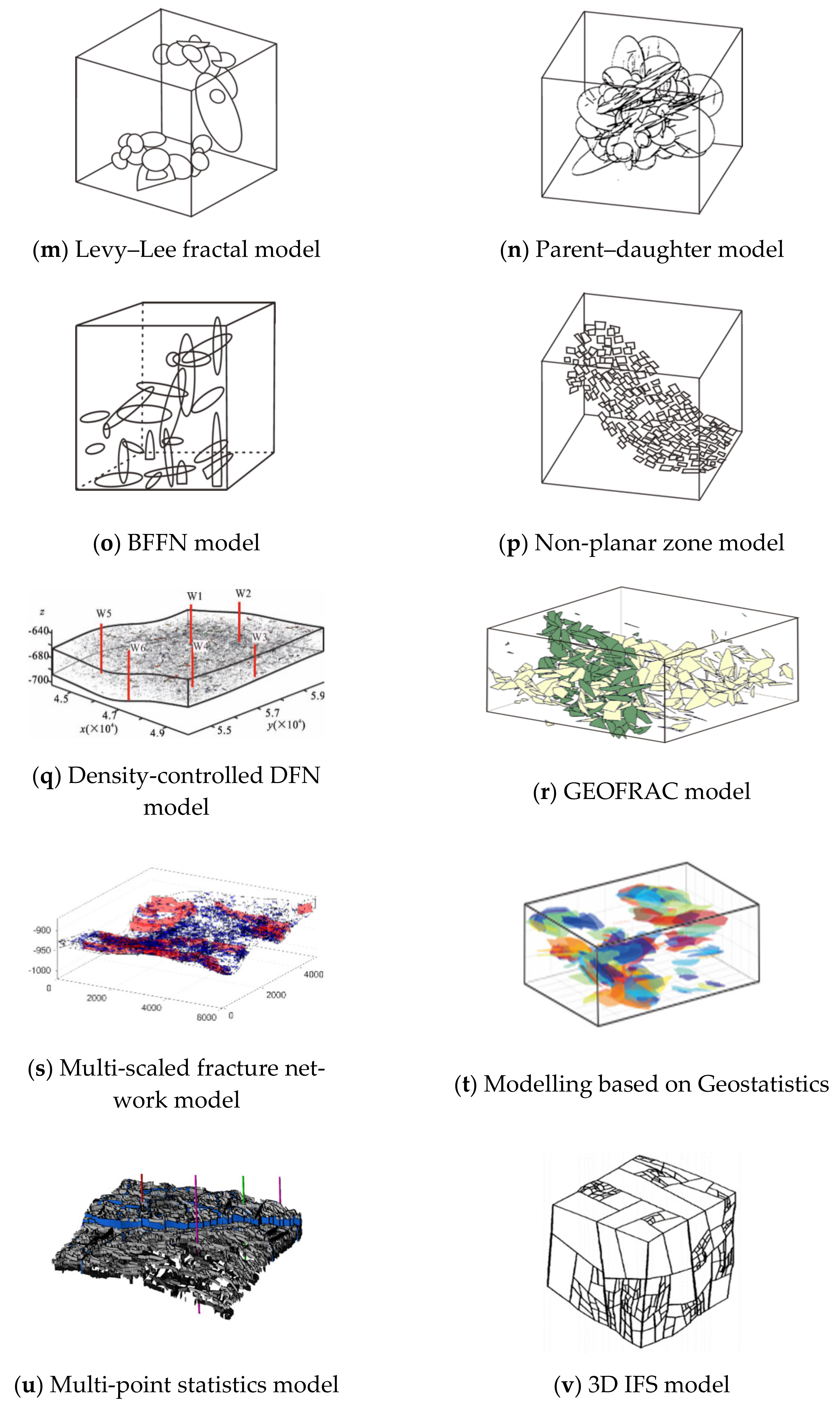
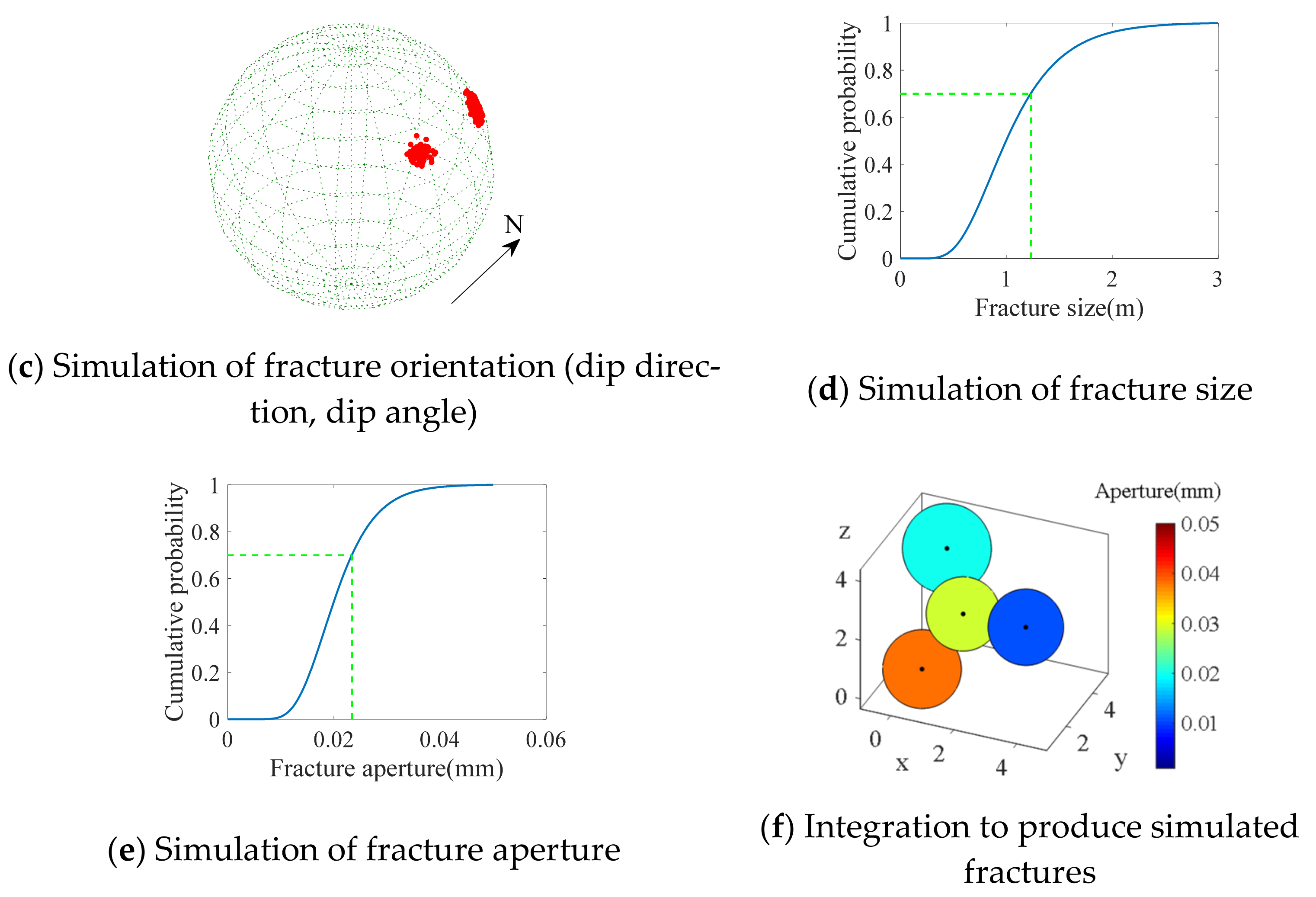
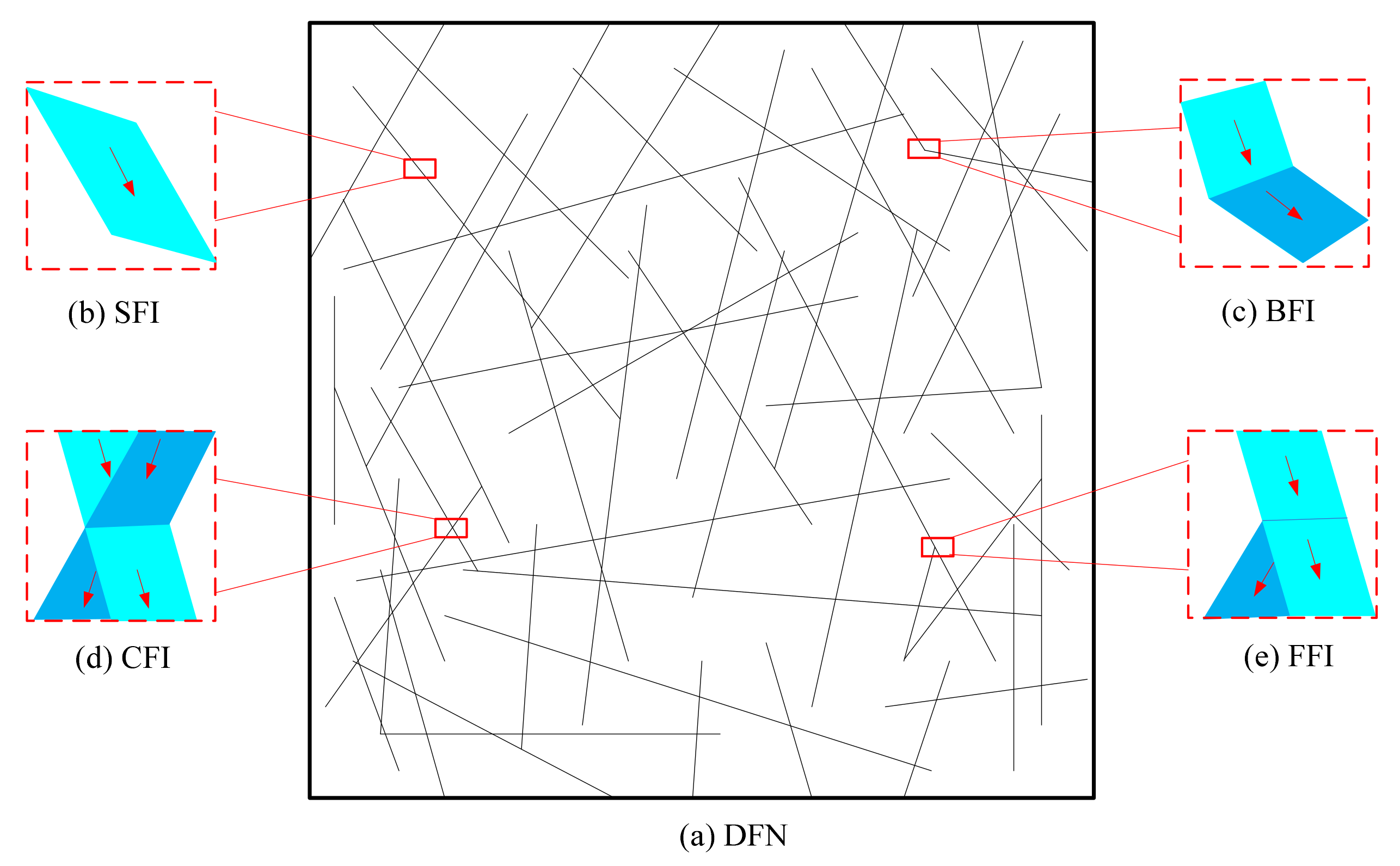
2. Modelling of Fracture Networks in Rock Masses
3. Modelling Fluid Flow through DFNs
3.1. Using COMSOL and FracSim3D to Model Fluid Flow through DFNs
3.2. Fluid Flow Modelling in a Single Fracture Considering Roughness, Void Structure, and Inertia Effects
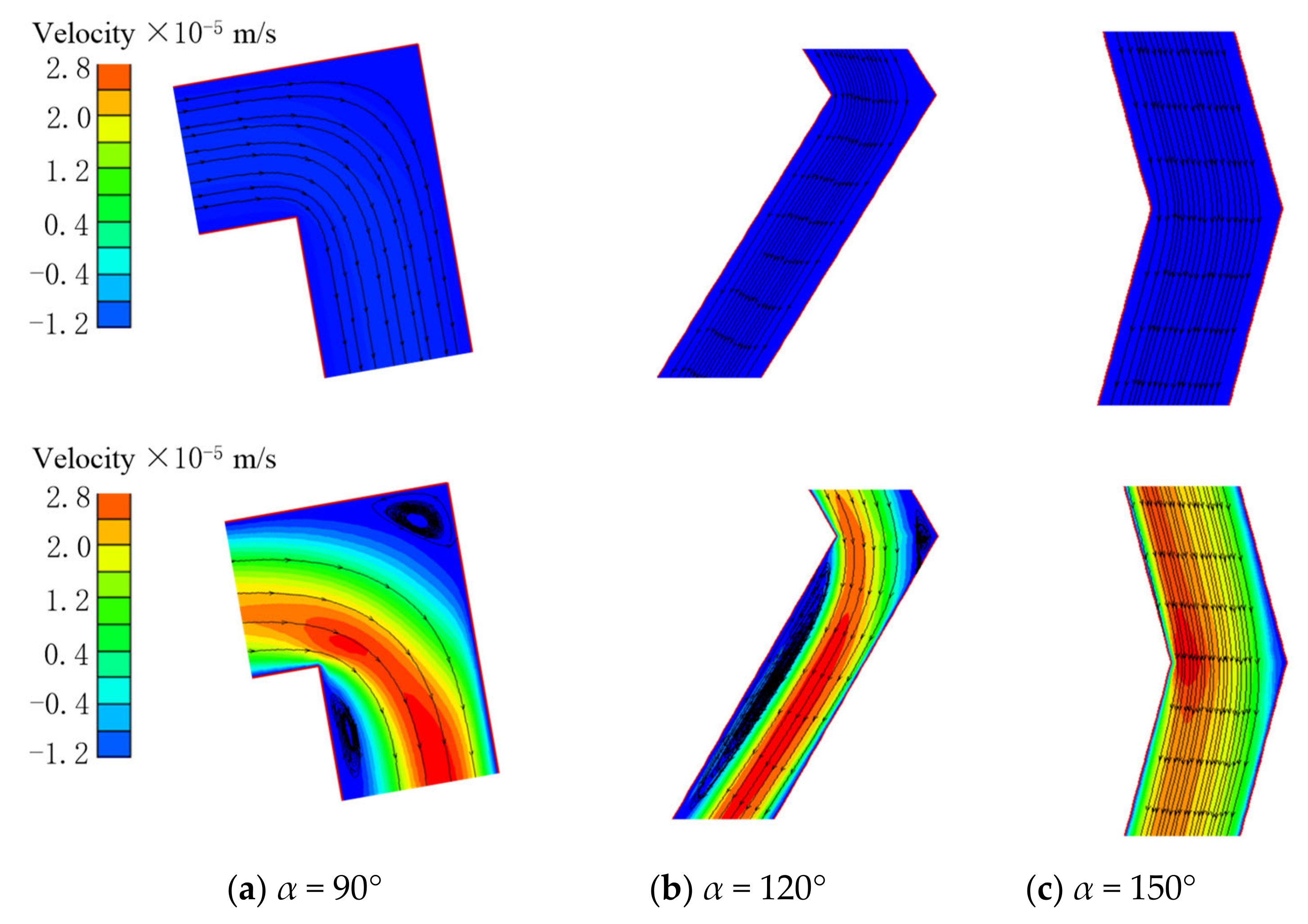
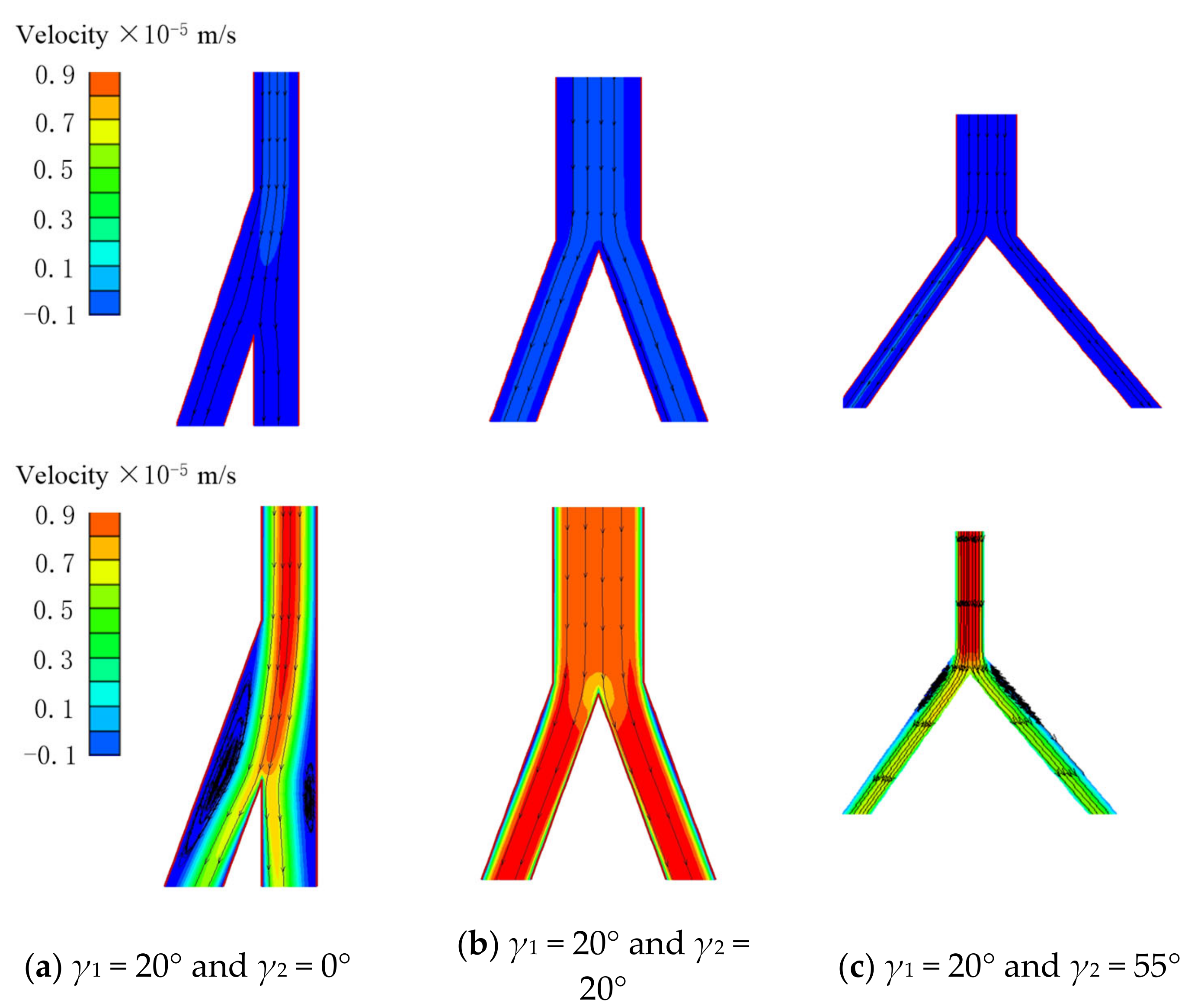
3.3. Non-Linear Fluid Flow Modelling in Fracture Intersections
3.4. Non-Linear Fluid Flow Modelling in DFNs
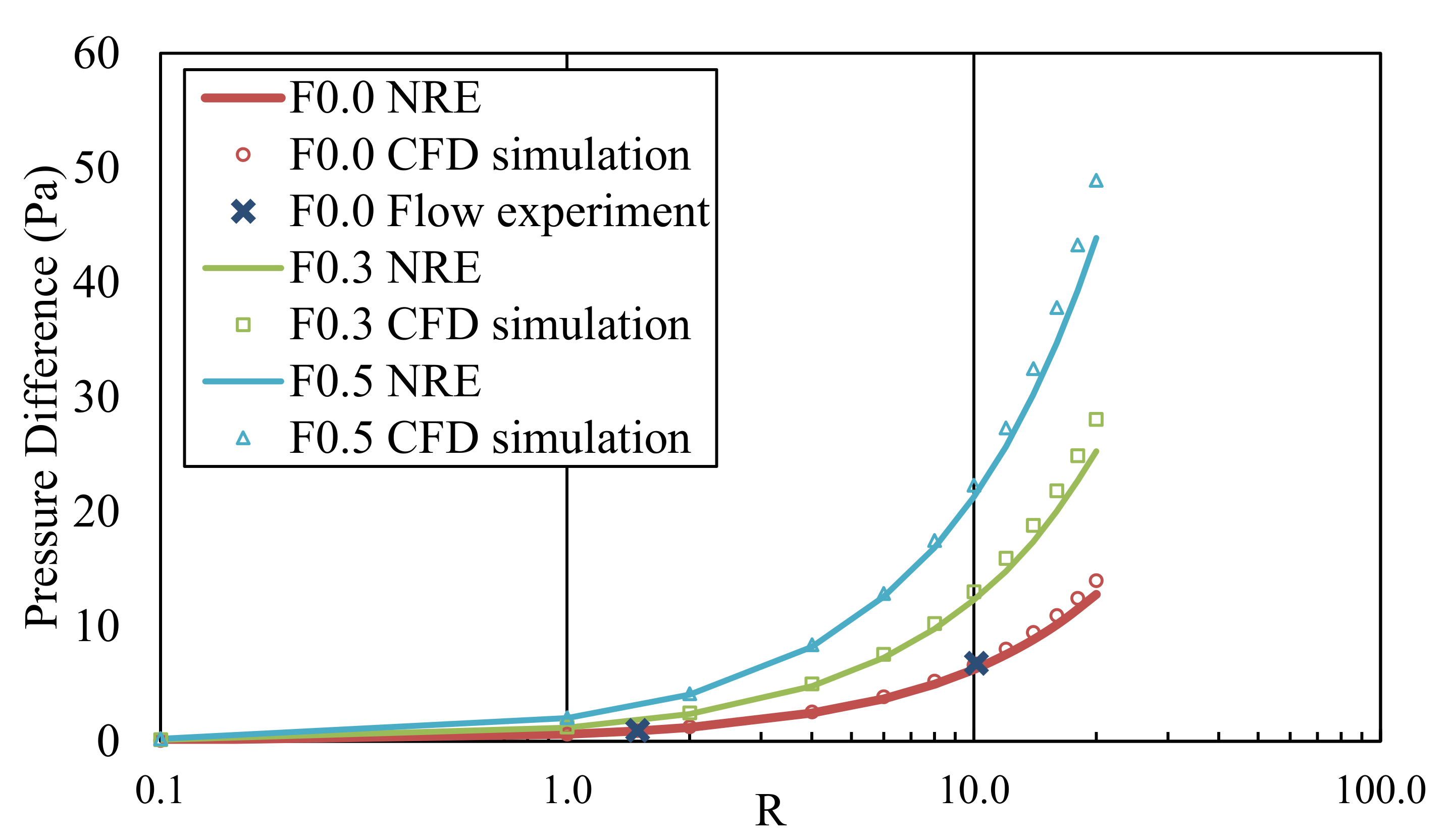
3.5. Experimental Studies of Non-Linear Fluid Flow through DFNs
4. Examples of Applications
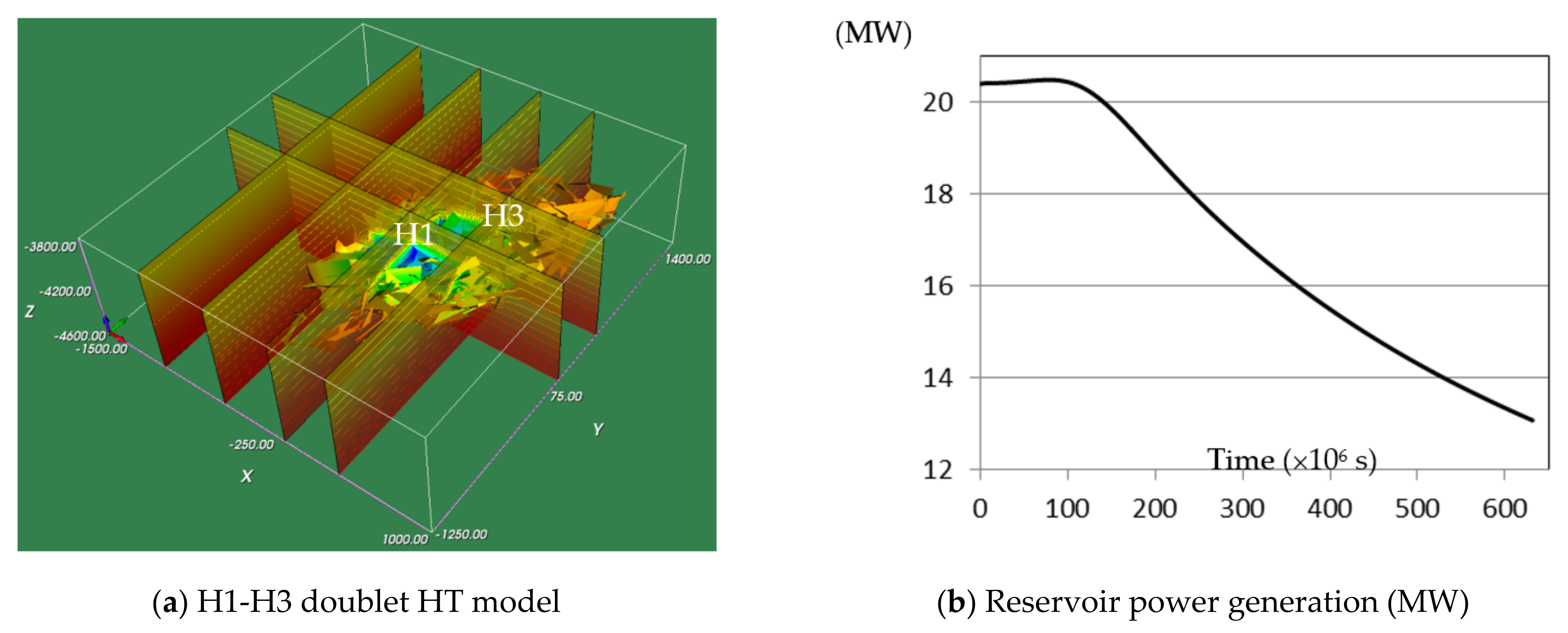
4.1. Habanero Geothermal Project
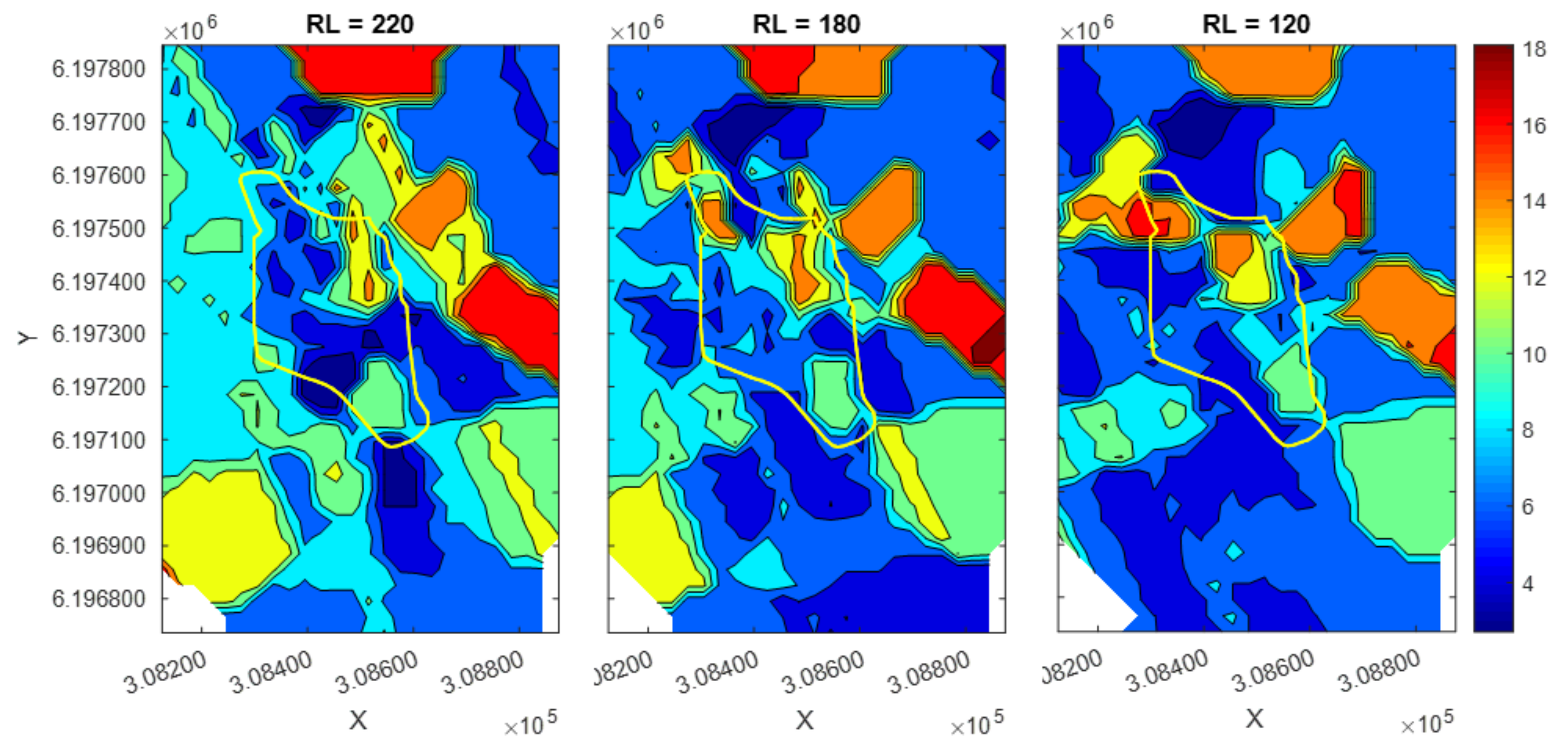
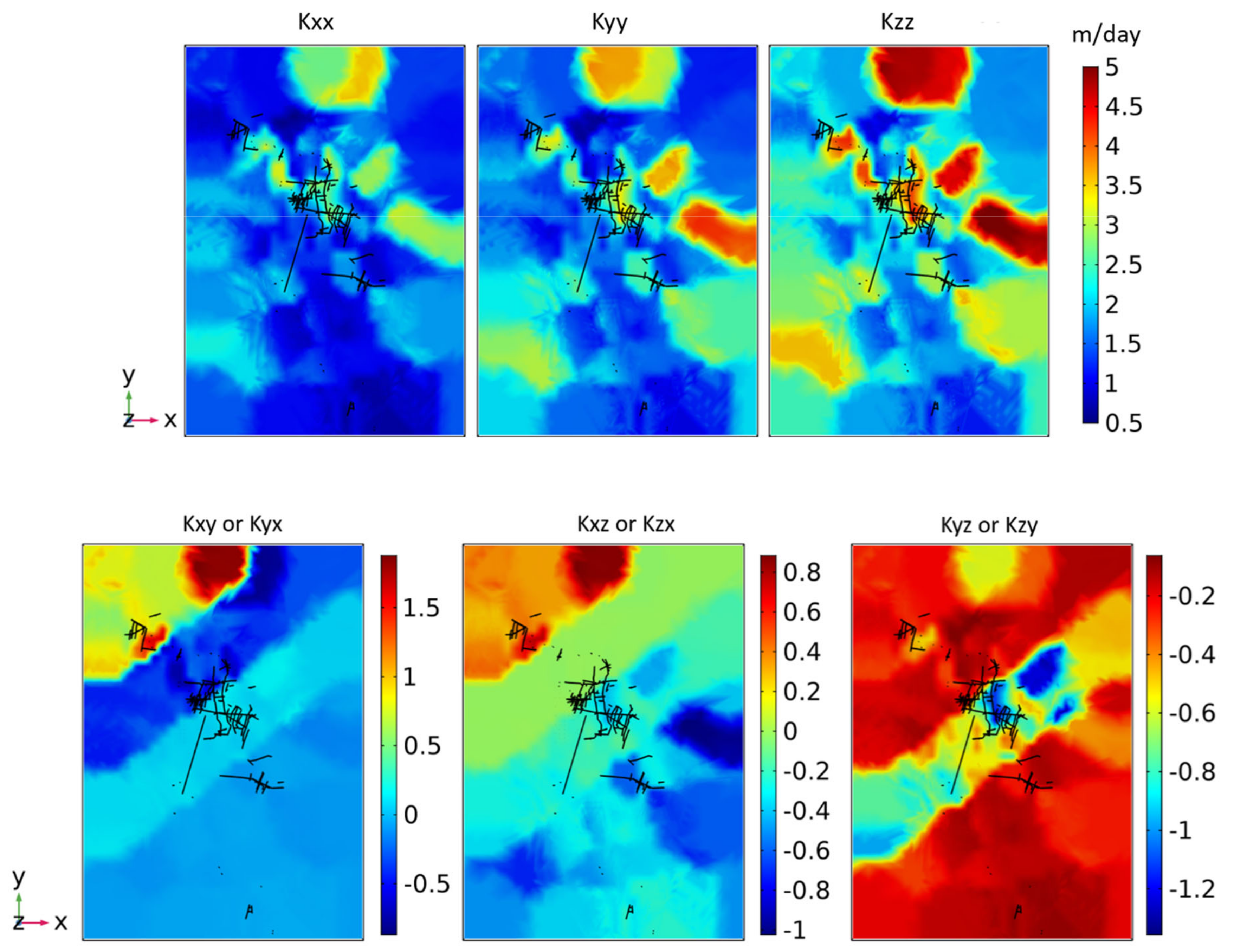
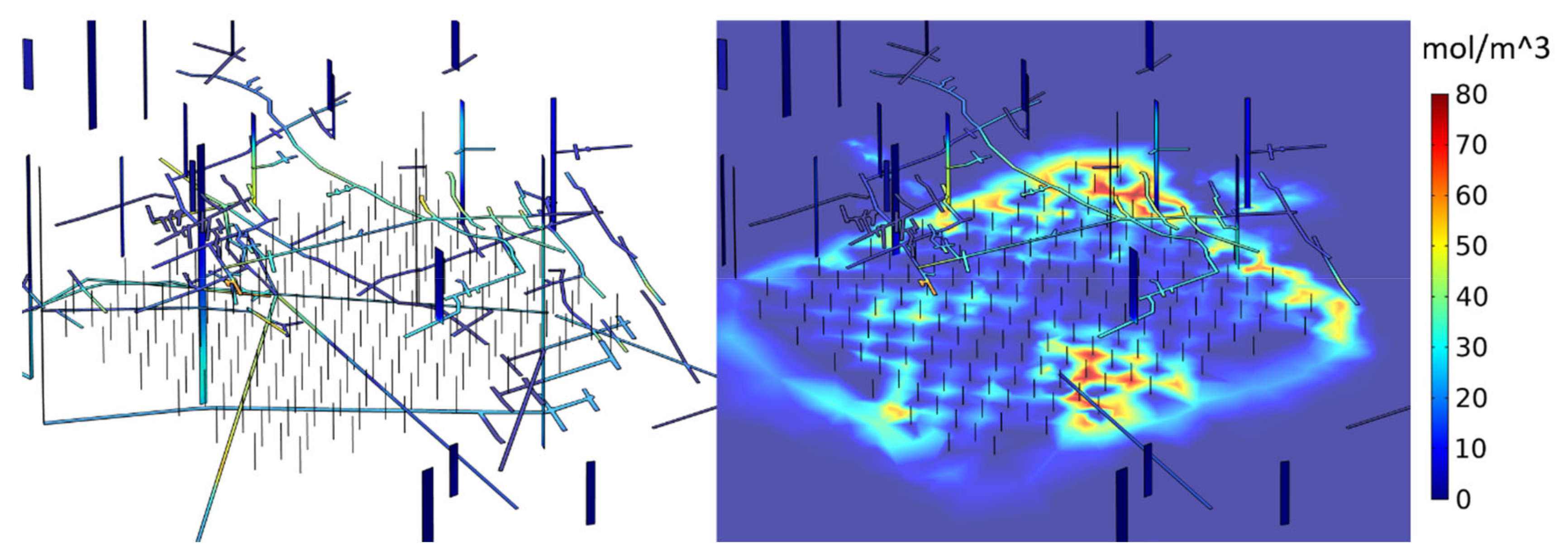
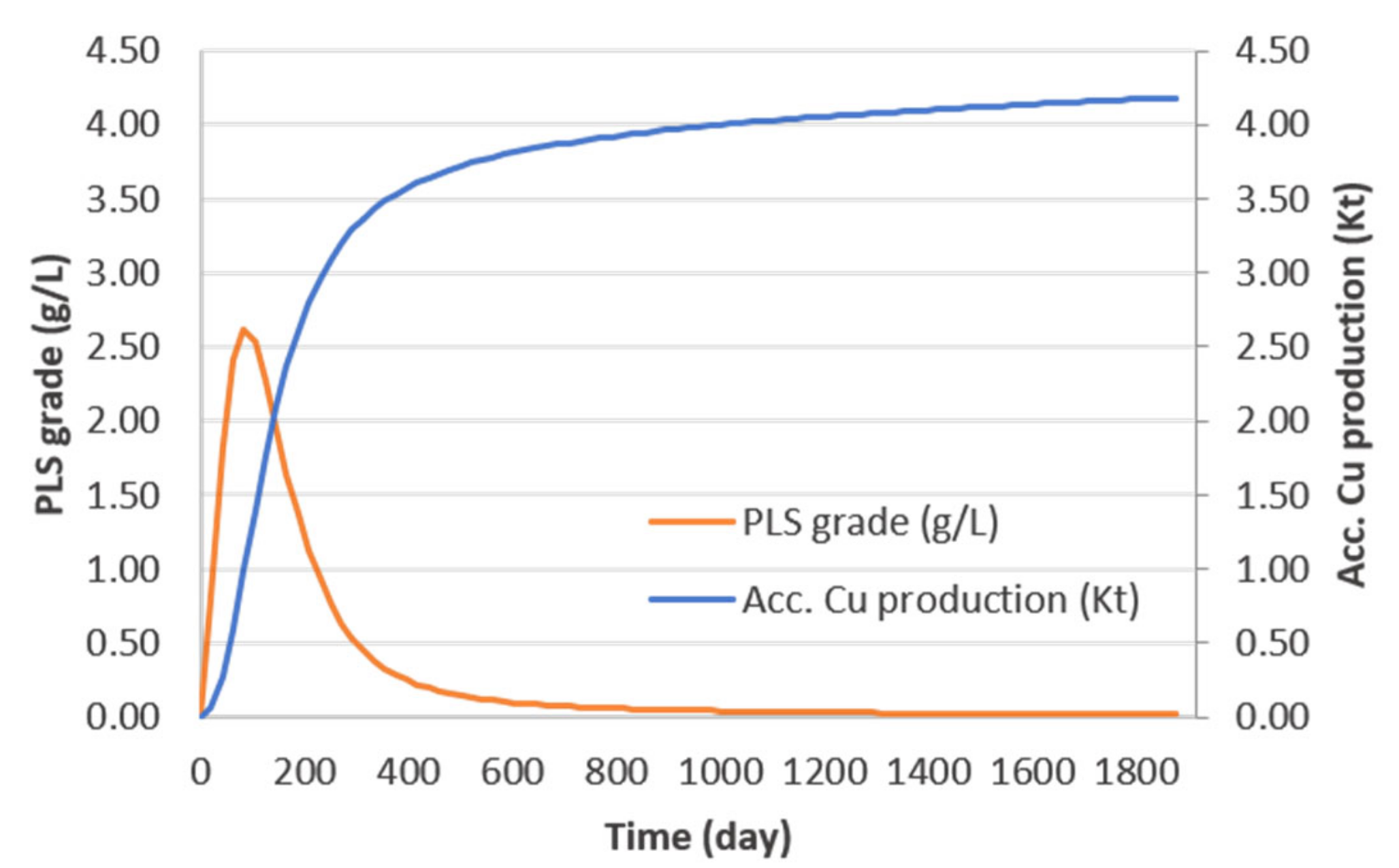
4.2. In-Situ Recovery of Copper Minerals in Kapunda Mine
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jing, L.; Stephansson, O. Fundamentals of Discrete Element Methods for Rock Engineering, Theory and Applications; Elsevier: Amsterdam, The Netherlands, 2007; ISBN 978-0-444-92937-5. [Google Scholar]
- Wang, Z.; Xu, C.; Dowd, P.A. Perturbation solutions for flow in a slowly varying fracture and the estimation of its transmissivity. Transp. Porous Media 2019, 128, 97–121. [Google Scholar] [CrossRef]
- Zimmerman, R.; Yeo, I. Fluid flow in rockfractures: From the Navier-Stokes equations to the Cubic Law. Dyn. Fluids Fract. Rock 2000, 122, 213–224. [Google Scholar] [CrossRef]
- Xiong, F.; Jiang, Q.; Xu, C.; Zhang, X.; Zhang, Q. Influences of connectivity and conductivity on nonlinear flow behaviours through three-dimension discrete fracture networks. Comput. Geotech. 2019, 107, 128–141. [Google Scholar] [CrossRef]
- Xiong, F.; Wei, W.; Xu, C.; Jiang, Q. Experimental and numerical investigation on nonlinear flow behaviour through three-dimensional fracture intersections and fracture networks. Comput. Geotech. 2020, 121. [Google Scholar] [CrossRef]
- Wang, Z.; Xu, C.; Dowd, P.A. A Modified Cubic Law for single-phase saturated laminar flow in rough rock fractures. Int. J. Rock Mech. Min. Sci. 2018, 103, 107–115. [Google Scholar] [CrossRef]
- Wang, Z.; Xu, C.; Dowd, P.A.; Wang, H.; Xiong, F. A non-linear version of the Reynolds equation for flow in rock fractures with complex void geometries. Water Resour. Res. 2020, 56, e2019WR026149. [Google Scholar] [CrossRef]
- Basha, H.A.; El-Asmar, W. The fracture flow equation and its perturbation solution. Water Resour. Res. 2003, 39, 1365. [Google Scholar] [CrossRef]
- Berkowitz, B. Characterizing flow and transport in fractured geological media: A review. Adv. Water Resour. 2002, 25, 861–884. [Google Scholar] [CrossRef]
- Oda, M. Permeability tensor for discontinuous rock masses. Geotechnique 1985, 35, 483–495. [Google Scholar] [CrossRef]
- Pruess, K.; Narasimhan, T. Practical method for modelling fluid &heat flow in porous media. Soc. Pet. Eng. J. 1985, 25, 14–26. [Google Scholar]
- Tsang, Y.W.; Tsang, C.F.; Hale, F.V.; Dverstorp, B. Tracer transport in a stochastic continuum model of fractured media. Water Resour. Res. 1996, 32, 3077–3092. [Google Scholar] [CrossRef]
- Lough, M.F.; Lee, S.H.; Kamath, J. An efficient boundary integral formulation for flow through fractured porous media. J. Comp. Phys. 1998, 143, 462–483. [Google Scholar] [CrossRef]
- Lee, S.; Lough, M.; Jensen, C. Hierarchical modelling of flow in naturally fractured formations. Water Resour. Res. 2001, 37, 443–455. [Google Scholar] [CrossRef]
- Min, K.B.; Jing, L.; Stephansson, O. Determining the equivalent permeability tensor for fractured rockmasses using a stochastic REV approach: Method and applicationto the field data from Sellafield, UK. Hydrogeol. J. 2004, 12, 497–510. [Google Scholar] [CrossRef]
- Dershowitz, W.S.; Fidelibus, C. Derivation of equivalent pipe network analogues for three-dimensional discrete fracture networks by boundary element method. Water Resour. Res. 1999, 35, 2685–2691. [Google Scholar] [CrossRef]
- Xu, C.; Fidelibus, C.; Dowd, P.A. Realistic Pipe Models for Flow Modelling in Discrete Fracture Networks. First International Discrete Fracture Network Engineering Conference, Vancouver, BC, Canada, 19–23 October 2014; Volume DFNE2014–132. [Google Scholar]
- Xu, C.; Fidelibus, C.; Dowd, P.; Wang, Z.; Tian, Z. An iterative procedure for the simulation of the steady-state fluid flow in rock fracture networks. Eng. Geol. 2018, 242, 160–168. [Google Scholar] [CrossRef]
- Xiong, F.; Jiang, Q.; Xu, C. Fast equivalent Micro-scale pipe network representation of rock fractures obtained by computed tomography for fluid flow simulations. Rock Mech. Rock Eng. 2021, 54, 937–953. [Google Scholar] [CrossRef]
- Dowd, P.A.; Martin, J.; Mardia, K.V.; Fowell, R.J.; Xu, C. A three-dimensional fracture network dataset for a block of granite. Int. J. Rock Mech. Min. Sci. 2009, 46, 811–818. [Google Scholar] [CrossRef]
- Xu, C.; Dowd, P.A. A new computer code for discrete fracture network modelling. Comput. Geosci. 2010, 36, 292–301. [Google Scholar] [CrossRef]
- Priest, S.D.; Hudson, J.A. Estimation of discontinuity spacing and trace length using scanline surveys. Int. J. Rock Mech. Min. Sci. 1981, 18, 181–197. [Google Scholar] [CrossRef]
- Song, J.-J.; Lee, C.-I. Estimation of joint length distribution using window sampling. Int. J. Rock Mech. Min. Sci. 2001, 38, 519–528. [Google Scholar] [CrossRef]
- Priest, S.D. Determination of discontinuity size distributions from scanline data. Rock Mech. Rock Eng. 2004, 37, 347–368. [Google Scholar] [CrossRef]
- Xu, C.; Dowd, P.A.; Nguyen, N. Non-parametric three-dimensional fracture modelling from fracture mapping data. Bol. Geol. Min. 2021, in press. [Google Scholar]
- Laslett, G.M. Censoring and edge effects in areal and line transect sampling of rock joint traces. Math. Geol. 1982, 14, 125–140. [Google Scholar] [CrossRef]
- Villaescusa, E.; Brown, E.T. Maximum likelihood estimation of joint size from trace length measurements. Rock Mech. Rock Eng. 1992, 25, 67–87. [Google Scholar] [CrossRef]
- Xu, C.; Dowd, P.A.; Wyborn, D. Optimisation of a Stochastic Rock Fracture Model Using Markov Chain Monte Carlo Simulation. Min. Technol. 2013, 122, 153–158. [Google Scholar] [CrossRef]
- Xu, C.; Dowd, P.A. Stochastic fracture propagation modelling for enhanced geothermal systems. Math. Geosci. 2014, 46, 665–690. [Google Scholar] [CrossRef]
- Guardiano, F.; Srivastava, R.M. Multivariate geostatistics: Beyond bivariate moments. In Geostatistics Troia 1; Soares, A., Ed.; Kluwer Academic: Dordrecht, The Netherlands, 1993; pp. 133–144. [Google Scholar]
- Dowd, P.A.; Xu, C.; Mardia, K.V.; Fowell, R.J. A comparison of methods for the simulation of rock fractures. Math. Geol. 2007, 39, 697–714. [Google Scholar] [CrossRef]
- Baecher, G.B. Statistical analysis of rock mass fracturing. Math. Geol. 1983, 15, 329–348. [Google Scholar] [CrossRef]
- Dershowitz, W.S. Rock Joint Systems. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1984. [Google Scholar]
- Ivanova, V.M. Three-Dimensional Schochastic Modelling of Rock Fracture Systems. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1995. [Google Scholar]
- Billaux, D.; Chiles, J.P.; Hestir, K.; Long, J. Three-dimensional statistical modelling of a fractured rock mass—An example from the Fanay-Augères mine. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1989, 26, 281–299. [Google Scholar] [CrossRef]
- Dong, S.; Zeng, L.; Cao, H.; Xu, C.; Wang, S. Principle and implementation of discrete fracture network modelling controlled by fracture density. Geol. Rev. 2018, 64, 1302–1314. [Google Scholar]
- Zeng, L.; Li, X. Fractures in sandstone reservoirs of ultra-low permeability: A case study of the Upper Triassic Yanchang Formation in the Ordos Basin, China. Aapg Bull. 2009, 93, 461–477. [Google Scholar]
- Dong, S.; Zeng, L.; Xu, C.; Cao, H.; Wang, S.; Lyu, W. Some progress in reservoir fracture stochastic modeling research. Oil Geophys. Prospect. 2018, 53, 625–641. [Google Scholar]
- Dong, S.; Zeng, L.; Dowd, P.A.; Xu, C.; Cao, H. A fast method for fracture intersection detection in discrete fracture networks. Comput. Geotech. 2018, 98, 205–216. [Google Scholar] [CrossRef]
- Dong, S.; Zeng, L.; Xia, D.; Lyu, W.; Wu, Y.; Guan, C. Three dimensional geological method for modelling multi-scale fractures in tight sandstone reservoir. Oil Gas Geol. 2019, 40, 101–109. [Google Scholar]
- Dershowitz, W.S.; Einstein, H.H. Characterizing rock joint geometry with joint system models. Rock Mech. Rock Eng. 1988, 21, 21–51. [Google Scholar] [CrossRef]
- Meng, Q.; Yan, L.; Chen, Y.; Zhang, Q. Generation of numerical models of anisotropic columnar jointed rock mass using modified centroidal Voronoi diagrams. Symmetry 2020, 10, 618. [Google Scholar] [CrossRef]
- Ivanova, V.M.; Sousa, R.; Murrihy, B.; Einstein, H.H. Mathematical algorithm development and parametric studies with the GEOFRAC three-dimensional stochastic model of natural rock fracture systems. Comput. Geosci. 2014, 67, 100–109. [Google Scholar] [CrossRef]
- Ghazvinian, E.; Diederichs, M.S.; Quey, R. 3D random Voronoi grain-based models for simulation of brittle rock damage and fabric-guided micro-fracturing. J. Rock Mech. Geotech. Eng. 2014, 6, 506–521. [Google Scholar] [CrossRef]
- Xu, C.; Dowd, P.A.; Wyborn, D.; Mohais, R. Connectivity Analysis of the Habanero Enhanced Geothermal System. In Proceedings of the 2012 Stanford Geothermal Workshop, Stanford, CA, USA, 30 January–1 February 2012. [Google Scholar]
- Alghalandis, Y.F. ADFNE: Open source software for discrete fracture network engineering, two and three dimensional applications. Comput. Geosci. 2017, 102, 1–11. [Google Scholar] [CrossRef]
- Acuna, J.A.; Yortsos, Y.C. Application of fractal geometry to the study of networks of fractures and their pressure transient. Water Resour. Res. 1995, 31, 527–540. [Google Scholar] [CrossRef]
- Wang, W.; Su, Y.; Yuan, B.; Wang, K.; Cao, X. Numerical simulation of fluid flow through fractal-based discrete fractured network. Energies 2018, 11, 286. [Google Scholar] [CrossRef]
- Koike, K.; Liu, C.; Sanga, T. Incorporation of fracture directions into 3D geostatistical methods for a rock fracture system. Environ. Earth Sci. 2012, 66, 1403–1414. [Google Scholar] [CrossRef]
- Baecher, G.B.; Lanney, N.A.; Einstein, H.H. Statistical description of rock properties and sampling. In Proceedings of the 18th U.S. Symposium on Rock Mechanics, Golden, CO, USA, 22–24 June 1977. [Google Scholar]
- Barton, C.M. Analysis of joint traces. In Proceedings of the 19th U.S. Symposium on Rock Mechanics, American Institute of Mining Engineers, Reno, NV, USA, 17–19 November 1978; pp. 39–40. [Google Scholar]
- Long, J.C.S.; Gilmour, P.; Witherspoon, P.A. A model for steady fluid flow in random three-dimensional networks of disc-shaped fractures. Water Resour. Res. 1985, 21, 1105–1115. [Google Scholar] [CrossRef]
- Andersson, J.; Shapiro, A.M.; Bear, J. A stochastic model of fractured rock conditioned by measured information. Water Resour. Res. 1984, 20, 79–88. [Google Scholar] [CrossRef]
- Alghalandis, Y.F. Stochastic Modelling of Fractures in Rock Masses. Ph.D. Thesis, University of Adelaide, Adelaide, SA, Australia, 2014. [Google Scholar]
- Masihi, M.; King, P. A correlated fracture network: Modelling and percolation properties. Water Resour. Res. 2007, 43, W07439. [Google Scholar] [CrossRef]
- Mahmoodpour, S.; Masihi, M. An improved simulated annealing algorithm in fracture network modelling. J. Nat. Gas Sci. Eng. 2016, 33, 538–550. [Google Scholar] [CrossRef]
- Xu, C.; Dowd, P.A.; Mardia, K.V.; Fowell, R.J.; Taylor, C.C. Simulating correlated marked point processes. J. Appl. Stat. 2007, 34, 1125–1134. [Google Scholar] [CrossRef]
- Lei, Q.; Latham, J.; Tsang, C. The use of discrete fracture networks for modelling coupled geomechanical and hydrological behaviour of fractured rocks. Comput. Geotech. 2017, 85, 151–176. [Google Scholar] [CrossRef]
- Chilès, J.P. Fractal and geostatistical methods for modelling of a fracture network. Math. Geol. 1988, 20, 631–654. [Google Scholar] [CrossRef]
- Nakaya, S.; Yoshida, T.; Shioiri, N. Percolation conditions in binary fractal fracture networks: Applications to rock fractures and active and seismogenic faults. J. Geophys. Res. Solid Earth 2003, 108, 1–13. [Google Scholar] [CrossRef]
- Nakaya, S.; Nakamura, K. Percolation conditions in fractured hard rocks: A numerical approach using the three-dimensional binary fractal fracture network (3D-BFFN) model. J. Geophys. Res. 2007, 112, 1–15. [Google Scholar] [CrossRef]
- Koike, K.; Kubo, T.; Liu, C.; Masoud, A.; Amano, K.; Kurihara, A.; Matsuoka, T.; Lanyon, B. 3D geostatistical modeling of fracture system in a granitic massif to characterize hydraulic properties and fracture distribution. Tectonophysics 2015, 660, 1–16. [Google Scholar] [CrossRef]
- Mohammadmoradi, P. Facies and fracture network modelling by a novel image processing based method. Geomaterials 2013, 3, 156–164. [Google Scholar] [CrossRef][Green Version]
- Jia, M.; Zhang, L.; Guo, J. Combining a connected-component labeling algorithm with FILTERSIM to simulate continuous discrete fracture networks. Environ. Earth Sci. 2017, 76, 327. [Google Scholar] [CrossRef]
- Liu, X.; Sanjay, S.; Dale, W. Geological Characterization of Naturally Fractured Reservoirs Using Multiple Point Geostatistics. In Proceedings of the SPE/DOE Improved Oil Recovery Symposium, Society of Petroleum Engineers, Tulsa, OK, USA, 3–5 April 2002. [Google Scholar]
- Chugunova, T.; Corpel, V.; Gomez, J.P. Explicit fracture network modelling: From multiple point statistics to dynamic simulation. Math. Geosci. 2017, 49, 541–553. [Google Scholar] [CrossRef]
- Seifollahi, S.; Dowd, P.A.; Xu, C.; Fadakar, A.A. spatial clustering approach for stochastic fracture network modelling. Rock Mech. Rock Eng. 2014, 47, 1225–1235. [Google Scholar] [CrossRef]
- Seifollahi, S.; Dowd, P.A.; Xu, C. An enhanced stochastic optimization in fracture network modelling conditional on seismic events. Comput. Geotech. 2014, 61, 85–95. [Google Scholar] [CrossRef][Green Version]
- Fadakar, A.Y.; Dowd, P.A.; Xu, C. The RANSAC method for generating fracture networks from micro-seismic event data. Math. Geosci. 2013, 45, 207–224. [Google Scholar] [CrossRef]
- Dershowitz, W. FracMan Version 7.4—Interactive Discrete Feature DataAnalysis, Geometric Modeling, and Exploration Simulation: User Documentation. 2014. Available online: https://www.golder.com/fracman/ (accessed on 12 March 2021).
- Hyman, J.D.; Karra, S.; Makedonska, N.; Gable, C.W.; Painter, S.L.; Viswanathan, H.S. DFNWorks: A discrete fracture network framework for modelling subsurface flow and transport. Comput. Geosci. 2015, 84, 10–19. [Google Scholar] [CrossRef]
- Zimmerman, R.; Bodvarsson, G. Hydraulic conductivity of rock fractures, Transp. Porous Media 1996, 23, 1–30. [Google Scholar] [CrossRef]
- Pyrak-Nolte, L.J.; Nolte, D.D. Approaching a universal scaling relationship between fracture stiffness and fluid flow. Nat. Commun. 2016, 7, 10663. [Google Scholar] [CrossRef] [PubMed]
- Renshaw, C.E. On the relationship between mechanical and hydraulic apertures in rough-walled fractures. J. Geophys. Res. 1995, 100, 24629–24636. [Google Scholar] [CrossRef]
- Cheng, J.; Morris, J.P.; Tran, J.; Lumsdaine, A.; Giordano, N.J. Single-phase flow in a rock fracture: Micro-model experiments and network flow simulation. Int. J. Rock Mech. Min. Sci. 2004, 41, 687–693. [Google Scholar] [CrossRef]
- Frampton, A.; Hyman, J.D.; Zou, L. Advective Transport in Discrete Fracture Networks With Connected and Disconnected Textures Representing Internal Aperture Variability. Water Resour. Res. 2019, 55, 5487–5501. [Google Scholar] [CrossRef]
- Huang, N.; Liu, R.; Jiang, Y.; Li, B.; Yu, L. Effects of fracture surface roughness and shear displacement on geometrical and hydraulic properties of three-dimensional crossed rock fracture models. Adv. Water Resour. 2018, 113, 30–41. [Google Scholar] [CrossRef]
- Brown, S.; Caprihan, A.; Hardy, R. Experimental observation of fluid flow channels in a single fracture. J. Geophys. Res. Solid Earth 1998, 103, 5125–5132. [Google Scholar] [CrossRef]
- Kang, P.K.; Brown, S.; Juanes, R. Emergence of anomalous transport in stressed rough fractures. Earth Planet. Sci. Lett. 2016, 454, 46–54. [Google Scholar] [CrossRef]
- Oron, A.P.; Berkowitz, B. Flow in rock fractures: The local cubic law assumption reexamined. Water Resour. Res. 1998, 34, 2811–2825. [Google Scholar] [CrossRef]
- Mohais, R.; Xu, C.; Dowd, P.A. Fluid flow and heat transfer within a single horizontal fracture in an enhanced geothermal system. ASME J. Heat Transf. 2011, 133, 112603. [Google Scholar] [CrossRef]
- Natarajan, N.; Xu, C.; Dowd, P.A.; Hand, M. Numerical modelling of thermal transport and quartz precipitation/dissolution in a coupled fracture-skin matrix system. Int. J. Heat Mass Transf. 2014, 78, 302–310. [Google Scholar] [CrossRef][Green Version]
- Tian, Z.F.; Xu, C.; Dowd, P.A. On the Study of Flows through Underground Fractures Using Finite Volume Methods, Flow and Transport in Subsurface Environment; Springer: Berlin/Heidelberg, Germany, 2018; pp. 119–140. ISBN 978-981-10-8772-1. [Google Scholar]
- Zimmerman, R.W.; Kumar, S.; Bodvarsson, G.S. Lubrication theory analysis of the permeability of rough-walled fractures. Int. J. Rock Mech. Min. Sci. 1991, 28, 325–331. [Google Scholar] [CrossRef]
- Brush, D.J.; Thomson, N.R. Fluid flow in synthetic rough-walled fractures: Navier-Stokes, Stokes, and local cubic law simulations. Water Resour. Res. 2003, 39, 1085. [Google Scholar] [CrossRef]
- Xiong, F.; Jiang, Q.; Ye, Z.; Zhang, X. Nonlinear flow behavior through rough-walled rock fractures: The effect of contact area. Comput. Geotech. 2018, 102, 179–195. [Google Scholar] [CrossRef]
- Zou, L.; Jing, L.; Cvetkovic, V. Shear-enhanced nonlinear flow in rough-walled rock fractures. Int. J. Rock Mech. Min. Sci. 2017, 97, 33–45. [Google Scholar] [CrossRef]
- Konzuk, J.S.; Kueper, B.H. Evaluation of cubic law based models describing single-phase flow through a rough-walled fracture. Water Resour. Res. 2004, 40, 1–17. [Google Scholar] [CrossRef]
- Olsson, R.; Barton, N. An improved model for hydromechanical coupling during shearing of rock joints. Int. J. Rock Mech. Min. Sci. 2001, 38, 317–329. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, H.S. An Average Flow Model for Determining Effects of Three-Dimensional Roughness on Partial Hydrodynamic Lubrication. J. Lubr. Technol. 1978, 100, 12–17. [Google Scholar] [CrossRef]
- Neuzil, C.E.; Tracy, J.V. Flow through fractures. Water Resour. Res. 1981, 17, 191–199. [Google Scholar] [CrossRef]
- Tsang, Y.W.; Witherspoon, P.A. Hydromechanical Behavior of a Deformable Rock Fracture Subject to Normal Stress. J. Geophys. Res. 1981, 86, 9287–9298. [Google Scholar] [CrossRef]
- Witherspoon, P.A.; Wang, J.S.Y.; Lwai, K.; Gale, J.E. Validity of Cubic Law for fluid flow in a deformable rock fracture. Water Resour. Res. 1980, 16, 1016–1024. [Google Scholar] [CrossRef]
- Nicholl, M.J.; Rajaram, H.; Glass, R.J.; Detwiler, R. Saturated flow in a single fracture: Evaluation of the Reynolds equation in measured aperture fields. Water Resour. Res. 1999, 35, 3361–3373. [Google Scholar] [CrossRef]
- Zimmerman, R.W.; Chen, D.W.; Cook, N.G.W. The effect of contact area on the permeability of fractures. J. Hydrol. 1992, 139, 79–96. [Google Scholar] [CrossRef]
- Bodin, J.; Delay, F.; de Marsily, G. Solute transport in a single fracture with negligible matrix permeability: 1. Fundamental mechanisms. Hydrogeol. J. 2003, 11, 418–433. [Google Scholar] [CrossRef]
- Zou, L.; Jing, L.; Cvetkovic, V. Modeling of Solute Transport in a 3D Rough-Walled Fracture–Matrix System. Transort Porous Media 2017, 116, 1005–1029. [Google Scholar] [CrossRef]
- Thompson, M.E.; Brown, S.R. The effect of anisotropic surface roughness on flow and transport in fractures. J. Geophys. Res. 1991, 96, 21923–21932. [Google Scholar] [CrossRef]
- Tsang, Y.W.; Tsang, C.F. Channel model of flow through fractured media. Water Resour. Res. 1987, 23, 467–479. [Google Scholar] [CrossRef]
- Moreno, L.; Tsang, Y.W.; Tsang, C.F.; Hale, F.V.; Neretnieks, I. Flow and tracer transport in a single fracture: A stochastic model and its relation to some field observations. Water Resour. Res. 1988, 24, 2033–2048. [Google Scholar] [CrossRef]
- Wang, H.; Wang, H.; Gao, F.; Zhou, P.; Zhai, Z. Literature review on pressure–velocity decoupling algorithms applied to built-environment CFD simulation. Build. Environ. 2018, 143, 671–678. [Google Scholar] [CrossRef]
- Zimmerman, R.W.; AL-Yaarubi, A.; Pain, C.C.; Grattoni, C.A. Non-linear regimes of fluid flow in rock fractures. Int. J. Rock Mech. Min. Sci. 2004, 41, 163–169. [Google Scholar] [CrossRef]
- Huang, N.; Jiang, Y.; Li, B.; Liu, R. A numerical method for simulation fluid flow through 3-D fracture networks. J. Nat. Gas Sci. Eng. 2017, 33, 1271–1281. [Google Scholar] [CrossRef]
- Zhang, X.; Sanderson, D.J.; Harkness, R.M.; Last, N.C. Evaluation of the 2-D permeability tensor for fractured rock masses. Int. J. Rock Mech. Min. Sci. 1996, 33, 17–37. [Google Scholar] [CrossRef]
- Yin, Q.; Jing, H.; Ma, G.; Su, H.; Liu, R. Investigating the roles of included angle and loading condition on the critical hydraulic gradient of real rock fracture networks. Rock Mech. Rock Eng. 2018, 51, 3167–3177. [Google Scholar] [CrossRef]
- Dang, W.; Wu, W.; Konietzky, H.; Qian, J. Effect of shear-induced aperture evolution on fluid flow in rock fractures. Comput. Geotech. 2019, 114, 103152. [Google Scholar] [CrossRef]
- Ji, Y.; Wanniarachchi, W.; Wu, W. Effect of fluid pressure heterogeneity on injection-induced fracture activation. Comput. Geotech. 2020, 123, 103589. [Google Scholar] [CrossRef]
- Geodynamics. Geodynamics Ltd.: 2014. In Hananero Geothermal Project Field Development Plan; Document Number: COM-FN-OT-PLN-01166; Geodynamics Ltd.: Milton, QLD, Australia, 2014. [Google Scholar]
- Mardia, K.V.; Nyirongo, V.B.; Walder, A.N.; Xu, C.; Dowd, P.A.; Fowell, R.J.; Kent, J.T. Markov Chain Monte Carlo implementation of rock fracture modeling. Math. Geol. 2007, 39, 355–381. [Google Scholar] [CrossRef]
- Vörös, R.; Weidler, R. Numerical Thermo-Hydraulic Simulation of a Large Scale Power Production in the Cooper Basin; Technical Report GDY018; Geodynamics Ltd.: Milton, QLD, Australia, 2006. [Google Scholar]
- Vörös, R.; Rothert, E. Simulation of the Thermal Drawdown for a Circulation between Habanero #1–Habanero #3; Technical Report GDY028; Geodynamics Ltd.: Milton, QLD, Australia, 2009. [Google Scholar]
- Pruess, K.; Oldenburg, C.; Moridis, G. TOUGH2 User’s Guide, Version 2.0; LBNL-43134; Ernest Orlando Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 1999.
- Xu, C.; Dowd, P.A.; Tian, Z.F. A simplified coupled hydro-thermal model for enhanced geothermal Systems. Appl. Energy 2015, 140, 135–145. [Google Scholar] [CrossRef]
- Xu, C.; Dowd, P.A.; Li, Q. Carbon sequestration potential of the Habanero reservoir when carbon dioxide is used as the heat exchange fluid. J. Rock Mech. Geotech. Eng. 2016, 8, 50–59. [Google Scholar] [CrossRef]
- Terramin Australia Limited 2018, ‘ASX Announcement ISR Copper Resource at Kapunda’. Available online: https://www.envirocopper.com.au/sites/envirocopper/media/banners/terramintzn-resource-feb-2018.pdf (accessed on 19 January 2021).
- Wang, H.; Xu, C.; Dowd, P.A.; Kuhar, L.; Faulkner, F. Numerical Modelling of in-Situ Recovery of Copper Minerals: A Case Study of Kapunda Mine, South Australia; Technical Report; University of Adelaide: Adelaide, SA, Australia, 2021. [Google Scholar]
- Nardi, A.; Idiart, A.; Trinchero, P.; de Vries, L.M.; Molinero, J. Interface COMSOL-PHREEQC (iCP), an efficient numerical framework for the solution of coupled multiphysics and geochemistry. Comput. Geosci. 2014, 69, 10–21. [Google Scholar] [CrossRef]





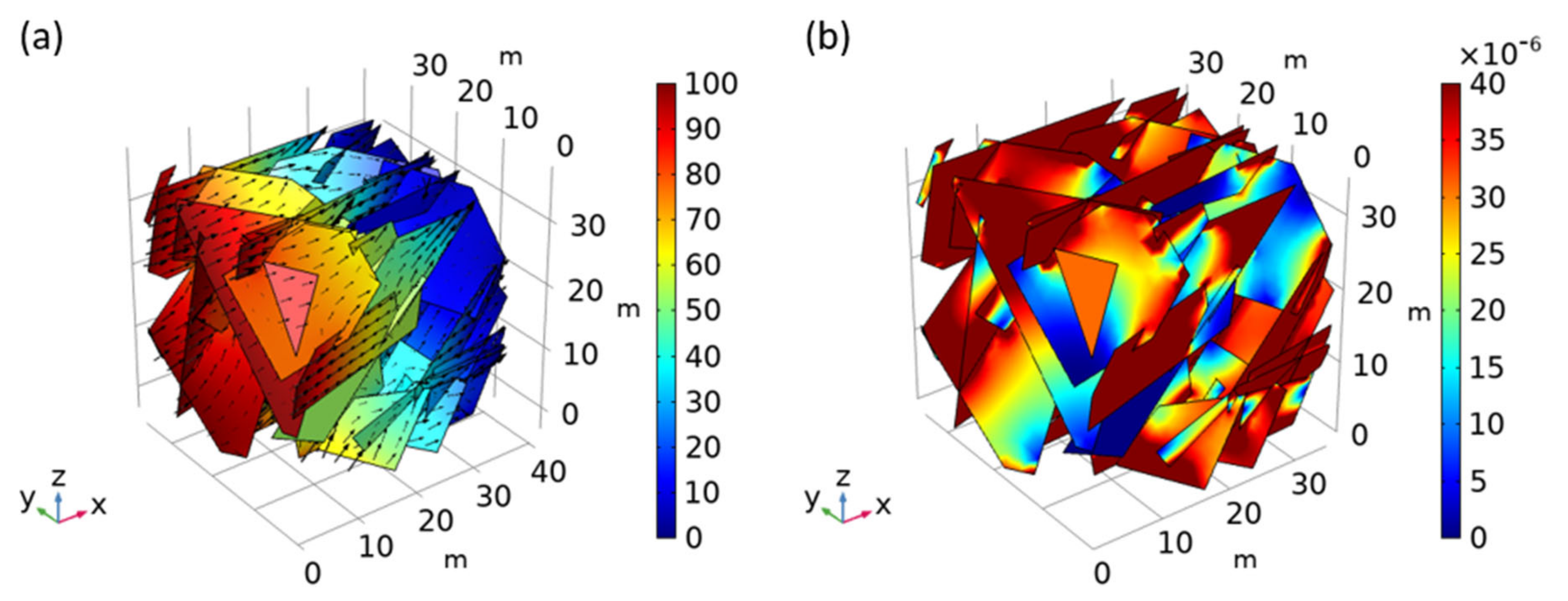


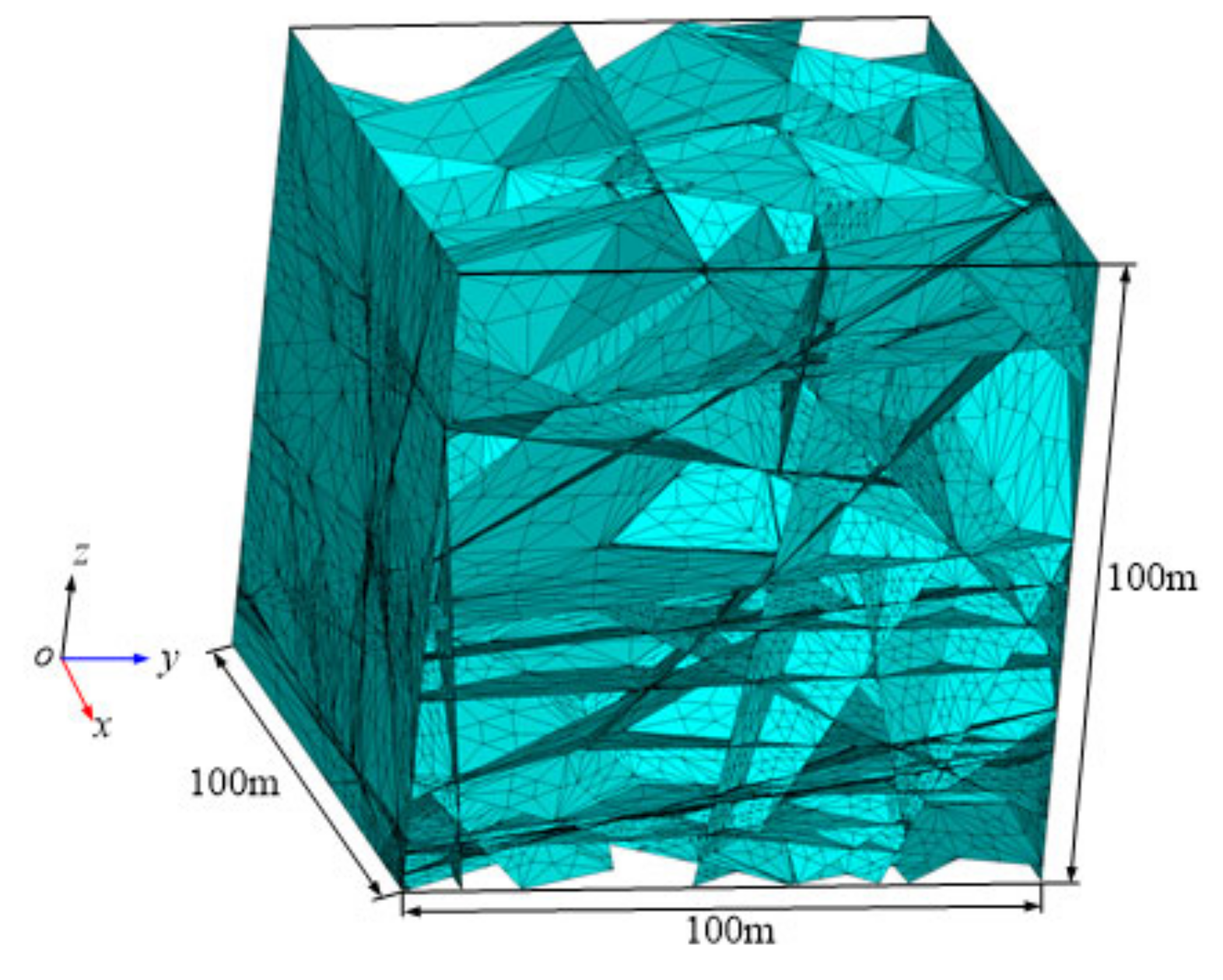


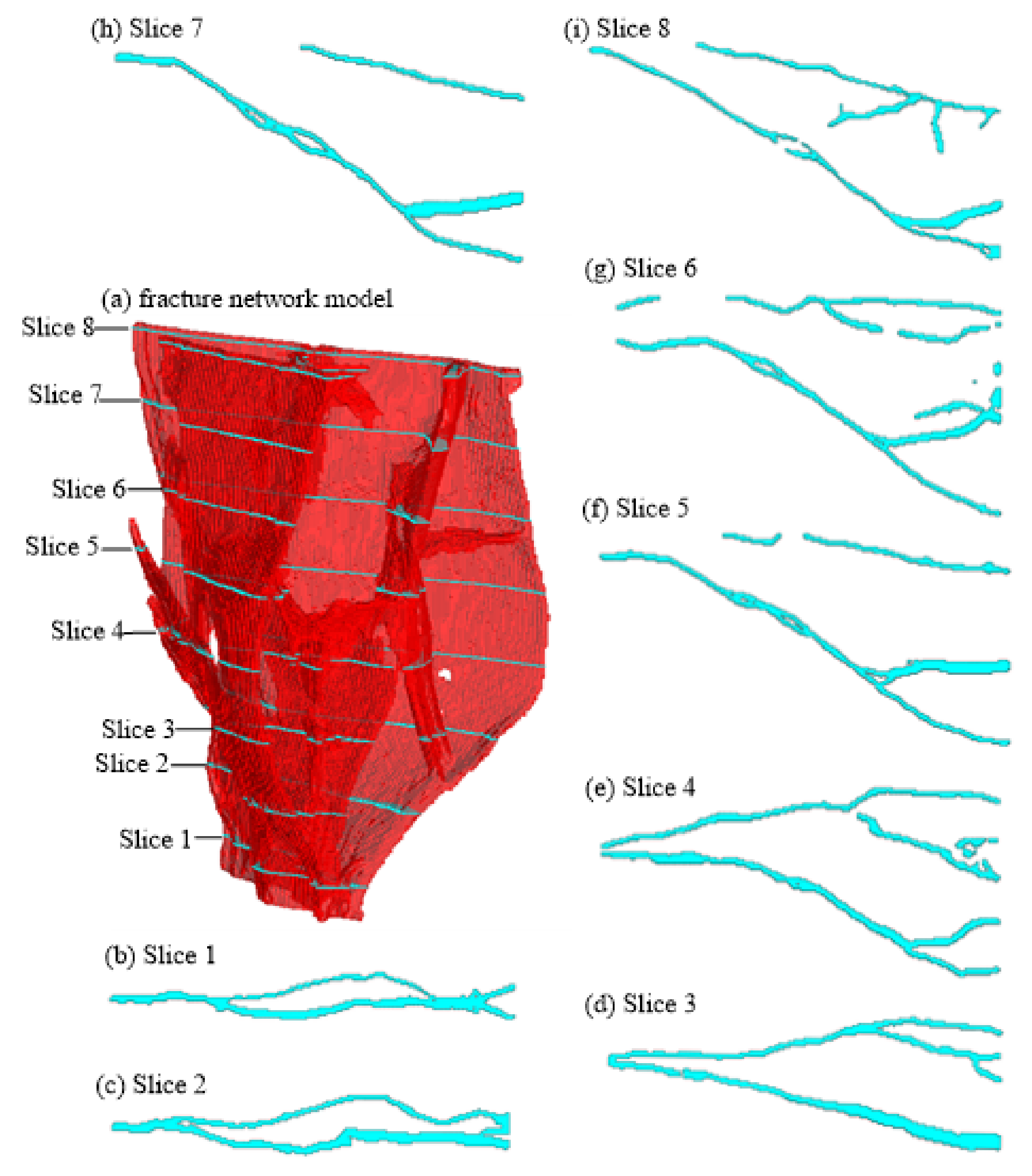
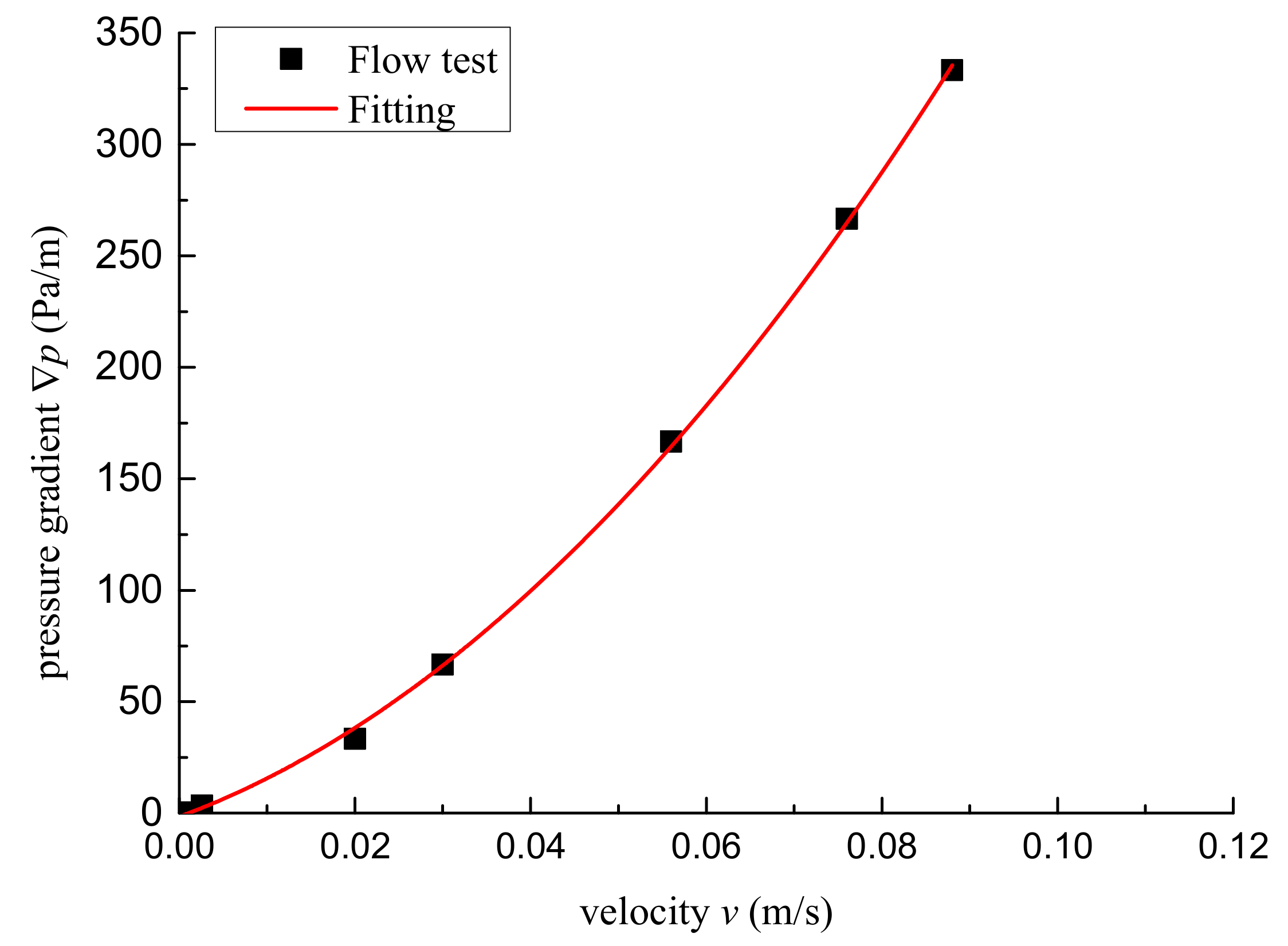
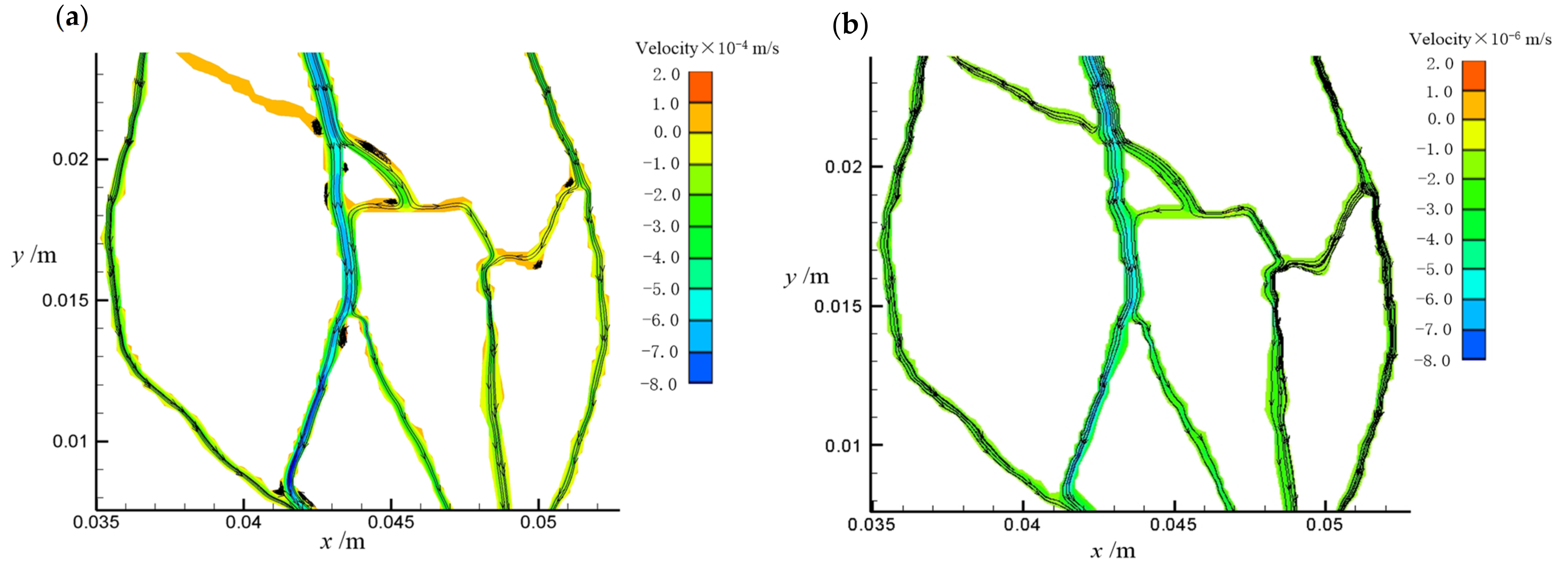



| Pressure Gradient Direction, Flow | Block Boundaries | |||||
|---|---|---|---|---|---|---|
| Left | Right | Front | Behind | Bottom | Top | |
| (x-) | (x+) | (y-) | (y+) | (z-) | (z+) | |
| x, Q (m3/s) | 2.90 × 10−6 | 4.75 × 10−6 | −1.38 × 10−9 | −1.98 × 10−7 | 2.32 × 10−6 | 6.75 × 10−7 |
| Pressure Gradient Direction, Flow | Block Boundaries | |||||
|---|---|---|---|---|---|---|
| Left | Right | Front | Behind | Bottom | Top | |
| (x-) | (x+) | (y-) | (y+) | (z-) | (z+) | |
| x, Q (m3/s) | 2.90 × 10−6 | 4.75 × 10−6 | −1.38 × 10−9 | −1.98 × 10−7 | 2.32 × 10−6 | 6.75 × 10−7 |
| y, Q (m3/s) | −1.15 × 10−8 | −5.72 × 10−7 | 2.40 × 10−6 | 3.56 × 10−6 | 6.23 × 10−7 | 1.70 × 10−8 |
| z, Q (m3/s) | 1.03 × 10−6 | 1.85 × 10−6 | −6.24 × 10−7 | 9.80 × 10−7 | 7.01 × 10−6 | 4.62 × 10−6 |
| Principal Permeability | Permeability (m2) | Principal Direction (°) | |
|---|---|---|---|
| Trend | Plunge | ||
| k11 | 1.903 × 10−12 | 4.4 | 62.1 |
| k22 | 9.510 × 10−13 | 135.4 | 19.1 |
| k33 | 7.823 × 10−13 | 232.4 | 19.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, C.; Dong, S.; Wang, H.; Wang, Z.; Xiong, F.; Jiang, Q.; Zeng, L.; Faulkner, L.; Tian, Z.F.; Dowd, P. Modelling of Coupled Hydro-Thermo-Chemical Fluid Flow through Rock Fracture Networks and Its Applications. Geosciences 2021, 11, 153. https://doi.org/10.3390/geosciences11040153
Xu C, Dong S, Wang H, Wang Z, Xiong F, Jiang Q, Zeng L, Faulkner L, Tian ZF, Dowd P. Modelling of Coupled Hydro-Thermo-Chemical Fluid Flow through Rock Fracture Networks and Its Applications. Geosciences. 2021; 11(4):153. https://doi.org/10.3390/geosciences11040153
Chicago/Turabian StyleXu, Chaoshui, Shaoqun Dong, Hang Wang, Zhihe Wang, Feng Xiong, Qinghui Jiang, Lianbo Zeng, Leon Faulkner, Zhao Feng Tian, and Peter Dowd. 2021. "Modelling of Coupled Hydro-Thermo-Chemical Fluid Flow through Rock Fracture Networks and Its Applications" Geosciences 11, no. 4: 153. https://doi.org/10.3390/geosciences11040153
APA StyleXu, C., Dong, S., Wang, H., Wang, Z., Xiong, F., Jiang, Q., Zeng, L., Faulkner, L., Tian, Z. F., & Dowd, P. (2021). Modelling of Coupled Hydro-Thermo-Chemical Fluid Flow through Rock Fracture Networks and Its Applications. Geosciences, 11(4), 153. https://doi.org/10.3390/geosciences11040153








