Experimental and Numerical Investigations of a River Embankment Model under Transient Seepage Conditions
Abstract
1. Introduction
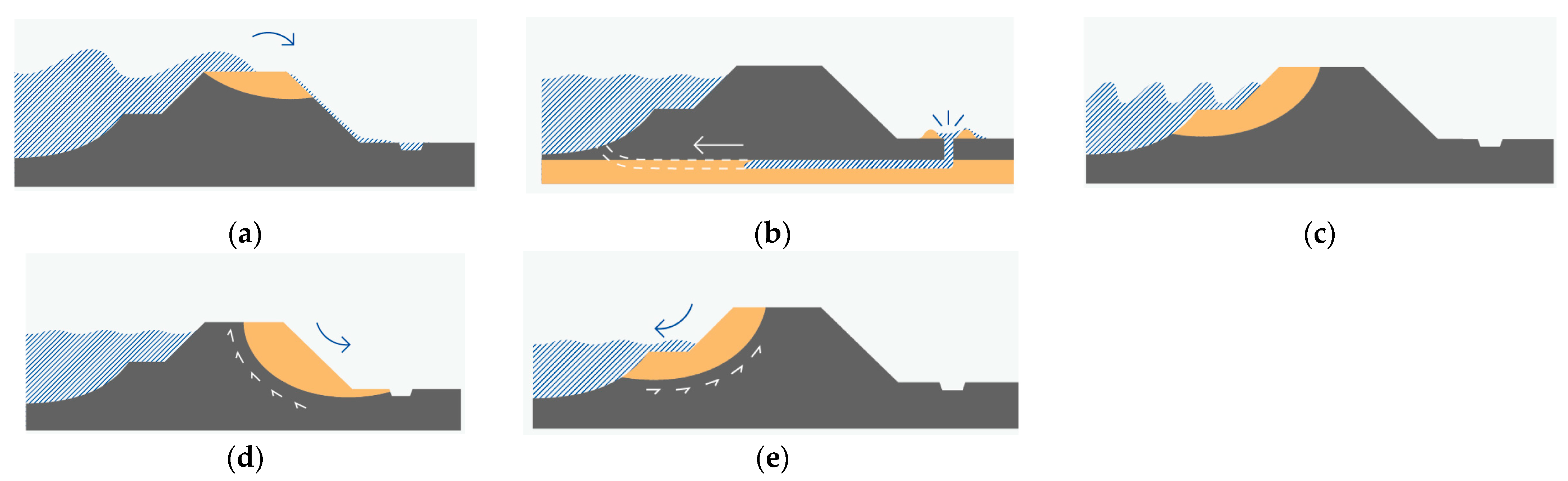
2. Materials and Methods
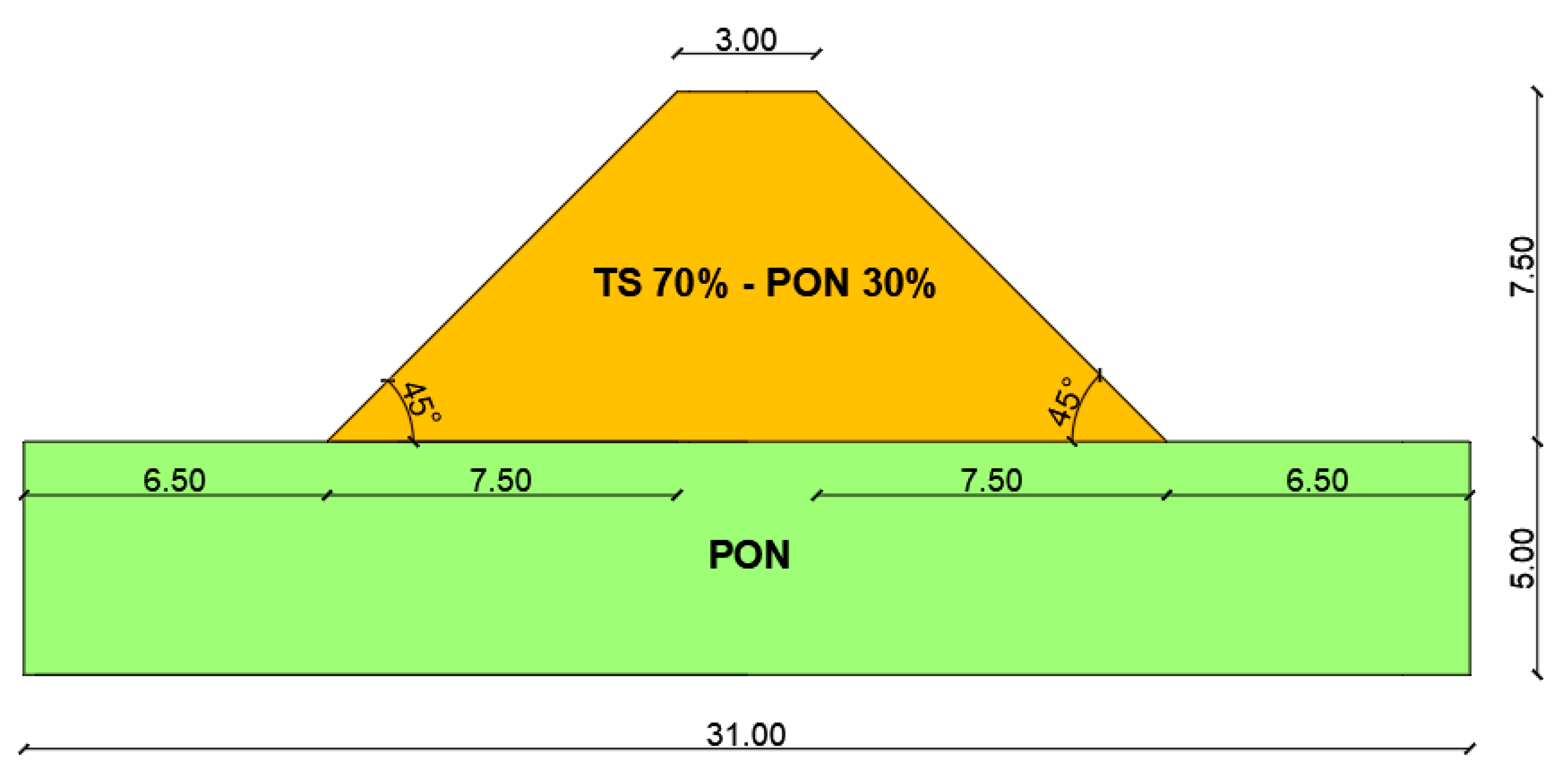
2.1. Case Study
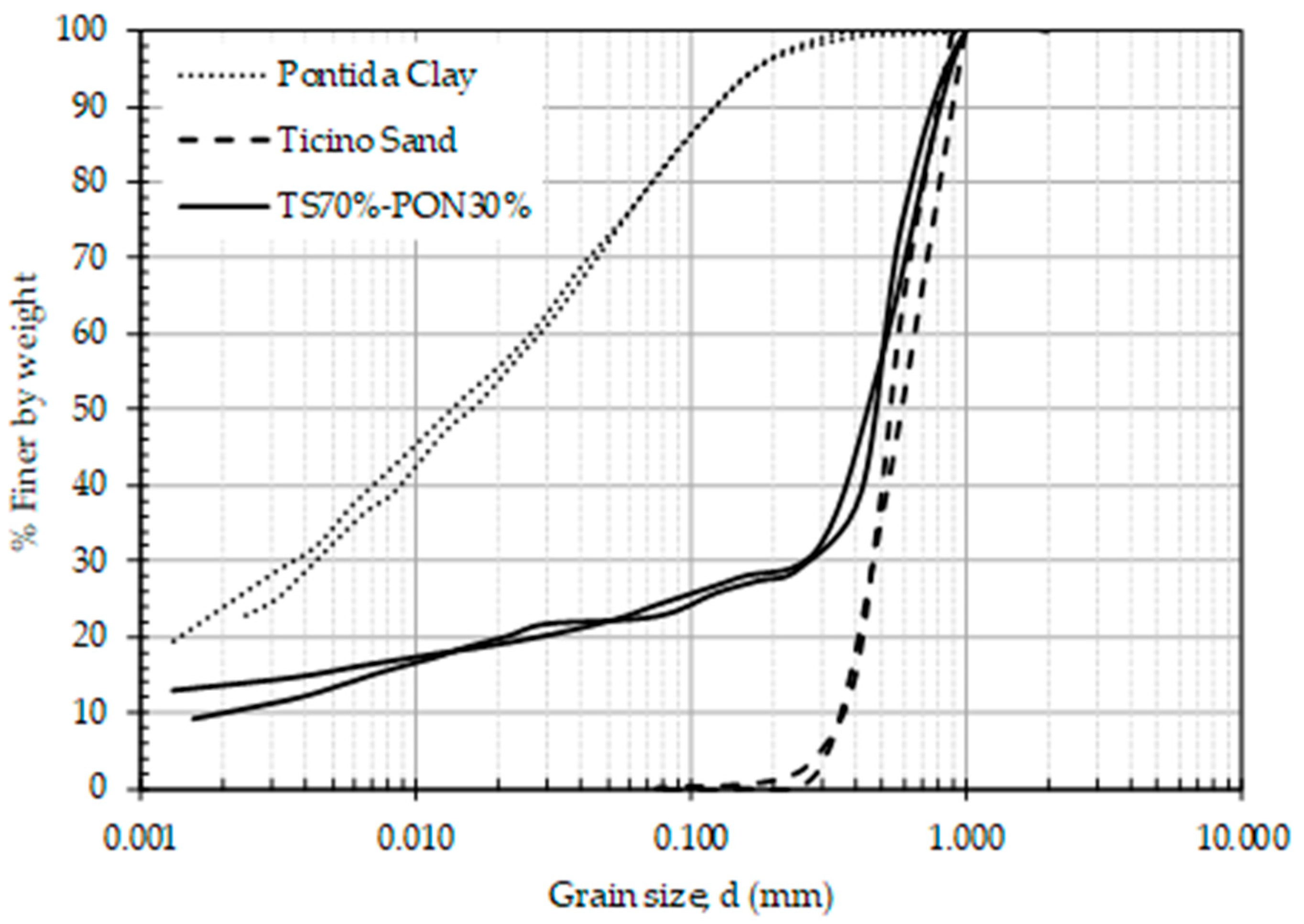
2.2. Soil Physical Properties
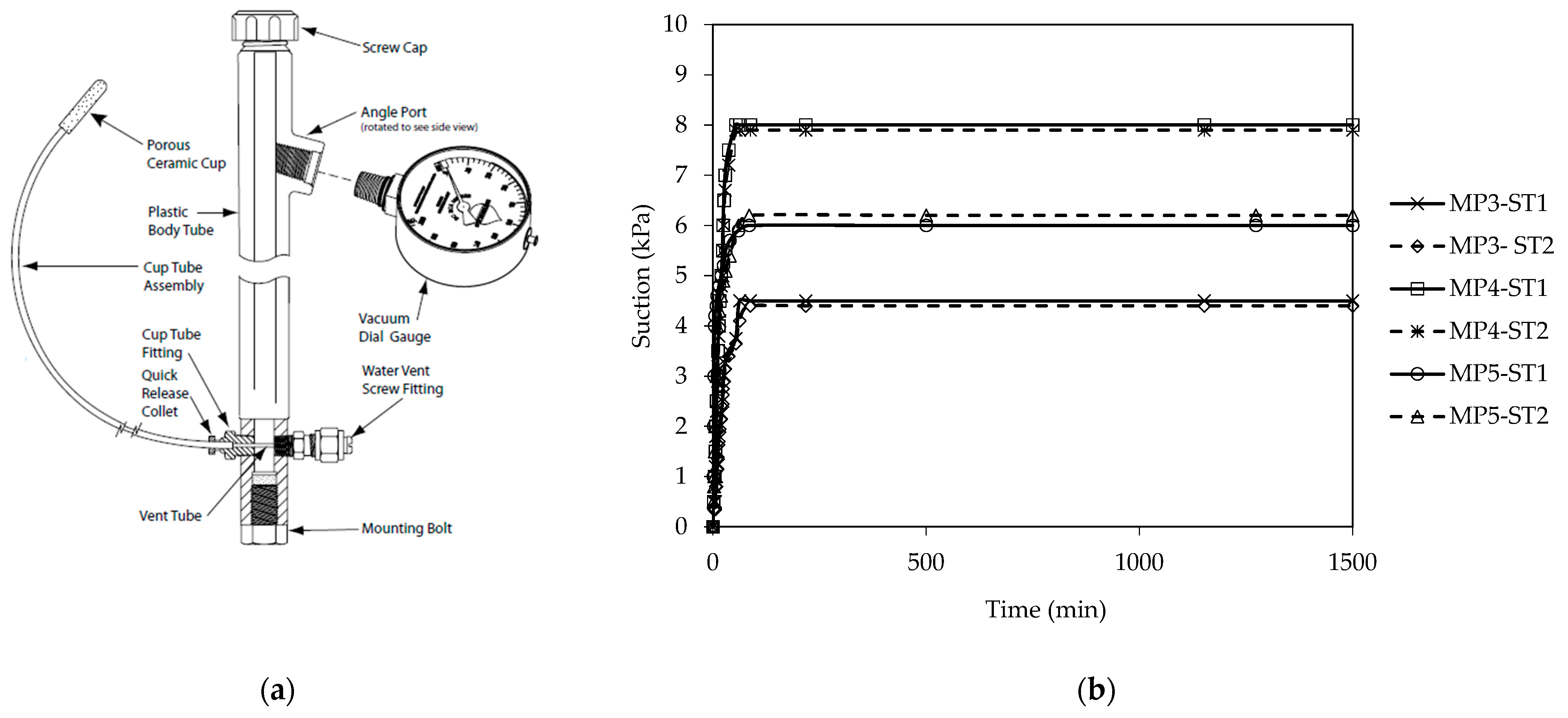
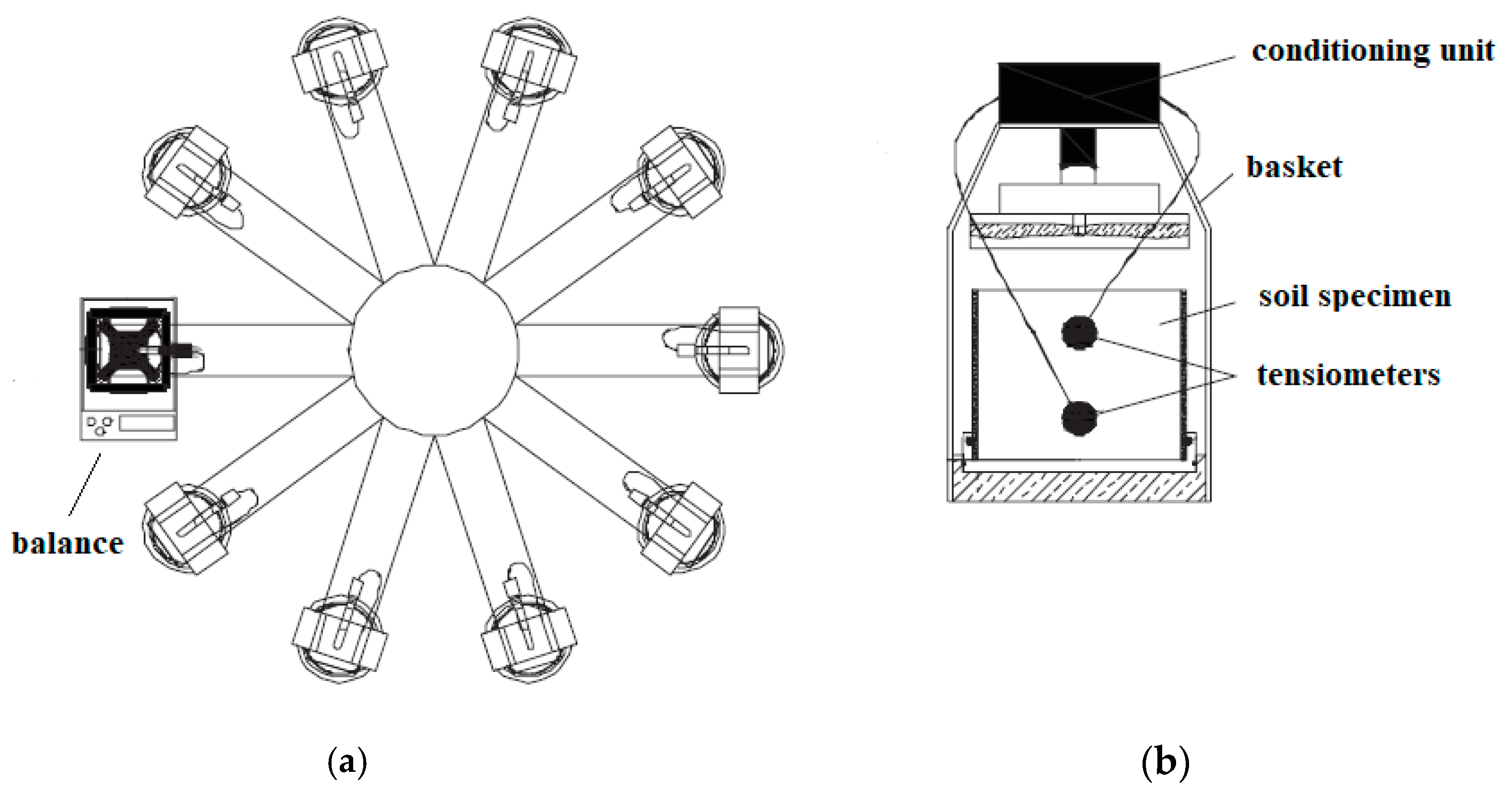
2.3. Specimen Preparation and Initial Condition
3. Soil Hydro-Mechanical Characterization
3.1. TS70%-PON30%
3.1.1. Saturated Permeability from Permeameter Test
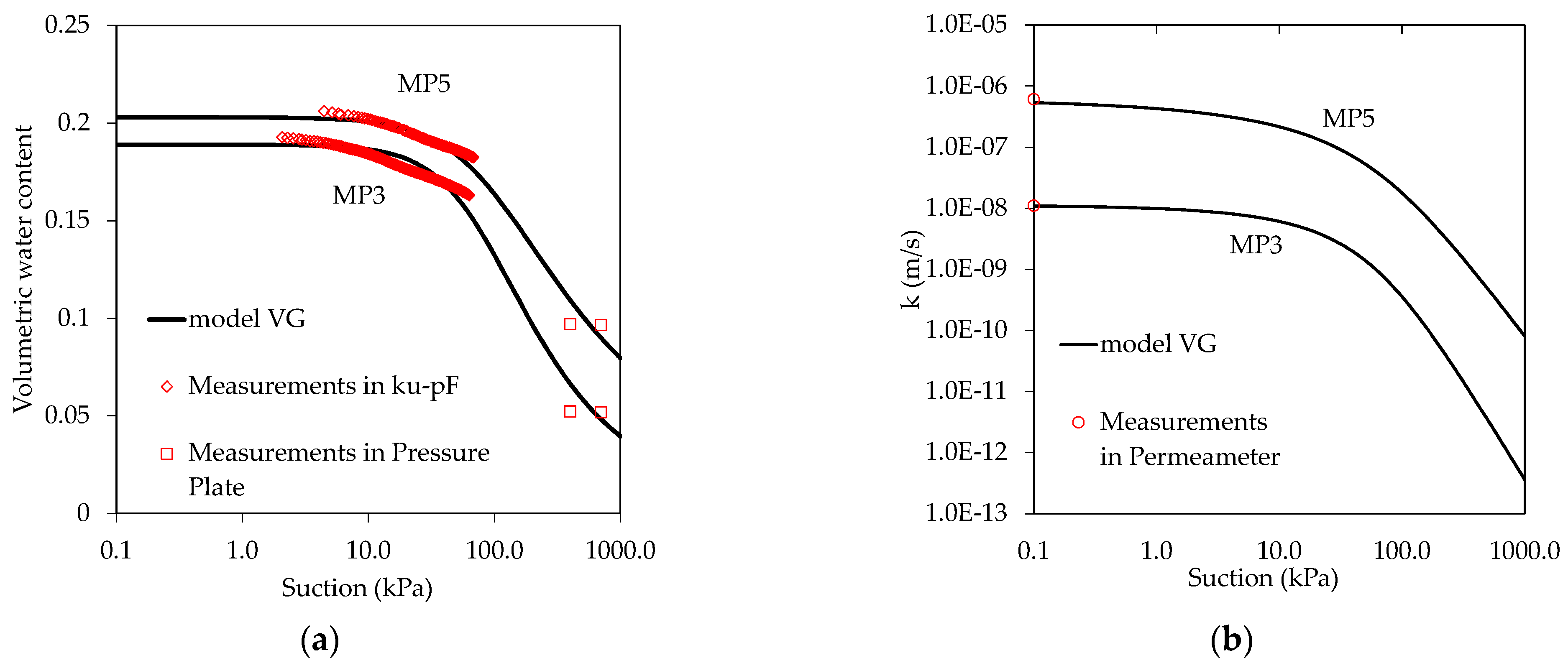
3.1.2. Soil Water Retention Curve (SWRC) and Hydraulic Conductivity Function (HCF)
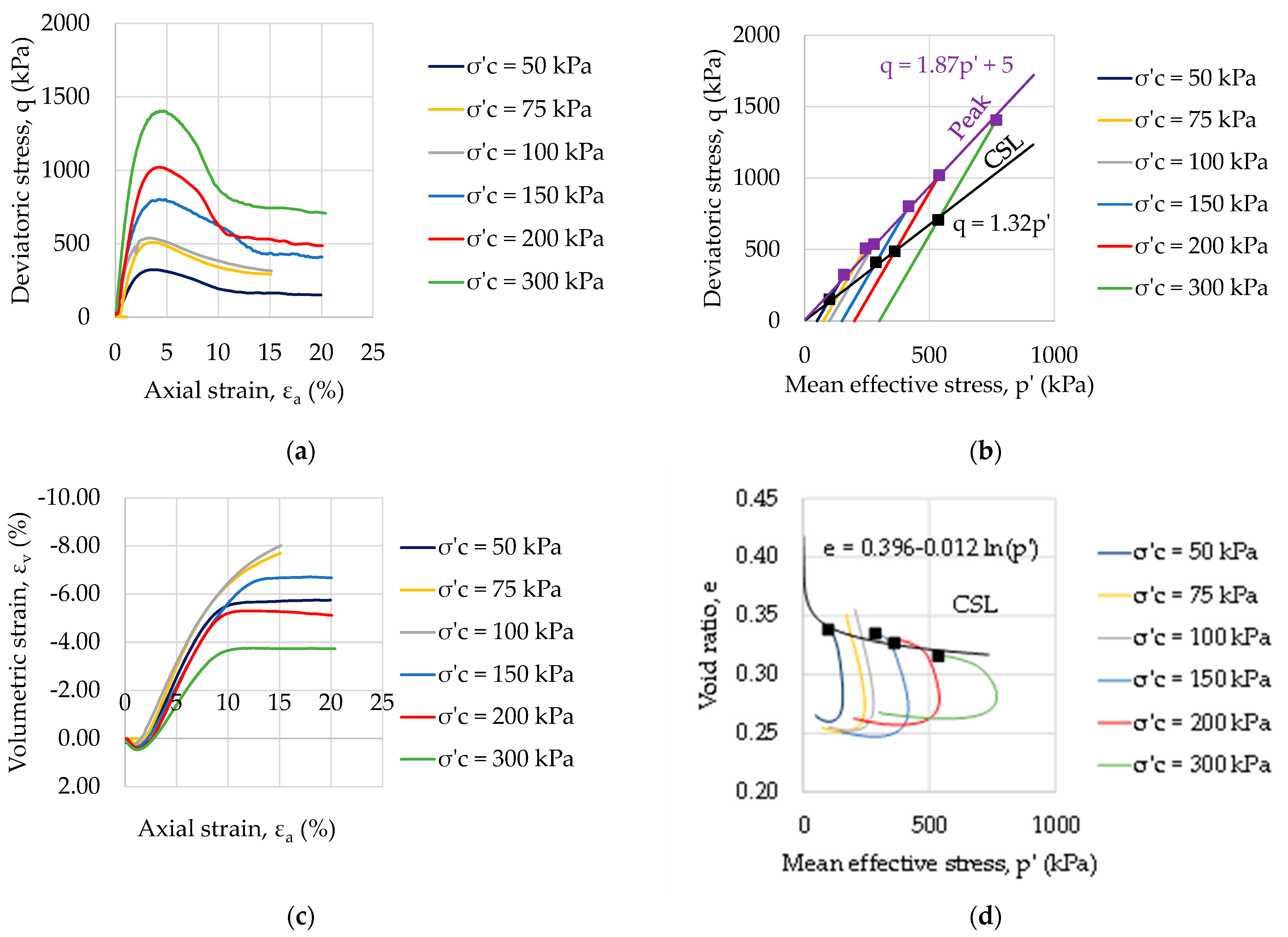
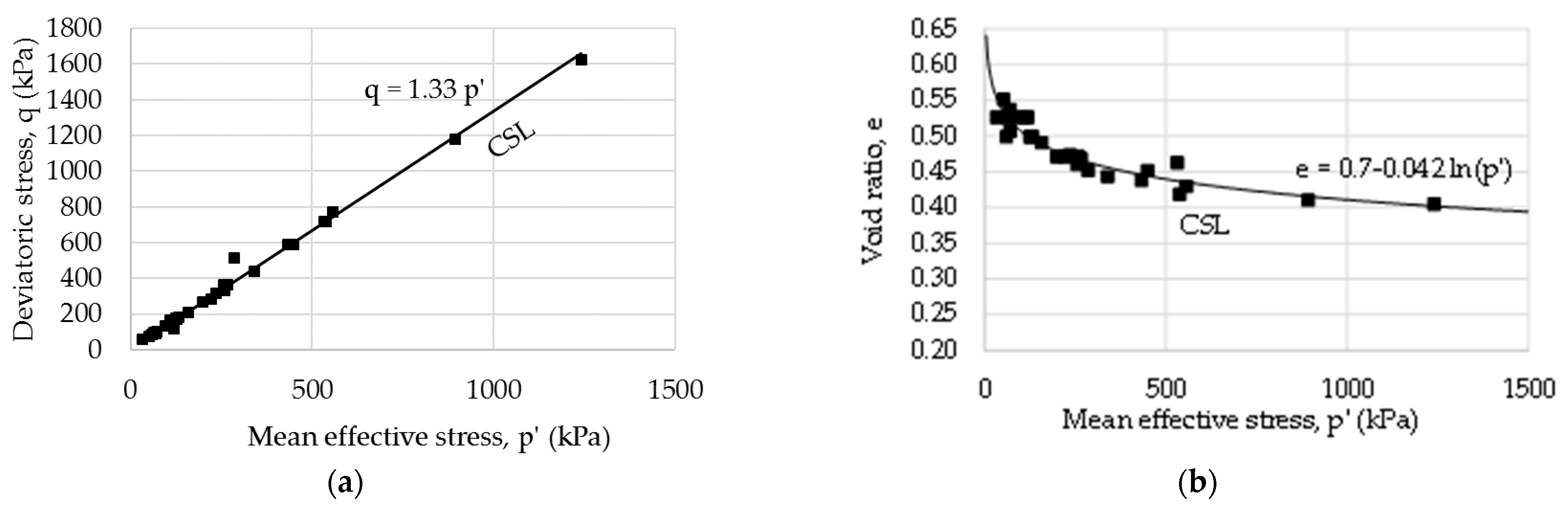
3.1.3. Mechanical Soil Properties at Full Saturation
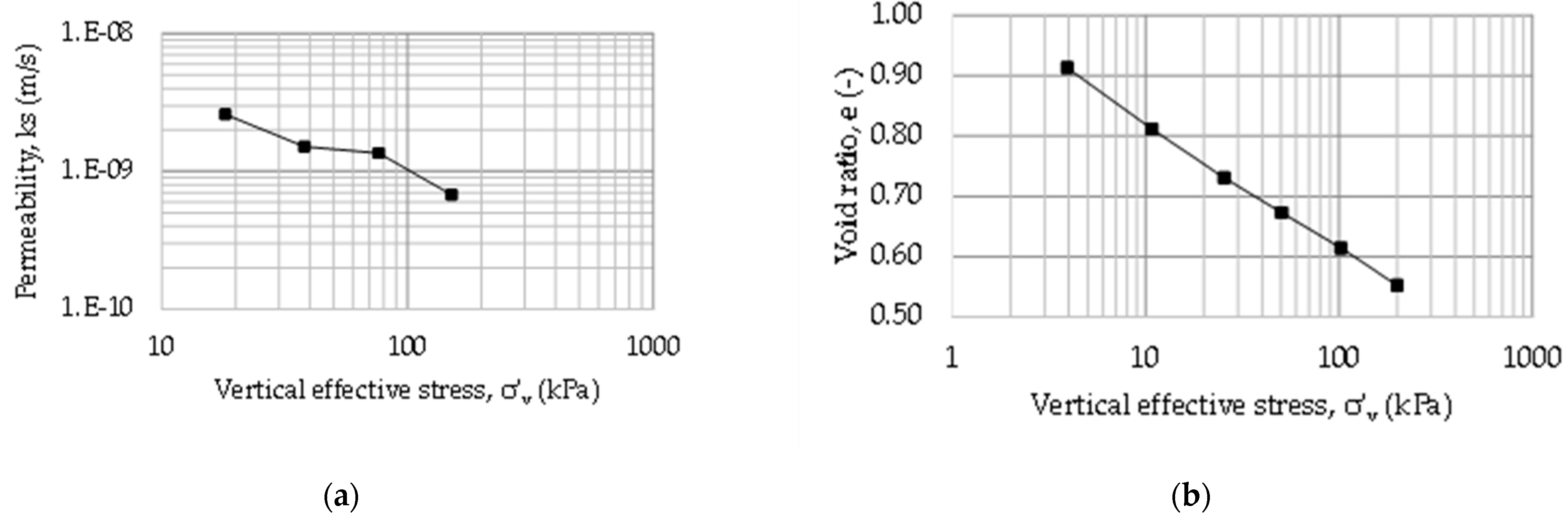
3.2. Pontida Clay
4. Numerical Analysis on the Hydraulic Response and Stability Assessment
4.1. Seepage Analyses
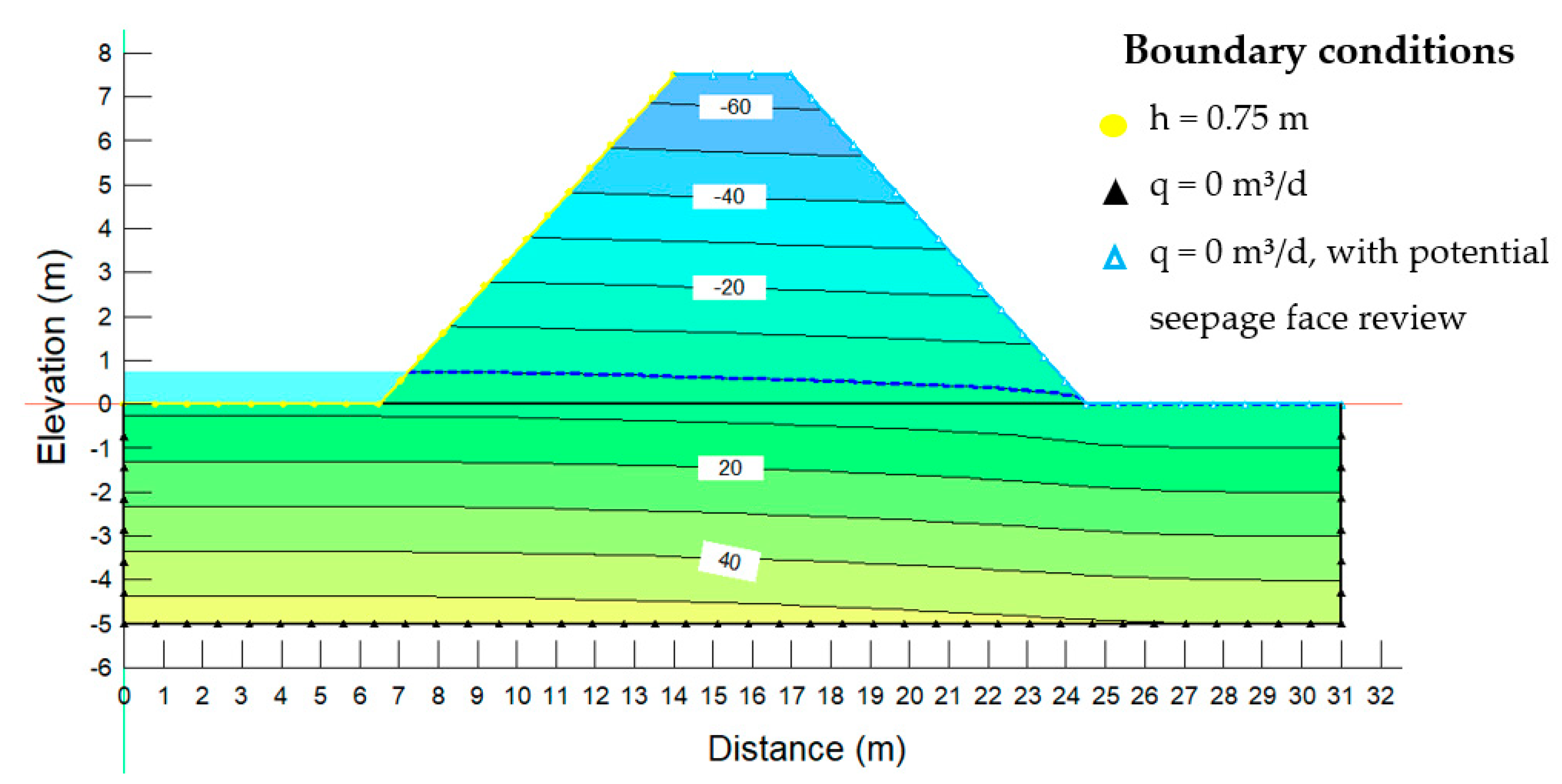
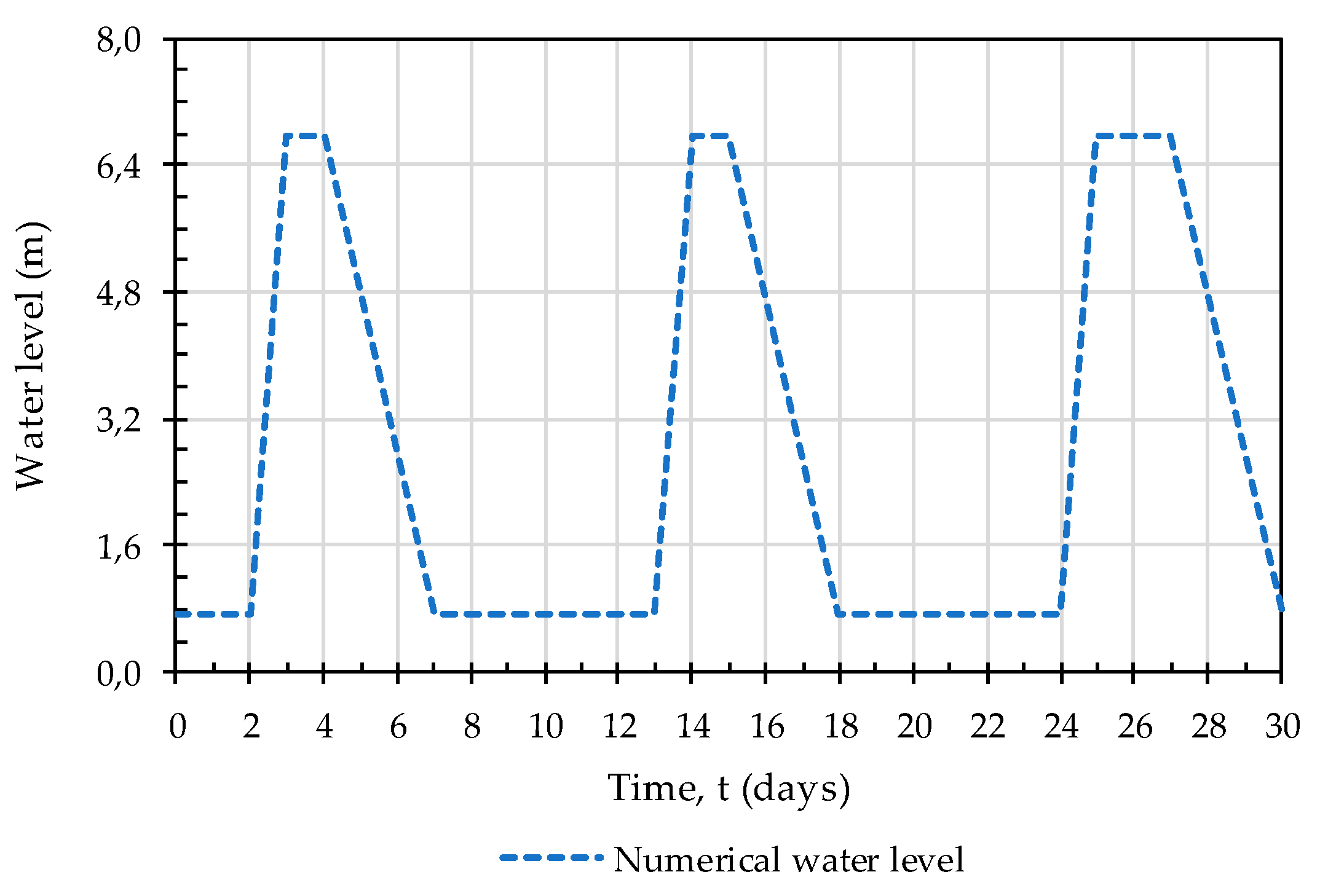
4.1.1. Boundary and Initial Conditions
4.2. Stability Analyses
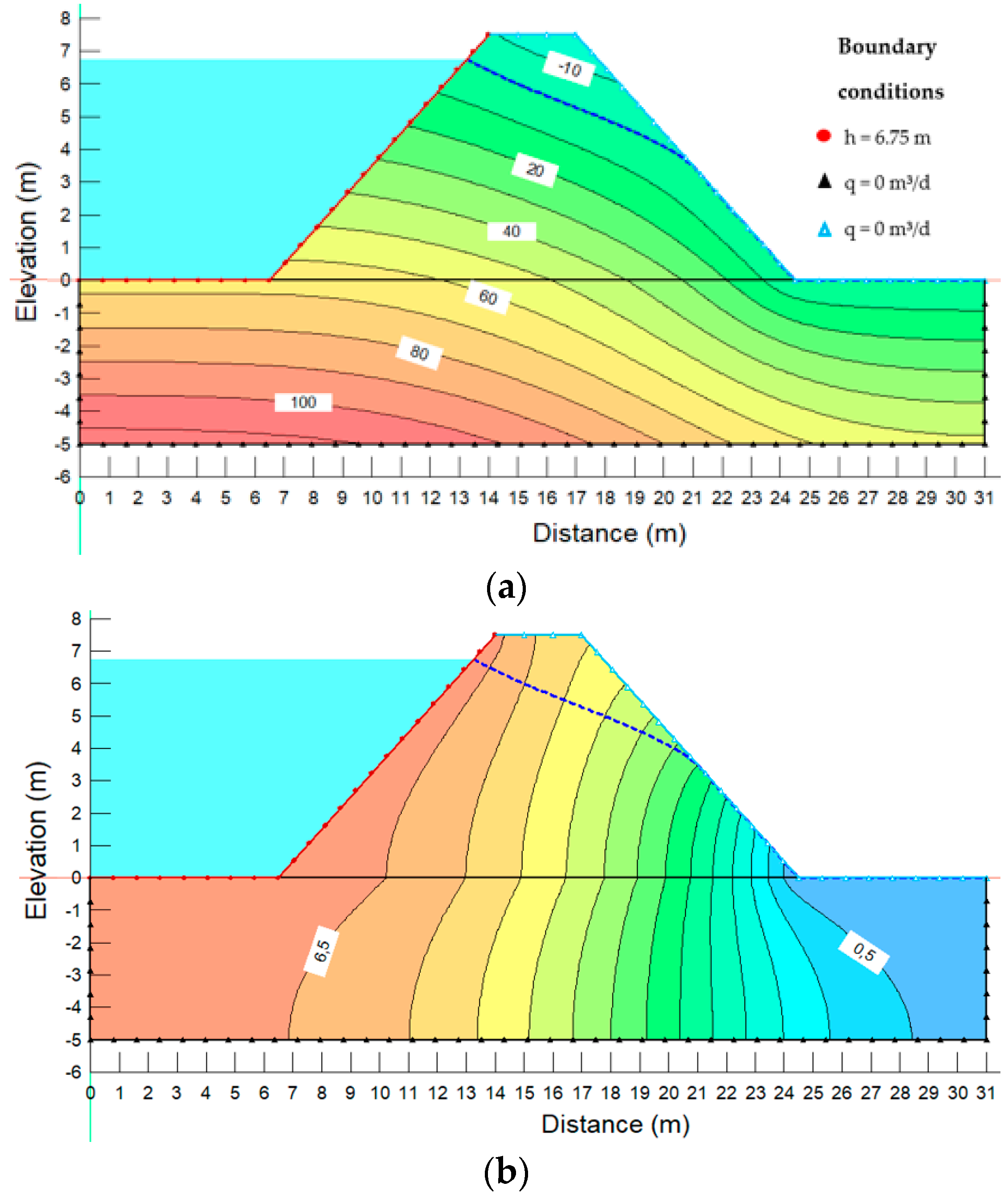
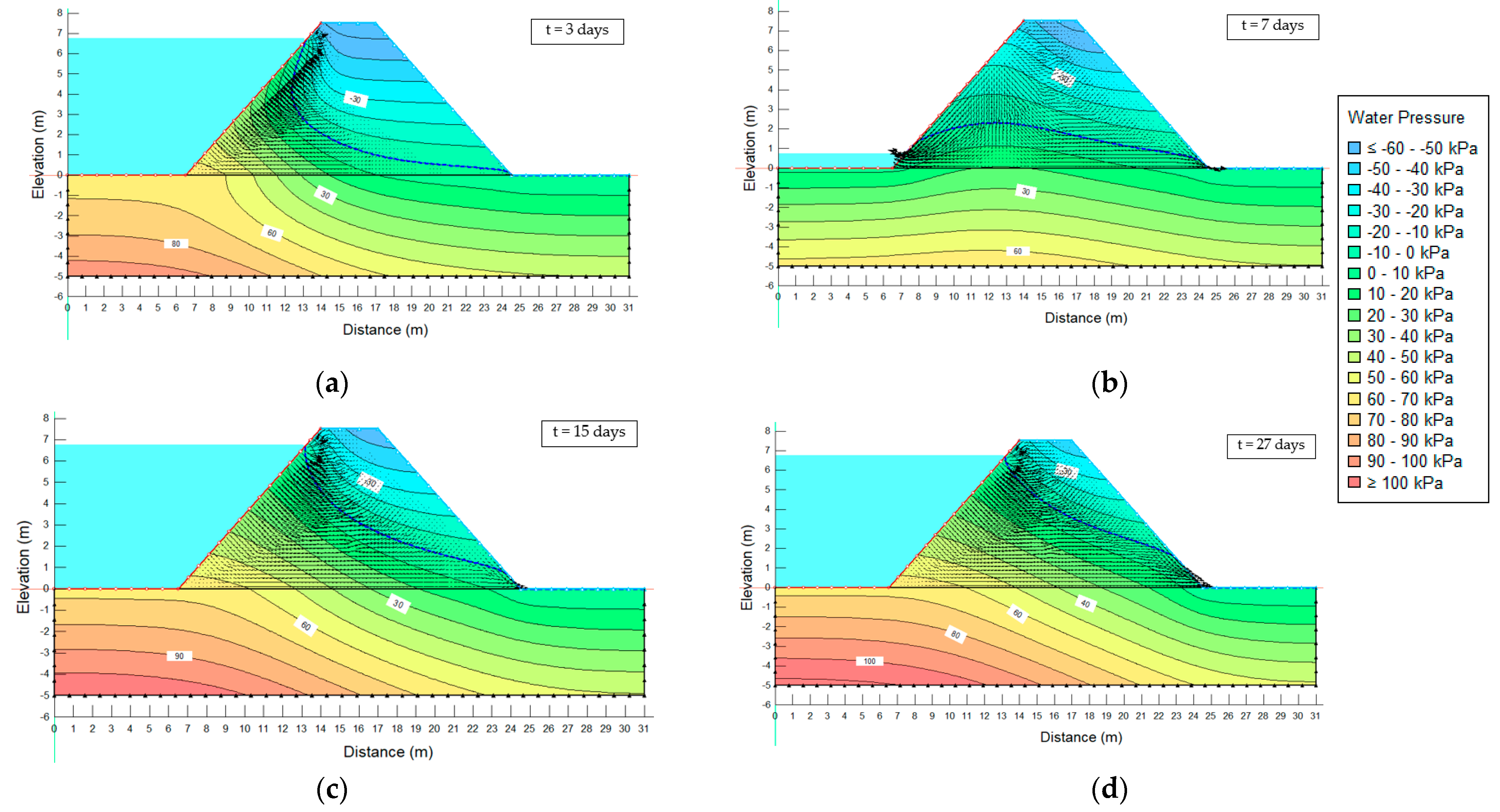
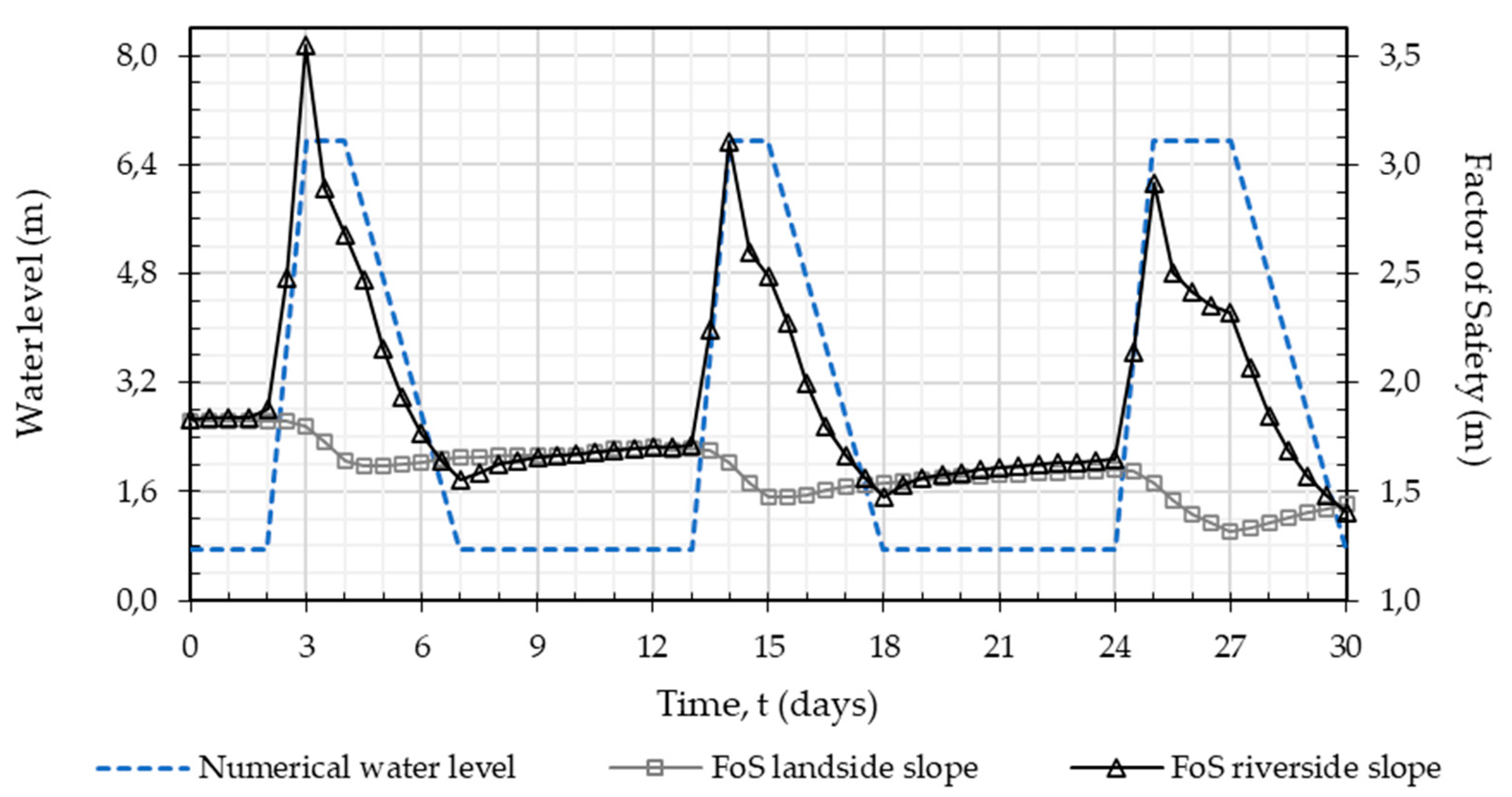
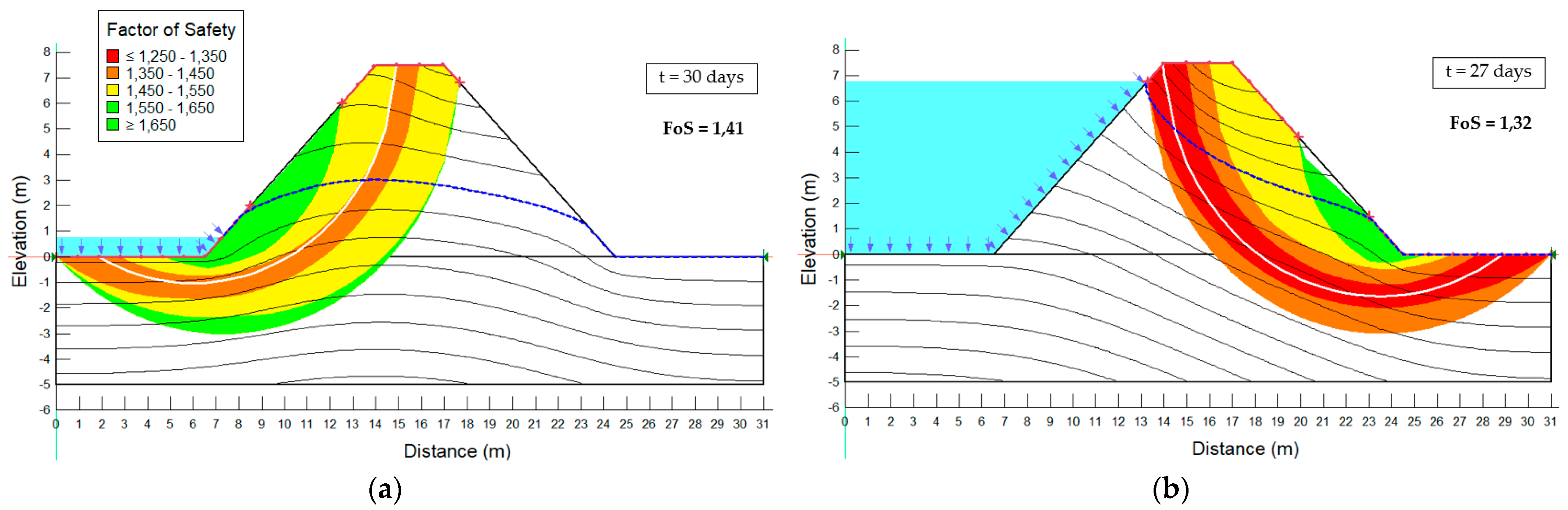
4.3. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- European Environment Agency. Floods. Available online: https://www.eea.europa.eu/archived/archived-content-water-topic/water-resources/floods (accessed on 23 April 2021).
- European Environment Agency. Economic Losses from Climate-Related Extremes in Europe. Available online: https://www.eea.europa.eu/data-and-maps/indicators/direct-losses-from-weather-disasters-4/assessment (accessed on 23 April 2021).
- Simonini, P.; Cola, S.; Bersan, S. Caratterizzazione Geotecnica, meccanismi di collasso e monitoraggio degli argini fluviali. In Proceedings of the XXV Convegno Nazionale di Geotecnica, Baveno, Italy, 4–6 June 2014; Volume 1, pp. 229–268. [Google Scholar]
- CIRIA; Ministry of Ecology of United Kingdom; USACE. The International Levee Handbook (C731); CIRIA: London, UK, 2013.
- Vannucchi, G.; Gottardi, G.; Madiai, C.; Marchi, M.; Tonni, L. Analisi della probabilità di collasso arginale dei grandi fiumi. In Proceedings of the XXV Convegno Nazionale di Geotecnica, Baveno, Italy, 4–6 June 2014; Volume 1, pp. 303–319. [Google Scholar]
- Wolman, M.G. Factors influencing the erosion of cohesive river banks. Am. J. Sci. 1959, 257, 204–216. [Google Scholar] [CrossRef]
- Hooke, J.M. An analysis of the processes of river bank erosion. J. Hydrol. 1979, 42, 39–62. [Google Scholar] [CrossRef]
- Thorne, C. Processes and mechanisms of river bank erosion. In Gravel-Bed Rivers: Fluvial Processes, Engineering and Management; John Wiley & Sons Inc.: Hoboken, NJ, USA, 1982; pp. 227–271. [Google Scholar]
- Rinaldi, M.; Casagli, N. Stability of streambanks formed in partially saturated soils and effects of negative pore water pressures: The Sieve River (Italy). Geomorphology 1999, 26, 253–277. [Google Scholar] [CrossRef]
- Federal Emergency Management Agency. Technical Manual for Dam Owners: Impacts of Animals on Earthen Dams; FEMA Rep. 47; FEMA: Washington, DC, USA, 2005.
- Kok, M.; TU Delft/HKV lijn in water; Jongejan, R.; Jongejan, R.M.C.; Nieuwjaar, M.; Waternet; Tánczos, I.; Ministerie van Infrastructuur en Milieu, Rijkswaterstaat, Expertise Netwerk Waterveiligheid (RWS, ENW). Fundamentals of Flood Protection; NPN Drukkers: Breda, The Netherlands, 2017. [Google Scholar]
- Lee, C.W.; Kim, Y.S.; Park, S.Y.; Kim, D.G.; Heo, G. The behavior characteristics of a reservoir levee subjected to increasing water levels. J. Civ. Eng. Manag. 2017, 23, 15–27. [Google Scholar] [CrossRef][Green Version]
- Saran, R.K.; Viswanadham, B.V.S. Centrifuge model tests on the use of geosynthetic layer as an internal drain in levees. Geotext. Geomembr. 2018, 46, 257–276. [Google Scholar] [CrossRef]
- Wang, Z.F.; Li, J.H.; Zhang, L.M. Influence of cracks on the stability of a cracked soil slope. In Proceedings of the 5th Asia-Pacific Conference on Unsaturated Soils, Pattaya, Thailand, 29 February–2 March 2012; Volume 2, pp. 594–600. [Google Scholar]
- Orlandini, S.; Moretti, G.; Albertson, J.D. Evidence of an emerging levee failure mechanism causing disastrous floods in Italy. Water Resour. Res. 2015, 51, 7995–8011. [Google Scholar] [CrossRef]
- Springer, F.M., Jr.; Ullrich, C.R.; Hagerty, D.J. Streambank stability. J. Geotech. Eng. 1985, 111, 624–640. [Google Scholar] [CrossRef]
- Lawler, D.M.; Thorne, C.R.; Hooke, J.M. Bank erosion and instability. In Fluvial Geomorphology for River Engineering and Management; Thorne, C.R., Hey, R.D., Newson, M.D., Eds.; John Wiley & Sons: Chichester, UK, 1997; pp. 137–172. [Google Scholar]
- Baldi, G.; Bellotti, R.; Crippa, V.; Fretti, C.; Ghionna, V.N.; Jamiolkowski, M.; Ostricati, D.; Pasqualini, E.; Pedroni, S. Laboratory validation of in situ tests. In Proceedings of the 11th International Conference on Soil Mechanics and Foundation Engineering, San Francisco, CA, USA, 12–16 August 1985. [Google Scholar]
- Baldi, G.; Bellotti, R.; Ghionna, V.N.; Jamiolkowski, M.; Pasqualini, E. Interpretation of CPT’s and CPTU’s. In Proceedings of the 4th International Geotechnical Seminar, Balkema, Singapore, 27 November 1986; pp. 3–10. [Google Scholar]
- Bellotti, R.; Jamiolkowski, M.; Lo Presti, D.C.F.; O’Neill, D.A. Anisotropy of small strain stiffness in Ticino sand. Géotechnique 1996, 46, 115–131. [Google Scholar] [CrossRef]
- Fioravante, V. Anisotropy of small strain stiffness of Ticino and Kenya sands from seismic wave propagation measured in triaxial testing. Soils Found. 2000, 40, 129–142. [Google Scholar] [CrossRef]
- Fioravante, V.; Giretti, D. Unidirectional cyclic resistance of Ticino and Toyoura sands from centrifuge cone penetration tests. Acta Geotech. 2016, 11, 953–968. [Google Scholar] [CrossRef]
- Jamiolkowski, M.B.; Lo Presti, D.C.F.; Manassero, M. Evaluation of relative density and shear strength from CPT and DMT. In Proceedings of the Soil behavior and soft ground construction, Ladd symposium, Reston, VA, USA, 5–6 October 2001; Germaine, T.C., Sheahan, T.C., Whitman, R.V., Eds.; ASCE: Reston, VA, USA, 2001; Volume 119, pp. 201–238. [Google Scholar]
- ASTM D1557-12e1. Standard Test Methods for Laboratory Compaction Characteristics of Soil Using Modified Effort (56,000 ft-lbf/ft3 (2700 kN-m/m3)); ASTM International: West Conshohocken, PA, USA, 2012; Available online: http://www.astm.org (accessed on 23 April 2021).
- Darcy, H. Les Fontaines Publiques de la Ville de Dijon: Exposition et Application des Principes a Suivre et des Formules a Employer dans les Questions de Distribution d’eau; Dalmont: Paris, France, 1856. [Google Scholar]
- Nicotera, M.; Papa, R.; Urciuoli, G. An experimental technique for determining the hydraulic properties of unsaturated pyroclastic soils. Geotech. Test. J. 2010, 33. [Google Scholar] [CrossRef]
- Schindler, U. Ein schnellverfahren zur messung der wasserleitfähigkeit im teilgesättigten boden an stechz, Arch. Acker Pfla-zenbau Bodenkd 1980, 24, 1–7. [Google Scholar]
- Richards, L.A. Porous plate apparatus for measuring moisture retention and transmission by soils. Soil Sci. 1948, 66, 105–110. [Google Scholar] [CrossRef]
- Richards, L.A. Physical condition of water in soil. In Methods of Soil Analysis. Part 1. Agronomy Monograph; Black, C.A., Ed.; ASA, SSSA: Madison, WI, USA, 1965; pp. 128–152. [Google Scholar]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 4, 892–898. [Google Scholar] [CrossRef]
- Šimůnek, J.; Šejna, M.; Saito, H.; Sakai, M.; van Genuchten, M.T. HYDRUS Software Series 3, Version 4.0; The HYDRUS-1D Software Package for Simulating the Movement of Water, Heat, and Multiple Solutes in Variably Saturated Media; Department of Environmental Sciences, University of California Riverside: Riverside, CA, USA, 2008.
- Marquardt, D.W. An algorithm for least-squares estimation of nonlinear parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Pirone, M.; Reder, A.; Rianna, G.; Pagano, L.; Nicotera, M.V.; Urciuoli, G. Laboratory and physical prototype tests for the investigation of hydraulic hysteresis of pyroclastic soils. Geosciences 2020, 10, 320. [Google Scholar] [CrossRef]
- Rianna, G.; Comegna, L.; Pagano, L.; Picarelli, L.; Reder, A. The role of hydraulic hysteresis on the hydrological response of pyroclastic silty covers. Water 2019, 11, 628. [Google Scholar] [CrossRef]
- Hueckel, T.; Baldi, G. Thermoplasticity of saturated clays: Experimental constitutive study. J. Geotech. Eng. 1990, 116. [Google Scholar] [CrossRef]
- Hueckel, T.; Pellegrini, R. Thermoplastic modelling of undrained failure of saturated clay due to heating. Soils Found. 1991, 31, 11–16. [Google Scholar] [CrossRef]
- Geo-slope International Ltd. Seep/W, Groundwater Seepage Analysis; GEO-SLOPE International Ltd.: Calgary, AB, Canada, 2012. [Google Scholar]
- Fredlund, D.G.; Rahardjo, H. Soil Mechanics for Unsaturated Soils; John Wiley & Sons: New York, NY, USA, 1993. [Google Scholar]
- Richards, L.A. Capillary conduction of liquids through porous medium. Int. J. Appl. Phys. 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Gottardi, G.; Gragnano, C.G.; Ranalli, M.; Tonni, L. Reliability analysis of riverbank stability accounting for the intrinsic variability of unsaturated soil parameters. Struct. Saf. 2020, 86, 01973. [Google Scholar] [CrossRef]
- Geo-slope International Ltd. Slope/W, Slope Stability Analysis; GEOSLOPE International Ltd.: Calgary, AB, Canada, 2012. [Google Scholar]
- Morgenstern, N.R.; Price, V.E. The analysis of the stability of general slip surfaces. Géotechnique 1965, 15, 79–93. [Google Scholar] [CrossRef]
- Vanapalli, S.K.; Fredlund, D.G.; Pufahl, D.E.; Clifton, A.W. Model for the prediction of shear strength with respect to soil suction. Can. Geotech. J. 1996, 33, 379–392. [Google Scholar] [CrossRef]
- Baker, R.; Leshchinsky, D. Spatial distribution of safety factors. J. Geotech. Geoenviron. 2001, 127, 135–145. [Google Scholar] [CrossRef]



| Soil | ɣmin | ɣmax | emin | emax | Gs | D50 | Uc | LL | PL | PI |
|---|---|---|---|---|---|---|---|---|---|---|
| kN/m3 | kN/m3 | - | - | - | mm | - | % | % | % | |
| TS | 13.64 | 16.67 | 0.574 | 0.923 | 2.671 1 | 0.574 1 | 1.83 1 | - | - | - |
| PON | - | - | - | - | 2.744 2 | 0.015 1 | - | 23.61 1 | 13.13 1 | 10.48 1 |
| TS70%-PON30% | 13.48 | 21.30 | 0.236 | 0.953 | 2.684 2 | 0.458 1 | 246.06 | 17.66 | 10.23 | 7.42 |
| Specimen | ɣd | w | n | e | Sr | Suction |
|---|---|---|---|---|---|---|
| kN/m3 | % | - | - | % | kPa | |
| MP1 | 20.89 | 8.20 | 0.207 | 0.261 | 84.47 | - |
| MP2 | 21.24 | 7.39 | 0.193 | 0.240 | 82.72 | - |
| MP3 | 20.79 | 7.80 | 0.211 | 0.267 | 78.53 | 4.5 |
| MP4 | 21.10 | 7.38 | 0.199 | 0.248 | 79.87 | 8 |
| MP5 | 20.82 | 7.30 | 0.209 | 0.265 | 74.00 | 6 |
| Average | 20.97 | 7.61 | 0.204 | 0.256 | 79.92 | 6.17 |
| Standard Deviation | 0.17 | 0.34 | 0.01 | 0.01 | 3.62 | 1.43 |
| Specimen | ksat | θr | θsat | α | nV | l | R2 |
|---|---|---|---|---|---|---|---|
| m/s | - | - | 1/kPa | - | - | - | |
| MP2 | 2.33 × 10−7 | - | - | - | - | - | - |
| MP3 | 1.10 × 10−8 | 0.005 | 0.190 | 0.013 | 1.650 | -0.030 | 0.920 |
| MP4 | 1.80 × 10−7 | - | - | - | - | - | - |
| MP5 | 6.08 × 10−7 | 0.017 | 0.200 | 0.011 | 1.400 | −0.330 | 0.930 |
| Logarithmic Mean | 1.29 × 10−7 | 0.011 | 0.195 | 0.012 | 1.525 | −0.180 | 0.925 |
| Standard Deviation | - | 0.006 | 0.005 | 0.001 | 0.125 | 0.150 | 0.005 |
| Sample | Specimen | γd | w | n | σ’c |
|---|---|---|---|---|---|
| (kN/m3) | (%) | (-) | (kPa) | ||
| MP6 | MP6_1 | 20.84 | 7.92 | 0.210 | 50 |
| MP6_2 | 21.01 | 7.54 | 0.203 | 100 | |
| MP6_3 | 20.89 | 7.57 | 0.208 | 200 | |
| MP7 | MP7_1 | 21.02 | 7.39 | 0.203 | 75 |
| MP7_2 | 21.07 | 7.40 | 0.201 | 150 | |
| MP7_3 | 20.79 | 7.21 | 0.212 | 300 | |
| Average | 20.94 | 7.51 | 0.206 | ||
| Standard Deviation | 0.10 | 0.22 | 0.004 |
| Material | γsat (kN/m2) | φ’ (°) | c’ (kPa) |
|---|---|---|---|
| Embankment Body | 22.96 | 45.50 | 5.00 |
| Foundation Layer | 21.14 | 33.00 | 2.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ventini, R.; Dodaro, E.; Gragnano, C.G.; Giretti, D.; Pirone, M. Experimental and Numerical Investigations of a River Embankment Model under Transient Seepage Conditions. Geosciences 2021, 11, 192. https://doi.org/10.3390/geosciences11050192
Ventini R, Dodaro E, Gragnano CG, Giretti D, Pirone M. Experimental and Numerical Investigations of a River Embankment Model under Transient Seepage Conditions. Geosciences. 2021; 11(5):192. https://doi.org/10.3390/geosciences11050192
Chicago/Turabian StyleVentini, Roberta, Elena Dodaro, Carmine Gerardo Gragnano, Daniela Giretti, and Marianna Pirone. 2021. "Experimental and Numerical Investigations of a River Embankment Model under Transient Seepage Conditions" Geosciences 11, no. 5: 192. https://doi.org/10.3390/geosciences11050192
APA StyleVentini, R., Dodaro, E., Gragnano, C. G., Giretti, D., & Pirone, M. (2021). Experimental and Numerical Investigations of a River Embankment Model under Transient Seepage Conditions. Geosciences, 11(5), 192. https://doi.org/10.3390/geosciences11050192






