Review of Processing and Interpretation of Self-Potential Anomalies: Transfer of Methodologies Developed in Magnetic Prospecting
Abstract
:1. Introduction
2. Self-Potential Observations: Analysis of Disturbances
2.1. Electrode Noise in SP Method
2.2. Temporal Variations in SP Method
2.3. Terrain Relief Correction
2.4. Calculation of SP Anomaly Distortion Due to Observations on Uneven Surface
2.5. Net Justification in Areal Observations
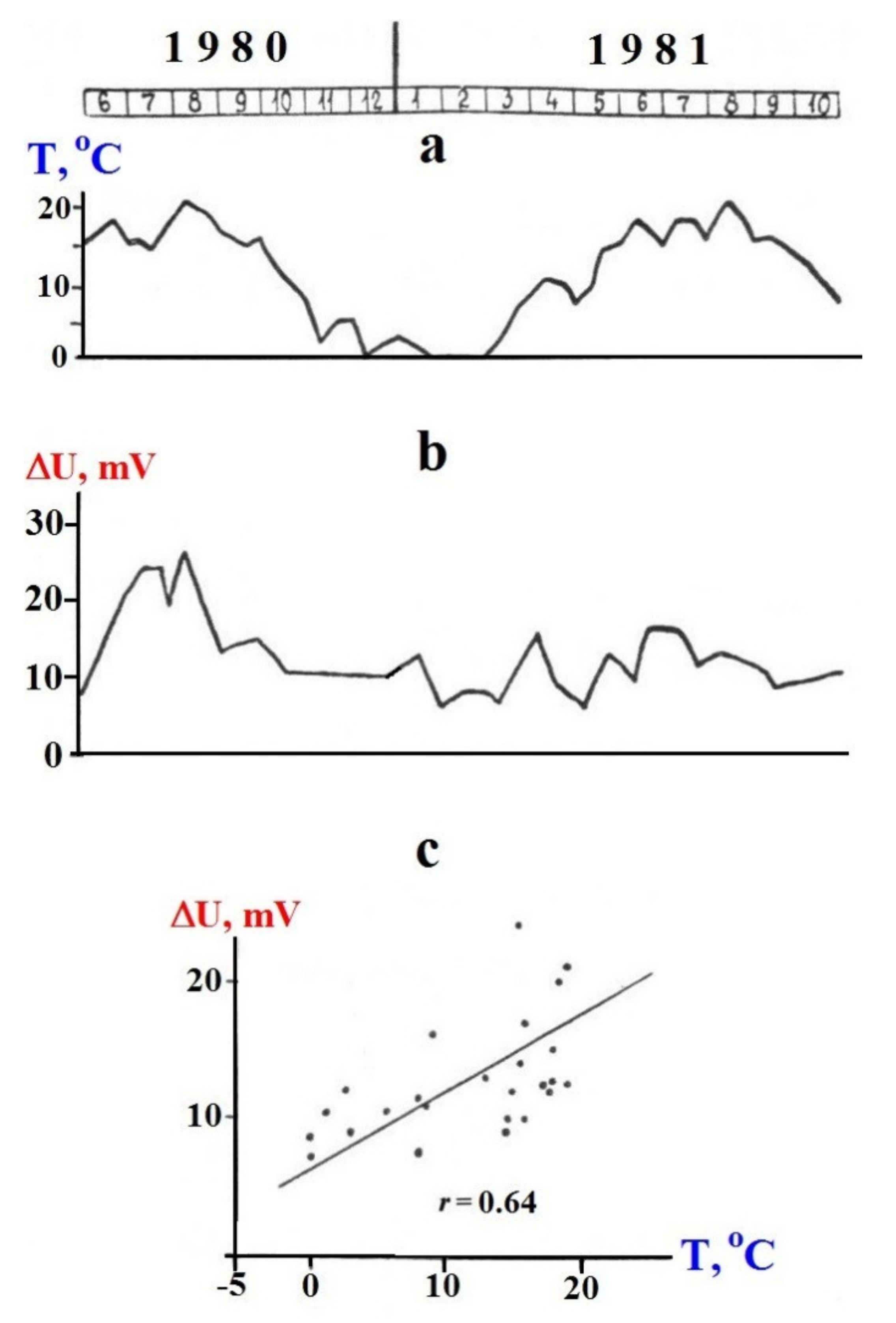
2.6. Influence of Meteorological Factors
2.7. Presence of Magmatic Associations
2.8. Some Environmental Factors
3. Review of Available Quantitative Interpretation Methods
4. Some Common Aspects of Magnetic and SP Fields
4.1. Quantitative Analysis of SP Anomalies by the Use of Advanced Methodologies Developed in Magnetic Prospecting
4.2. SP Observations on an Inclined Profile
5. Quantitative Analysis of SP Anomalies
5.1. Testing on Theoretical Models
5.2. Mining Geophysics
5.2.1. Chyragdere Sulfur Deposit (Central Azerbaijan)
5.2.2. Sariyer Sulphide-Pyrite Deposit (Near Istanbul, Turkey)
5.2.3. Polymetallic Deposit (Russia)
5.2.4. Katsdag Polymetallic Deposit (Azerbaijan)
5.2.5. Filizchai Polymetallic Deposit (Azerbaijan)
5.2.6. Uchambo Ore Field (Georgia)
5.2.7. Potentsialnoe Polymetallic Deposit (Rudnyi Altai, Russia)
5.2.8. Canyon Makhtesh Ramon (Negev Desert, Southern Israel)
5.3. Archaeological Sites
5.3.1. Roman Site of Banias (Northern Continuation) (Northern Israel)
5.3.2. Nabatean Site of Halutza (Southern Israel)
5.3.3. Christian Site of Emmaus-Nikopolis (Central Israel)
5.4. Environmental Geophysics
5.4.1. Buried Cavities in Dolomitic Limestone (Southern Italy)
5.4.2. Cavities in the Djuanda Forest Park (Bandung, Indonesia)
5.4.3. Subvertical Fissure Zone (Russia)
5.5. Technogenic Geophysics
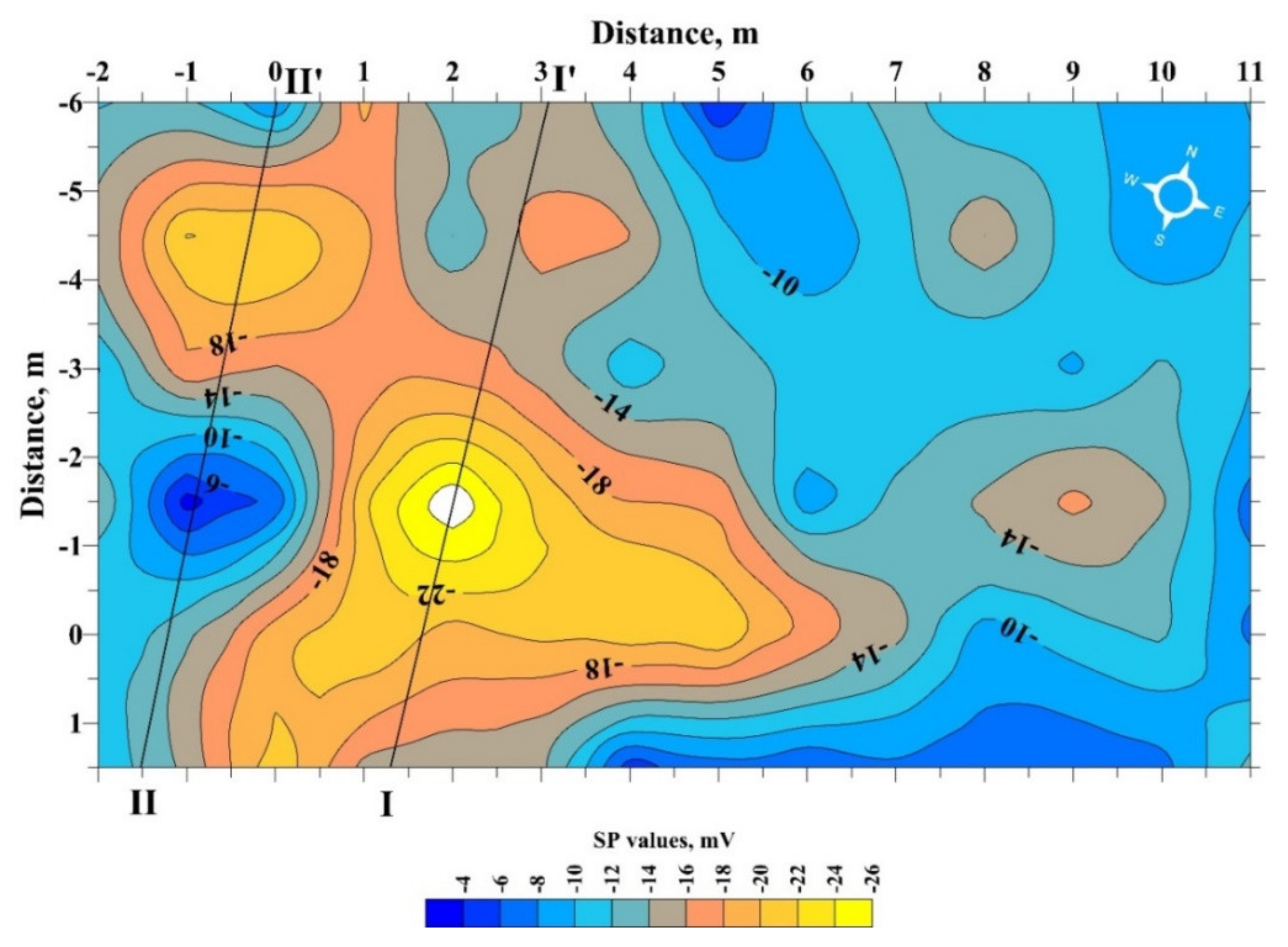
Underground Metallic Water-Pipe (Southern Russia)
5.6. Generalization of the Calculated Self-Potential Moments
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sato, M.; Mooney, H.M. The electrochemical mechanism of sulfide self-potentials. Geophysics 1960, 25, 226–249. [Google Scholar] [CrossRef]
- Fox, R.W. On the electromagnetic properties of metalliferous veins in the mines of Cornwall. R. Soc. Philos. Trans. 1833, 2, 399–414. [Google Scholar]
- Semenov, A.S. Electric Prospecting by Self-Potential Method, 4th ed.; revised and supplemented; Nedra: Leningrad, Russia, 1980. (In Russian) [Google Scholar]
- Parasnis, D.S. Principles of Applied Geophysics, 4th ed.; revised and supplemented; Chapman & Hall: London, UK, 1986. [Google Scholar]
- Corry, C.E. Spontaneous polarization associated with porphyry sulfide mineralization. Geophysics 1985, 50. [Google Scholar] [CrossRef] [Green Version]
- Babu, R.H.V.; Rao, A.D. Inversion of self-potential anomalies in mineral exploration. Comput. Geosci. 1988, 14, 377–387. [Google Scholar] [CrossRef]
- Lile, O.B. Self potential anomaly over a sulphide conductor tested for use as a current source. J. Appl. Geophys. 1996, 36, 97–104. [Google Scholar] [CrossRef]
- Goldie, M. Self-potentials associated with the Yanacocha high-sulfidation gold deposit in Peru. Geophysics 2002, 67, 684–689. [Google Scholar] [CrossRef]
- Bhattacharya, B.B.; Shalivakhan, J.A.; Bera, A. Three-dimensional probability tomography of self-potential anomalies of graphite and sulphide mineralization in Orissa and Rajasthan, India. First Break 2007, 5, 223–230. [Google Scholar] [CrossRef]
- Dmitriev, A.N. Direct and inverse SP modeling on the basis of exact model of self-potential field nature. Geol. Geophys. 2012, 53, 797–812. [Google Scholar] [CrossRef]
- Fedi, M.; Abbas, M. A fast interpretation of self-potential data using the depth from extreme points method. Geophysics 2013, 78, E107–E116. [Google Scholar] [CrossRef]
- Biswas, A.; Sharma, S.P. Integrated geophysical studies to elicit the structure associated with uranium mineralization around South Purulia shear zone, India: A review. Ore Geol. Rev. 2016, 72, 1307–1326. [Google Scholar] [CrossRef]
- Eppelbaum, L.V. Geophysical Potential Fields: Geological and Environmental Applications; Elsevier: Amsterdam, The Netherlands; New York, NY, USA, 2019. [Google Scholar]
- Eppelbaum, L.V. Advanced system of self-potential field analysis in ore deposits of the South Caucasus. Proc. Natl. Azerbaijan Acad. Sci. 2019, 2, 21–35. [Google Scholar] [CrossRef]
- Wynn, J.C.; Sherwood, S.I. The self-potential (SP) method: An inexpensive reconnaissance and archaeological mapping tool. J. Field Archaeol. 1984, 11, 195–204. [Google Scholar] [CrossRef]
- Mauriello, P.; Monna, D.; Patella, D. 3D geoelectric tomography and archaeological applications. Geophys. Prospect. 1998, 46, 543–570. [Google Scholar] [CrossRef]
- Eppelbaum, L.; Ben-Avraham, Z.; Itkis, S. Ancient Roman remains in Israel provide a challenge for physical-archaeological modeling techniques. First Break 2003, 21, 51–61. [Google Scholar] [CrossRef]
- Eppelbaum, L.V.; Ben-Avraham, Z.; Itkis, S.E. Integrated geophysical investigations at the Halutza archaeological site. In Proceedings of the 64 EAGE Conference, Florence, Italy, 27–30 May 2002; pp. 1–4. [Google Scholar] [CrossRef]
- Drahor, M.G. Application of the self-potential method to archaeological prospection: Some case histories. Archaeol. Prospect. 2004, 11, 77–105. [Google Scholar] [CrossRef]
- Di Maio, R.; Fedi, M.; Lamanna, M.; Grimaldi, M.; Pappaladro, U. The Contribution of Geophysical Prospecting in the Reconstruction of the Buried Ancient Environments of the House of Marcus Fabius Rufus (Pompeii, Italy). Archaeol. Prospect. 2010, 17, 259–269. [Google Scholar] [CrossRef]
- Shevnin, V.A.; Bobachev, A.A.; Ivanova, S.V.; Baranchuk, K.I. Joint analysis of self potential and electrical resistivity tomography data for studying Alexandrovsky settlement. In Proceedings of the 20th European Meeting of Environmental and Engineering Geophysics, Athens, Greece, 14–18 September 2014; pp. 1–5. [Google Scholar] [CrossRef]
- De Giorgi, L.; Leucci, G. The archaeological site of Sagalassos (Turkey): Exploring the mysteries of the invisible layers using geophysical methods. Explor. Geophys. 2017, 49, 751–761. [Google Scholar] [CrossRef]
- De Giorgi, L.; Leucci, G. Passive and Active Electric Methods: New Frontiers of Application. In Innovation in Near-Surface Geophysics; Persico, R., Piro, S., Linford, N., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 1–21. [Google Scholar] [CrossRef]
- Corwin, R.F. Application of the Self-Potential Method for Engineering and Environmental Investigations. In SAGEEP Proceedings; Society of Exploration Geophysicists: Tulsa, OK, USA, 1990; pp. 107–121. [Google Scholar]
- Quarto, R.; Schiavone, D. Detection of cavities by the self-potential method. First Break 1996, 14, 419–430. [Google Scholar] [CrossRef]
- Jardani, A.; Dupont, J.; Revil, A. Self-potential signals associated with preferential groundwater flow pathways in sinkholes. J. Geophys. Res. 2006, 111, B09204. [Google Scholar] [CrossRef] [Green Version]
- Eppelbaum, L.V. Revealing of subterranean karst using modern analysis of potential and quasi-potential fields. In Proceedings of the 2007 SAGEEP Conference, Denver, CO, USA, 1–5 April 2007; pp. 797–810. [Google Scholar] [CrossRef]
- Srigutomo, W.; Arkanuddin, M.R.; Pratomo, P.M.; Novana, E.C.; Agustina, R.D. Application of qualitative and quantitative analyses of self potential anomaly in caves detection in Djuanda Forest Park, Bandung. Am. Inst. Phys. Proc. 2010, 1325, 164–167. [Google Scholar] [CrossRef]
- Chen, Y.; Qin, X.; Huang, Q.; Gan, F.; Han, K.; Zheng, Z.; Meng, Y. Anomalous spontaneous electrical potential characteristics of epi-karst in the Longrui Depression, Southern Guangxi Province, China. Environ. Earth Sci. 2018, 77, 1–9. [Google Scholar] [CrossRef]
- Gusev, A.P.; Kaleichik, P.A.; Fedorsky, M.S.; Shavrin, I.A. Dynamics of self-potential field as indicator of dangerous rock-slide areas in industrial landscape (on example of Belarus). Bull. Perm Univ. 2018, 17, 120–127. (In Russian) [Google Scholar]
- Oliveti, I.; Cardarelli, E. Self-Potential data inversion for environmental and hydrogeological investigations. Pure Appl. Geophys. 2019, 176, 3607–3628. [Google Scholar] [CrossRef]
- Castermant, J.; Mendonça, C.; Revil, A.; Trolard, F.; Bourrie, G.; Linde, N. Redox potential distribution inferred from self-potential measurements associated with the corrosion of a burden metallic body. Geophys. Prospect. 2008, 56, 269–282. [Google Scholar] [CrossRef]
- Fomenko, N.E. Ecological Geophysics; South State University: Rostov-on-Don, Russia, 2010. (In Russian) [Google Scholar]
- Onojasun, O.E.; Takum, E. Geophysical investigation using self-potential techniques: A case of locating underground water pipeline at Kwinana industrial area, Perth. Afr. J. Geo-Sci. Res. 2015, 3, 19–23. [Google Scholar]
- Cui, Y.; Zhu, X.; Wei, W.; Liu, J.; Tong, T. Dynamic imaging of metallic contamination plume based on self-potential data. Trans. Nonferrous Met. Soc. China 2017, 27, 1822–1830. [Google Scholar] [CrossRef]
- Perrier, F.; Pant, S.R. Noise reduction in long-term self-potential monitoring with travelling electrode referencing. Pure Appl. Geophys. 2005, 162, 165–179. [Google Scholar] [CrossRef]
- Zaborovsky, A.I. Electric Prospecting; Gostoptekhizdat: Moscow, Russia, 1963. (In Russian) [Google Scholar]
- Khesin, B.E.; Alexeyev, V.V.; Eppelbaum, L.V. Interpretation of Geophysical Fields in Complicated Environments; Modern Approaches in Geophysics, Boston–Dordrecht–London; Kluwer Academic Publishers (Springer): Amsterdam, The Netherlands, 1996. [Google Scholar]
- Ernstson, K.; Scherer, V. Self-potential variations with time and their relation to hydrogeologic and meteorological parameters. Geophysics 1986, 51, 1967–1977. [Google Scholar] [CrossRef]
- Eppelbaum, L.V.; Mishne, A.R. Unmanned Airborne Magnetic and VLF investigations: Effective Geophysical Methodology of the Near Future. Positioning 2011, 2, 112–133. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.-H.; Geng, Y. Terrain correction in the gradient calculation of spontaneous potential data. Chin. J. Geophys. 2015, 58, 654–664. [Google Scholar] [CrossRef]
- Telford, W.M.; Geldart, L.P.; Sheriff, R.E. Applied Geophysics, 2nd ed.; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Revil, A.; Jardani, A. The Self-Potential Method: Theory and Applications in Environmental Geosciences; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Perrier, F.; Morat, P. Characterization of electrical daily variations induced by capillary flow in the non-saturated zone. Pure Appl. Geophys. 2000, 157, 785–810. [Google Scholar] [CrossRef]
- Jardani, A.; Revil, A. Stochastic joint inversion of temperature and self-potential data. Geophys. J. Int. 2009, 179, 640–654. [Google Scholar] [CrossRef] [Green Version]
- Petrovsky, A. The problem of a hidden polarized sphere. Philos. Mag. 1928, 5, 914–933. [Google Scholar] [CrossRef]
- Murty, B.V.; Haricharan, P. A simple approach toward interpretation SP anomaly due to 2-D sheet model of short dipole length. Geophys. Res. Bull. 1984, 22, 213–218. [Google Scholar]
- Fitterman, D.V. Calculation of self-potential anomalies near vertical contacts. Geophysics 1979, 44, 195–205. [Google Scholar] [CrossRef]
- Rao, D.A.; Babu, H.V.; Sivakumar, G.D.J. A Fourier transform method for the interpretation of SP anomalies due to two-dimensional inclined sheets of finite depth extent. Pure Appl. Geophys. 1982, 120, 365–374. [Google Scholar] [CrossRef]
- Rao, S.V.S.; Mohan, N.L. Spectral interpretation of self-potential anomaly due to an inclined sheet. Curr. Sci. 1984, 53, 474–477. [Google Scholar]
- Banerjee, B.; Pal, B.P. Frequency domain interpretation of Self-Potential anomalies. Gerlands Beitr. Geophys. 1990, 99, 531–538. [Google Scholar]
- Skianis, G.A.; Papadopoulos, T.D.; Vaiopoulos, D.A. 1-D and 2-D spatial frequency analysis of SP field anomalies produced by a polarized sphere. Pure Appl. Geophys. 1991, 137, 251–260. [Google Scholar] [CrossRef]
- Skianis, G.; Papadopoulos, T.; Vaiopoulos, D.A.; Nikolaou, S. A new method of quantitative interpretation of SP anomalies produced by a polarized inclined sheet. Geophys. Prospect. 1995, 43, 677–691. [Google Scholar] [CrossRef]
- Abdelrahman, E.M.; Sharafeldin, S.M. A least squares approach to depth determination from residual self-potential anomalies caused by horizontal cylinders and spheres. Geophysics 1997, 62, 44–48. [Google Scholar] [CrossRef]
- Abdelrahman, E.M.; El-Araby, T.M.; Ammar, A.A.; Hassanein, H.I. A least-squares approach to shape determination from selfpotential anomalies. Pure Appl. Geophys. 1997, 150, 121–128. [Google Scholar] [CrossRef]
- Abdelrahman, E.M.; Ammar, A.A.; Hassanein, H.I.; Hafez, M.A. Derivative analysis of SP anomalies. Geophysics 1998, 63, 890–897. [Google Scholar] [CrossRef]
- El-Araby, H.M. A new method for complete quantitative interpretation of self-potential anomalies. J. Appl. Geophys. 2004, 55, 211–224. [Google Scholar] [CrossRef]
- Essa, K.; Mehanee, S.; Smith, P.D. A new inversion algorithm for estimating the best fitting parameters of some geometrically simple body to measured self-potential anomalies. Explor. Geophys. 2008, 39, 155–163. [Google Scholar] [CrossRef]
- Gibert, D.; Pessel, M. Identification of sources of potential fields with the continuous wavelet transform: Application to SP profiles. Geophys. Res. Lett. 2001, 28, 1863–1866. [Google Scholar] [CrossRef]
- Sailhac, P.; Marquis, G. Analytic potentials for the forward and inverse modeling of SP anomalies caused by subsurface fluid flow. Geophys. Res. Lett. 2001, 28, 1851–1854. [Google Scholar] [CrossRef] [Green Version]
- Patella, D. Introduction to ground surface self-potential tomography. Geophys. Prospect. 1997, 45, 653–681. [Google Scholar] [CrossRef]
- Di Maio, R.; Piegari, E.; Rani, P.; Avella, A. Self-Potential data inversion through the integration of spectral analysis and tomographic approaches. Geophys. J. Int. 2016, 206, 1204–1220. [Google Scholar] [CrossRef]
- Mendonça, C.A. Forward and inverse self-potential modeling in mineral exploration. Geophysics 2008, 73, F33–F43. [Google Scholar] [CrossRef]
- Srivastava, S.; Agarwal, B.N.P. Interpretation of self-potential anomalies by enhanced local wave number technique. J. Appl. Geophys. 2009, 68, 259–268. [Google Scholar] [CrossRef]
- Al-Garni, M.A. Interpretation of spontaneous potential anomalies from some simple geometrically shaped bodies using neural network inversion. Acta Geophys. 2017, 58, 143–162. [Google Scholar] [CrossRef]
- Hristenko, L.A.; Stepanov, Y.I. Transformation of SP observations for solving engineering-geological problems. Min. Inf. Anal. Bull. 2012, 169–173. (In Russian) [Google Scholar]
- Gobashy, M.; Abdelazeem, M.; Abdrabou, M.; Khalil, M.H. Estimating model parameters from self-potential anomaly of 2D inclined sheet using whale optimization algorithm: Applications to mineral exploration and tracing shear zones. Nat. Resour. Res. 2020, 29, 499–519. [Google Scholar] [CrossRef]
- Rao, K.; Jain, S.; Biswas, A. Global optimization for delineation of self-potential anomaly of a 2D inclined plate. Nat. Resour. Res. 2021, 30, 175–189. [Google Scholar] [CrossRef]
- Tlas, M.; Asfahani, J. An approach for interpretation of self-potential anomalies due to simple geometrical structures using Fair function minimization. Pure Appl. Geophys. 2013, 170, 895–905. [Google Scholar] [CrossRef]
- Giannakis, I.; Tsourlos, P.; Papazachos, C.; Vargemezis, G.; Giannopoulos, A.; Papadopoulos, N.; Tosti, F.; Alani, A. A hybrid optimization scheme for self-potential measurements due to multiple sheet-like bodies in arbitrary 2D resistivity distributions. Geophys. Prospect. 2019, 67, 1948–1964. [Google Scholar] [CrossRef]
- Kilty, K.T. On the origin and interpretation of self-potential anomalies. Geophys. Prospect. 1984, 32, 51–62. [Google Scholar] [CrossRef]
- Eppelbaum, L.V.; Khesin, B.E. Geophysical Studies in the Caucasus; Springer: Heidelberg, Germany; New York, NY, USA, 2012. [Google Scholar]
- Zhdanov, M.S.; Keller, G.V. The Geoelecrical Methods in Geophysical Exploration; Elsevier: Amsterdam, The Netherlands, 1994. [Google Scholar]
- Jardani, A.; Revil, A.; Bolève, A.; Dupont, J.P. Three-dimensional inversion of self-potential data used to constrain the pattern of groundwater flow in geothermal fields. J. Geophys. Res. 2008, 113, B09204. [Google Scholar] [CrossRef]
- Akgün, M. Estimation of some bodies parameters from the self potential method using Hilbert transform. J. Balk. Geophys. Soc. 2001, 4, 29–44. [Google Scholar]
- Sindirgi, P.; Pamukçu, O.; Özyalin, S. Application of normalized full gradient method to self potential (SP) data. Pure Appl. Geophys. 2008, 165, 409–427. [Google Scholar] [CrossRef]
- Sindrigi, P.; Özyalin, S. Estimating the location of a causative body from a self-potential anomaly using 2D and 3D normalized full gradient and Euler deconvolution. Turk. J. Earth Sci. 2019, 28, 640–659. [Google Scholar] [CrossRef]
- Agarwal, B.N.P.; Srivastava, S. Analyses of self-potential anomalies by conventional and extended Euler deconvolution techniques. Comput. Geosci. 2009, 35, 2231–2238. [Google Scholar] [CrossRef]
- Biswas, A. Inversion of Amplitude from the 2-D Analytic Signal of Self-Potential Anomalies. In Minerals; Essa, K.S., Ed.; IntechOpen: London, UK, 2018; pp. 13–45. [Google Scholar] [CrossRef] [Green Version]
- Sungkono. Robust interpretation of single and multiple self-potential anomalies via flower pollination algorithm. Arab. J. Geosci. 2020, 13, 1–15. [Google Scholar] [CrossRef]
- Eppelbaum, L.V.; Khesin, B.E.; Itkis, S.E. Prompt magnetic investigations of archaeological remains in areas of infrastructure development: Israeli experience. Archaeol. Prospect. 2001, 8, 163–185. [Google Scholar] [CrossRef]
- Eppelbaum, L.V. Quantitative interpretation of magnetic anomalies from bodies approximated by thick bed models in complex environments. Environ. Earth Sci. 2015, 74, 5971–5988. [Google Scholar] [CrossRef]
- Göktürkler, G.; Balkaya, Ç. Inversion of self-potential anomalies caused by simple-geometry bodies using global optimization algorithms. J. Geophys. Eng. 2012, 10, 498–507. [Google Scholar] [CrossRef]
- Stern, W. Relation between spontaneous polarization curves and depth, size, and dip of ore bodies. Trans. Am. Inst. Min. Metallurg. Petr. Eng. 1945, 164, 189–196. [Google Scholar]
- Yüngül, S. Spontaneous-potential survey of a copper deposit at Sariyer, Turkey. Geophysics 1954, 19, 455–458. [Google Scholar] [CrossRef]
- Sengupta, S.N.; Bose, R.N.; Mitra, S.K. Geophysical investigations for copper ores in the Singhana-Gotpo area, Khetri copper belt, Rajasthan (India). Geoexpoloration 1969, 7, 73–82. [Google Scholar] [CrossRef]
- Logn, O.; Bolviken, B. Self potentials at the Joma pyrite deposit, Norway. Geoexploration 1974, 12, 11–28. [Google Scholar] [CrossRef]
- Cowan, D.R.; Allchurch, P.D.; Omnes, G. An integrated geo-electrical survey on the Nangaroo copper-zinc prospect, near Leonora, Western Australia. Geoexploration 1975, 13, 77–98. [Google Scholar] [CrossRef]
- Nayak, P.N. Electromechanical potential in surveys for sulphide. Geoexploration 1981, 18, 311–320. [Google Scholar] [CrossRef]
- Alizadeh, A.M.; Guliyev, I.S.; Kadirov, F.A.; Eppelbaum, L.V. Geosciences in Azerbaijan. Volume II: Economic Minerals and Applied Geophysics; Springer: Heidelberg, Germany; New York, NY, USA, 2017. [Google Scholar]
- Erofeev, L.Y.; Orekhov, A.N.; Erofeeva, G.V. Natural electric fields in Siberian gold deposits: Structure, origin, and relationship with gold orebodies. Geol. Geophys. 2017, 58, 984–989. [Google Scholar] [CrossRef]
- Safipour, R.; Hölz, S.; Halbach, J.; Jegen, M.; Petersen, S.; Swidinsky, A. A self-potential investigation of submarine massive sulfides, Palinuro Seamount, Tyrrhenian Sea. Geophysics 2017, 82, A51–A56. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Z.; Shen, J.; Tao, C.; Deng, X.; Wu, T.; Nie, Z.; Wang, W.; Su, Z. Autonomous underwater vehicle based marine multi-component self-potential method: Observation scheme and navigational correction. Geosci. Instrum. Methods Data Syst. 2020, 10, 1–25. [Google Scholar] [CrossRef]
- Bukhnikashvili, A.V.; Kebuladze, V.V.; Tabagua, G.G.; Dzhashi, G.G.; Gugunava, G.E.; Tatishvili, O.V.; Gogua, R.A. Geophysical Exploration of Adjar Group of Copper-Polymetallic Deposits; Metsniereba: Tbilisi, Russia, 1974. (In Russian) [Google Scholar]
- Semenov, M.V. Principles of Prospecting and Investigating Pyrite-Polymetallic Ore Fields by Geophysical Methods; Nedra: Leningrad, Russia, 1975. (In Russian) [Google Scholar]
- Eppelbaum, L.V.; Vaksman, V.L.; Kouznetsov, S.V.; Sazonova, L.M.; Smirnov, S.A.; Surkov, A.V.; Bezlepkin, B.; Katz, Y.; Korotaeva, N.N.; Belovitskaya, G. Discovering of microdiamonds and minerals-satellites in Canyon Makhtesh Ramon (Negev desert, Israel). Dokl. Earth Sci. 2006, 407, 202–204. [Google Scholar] [CrossRef]
- Drahor, M.G.; Akyol, A.L.; Dilaver, N. An application of the self-potential (SP) method in archaeogeophysical prospection. Archaeol. Prospect. 2006, 3, 141–158. [Google Scholar] [CrossRef]
- Tsokas, G.N.; Tourlos, P.I.; Kim, J.-H.; Papazachos, C.B.; Vargemezis, G.; Bogiatzis, P. Assessing the condition of the rock mass over the tunnel of Eupalinus in Samos (Greece) using both conventional geophysical methods and surface to tunnel electrical resistivity tomography. Archaeol. Prospect. 2014, 21, 277–291. [Google Scholar] [CrossRef]
- Eppelbaum, L.V.; Khesin, B.E.; Itkis, S.E.; Ben-Avraham, Z. Advanced analysis of self-potential data in ore deposits and archaeological sites. In Proceedings of the 10th European Meeting of Environmental and Engineering Geophysics, Utrecht, The Netherlands, 6–9 September 2004; pp. 1–4. [Google Scholar] [CrossRef]
- Eppelbaum, L.V. Quantitative analysis of self-potential anomalies in archaeological sites of Israel: An overview. Environ. Earth Sci. 2020, 79, 1–15. [Google Scholar] [CrossRef]
- Meyers, E.M. (Ed.) The Oxford Encyclopedia of Archaeology in the Near East; Oxford University Press: Oxford, UK, 1996; Volume 5. [Google Scholar]
- Hartal, M. Banias, the Aqeduct. Excav. Surv. Isr. 1997, 16, 5–8. [Google Scholar]
- Kenyon, K.M. Archaeology in the Holy Land; Norton: New York, NY, USA, 1979. [Google Scholar]
- Kempinski, A.; Reich, R. (Eds.) The Architecture of Ancient Israel; Israel Exploration Society: Jerusalem, Israel, 1992. [Google Scholar]
- Ogilvy, A.A.; Bogoslovsky, V.A. The possibilities of geophysical methods applied for investigating the impact of man on the geological medium. Geophys. Prospect. 1979, 27, 775–789. [Google Scholar] [CrossRef]
- Corwin, R.F. The Self-Potential Method for Environmental and Engineering Application. In Geotechnical and Environmental Geophysics; Ward, S.H., Ed.; Society of Exploration Geophysicists: Tulsa, OK, USA, 1996; Volume 1, pp. 127–145. [Google Scholar]
- Gurk, M.; Bosch, F. Cave detection using the Self-Potential-Surface (SPS) technique on a karstic terrain in the Jura Mountains (Switzerland). In Proceedings of the Kolloquium Elektromagnetische Tiefenforschung, Burg Ludwigstein, Germany, 9–13 March 2001; pp. 283–291. [Google Scholar]
- Vichabian, Y.; Morgan, F.D. Self-potentials in cave detection. Lead. Edge 2002, 21, 866–871. [Google Scholar] [CrossRef]
- Lapenna, V.; Lorenzo, P.; Perrone, A.; Piscitelli, S.; Sdao, F.; Rizzo, E. High-resolution geoelectrical tomographies in the study of Giarrossa landslide (southern Italy). Bull. Eng. Geol. Environ. 2003, 62, 259–268. [Google Scholar] [CrossRef]
- Jardani, A.; Revil, A.; Dupont, J. Self-potential tomography applied to the determination of cavities. Geophys. Res. Lett. 2006, 23, L13401. [Google Scholar] [CrossRef]
- Jardani, A.; Revil, A.; Santos, F.; Fauchard, C.; Dupont, J. Detection of preferential infiltration pathways in sinkholes using joint inversion of self-potential and EM-34 conductivity data. Geophys. Prospect. 2007, 55, 749–760. [Google Scholar] [CrossRef]
- Rozycki, A.; Fonticiella, J.M.R.; Cuadra, A. Detection and evaluation of horizontal fractures in Earth dams using self-potential method. Eng. Geol. 2006, 82, 145–153. [Google Scholar] [CrossRef]
- Gibert, D.; Sailhac, P. Comment on ‘‘Self-potential signals associated with preferential groundwater flow pathways in sinkholes’’ by A. Jardani, J.P. Dupont, and A. Revil, J. of Geophys. Res.; 113, B03210. J. Geophys. Res. 2008, 113, B03210. [Google Scholar] [CrossRef] [Green Version]
- Tripathi, G.N.; Frayar, A.E. Integrated surface geophysical approach to locate a karst conduit: A case study from Royal Spring Basin, Kentucky, USA. J. Nepal Geol. Soc. 2016, 51, 27–37. [Google Scholar] [CrossRef]
- Shevnin, V.A. Identification of self-potential anomalies of a diffusion-absorption origin. Mosc. Univ. Geol. Bull. 2018, 73, 306–311. [Google Scholar] [CrossRef]
- Ekine, A.S.; Emujakporue, G.O. Investigation of corrosion of buried oil pipeline by the electrical geophysical methods. J. Appl. Sci. Environ. Manage. 2010, 14, 63–65. [Google Scholar] [CrossRef]
- Rittgers, J.B.; Revil, A.; Karaoulis, M.; Mooney, M.A.; Slater, L.D.; Atekwana, E.A. Self-potential signals generated by the corrosion of buried metallic objects with application to contaminant plumes. Geophysics 2013, 78, EN65–EN82. [Google Scholar] [CrossRef]



















| Method | Gravity | Magnetic | Resistivity | Self-Potential |
|---|---|---|---|---|
| Price of equipment US $ | 60,000–110,000 | 20,000–25,000 | 35,000–55,000 | 150–200 |
| Field | Analytical Expression | |
|---|---|---|
| Magnetic | Thin bed (TB) (12) | Point source (rod) (13) |
| Self- Potential | Horizontal circular cylinder (HCC) (14) | Sphere (15) |
| Parameters Necessary for Examination | Parameters Derived from Anomalies from Models | Formulas for Calculation of Parameters Necessary for Quantitative Analysis | ||
|---|---|---|---|---|
| Thin Bed | HCC | Thin Bed | HCC | |
| Generalized Angle θ | d1, d2 d1r d1, d5 d1r, d5 | |||
| Depth h0, hc | d1, d2, θ d1r, θ d5, θ | |||
| Horizontal Displacement x0, xc | h, θ, xmax, xmin,r | |||
| Normal Background | ∆Umin, ∆UA, θ | |||
| Self-Potential Moment | ∆Ua, h0, hc, Q | |||
| Variable | Description |
|---|---|
| θ | Generalized angle reflecting the degree of SP anomaly asymmetry as a function relation of an anomalous body depth of occurrence, geometric form, value of polarization |
| x0 | Horizontal displacement of projection of the middle of the upper edge of thin bed to the earth’s surface due to oblique polarization |
| xc | Horizontal displacement of projection of the center of the HCC to the earth’s surface due to oblique polarization |
| h0 | Depth to the upper edge of thin bed |
| hc | Depth to the center of HCC |
| ∆Umax | Maximum value of SP anomaly |
| ∆Umin | Minimum value of SP anomaly |
| ∆UA | Total amplitude of SP anomaly |
| d1 | Difference of extremum abscissae for thin bed |
| d1r | Difference of extremum abscissae for HCC |
| d2 | Difference of semiamplitude point abscissae |
| d5 | Difference of inflection point abscissae |
| xr | Right inflection abscissae point |
| xl | Left inflection abscissae point |
| ∆Ubackr | Normal background level of SP anomaly |
| Self-potential moment for the models of thin bed or HCC |
| Object | Location | Approximation Model | Value of Self-Potential Moment |
|---|---|---|---|
| I. Ore geophysics | |||
| Sariyer sulphide-pyrite deposit | near Istanbul, Turkey | HCC | |
| Polymetallic deposit | Russia | thin bed | |
| Katsdag polymetallic deposit | Southern Greater Caucasus, Azerbaijan | thin bed | |
| Filizchai polymetallic deposit (Azerbaijan) | Southern Greater Caucasus, Azerbaijan | thin bed | 14,600 mV·m |
| Uchambo ore field | Lesser Caucasus, Georgia | HCC | |
| Potentsialnoe polymetallic deposit | Rudnyi Altai, Russia | thin bed, thick bed, HCC | (for HCC) |
| II. Archaeogeophysics | |||
| Banias (anomaly I) | northern Israel | thin bed | |
| Banias (anomaly II) | “—” | HCC | |
| Halutza | southern Israel | thin bed | |
| Emmaus-Nikopolis | central Israel | HCC | 4.5 mV·m2 |
| III. Environmental Geophysics | |||
| Underground cave | southern Italy | HCC | |
| Underground cave | Bandung, Indonesia | thin bed | |
| Fissured zone | Russia | thin bed | |
| IV. Technogenic geophysics | |||
| Underground metallic water-pipe | southern Russia | HCC | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eppelbaum, L.V. Review of Processing and Interpretation of Self-Potential Anomalies: Transfer of Methodologies Developed in Magnetic Prospecting. Geosciences 2021, 11, 194. https://doi.org/10.3390/geosciences11050194
Eppelbaum LV. Review of Processing and Interpretation of Self-Potential Anomalies: Transfer of Methodologies Developed in Magnetic Prospecting. Geosciences. 2021; 11(5):194. https://doi.org/10.3390/geosciences11050194
Chicago/Turabian StyleEppelbaum, Lev V. 2021. "Review of Processing and Interpretation of Self-Potential Anomalies: Transfer of Methodologies Developed in Magnetic Prospecting" Geosciences 11, no. 5: 194. https://doi.org/10.3390/geosciences11050194
APA StyleEppelbaum, L. V. (2021). Review of Processing and Interpretation of Self-Potential Anomalies: Transfer of Methodologies Developed in Magnetic Prospecting. Geosciences, 11(5), 194. https://doi.org/10.3390/geosciences11050194






