Practical Estimation of Landslide Kinematics Using PSI Data
Abstract
1. Introduction
2. Case Studies
3. Workflow and Analyses
- 1-
- PSI data post-processing to extract quantities suitable to describe landslide kinematics;
- 2-
- spatial analysis of (point-like) PSI data to select profile traces representative of landside complexity (swath profiles) and distribute the information over landslide area (interpolation);
- 3-
- extraction of 2D profiles and assessment of the most suitable approach;
- 4-
- interpretation of 2D profiles using non-specific templates derived from simplified 2D FEM models and comparison to field evidence of selected case studies.
3.1. PSI Datasets Post-Processing and Kinematic Descriptors
3.2. Data Spatialization
3.3. Profiles Extraction
3.4. Profiles Interpretation
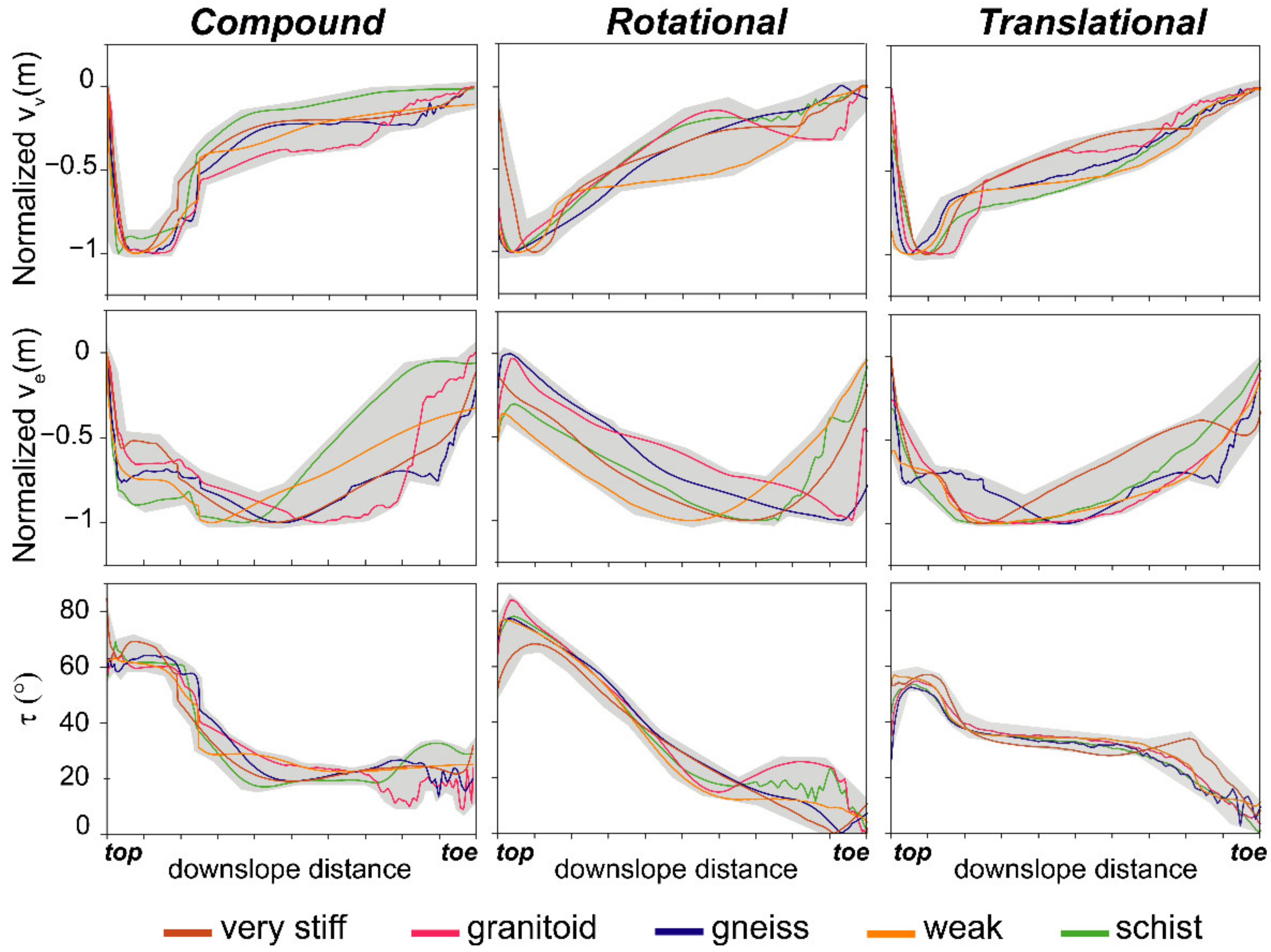
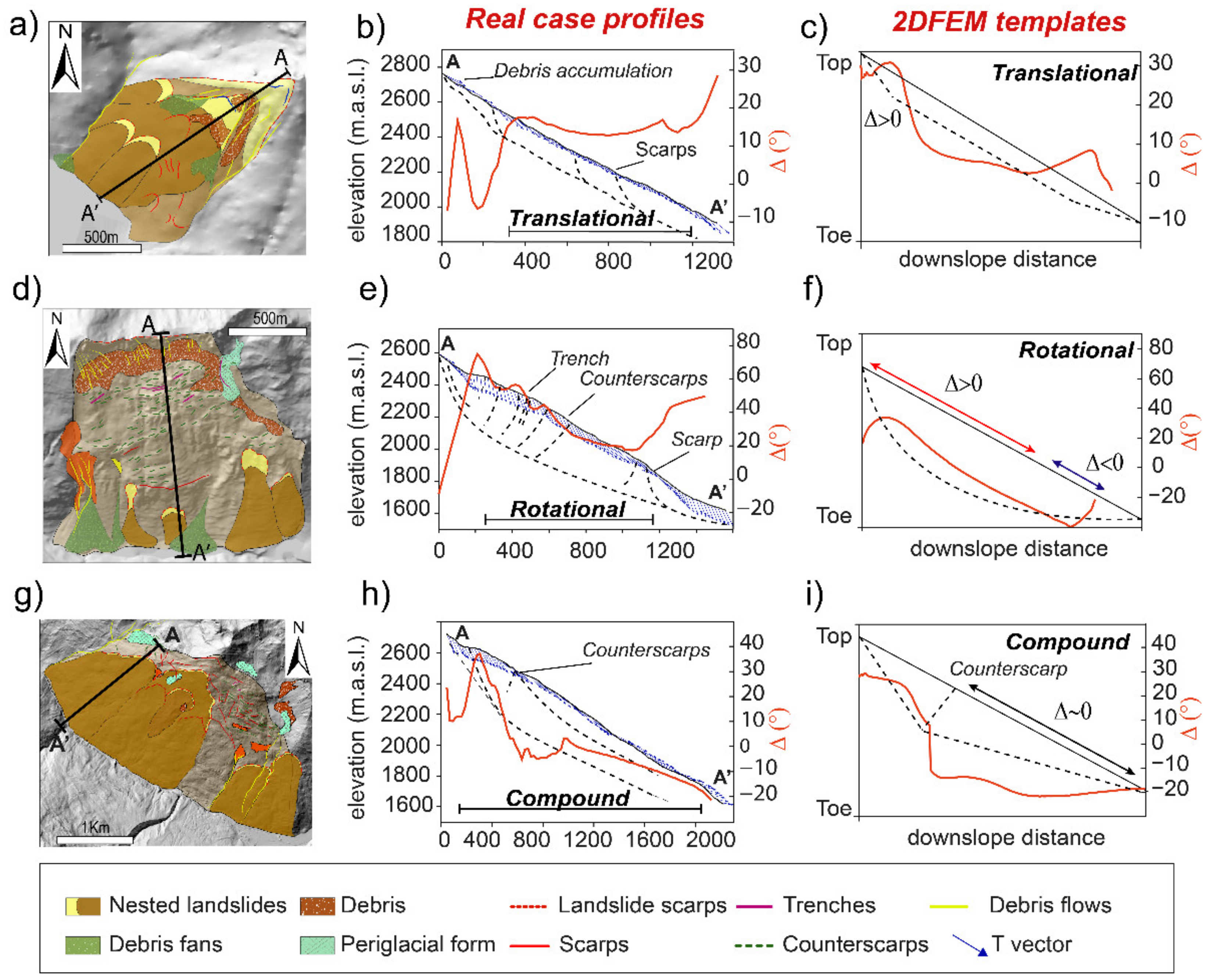
3.4.1. DFEM Interpretation Templates
3.4.2. Interpretation Using Geomorphological Mapping
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Crippa, C.; Valbuzzi, E.; Frattini, P.; Crosta, G.B.; Spreafico, M.C.; Agliardi, F. Semi-automated regional classification of the style of activity of slow rock-slope deformations using PS InSAR and SqueeSAR velocity data. Landslides 2021. [Google Scholar] [CrossRef]
- Aslan, G.; Foumelis, M.; Raucoules, D.; De Michele, M.; Bernardie, S.; Cakir, Z. Landslide mapping and monitoring using persistent scatterer interferometry (PSI) technique in the French alps. Remote Sens. 2020, 12, 1305. [Google Scholar] [CrossRef]
- Gullà, G.; Peduto, D.; Borrelli, L.; Antronico, L.; Fornaro, G. Geometric and kinematic characterization of landslides affecting urban areas: The Lungro case study (Calabria, Southern Italy). Landslides 2017, 14, 171–188. [Google Scholar] [CrossRef]
- Brückl, E.; Brunner, F.K.; Kraus, K. Kinematics of a deep-seated landslide derived from photogrammetric, GPS and geophysical data. Eng. Geol. 2006, 88, 149–159. [Google Scholar] [CrossRef]
- Travelletti, J.; Malet, J.-P. Characterization of the 3D geometry of flow-like landslides: A methodology based on the integration of heterogeneous multi-source data. Eng. Geol. 2012, 128, 30–48. [Google Scholar] [CrossRef]
- Wasowski, J.; Pisano, L. Long-term InSAR, borehole inclinometer, and rainfall records provide insight into the mechanism and activity patterns of an extremely slow urbanized landslide. Landslides 2020, 17, 445–457. [Google Scholar] [CrossRef]
- Wasowski, J.; Bovenga, F. Investigating landslides and unstable slopes with satellite Multi Temporal Interferometry: Current issues and future perspectives. Eng. Geol. 2014, 174, 103–138. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Schlögel, R.; Doubre, C.; Malet, J.P.; Masson, F. Landslide deformation monitoring with ALOS/PALSAR imagery: A D-InSAR geomorphological interpretation method. Geomorphology 2015, 231, 314–330. [Google Scholar] [CrossRef]
- Eriksen, H.Ø.; Lauknes, T.R.; Larsen, Y.; Corner, G.D.; Bergh, S.G.; Dehls, J.; Kierulf, H.P. Visualizing and interpreting surface displacement patterns on unstable slopes using multi-geometry satellite SAR interferometry (2D InSAR). Remote Sens. Environ. 2017, 191, 297–312. [Google Scholar] [CrossRef]
- Frattini, P.; Crosta, G.B.; Rossini, M.; Allievi, J. Activity and kinematic behaviour of deep-seated landslides from PS-InSAR displacement rate measurements. Landslides 2018, 15, 1053–1070. [Google Scholar] [CrossRef]
- Agliardi, F.; Riva, F.; Barbarano, M.; Zanchetta, S.; Scotti, R.; Zanchi, A. Effects of tectonic structures and long-term seismicity on paraglacial giant slope deformations: Piz Dora (Switzerland). Eng. Geol. 2019, 263, 105353. [Google Scholar] [CrossRef]
- Agliardi, F.; Crosta, G.B.; Frattini, P. Slow rock-slope deformation. In Landslides: Types, Mechanisms and Modeling; Cambridge University Press: Cambridge, UK, 2012; p. 207. [Google Scholar]
- Crosta, G.B.; Frattini, P.; Agliardi, F. Deep seated gravitational slope deformations in the European Alps. Tectonophysics 2013, 605, 13–33. [Google Scholar] [CrossRef]
- Chigira, M. September 2005 rain-induced catastrophic rockslides on slopes affected by deep-seated gravitational deformations, Kyushu, southern Japan. Eng. Geol. 2009, 108, 1–15. [Google Scholar] [CrossRef]
- Audemard, F.A.; Beck, C.; Carrillo, E. Deep-seated gravitational slope deformations along the active Boconó Fault in the central portion of the Mérida Andes, western Venezuela. Geomorphology 2010, 124, 164–177. [Google Scholar] [CrossRef]
- Lin, C.W.; Tseng, C.M.; Tseng, Y.H.; Fei, L.Y.; Hsieh, Y.C.; Tarolli, P. Recognition of large scale deep-seated landslides in forest areas of Taiwan using high resolution topography. J. Asian Earth Sci. 2013, 62, 389–400. [Google Scholar] [CrossRef]
- Agliardi, F.; Crosta, G.B.; Frattini, P.; Malusà, M.G. Giant non-catastrophic landslides and the long-term exhumation of the European Alps. Earth Planet. Sci. Lett. 2013, 365, 263–274. [Google Scholar] [CrossRef]
- Bovis, M.J.; Evans, S.G. Extensive deformations of rock slopes in southern Coast Mountains, southwest British Columbia, Canada. Eng. Geol. 1996, 44, 163–182. [Google Scholar] [CrossRef]
- Agliardi, F.; Crosta, G.B.; Zanchi, A. Structural constraints on deep-seated slope deformation kinematics. Eng. Geol. 2001, 59, 83–102. [Google Scholar] [CrossRef]
- Crosta, G.B.; di Prisco, C.; Frattini, P.; Frigerio, G.; Castellanza, R.; Agliardi, F. Chasing a complete understanding of the triggering mechanisms of a large rapidly evolving rockslide. Landslides 2013, 11, 747–764. [Google Scholar] [CrossRef]
- Grämiger, L.M.; Moore, J.R.; Gischig, V.S.; Ivy-Ochs, S.; Loew, S. Beyond debuttressing: Mechanics of paraglacial rock slope damage during repeat glacial cycles. J. Geophys. Res. Earth Surf. 2017, 122, 1004–1036. [Google Scholar] [CrossRef]
- Riva, F.; Agliardi, F.; Amitrano, D.; Crosta, G.B. Damage-Based Time-Dependent Modeling of Paraglacial to Postglacial Progressive Failure of Large Rock Slopes. J. Geophys. Res. Earth Surf. 2018, 123, 124–141. [Google Scholar] [CrossRef]
- Ambrosi, C.; Crosta, G.B. Large sackung along major tectonic features in the Central Italian Alps. Eng. Geol. 2006, 83, 183–200. [Google Scholar] [CrossRef]
- Frattini, P.; Crosta, G.B.; Allievi, J. Damage to buildings in large slope rock instabilities monitored with the PSinSAR™ technique. Remote Sens. 2013, 5, 4753–4773. [Google Scholar] [CrossRef]
- Crosta, G.B.; Imposimato, S.; Roddeman, D.G. Numerical modelling of large landslides stability and runout. Nat. Hazards Earth Syst. Sci. 2003, 3, 523–538. [Google Scholar] [CrossRef]
- Eberhardt, E.; Stead, D.; Coggan, J.S. Numerical analysis of initiation and progressive failure in natural rock slopes-the 1991 Randa rockslide. Int. J. Rock Mech. Min. Sci. 2004, 41, 69–87. [Google Scholar] [CrossRef]
- Rott, H.; Scheuchl, B.; Siegel, A.; Grasemann, B. Monitoring very slow slope movements by means of SAR interferometry: A case study from a mass waste above a reservoir in the Otztal Alps, Austria. Geophys. Res. Lett. 1999, 26, 1629–1632. [Google Scholar] [CrossRef]
- Agliardi, F.; Crippa, C.; Spreafico, M.C.; Manconi, A.; Bourlès, D.; Braucher, R.; Cola, G.; Zanchetta, S. Strain partitioning and heterogeneous evolution in a giant slope deformation revealed by InSAR, dating and modelling. In Proceedings of the Geophysical Research Abstracts, Vienna, Austria, 7–12 April 2019; Volume 21. [Google Scholar]
- Jongmans, D.; Garambois, S. Geophysical investigation of landslides: A review. Bull. Soc. Géol. Fr. 2007, 178, 101–112. [Google Scholar] [CrossRef]
- Bovis, M.J. Rock-slope deformation at Affliction Creek, southern Coast Mountains, British Columbia. Can. J. Earth Sci. 1990, 27, 243–254. [Google Scholar] [CrossRef]
- Ferretti, A.; Fumagalli, A.; Novali, F.; Prati, C.; Rocca, F.; Rucci, A. A new algorithm for processing interferometric data-stacks: SqueeSAR. In IEEE Transactions on Geoscience and Remote Sensing; IEEE: Piscataway, NJ, USA, 2011. [Google Scholar]
- Colesanti, C.; Ferretti, A.; Prati, C.; Rocca, F. Monitoring landslides and tectonic motions with the Permanent Scatterers Technique. Eng. Geol. 2003, 68, 3–14. [Google Scholar] [CrossRef]
- Colesanti, C.; Wasowski, J. Investigating landslides with space-borne Synthetic Aperture Radar (SAR) interferometry. Eng. Geol. 2006, 88, 173–199. [Google Scholar] [CrossRef]
- Rosi, A.; Agostini, A.; Tofani, V.; Casagli, N. A Procedure to map subsidence at the regional scale using the persistent scatterer interferometry (PSI) technique. Remote Sens. 2014, 6, 10510–10522. [Google Scholar] [CrossRef]
- Agliardi, F.; Spreafico, M.C.; Zanchetta, S.; Castellanza, R.; Asnaghi, R.; Paternoster, J.; Crippa, C.; Crosta, G. Gravitational transfer zones influence DSGSD mechanisms and activity. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 4–13 April 2018; Volume 20, p. 13819. [Google Scholar]
- Schmid, S.M.; Fügenschuh, B.; Kissling, E.; Schuster, R. Tectonic map and overall architecture of the Alpine orogen. Eclogae Geol. Helv. 2004, 97, 93–117. [Google Scholar] [CrossRef]
- Ferrari, F.; Giani, G.P.; Apuani, T. Towards the comprehension of rockfall motion, with the aid of in situ tests. In Proceedings of the Vajont Thoughts and Analyses after 50 Years Since the Catastrophic Landslide, Padua, Italy, 8–10 October 2013; Sapienza Università Editrice: Roma, Italy; pp. 163–171. [Google Scholar]
- Henderson, I.H.C.; Lauknes, T.R.; Osmundsen, P.T.; Dehls, J.; Larsen, Y.; Redfield, T.F. A structural, geomorphological and InSAR study of an active rock slope failure development. Geol. Soc. London, Spec. Publ. 2011, 351, 185–199. [Google Scholar] [CrossRef]
- Notti, D.; Herrera, G.; Bianchini, S.; Meisina, C.; García-Davalillo, J.C.; Zucca, F. A methodology for improving landslide PSI data analysis. Int. J. Remote Sens. 2014, 35, 2186–2214. [Google Scholar] [CrossRef]
- Joughin, L.R.; Kwok, R.; Fahnestock, M.A. Interferometric estimation of three-dimensional ice-flow using ascending and descending passes. IEEE Trans. Geosci. Remote Sens. 1998, 36, 25–37. [Google Scholar] [CrossRef]
- Notti, D.; Meisina, C.; Zucca, F.; Colombo, A. Models To Predict Persistent Scatterers Data Distribution and Their Capacity To Register Movement Along the Slope. In Proceedings of the Fringe 2011, Frascati, Italy, 19–23 September 2011; pp. 19–23. [Google Scholar]
- Meisina, C.; Zucca, F.; Notti, D.; Colombo, A.; Cucchi, A.; Savio, G.; Giannico, C.; Bianchi, M. Geological interpretation of PSInSAR Data at regional scale. Sensors 2008, 8, 7469–7492. [Google Scholar] [CrossRef] [PubMed]
- Manzo, M.; Ricciardi, G.P.P.; Casu, F.; Ventura, G.; Zeni, G.; Borgström, S.; Berardino, P.; Del Gaudio, C.; Lanari, R. Surface deformation analysis in the Ischia Island (Italy) based on spaceborne radar interferometry. J. Volcanol. Geotherm. Res. 2006, 151, 399–416. [Google Scholar] [CrossRef]
- Dalla Via, G.; Crosetto, M.; Crippa, B. Resolving vertical and east-west horizontal motion from differential interferometric synthetic aperture radar: The L’Aquila earthquake. J. Geophys. Res. Solid Earth 2012, 117. [Google Scholar] [CrossRef]
- Ferretti, A. Satellite InSAR Data: Reservoir Monitoring from Space; EAGE Publications: Houten, The Netherlands, 2014; ISBN 978-90-73834-71-2. [Google Scholar]
- Baulig, H. Sur une méthode altimétrique d’analyse morphologique appliquée à la Bretagne péninsulaire. Bull. Assoc. Geogr. Fr. 1926, 3, 7–9. [Google Scholar] [CrossRef]
- Grohmann, C.H. Morphometric analysis in geographic information systems: Applications of free software GRASS and R. Comput. Geosci. 2004, 30, 1055–1067. [Google Scholar] [CrossRef]
- Sibson, R. A Brief Description of Natural Neighbor Interpolation chapter 2. In Interpolating Multivariate Data; John Wiley & Sons: New York, NY, USA, 1981; pp. 21–36. [Google Scholar]
- Hammah, R.E.; Yacoub, T.; Corkum, B.; Curran, J.H. The practical modelling of discontinuous rock masses with finite element analysis. In Proceedings of the The 42nd US Rock Mechanics Symposium (USRMS), San Francisc, CA, USA, 29 June–2 July 2008. [Google Scholar]
- Riahi, A.; Hammah, E.R.; Curran, J.H. Limits of applicability of the finite element explicit joint model in the analysis of jointed rock problems. In Proceedings of the 44th US Rock Mechanics Symposium and 5th US-Canada Rock Mechanics Symposium, Salt Lake City, UT, USA, 27–30 June 2010. [Google Scholar]
- Dawson, E.M.; Roth, W.H.; Drescher, A. Slope stability analysis by strength reduction. Geotechnique 1999, 49, 835–840. [Google Scholar] [CrossRef]
- Agliardi, F.; Scuderi, M.M.; Fusi, N.; Collettini, C. Slow-to-fast transition of giant creeping rockslides modulated by undrained loading in basal shear zones. Nat. Commun. 2020, 11, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Peduto, D.; Ferlisi, S.; Nicodemo, G.; Reale, D.; Pisciotta, G.; Gullà, G. Empirical fragility and vulnerability curves for buildings exposed to slow-moving landslides at medium and large scales. Landslides 2017, 14, 1993–2007. [Google Scholar] [CrossRef]
- Uzielli, M.; Catani, F.; Tofani, V.; Casagli, N. Risk analysis for the Ancona landslide—I: Characterization of landslide kinematics. Landslides 2015, 12, 69–82. [Google Scholar] [CrossRef]
- Intrieri, E.; Frodella, W.; Raspini, F.; Bardi, F.; Tofani, V. Using satellite interferometry to infer landslide sliding surface depth and geometry. Remote Sens. 2020, 12, 1462. [Google Scholar] [CrossRef]
- Eriksen, H.Ø. Combining Satellite and Terrestrial Interferometric Radar Data to Investigate Surface Displacement in the Storfjord and Kåfjord Area, Northern Norway. Ph.D. Thesis, The Arctic University of Norway, Tromsø, Norway, 2017. [Google Scholar]










| Satellite | PSI Technique | Mode | Θ (°) | Δ (°) | Revisit Time (Days) | Time Interval (Years) |
|---|---|---|---|---|---|---|
| Sentinel 1A/B | SqueeSAR™ | Ascending | 41.99 | 10.23 | 12 (6 after 2016) | 2015–2017 |
| Sentinel 1A/B | SqueeSAR™ | Descending | 41.78 | 8.89 | 2015–2017 |
| Slope Material below Unstable Mass | Very Stiff | Weak | Schist | Gneiss | Granitoid | |
|---|---|---|---|---|---|---|
| Unit Weight (MN/m3) | 0.027 | 0.027 | 0.027 | 0.027 | 0.027 | 0.027 |
| Stiffness | isotropic | isotropic | isotropic | isotropic | isotropic | isotropic |
| Poisson Ratio | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 |
| Young Modulus | 100,000 | 100,000 | 10,000 | 19,000 | 31,000 | 41,000 |
| Material Type | elastic | plastic | plastic | plastic | plastic | plastic |
| Peak Tensile Strength (MPa) | 5 | 0.4 | 0.4 | 0.1 | 0.15 | 0.2 |
| Peak Cohesion (MPa) | 5 | 0.75 | 0.3 | 0.4 | 0.5 | 0.7 |
| Peak Friction Angle (°) | 35 | 35 | 30 | 36 | 47 | 50 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Crippa, C.; Agliardi, F. Practical Estimation of Landslide Kinematics Using PSI Data. Geosciences 2021, 11, 214. https://doi.org/10.3390/geosciences11050214
Crippa C, Agliardi F. Practical Estimation of Landslide Kinematics Using PSI Data. Geosciences. 2021; 11(5):214. https://doi.org/10.3390/geosciences11050214
Chicago/Turabian StyleCrippa, Chiara, and Federico Agliardi. 2021. "Practical Estimation of Landslide Kinematics Using PSI Data" Geosciences 11, no. 5: 214. https://doi.org/10.3390/geosciences11050214
APA StyleCrippa, C., & Agliardi, F. (2021). Practical Estimation of Landslide Kinematics Using PSI Data. Geosciences, 11(5), 214. https://doi.org/10.3390/geosciences11050214







