Uncertainty Assessment of Entropy-Based Circular Channel Shear Stress Prediction Models Using a Novel Method
Abstract
:1. Introduction
2. Materials and Methods
2.1. Entropy Models
2.1.1. Shannon Model
2.1.2. Shannon PL Model
2.1.3. Tsallis Entropy Model
2.1.4. Renyi Model
2.2. Global Shear Stress (ρgRs)
2.3. Data Collection
2.4. Uncertainty Analysis
2.4.1. HBMES-1 Uncertainty Method
2.4.2. HBMES-2 Uncertainty Method
- Determining the OCBi and its borders;
- 2.
- Assessment of the final OCB (OCBn);
- 3.
- Introducing the uncertainty index of FOCB.
3. Results and Discussion
3.1. Calibration
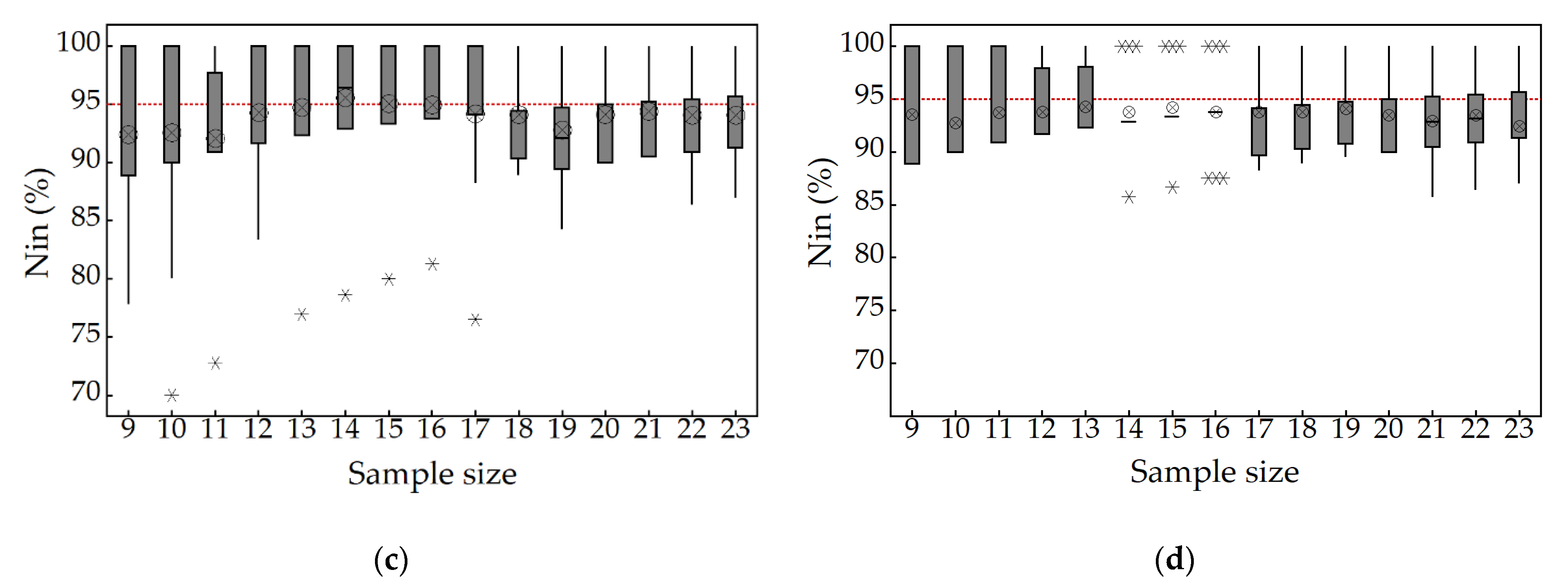
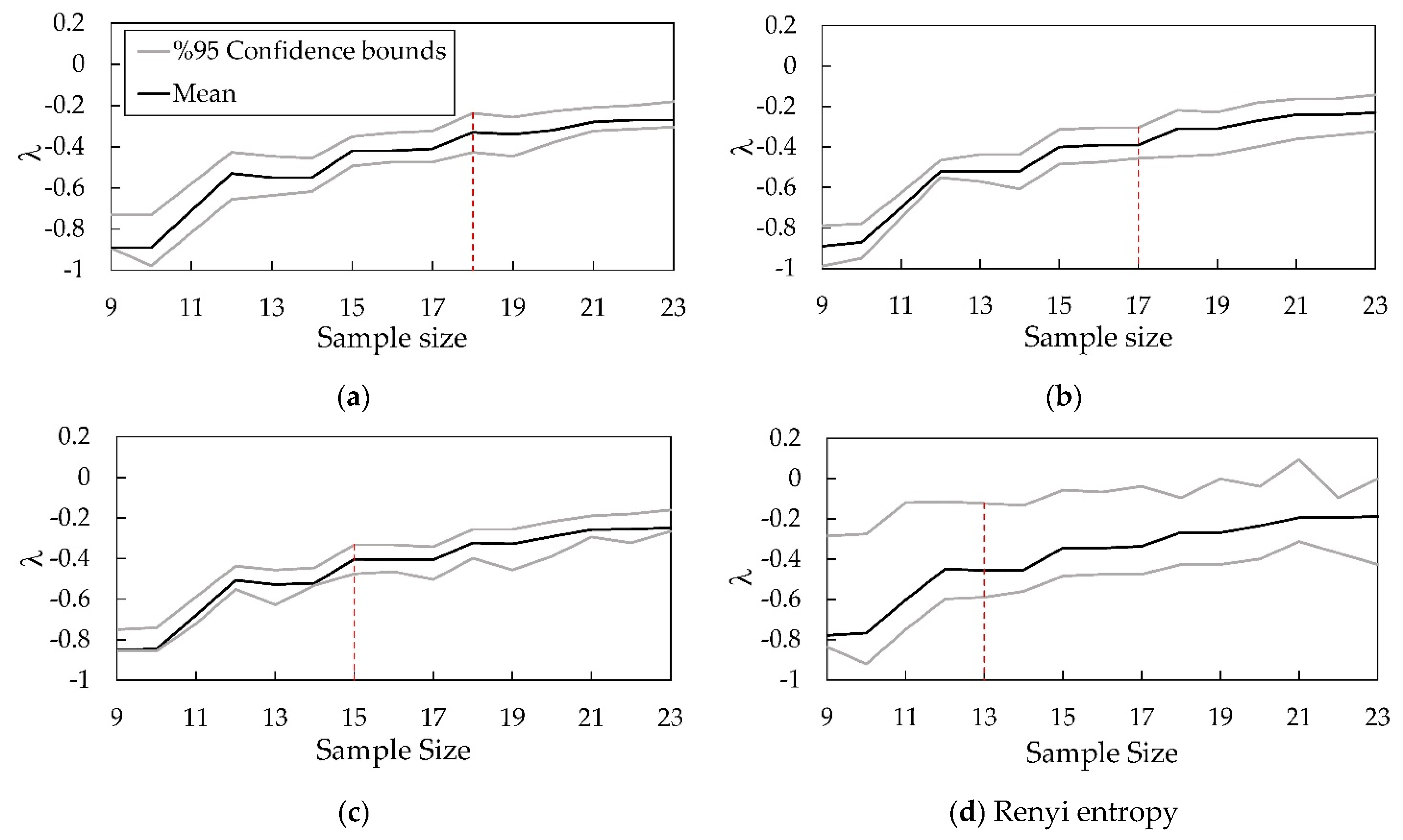
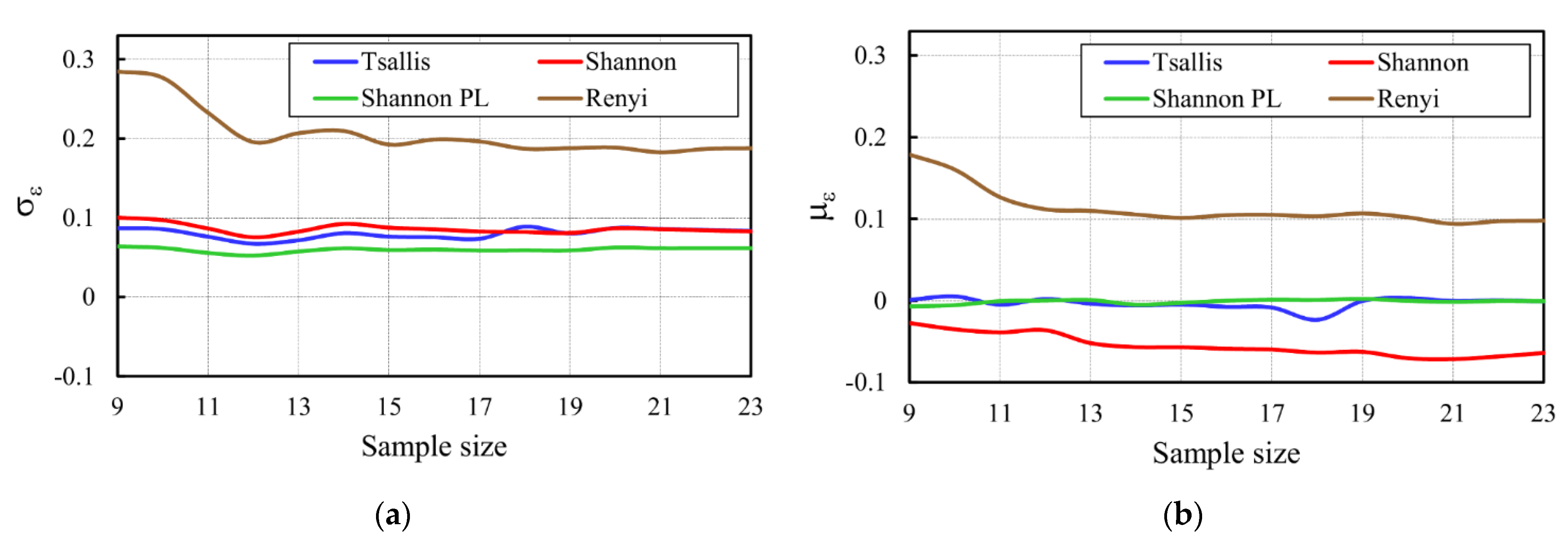
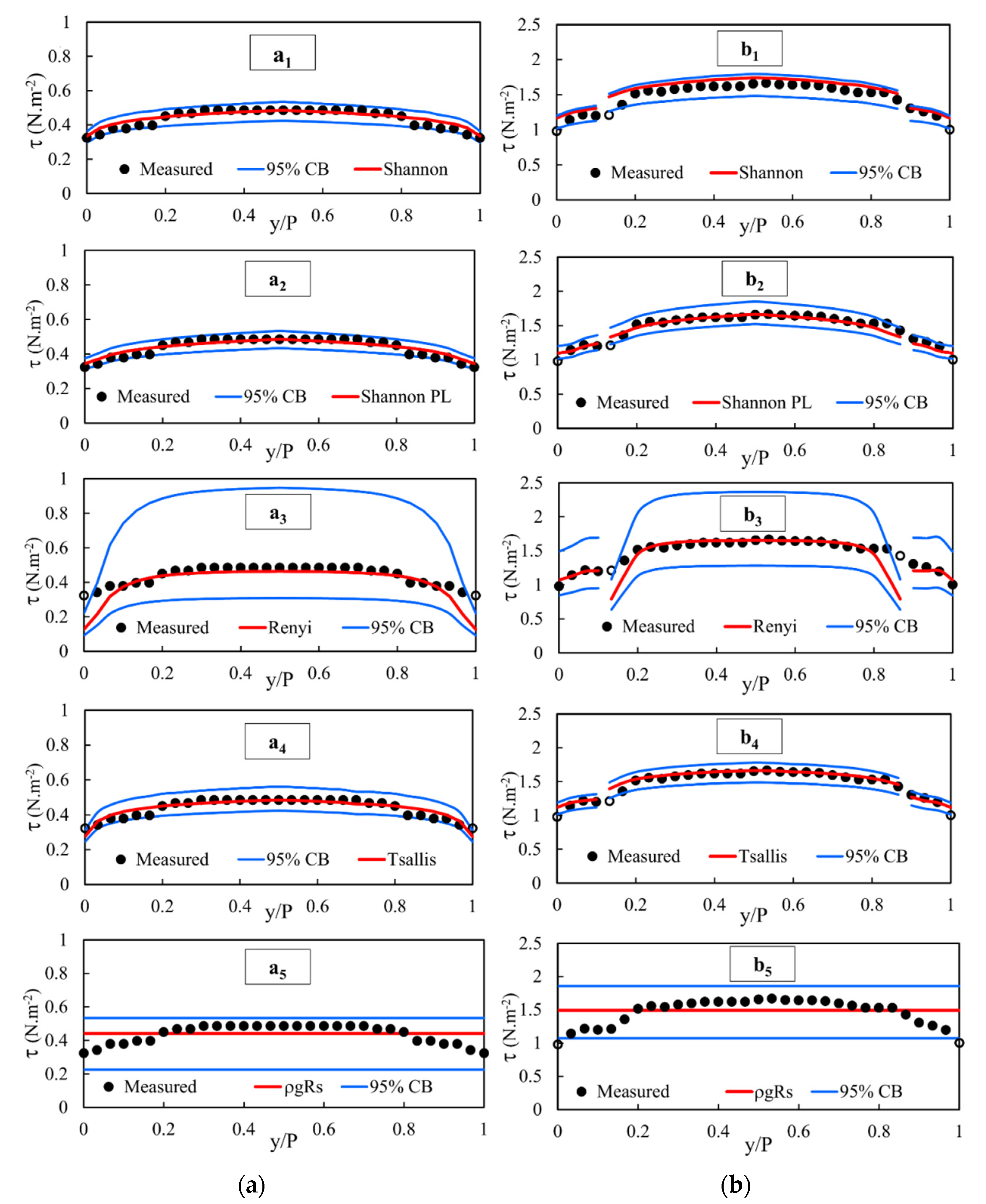
3.2. Assessment of Uncertainty of Four Entropy Models Using the HBMES-1 Method
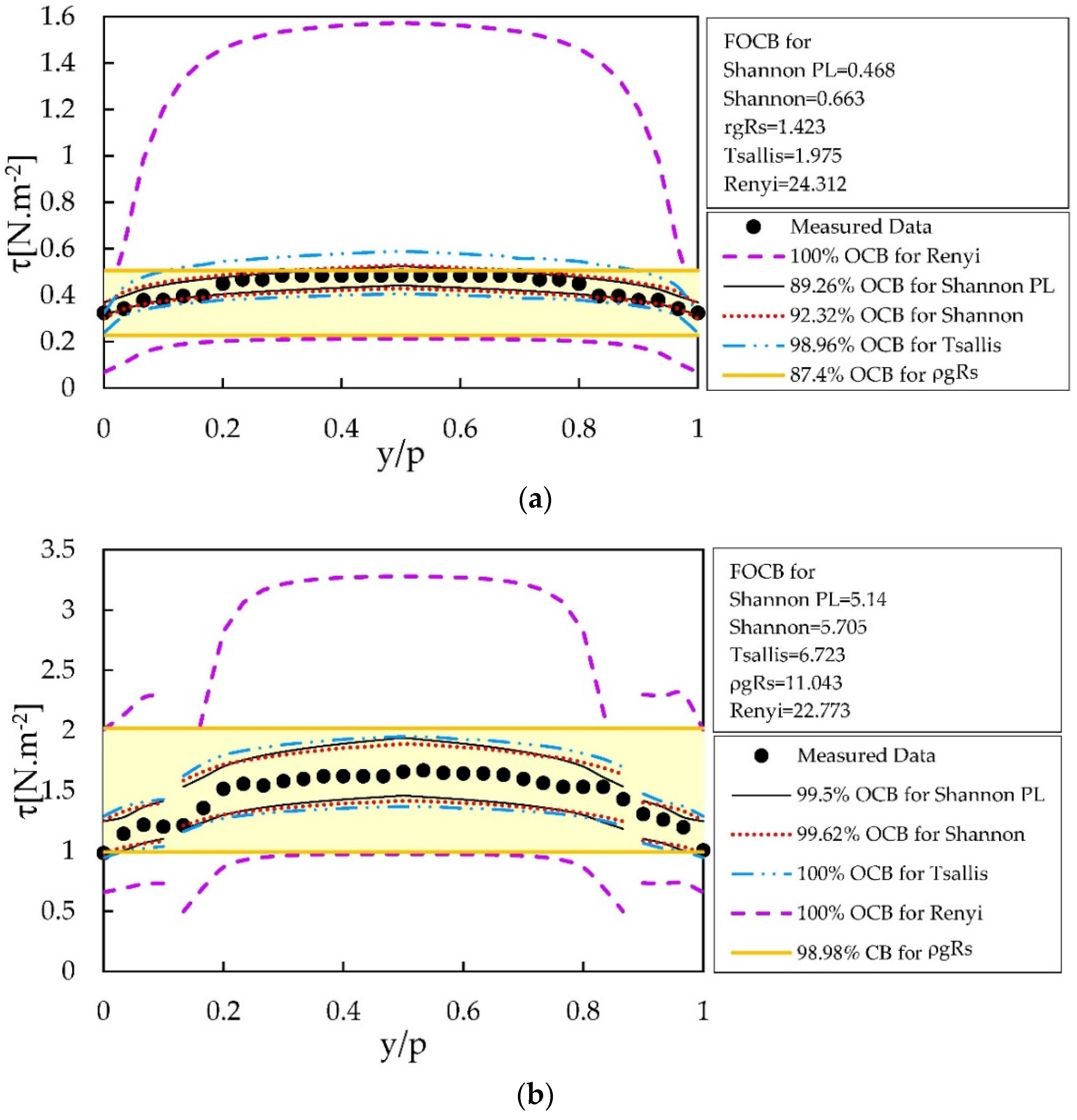
3.3. Comparison of the Uncertainty of Four Entropy Models Using HBMES-2 Method
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Perrusquia, G. Bedload Transport in Storm Sewers. Stream Traction in Pipe Channels. Ph.D. Thesis, Chalmers University of Technology, Gothenburg, Sweden, 1991. [Google Scholar]
- Kleijwegt, R.A. On Sediment Transport in Circular Sewers with Non-Cohesive Deposits. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 1992. [Google Scholar]
- Knight, D.W.; Sterling, M. Boundary shear in circular pipes running partially full. J. Hydraul. Eng. 2000, 126, 263–275. [Google Scholar] [CrossRef]
- Berlamont, J.E.; Trouw, K.; Luyckx., G. Shear stress distribution in partially filled pipes. J. Hydraul. Eng. 2003, 129, 697–705. [Google Scholar] [CrossRef]
- Bares, V.; Jirak, J.; Pollert, J. Bottom shear stress in unsteady sewer flow. Water Sci. Technol. 2006, 54, 93–100. [Google Scholar] [CrossRef]
- Yu, G.; Tan, S.K. Estimation of boundary shear stress distribution in open channels using flownet. JHR 2007, 45, 486–496. [Google Scholar] [CrossRef]
- Shameem, A.J.; Valyrakis, M.; Zare-Behtash, H. A Fluid Dynamics Approach for Assessing the Intelligent Geomorphic Design of the Japanese Pufferfish Nest. Geosciences 2021, 11, 22. [Google Scholar] [CrossRef]
- Gholami, A.; Bonakdari, H.; Ebtehaj, I.; Gharabaghi, B.; Khodashenas, S.R.; Talesh, S.H.A.; Jamali, A. A methodological approach of predicting threshold channel bank profile by multi-objective evolutionary optimization of ANFIS. Eng. Geol. 2018, 239, 298–309. [Google Scholar] [CrossRef]
- Fotovatikhah, F.; Herrera, M.; Shamshirband, S.; Chau, K.W.; Faizollahzadeh Ardabili, S.; Piran, M.J. Survey of computational intelligence as basis to big flood management: Challenges, research directions and future work. Eng. Appl. Comput. Fluid Mech. 2018, 12, 411–437. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.Y.; Chau, K.W. Uncertainty Analysis on Hybrid Double Feedforward Neural Network Model for Sediment Load Estimation with LUBE Method. Water Resour. Manag. 2019, 33, 3563–3577. [Google Scholar] [CrossRef]
- Shende, S.; Chau, K.W. Design of water distribution systems using an intelligent simple benchmarking algorithm with respect to cost optimization and computational efficiency. Water Supply 2019, 19, 1892–1898. [Google Scholar] [CrossRef]
- Bonakdari, H.; Gholami, A.; Sattar, A.M.; Gharabaghi, B. Development of robust evolutionary polynomial regression network in the estimation of stable alluvial channel dimensions. Geomorphology 2020, 350, 106895. [Google Scholar] [CrossRef]
- Danandeh Mehr, A.; Safari, M.J.S. Application of Soft Computing Techniques for Particle Froude Number Estimation in Sewer Pipes. J. Pipeline Syst. Eng. Pract. 2020, 11, 04020002. [Google Scholar] [CrossRef]
- Malik, A.; Kumar, A.; Kim, S.; Kashani, M.H.; Karimi, V.; Ghorbani, M.A.; Al-Ansari, N.; Salih, S.Q.; Yaseen, Z.M.; Chau, K.W. Modeling monthly pan evaporation process over the Indian central Himalayas: Application of multiple learning artificial intelligence model. Eng. Appl. Comput. Fluid Mech. 2020, 14, 323–338. [Google Scholar] [CrossRef] [Green Version]
- Kargar, K.; Samadianfard, S.; Parsa, J.; Nabipour, N.; Shamshirband, S.; Mosavi, A.; Chau, K.W. Estimating longitudinal dispersion coefficient in natural streams using empirical models and machine learning algorithms. Eng. Appl. Comput. Fluid Mech. 2020, 14, 311–322. [Google Scholar] [CrossRef]
- Wang, W.C.; Xu, L.; Chau, K.W.; Xu, D.M. Yin-Yang firefly algorithm based on dimensionally Cauchy mutation. Expert Syst. Appl. 2020, 150, 113216. [Google Scholar] [CrossRef]
- Farina, G.; Alvisi, S.; Franchini, M.; Moramarco, T. Three methods for estimating the entropy parameter M based on a decreasing number of velocity measurements in a river cross-section. Entropy 2014, 16, 2512–2529. [Google Scholar] [CrossRef] [Green Version]
- Mihaliović, D.T.; Mimić, G.; Gualtieri, P.; Arsenić, I.; Gualtieri, C. Randomness representation in turbulent flows with bed roughness elements using the spectrum of the Kolmogorov complexity. In Proceedings of the iEMSs Eight Biennial Meeting: International Congress on Environmental Modeling and Software (iEMSs), Toulouse, France, 10–14 July 2016. [Google Scholar]
- Mihaliović, D.T.; Mimić, G.; Gualtieri, P.; Arsenić, I.; Gualtieri, C. Randomness Representation of Turbulence in Canopy Flows Using Kolmogorov Complexity Meaures. Entropy 2017, 19, 519. [Google Scholar] [CrossRef] [Green Version]
- Gholami, A.; Bonakdari, H.; Mohammadian, M.; Zaji, A.H.; Gharabaghi, B. Assessment of geomorphological bank evolution of the alluvial threshold rivers based on entropy concept parameters. Hydrol. Sci. J. 2019, 64, 856–872. [Google Scholar] [CrossRef]
- Gholami, A.; Bonakdari, H.; Mohammadian, M. Enhanced formulation of the probability principle based on maximum entropy to design the bank profile of channels in geomorphic threshold. Stoch. Hydrol. Hydraul. 2019, 33, 1013–1034. [Google Scholar] [CrossRef]
- Khozani, Z.S.; Bonakdari, H. Formulating the shear stress distribution in circular open channels based on the Renyi entropy. Phys. A 2018, 490, 114–126. [Google Scholar] [CrossRef]
- Chiu, C.L. Entropy and probability concepts in hydraulics. J. Hydraul. Eng. 1987, 113, 583–599. [Google Scholar] [CrossRef]
- Sterling, M.; Knight, D.W. An attempt at using the entropy approach to predict the transverse distribution of boundary shear stress in open channel flow. Stoch. Hydrol. Hydraul. 2002, 16, 127–142. [Google Scholar] [CrossRef]
- Sheikh, Z.; Bonakdari, H. Prediction of boundary shear stress in circular and trapezoidal channels with entropy concept. Urban Water J. 2015, 13, 629–636. [Google Scholar] [CrossRef]
- Renyi, A. On measures of entropy and information. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability; The Regents of the University of California: Oakland, CA, USA, 1961; Volume 1, pp. 547–561. [Google Scholar]
- Jozsa, R. Quantum Information and Its Properties. In Introduction to Quantum Computation and Information; Lo, H.K., Popescu, S., Spiller, T., Eds.; World Scientific: Singapore, 1998. [Google Scholar]
- Titchener, M.R.; Nicolescu, R.; Staiger, L.; Gulliver, A.; Speidel, U. Deterministic Complexity and Entropy. J. Fundam. Inf. 2004, 64, 443–461. [Google Scholar]
- Tsallis, C. Possible generalization of Boltzmann–Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Tsallis, C.; Brigatti, E. Nonextensive statistical mechanics: A brief introduction. Contin. Mech. Thermodyn. 2004, 16, 223–235. [Google Scholar] [CrossRef] [Green Version]
- Gholami, A.; Bonakdari, H.; Mohammadian, A. A method based on the Tsallis entropy for characterizing threshold channel bank profiles. Phys. A Stat. Mech. Appl. 2016, 526, 121089. [Google Scholar] [CrossRef]
- Ghoshal, K.; Kumbhakar, M.; Singh, V.P. Distribution of sediment concentration in debris flow using Rényi entropy. Phys. A Stat. Mech. Appl. 2019, 521, 267–281. [Google Scholar] [CrossRef]
- Bonakdari, H.; Sheikh, Z.; Tooshmalani, M. Comparison between Shannon and Tsallis entropies for prediction of shear stress distribution in open channels. Stoch. Hydrol. Hydraul. 2015, 29, 1–11. [Google Scholar] [CrossRef]
- Hastings, W.K. Monte Carlo sampling methods using Markov chains and their applications. Biometrika 1970, 57, 97–109. [Google Scholar] [CrossRef]
- Watt, W.E.; Paine, J.D. Flood risk mapping in Canada: 1. Uncertainty considerations. Can. Water Resour. J. 1992, 17, 129–138. [Google Scholar] [CrossRef]
- Misirli, F.; Gupta, H.V.; Sorooshian, S.; Thiemann, M. Bayesian recursive estimation of parameter and output uncertainty for watershed models. Calibration Watershed Models Water Sci. Appl. 2003, 6, 113–124. [Google Scholar]
- Montanari, A.; Brath, A. A stochastic approach for assessing the uncertainty of rainfall-runoff simulations. Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef]
- Iyer, V.A.; Woodmansee, M.A. Uncertainty analysis of laser-doppler-velocimetry measurements fin a swirling flowfield. AIAA J. 2005, 43, 512–519. [Google Scholar] [CrossRef]
- Gabellani, S.; Boni, G.; Ferraris, L.; Hardenberg, J.V.; Provenzale., A. Propagation of uncertainty from rainfall to runoff: A case study with a stochastic rainfall generator. Adv. Water Resour. 2007, 30, 2061–2071. [Google Scholar] [CrossRef]
- Iskra, I.; Droste, R. Parameter uncertainty of a watershed model. Can. Water Resour. J. 2008, 33, 5–22. [Google Scholar] [CrossRef] [Green Version]
- Baldassarre, G.D.; Montanari, A. Uncertainty in river discharge observations: A quantitative analysis. Hydrol. Earth Syst. Sci. 2009, 13, 913–921. [Google Scholar] [CrossRef] [Green Version]
- Hamilton, A.S.; Moore, R.D. Quantifying uncertainty in streamflow records. Can. Water Resour. J. 2012, 37, 3–21. [Google Scholar] [CrossRef]
- Ghorbani, M.A.; Zadeh, H.A.; Isazadeh, M.; Terzi., O. A comparative study of artificial neural network (MLP, RBF) and support vector machine models for river flow prediction. Environ. Earth Sci. 2016, 75, 476. [Google Scholar] [CrossRef]
- Arnaud, P.; Cantet, P.; Odry, J. Uncertainties of flood frequency estimation approaches based on continuous simulation using data resampling. J. Hydrol. 2017, 554, 360–369. [Google Scholar] [CrossRef] [Green Version]
- Beven, K.; Lamb, R. The uncertainty cascade in model fusion. J. Geol. Soc. 2017, 408, 255–266. [Google Scholar] [CrossRef]
- Gholami, A.; Bonakdari, H.; Ebtehaj, I.; Khodashenas, S.R. Reliability and sensitivity analysis of robust learning machine in prediction of bank profile morphology of threshold sand rivers. Measurement 2020, 153, 107411. [Google Scholar] [CrossRef]
- Vidrio-Sahagún, C.T.; He, J. Flood Hazard Estimation under Nonstationarity Using the Particle Filter. Geosciences 2021, 11, 13. [Google Scholar] [CrossRef]
- Thiemann, M.; Trosset, M.; Gupta, H.; Sorooshian, S. Bayesian recursive parameter estimation for hydrologic models. Water Resour. Res. 2001, 37, 2521–2535. [Google Scholar] [CrossRef]
- Corato, G.; Melone, F.; Moramarco, T.; Singh, V.P. Uncertainty analysis of flow velocity estimation by a simplified entropy model. Hydrol. Process. 2014, 28, 581–590. [Google Scholar] [CrossRef]
- Kazemian-Kale-Kale, A.; Bonakdari, H.; Gholami, A.; Khozani, Z.S.; Akhtari, A.A.; Gharabaghi, B. Uncertainty analysis of shear stress estimation in circular channels by Tsallis entropy. Phys. A Stat. Mech. Its Appl. 2018, 510, 558–576. [Google Scholar] [CrossRef]
- Kazemian-Kale-Kale, A.; Bonakdari, H.; Gholami, A.; Gharabaghi, B. The uncertainty of the Shannon entropy model for shear stress distribution in circular channels. Int. J. Sediment Res. 2020, 35, 57–68. [Google Scholar] [CrossRef]
- Knight, D.W.; Yuen, K.W.H.; Alhamid, A.A.I. Boundary Shear Stress Distributions in Open Channel Flow. Physical Mechanisms of Mixing and Transport in the Environment; John Wiley: New York, NY, USA, 1993. [Google Scholar]
- Chow, V.T. Open Channel Hydraulics; McGraw-Hill Civil Engineering Series; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Sterling, M. A Study of Boundary Shear Stress, Flow Resistance and the Free Overfall in Open Channels with a Circular Cross-Section. Ph.D. Thesis, University of Birmingham, Birmingham, UK, 1998. [Google Scholar]
- Khozani, Z.S.; Bonakdari, H.; Zaji, A.H. Estimating the shear stress distribution in circular channels based on the randomized neural networks technique. Appl. Soft. Comput. 2017, 58, 441–448. [Google Scholar] [CrossRef]
- Andersson, D.E.; Shyr, O.F.; Fu, J. Does high-speed rail accessibility influence residential property prices? Hedonic estimates from southern Taiwan. J. Transp. Geogr. 2010, 18, 166–174. [Google Scholar] [CrossRef]
- Malik, W.A.; Piepho, H.P. On generalized exponential transformations for proportions. Commun. Stat. Theory Methods 2016, 45, 5857–5870. [Google Scholar] [CrossRef]
- He, Y.; Zheng, Y. Short-term power load probability density forecasting based on Yeo-Johnson transformation quantile regression and Gaussian kernel function. Energy 2018, 154, 143–156. [Google Scholar] [CrossRef]
- Rohlf, F.J.; Sokal, R.R. Statistical Tables; Macmillan: Basingstoke, UK, 1995. [Google Scholar]
- Mudholkar, G.S.; Tian, L. An entropy characterization of the inverse Gaussian distribution and related goodness-of-fit test. J. Stat. Plan. Inference 2002, 102, 211–221. [Google Scholar] [CrossRef]
- Jorgensen, B. Statistical Properties of the Generalized Inverse Gaussian Distribution; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Abbaspour, K.C.; Johnson, C.A.; Van Genuchten, M.T. Estimating uncertain flow and transport parameters using a sequential uncertainty fitting procedure. Vadose Zone J. 2004, 3, 1340–1352. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Yang, J.; Maximov, I.; Siber, R.; Bogner, K.; Mieleitner, J.; Srinivasan, R. Modelling hydrology and water quality in the pre-alpine/alpine Thur watershed using SWAT. J. Hydrol. 2007, 333, 413–430. [Google Scholar] [CrossRef]
- Gholami, A.; Bonakdari, H.; Ebtehaj, I.; Mohammadian, M.; Gharabaghi, B.; Khodashenas, S.R. Uncertainty analysis of intelligent model of hybrid genetic algorithm and particle swarm optimization with ANFIS to predict threshold bank profile shape based on digital laser approach sensing. Measurement 2018, 121, 294–303. [Google Scholar] [CrossRef]
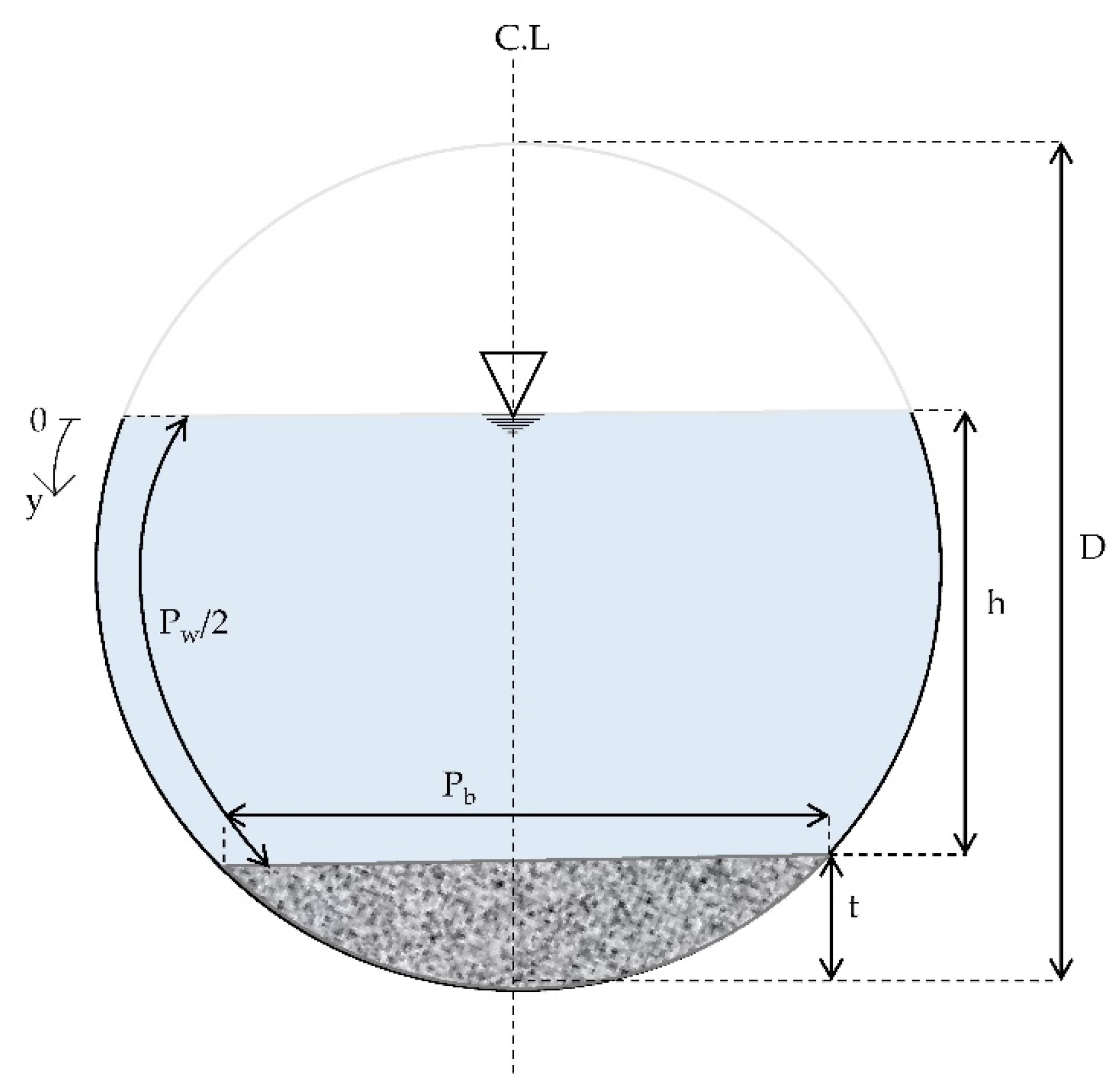


| Sample | Section | t/D | h + t/D | S0 × 103 | Fr | Q (l/s) |
|---|---|---|---|---|---|---|
| 1 | Circular | 0 | 0.333 | 1 | 0.516 | 5.36 |
| 2 | 0.506 | 1 | 0.505 | 11.7 | ||
| 3 | 0.666 | 1 | 0.441 | 17.3 | ||
| 4 | 0.826 | 1 | 0.375 | 22.9 | ||
| 5 | Circular with flat bed | 0.25 | 0.332 | 1.96 | 0.671 | 1.32 |
| 6 | 0.499 | 1.96 | 0.748 | 8 | ||
| 7 | 0.398 | 1.96 | 0.656 | 3.3 | ||
| 8 | 0.666 | 1.96 | 0.68 | 16.5 | ||
| 9 | 0.755 | 1.96 | 0.663 | 22.1 | ||
| 10 | 0.795 | 1.96 | 0.626 | 23.8 | ||
| 11 | 0.333 | 8.62 | 1.71 | 3.39 | ||
| 12 | 0.499 | 8.62 | 1.7 | 18.2 | ||
| 13 | 0.666 | 8.62 | 1.59 | 38.9 | ||
| 14 | Circular with flat bed | 0.332 | 0.499 | 2 | 0.718 | 4.4 |
| 15 | 0.666 | 2 | 0.685 | 12.2 | ||
| 16 | 0.75 | 2 | 0.669 | 17 | ||
| 17 | 0.8 | 2 | 0.721 | 22.1 | ||
| 18 | 0.499 | 2 | 1.96 | 12 | ||
| 19 | Circular with flat bed | 0.5 | 0.666 | 9 | 1.4 | 8.4 |
| 20 | 0.75 | 9 | 1.42 | 16 | ||
| 21 | 0.8 | 9 | 1.33 | 20 | ||
| 22 | Circular with flat bed | 0.664 | 0.75 | 8.8 | 1.44 | 3.09 |
| 23 | 0.8 | 8.8 | 1.55 | 4.93 |
| Models | Nin | |FP| | |FN| | FREE | |
|---|---|---|---|---|---|
| Entropy | Shannon | 94.81 | 6.521 | 0.096 | 6.617 |
| Shannon PL | 93.41 | 6.018 | 0.107 | 6.125 | |
| Tsallis | 92.43 | 8.525 | 0.239 | 8.764 | |
| Renyi | 91.58 | 26.041 | 0.658 | 26.699 | |
| Conventional | ρgRs | 85.41 | 8.124 | 1.715 | 9.839 |
| Samples | Models | OCB | FREEopt | FOCB |
|---|---|---|---|---|
| 1 | Shannon PL | 89.26 | 0.525 | 0.469 |
| Tsallis | 98.96 | 1.995 | 1.974 | |
| Shannon | 92.32 | 0.718 | 0.663 | |
| Renyi | 100 | 24.312 | 24.312 | |
| ρgRs | 87.4 | 1.628 | 1.423 | |
| 2 | Shannon PL | 98.44 | 0.768 | 0.756 |
| Tsallis | 100 | 4.057 | 4.057 | |
| Shannon | 95.86 | 0.975 | 0.935 | |
| Renyi | 100 | 60.569 | 60.569 | |
| ρgRs | 93.14 | 1.48 | 1.379 | |
| 8 | Shannon PL | 94.76 | 1.927 | 1.826 |
| Tsallis | 97.6 | 1.953 | 1.906 | |
| Shannon | 96.06 | 2.931 | 2.815 | |
| Renyi | 99.02 | 29.049 | 28.764 | |
| ρgRs | 99.14 | 4.92 | 4.878 | |
| 11 | Shannon PL | 99.5 | 5.166 | 5.14 |
| Tsallis | 100 | 6.723 | 6.723 | |
| Shannon | 99.62 | 5.727 | 5.705 | |
| Renyi | 100 | 22.773 | 22.773 | |
| ρgRs | 98.98 | 11.157 | 11.043 | |
| 18 | Shannon PL | 100 | 17.426 | 17.426 |
| Tsallis | 100 | 22.231 | 22.231 | |
| Shannon | 100 | 16.049 | 16.049 | |
| Renyi | 100 | 41.814 | 41.814 | |
| ρgRs | 99.56 | 21.233 | 21.139 |
| Section | FOCB | ||||
|---|---|---|---|---|---|
| Shannon PL | Shannon | Tsallis | Renyi | ρgRs | |
| Circular | 1.339 | 2.432 | 2.961 | 58.457 | 2.026 |
| Circular with flat bed | 11.591 | 10.118 | 17.407 | 57.569 | 17.115 |
| Average | 9.808 | 8.781 | 14.895 | 57.726 | 14.491 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kazemian-Kale-Kale, A.; Gholami, A.; Rezaie-Balf, M.; Mosavi, A.; Sattar, A.A.; Azimi, A.H.; Gharabaghi, B.; Bonakdari, H. Uncertainty Assessment of Entropy-Based Circular Channel Shear Stress Prediction Models Using a Novel Method. Geosciences 2021, 11, 308. https://doi.org/10.3390/geosciences11080308
Kazemian-Kale-Kale A, Gholami A, Rezaie-Balf M, Mosavi A, Sattar AA, Azimi AH, Gharabaghi B, Bonakdari H. Uncertainty Assessment of Entropy-Based Circular Channel Shear Stress Prediction Models Using a Novel Method. Geosciences. 2021; 11(8):308. https://doi.org/10.3390/geosciences11080308
Chicago/Turabian StyleKazemian-Kale-Kale, Amin, Azadeh Gholami, Mohammad Rezaie-Balf, Amir Mosavi, Ahmed A. Sattar, Amir H. Azimi, Bahram Gharabaghi, and Hossein Bonakdari. 2021. "Uncertainty Assessment of Entropy-Based Circular Channel Shear Stress Prediction Models Using a Novel Method" Geosciences 11, no. 8: 308. https://doi.org/10.3390/geosciences11080308
APA StyleKazemian-Kale-Kale, A., Gholami, A., Rezaie-Balf, M., Mosavi, A., Sattar, A. A., Azimi, A. H., Gharabaghi, B., & Bonakdari, H. (2021). Uncertainty Assessment of Entropy-Based Circular Channel Shear Stress Prediction Models Using a Novel Method. Geosciences, 11(8), 308. https://doi.org/10.3390/geosciences11080308










