SNR-Based GNSS-R for Coastal Sea-Level Altimetry
Abstract
:1. Introduction
2. Geodetic GNSS-R Footprint
3. Geodetic GNSS-R Model
4. Port-au-Prince Tide Gauge Station
5. GNSS-R Sea Level Altimetry
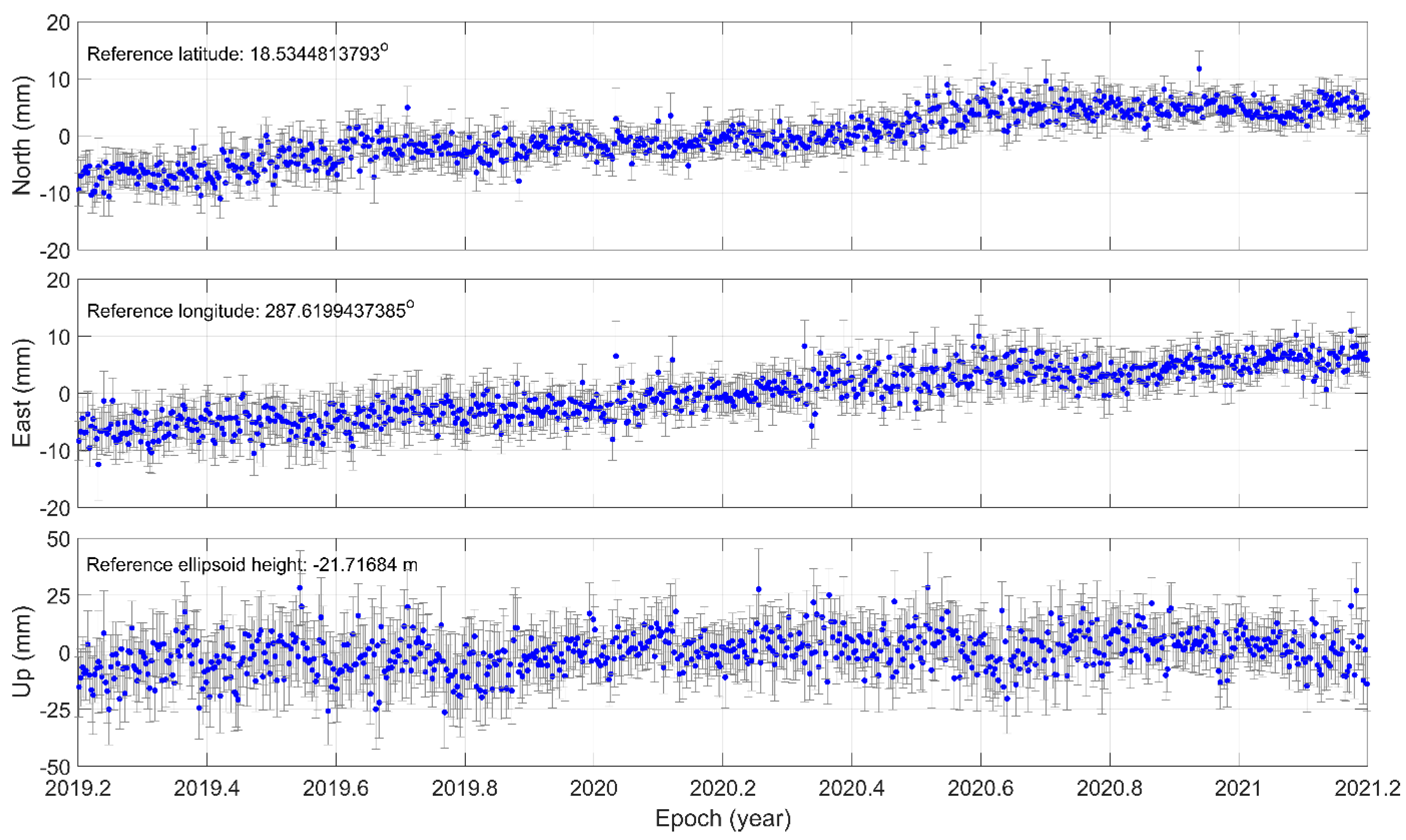
6. Absolute Sea Level Altimetry
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Misra, P.; Enge, P. Global Positioning System: Signals, Measurements, and Performance; Ganga-Jamuna Press: Lincoln, MA, USA, 2011. [Google Scholar]
- Gao, Z.; Ge, M.; Li, Y.; Shen, W.; Zhang, H.; Schuh, H. Railway irregularity measuring using Rauch–Tung–Striebel smoothed multi-sensors fusion system: Quad-GNSS PPP, IMU, odometer, and track gauge. GPS Solut. 2018, 22, 36. [Google Scholar] [CrossRef]
- Liu, W.; Shi, X.; Zhu, F.; Tao, X.; Wang, F. Quality analysis of multi-GNSS raw observations and a velocity-aided positioning approach based on smartphones. Adv. Space Res. 2019, 63, 2358–2377. [Google Scholar] [CrossRef]
- Kavak, A.; Vogel, W.; Xu, G. Using GPS to measure ground complex permittivity. Electron. Lett. 1998, 34, 254–255. [Google Scholar] [CrossRef]
- Larson, K.; Löfgren, J.; Haas, R. Coastal sea level measurements using a single geodetic GPS receiver. Adv. Space Res. 2013, 51, 1301–1310. [Google Scholar] [CrossRef] [Green Version]
- Larson, K.; Ray, R.D.; Geremia-Nievinski, F.; Freymueller, J. The Accidental Tide Gauge: A GPS Reflection Case Study from Kachemak Bay, Alaska. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1200–1204. [Google Scholar] [CrossRef] [Green Version]
- Löfgren, J.S.; Haas, R.; Scherneck, H.-G. Sea level time series and ocean tide analysis from multipath signals at five GPS sites in different parts of the world. J. Geodyn. 2014, 80, 66–80. [Google Scholar] [CrossRef] [Green Version]
- Larson, K.M.; Ray, R.D.; Williams, S. A 10-Year Comparison of Water Levels Measured with a Geodetic GPS Receiver versus a Conventional Tide Gauge. J. Atmos. Ocean. Technol. 2017, 34, 295–307. [Google Scholar] [CrossRef] [Green Version]
- Tabibi, S.; Geremia-Nievinski, F.; Francis, O.; van Dam, T. Tidal analysis of GNSS reflectometry applied for coastal sea level sensing in Antarctica and Greenland. Remote Sens. Environ. 2020, 248, 111959. [Google Scholar] [CrossRef]
- Tabibi, S.; Francis, O. Can GNSS-R Detect Abrupt Water Level Changes? Remote Sens. 2020, 12, 3614. [Google Scholar] [CrossRef]
- Geremia-Nievinski, F.; Hobiger, T.; Haas, R.; Liu, W.; Strandberg, J.; Tabibi, S.; Vey, S.; Wickert, J.; Williams, S. SNR-based GNSS reflectometry for coastal sea-level altimetry: Results from the first IAG inter-comparison campaign. J. Geod. 2020, 94, 1–15. [Google Scholar] [CrossRef]
- Fagundes, M.A.R.; Mendonça-Tinti, I.; Iescheck, A.L.; Akos, D.M.; Geremia-Nievinski, F. An open-source low-cost sensor for SNR-based GNSS reflectometry: Design and long-term validation towards sea-level altimetry. GPS Solut. 2021, 25, 73. [Google Scholar] [CrossRef]
- Calais, E.; Symithe, S.; de Lépinay, B.M.; Prépetit, C. Plate boundary segmentation in the northeastern Caribbean from geodetic measurements and Neogene geological observations. Comptes Rendus Geosci. 2016, 348, 42–51. [Google Scholar] [CrossRef]
- GFDRR Climate Risk and Adaptation Country Profile: Haiti. Available online: https://www.gfdrr.org/en/publication/climate-risk-and-adaptation-country-profile-haiti (accessed on 26 August 2021).
- World Bank Rapidly Assessing the Impact of Hurricane Matthew in Haiti. World Bank. Available online: https://www.worldbank.org/en/results/2017/10/20/rapidly-assessing-the-impact-of-hurricane-matthew-in-haiti (accessed on 26 August 2021).
- Intergovernmental Panel on Climate. Small Islands. In Climate Change 2014—Impacts, Adaptation and Vulnerability: Part B: Regional Aspects: Working Group II Contribution to the IPCC Fifth Assessment Report; Cambridge University Press: Cambridge, UK, 2014; pp. 1613–1654. [Google Scholar]
- Hristov, H.D. Fresnal Zones in Wireless Links, Zone Plate Lenses and Antennas, 1st ed.; Artech House, Inc.: Norwood, MA, USA, 2000. [Google Scholar]
- Larson, K.M.; Geremia-Nievinski, F. GPS snow sensing: Results from the EarthScope Plate Boundary Observatory. GPS Solut. 2012, 17, 41–52. [Google Scholar] [CrossRef]
- Geremia-Nievinski, F.; Larson, K. Inverse Modeling of GPS Multipath for Snow Depth Estimation—Part I: Formulation and Simulations. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6555–6563. [Google Scholar] [CrossRef]
- Nievinski, F.G.; Larson, K.M. Forward modeling of GPS multipath for near-surface reflectometry and positioning applications. GPS Solut. 2013, 18, 309–322. [Google Scholar] [CrossRef]
- Beckmann, P.; Spizzichino, A. The Scattering of Electromagnetic Waves from Rough Surfaces; Artech House, Inc.: Norwood, MA, USA, 1987; p. 511. [Google Scholar]
- Tabibi, S.; Nievinski, F.G.; van Dam, T.; Monico, J.F. Assessment of modernized GPS L5 SNR for ground-based multipath reflectometry applications. Adv. Space Res. 2014, 55, 1104–1116. [Google Scholar] [CrossRef] [Green Version]
- Georgiadou, P.Y.; Kleusberg, A. On carrier signal multipath effects in relative GPS positioning. Manuscrip-Ta Geod. 1988, 13, 172–179. [Google Scholar]
- Tabibi, S.; Geremia-Nievinski, F.; Van Dam, T. Statistical Comparison and Combination of GPS, GLONASS, and Multi-GNSS Multipath Reflectometry Applied to Snow Depth Retrieval. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3773–3785. [Google Scholar] [CrossRef]
- Geremia-Nievinski, F.; Larson, K. Inverse Modeling of GPS Multipath for Snow Depth Estimation—Part II: Application and Validation. IEEE Trans. Geosci. Remote. Sens. 2014, 52, 6564–6573. [Google Scholar] [CrossRef]
- Nikolaidou, T.; Santos, M.C.; Williams, S.D.P.; Geremia-Nievinski, F. Raytracing atmospheric delays in ground-based GNSS reflectometry. J. Geod. 2020, 94, 1–12. [Google Scholar] [CrossRef]
- Landskron, D.; Böhm, J. VMF3/GPT3: Refined discrete and empirical troposphere mapping functions. J. Geod. 2017, 92, 349–360. [Google Scholar] [CrossRef]
- Williams, S.D.P.; Nievinski, F.G. Tropospheric delays in ground-based GNSS multipath reflectometry-Experimental evidence from coastal sites. J. Geophys. Res. Solid Earth 2017, 122, 2310–2327. [Google Scholar] [CrossRef] [Green Version]
- Garrison, J.; Zavorotny, V.U.; Egido, A.; Nievinski, F.G.; Martin, F.; Mollfulleda, A.; Ruffini, G.; Garrison, J.; Larson, K.M. GNSS Reflectometry for Earth Remote Sensing. In Position, Navigation, and Timing Technologies in the 21st Century; John Wiley & Sons, Ltd.: New York, NY, USA, 2020; pp. 1015–1114. [Google Scholar]
- Rebischung, P.; Schmid, R. IGS14/igs14.atx: A new Framework for the IGS Products. In Proceedings of the AGU Fall Meeting, San Francisco, CA, USA, 12–16 December 2016. [Google Scholar]
- Bradshaw, E.; Rickards, L.; Aarup, T. Sea level data archaeology and the Global Sea Level Observing System (GLOSS). GeoResJ 2015, 6, 9–16. [Google Scholar] [CrossRef] [Green Version]
- S12C SDI-12 Seawater Pressure & Temperature Transducer. Available online: https://www.sensorsone.com/s12c-sdi-12-seawater-pressure-and-temperature-transducer/ (accessed on 24 June 2021).
- OTT RLS—Radar Level Sensor—OTT Hydromet. Available online: https://www.ott.com/products/water-level-1/ott-rls-radar-level-sensor-861/ (accessed on 22 June 2021).
- Foreman, M.; Henry, R. The harmonic analysis of tidal model time series. Adv. Water Resour. 1989, 12, 109–120. [Google Scholar] [CrossRef]
- Herring, T.A.; King, R.W.; Floyd, M.A.; McClusky, S.C. GAMIT Reference Manual Release 10.7; Massachusetts Institute of Technology: Cambridge, MA, USA, 2018. [Google Scholar]
- Altamimi, Z.; Rebischung, P.; Métivier, L.; Collilieux, X. ITRF2014: A new release of the International Terrestrial Reference Frame modeling nonlinear station motions. J. Geophys. Res. Solid Earth 2016, 121, 6109–6131. [Google Scholar] [CrossRef] [Green Version]
- Petit, G.; Luzum, B. IERS Conventions; Verlag des Bundesamts für Kartographie und Geodäsie: Frankfurt am Main, Germany, 2010; 179p, ISBN 3-89888-989-6. [Google Scholar]
- Boehm, J.; Niell, A.; Tregoning, P.; Schuh, H. Global Mapping Function (GMF): A new empirical mapping function based on numerical weather model data. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef] [Green Version]
- Schmid, R.; Steigenberger, P.; Gendt, G.; Ge, M.; Rothacher, M. Generation of a consistent absolute phase-center correction model for GPS receiver and satellite antennas. J. Geod. 2007, 81, 781–798. [Google Scholar] [CrossRef] [Green Version]
- Lyard, F.; Lefevre, F.; Letellier, T.; Francis, O. Modelling the global ocean tides: Modern insights from FES2004. Ocean Dyn. 2006, 56, 394–415. [Google Scholar] [CrossRef]
- Tregoning, P.; Van Dam, T. Atmospheric pressure loading corrections applied to GPS data at the observation level. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef] [Green Version]
- Herring, T.A.; King, R.W.; Floyd, M.A.; McClusky, S.C. GLOBK Reference Manual Release 10.6; Massachusetts Institute of Technology: Cambridge, MA, USA, 2018. [Google Scholar]
- Blewitt, G.; Kreemer, C.; Hammond, W.C.; Gazeaux, J. MIDAS robust trend estimator for accurate GPS station velocities without step detection. J. Geophys. Res. Solid Earth 2016, 121, 2054–2068. [Google Scholar] [CrossRef] [PubMed]
- Intergovernmental Oceanographic Commission. Workshop on Sea-Level Measurements in Hostile Conditions, Moscow, Russian Federation, 13–15 March 2018; UNESCO: Paris, France, 2018; 28p. [Google Scholar]




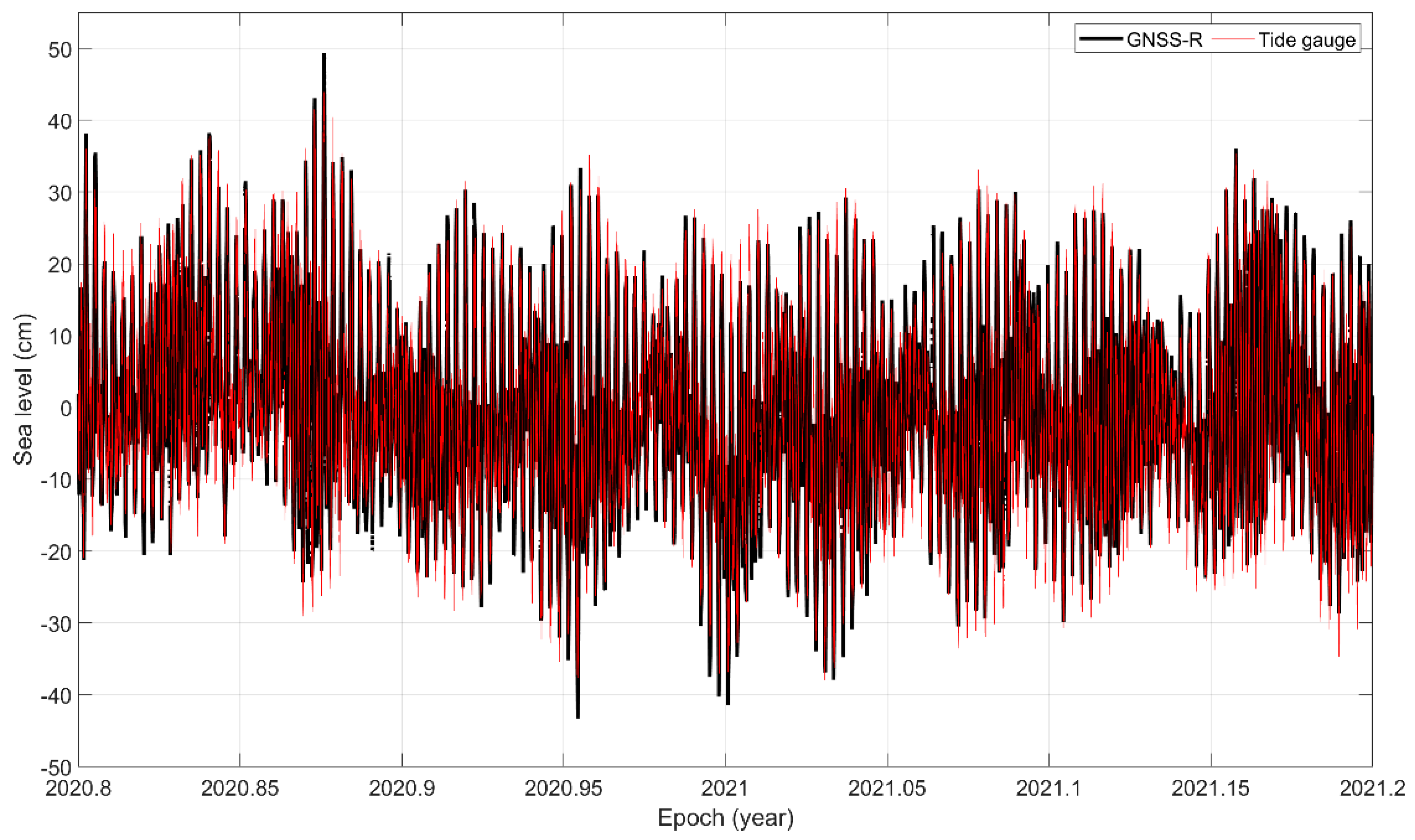
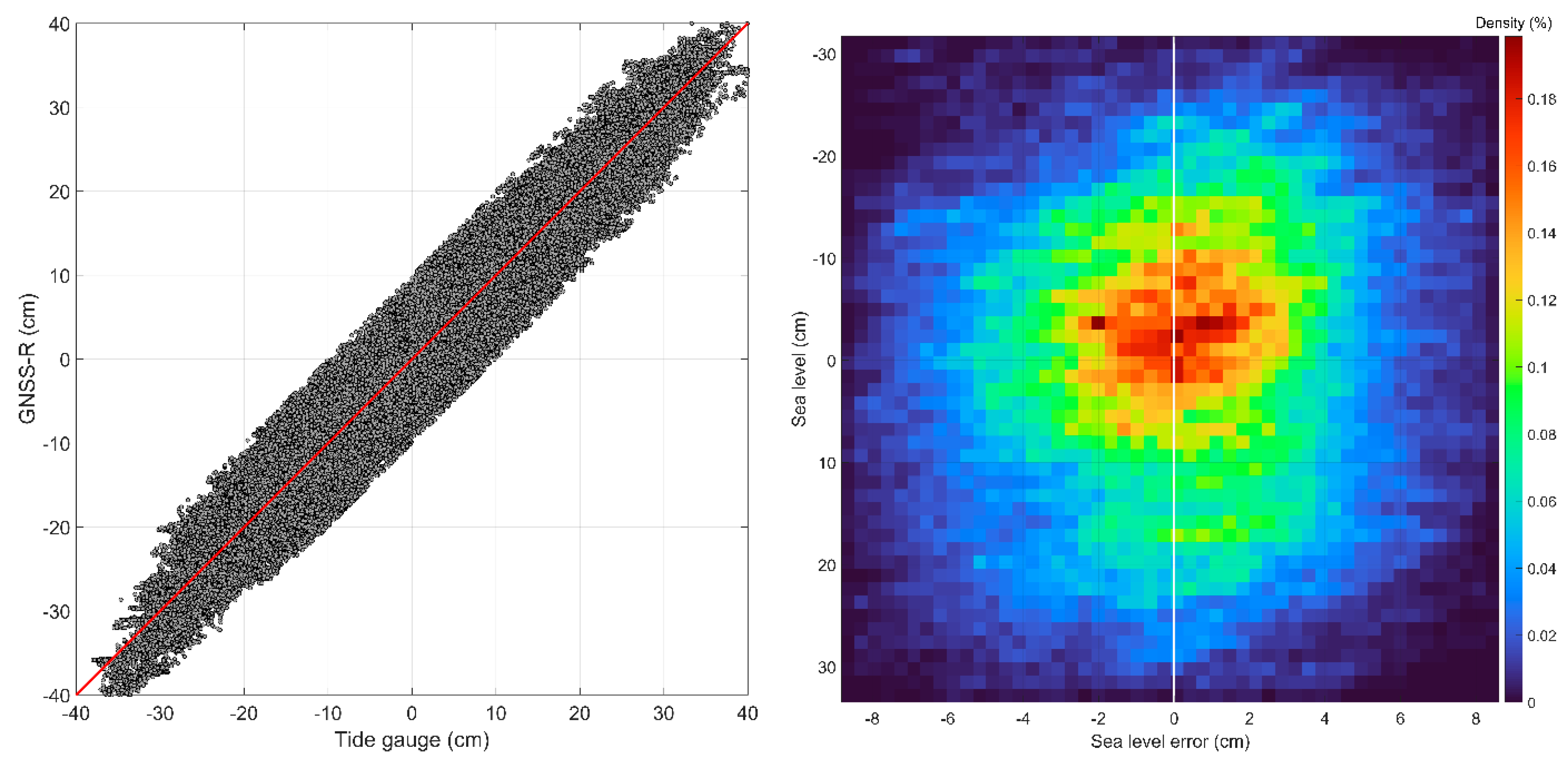
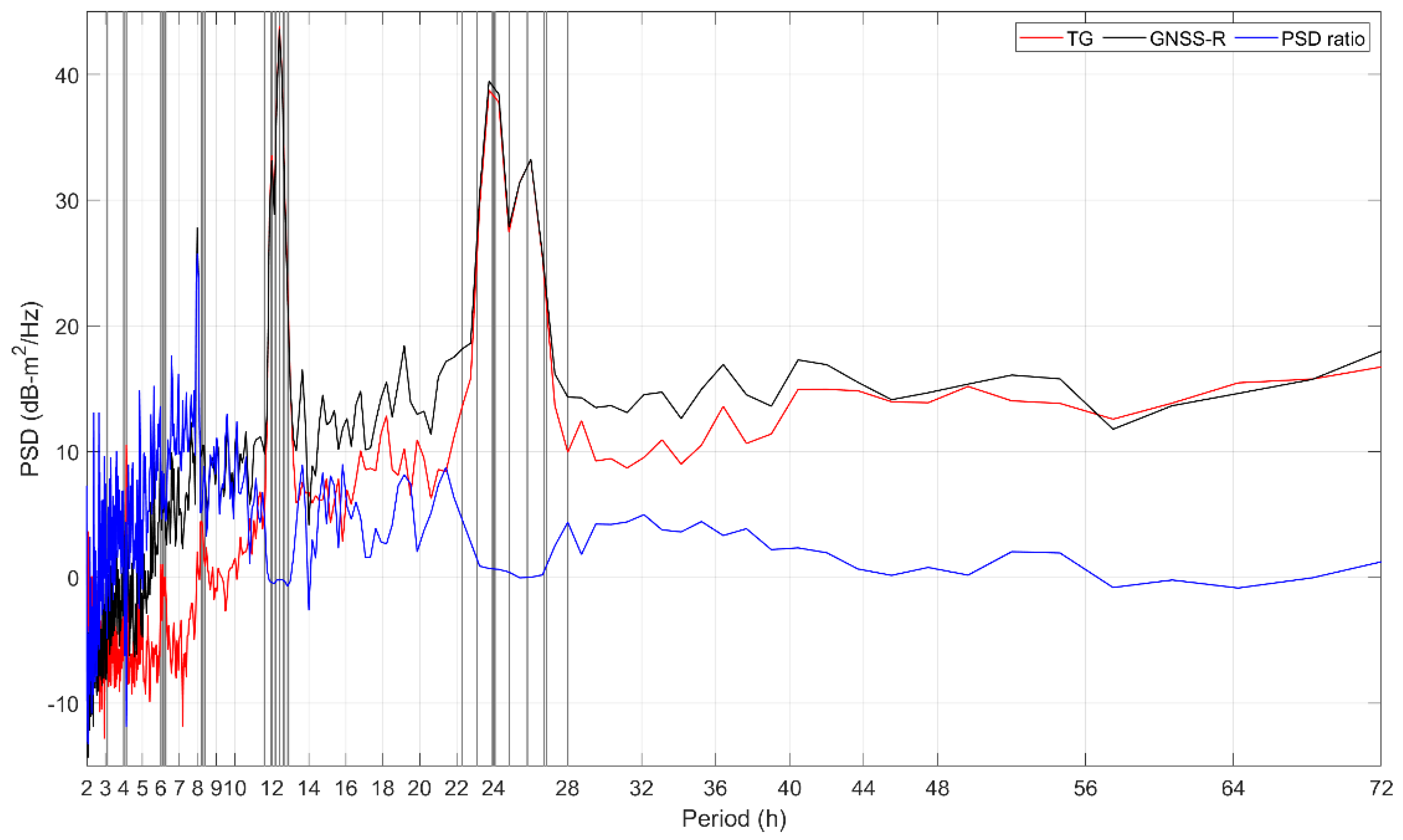

| 3-h | 4-h | 6-h | 12-h | 24-h | |
|---|---|---|---|---|---|
| Correlation | 0.43 | 0.66 | 0.94 | 0.97 | 0.97 |
| RMSE (cm) | 1.81 | 2.28 | 2.74 | 3.10 | 3.17 |
| Slope deviation () | 0.04 | 0.02 |
| Wave | Period (h) | OTT RLS | GNSS-R | Vec. Diff (cm) | ||
|---|---|---|---|---|---|---|
| Amp. (cm) | Phase (°) | Amp. (cm) | Phase (°) | |||
| 26.8683 | 0.43 | 231.51 | 0.47 | 229.14 | 0.04 | |
| 25.8193 | 4.10 | 214.62 | 4.09 | 211.35 | 0.23 | |
| 24.0658 | 2.81 | 243.31 | 2.62 | 240.67 | 0.23 | |
| 23.9344 | 7.48 | 232.84 | 8.25 | 229.20 | 0.91 | |
| 12.6583 | 3.12 | 23.13 | 2.95 | 21.49 | 0.19 | |
| 12.4206 | 14.35 | 34.26 | 14.03 | 32.85 | 0.47 | |
| 12.0000 | 4.18 | 51.46 | 3.98 | 48.63 | 0.28 | |
| 11.96723606 | 1.29 | 48.82 | 1.33 | 54.25 | 0.13 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tabibi, S.; Sauveur, R.; Guerrier, K.; Metayer, G.; Francis, O. SNR-Based GNSS-R for Coastal Sea-Level Altimetry. Geosciences 2021, 11, 391. https://doi.org/10.3390/geosciences11090391
Tabibi S, Sauveur R, Guerrier K, Metayer G, Francis O. SNR-Based GNSS-R for Coastal Sea-Level Altimetry. Geosciences. 2021; 11(9):391. https://doi.org/10.3390/geosciences11090391
Chicago/Turabian StyleTabibi, Sajad, Renaldo Sauveur, Kelly Guerrier, Gerard Metayer, and Olivier Francis. 2021. "SNR-Based GNSS-R for Coastal Sea-Level Altimetry" Geosciences 11, no. 9: 391. https://doi.org/10.3390/geosciences11090391
APA StyleTabibi, S., Sauveur, R., Guerrier, K., Metayer, G., & Francis, O. (2021). SNR-Based GNSS-R for Coastal Sea-Level Altimetry. Geosciences, 11(9), 391. https://doi.org/10.3390/geosciences11090391







