Next Article in Journal
Micromorphological Analysis of Archaeological Abenaki Pit Features from the Fort Odanak Site (CaFe-7), Québec, Canada
Previous Article in Journal
A Tool for Performing Automatic Kinematic Analysis on Rock Outcrops
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Geosciences
Volume 12
Issue 12
10.3390/geosciences12120436
geosciences-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

The Usage of GIS Tools on Vintage Aerogeophysical Data for Simple and Fast Processing with a Focus on Fault Interpretation: An Austrian Case Study

by
Ingrid Schattauer
1,*,
Esther Hintersberger
1,
Christian Ullrich
2,
Robert Supper
1 and
Klaus Motschka
1
1
Geological Survey of Austria (GBA), Neulinggasse 38, 1030 Vienna, Austria
2
Federal Office of Metrology and Surveying (BEV), Schiffamtsgasse 1-3, 1020 Vienna, Austria
*
Author to whom correspondence should be addressed.
Geosciences 2022, 12(12), 436; https://doi.org/10.3390/geosciences12120436
Submission received: 28 July 2022 / Revised: 18 November 2022 / Accepted: 21 November 2022 / Published: 25 November 2022
(This article belongs to the Section Geophysics)
Browse Figures
Versions Notes

Abstract

:
The reuse of vintage datasets which were acquired in the 20th century can pose challenges for modern geophysical modeling due to missing detailed preprocessing information, significant uncertainties, or lack of precise tracking, etc. Nevertheless, they are often the only available datasets in a target region. We explore here the potential of such vintage airborne geophysical datasets (magnetics, AEM, radiometrics) to detect the location and dip direction of geological faults, using a non-modeling interpretation approach based on multiple GIS tools. We apply our approach in a geologically well-known region where four different types of faults are mapped. The applicability of the tools used in this study depend on the geological setting of each fault and is evaluated based on the comparison with geological and—where available—with modeling data. In general, the GIS tools, especially used on a combination of datasets, show reliable results concerning the location and strike of faults, and even seem to be able to predict the dip direction of a fault.

1. Introduction

Nowadays, increasing quality of technology and digital data storage capacity has led to an increase in data availability. However, “vintage” geophysical datasets, e.g., datasets that were acquired and processed during the 20th century, are sometimes hard to update or to replace. Such datasets are normally not comparable to modern quality standards; they might be nevertheless a rich source of information in regions with no comparable modern data. For example, in the north of Austria, about 40 square kilometers are covered by a set of airborne geophysical data, acquired in the 1980s and 1990s by the Geological Survey of Austria (GBA) [1,2,3,4,5]. At that time, the individual sets were processed, interpreted, and compiled into reports, which, at that time, reflected the state-of-the-art knowledge. In the meantime, the processing tools have improved significantly. Therefore, we want to explore the re-use of this existing data set in regards of its potential to identify and locate geological structures. In general, an integrated use of airborne magnetic, gamma ray and electromagnetic data is known to discover important types of geological information, including faults [6].
The usage of such vintage data can be challenging, not only because of factors such as the lack of the original unprocessed data or inconsistent elevation measurement during different campaigns, but also because of the lack of suitable modeling software. The application of GIS technologies opens up an opportunity for rapid processing of geophysical datasets, nearly independent of their quality and precision. In addition, the data visualization tools and the possibilities for handling and combining multiple geospatial datasets make GIS attractive for fault characterization. Nevertheless, the question remains how reliable the results of such non-modeling approaches are and if they are applicable to the study of tectonic problems.
In this study, we apply GIS–based tools on vintage airborne geophysical data together with gravity data provided by the Austrian Federal Office of Metrology and Surveying (BEV). In order to evaluate the application of the methods to the datasets mentioned above and to detect tectonic structures, we target the most prominent tectonic structure within the area covered by all surveys, the Diendorf Fault System (DFS, Figure 1a). The DFS is a ca. 150 km long, steeply dipping, approximately NE-SW trending fault system that forms the eastern margin of the Bohemian Massif in Austria [7,8,9]. The DFS is the southern part of the Diendorf-Boskovice Fault System, which extends northwards to Brno (CZ), where it is supposed to be kinematically linked to the Boskovice Fault [10 and references therein]. Showing a long-lasting and multiphase history, evidence of NE-SW-striking sinistral strike-slip partly ductile, mylonitic shear zones during Upper Carboniferous and Permian times is observed along the DFS. Several studies show not only insights of continuous transtensional left-lateral strike-slip faulting during Miocene, but also recent tectonic activity [10,11]. The two most prominent structures of the DFS are the NE-SW striking Diendorf Fault (DF), which extends from Purgstall in the south to Maissau [11,12], and in the northwest, the Waitzendorf Fault (WF) striking NNE-SSW between the villages of Pulkau (A) and Znojmo (CZ) [10]. Total sinistral displacement along the DF is estimated between 25 km, derived from offset of granitic blocks [8] and about 40 km, derived from offset of magnetic anomalies [13]. Figdor & Scheidegger [13] also conducted a gravity ground survey with subbases along the DF, where the DF can be identified as an elongated gravity minimum, supporting the NE-SW trend.
Both faults, the DF and the WF, are clearly visible as lineaments in digital elevation models, as they separate the crystalline rocks in the NW from the Neogene sediments of the Molasse basin in the SE. However, neither geomorphology nor surface geological mapping identify the northern part of the DF, where it runs parallel to the WF, where it is assumed to continue mostly under Quaternary loess cover within the Molasse basin.
The DFS limits the tectonic Thaya Window towards the east, where the Moravian Superunit is exposed (Figure 1b). Towards the west, the Thaya Window is limited by the SW-dipping Moldanubian Shearzone (MSZ), separating it from the Moldanubian Superunit. The Moldanubian Superunit was thrust onto the Moravian Superunit along the MSZ during the Variscan orogeny. Within the Thaya Window, one major SSW-dipping, roughly N-S striking regional thrust separates the Pleißing and the Pulkau nappes, consisting both of orthogneisses of different compositions [14]. This nappe boundary is indicated as NB in the following figures. For comparison, all available data are plotted along a NE-SW trending profile A that crosses all four faults, in order to evaluate the relevance of individual datasets and the correlation between them concerning the recognition of tectonic boundaries. For orientation, the location of profile A is shown in all figures representing the data.

2. Materials and Methods

2.1. Acquisition and Processing of Aerogeophysical Data

Since 1982, the Geological Survey of Austria (GBA) has been performing aerogeophysical helicopter surveys in Austria. The main elements of the airborne system are an electromagnetic (EM) device, a gamma spectrometer, and a magnetic total intensity instrument. All parameters were recorded simultaneously and the intended flight altitude for all survey sites was 80 m above ground. The instrumentation has been changed and improved several times over the years (see Table 1), which resulted in considerable weight reductions and better accuracy.
At the beginning, a proton precision magnetometer was carried 20 m below the helicopter in a separate “bird” with analog data recording at a sampling rate of one sample per second. By the end of the 80′s, digital data recording was introduced and in 1994, the instrument was replaced by a cesium vapor magnetometer, with the position of the sensor moved inside the EM-bird, 30 m below the helicopter. These changes led to an improvement in accuracy (i.e., increased sensor distance to the helicopter and better sensor accuracy), an increased data-sampling rate (10 samples per second) as well as an easier helicopter take-off procedure (only one bird). In 1996, the proton precession magnetometer used as base-station on the ground for measuring the daily variation of the earth’s magnetic field was replaced also by a cesium vapor magnetometer. This raised the sampling rate from one per 30 s to 10 per second. Additionally, a self-sufficient power supply for the sensor was developed, which allowed the base station to be located far away from noisy influences, which leads to an improved accuracy of the data.
Before 1993, video recording and Doppler-navigation were used for position recording, with the altitude measured by radar altimeter. Pilots did in-flight-navigation visually. In a time-consuming post-processing step, the flight-path video was used to correct for the drift of the Doppler-navigation system. The final horizontal accuracy of the position was nevertheless very poor (+/− 100 m). The height above ground was available from the radar-altimeter (depending on the earth’s vegetation cover with an error of up to 30 m). In 1993, a GPS-receiver was added to the system, but because selective availability (SA) by the US-government was active, the position error was still in the range of +/− 100 m. Nevertheless, flying and post-processing times were significantly reduced. In addition, a first-reflection laser-altimeter was installed. In 1997, the GPS-receiver was replaced by a GPS/GLONASS-receiver and the position error was reduced to a few tens of meters. In summary, all the before-mentioned improvements led over time to faster, more accurate data acquisition and an easier and quicker post-processing for the airborne magnetic field measurements. This is also valid for the EM and gamma-ray measurements.
The area covered by the different surveys and used in this study is shown in Figure 1a. As the quality of each single dataset is based on the type of the recording instrument and the accuracy of determination of height and coordinates, the technical improvements concerning the latter are described in the following and are summarized in Table 1 showing the various technical equipment and survey specifications that have been used over a period of 14 years. Airborne total magnetic intensity maps have the potential to reveal both deep (up to tens of kilometers) and shallow tectonic structures, whether outcropping at the surface or buried under Quaternary or Neogene sediments.
Until 1994, the magnetic data was obtained using a proton precision magnetometer (G-801/3). Then, the instrument was replaced with a more accurate cesium vapor magnetometer (Scrintrex CS-2), which was located inside the EM-bird (Table 1). Both devices were carried below the helicopter - the magnetometer 20m and the EM-bird 30m. Further recording details can be found in the survey-specific technical reports [1,2,3,4,5]. In 1998, the individual geomagnetic datasets covering the DFS (see red boxes in Figure 1a) were reprocessed and combined to a single data set. The reprocessing involved the following steps: (i) the fully automatic processing that was common at that time was expanded to include interactive programs that enabled the editor to visually check the data quality, in order to remove spikes and gaps. (ii) The International Geomagnetic Reference Field (IGRF) was removed. (iii) A heading error correction was introduced to remove the influence of the moving helicopter. (iv) The correction of daily magnetic field variations was applied. (v) Correction factors in order to match the individual datasets were applied [17]. (vi) A reduction to the pole was applied [18]. The resulting data set is provided in the form of a grid with a resolution of 250 m × 250 m (Figure 2) and was used for modeling in this study.
The interpretation of aero-electromagnetic (AEM) measurements is based on the model concept that the measured data can be explained by modeling the distribution of electrical resistivity in the subsoil. The task of the quantitative interpretation of AEM data is to find a physical earth model (distribution of resistivity in the subsoil) that explains this measurement result and, at the same time, agrees with already known geological data about the survey area. The volume involved in each of the frequency domain measurements depends on the used frequencies (Table 1), the conductivity of the surface, and the altitude of the measuring device [19]. Therefore, the exploration depth can vary up to the maximum of 100–150 m (which applies to the coil specifications used in this context) [1,2,3,4,5]. Since height determination in the 1980s and 1990s was error-prone, one of the tasks of this study was to evaluate the usability of old AEM maps for large-scale geological applications, such as fault identification. In addition to the aspects mentioned above, there are further methodical limits to the detection of faults in AEM data. First, a resistivity contrast between the two adjoining lithological units or at least between the fractured fault zone and its surrounding is needed. Second, the fault should be outcropping at the surface, or at least has only a relatively thin cover of not more than a few tens of meters.
In 1998, all individual AEM datasets (Table 1) acquired by the GBA in the study area were reprocessed and homogenized. This map is available for the present study and shows the distribution of apparent electrical resistivity calculated for the homogenous half -space model. (Figure 3).
Airborne gamma-ray maps show the distribution of natural radioactivity of surface rocks and soils down to a depth of a few decimeters below the surface. Therefore, they are useful to distinguish regions of contrasting mineralogical content of outcropping rocks [20]. Under certain circumstances, straight linear boundaries can be interpreted as faults.
Two different gamma-ray spectrometers were used during the airborne survey period of the study area (Table 1). Geometrics GR-800B, used in the 1980’s contains eight sodium-iodide crystals with a total volume of 33.6 L. The light pulses, stimulated by gamma-rays are sampled into 256 energy channels covering the energy range from 0 to 3 MeV. Scintrex PGAM-1000 has the same specifications as Geometrics GR-800B but with the addition of an upward looking sodium-iodide crystal (for ambient radon-correction). The total volume of this device is 37.8 L. The following processing steps were applied: (i) reduction of cosmic radiation, (ii) reduction of the background, (iii) reduction of the Compton effect, (iv) radon correction (only at the survey areas conducted in the nineties), (v) height correction. Attenuation coefficients were determined by climb flights in the survey area.
The three most commonly used radiometric data sets (uranium, thorium, and potassium) are available for the study area. They were acquired along with the magnetic and electromagnetic data and later post-processed in a framework aimed at homogenizing airborne radiometric data [21]. This data, compiled in 2007, was used for fault interpretation in this study (Figure 4a–c) in order to evaluate its usability.

2.2. Acquisition and Processing of Gravity Data

Processed gravity data is helpful in solving a variety of engineering and environmental problems, including estimating the spatial extent of faults [22]. It is often used in conjunction with aeromagnetic modeling data, as both methods are based on potential field interpretation and therefore can be suitable under favorable circumstances for solving problems that require investigation depths of up to ten kilometers [23]. The Bouguer anomaly is used to model and identify faults because of its sensitivity regarding density inhomogeneities within the subsurface [24].
The gravity data available in Austria has been acquired by various organizations for more than 50 years and are now maintained by the BEV. The gravity base reference in Austria is a ballistic absolute gravimeter of the JILAg6 type (between 1986 and 2009) and the FG5 absolute gravimeter (since 2010). The gravity base station absolute values are tied to stations of the Austrian Gravity frame (ÖSGN) and are continuously checked and re-measured. All of the ÖSGN stations are tied to absolute gravity stations. The calibration of individual gravimeters was controlled by observations at the Hochkar Calibration Line (HCL) in Austria. In 2007, Meurers and Ruess published a complete review of the gravity values measured in Austria based on 54,000 land gravimetric data [25]. For determining the Bouguer anomaly, the observed gravity from the gravity data base was corrected for the normal gravity at elevation h, the mass correction, and atmospheric correction with the normal gravity at elevation h resulting from a Taylor series expansion to the 2nd order, both in h and geometrical flattening [26]. The elevation h corresponds to normal orthometric elevation, which is the official elevation system in Austria. A spherical mass terrain correction (167 km radius, Hayford zone O2) assuming a constant density of 2670 kgm−3 was applied, with a truncation of the mass correction area beyond 167 km. Rock densities measured in situ and in drill cores in 1991 vary widely within the Bohemian Massif, but generally confirm this assumed average value of 2670 kgm−3 [27]. For the terrain correction, a digital terrain model with a spatial resolution of 50 m was used and the topography close to gravity stations (<1000 m) was approximated by a polyhedral surface.
The irregularly distributed data were interpolated onto a 500 m x 500 m square grid using an inverse-distance-to-2nd power algorithm (Figure 5). This grid size was chosen on one hand to obtain an adequate density to solve the problem of tracing faults, and on the other hand to avoid artefacts caused by improper interpolation.

2.3. GIS-Based Reprocessing Methods Used for Geological Fault Interpretation

GIS tools developed to analyze digital elevation models can also be used to explore and visualize geophysical data. These tools are helpful in gaining insight into the nature of data before modeling, or in cases where no modeling software is available [28,29]. The feasibility of detecting geological faults in geophysical data sets relies on abrupt gradients of geophysical properties on both sides of the fault. Determining these lateral magnetization contrasts has long been an important topic in fault interpretation research, and many edge detection routines have been developed [30,31,32,33,34].
A variety of GIS tools are capable of performing edge-approximating techniques, which are used to detect faults. Alignment of geophysical anomalies using derivatives of the 1st and 2nd order provide information for structural analysis. Nevertheless, it requires experience and knowledge of the geological setting to interpret the lineaments correctly. We applied several GIS tools, e.g., Raster to TIN [35], Slope [36], Profile curvature [37] and Aspect—Slope [38], applying varying starting conditions described in the following. We then look for linear features in each of the datasets individually and finally compare the positions of the obtained lineaments with mapped faults in the respective area. Based on this comparison, we qualitatively evaluate the usefulness of each data set separately and the combined data set in respect to detect geological faults and their characteristics. In the following, the applied GIS tools are shortly described.
The accuracy of calculated magnetic models depends—among other things—on the accuracy of the spatial position [39]. In particular, the height and orientation measurements of the magnetometer device were imprecise in earlier times (see Section 2.1). Therefore, when dealing with vintage data, the focus of the interpretation should lie on strong variations of the magnetic field to avoid the misinterpretation of noise or artefacts. The GIS tool Raster to TIN [35] transforms a raster into a Triangular irregular network (TIN) which has the ability to describe the surface at different levels of resolution. This tool is widely used to convert digital elevation models, but it can also be applied to geophysical raster data [40,41]. Because nodes can be placed irregularly over a surface, TINs can have a higher resolution in areas where a surface is highly variable or where more detail is desired and a lower resolution in areas that are less variable (see cell sizes in Supplementary Figure S3). Thus, applied on magnetic field data, sections with steep gradients will be amplified whereas sections with less distinct gradients will appear underrepresented. The z-factor adjusts the units of measure in z direction (depth or height) in case they differ from the measure units in x and y direction (map view), with the default value of 1 in case the measured units are identical in all directions. In the case of non-elevation data, the z factor can be used to amplify the shown data (= z component) in order get an equivalent to the vertical derivation often used in the course of edge detection techniques. The z-tolerance is the maximum number of units by which the TIN surface may differ between two neighboring cells from the input raster. Choosing a low z-tolerance (e.g., 20 nT for the magnetic total intensity) yields a result similar to the input raster resolution (see Figure 2, but with better visible edges. In addition, if combined with a high z-factor (e.g., 20, see Figure 6), small variations in the data are highlighted.
The derivatives of magnetic or gravimetric anomalies caused by faults have associated peaks or ridges that are more or less offset laterally from their associated sources. The shallower the dip of the fault plane and the deeper the structure extends, the greater the offset [42]. Slope computation is a viable technique for delineating edges in potential field data, and is therefore useful for visually proving the presence of faults. The GIS tool Slope [36] identifies the steepest gradient from each cell in a raster. The calculation is performed on a projected flat plane using a 2D Cartesian coordinate system. Here, we again choose a z-factor, which leads to an exaggeration of the z-component of the resulting field. Figure 7 shows the slope amplitude of the magnetic total intensity with z- factor 20 of the triangulated magnetic field (with low z-tolerance, Figure 6). Areas colored mainly in blue show “flat areas”, e.g., small lateral changes in total intensity. Red colors highlight abrupt changes. In general, the blue flat areas are mostly bonded by as linear features of yellow and red colors, indicating abrupt lateral changes of geophysical parameters. These can be interpreted as faults or other geological contacts. However, if the change of the measured parameters across a fault is not seen, e.g., due to a small offset or a gently dipping fault, the fault might not be identified within this illustration.
The GIS function Aspect-Slope [38] is designed to simultaneously display the aspect and the slope of a digital elevation model. The utilized color scheme allows accurate terrain visualization while simultaneously categorizing the surface into explicit aspect and three slope classes represented within a single, two-dimensional map [43]. Applied on potential field data, this tool converts magnetic or gravimetric data into 3D appearing “landscapes” in which strong field variations and their spatial orientation come forward, whereas regions with small lateral changes tend to disappear in grayish hues. “Flat areas”, e.g., areas where the potential field values do not change, are shown in gray (Figure S1 in the supplementary information). In order to achieve an even stronger visual effect highlighting smaller changes, a scaling factor (z-factor) of 5 (Figure S2 in the supplementary information) and 10 was used for the z component when processing the total intensity data (Figure 8a). For gravimetric data (Figure 8b), no z-factor was applied, because using it does not add any additional value to the resulting aspect slope map. The visible lineaments are the same no matter which z-factor is selected. This is because the dynamics of the values across the study area differ from the dynamics of the magnetic data. The interpretation of the aspect–slope approach is similar to that of the Slope approach, but provides directly additional information of the dipping direction of the geological contact.
Curvature anomaly maps of potential field data can be used to improve the localization of geological boundaries [44,45,46,47]. GIS provides the tool Curvature [37], whose primary output is the curvature of the surface on a cell-by-cell basis, as fitted through that cell and its eight surrounding neighbors. Two optional output curvature types are possible: the profile curvature is in the direction of the maximum slope, and the plan curvature is perpendicular to the direction of the maximum slope [48]. In this study, we used the profile curvature method, as it has become the more popular method in the last dozen years [49,50]. The calculated field shows isolines with constant rate of change of the steepest slope across the surface and therefore is useful to localize edges of gravity or magnetic source bodies. In this study, we calculated the profile curvature of both, the magnetic and gravimetric data (Figure 9) but chose to use only the gravimetric map for interpretation since the magnetic curvature map shows no additional value compared to the magnetic or the magnetic slope map. In contrast, the slope map of the gravimetric data shows less informative value compared to the calculated profile curvature map (Figure 9), and is therefore not used for further interpretation.

3. Results

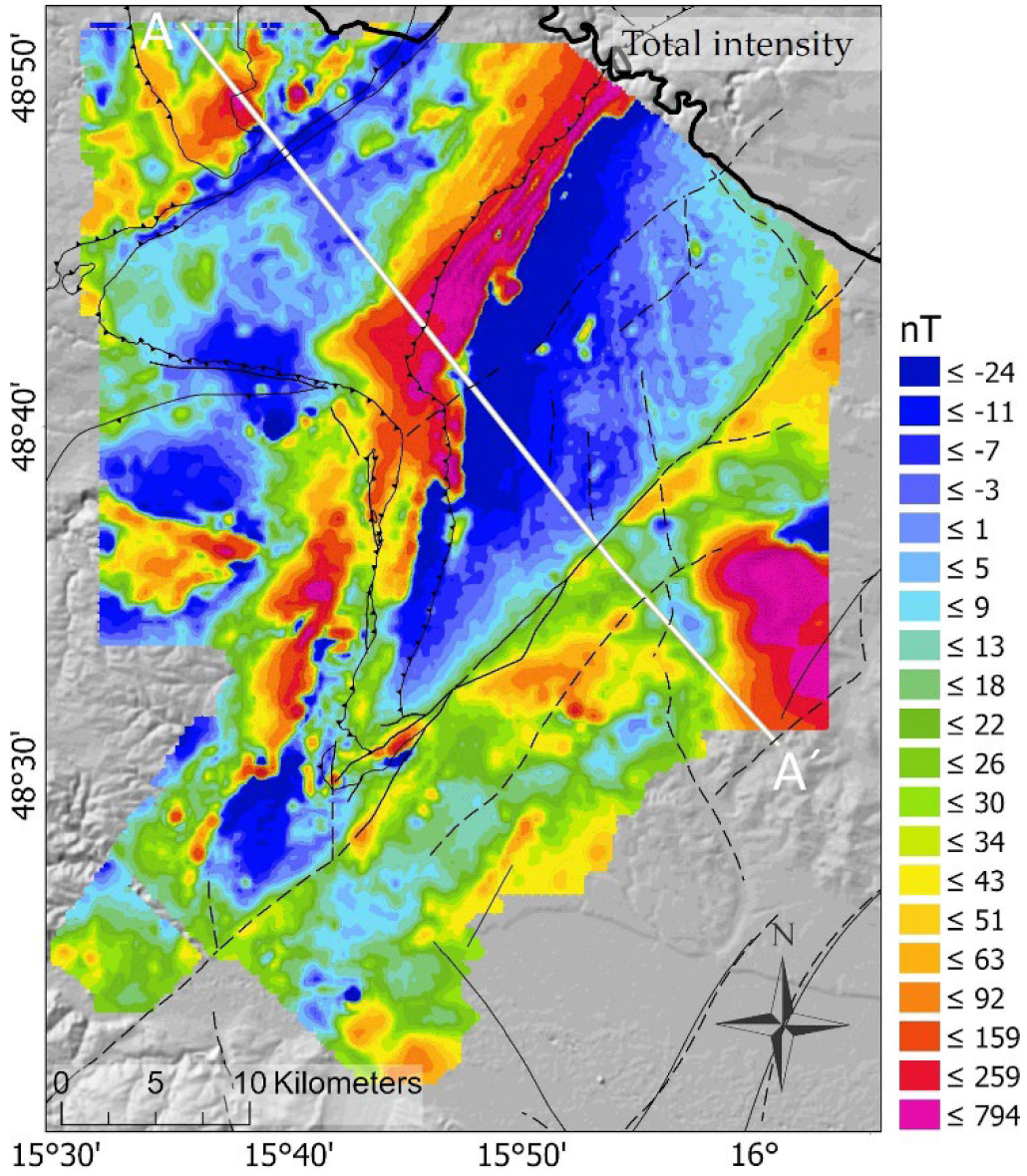
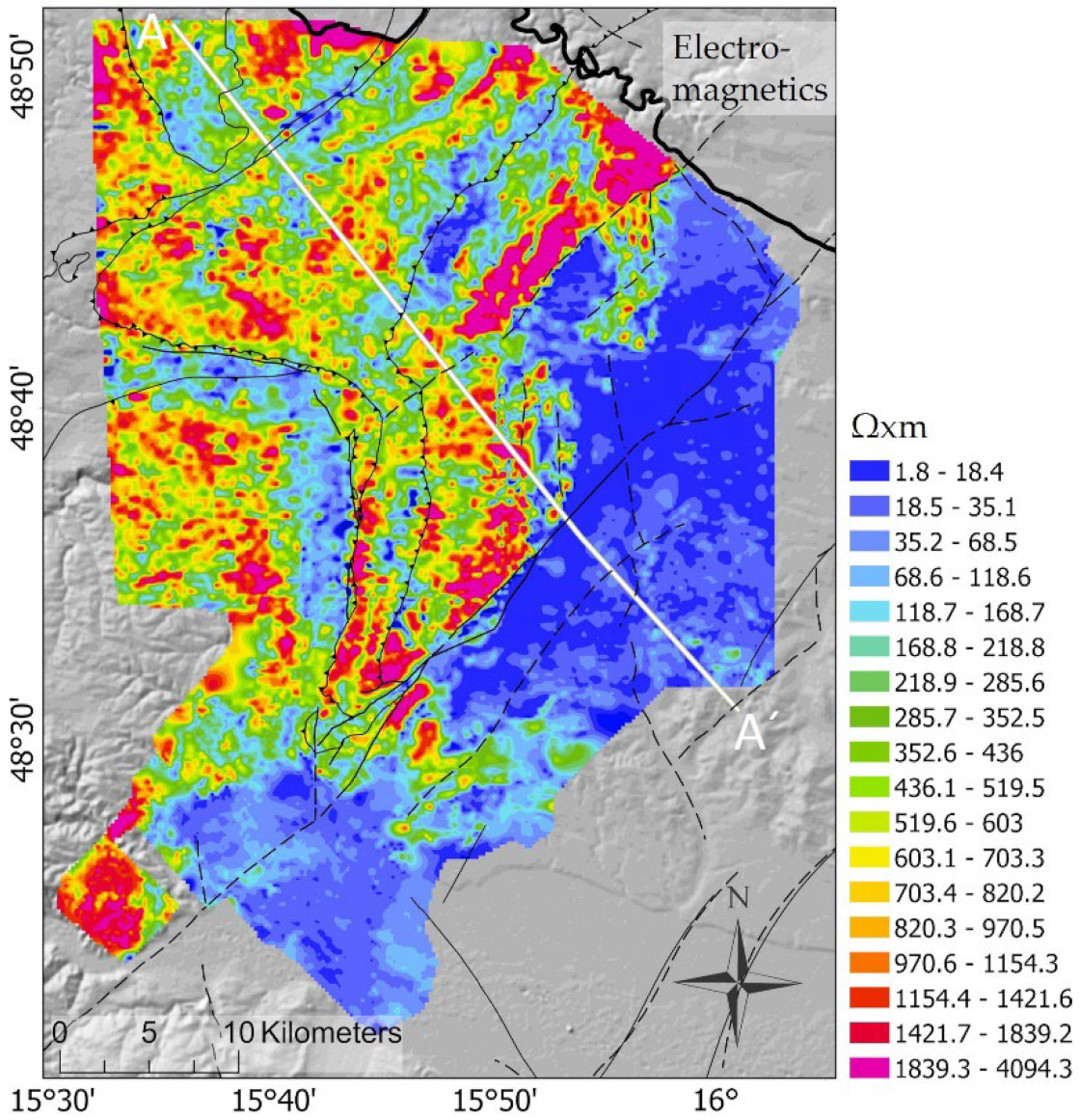
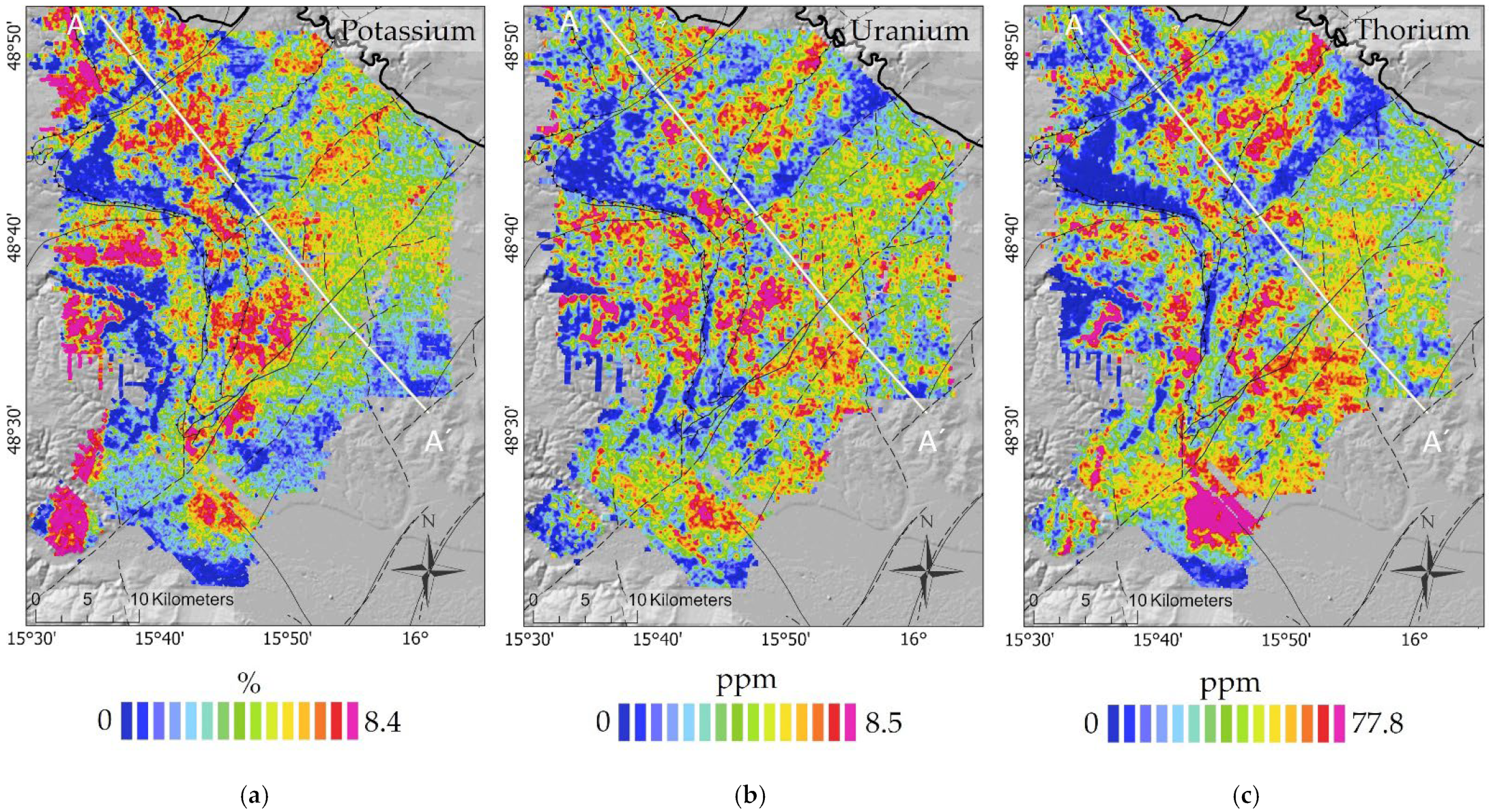
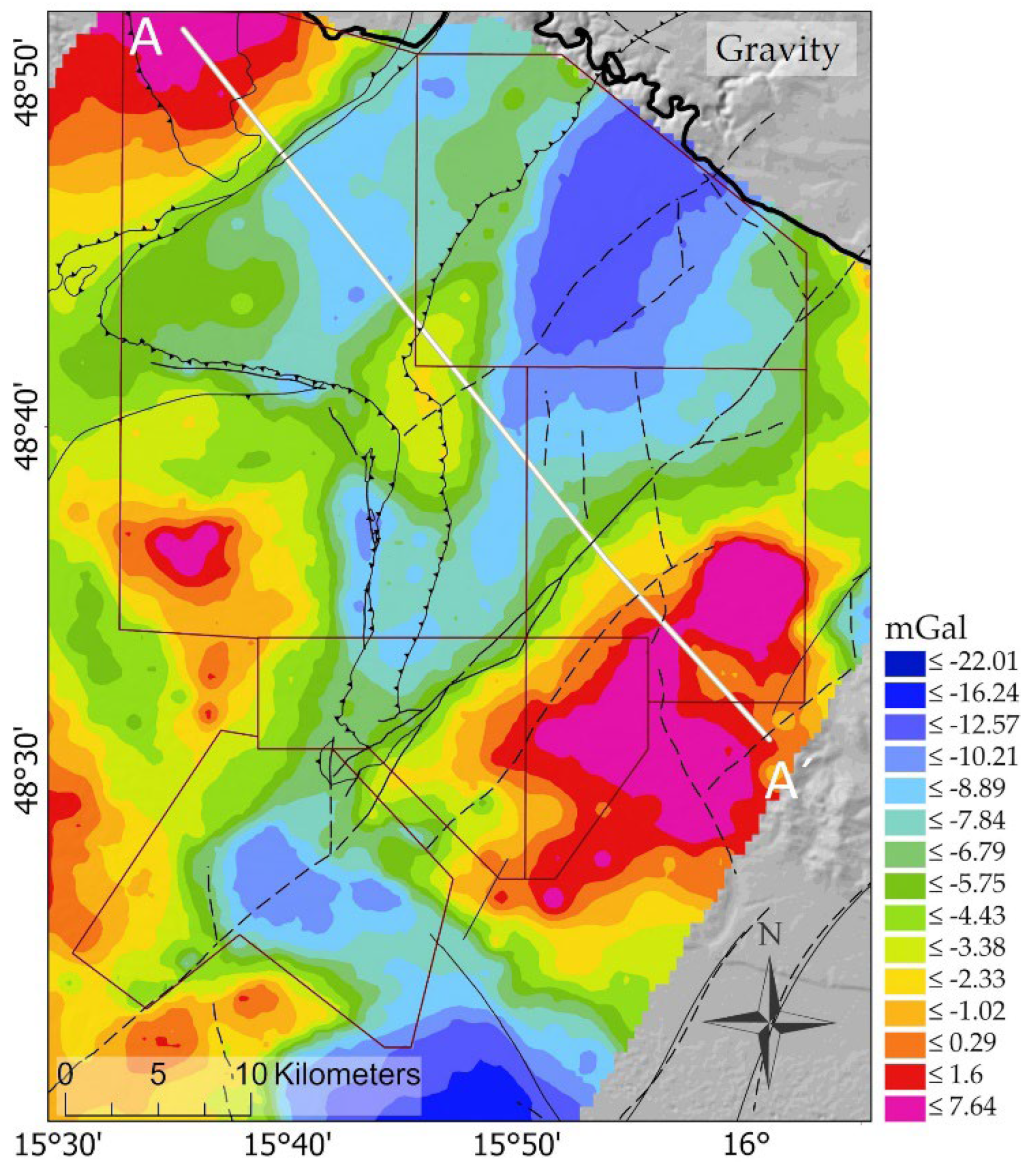
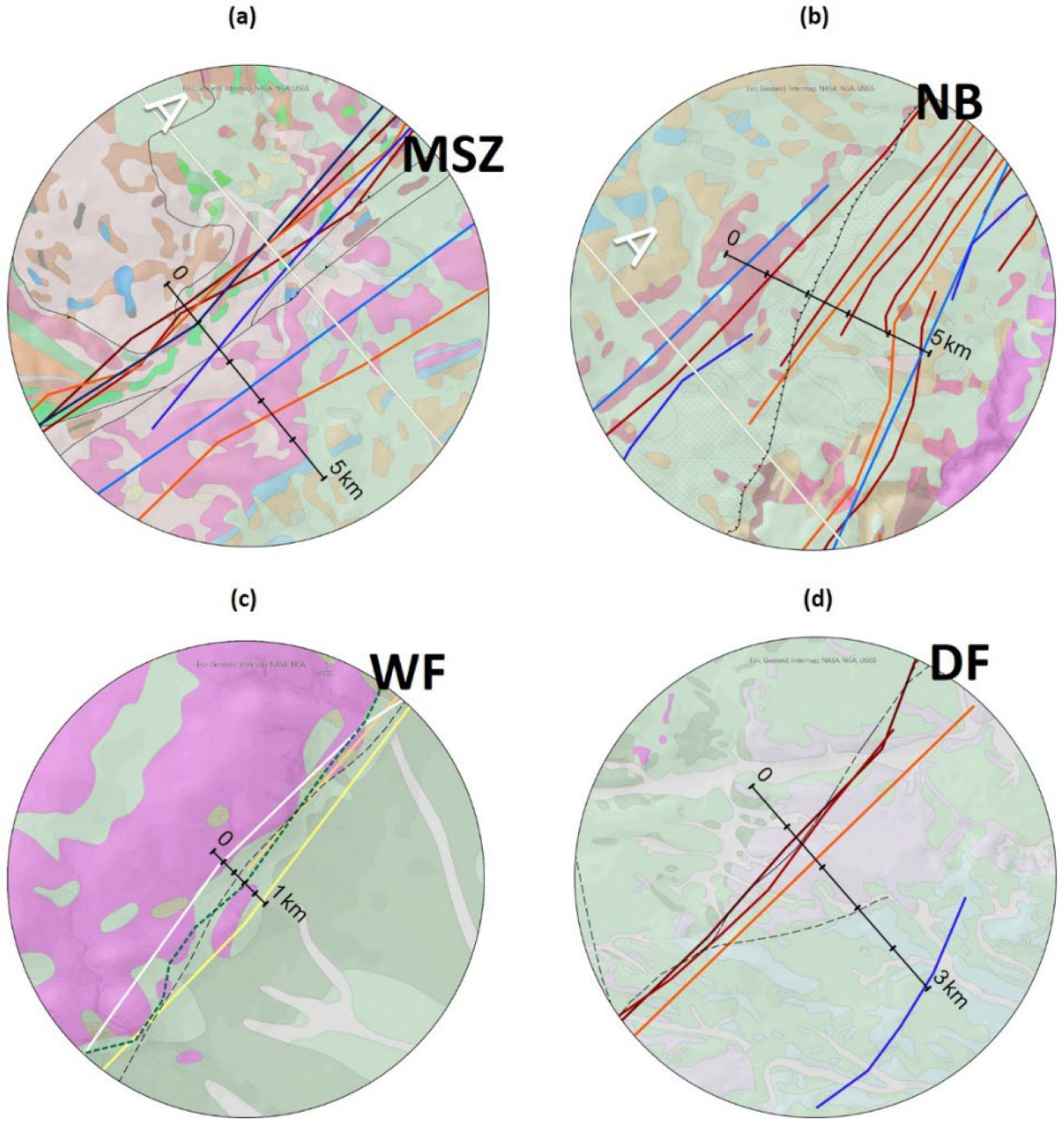
3.1. Fault Lineaments in Map View

Abrupt geophysical parameter changes often indicate sudden changes in lithology at the subsurface. Often, especially if they appear linear, these zones can be associated with tectonic structures or other geological contacts. If these linear features are observed within multiple geophysical data sets, the likelihood that they represent a tectonic structure increases. The lineaments in this study were interpreted and placed visually, although there are GIS-routines capable of automatically detecting lineaments from a map [51]. The reason for this is that focusing on the verification of the four main faults requires a simplification of the original and processed datasets. Figure 10 shows the resultant lineations derived from all data sets presented in Section 2. Figure 10a, shows lineaments derived from gravity and magnetic data representing deep-seated sources, whereas lineaments in Figure 10b represent data from shallow sources (radiometry) and from sources of intermediate depths (AEM). Comparing the lineaments with the major tectonic structures marked as MSZ, NB, WF, and DF in Figure 10, they generally correspond well. For better visibility, detailed views of the surrounding of each fault along profile A are presented in Figure 11.
The DF, MSZ, and NB, are well represented in datasets shown in Figure 10a: The DF generally shows a dense bundle of lineaments within ~1 km around the mapped fault location, except for the Aspect-Slope representation of the Bouguer anomaly. Lineaments related to the MZS and the NB are also represented clearly, but are spread over ~5 km. The WF, however, is only visible in the AEM data.
In contrast, lineaments related to the WF can be observed in Figure 10b, also representing a concentrated bundle of ~1 km width. Lineaments related to the DF are observed in Figure 10b only for its southern part. The MSZ is also associated with short lineaments, but not as abundantly and clear as in Figure 10a, whereas the NB is only seen in the TIN representation of the magnetic data with high z tolerance (Figure S3).
In order to investigate if the different appearances of the observed faults can be probably explained by the different geological situations and geometries of the four faults, we will discuss each of the larger tectonic structures, their visibility in the different data sets and the possible reasons in the following.
In the TIN (Delauny Triangulation) representation of the magnetic data, the DF is clearly seen as a linear feature in the TIN representation (Figure 6 and black solid line in Figure 10a and Figure 11d). It seems that the TIN representation of the magnetic data highlights edges that are already visible in the normal raster representation (comparison of Figure 2 and Figure 6). However, the high z-factor of 20 for the TIN representation leads to extreme values for the lowest and the highest values of the dataset. This results in a kind of saturation of the color bar for both extremes of the total intensity scale, which might obscure variations between high and higher (or low and lower) values. This might be the reason why the WF is not seen in this visualization.
The lineaments observed in the TIN show a good fit with those lineaments that are generally assumed to be derived from deeper sources. In addition, a Neogene-Quaternary sedimentary basin fill covers the northern part of the DF, while the WF is clearly visible at the surface. It also appears that the WF has little vertical displacement, so that at greater depths, the rocks on both sides of the fault are identical. Therefore, the TIN representation of the magnetic total intensity might be used as a quick way to identify deeper seated sources (low z-tolerance and high z-factor).
The lineaments obtained from the Slope and Aspect–Slope calculations (Figure 7 and Figure 8) for the Bouguer anomaly and the magnetic total intensity are marked as blue and orange lines in Figure 10a and Figure 11, respectively. The combined information of the location and the direction of the steep gradient in the magnetic total intensity highlights those faults as areas of unidirectional gradients. The DF is clearly seen as a narrow, linear area of linear changes in the magnetic data, being a textbook example for the application of those methods. In addition, N-S to NW-SE striking faults between the WF and the DF can be also identified in a similar, but more subtle way.
The northern part of the MSZ separates an area with little change in its SE from an area showing a high fluctuation. This separation follows very well the geologically mapped feature. Since such highly changing environment also characterizes the eastern Thaya Window around the NB, we assume that this is an expression of the high measured magnetic total intensity values in these areas (see Figure 2). As the gradient calculation is made on the absolute values, a change of a few percent between measured magnetic intensities of 200 nT and higher leads to larger gradients than the same deviation at lower magnetic intensities in the range of less than 100 nT. Considering this, the larger areas of high gradients can also be interpreted as areas of predominantly granitic or granulitic rocks, which are generally associated with higher magnetic intensities. Therefore, the northern part of the MSZ can be mapped along the boundary between the blue and the dark red areas.
In addition to the linear features, this visualization method also highlights smaller circular areas. Following the argumentation above, they could be interpreted as singular small granitic lenses close to or at the surface. Another possible interpretation would be that of manmade artificial sources at the surface [52].
The application of the Aspect-slope calculation on the Bouguer gravity anomaly data shows less variation (Figure 8b), most probably due to the larger grid sizes of the gravity interpolation. In general, this data consists mostly of steep gradients. Therefore, the data is less intuitive to interpret. Nevertheless, the main features observed within Figure 8a can also be identified, although less precisely: The MSZ can be identified as a linear change between a generally S-dipping (pink) and a generally N-dipping (green) area. In addition, the NB seems to be located around the maximum of the granitic rock unit of the Thaya Window, as it correlates roughly with the change between E-dipping (blue) and NW-dipping (yellow) areas.
However, in general, the Aspect–Slope and Slope tools as applied here seem not to help to interpret the Bouguer anomaly data. Therefore, we tested if the second derivative of the data would provide insights that are more precise. In Figure 9, the curvature along the maximum slope for the Bouguer anomaly data is plotted. Despite the high noise in this map, longer linear features consisting of negative and positive lines can be observed parallel to the main fault zones, except for the WF, which is not visible in the data set. The MSZ and the respective lineament correlate well, especially its southern N-S striking part, where the MSZ juxtaposes granitic rocks on the east and sedimentary basin fill on the west. In addition, the outlines of the granitic body within the Thaya Window around the NB that has been distinguished in the magnetic total intensity aspect-slope map (see Figure 8a) can be also identified here. Furthermore, the DF can be located as a more or less continued NE-SW striking line. The comparison with the original Bouguer anomaly raster and the Aspect–Slope and Slope calculation results suggest that, for gravity data, the curvature map is the best to locate potential fault zones, if a large enough density contrast exists. The lack of a large density contrast might be also the reason that the WF is not detected in any of the gravity data visualizations.
Lineaments on AEM (Figure 3) and aero-radiometric data (Figure 4) have been identified only based on the visualization of the data as shown in the respective figures. Lineaments identified within the AEM data set correlate well with the major faults, where the faults are present in the landscape as geomorphological fault scarps. This is generally the case where the faults act as margins for sedimentary basins, e.g., the central part of the DFS, the northern part of the WF as western limits of the Molasse basin, and the southern part of the MSZ, where it is the northern and eastern boundary of the Horn basin. Here, the granitic and/or gneissic rocks of the Bohemian Massif are located at one side of the respective fault, and the adjacent sedimentary deposits of the basins on the other side. Thus, there are strong material contrasts across the fault more or less directly at the surface or at very shallow depths. As the measured AEM values are low, the expected penetration depth for this method is around 50 m. Therefore, these material-contrasts close to or at the surface are depicted well in the AEM data. The radiometric data correlates well with the distribution of sedimentary deposits, showing slightly elevated values in the Uranium and Thorium distributions.

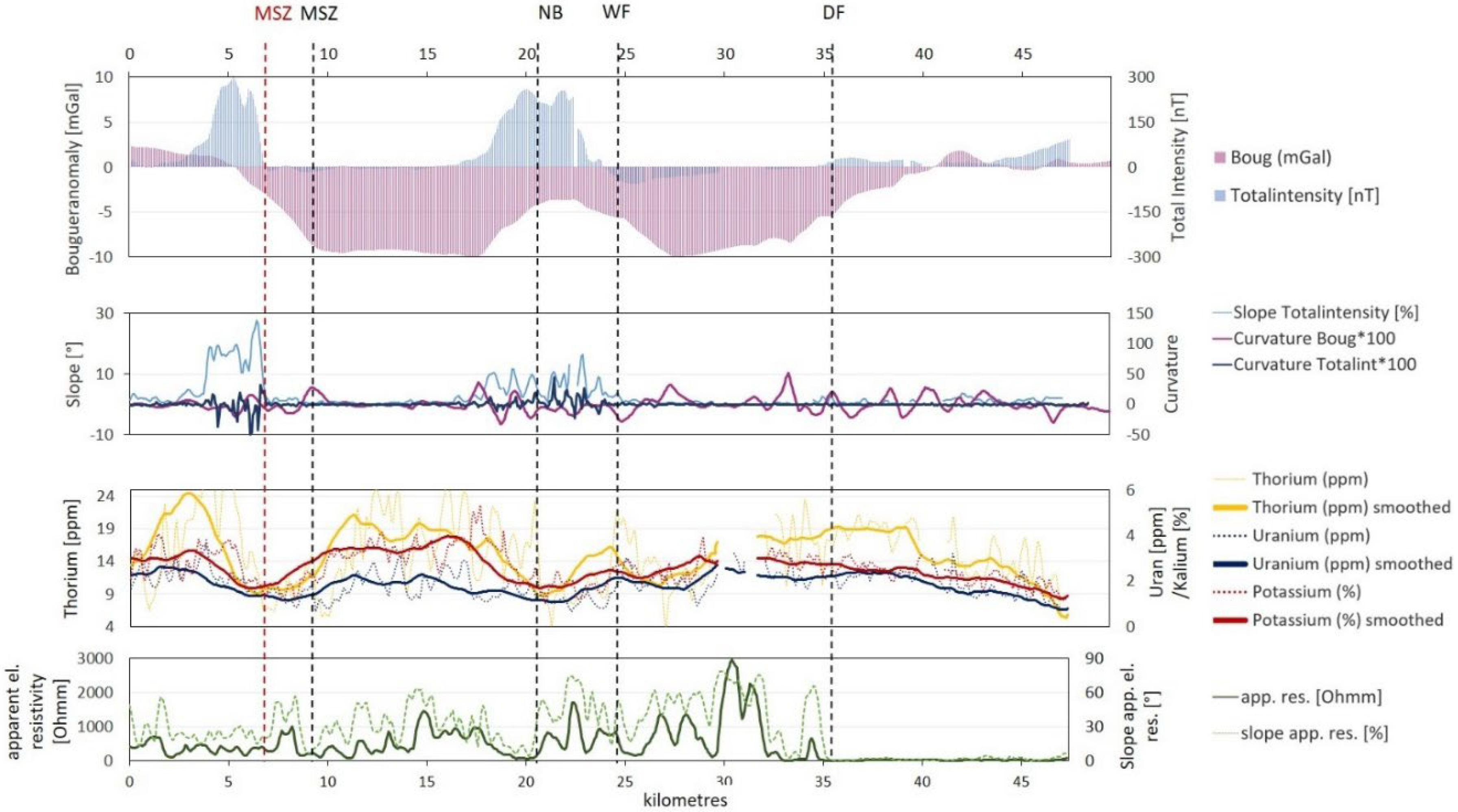
3.2. Comparison along Profile A

For the comparison of the different datasets, we looked at all data along profile A, which includes four of the most prominent faults located at this study site. As a reliable basis for evaluation of the airborne datasets serves the location of the geological faults taken from the geological map of Lower Austria [15,16] (Figure 1b). All aerogeophysical data plotted in GIS (Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9) were extracted at defined point locations along profile A. After creating the line feature of profile A, the GIS tools Generate Points along Lines and Extract Multi Values to Points were applied. Generate Points along Lines created point features along profile A at a fixed interval of 100 m. Subsequently, the tool Extract Multi Values to Points, applied as a batch tool, extracted magnetic, gravity, radiometric, and electromagnetic data at the calculated point locations. As the extracted points are measured by map units given in degrees of latitude and longitude, the 100 m distance between the points along profile A had to be projected on degrees of longitude in order to plot the curves shown in Figure 12.
Evaluating the visibility of the four major faults within the different datasets along profile A, we come to the following observations relative to each of the four major fault structures:
(1) The Molanubian Shearzone (MSZ) is indicated as a strong change in almost all data sets at a similar position, as presented by the red dashed line in Figure 12. However, in comparison with its surface trace on the geological map and profile (black dashed line), this position is shifted towards the NW for two kilometers. This might be the effect of its NW-dipping geometry.
(2) The Nappe boundary (NB) within the Thaya Window is more difficult to identify, as the changes in each data set are not as prominent as in the case of the MSZ. However, changes can be observed especially in the magnetic total intensity and its derivatives, the distribution of Thorium/Potassium and the AEM data. Interestingly, the changes for the latter coincide with the location of the fault on the geological map and profile (black dashed line in Figure 12), whereas the change in the observed magnetic data is shifted again towards the NW. Again, this is probably caused by a NW-dipping geometry.
(3) Profile A crosses the Waitzendorf Fault (WF) at the southern part of the fault, south of the visible and prominent geomorphological scarp. Nevertheless, there are minor changes in the magnetic total intensity and even in the gravity data, although they are smooth and over a larger distance. However, the slope of the magnetic total intensity shows a more localized change at the place of the WF. The fault can be clearly seen in the non-smoothed radiometric data. In addition, there is also a change within the apparent resistivity of the AEM data, but this signal is not distinct.
(4) The Diendorf Fault (DF), in contrast, shows a drastic change in the AEM data precisely where the fault is mapped. NW of the DF, values up to 3000 Ohmm are observed, whereas the values in its SE do not exceed 100 Ohmm. This is reflected also in the magnetic total intensity, where an increase is observed around the location of the DF, but not as strong as at the location of the faults that are outcropping at the surface (MSZ, WF).

4. Discussion

4.1. Comparison of Different Data Sets Using Various GIS Tools

In general, our study shows that, depending on the nature of the fault, differently transformed geophysical field data executed with GIS tools lead to good results consistent with the location of the geologic contacts at all four mapped faults. The magnetic total intensity is especially useful to detect the trace of the DF under the sedimentary cover of the Molasse Basin. In general, the magnetic and the gravimetric data show reliable results for deeper sources. The capability of gravity data to detect sources at different depths depends on the extent of the study area and the density of the measured grid: a larger extent of the study area allows detecting deeper and larger sources. On the other hand, a higher density of measurements per square kilometer permits a higher resolution of anomalies and discrimination between small anomalies. AEM data represent sources, which are located in a layer with a thickness of 80 to 150 m lying directly beneath the surface. The results of radiometric surveys on the other hand image the geologic structure of the surface, since the exploration depth is only a few decimeters. Thus, as the summary in Table 2 shows, comparing the results of these different methods can provide information not only on the depth extent of the sources of the anomaly, but also on whether or not the geological structure is buried. For these investigations, it is essential to have good geologic knowledge about whether the expected geophysical contrast in the present case is shown in the method under consideration.

4.2. Location of Profile A

The position of profile A was selected in order to investigate four geologic boundaries with different characteristics. The fact that all contacts are mapped (partly) on the surface enables us to evaluate whether anomalies apparent in geophysical data are plausible. Profile A is more or less perpendicular to the fault structures, and provides therefore a good position to evaluate the anomalies. The chosen position is more or less the only option, where all four major faults are crossed by a single transect. However, profile A crosses the WF only at its southernmost part, where the prominent geomorphological fault scarp is no longer observed. Even though we still see some changes in almost all datasets, they are less prominent than those associated with other faults. If the profile A would run across at the center of the WF, the picture would look differently. A similar situation is given for the DF where profile A crosses north of the geomorphologically prominent fault scarp where the fault is buried below Quaternary and Neogene sedimentary cover. Even though the fault can be observed with the geophysical methods describing deep-seated anomalies (magnetics and gravity, and their derivatives), there is no sign for a fault in the radiometric data set that is insights for shallow sources.

4.3. Map View vs. Profile

As discussed in the section above, the view along one single profile has its limitations. Especially the evaluation of the suitability of an applied method depends strongly on the location of the profile. Nevertheless, comparison of the edge-approximation results of various geophysical methods along a profile is helpful to understand the vertical distribution of the anomalies. For example, the comparison between methods detecting shallow and deeper sources, respectively, along a profile allows also to indicate the direction of the fault dip, e.g., for the MSZ and NB in Figure 12.
In addition, the map view of each edge-approximate result (Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10) provides information regarding the orientation and the length of the observed fault. In addition, the differences in width between the location of the lineaments obtained from different sources might be an indicator for vertical (WF and DF) versus dipping (MSZ and NB) fault geometries (Figure 11). Therefore, we recommend the evaluation of the different datasets both in map view and along along a profile in order to assess their usability and reliability.

4.4. Comparison with Results from Modeling

The same aeromagnetic dataset used in this study has been studied by Paoletti et al. [53]. They used potential field multiscale techniques for source-edge location and characterization of sources at depth with a focus on characterization of subsurface structures. In general, the major lineaments and structures such as the DF, the MSZ, and the WF have been identified by both approaches. Additionally, the identified locations are in good agreement, and the information derived from modeling is also more detailed. Nevertheless, the comparison shows that good results can be achieved with simple GIS tools even without modeling software.

4.5. Precision of Vintage Aerogeophysical Data

Usually, vintage geophysical data show a lower acquisition density than modern data, especially in the case of regional surveys. Combined with the fact that faults are only visible if related with density and/or magnetization contrasts, the possibility to identify faults in vintage potential data is limited to larger offsets associated with strong contrasts. Another aspect related to the low acquisition density is the uncertainties regarding the exact fault locations. As the interpretation is generally based on interpolated data grids, low data density plays a major role in increasing the uncertainties in this aspect.
Typically, accurate modeling of magnetic data requires applying field continuation to a horizontal plane [54,55]. However, the study area is a region of generally low and rather flat topography. In addition, due to their age, the used datasets have rather poor horizontal (+/− 100 m) and vertical precision (~30 m), which also varies not only between survey campaigns, but also between single survey locations. Therefore, it is doubtful if the application of field continuation to a horizontal plane would increase the data quality significantly.
In addition, vintage airborne geophysical maps are sometimes difficult to evaluate due to unknown details of their production. If there is enough evidence provided to trust the reliability of a dataset in parts where several datasets exist, the data can be used in areas where less information of other data sets is available. In view of the fact that the original magnetic data in this study were no longer available and the data that was reprocessed in 1997 is not documented in detail, it can be said that this data is still worth using for interpretation and analysis. In general, we recommend considering the scale of the studied issue and then deciding whether to reprocess the data or not. In the case of localizing faults which is a larger-scale problem, it is possible to gain additional information using the datasets of variable quality, such as the ones existing in the study area.

4.6. Experimenting with GIS Tools

This study intends to show that there are many possibilities to “play around” with geophysical data by using different GIS tools to gain more insight into the characteristics of the data. When using common field transformation tools such as Slope and Curvature, the results are expectable, but when using methodologies which are not as well established, e.g., the TIN representation, it is necessary to think about the reliability of the obtained results. Applying the scaling of the Z-component in the Raster to TIN tool, one has to be aware of that this procedure manipulates the original data. Using a z-tolerance implies terracing of the data [56]. Choosing both factors together may lead to artefacts which might have no significance at all (Figure S3). Nevertheless, the lineaments highlighted in this high z-tolerance/large z-component scaling TIN agree well with other lineaments derived from shallow sources. In addition, a Neogene-Quaternary sedimentary basin fill covers the northern part of the DF, while the WF is clearly visible at the surface. It is also suggested that the WF has not much vertical displacement, so that in greater depths, the rocks on both sides of the fault are identical. This might be purely coincidental, but maybe “playing around” carefully with the settings of the TIN representation of the magnetic total intensity might be used as a quick way to differentiate between deeper seated sources (low z-tolerance and high z-factor) and shallow sources (high z-tolerance).

4.7. Applicability for Regions with Less or No Geological Information

Here, we have shown that vintage aerogeophysical data have the potential to help identify geological contacts and faults, when put in a well-known geological context. However, the question remains how this knowledge can be transferred to areas where geological information is low, especially considering the limitations that come with using vintage data.
By comparing a fairly large amount of various data sets covering different methods and production origins, this nevertheless enables a geoscientist to assess whether a certain data set is useful for a particular problem or not. This is done by evaluating the correspondence from one data set to another. Gravitational, magnetic, and geoelectric surveys may be used as indirect evidence for faults at depth that juxtapose rocks with different densities, magnetic, and electric resistivity properties. Geophysical field data however can be used in conjunction with sparse 2D seismic data to resolve the trace of a fault over very long distances. Even on a regional scale, large lateral offset of rock bodies can be inferred from gravity or magnetic data.

5. Conclusions

Vintage airborne geophysical data from different generations were reprocessed and compared to gravity data using various GIS tools. The lineaments identified in the different datasets were compared with the tectonic map to assess the usefulness of this approach to detect geological structures. The main findings of this study are:
  • In general, even if vintage aerogeophysical data lacks today´s accuracy due to less sophisticated technical equipment, they contain valuable information that can be extracted using GIS tools.
  • GIS tools prove to be useful for rapid data visualization and interpretation (especially first and second order derivatives and aspect-slope visualization). The comparison of differently transformed fields of various geophysical methods and spatial views can refine the understanding of tectonic structures.
  • Lineaments extracted from geophysical data show generally good agreement with the boundaries of geological units and faults. Deep seated and buried sources can be identified by lineaments of magnetic and gravity data and their field transformations—they run mainly parallel to each other. Lineaments identified by methods with shallower investigation depth (AEM and radiometry) can give hints as to whether the geologic structure is buried or not.
  • The differences between the positions of lineaments from different methods and datasets can be an indicator for vertical (WF and DF) versus dipping (MSZ and NB) fault geometries.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/geosciences12120436/s1, Figure S1: Aspect - slope applied to the magnetic total intensity without any vertical exaggeration; Figure S2: Aspect - slope applied to the magnetic total intensity with a vertical exaggeration factor (z factor) of 5; Figure S3: Triangulated field (TIN) of the magnetic total intensity with z-tolerance 106 and no z-factor.

Author Contributions

Conceptualization, I.S. and E.H.; methodology, I.S., C.U., K.M., R.S.; formal analysis, I.S., C.U.; interpretation, E.H., I.S.; writing—original draft preparation, I.S., E.H., C.U., K.M., R.S.; writing—review and editing, I.S., E.H.; visualization, I.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research received funding by the GeoERA project HIKE via the European Union’s Horizon 2020 research and innovation programme under grant agreement No 731166 and by the Bundesministerium Bildung, Wissenschaft und Forschung (Austrian Federal Ministry of Education, Science and Research) under grant number UELG-74.

Data Availability Statement

The datasets analyzed in this study are available on request from the corresponding author and will be soon openly available on the Tethys Research Data Repository [https://tethys.at/] (accessed on 27 July 2022).

Acknowledgments

We thank the three anonymous reviewers whose comments and suggestions helped improve and clarify this manuscript.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study nor in the collection, analyses, nor interpretation of data, nor in the writing of the manuscript, nor in the decision to publish the results.

References

  1. Seiberl, W.; Heinz, H. Aerogeophysikalische Vermessung im Bereich der Kremser Bucht; Technical report BC-2c/83; Geological Survey of Austria: Vienna, Austria, 1986; Available online: http://opac.geologie.ac.at/ais312/dokumente/AeroGeoPh_1986_KremserBucht.pdf (accessed on 27 July 2022).
  2. Seiberl, W.; Heinz, H. Aerogeophysikalische Vermessung im Raum Ziersdorf; Technical report OC-1d/85; Geological Survey of Austria: Vienna, Austria, 1986; Available online: http://opac.geologie.ac.at/ais312/dokumente/AeroGeoPh_1986_Ziersdorf.pdf (accessed on 27 July 2022).
  3. Seiberl, W.; Roetzel, R. Aerogeophysikalische Vermessung im Bereich Geras, Niederösterreich; Technical report ÜLG-20/96-97; Geological Survey of Austria: Vienna, Austria, 1998; Available online: http://opac.geologie.ac.at/ais312/dokumente/AeroGeoPh_1998_Geras.pdf (accessed on 27 July 2022).
  4. Seiberl, W.; Roetzel, R.; Pirkl, H.R. Aerogeophysikalische Vermessung im Bereich von Pulkau/NÖ; Technical report ÜLG-20/94-1; Geological Survey of Austria: Vienna, Austria, 1996; Available online: http://opac.geologie.ac.at/ais312/dokumente/AeroGeoPh_1996_Pulkau.pdf (accessed on 27 July 2022).
  5. Seiberl, W.; Roetzel, R. Aerogeophysikalische Vermessung im Bereich von Pulkau-Nord/NÖ; Technical report ÜLG-20/95-2; Geological Survey of Austria: Vienna, Austria, 1997; Available online: http://opac.geologie.ac.at/ais312/dokumente/AeroGeoPh_1997_PulkauNordNoe.pdf (accessed on 27 July 2022).
  6. Meri-Liisa, A. Regional Interpretation of Aerogeophysical Data: Extracting Compositional and Structural Features; Special Paper 39; Geological Survey of Finland: Espoo, Finland, 2005. [Google Scholar]
  7. Scharbert, H.G. Die Granulite der südlichen Böhmischen Masse. In Geologische Rundschau; Enke: Stuttgart, Germany, 1962; Volume 52, pp. 112–123. [Google Scholar]
  8. Schermann, O. Über Horizontalseitenverschiebungen arn Ostrand der Böhmischen Masse. Mitt. Ges. Geol. Bergbaustud 1965, 16, 89–103. [Google Scholar]
  9. Scheidegger, A.E. Untersuchungen des Beanspruchungsplanes im Einflußgebiet der Diendorfer Störung. In Jahrbuch der Geologischen Bundesanstalt; Verlag der Geologischen Bundesanstalt (GBA): Vienna, Austria, 1976; Volume 119, pp. 83–95. [Google Scholar]
  10. Roštínský, P.; Pospíšil, L.; Švábenský, O. Recent geodynamic and geomorphological analyses of the Diendorf–Čebín Tectonic Zone, Czech Republic. Tectonophysics 2013, 599, 45–66. [Google Scholar] [CrossRef]
  11. Decker, K. Tektonische Auswertung Integrierter Geologischer, Geophysikalischer, Morphologischer und Strukturgeologischer Daten; Technical report; Geogenes Naturraumpotential Horn-Hollabrunn etc., Projektbericht Bund-Bundesländerkooperation; Geological Survey of Austria: Vienna, Austria, 1999. [Google Scholar]
  12. Roetzel, R. Bericht 1994–1995 über geologische Aufnahmen im Tertiär und Quartär auf Blatt 22 Hollabrunn mit Bemerkung zur Tektonik am Diendorfer Störungssystem; Report; Geologische Bundesanstalt: Vienna, Austria, 1996. [Google Scholar]
  13. Figdor, H.; Scheidegger, A.E. Geophysikalische Untersuchungen an der Diendorfer Störung. In Verhandlungen der Geologischen Bundesanstalt; Verlag der Geologischen Bundesanstalt (GBA): Vienna, Austria, 1977; pp. 243–270. [Google Scholar]
  14. Linner, M.; Reinhard, R.; Benjamin, H.; Hintersberger, E. Two Nappes in the Austrian Part of the Moravian Superunit. In Proceedings of the CETEG 2019: 17th Meeting of the Central European Tectonic Groups, Rozdrojovice, Czech Republic, 24–27 April 2019; Available online: http://opac.geologie.ac.at/ais312/dokumente/Linner_Roetzel_Huet_Hintersberger_2019_Nappes_Austrian_Moravian_Superunit.pdf (accessed on 27 July 2022).
  15. Schnabel, W.; Fuchs,, G.; Matura, A.; Roetzel, R.; Scharbert, S.; Krenmayr, H.-G.; Egger, J.; Schnabel, W.; Bryda, G.; Mandl, G.W.; et al. Geologische Karte von Niederösterreich (Geological Map of Lower Austria) 1:200.000; Geological Survey of Austria: Vienna, Austria, 2002. [Google Scholar]
  16. Schnabel, W.; Krenmayr, H.-G.; Mandl, G.W.; Nowotny, A.; Roetzel, R.; Scharbert, S.; Schnabel, W. Geologische Karte von Niederösterreich (Geological map of Lower Austria) 1:200.000, Legende und kurze Erläuterung (Legend and short description). Verlag der GBA: Vienna, Austria, 2002; ISBN 3-85316-017-4. [Google Scholar]
  17. Supper, R. Auswertung Aerogeophysikalischer Messungen im Bereich Niederösterreich Nord; Internal report; Geological Survey of Austria: Vienna, Austria, 1999. [Google Scholar]
  18. Baranov, V. A New Method for Interpretation of Aeromagnetic Maps: Pseudo-Gravimetric Anomalies. Geophysics 1957, 22, 359–382. [Google Scholar] [CrossRef]
  19. Beamish, D. Airborne EM Skin Depths. Geophys. Prospect. 2004, 52, 439–449. [Google Scholar] [CrossRef] [Green Version]
  20. Dantas, E.L.; Silva, A.M.; Almeida, T.; De Moraes, R.A.V. Old Geophysical Data Applied to Modern Geological Mapping Problems: A Case-Study in the Seridó Belt, NE Brazil. Rev. Bras. De Geociências 2003, 33, 65–72. [Google Scholar] [CrossRef] [Green Version]
  21. Motschka, K. Gammastrahlenspektroskopie in Österreich. In Geo-Atlas Österreich; Hofmann, T., Schönlaub, H.P., Eds.; Böhlau-Verlag: Vienna, Austria, 2007; pp. 102–103. [Google Scholar]
  22. Mickus, K. Gravity Method: Environmental and Engineering Applications; Department of Geosciences, Southwest Missouri State University: Springfield, MI, USA, 2003; Available online: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.522.2552&rep=rep1&type=pdf (accessed on 27 July 2022).
  23. Khalaf, A.K.A.; Kordik, P.; Khalil, A.; Mekkawi, M.; El-Bohoty, M.; Rabeh, T.; Refai, M.K.; El-Mahdy, A. Interpretation of Geophysical Data at EL Fayoum—Dahshour Area, Egypt Using Three Dimensional Models. Arab. J. Sci. Eng. 2013, 38, 1769–1784. [Google Scholar] [CrossRef]
  24. Nabighian, M.N.; Ander, M.E.; Grauch, V.J.S.; Hansen, R.O.; LaFehr, T.R.; Li, Y.; Pearson, W.C.; Peirce, J.W.; Phillips, J.D.; Ruder, M.E. Historical Development of the Gravity Method in Exploration. Geophysics 2005, 70, 63ND–89ND. [Google Scholar] [CrossRef] [Green Version]
  25. Meurers, B.; Ruess, D. Compilation of a New Bouguer Gravity Data Base in Austria. VGI Osterr. Z. Für Vermess. Und Geoinf. 2007, 2, 90–94. [Google Scholar]
  26. Meurers, B.; Ruess, D.; Graf, J. A Program System for High Precise Bouguer Gravity Determination. In Proceedings of the 8th International Meeting on Alpine Gravimetry, Leoben, Austria, 4–5 May 2000; pp. 217–226. [Google Scholar]
  27. Aric, K.; Gutdeutsch, R.; Heinz, H.; Meurers, B.; Seiberl, W.; Adam, A.; Smythe, D. Geophysical Investigations in the Southern Bohemian Massif. Jahrb. Der Geol. Bundesanst. 1997, 140, 9–28. [Google Scholar]
  28. Kumar, U.; Pal, S.K.; Sahoo, S.D.; Narayan, S.; Mondal, S.; Ganguli, S.S. Lineament Mapping over Sir Creek Offshore and its Surroundings using High Resolution EGM2008 Gravity Data: An Integrated Derivative Approach. J. Geol. Soc. India 2018, 91, 671–678. [Google Scholar] [CrossRef]
  29. Lobatskaya, R.M.; Strelchenko, I.P. GIS-Based Analysis of Fault Patterns in Urban Areas: A Case Study of Irkutsk City, Russia. Spec. Issue Exhum. Asia 2016, 7, 287–294. [Google Scholar] [CrossRef] [Green Version]
  30. Pilkington, M.; Tschirhart, V. Practical considerations in the use of edge detectors for geologic mapping using magnetic data. Geophysics 2017, 82, J1–J8. [Google Scholar] [CrossRef]
  31. Tschirhart, P.; Morris, B. Improved edge detection mapping through stacking and integration: A case study in the Bathurst Mining Camp. Geophys. Prospect. 2015, 63, 283–295. [Google Scholar] [CrossRef]
  32. Keating, P.; Pilkington, M. An automated method for the interpretation of magnetic vertical-gradient anomalies. Geophysics 1990, 55, 336. [Google Scholar] [CrossRef]
  33. Miller, H.G.; Singh, V. Potential field tilt—A new concept for location of potential field sources. J. Appl. Geophys. 1994, 32, 213–217. [Google Scholar] [CrossRef]
  34. Blakely, R.J.; Simpson, R.W. Approximating Edges of Source Bodies from Magnetic or Gravity Anomalies. Geophysics 1986, 51, 1494–1498. [Google Scholar] [CrossRef]
  35. Raster to TIN. Available online: https://pro.arcgis.com/en/pro-app/latest/tool-reference/3d-analyst/raster-to-tin.htm (accessed on 27 July 2022).
  36. Slope. Available online: https://pro.arcgis.com/en/pro-app/latest/tool-reference/spatial-analyst/slope.htm (accessed on 27 July 2022).
  37. Curvature Tool. Available online: https://pro.arcgis.com/en/pro-app/latest/tool-reference/spatial-analyst/curvature.htm (accessed on 27 July 2022).
  38. Aspect–Slope. Available online: https://pro.arcgis.com/en/pro-app/latest/help/analysis/raster-functions/aspect-slope-function.htm (accessed on 27 July 2022).
  39. Xie, R.; Xiong, S.; Duan, S.; Wang, J.; Wang, P.; Luo, Y.; Liu, H.; Fan, Z. Noise Estimation in Vector Magnetic Data Derived from Airborne Vector Magnetic System. Geophysics 2020, 85, J71–J83. [Google Scholar] [CrossRef]
  40. Morris, B.; Leblanc, G.; Prevec, L. An Alternative Simple Procedure to Identify Magnetic and Other Geophysical Anomalies Due to Kimberlite Pipes. In Proceedings of the 2002 SEG Annual Meeting, Salt Lake City, UT, USA, 6–11 October 2002; p. SEG-2002-0712. [Google Scholar]
  41. Lee, S.; Ross, W.S. 3-D Mitigation of Surface-wave Noise in Spatially Inhomogeneous Media. In Proceedings of the 2008 SEG Annual Meeting, Las Vegas, NV, USA, 9–14 November 2008; p. SEG-2008-2561. [Google Scholar]
  42. Grauch, V.J.S.; Hudson, M.R. Guides to Understanding the Aeromagnetic Expression of Faults in Sedimentary Basins: Lessons Learned from the Central Rio Grande Rift, New Mexico. Geosphere 2007, 3, 596. [Google Scholar] [CrossRef] [Green Version]
  43. Brewer, C.A.; Marlow, K.A. Color Representation of Aspect and Slope Simultaneously. In Proceedings of the AutoCarto Conference, Minneapolis, MI, USA, 30 October–1 November 1993; Available online: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.453.8620&rep=rep1&type=pdf (accessed on 27 July 2022).
  44. Roberts, A. Curvature attributes and their application to 3D interpreted horizons. First Break 2001, 19, 85–100. [Google Scholar] [CrossRef]
  45. Lee, M.; Morris, W.; Leblanc, G.; Harris, J. Curvature analysis to differentiate magnetic sources for geologic mapping’, Geophys. Prospect. 2012, 61, 572–585. [Google Scholar] [CrossRef]
  46. Cevallos, C.; Kovac, P.; Lowe, S.J. Application of curvatures to airborne gravity gradient data in oil exploration. Geophysics 2013, 78, G81–G88. [Google Scholar] [CrossRef]
  47. Phillips, J.D.; Hansen, R.O.; Blakely, R.J. The Use of Curvature in Potential-Field Interpretation. Explor. Geophys. 2007, 38, 111–119. [Google Scholar] [CrossRef]
  48. Florinsky, I. Digital Terrain Analysis in Soil Science and Geology; Academic Press: Cambridge, MA, USA, 2016; p. 486. [Google Scholar]
  49. Cooper, G.R. Balancing Images of Potential-Field Data. Geophysics 2009, 74, L17–L20. [Google Scholar] [CrossRef]
  50. Cooper, G.R.J. An Improved Tilt Angle Filter for Potential Field Data. Lead. Edge 2012, 31, 514–517. [Google Scholar] [CrossRef]
  51. Lee, M.; Morris, W.; Harris, J.; Leblanc, G. An automatic network-extraction algorithm applied to magnetic survey data for the identification and extraction of geologic lineaments. Lead. Edge 2012, 31, 26–31. [Google Scholar] [CrossRef]
  52. Morris, W.; Ugalde, H.; Kirsch, M.; Gloaguen, R.; Seht, M.; Siemon, B.; Meyer, U. A multi-parameter approach for recognition of anthropogenic noise in aeromagnetic data collected over populated areas: Erzgebirge, Germany. Geophys. Prospect. 2021, 70, 593–617. [Google Scholar] [CrossRef]
  53. Paoletti, V.; Hintersberger, E.; Schattauer, I.; Milano, M.; Deidda, G.P.; Supper, R. Geophysical Study of the Diendsorf-Boskovice Fault System (Austria). Remote Sens. 2022, 14, 1807. [Google Scholar] [CrossRef]
  54. Szitkar, F.; Dyment, J. Near-seafloor magnetics reveal tectonic rotation and deep structure at the TAG (Trans-Atlantic Geotraverse) hydrothermal site (Mid-Atlantic Ridge, 26° N). Geology 2015, 43, 87–90. [Google Scholar] [CrossRef]
  55. Tivey, M.A.; Rona, P.A.; Schouten, H. Reduced crustal magnetization beneath the active sulfide mound, TAG hydrothermal field, Mid-Atlantic Ridge at 26 °N. Earth Planet. Sci. Lett. 1993, 115, 101–115. [Google Scholar] [CrossRef]
  56. Cooper, G.R.J. An improved terracing algorithm for potential-field data. Geophysics 2020, 85, G109–G113. [Google Scholar] [CrossRef]
Geosciences 12 00436 g001 550
Figure 1. (a) Location of provided gravity measurements and airborne datasets acquired in 1983–1997 (inset shows study area location in Europe), background map: open street map. (b) Tectonic map of the study area, major faults for this study are marked: DF—Diendorf Fault, MSZ—Moldanubian Shearzone, NB—Nappe boundary between Pleißing and Pulkau nappes within the Thaya Window, WF—Waitzendorf Fault. Location of airborne datasets outlined in green is shown as reference, background map: tectonic units of the geological map of Lower Austria at the scale of 1:200.000, adapted with permission from [15,16], Geological Survey of Austria (GBA), 2022.
Figure 1. (a) Location of provided gravity measurements and airborne datasets acquired in 1983–1997 (inset shows study area location in Europe), background map: open street map. (b) Tectonic map of the study area, major faults for this study are marked: DF—Diendorf Fault, MSZ—Moldanubian Shearzone, NB—Nappe boundary between Pleißing and Pulkau nappes within the Thaya Window, WF—Waitzendorf Fault. Location of airborne datasets outlined in green is shown as reference, background map: tectonic units of the geological map of Lower Austria at the scale of 1:200.000, adapted with permission from [15,16], Geological Survey of Austria (GBA), 2022.
Geosciences 12 00436 g001
Geosciences 12 00436 g002 550
Figure 2. Reprocessed magnetic total intensity in Nanotesla (nT) covered by the vintage airborne data (red boxes in Figure 1a); the white line shows the location of profile A where different geophysical datasets are compared, legend for tectonic structures: see Figure 1b. Background map: Lidar image with a 10 × 10 m resolution.
Figure 2. Reprocessed magnetic total intensity in Nanotesla (nT) covered by the vintage airborne data (red boxes in Figure 1a); the white line shows the location of profile A where different geophysical datasets are compared, legend for tectonic structures: see Figure 1b. Background map: Lidar image with a 10 × 10 m resolution.
Geosciences 12 00436 g002
Geosciences 12 00436 g003 550
Figure 3. Apparent electrical resistivity map in ohm-meter (Ω × m). Location of profile A (white line) is shown for orientation, black lines indicate geological faults, see legend in Figure 1b for details. Background map: Lidar image with a 10 × 10 m resolution.
Figure 3. Apparent electrical resistivity map in ohm-meter (Ω × m). Location of profile A (white line) is shown for orientation, black lines indicate geological faults, see legend in Figure 1b for details. Background map: Lidar image with a 10 × 10 m resolution.
Geosciences 12 00436 g003
Geosciences 12 00436 g004 550
Figure 4. (a) Potassium map (b) Uranium map (c) Thorium map. Location of profile A (white line) is shown for orientation. Black lines indicate geological faults; see legend in Figure 1b for details. Background map: Lidar image with a 10 × 10 m resolution.
Figure 4. (a) Potassium map (b) Uranium map (c) Thorium map. Location of profile A (white line) is shown for orientation. Black lines indicate geological faults; see legend in Figure 1b for details. Background map: Lidar image with a 10 × 10 m resolution.
Geosciences 12 00436 g004
Geosciences 12 00436 g005 550
Figure 5. Bouguer anomaly map calculated with reference density 2670 kg × m−3 (data provided by BEV). For processing details, see description in text. Outline of airborne geophysical data sets are shown for reference. Black lines indicate geological faults; see legend in Figure 1b for details. Background map: Lidar image with a 10 × 10 m resolution.
Figure 5. Bouguer anomaly map calculated with reference density 2670 kg × m−3 (data provided by BEV). For processing details, see description in text. Outline of airborne geophysical data sets are shown for reference. Black lines indicate geological faults; see legend in Figure 1b for details. Background map: Lidar image with a 10 × 10 m resolution.
Geosciences 12 00436 g005
Geosciences 12 00436 g006 550
Figure 6. Magnetic total intensity—triangulated field with low z-tolerance (20 nT) and z-factor 20. Background map: Lidar image with a 10 × 10 m resolution.
Figure 6. Magnetic total intensity—triangulated field with low z-tolerance (20 nT) and z-factor 20. Background map: Lidar image with a 10 × 10 m resolution.
Geosciences 12 00436 g006
Geosciences 12 00436 g007 550
Figure 7. Slope amplitude [in degrees] of magnetic total intensity (triangulated field) with z- factor 20. Background map: Lidar image with a 10 × 10 m resolution.
Figure 7. Slope amplitude [in degrees] of magnetic total intensity (triangulated field) with z- factor 20. Background map: Lidar image with a 10 × 10 m resolution.
Geosciences 12 00436 g007
Geosciences 12 00436 g008 550
Figure 8. (a) Aspect—slope applied to the magnetic total intensity with z-factor 10 and (b) to the Bouguer gravity anomaly. Color saturation represents the steepness and hue (color) represents the direction of the aspect. Background map: Lidar image with a 10 × 10 m resolution.
Figure 8. (a) Aspect—slope applied to the magnetic total intensity with z-factor 10 and (b) to the Bouguer gravity anomaly. Color saturation represents the steepness and hue (color) represents the direction of the aspect. Background map: Lidar image with a 10 × 10 m resolution.
Geosciences 12 00436 g008
Geosciences 12 00436 g009 550
Figure 9. Profile curvature map of Bouguer anomaly data. Background map: Lidar image with a 10 × 10 m resolution.
Figure 9. Profile curvature map of Bouguer anomaly data. Background map: Lidar image with a 10 × 10 m resolution.
Geosciences 12 00436 g009
Geosciences 12 00436 g010 550
Figure 10. (a) Compilation of all visually derived lineaments extracted from geophysical data relying on deeper sources: gravity and magnetic data. (b) Compilation of all visually derived lineaments extracted from data relying on shallow sources: radiometric and electromagnetic data. In the background of both (a,b), a section of the 1:200.000 geological map of Lower Austria at the scale of 1:200.000, reprinted with permission from [15,16], Geological Survey of Austria (GBA), 2002. is shown to indicate the mapped changes in lithology.
Figure 10. (a) Compilation of all visually derived lineaments extracted from geophysical data relying on deeper sources: gravity and magnetic data. (b) Compilation of all visually derived lineaments extracted from data relying on shallow sources: radiometric and electromagnetic data. In the background of both (a,b), a section of the 1:200.000 geological map of Lower Austria at the scale of 1:200.000, reprinted with permission from [15,16], Geological Survey of Austria (GBA), 2002. is shown to indicate the mapped changes in lithology.
Geosciences 12 00436 g010
Geosciences 12 00436 g011 550
Figure 11. Detailed view of Figure 10 at the faults of concern along profile A. (a) Detailed view from Figure 10a of lineament position at MSZ, (b) at the nappe boundary NB, (c) at DF. (d) Detailed view from Figure 10b of lineament position at WF. Legends see Figure 10a,b, respectively.
Figure 11. Detailed view of Figure 10 at the faults of concern along profile A. (a) Detailed view from Figure 10a of lineament position at MSZ, (b) at the nappe boundary NB, (c) at DF. (d) Detailed view from Figure 10b of lineament position at WF. Legends see Figure 10a,b, respectively.
Geosciences 12 00436 g011
Geosciences 12 00436 g012 550
Figure 12. Comparison of different geophysical datasets and their respective derivatives with the position of mapped geological faults along profile A. Locations of the major faults visible in the tectonic map (Figure 1b) are marked by vertical black dashed lines (MSZ = Moldanubian Shearzone, NB = nappe boundary, WZ = Waitzendorf Fault, DF = Diendorf Fault). The vertical red dashed line indicate the position of MSZ based on the common shifts within the presented data and their derivations, most probably due to a westward inclination of the respective fault plane.
Figure 12. Comparison of different geophysical datasets and their respective derivatives with the position of mapped geological faults along profile A. Locations of the major faults visible in the tectonic map (Figure 1b) are marked by vertical black dashed lines (MSZ = Moldanubian Shearzone, NB = nappe boundary, WZ = Waitzendorf Fault, DF = Diendorf Fault). The vertical red dashed line indicate the position of MSZ based on the common shifts within the presented data and their derivations, most probably due to a westward inclination of the respective fault plane.
Geosciences 12 00436 g012
Table
Table 1. Varying technical equipment and survey specification of aerogeophysical data survey which builds the basis of new processing steps.
Table 1. Varying technical equipment and survey specification of aerogeophysical data survey which builds the basis of new processing steps.
Aerogeohysical
Survey/Year		Magnetic DeviceElectromagnetic Device/FrequenciesRadiometric DeviceData Per Sec (Mag/EM/Rad)Average Line Spacing [m]
Kremser Bucht/1983G-801/3DIGHEM II/900 Hz (vert./coaxial), 3600 Hz (horiz./coplanar)GR-800 B1/4/1200
Kamptal-Ziersdorf/1983G-801/3DIGHEM II/900 Hz (vert./coaxial), 3600 Hz (horiz./coplanar)GR-800 B1/4/1200
Pulkau/1994Scintrex CS-2DIGHEM II/900 Hz (vert./coaxial), 7200 Hz (horiz./coplanar)Scintrex PGAM-100010/10/1250
Pulkau north/1995Scintrex CS-2DIGHEM II/900 Hz (vert./coaxial), 7200 Hz (horiz./coplanar)Scintrex PGAM-100010/10/1200
Geras/1996–1997Scintrex CS-2GEOTECH “Hummingbird”/434 Hz (vertic./coplanar), 3212 Hz (horiz./coaxial), 7002 Hz (vertic./coplanar), 34,133 Hz (horiz./coaxial)Scintrex PGAM-100010/10/1200
Mag = magnetic data, EM = electromagnetic data, Rad = radiometric data.
Table
Table 2. Summary of the interpreted results and an evaluation of their applicability to each of the major faults within the study area.
Table 2. Summary of the interpreted results and an evaluation of their applicability to each of the major faults within the study area.
ViewMethodField under ConsiderationTectonic StructureApplied Key GIS-ToolFigure
MSZNBWFDF
Profile AGravityBougueranomaly (BA) IDWFigure 12
Profile Curvature of BA Profile Curvature
MagneticsTotal Intensity (TI) IDW
Slope of TI Slope
Curvature of TI Profile Curvature
AEMApparent Resistivity IDW
RadiometricsUranium IDW
Potassium IDW
Thorium IDW
Map view GravityBougueranomaly IDWFigure 5
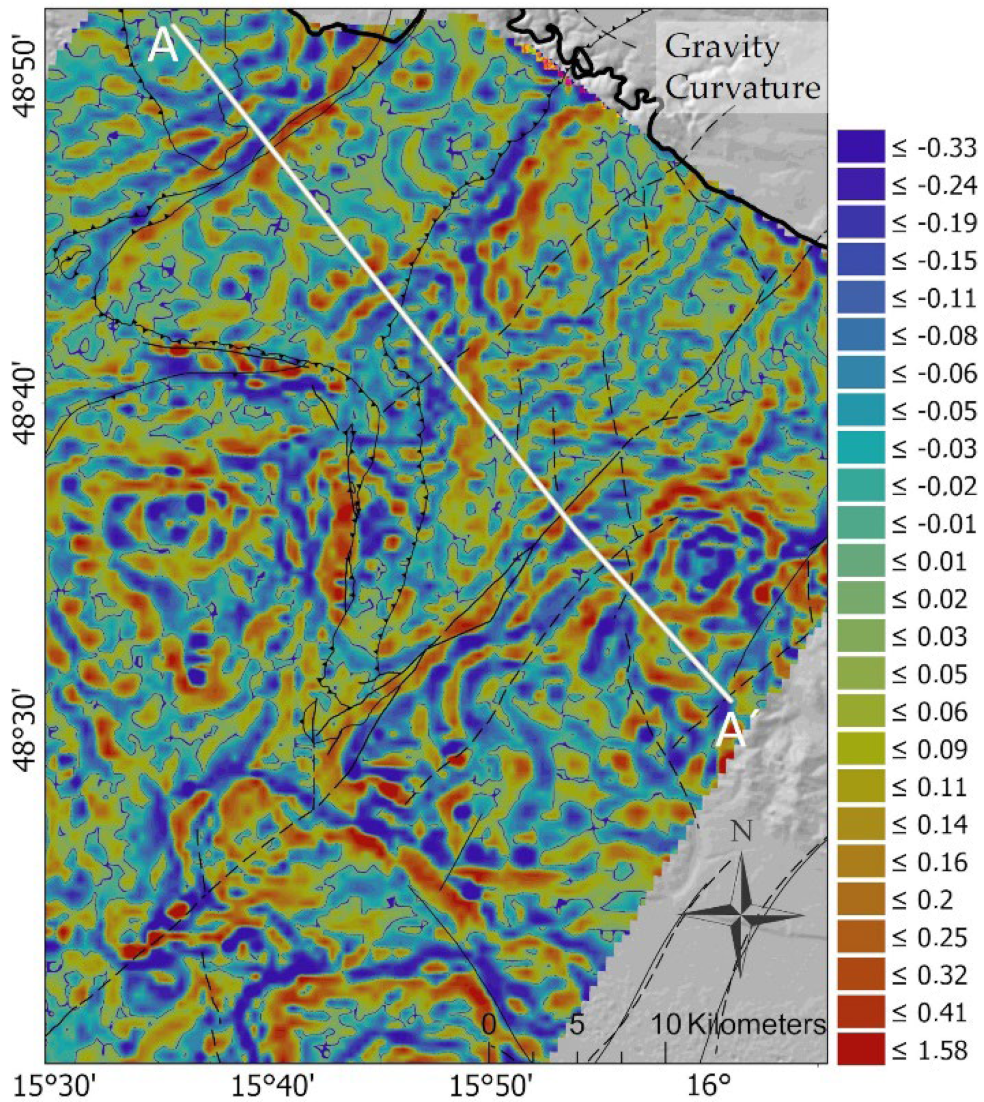
Profile Curvature of BA Profile CurvatureFigure 9
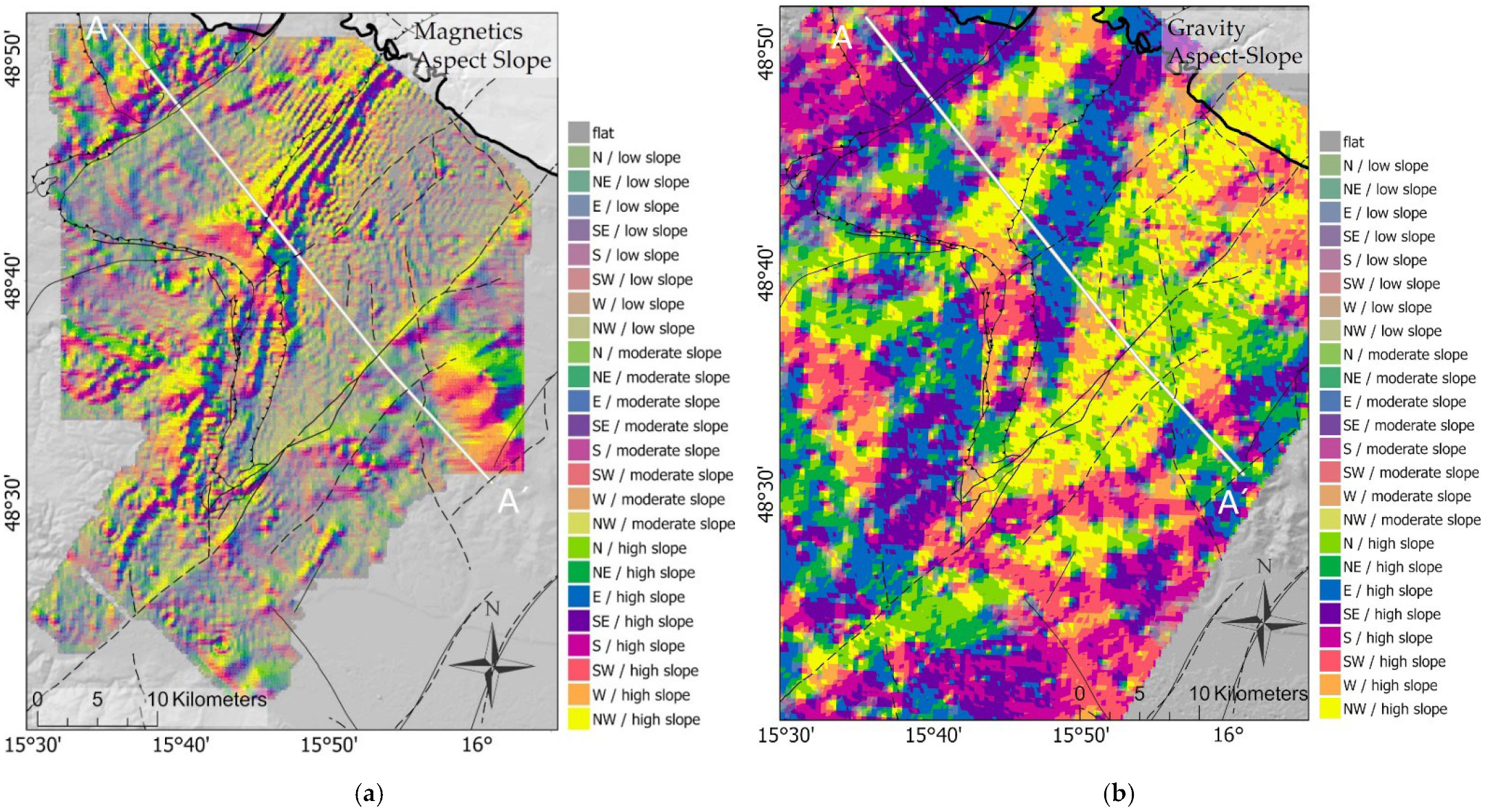
Aspect Slope of BA Aspect SlopeFigure 8b
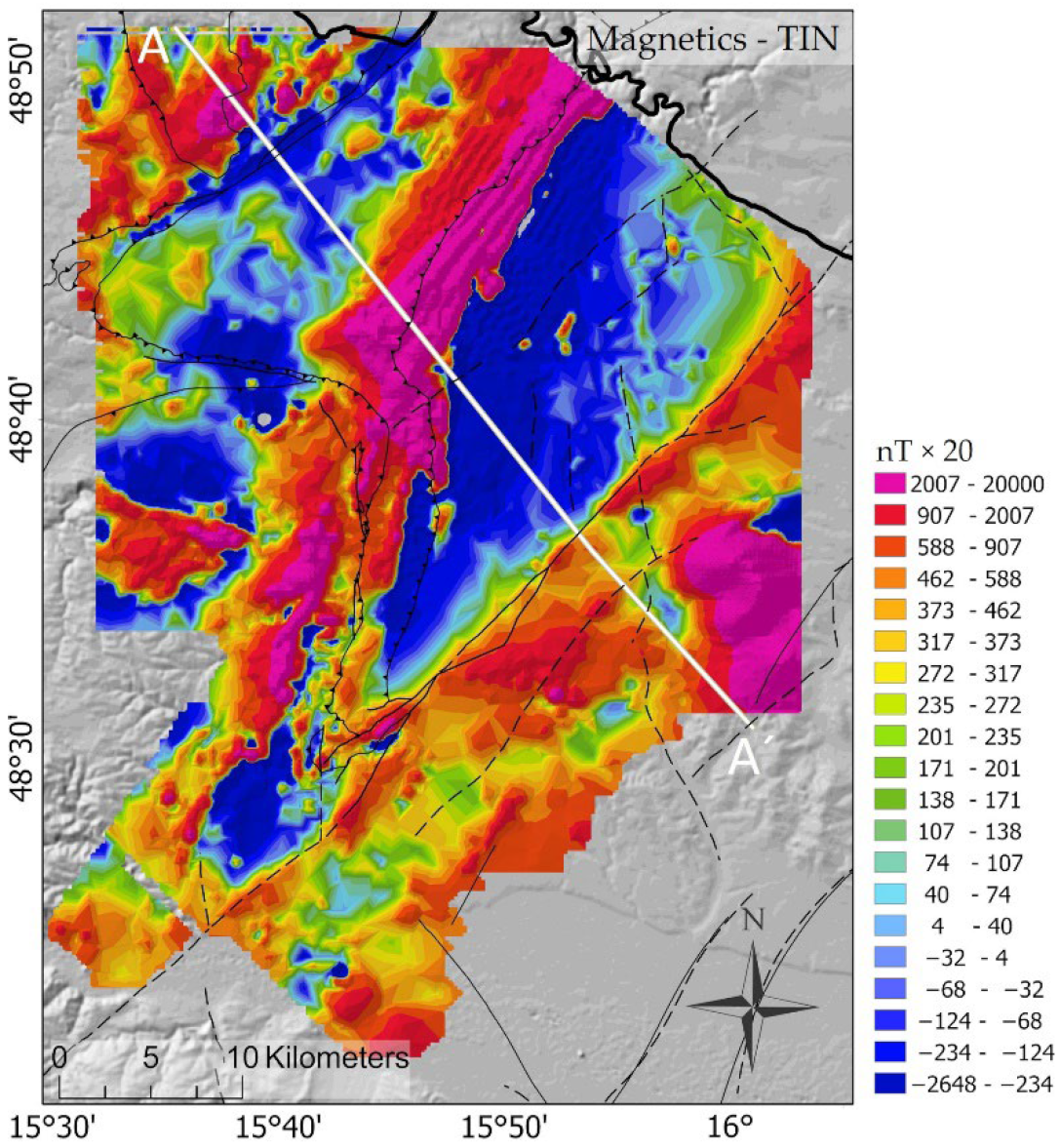
MagneticsTotal Intensity (TI) IDWFigure 2
TI TIN Raster to TIN Figure 6
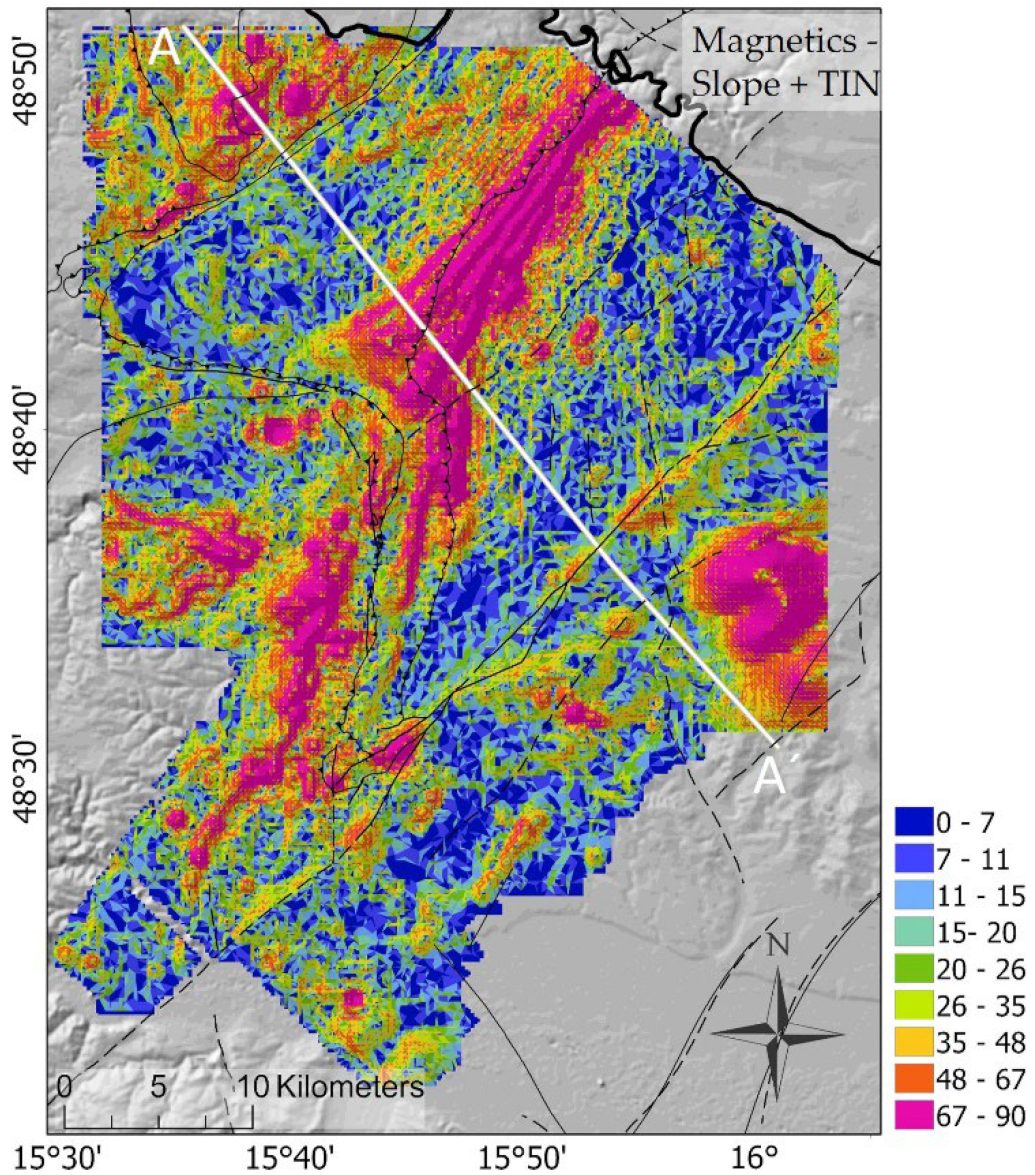
Slope of TI Raster to TIN/SlopeFigure 7
Aspect slope of TI Aspect SlopeFigure 8a
AEMApparent Resistivity IDWFigure 3
RadiometricsPotassium IDWFigure 4a
Uranium IDWFigure 4b
Thorium IDWFigure 4c
TIN = triangulated network visible
Magn. Intensity = Magnetization Intensity [A/m] visible with limitations
not visible
MSZ = Moldanubian Shear Zone, NB = nappe boundary between Pulkau and Pleißing nappes, WF = Waitzendorf Fault, DF = Diendorf Fault.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Schattauer, I.; Hintersberger, E.; Ullrich, C.; Supper, R.; Motschka, K. The Usage of GIS Tools on Vintage Aerogeophysical Data for Simple and Fast Processing with a Focus on Fault Interpretation: An Austrian Case Study. Geosciences 2022, 12, 436. https://doi.org/10.3390/geosciences12120436

AMA Style

Schattauer I, Hintersberger E, Ullrich C, Supper R, Motschka K. The Usage of GIS Tools on Vintage Aerogeophysical Data for Simple and Fast Processing with a Focus on Fault Interpretation: An Austrian Case Study. Geosciences. 2022; 12(12):436. https://doi.org/10.3390/geosciences12120436

Chicago/Turabian Style

Schattauer, Ingrid, Esther Hintersberger, Christian Ullrich, Robert Supper, and Klaus Motschka. 2022. "The Usage of GIS Tools on Vintage Aerogeophysical Data for Simple and Fast Processing with a Focus on Fault Interpretation: An Austrian Case Study" Geosciences 12, no. 12: 436. https://doi.org/10.3390/geosciences12120436

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop