3D Migration Depth Focus Velocity Analysis of Hand-Held Ground Penetrating Radar
Abstract
:1. Introduction
2. 3D Migration Depth Focus Velocity Analysis
2.1. 3D Diffraction Stacking Migration
2.2. Depth Focus Velocity Analysis
2.2.1. Cross-Correlation
2.2.2. Standard Deviation
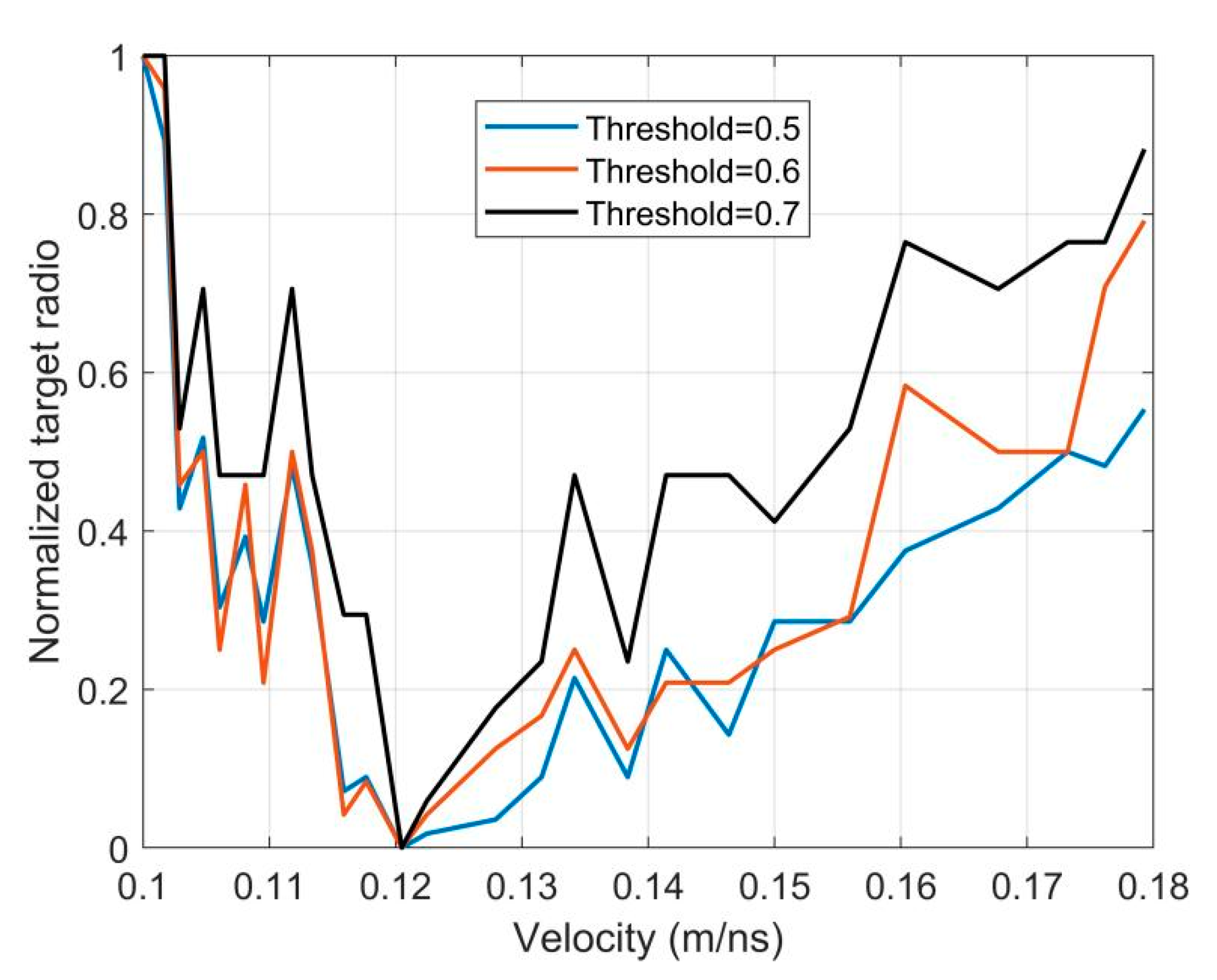
2.2.3. Velocity Analysis
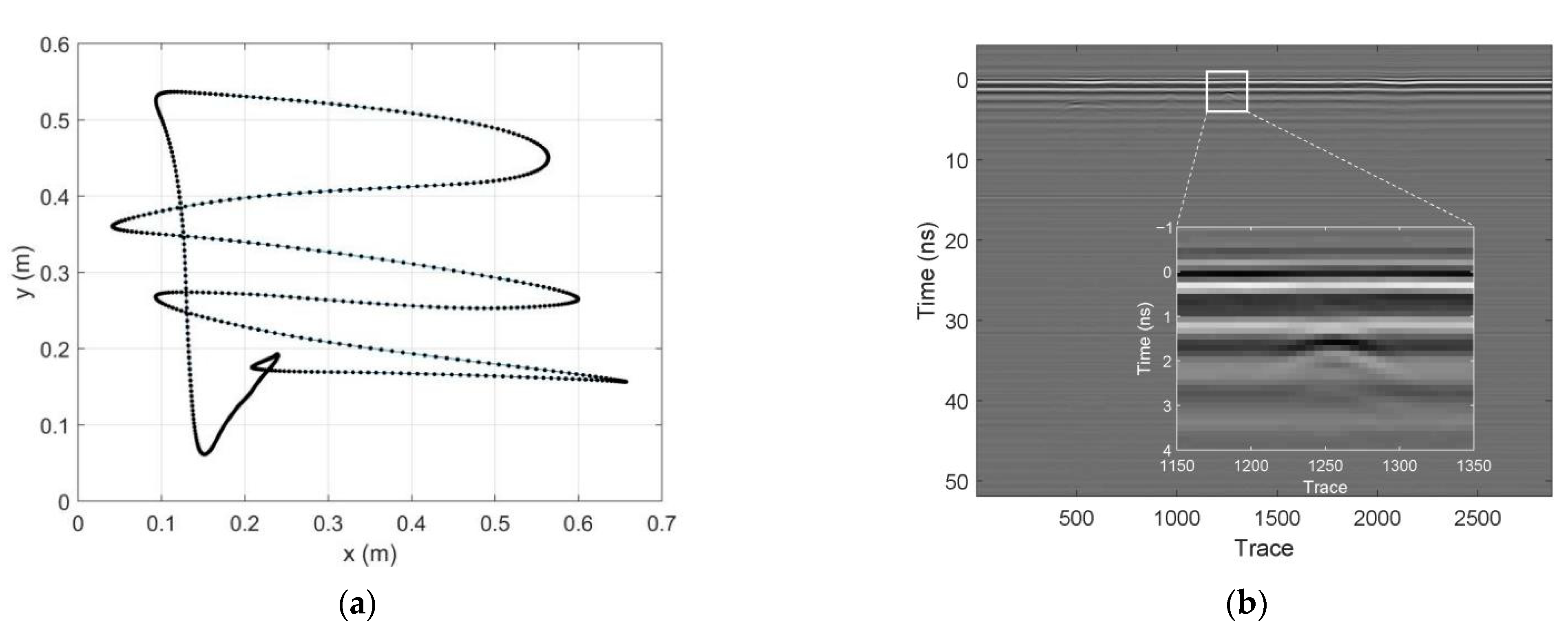
3. Application to Experimental Data
3.1. Experiment Description
3.2. Signal Processing
4. Discussions
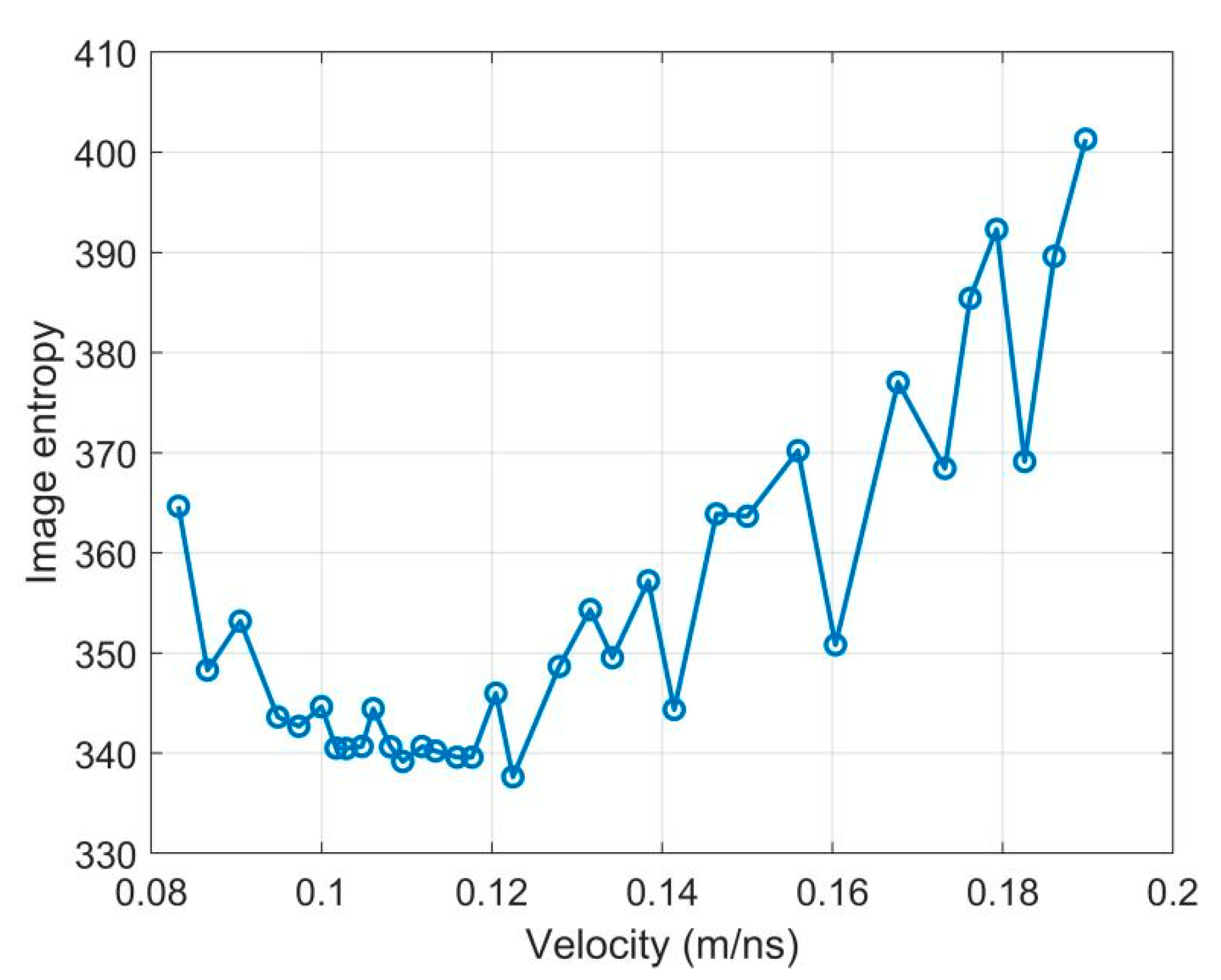
4.1. Comparison with Entropy-Based Migration Velocity Analysis Method
4.2. Advantages, Limitations, and Significance
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhou, H.; Sato, M.; Liu, H. Migration velocity analysis and prestack migration of common-transmitter GPR data. IEEE Trans. Geosci. Remote Sens. 2005, 43, 86–91. [Google Scholar] [CrossRef]
- Daniels, D.J. Ground Penetrating Radar, 2nd ed.; IEEE: London, UK, 2004. [Google Scholar]
- Feng, X.; Yu, Y.; Liu, C.; Fehler, M. Combination of H-Alpha decomposition and migration for enhancing subsurface target classification of GPR. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4852–4861. [Google Scholar] [CrossRef]
- Feng, X.; Yu, Y.; Liu, C.; Fehler, M. Subsurface polarimetric migration imaging for full polarimetric ground-penetrating radar. Geophys. J. Int. 2015, 202, 1324–1338. [Google Scholar] [CrossRef] [Green Version]
- Feng, X.; Sato, M. Landmine imaging by a Hand-held GPR and metal detector sensor (ALIS). In Proceedings of the 2005 IEEE International Geoscience and Remote Sensing Symposium, IGARSS’05, Seoul, Korea, 29 July 2005; Volume 1, pp. 379–382. [Google Scholar]
- Feng, X.; Fujiwara, J.; Zhou, Z.; Kobayashi, T.; Sato, M. Migration and interpolation for the hand-held GPR MD sensor system (ALIS). In Proceedings of the Detection and Remediation Technologies for Mines and Minelike Targets XI, SPIE, Orlando, FL, USA, 17–21 April 2006; Volume 6217, pp. 67–73. [Google Scholar]
- Feng, X.; Fujiwara, J.; Zhou, Z.; Kobayashi, T.; Sato, M. Imaging algorithm of a Hand-held GPR MD sensor (ALIS). In Proceedings of the Detection and Remediation Technologies for Mines and Minelike Targets X, SPIE, Tokyo, Japan, 21–23 June 2005; Volume 5794, pp. 1192–1199. [Google Scholar]
- Sato, M.; Fujiwara, J.; Feng, X.; Zhou, Z.; Kobayashi, T. Development of a hand-held GPR MD sensor system (ALIS). In Proceedings of the Detection and Remediation Technologies for Mines and Minelike Targets X, SPIE, Tokyo, Japan, 21–23 June 2005; Volume 5794, pp. 1000–1007. [Google Scholar]
- Sato, M.; Kikuta, K. Dual sensor ‘Alis’ for humanitarian demining. In Proceedings of the IGARSS 2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 8428–8431. [Google Scholar]
- Sato, M.; Kikuta, K. Image reconstruction and processing algorithm of GPR for humanitarian demining sensor ALIS. In Proceedings of the 2018 International Conference on Electromagnetics in Advanced Applications (ICEAA), Cartagena de Indias, Colombia, 10–14 September 2018; pp. 118–121. [Google Scholar]
- Schleicher, J.; Daniels, D.; Hammerton, P. A multiple migration and stacking algorithm designed for land mine detection. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6983–6988. [Google Scholar]
- Novais, A.; Costa, J.; Schleicher, J. GPR velocity determination by image-wave remigration. J. Appl. Geophys. 2008, 65, 65–72. [Google Scholar] [CrossRef]
- Yilmaz, Ö. Seismic Data Analysis; Society of Exploration Geophysicists: Tulsa, OK, USA, 2001. [Google Scholar]
- Leparoux, D.; Gibert, D.; Cote, P. Adaptation of prestack migration to multi-offset ground-penetrating radar (GPR) data. Geophys. Prospect. 2001, 49, 374–386. [Google Scholar] [CrossRef]
- Feng, X.; Sato, M. Pre-stack migration applied to GPR for landmine detection. Inverse Probl. 2004, 20, S99–S115. [Google Scholar] [CrossRef]
- Hagedoorn, J.G. A process of seismic reflection interpretation. Geophys. Prospect. 1954, 2, 85–127. [Google Scholar] [CrossRef]
- Feng, X.; Sato, M.; Liu, C. Hand-held GPR imaging using migration for irregular data. IEEE J. Sel. Topics Appl Earth Observ. Remote Sens. 2011, 4, 799–803. [Google Scholar] [CrossRef]
- Gonzalez-Huici, M.A. Adaptative Stolt migration via contrast maximization for GPR applications. In Proceedings of the 6th International Workshop on Advanced Ground Penetrating Radar (IWAGPR), Aachen, Germany, 22–24 June 2011; pp. 1–5. [Google Scholar]
- Economou, N.; Vafidis, A.; Bano, M.; Hamdan, H.; Ortega-Ramirez, J. Ground-penetrating radar data diffraction focusing without a velocity model. Geophysics 2020, 85, 1MJ–Z13. [Google Scholar] [CrossRef]
- Lopez-Sanchez, J.M.; Fortuny-Guasch, J. 3-D radar imaging using range migration techniques. IEEE Trans. Antennas Propag. 2000, 48, 728–737. [Google Scholar] [CrossRef]
- Zhuge, X.; Savelyev, T.G.; Yarovoy, A.G.; Ligthart, L.P.; Levitas, B. Comparison of different migration techniques for UWB short-range imaging. In Proceedings of the European Radar Conference (EuRAD), Rome, Italy, 30 September–2 October 2009; pp. 184–187. [Google Scholar]
- Schneider, W.A. Integral formulation for migration in two and three dimensions. Geophysics 1978, 43, 49–76. [Google Scholar] [CrossRef]
- Kondo, T.; Kikuta, K.; Sato, M. Ground surface reflection compensation for hand-held GPR. IEEE Geosci. Remote Sens. Lett. 2022, 19, 3501605. [Google Scholar] [CrossRef]
- Xu, X.; Miller, E.L.; Rappaport, C.R. Minimum entropy regularization in frequency-wavenumber migration to localize subsurface objects. IEEE Trans. Geosci. Remote Sens. 2003, 41, 8. [Google Scholar]
- Zhou, H.; Feng, X.; Ding, C.; Dong, Z.; Liu, C.; Zhang, Y.; Meng, Z. Yutu-2 radar sounding evidence of a buried crater at Chang’E-4 landing site. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4600419. [Google Scholar] [CrossRef]
- Zhou, H.; Feng, X.; Dong, Z.; Liu, C.; Liang, W. Application of denoising CNN for noise suppression and weak signal extraction of lunar penetrating radar data. Remote Sens. 2021, 13, 779. [Google Scholar] [CrossRef]
- Feng, J.; Su, Y.; Ding, C.; Xing, S.; Dai, S.; Zou, Y. Dielectric properties estimation of the lunar regolith at CE-3 landing site using lunar penetrating radar data. Icarus 2017, 284, 424–430. [Google Scholar]
- Dong, Z.; Feng, X.; Zhou, H.; Liu, C.; Zeng, Z.; Li, J.; Liang, W. Properties analysis of lunar regolith at Chang’E-4 landing site based on 3D velocity spectrum of lunar penetrating radar. Remote Sens. 2020, 12, 629. [Google Scholar] [CrossRef] [Green Version]
- Alvarez Lopez, Y.; Garcia Fernandez, M.; Arboleya Arboleya, A.; Gonzalez-Valdes, B.; Rodriguez Vaqueiro, Y.; Las-Heras Andres, F.; Pino García, A. SAR-based technique for soil permittivity estimation. Int. J. Remote Sens. 2017, 38, 5168–5185. [Google Scholar] [CrossRef]
- Yuan, Y.; Zhu, P.; Zhao, N.; Xiao, L.; Garnero, E.; Xiao, Z.; Zhao, J.; Qiao, L. The 3-D geological model around Chang’E-3 landing site based on lunar penetrating radar Channel 1 data. Geophys. Res. Lett. 2017, 44, 6553–6561. [Google Scholar] [CrossRef] [Green Version]
- Lai, J.; Xu, Y.; Bugiolacchi, R.; Meng, X.; Xiao, L.; Xie, M.; Liu, B.; Di, K.; Zhang, X.; Zhou, B.; et al. First look by the Yutu-2 rover at the deep subsurface structure at the lunar farside. Nat. Commun. 2020, 11, 3426. [Google Scholar] [CrossRef] [PubMed]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, Z.; Feng, X.; Zhou, H.; Zou, L.; Sato, M. 3D Migration Depth Focus Velocity Analysis of Hand-Held Ground Penetrating Radar. Geosciences 2022, 12, 178. https://doi.org/10.3390/geosciences12040178
Dong Z, Feng X, Zhou H, Zou L, Sato M. 3D Migration Depth Focus Velocity Analysis of Hand-Held Ground Penetrating Radar. Geosciences. 2022; 12(4):178. https://doi.org/10.3390/geosciences12040178
Chicago/Turabian StyleDong, Zejun, Xuan Feng, Haoqiu Zhou, Lilong Zou, and Motoyuki Sato. 2022. "3D Migration Depth Focus Velocity Analysis of Hand-Held Ground Penetrating Radar" Geosciences 12, no. 4: 178. https://doi.org/10.3390/geosciences12040178
APA StyleDong, Z., Feng, X., Zhou, H., Zou, L., & Sato, M. (2022). 3D Migration Depth Focus Velocity Analysis of Hand-Held Ground Penetrating Radar. Geosciences, 12(4), 178. https://doi.org/10.3390/geosciences12040178








