A More Comprehensive Way to Analyze Foam Stability for EPB Tunnelling—Introduction of a Mathematical Characterization
Abstract
:1. Introduction
1.1. Soil Conditioning
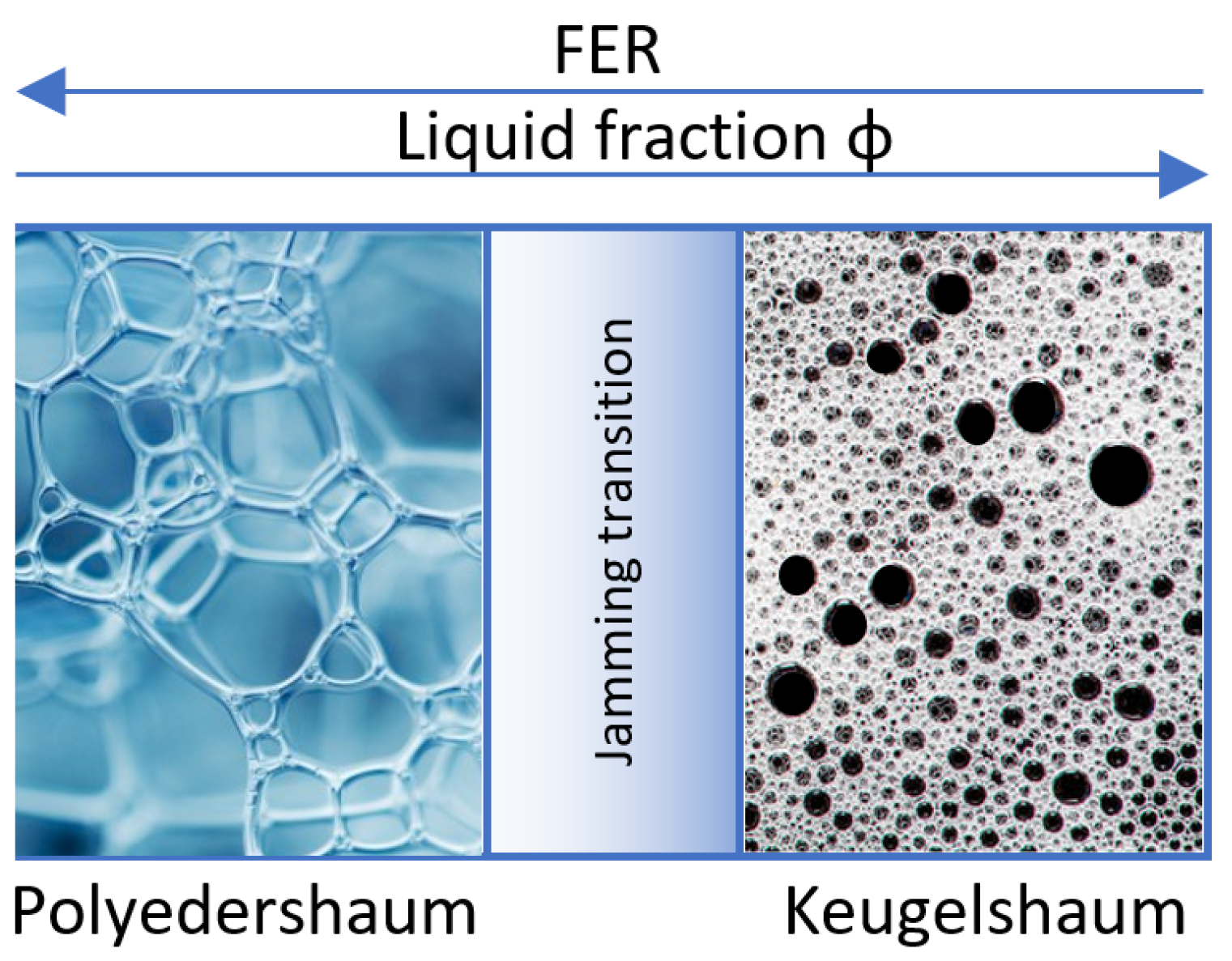
1.2. Foam Generation and Characterization
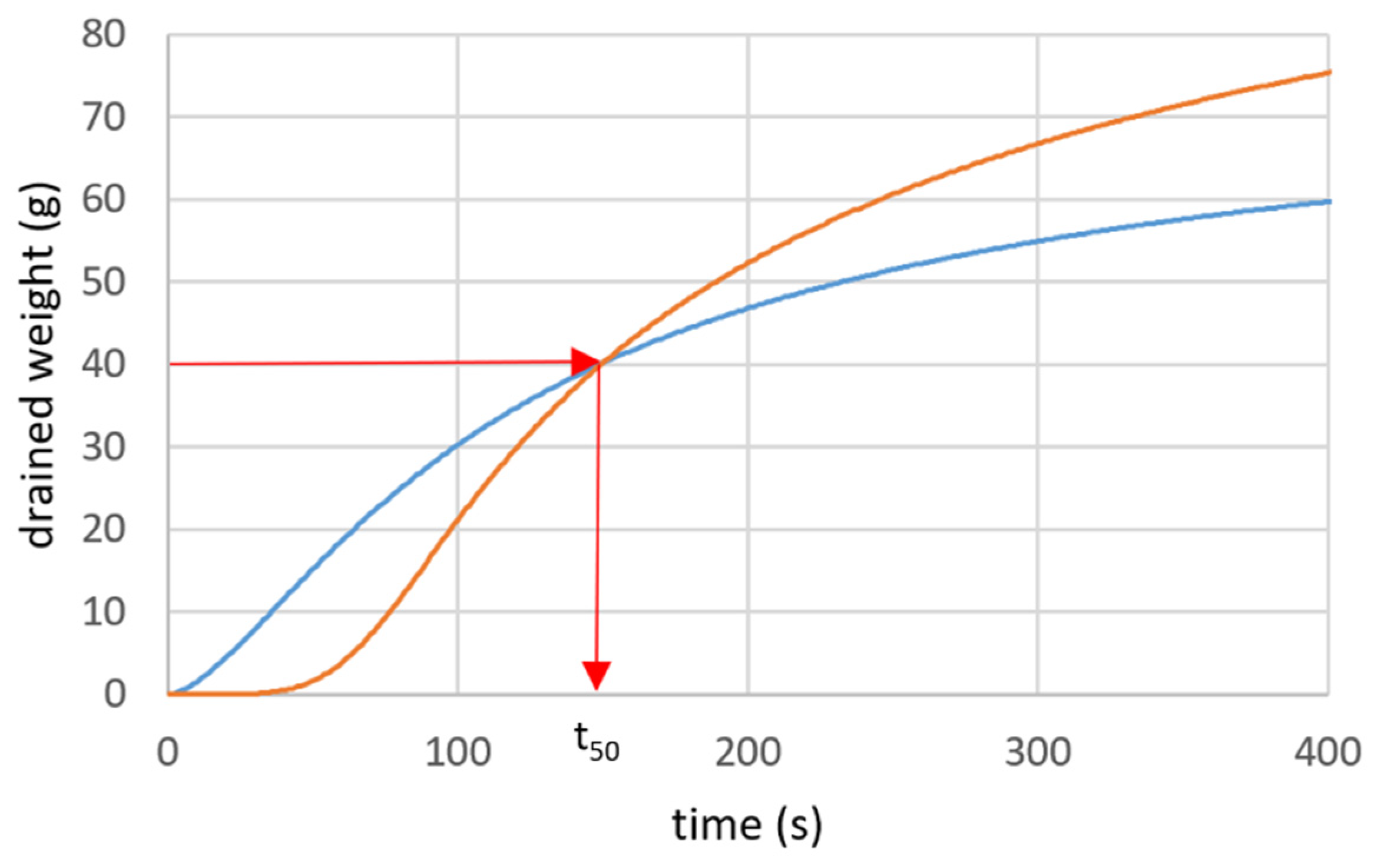
1.3. Half-Life Test
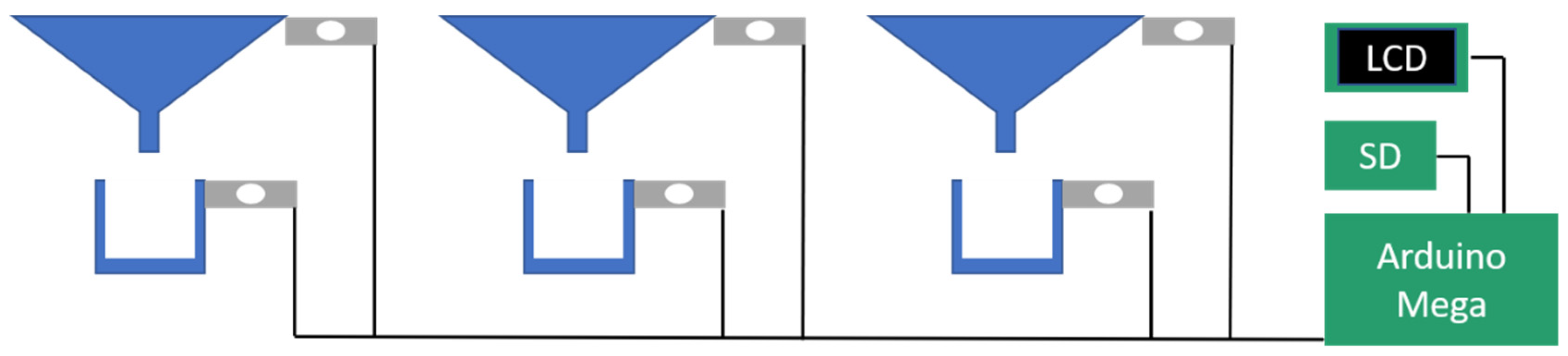
2. Materials and Methods
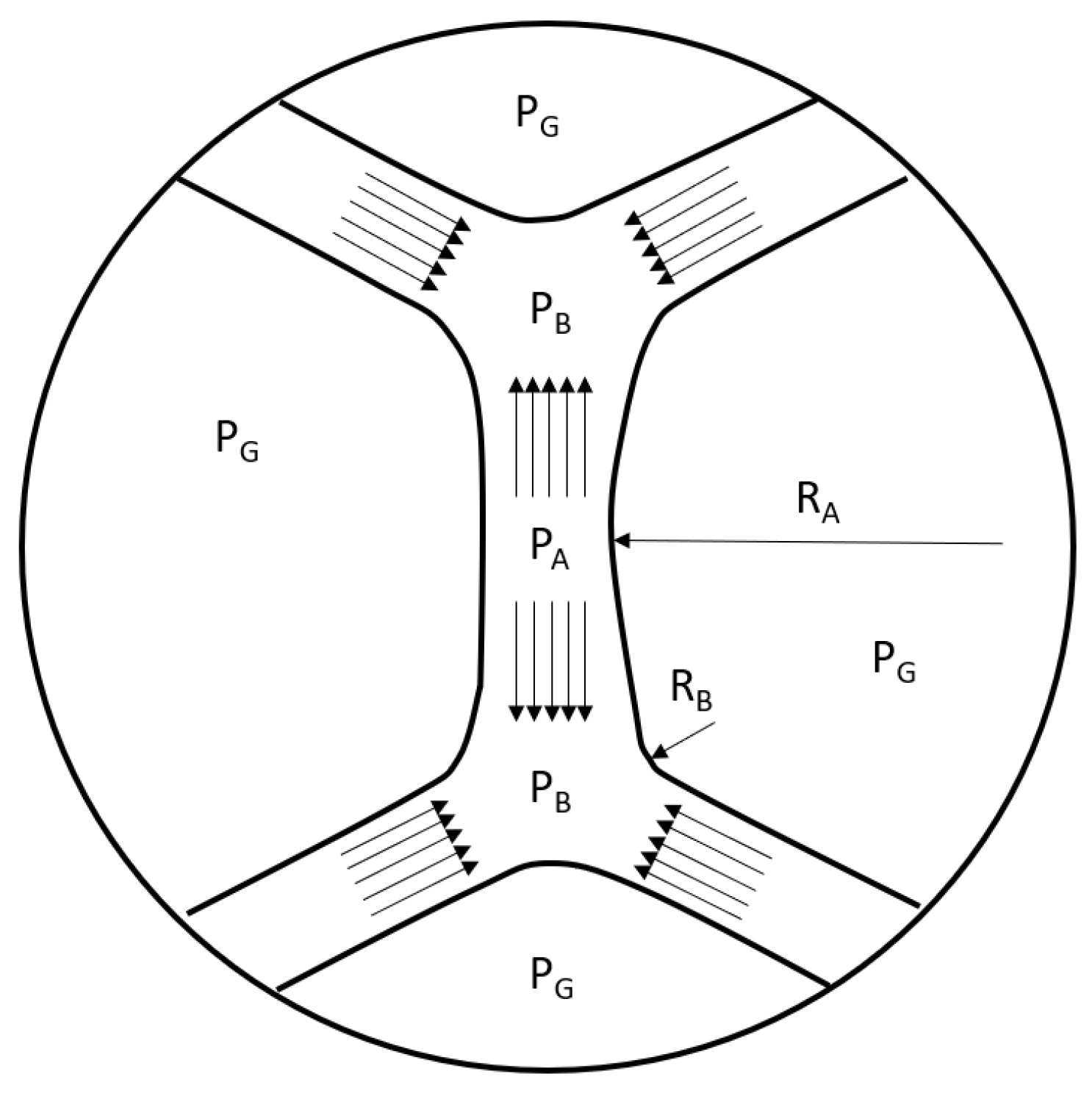
3. Mathematical Formulation
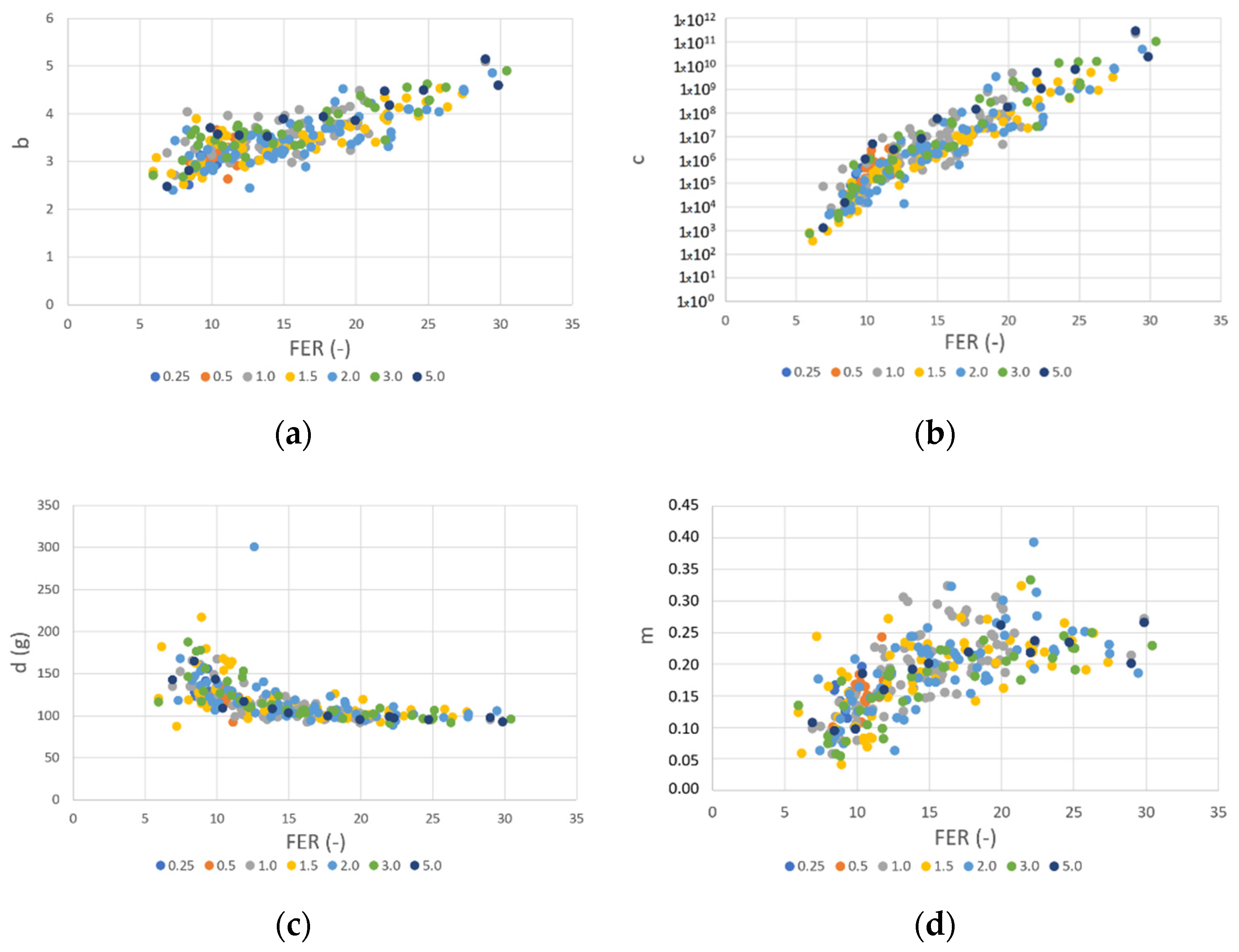
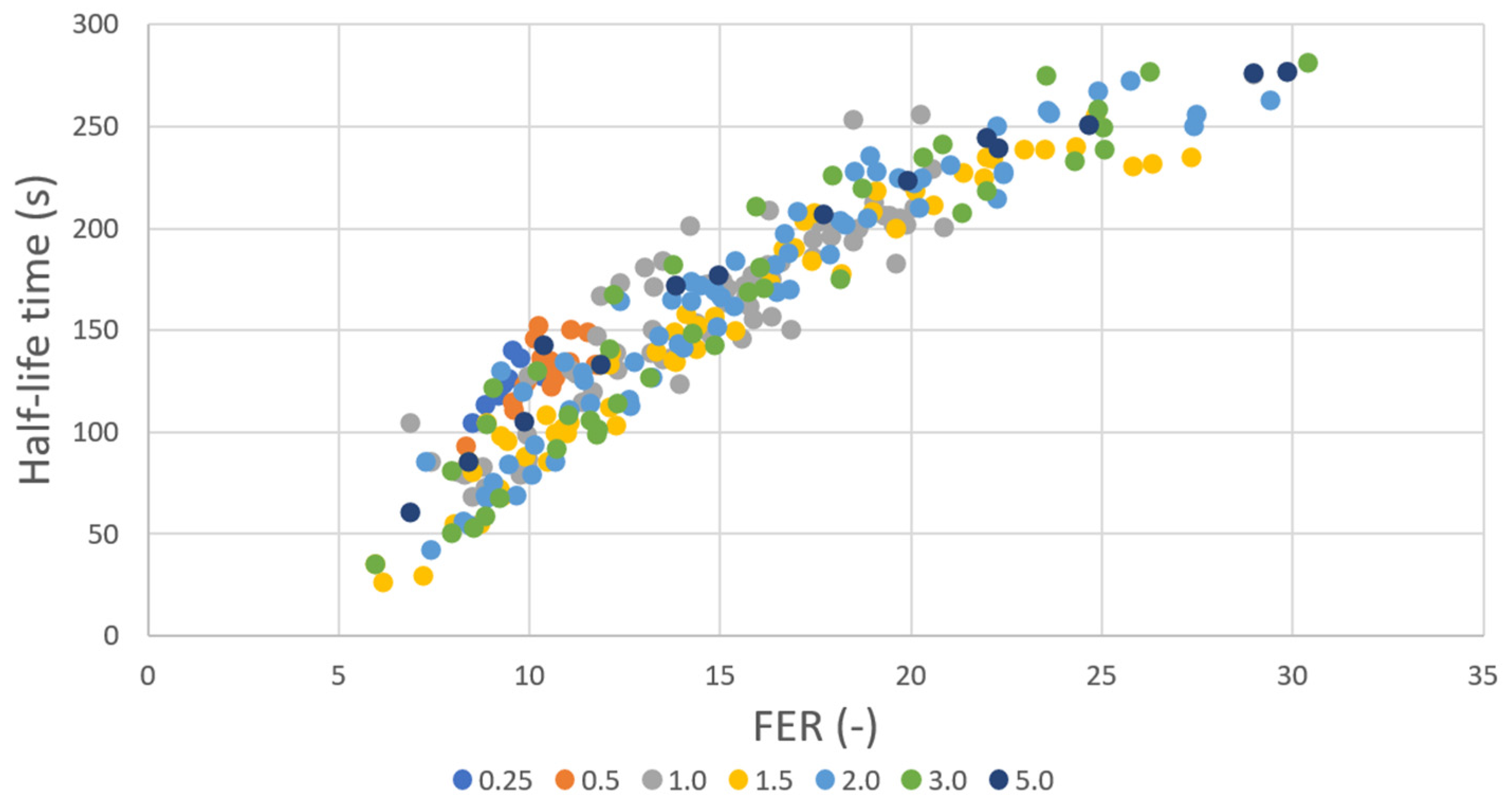
4. Influence of Concentration
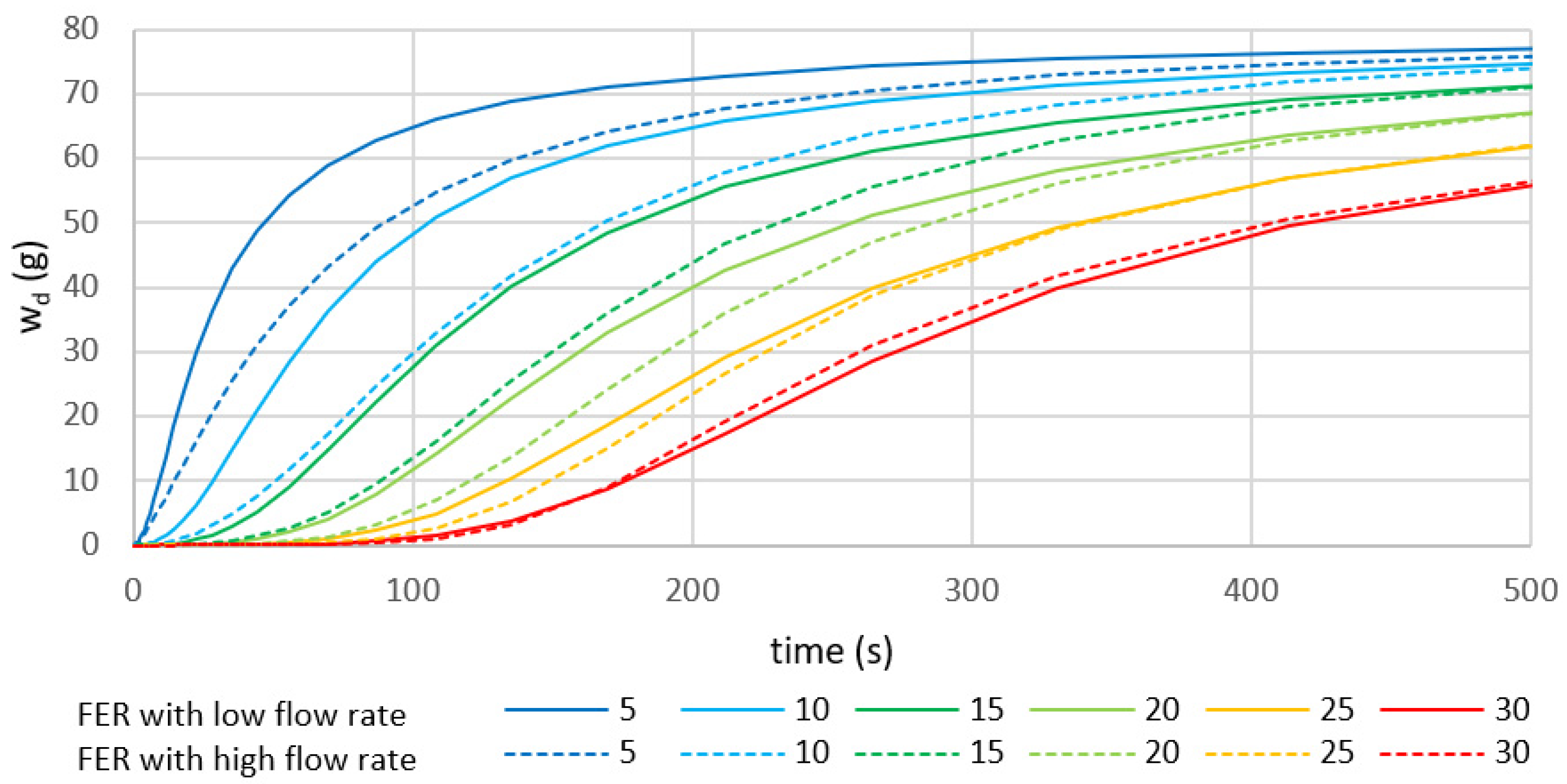
Influence of the Flow Rate
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Peila, D.; Oggeri, C.; Borio, L. Using the slump test to assess the behaviour of conditioned soil for EPB tunneling. Environ. Eng. Geosci. 2009, 15, 167–174. [Google Scholar] [CrossRef]
- Thewes, M.; Budach, C. Soil conditioning with foam during EPB tunnelling. Geomech. Tunn. 2010, 3, 256–267. [Google Scholar] [CrossRef]
- Liu, X.; Shen, S.; Zhou, A.; Xu, Y. Evaluation of foam conditioning effect on groundwater inflow at tunnel cutting face. Int. J. Numer. Anal. Methods Geomech. 2018, 43, 463–481. [Google Scholar] [CrossRef]
- Carigi, A.; Todaro, C.; Martinelli, D.; Amoroso, C.; Peila, D. Evaluation of the geo-mechanical properties property recovery in time ofconditioned soil for EPB-TBM tunnelling. Geosciences 2020, 10, 438. [Google Scholar] [CrossRef]
- Martinelli, D.; Winderholler, R.; Peila, D. Undreained behaviour of granular soils conditioned for EPB tunnelling—A new experimental procedure tunnelling. Geomechanick und Tunnelbau 2017, 10, 81–89. [Google Scholar] [CrossRef]
- Mori, L.; Mooney, M.A.; Cha, M. Characterizing the influence of stress on foam conditioned sand for EPB tunneling. Tunn. Undergr. Space Technol. 2018, 71, 454–465. [Google Scholar] [CrossRef]
- Todaro, C. Analysis on the penetration of foams in the excavation with EPB. GEAM—Geoing. Ambient. E Min. 2016, 147, 49–52. [Google Scholar]
- Mori, L.; Alavi, E.; Mooney, M.A. Apparent density evaluation methods to assess the effectiveness of soil conditioning. Tunn. Undergr. Space Technol. 2017, 67, 175–186. [Google Scholar] [CrossRef]
- Peña, M. Soil conditioning for sands. Tunn. Tunn. Int. 2003, 35, 40–42. [Google Scholar]
- Borio, L.; Peila, D. Study of the permeability of foam conditioned soils with laboratory tests. Am. J. Environ. Sci. 2010, 6, 365. [Google Scholar] [CrossRef] [Green Version]
- Oñate Salazar, C.G.; Martinelli, D.; Todaro, C.; Luciani, A.; Boscaro, A.; Peila, D. Preliminary study of wear induced by granular soil on metallic parts of EPB tunnelling machines. GEAM—Geoing. Ambient. E Min. 2016, 53, 67–70. [Google Scholar]
- Hollmann, F.S.; Thewes, M. Assessment method for clay clogging and disintegration of fines in mechanised tunnelling. Tunn. Undergr. Space Technol. 2013, 37, 96–106. [Google Scholar] [CrossRef]
- Carigi, A.; Luciani, A.; Todaro, C.; Martinelli, D.; Peila, D. Influence of conditioning on the behaviour of alluvial soils with cobbles. Tunn. Undergr. Space Technol. 2020, 96, 103225. [Google Scholar] [CrossRef]
- Todaro, C.; Carigi, A.; Peila, L.; Martinelli, D.; Peila, D. Soil conditioning tests of clay for EPB tunnelling. Undergr. Space 2021. [Google Scholar] [CrossRef]
- Barra Caracciolo, A.; Cardoni, M.; Pescatore, T.; Patrolecco, L. Characteristics and environmental fate of the anionic surfactant sodium lauryl ether sulphate SLES used as the main component in foaming agents for mechanized tunnelling. Environ. Pollut. 2017, 226, 94–103. [Google Scholar] [CrossRef] [PubMed]
- Firouzei, Y.; Grenni, P.; Barra Caracciolo, A.; Patrolecco, L.; Todaro, C.; Martinelli, D.; Carigi, A.; Hajipour, G.; Hassanpour, J.; Peila, D. The most common laboratory procedures for the evaluation of EPB TBMs excavated material ecotoxicity in Italy: A review. GEAM—Geoing. Ambient. E Min. 2020, 160, 44–56. [Google Scholar]
- Vinai, R.; Peila, D.; Oggeri, C.; Pelizza, S. Laboratory tests for EPB tunnelling soil conditioning. In Proceedings of the 33rd ITA-AITES World Tunnel Congress–Underground Space—The 4th Dimension of Metropolises, Prague, Czech Republic, 5–10 May 2007; Taylor & Francis Group: London, UK, 2007; pp. 273–278. [Google Scholar]
- Peila, D.; Martinelli, D.; Todaro, C.; Luciani, A. Soil conditioning in EPB shield tunnelling—An overview of laboratory tests. Geomech. Tunn. 2019, 12, 491–498. [Google Scholar] [CrossRef]
- Thewes, M.; Budach, C.; Bezuijen, A. Foam conditioning in EPB tunnelling. In Geotechnical Aspects of Underground Construction in Soft Ground; Taylor & Francis Group: London, UK, 2012; Volume 127, ISBN 978-0-415-68367-8. [Google Scholar]
- Wu, Y.; Mooney, M.A.; Cha, M. An experimental examination of foam stability under pressure for EPB TBM tunneling. Tunn. Undergr. Space Technol. 2018, 77, 80–93. [Google Scholar] [CrossRef]
- Al Yousef, Z.A.; Almobarky, M.A.; Schechter, D.S. The effect of nanoparticle aggregation on surfactant foam stability. J. Colloid Interface Sci. 2018, 511, 365–373. [Google Scholar] [CrossRef]
- Fameau, A.L.; Salonen, A. Effect of particles and aggregated structures on the foam stability and aging. Comptes Rendus Phys. 2014, 15, 748–760. [Google Scholar] [CrossRef]
- Horozov, T.S. Foams and foam films stabilised by solid particles. Curr. Opin. Colloid Interface Sci. 2008, 13, 134–140. [Google Scholar] [CrossRef]
- Bikerman, J.J. Foams; Springer Science & Business Media: New York, NY, USA, 2013; Volume 10. [Google Scholar]
- Butt, H.J.; Graf, K.; Kappl, M. Physics and Chemistry of Interfaces; John Wiley & Sons: New York, NY, USA, 2013. [Google Scholar]
- Langevin, D. Aqueous foams and foam films stabilised by surfactants. Gravity-free studies. Comptes Rendus Mech. 2016, 345, 47–55. [Google Scholar] [CrossRef] [Green Version]
- Schramm, L.L. Foams: Fundamentals and Applications in the Petroleum Industry; American Chemical Society: Washington, DC, USA, 1994. [Google Scholar]
- Stevenson, P. Inter-bubble gas diffusion in liquid foam. Curr. Opin. Colloid Interface Sci. 2010, 15, 374–381. [Google Scholar] [CrossRef]
- Bhakta, A.; Ruckenstein, E. Drainage and Coalescence in Standing Foams. J. Colloid Ad Interface Sci. 1997, 191, 184–201. [Google Scholar] [CrossRef] [PubMed]
- Moll, P.; Grossmann, L.; Kutzli, I.; Weiss, J. Influence of energy density and viscosity on foam stability—A study with pea protein Pisum sativum L. J. Dispers. Sci. Technol. 2019, 41, 1789–1796. [Google Scholar] [CrossRef]
- EFNARC. Specification and Guidelines for the Use of Specialist Products for Mechanized Tunnelling (TBM) in Soft Ground and Hard Rock Recommendation; EFNARC: Farnham, UK, 2005. [Google Scholar]
- Galli, M.; Thewes, M. Rheological characterisation of foam-conditioned sands in EPB tunneling. Int. J. Civil Eng. 2019, 17, 145–160. [Google Scholar] [CrossRef]
- Sebastiani, D.; Vilardi, D.; Bavasso, I.; Di Palma, L.; Miliziano, S. Classification of foam and foaming products for EPB mechanized tunnelling based on half-life time. Tunn. Undergr. Space Technol. 2019, 92, 103044. [Google Scholar] [CrossRef]
- Zhao, S.; Li, S.; Wan, Z.; Wang, X.; Wang, M.; Yuan, C. Effects of anti-clay agents on bubble size distribution and stability of acquous foam under pressure for earth pressure balance shield tunnelling. Colloid Interface Sci. Commun. 2021, 42, 100424. [Google Scholar] [CrossRef]
- Zhou, X.; Yang, Y. Effect of foam parameters on cohesionless soil permeability and its application to prevent the water speweing. Appl. Sci. 2020, 10, 1787. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Chang, Z.; Luo, W.; Gu, S.; Li, W.; An, J. Effect of starch particles on foam stability and dilational viscoelasticity of aqueous-foam. Chin. J. Chem. Eng. 2015, 23, 276–280. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carigi, A.; Todaro, C.; Martinelli, D.; Peila, D. A More Comprehensive Way to Analyze Foam Stability for EPB Tunnelling—Introduction of a Mathematical Characterization. Geosciences 2022, 12, 191. https://doi.org/10.3390/geosciences12050191
Carigi A, Todaro C, Martinelli D, Peila D. A More Comprehensive Way to Analyze Foam Stability for EPB Tunnelling—Introduction of a Mathematical Characterization. Geosciences. 2022; 12(5):191. https://doi.org/10.3390/geosciences12050191
Chicago/Turabian StyleCarigi, Andrea, Carmine Todaro, Daniele Martinelli, and Daniele Peila. 2022. "A More Comprehensive Way to Analyze Foam Stability for EPB Tunnelling—Introduction of a Mathematical Characterization" Geosciences 12, no. 5: 191. https://doi.org/10.3390/geosciences12050191
APA StyleCarigi, A., Todaro, C., Martinelli, D., & Peila, D. (2022). A More Comprehensive Way to Analyze Foam Stability for EPB Tunnelling—Introduction of a Mathematical Characterization. Geosciences, 12(5), 191. https://doi.org/10.3390/geosciences12050191







