Regional-Scale Seismic Liquefaction Susceptibility Mapping via an Empirical Approach Validated by Site-Specific Analyses
Abstract
:1. Introduction
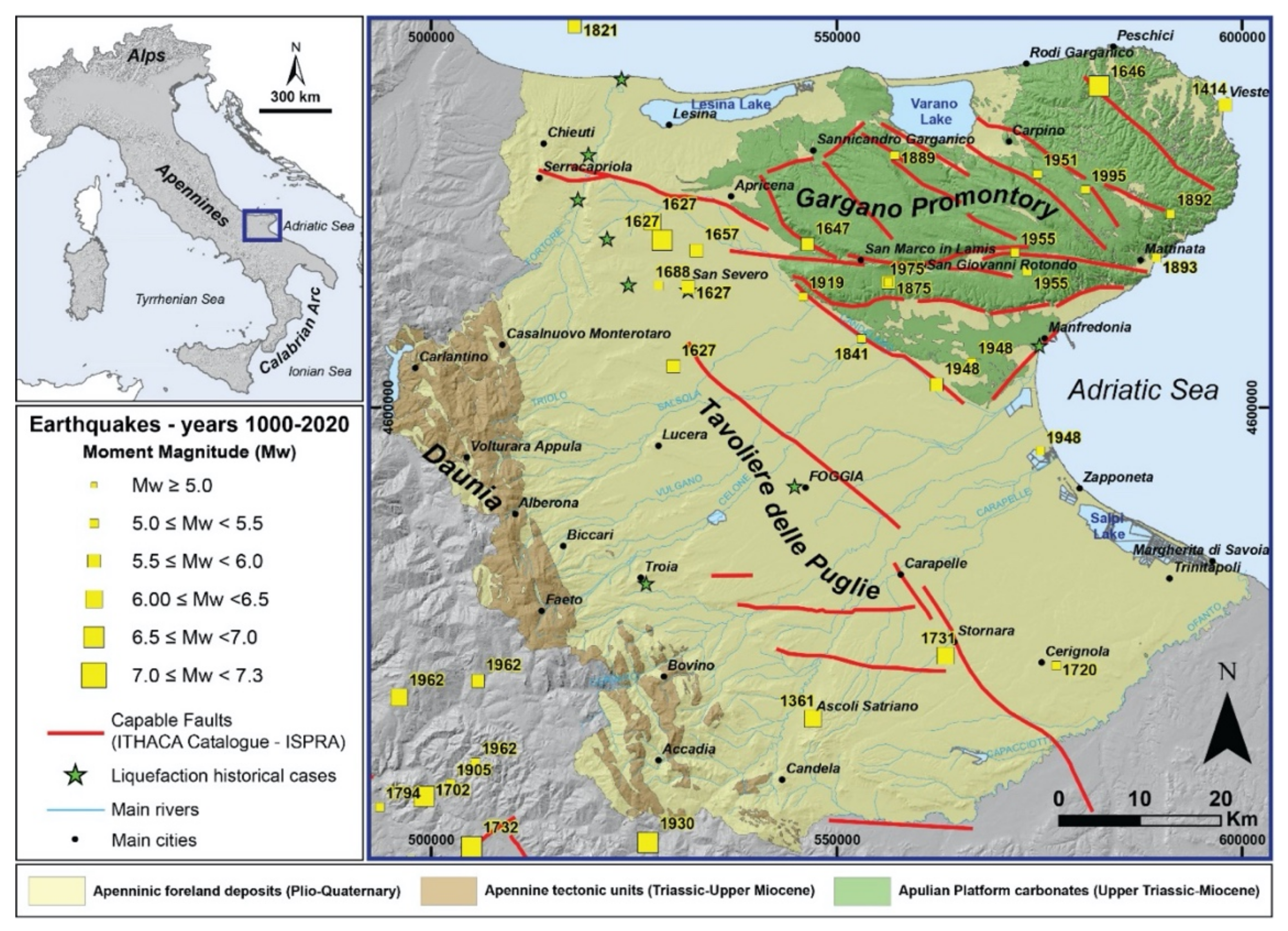
2. Study Area
3. Susceptibility Model
Method
4. Validation Dataset Preparation
4.1. Data Collection
4.2. Method for Liquefaction Evaluation
5. Results
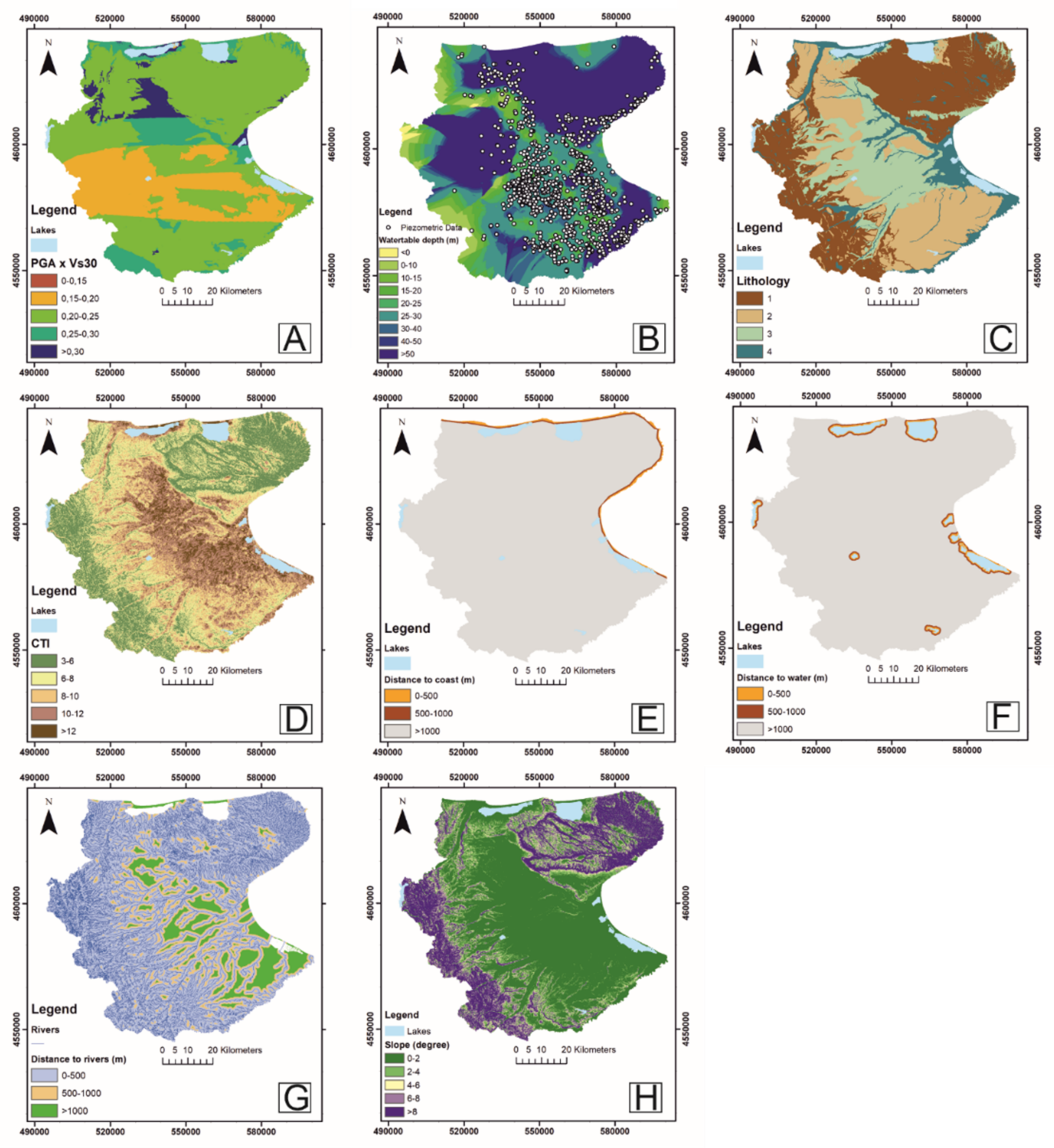
5.1. Geospatial Predictors
5.2. Validation Dataset
5.3. Susceptibility Map
6. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bird, J.F.; Bommer, J.J.; Crowley, H.; Pinho, R. Modelling liquefaction-induced building damage in earthquake loss estimation. Soil Dyn. Earthq. Eng. 2006, 26, 15–30. [Google Scholar] [CrossRef]
- Galli, P.; Castenetto, S.; Peronace, E. The MCS macroseismic survey of the Emilia 2012 earthquakes. Ann. Geophys. 2012, 55, 663–672. [Google Scholar] [CrossRef]
- Huang, Y.; Yu, M. Review of soil liquefaction characteristics during major earthquakes of the twenty-first century. Nat. Hazards 2013, 3, 2375–2384. [Google Scholar] [CrossRef]
- Matsuoka, M.; Wakamatsu, K.; Hashimoto, M.; Senna, S.; Midorikawa, S. Evaluation of liquefaction potential for large areas based on geomorphologic classification. Earthq. Spectra 2015, 31, 2375–2395. [Google Scholar] [CrossRef]
- Chen, J.; Hideyuki, O.; Takeyama, T.; Oishi, S.; Hori, M. Toward a numerical-simulation-based liquefaction hazard assessment for urban regions using high-performance computing. Eng. Geol. 2019, 258, 105153. [Google Scholar] [CrossRef]
- Rashidian, V.; Baise, L.G. Regional efficacy of a global geospatial liquefaction model. Eng. Geol. 2020, 272, 105644. [Google Scholar] [CrossRef]
- Pudi, R.; Martha, T.R.; Roy, P.; Kumar, K.V.; Rao, P.R. Regional liquefaction susceptibility mapping in the Himalayas using geospatial data and AHP technique. Curr. Sci. 2019, 116, 1868–1877. [Google Scholar] [CrossRef]
- Zhu, J.; Baise, L.G.; Thompson, E.M. An updated geospatial liquefaction model for global application. Bull. Seismol. Soc. Am. 2017, 107, 1365–1385. [Google Scholar] [CrossRef]
- Monaco, P.; Santucci de Magistris, F.; Grasso, S.; Marchetti, S.; Maugeri, M.; Totani, G. Analysis of the liquefaction phenomena in the village of Vittorito (L’Aquila). Bull. Earthq. Eng. 2011, 9, 231–261. [Google Scholar] [CrossRef]
- Papathanassiou, G.; Caputo, R.; Rapti-Caputo, D. Liquefaction phenomena along the paleo-Reno River caused by the May 20, 2012, Emilia (northern Italy) earthquake. Ann. Geophys. 2012, 55, 735–742. [Google Scholar] [CrossRef]
- Lanfredi Sofia, C.; Castaldini, D. Inventory of coseismic effects in seismic hazard assessment and communication: The case study of 2012 Emilia Earthquakes [Inventario de efeitos co-sismicos para a avaliação local do risco sísmico local e comunicação. O estudo de caso dossismos de Emilia 2012. In Proceedings of the VII Congresso Nacional De Geomorfologia, Lisboa, Portugal, 8–9 October 2015; Geomorfologia 2015. Associação Portuguesa de Geomorfólogos: Porto, Portugal, 2015; Volume 9, pp. 291–298. [Google Scholar]
- Yilmaz, C.; Silva, V.; Weatherill, G. Probabilistic framework for regional loss assessment due to earthquake-induced liquefaction including epistemic uncertainty. Soil Dyn. Earthq. Eng. 2021, 141, 106493. [Google Scholar] [CrossRef]
- Marcuson, W.F.; Wahls, H.E. Effects of Time on Damping Ratio of Clays; ASTM American Society for Testing Materials; ASTM: West Conshohocken, PA, USA, 1978; pp. 126–147. [Google Scholar]
- Youd, T.L.; Idriss, I.M. Liquefaction resistance of soils: Summary report from the 1996 NCEER and 1998 NCEER/NSF workshops on evaluation of liquefaction resistance of soils. J. Geotech. Geoenvironmental Eng. 2001, 127, 297–313. [Google Scholar] [CrossRef] [Green Version]
- Seed, H.B.; Idriss, I.M. Simplified procedure for evaluating soil liquefaction potential. J. Soil Mech. Found. Div. 1971, 97, 1249–1273. [Google Scholar] [CrossRef]
- Seed, H.B. Soil liquefaction and cyclic mobility evaluation for level ground during earthquakes. J. Geotech. Eng. Div. 1979, 105, 201–255. [Google Scholar] [CrossRef]
- Seed, H.B. Ground Motions and Soil Liquefaction during Earthquakes; Earthquake Engineering Research Insititue: Berkeley, CA, USA, 1982; p. 134. [Google Scholar]
- Youd, T.L.; Hoose, S.N. Liquefaction susceptibility and geologic setting. In Proceedings of the 6th World Conf. on Earthquake Engineering, New Delhi, India, 10–14 January 1977; Indian Society of Earthquake Technology: Roorkee, India, 1977; Volume 6, pp. 37–42. [Google Scholar]
- Zhu, J.; Daley, D.; Baise, L.G.; Thompson, E.M.; Wald, D.J.; Knudsen, K.L. A geospatial liquefaction model for rapid response and loss estimation. Earthq. Spectra 2015, 31, 1813–1837. [Google Scholar] [CrossRef]
- Bozzoni, F.; Bonì, R.; Conca, D.; Lai, C.G.; Zuccolo, E.; Meisina, C. Megazonation of earthquake-induced soil liquefaction hazard in continental Europe. Bull. Earthq. Eng. 2020, 19, 4059–4082. [Google Scholar] [CrossRef]
- Norini, G.; Aghib, F.S.; Di Capua, A.; Facciorusso, J.; Castaldini, D.; Marchetti, M.; Cavallin, A.; Pini, R.; Ravazzi, C.; Zuluaga, M.C.; et al. Assessment of liquefaction potential in the central Po plain from integrated geomorphological, stratigraphic and geotechnical analysis. Eng. Geol. 2021, 282, 105997. [Google Scholar] [CrossRef]
- Baise, L.G.; Daley, D.; Zhu, J.; Thompson, E.M.; Knudsen, K. Geospatial liquefaction hazard model for Kobe, Japan and Christchurch, New Zealand. Seism. Res. Lett. 2012, 83, 458. [Google Scholar]
- Maurer, B.W.; van Ballegooy, S.; Bradley, B.A. Fragility functions for performance-based damage assessment of soil liquefaction. In Proceedings of the 3rd International Conference on Performance based Design in Earthquake Geotechnical Engineering, Online, 16–19 July 2017. [Google Scholar]
- Geyin, M.; Baird, A.J.; Maurer, B.W. Field assessment of liquefaction prediction models based on geotechnical versus geospatial data, with lessons for each. Earthq. Spectra 2020, 36, 1386–1411. [Google Scholar] [CrossRef]
- Lai, C.G.; Bozzoni, F.; De Marco, M.C.; Zuccolo, E.; Bandera, S.; Mazzocchi, G. LIQUEFACT Project-DELIVERABLE D2.4. In GIS Database of the Historical Liquefaction Occurrences in Europe and European Empirical Correlations to Predict the Liquefaction Occurrence Starting from the Main Seismological Information v 1.0; Università degli Studi di Pavia/Eucentre: Pavia, Italy, 2018; p. 5571183. [Google Scholar]
- Saaty, T.L. The Analytic Hierarchy Process: Planning, Priority Setting, Resources Allocation; Hill Book CO: New York, NJ, USA, 1980. [Google Scholar]
- Karpouza, M.; Chousianitis, K.; Bathrellos, G.D.; Skilodimou, H.D.; Kaviris, G.; Antonarakou, A. Hazard zonation mapping of earthquake-induced secondary effects using spatial multi-criteria analysis. Nat. Hazards 2021, 109, 637–669. [Google Scholar] [CrossRef]
- Castellanos Abella, E.A.; van Westen, C.J. Generation of a landslide risk index map for Cuba using spatial multi-criteria evaluation. Landslides 2007, 4, 311–325. [Google Scholar] [CrossRef] [Green Version]
- Gorsevski, P.V.; Jankowski, P. An optimized solution of multi-criteria evaluation analysis of landslide susceptibility using fuzzy sets and Kalman filter. Comput. Geosci. 2010, 36, 1005–1020. [Google Scholar] [CrossRef]
- Pisano, L.; Zumpano, V.; Malek, Z.; Rosskopf, C.M.; Parise, M. Variations in the susceptibility to landslides, as a consequence of land cover changes: A look to the past, and another towards the future. Sci. Total Environ. 2017, 601–602, 1147–1159. [Google Scholar] [CrossRef] [PubMed]
- Galli, P.; Meloni, F. Nuovo catalogo nazionale dei processi di liquefazione avvenuti in occasione dei terremoti storici in Italia. Alp. Mediterr. Quat. 1993, 6, 271–292. [Google Scholar]
- Vessia, G.; Venisti, N. Liquefaction damage potential for seismic hazard evaluation in urbanized areas. Soil Dyn. Earthq. Eng. 2011, 31, 1094–1105. [Google Scholar] [CrossRef]
- Crostella, A.; Vezzani, L. La geologia dell’Appennino foggiano. Boll. Soc. Geol. It 1964, 83, 121–141. [Google Scholar]
- CARG-Carta Geologica d’Italia at a 1:50,000 Scale, Sheet 407 San Bartolomeo in Galdo; CARG Project; ISPRA, SystemCart: Rome, Italy, 2011.
- Azzaroli, A.; Perno, U.; Radina, B. Note Illustrative Della Carta Geologica d’Italia. In Gravina di Puglia; Servizio Geologico d’Italia: Rome, Italy, 1968; pp. 1–57. [Google Scholar]
- CARG-Carta Geologica d’Italia at a 1:50,000 Scale, Sheet 396 San Severo; CARG Project; ISPRA, SystemCart: Rome, Italy, 2011.
- CARG-Carta Geologica d’Italia at a 1:50,000 Scale, Sheet 421 Ascoli Satriano; CARG Project; ISPRA, SystemCart: Rome, Italy, 2011.
- CARG-Carta Geologica d’Italia at a 1:50,000 Scale, Sheet 408 Foggia; CARG Project; ISPRA, SystemCart: Rome, Italy, 2011.
- Maggiore, M.; Nuovo, G.; Pagliarulo, P. Caratteristiche idrogeologiche e principali differenze idrochimiche delle falde sotterranee del Tavoliere di Puglia. Mem. Soc. Geol. It 1996, 51, 669–684. [Google Scholar]
- Maggiore, M.; Pagliarulo, P. Siccità e disponibilità idriche sotterranee del tavoliere di Puglia. Geol. Dell’ambiente SIGEA 2003, 11, 35–40. [Google Scholar]
- Cotecchia, V.; Ferrari, G.; Fidelibus, M.D.; Polemio, M.; Tadolini, T.; Tulipano, L. Considerazioni sull’origine delle acque presenti in livelli sabbiosi profondi del Tavoliere di Puglia. Quad. di Geol. Appl. 1995, 1, 1163–1173. [Google Scholar]
- Rovida, A.; Locati, M.; Camassi, R.; Lolli, B.; Gasperini, P. The Italian earthquake catalogue CPTI15. Bull. Earthq. Eng. 2020, 18, 2953–2984. [Google Scholar] [CrossRef]
- Rovida, A.; Locati, M.; Camassi, R.; Lolli, B.; Gasperini, P.; Antonucci, A. Italian Parametric Earthquake Catalogue (CPTI15), Version 4.0; Istituto Nazionale di Geofisica e Vulcanologia (INGV): Rome, Italy, 2022. [CrossRef]
- ITHACA Working Group. ITHACA (ITaly HAzard from CApable Faulting), A Database of Active Capable Faults of the Italian Territory. Version December 2019. ISPRA Geological Survey of Italy. Available online: http://sgi2.isprambiente.it/ithacaweb/Mappatura.aspx (accessed on 12 April 2022).
- Miccolis, S.; Filippucci, M.; De Lorenzo, S.; Frepoli, A.; Pierri, P.; Tallarico, A. Seismogenic Structure Orientation and Stress Field of the Gargano Promontory (Southern Italy) From Microseismicity Analysis. Front. Earth Sci. 2021, 9, 589332. [Google Scholar] [CrossRef]
- Crespellani, T.; Facciorusso, J.; Ghinelli, A.; Madiai, C.; Renzi, S.; Vannucchi, G. Rapporto Preliminare sui Diffusi Fenomeni di liquefazione Verificatisi Durante il Terremoto in Pianura Padana Emiliana del Maggio 2012; Università degli Studi di Firenze, Dipartimento di Ingegneria Civile e Ambientale-Sezione Geotecnica: Florence, Italy, 2012; pp. 1–33. [Google Scholar]
- Galli, P.; Meloni, F. Liquefazione Storica. Un catalogo nazionale. Quat. Ital. J. Quat. Sci. 1993, 6, 271–292. [Google Scholar]
- Galli, P. New empirical relationships between magnitude and distance for liquefaction. Tectonophysics 2000, 324, 169–187. [Google Scholar] [CrossRef]
- Fortunato, C.; Martino, S.; Prestininzi, A.; Romeo, R.W.; Fantini, A.; Sanandrea, P. New release of the Italian catalogue of earthquake-induced ground failures (CEDIT). Ital. J. Eng. Geol. Environ. 2012, 2, 63–74. [Google Scholar] [CrossRef]
- Bozzoni, F.; Bonì, R.; Conca, D.; Meisina, C.; Lai, C.G.; Zuccolo, E. A geospatial approach for mapping the earthquake-induced liquefaction risk at the european scale. Geosciences 2021, 11, 32. [Google Scholar] [CrossRef]
- Martino, S.; Caprari, P.; Fiorucci, M.; Marmoni, G.M. Il Catalogo CEDIT: Dall’inventario degli effetti sismoindotti all’analisi di scenario. Mem. Descr. Carta Geol. D’it 2020, 107, 441–450. [Google Scholar]
- Martino, S.; Prestininzi, A.; Romeo, R.W. Earthquake-induced ground failures in Italy from a reviewed database. Nat. Hazards Earth Syst. Sci. 2014, 14, 799–814. [Google Scholar] [CrossRef] [Green Version]
- Saaty, T.L. A scaling method for priorities in hierarchical structures. J. Math. Psychol. 1977, 15, 234–281. [Google Scholar] [CrossRef]
- Eastman, R. The IDRISI Selva Help; Clark Labs: Worcester, MA, USA, 2012. [Google Scholar]
- Poudyal, C.P.; Chang, C.; Oh, H.-J.; Lee, S. Landslide susceptibility maps comparing frequency ratio and artificial neural networks: A case study from the Nepal Himalaya. Environ. Earth Sci. 2010, 61, 1049–1064. [Google Scholar] [CrossRef]
- Feizizadeh, B.; Blaschke, T. GIS-multicriteria decision analysis for landslide susceptibility mapping: Comparing three methods for the Urmia lake basin, Iran. Nat. Hazards 2013, 65, 2105–2128. [Google Scholar] [CrossRef]
- Saaty, T.L.; Vargas, L.G. Modeling behavior in competition: The analytic hierarchy process. Appl. Math. Comput. 1985, 16, 49–92. [Google Scholar] [CrossRef]
- Bathrellos, G.D.; Gaki-Papanastassiou, K.; Skilodimou, H.D.; Skianis, G.A.; Chousianitis, K.G. Assessment of rural community and agricultural development using geomorphological-geological factors and GIS in the Trikala prefecture (Central Greece). Stoch. Environ. Res. Risk Assess. 2013, 27, 573–588. [Google Scholar] [CrossRef]
- Chen, Y.; Yu, J.; Khan, S. Spatial sensitivity analysis of multi-criteria weights in GIS-based land suitability evaluation. Environ. Model. Softw. 2010, 25, 1582–1591. [Google Scholar] [CrossRef]
- Silvestri, F.; Simonelli, A.L. Principi di progettazione metodologie di analisi. In Aspetti Geotecnici della Progettazione in Zona sismica, Linee Guida; Pàtron Editore: Bologna, Italy, 2005; pp. 37–52. [Google Scholar]
- Facciorusso, J.; Vannucchi, G. Esempio di valutazione del potenziale di liquefazione su scala regionale secondo l’approccio deterministico e probabilistico. Riv. Ital. di Geotec. 2009, 2, 34–56. [Google Scholar]
- Eurocode 8. Design of Structures for Earthquake Resistance: Part 5. Foundations, Retaining Structures and Geotechnical Aspects; Final Draft; PrEN 1998-5; CEN: Brussels, Belgium, 1998.
- Idriss, I.M.; Boulanger, R.W. Semi-empirical procedures for evaluating liquefaction potential during earthquakes. Soil Dyn. Earthq. Eng. 2006, 26, 115–130. [Google Scholar] [CrossRef]
- Boulanger, R.W. High overburden stress effects in liquefaction analyses. J. Geotech. Geoenvironmental Eng. 2003, 129, 1071–1082. [Google Scholar] [CrossRef]
- Idriss, I.M. An update to the Seed-Idriss simplified procedure for evaluating liquefaction potential. In TRB Workshop on New Approaches to Liquefaction, January; Publication No. FHWA-RD-99-165; Federal Highway Administration: Washington, DC, USA, 1999. [Google Scholar]
- Boulanger, R.W.; Idriss, I.M. State normalization of penetration resistance and the effect of overburden stress on liquefaction resistance. In Proceedings of the 11th International Conference on Soil Dynamics and Earthquake Engineering and 3rd International Conference on Earthquake Geotechnical Engineering, University of California, Berkeley, CA, USA, 7–9 January 2004. [Google Scholar]
- Seed, H.B.; Mori, K.; Chan, C.K. Influence of Seismic History on the Liquefaction Characteristics of Sands; Report No. EERC 75-25; Earthquake Engineering Research Center, University of California: Berkeley, CA, USA, 1975. [Google Scholar]
- Seed, H.B.; Tokimatsu, K.; Harder, L.F., Jr.; Chung, R. The Influence of SPT Procedures on Soil Liquefaction Resistance Evaluations; Report, No. UCB/EERC-84/15; Earthquake Engineering Research Center, University of California: Berkeley, CA, USA, 1984. [Google Scholar]
- Seed, H.B.; Tokimatsu, K.; Harder, L.F., Jr.; Chung, R. Influence of SPT procedures in soil liquefaction resistance evaluations. J. Geotech. Eng. ASCE 1985, 111, 1425–1445. [Google Scholar] [CrossRef]
- Seed, H.B. Earthquake resistant design of earth dams. In Proceedings of the Symposium on Seismic Design of Embankments and Caverns, ASCE; National Convention, Philadelphia, PA, USA, 16–20 May 1983; American Society of Civil Engineers: New York, NY, USA, 1983; pp. 41–64. [Google Scholar]
- Knudsen, K.; Bott, J. Geologic and geomorphic evaluation of liquefaction case histories for rapid hazard mapping. Seism. Res. Lett. 2011, 82, 334. [Google Scholar]
- Stucchi, M.; Akinci, A.; Faccioli, E.; Gasperini, P.; Malagnini, L.; Meletti, C.; Montaldo, V.; Valensise, G. Redazione della Mappa di Pericolosità Sismica prevista dall’Ordinanza PC del 20 marzo 2003, n. 3274, All. In 1 Rapporto Conclusivo; Istituto Nazionale di Geofisica e Vulcanologia: Rome, Italy, 2004. [Google Scholar]
- NTC 2018. Norme Tecniche per le Costruzioni, D.M. 17 Gennaio 2018, Gazzetta Ufficiale, n. 42 del 20 Febbraio 2008. Supplemento Ordinario n. 8, Istituto Poligrafico e Zecca dello Stato, Roma. Available online: https://www.gazzettaufficiale.it/eli/gu/2018/02/20/42/so/8/sg/pdf (accessed on 25 April 2022).
- Di Capua, G.; Peppoloni, S.; Amanti, M.; Cipolloni, C.; Conte, G. Site classification map of Italy based on surface geology. Geol. Soc. Eng. Geol. Spec. Publ. 2016, 27, 147–156. [Google Scholar] [CrossRef]
- Mori, F.; Mendicelli, A.; Moscatelli, M.; Romagnoli, G.; Peronace, E.; Naso, G. A new Vs30 map for Italy based on the seismic microzonation dataset. Eng. Geol. 2020, 275, 105745. [Google Scholar] [CrossRef]
- Beven, K.J.; Kirkby, M.J. A physically based, variable contributing area model of basin hydrology/Un modèle à base physique de zone d’appel variable de l’hydrologie du bassin versant. Hydrol. Sci. J. 1979, 24, 43–69. [Google Scholar] [CrossRef] [Green Version]
- Youd, T.L. Liquefaction, Flow, and Associated Ground Failure; US Geological Survey Circular 688; US Geological Survey: Reston, VA, USA, 1973.
- Obermeier, S.F. Use of liquefaction-induced features for paleoseismic analysis—An overview of how seismic liquefaction features can be distinguished from other features and how their regional distribution and properties of source sediment can be used to infer the location and strength of Holocene paleo-earthquakes. Eng. Geol. 1996, 44, 1–76. [Google Scholar]
- Swets, J.A. 1988 Measuring the accuracy of diagnostic systems. Science 1988, 240, 1285–1293. [Google Scholar] [CrossRef] [Green Version]
- Fawcett, T. An introduction to ROC analysis. Pattern Recogn. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]



| Year | Site | Magnitude |
|---|---|---|
| 1627 | Capitanata | Mw 6.66 ± 0.10 |
| 1361 | Subappennino Dauno | Mw 6.03 ± 0.46 |
| 1627 | Capitanata | Mw 5.80 ± 0.46 |
| 1627 | Capitanata | Mw 6.03 ± 0.46 |
| 1646 | Gargano | Mw 6.72 ± 0.25 |
| 1657 | Capitanata | Mw 5.96 ± 0.15 |
| 1731 | Tavoliere delle Puglie | Mw 6.33 ± 0.13 |
| 1857 | Capitanata | Mw 5.86 ± 0.12 |
| Main Variables | Distance to River (m) | Distance to Coast (m) | Slope (°) | Water Table Depth (m) | Distance to Water Body (m) | Lithology | PGA-VS30 | CTI | Weights |
|---|---|---|---|---|---|---|---|---|---|
| Distance to river (m) | 1 | 0.033 | |||||||
| Distance to coast (m) | 4 | 1 | 0.135 | ||||||
| Slope (°) | 1/2 | 1/4 | 1 | 0.031 | |||||
| Water table depth (m) | 7 | 2 | 6 | 1 | 0.232 | ||||
| Distance to water body (m) | 1 | 1/7 | 1/2 | 1/6 | 1 | 0.026 | |||
| Lithology | 9 | 2 | 8 | 1/2 | 8 | 1 | 0.213 | ||
| PGA-VS30 | 9 | 4 | 7 | 1 | 8 | 1 | 1 | 0.259 | |
| CTI | 2 | 1/4 | 4 | 1/3 | 3 | 1/3 | 1/4 | 1 | 0.071 |
| Consistency ratio: 0.042 < 0.1 (acceptable) | |||||||||
| Main Variables | Weights | Subclass | CR | Weights | Cumulative Weight |
|---|---|---|---|---|---|
| Lithology | 0.213 | 1 | 0.08 | 0.048 | 0.01 |
| 2 | 0.09 | 0.019 | |||
| 3 | 0.244 | 0.052 | |||
| 4 | 0.618 | 0.132 | |||
| PGA-VS30 | 0.259 | 0–0.15 | 0.02 | 0.09 | 0.023 |
| 0.15–0.20 | 0.11 | 0.028 | |||
| 0.20–0.25 | 0.19 | 0.049 | |||
| 0.25–0.30 | 0.29 | 0.075 | |||
| >0.30 | 0.33 | 0.085 | |||
| Distance to coast (m) | 0.135 | 0–500 | 0.033 | 0.8 | 0.108 |
| 500–1000 | 0.124 | 0.017 | |||
| >1000 | 0.075 | 0.010 | |||
| Distance to river (m) | 0.033 | 0–500 | 0.033 | 0.8 | 0.026 |
| 500–1000 | 0.124 | 0.004 | |||
| >1000 | 0.075 | 0.002 | |||
| Distance to water body (m) | 0.026 | 0–500 | 0.033 | 0.8 | 0.021 |
| 500–1000 | 0.124 | 0.002 | |||
| >1000 | 0.075 | 0.002 | |||
| Water table depth (m) | 0.232 | <0 | 0.012 | 0.191 | 0.044 |
| 0–10 | 0.175 | 0.041 | |||
| 10–15 | 0.175 | 0.041 | |||
| 15–20 | 0.167 | 0.039 | |||
| 20–25 | 0.151 | 0.035 | |||
| 25–30 | 0.074 | 0.019 | |||
| 30–40 | 0.032 | 0.007 | |||
| 40–50 | 0.02 | 0.005 | |||
| >50 | 0.017 | 0.004 | |||
| Slope (°) | 0.031 | 0–2 | 0.02 | 0.33 | 0.010 |
| 2–4 | 0.29 | 0.009 | |||
| 4–6 | 0.19 | 0.006 | |||
| 6–8 | 0.11 | 0.003 | |||
| >8 | 0.09 | 0.003 | |||
| CTI | 0.071 | 3–6 | 0.02 | 0.33 | 0.023 |
| 6–8 | 0.29 | 0.021 | |||
| 8–10 | 0.19 | 0.013 | |||
| 10–12 | 0.11 | 0.008 | |||
| >12 | 0.09 | 0.006 |
| Observed | |||
|---|---|---|---|
| Predicted | Liq pixel | No-Liq Pixel | |
| Liq pixel | 29 (TP) | 26 (FP) | |
| No-Liq Pixel | 2 (FN) | 109 (TN) | |
| Overall Accuracy | 83.1% | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zumpano, V.; Pisano, L.; Filice, F.; Ugenti, A.; de Lucia, D.; Wasowski, J.; Santaloia, F.; Lollino, P. Regional-Scale Seismic Liquefaction Susceptibility Mapping via an Empirical Approach Validated by Site-Specific Analyses. Geosciences 2022, 12, 215. https://doi.org/10.3390/geosciences12050215
Zumpano V, Pisano L, Filice F, Ugenti A, de Lucia D, Wasowski J, Santaloia F, Lollino P. Regional-Scale Seismic Liquefaction Susceptibility Mapping via an Empirical Approach Validated by Site-Specific Analyses. Geosciences. 2022; 12(5):215. https://doi.org/10.3390/geosciences12050215
Chicago/Turabian StyleZumpano, Veronica, Luca Pisano, Francesco Filice, Angelo Ugenti, Daniela de Lucia, Janusz Wasowski, Francesca Santaloia, and Piernicola Lollino. 2022. "Regional-Scale Seismic Liquefaction Susceptibility Mapping via an Empirical Approach Validated by Site-Specific Analyses" Geosciences 12, no. 5: 215. https://doi.org/10.3390/geosciences12050215
APA StyleZumpano, V., Pisano, L., Filice, F., Ugenti, A., de Lucia, D., Wasowski, J., Santaloia, F., & Lollino, P. (2022). Regional-Scale Seismic Liquefaction Susceptibility Mapping via an Empirical Approach Validated by Site-Specific Analyses. Geosciences, 12(5), 215. https://doi.org/10.3390/geosciences12050215








