Tsunamis Generated and Amplified by Atmospheric Pressure Waves Due to an Eruption over Seabed Topography
Abstract
:1. Introduction
2. Numerical Method and Conditions
2.1. Numerical Method and Atmospheric Pressure Wave Model
- (1)
- The phase velocity of a tsunami that effectively resonates with atmospheric pressure waves with the same traveling velocity over water with the same depth may be different.
- (2)
- In the tsunami-generation process, free-wave components may be evaluated differently.
- (3)
- In the tsunami-propagation process, tsunami profiles are calculated differently when traveling as free waves after leaving the atmospheric pressure waves.
2.2. Seabed Topography
3. Amplification of an Existing Tsunami Caught up or Passed by Atmospheric Pressure Waves over Seabed Topography
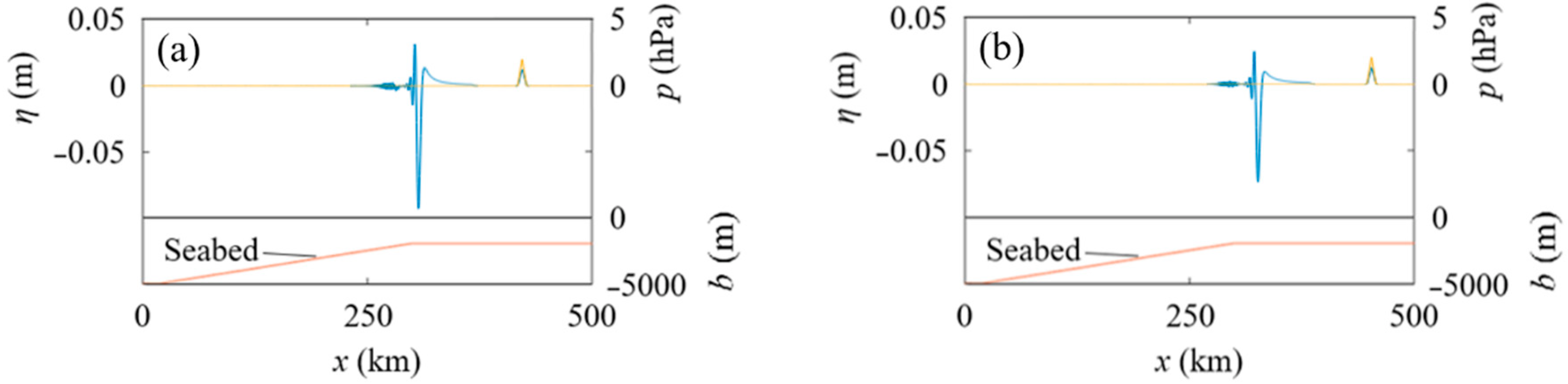
3.1. Amplification of an Existing Tsunami Caught up by an Atmospheric Pressure Wave over an Abrupt Change in Water Depth
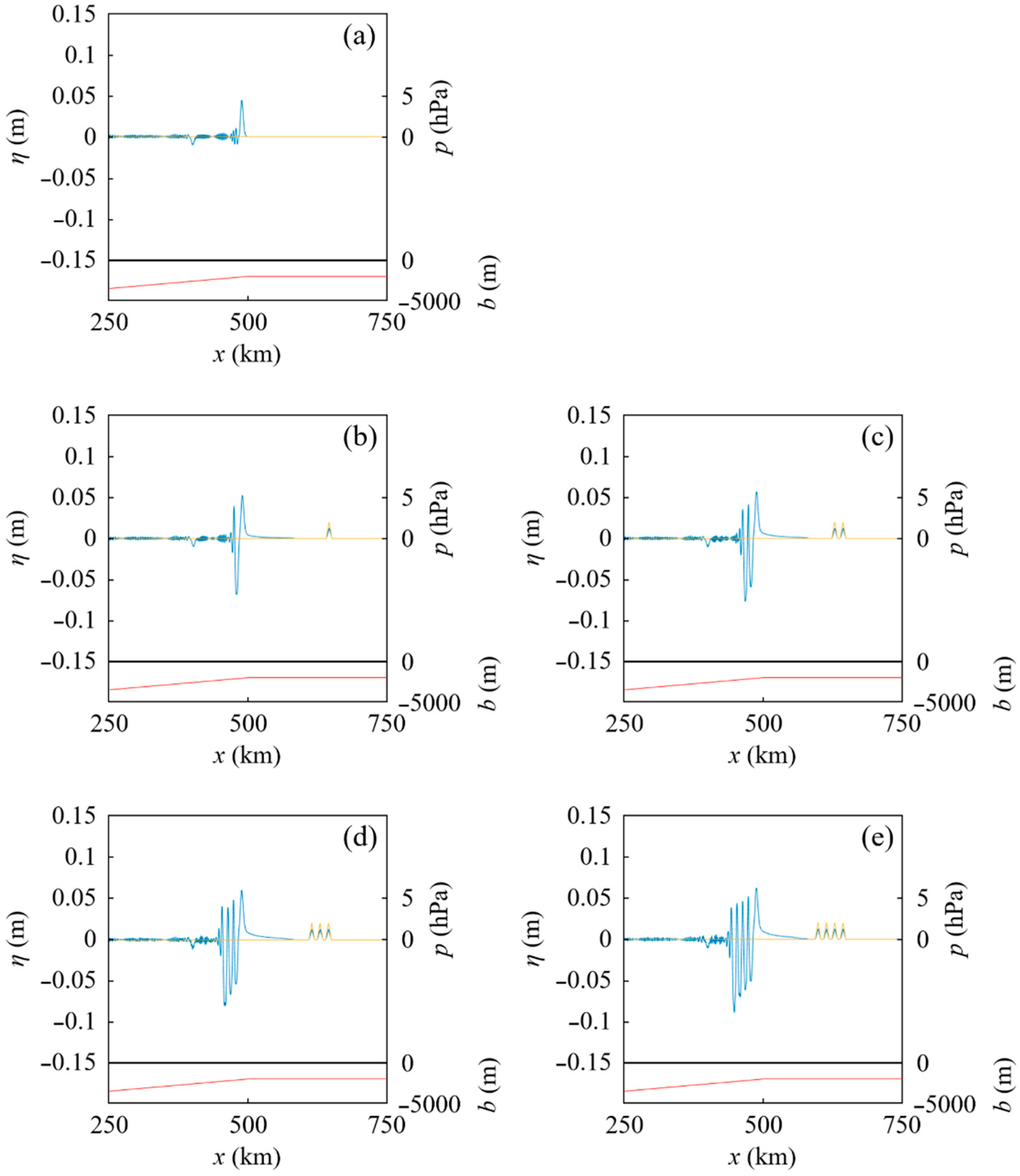
3.2. Amplification of an Existing Tsunami Passed by Atmospheric Pressure Waves over a Sloping Seabed
4. Tsunamis Generated by an Atmospheric Pressure Wave Train over Seabed Topography
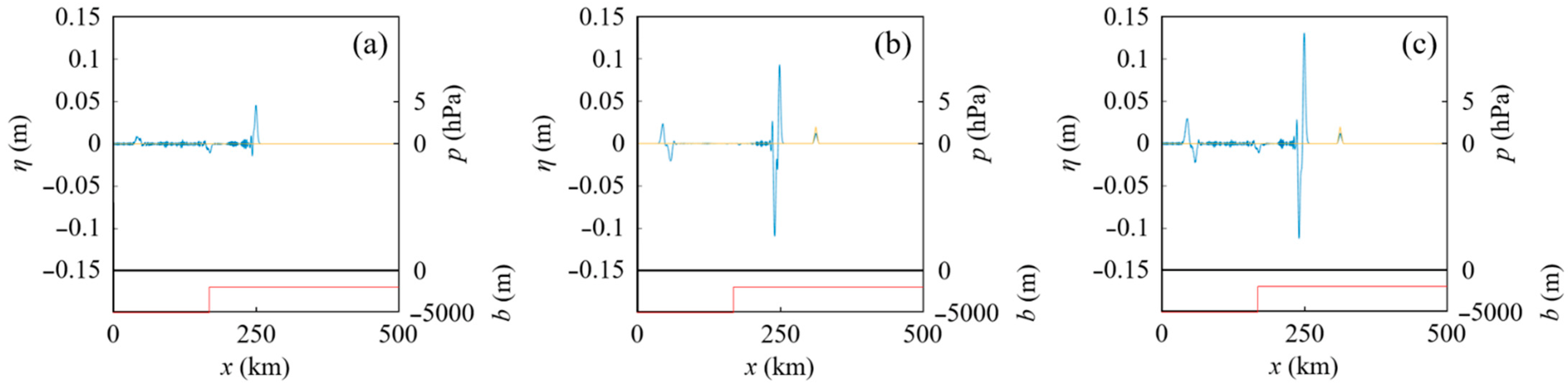
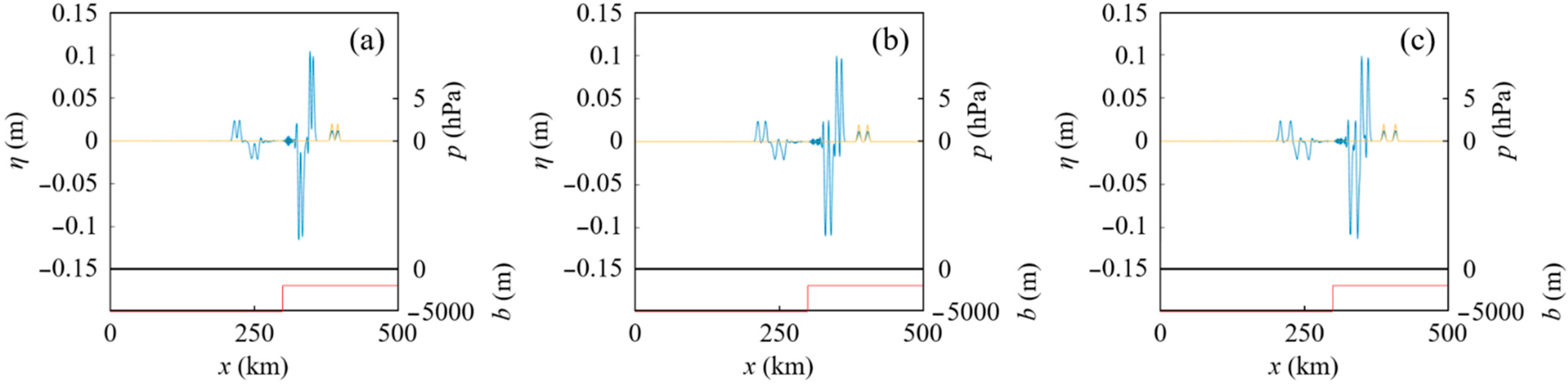
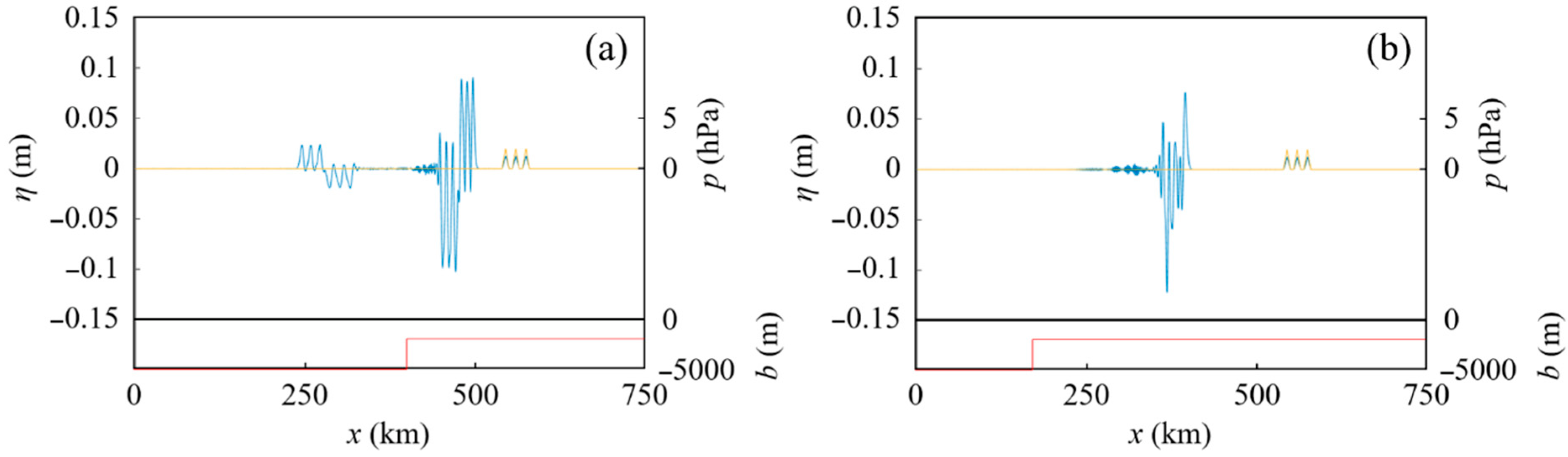
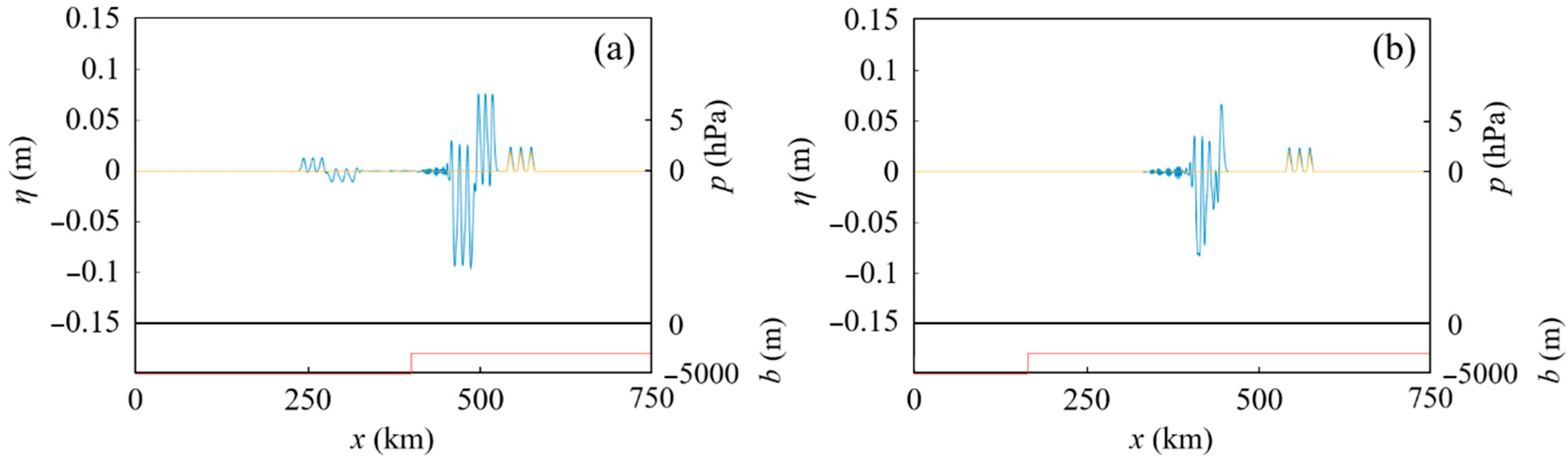
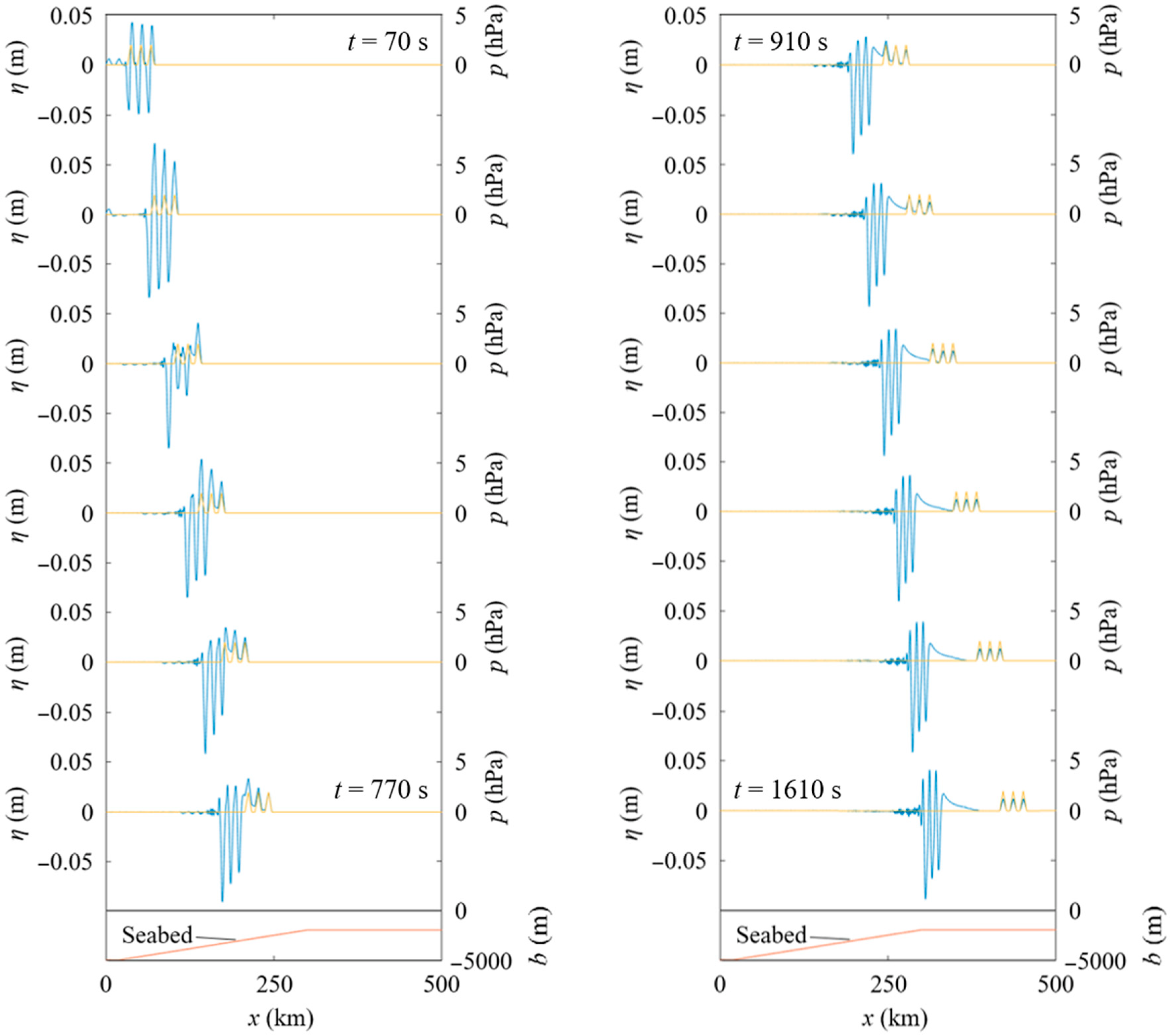
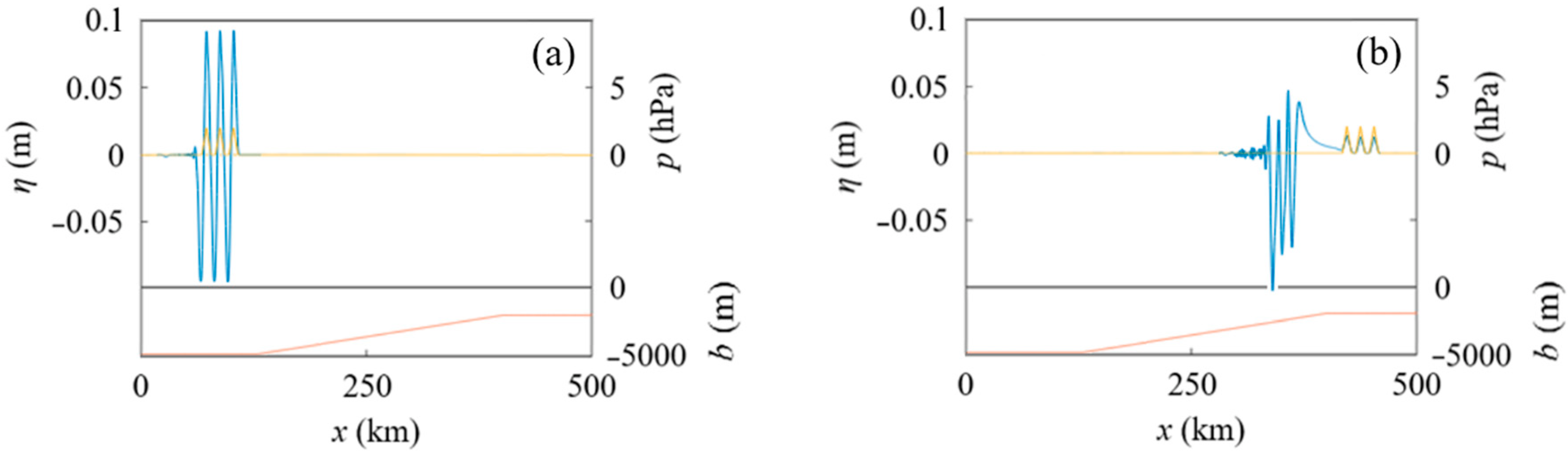
4.1. Tsunamis Generated by an Atmospheric Pressure Wave Train over a Stepped Seabed
4.1.1. Effect of the Interval of Atmospheric Pressure Waves on the Resultant Tsunamis over a Stepped Seabed
4.1.2. Effect of the Phase of a Tsunami-Generation Process Due to an Atmospheric Pressure Wave Train on the Resultant Tsunamis over a Stepped Seabed
4.1.3. Effect of the Difference between Two Water Depths over a Stepped Seabed on Tsunamis Generated by an Atmospheric Pressure Wave Train
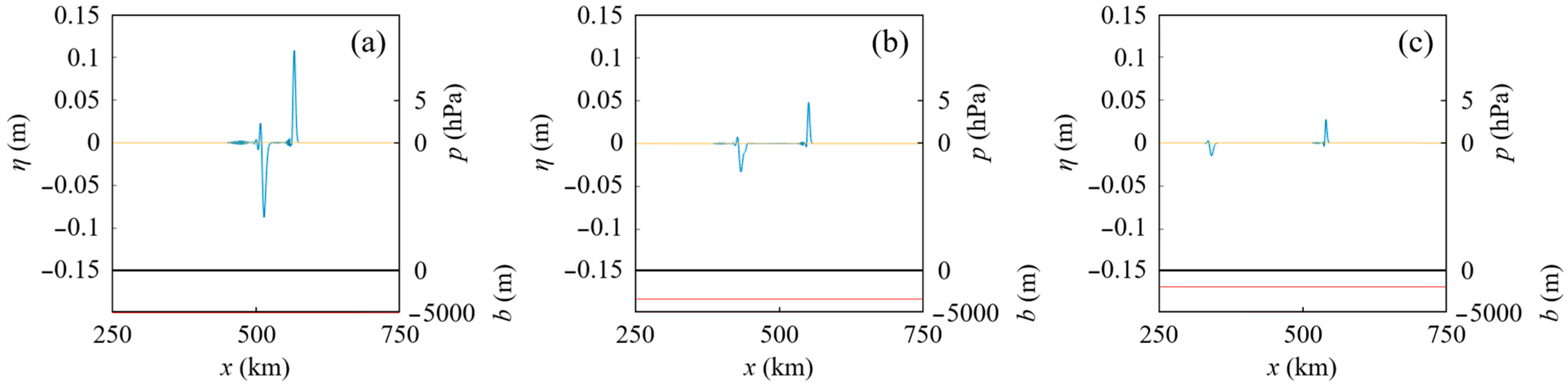
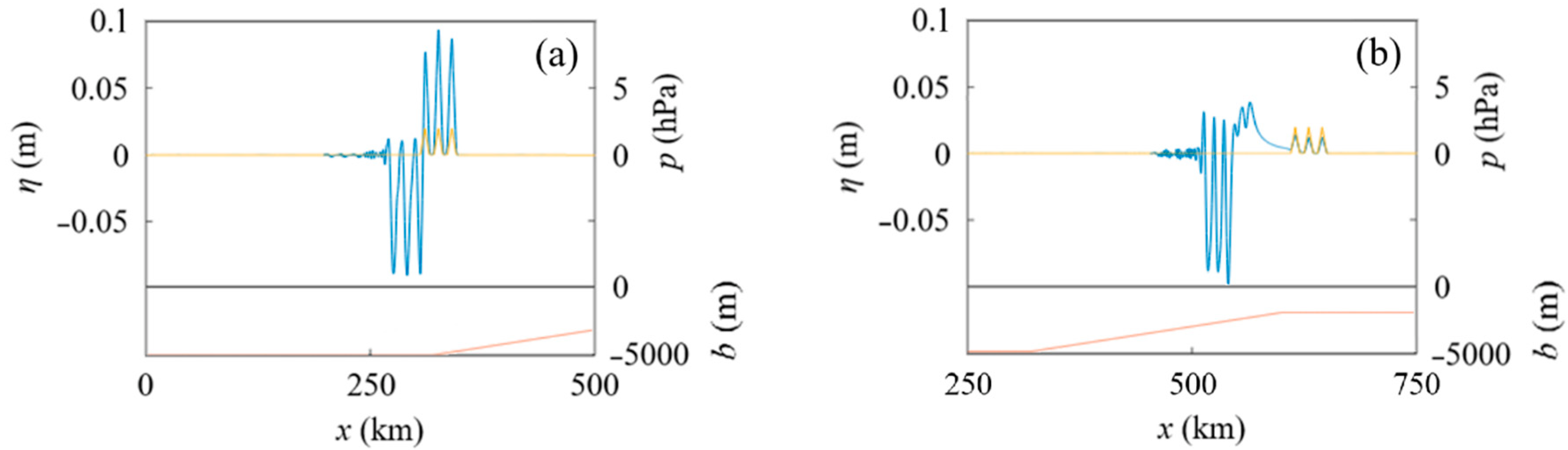
4.2. Tsunamis Generated by an Atmospheric Pressure Wave Train over a Sloping Seabed
5. Brief Discussion on a Tide-Gauge Record
6. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Japan Meteorological Agency Earthquake Volcano Department. On the tide level change due to the large eruption of Hunga Tonga-Hunga Ha’apai volcano near the Tonga Islands around 13:00 on January 15, 2022. Jpn. Meteorol. Agency Press Release 2022, 11, 23. Available online: https://www.jma.go.jp/jma/press/2201/16a/kaisetsu202201160200.pdf (accessed on 10 May 2022). (In Japanese).
- Proudman, J. The effects on the sea of changes in atmospheric pressure. Geophys. J. Int. 1929, 2, 197–209. [Google Scholar] [CrossRef]
- Kakinuma, T. Long-wave generation due to atmospheric pressure variation and harbor oscillation in harbors of various shapes and countermeasures against meteotsunamis. In Natural Hazards—Risk, Exposure, Response, and Resilience; Tiefenbacher, J., Ed.; InTech: London, UK, 2019; pp. 81–109. [Google Scholar] [CrossRef] [Green Version]
- Verbeek, R.D.M. Krakatau; Government Press: Batavia, IL, USA, 1885; 495p. [Google Scholar]
- Symons, G.J. (Ed.) The Eruption of Krakatoa, and Subsequent Phenomena, Report of the Krakatoa Committee of the Royal Society; Trübner and Co.: London, UK, 1888; 494p. [Google Scholar]
- Imamura, A. Observation of Krakatau explosion tsunami in Japan: Earthquake Chat (10). Earthquake 1934, 1, 158–160. (In Japanese) [Google Scholar]
- Harkrider, D.; Press, F. The Krakatoa air-sea waves: An example of pulse propagation in coupled systems. Geophys. J. R. Astron. Soc. 1967, 13, 149–159. [Google Scholar] [CrossRef] [Green Version]
- Garrett, C.J.R. A theory of the Krakatoa tide gauge disturbances. Tellus 1970, 22, 43–52. [Google Scholar] [CrossRef]
- Yokoyama, I. A geophysical interpretation of the 1883 Krakatau eruption. J. Volcanol. Geotherm. Res. 1981, 9, 359–378. [Google Scholar] [CrossRef]
- Yokoyama, I. A scenario of the 1883 Krakatau tsunami. J. Volcanol. Geotherm. Res. 1987, 34, 123–132. [Google Scholar] [CrossRef]
- Pelinovsky, E.; Choi, B.H.; Stromkov, A.; Didenkulova, I.; Kim, H.-S. Analysis of tide-gauge records of the 1883 Krakatau Tsunami. In Tsunamis: Case Studies and Recent Developments, Advances in Natural and Technological Hazards Research, 23; Satake, K., Ed.; Springer: Dordrecht, The Netherlands, 2005; pp. 57–77. [Google Scholar] [CrossRef]
- Soloviev, S.L. Basic data of tsunamis in the Pacific coast of USSR, 1937–1976. In A Study of Tsunamis in the Open Sea; Academii Nauk: Moscow, Russia, 1978; pp. 61–136. (In Russian) [Google Scholar]
- Kobayashi, T.; Kakinuma, T. Tsunamis propagated by airwaves generated by explosive volcanic eruptions: The 1883 Krakatau and the 1956 Bezymianny eruptions. In Proceedings of the International Meeting on Eruptive History and Informatics 2021-2, Fukuoka, Japan, 5–6 March 2022; pp. 93–105. (In Japanese). [Google Scholar]
- Sekizawa, S.; Kohyama, T. Meteotsunami observed in Japan following the Hunga Tonga eruption in 2022 investigated using a one-dimensional shallow-water model. SOLA 2022. preprint. [Google Scholar] [CrossRef]
- Tanioka, Y.; Yamanaka, Y.; Nakagaki, T. Characteristics of the deep sea tsunami excited offshore Japan due to the air wave from the 2022 Tonga eruption. Earth Planets Space 2022, 74, 61. [Google Scholar] [CrossRef]
- Kubota, T.; Saito, T.; Nishida, K. Global fast-traveling tsunamis driven by atmospheric Lamb waves on the 2022 Tonga eruption. Science 2022, eabo4364. [Google Scholar] [CrossRef] [PubMed]
- Pakoksung, K.; Suppasri, A.; Imamura, F. Tsunami Simulation (without Air-Sea Waves) on the 2022/01/15 Hunga Tonga-Hunga Ha’apai Submarine Volcanic Explosion. 2022. Available online: https://irides.tohoku.ac.jp/research/prompt_investigation/2022_tonga-vol-tsunami.html (accessed on 10 May 2022).
- Ramírez-Herrera, M.T.; Coca, O.; Vargas-Espinosa, V. Tsunami effects on the Coast of Mexico by the Hunga Tonga-Hunga Ha’apai volcano eruption, Tonga. Pure Appl. Geophys. 2022, 179, 1117–1137. [Google Scholar] [CrossRef] [PubMed]
- Carvajal, M.; Sepúlveda, I.; Gubler, A.; Garreaud, R. Worldwide signature of the 2022 Tonga volcanic tsunami. Geophys. Res. Lett. 2022, 49, e2022GL098153. [Google Scholar] [CrossRef]
- Hibiya, T.; Kajiura, K. Origin of the Abiki phenomenon (a kind of seiche) in Nagasaki Bay. J. Oceanogr. Soc. Jpn. 1982, 38, 172–182. [Google Scholar] [CrossRef]
- Vilibić, I.; Monserrat, S.; Rabinovich, A.; Mihanović, H. Numerical modelling of the destructive meteotsunami of 15 June, 2006 on the coast of the Balearic Islands. Pure Appl. Geophys. 2008, 165, 2169–2195. [Google Scholar] [CrossRef]
- Asano, T.; Yamashiro, T.; Nishimura, N. Field observations of meteotsunami locally called “abiki” in Urauchi Bay, Kami-Koshiki Island, Japan. Nat. Hazards 2012, 64, 1685–1706. [Google Scholar] [CrossRef]
- Bailey, K.E.; DiVeglio, C.; Welty, A. An examination of the June 2013 East Coast meteotsunami captured by NOAA observing systems. NOAA Tech. Rep. NOS CO-OPS 2014, 79, 42. Available online: https://repository.library.noaa.gov/view/noaa/14435 (accessed on 10 May 2022).
- Tanaka, K.; Ito, D. Multiscale meteorological systems resulted in meteorological tsunamis. In Tsunami; Mokhtari, M., Ed.; InTech: Rijeka, Balkans, 2016; pp. 13–33. [Google Scholar] [CrossRef] [Green Version]
- Iwase, H.; Mikami, T.; Goto, C. Practical tsunami numerical simulation model by use of non-linear dispersive long wave theory. J. JSCE 1998, 1998, 119–124. [Google Scholar] [CrossRef] [Green Version]
- Peregrine, D.H. Long waves on a beach. J. Fluid Mech. 1967, 27, 815–827. [Google Scholar] [CrossRef]
- Baba, T.; Allgeyer, S.; Hossen, J.; Cummins, P.R.; Tsushima, H.; Imai, K.; Yamashita, K.; Kato, T. Accurate numerical simulation of the far-field tsunami caused by the 2011 Tohoku earthquake, including the effects of Boussinesq dispersion, seawater density stratification, elastic loading, and gravitational potential change. Ocean Model. 2017, 111, 46–54. [Google Scholar] [CrossRef]
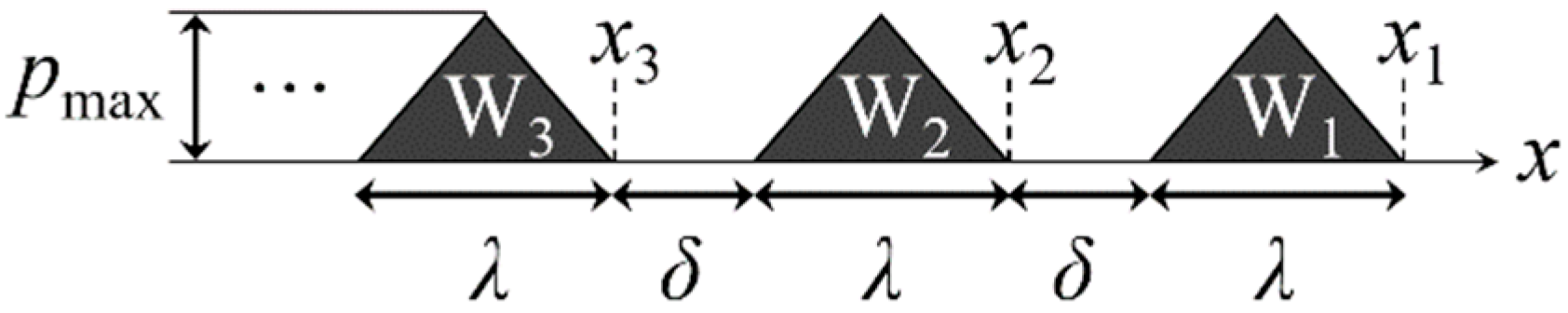



| Case | Existing Tsunami TLamb | Number of Atmospheric Pressure Waves | Interval of Atmospheric Pressure Waves, δ | Initial Position of the nth Atmospheric Pressure Wave, xn | Seabed Topography | Still-Water Depth in the Onshore Shallowest Area, hon | Offshore End Location of the Onshore Shallowest Area, xon | Offshore End Location of the Slope, xslope |
|---|---|---|---|---|---|---|---|---|
| A | Presence | 0 | — | x1 = 55 km | Stepped | 2000 m | 170 km | — |
| 1 | ||||||||
| Absence | 1 | |||||||
| B | Presence | 0 | — | x1 = 55 km | Partially Sloping β = 6.25 × 10−3 | 2000 m | 500 km | 20 km |
| 1 | ||||||||
| 2 | 5 km | |||||||
| 3 | ||||||||
| 4 | ||||||||
| C | Absence | 2 | 0 km 5 km 10 km | x2 = 40 km | Stepped | 2000 m | 300 km | — |
| D | Absence | 3 | 5 km | x1 = 55 km | Stepped | 2000 m | 170 km 400 km | — |
| E | Absence | 3 | 5 km | x1 = 55 km | Stepped | 3000 m | 170 km 400 km | — |
| F | Absence | 3 | 5 km | x1 = 55 km | Partially Sloping β = 1.07 × 10−2 | 2000 m | 300 km | 20 km |
| G | Absence | 1 | — | x1 = 55 km | Flat | 2000 m 3500 m 5000 m | 0 km | — |
| H | Absence | 1 | — | x1 = 25 km, x1 = 55 km | Partially Sloping β = 1.07 × 10−2 | 2000 m | 300 km | 20 km |
| I | Absence | 3 | 5 km | x1 = 55 km | Partially Sloping β = 1.07 × 10−2 | 2000 m | 400 km | 120 km |
| 600 km | 320 km |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kakinuma, T. Tsunamis Generated and Amplified by Atmospheric Pressure Waves Due to an Eruption over Seabed Topography. Geosciences 2022, 12, 232. https://doi.org/10.3390/geosciences12060232
Kakinuma T. Tsunamis Generated and Amplified by Atmospheric Pressure Waves Due to an Eruption over Seabed Topography. Geosciences. 2022; 12(6):232. https://doi.org/10.3390/geosciences12060232
Chicago/Turabian StyleKakinuma, Taro. 2022. "Tsunamis Generated and Amplified by Atmospheric Pressure Waves Due to an Eruption over Seabed Topography" Geosciences 12, no. 6: 232. https://doi.org/10.3390/geosciences12060232
APA StyleKakinuma, T. (2022). Tsunamis Generated and Amplified by Atmospheric Pressure Waves Due to an Eruption over Seabed Topography. Geosciences, 12(6), 232. https://doi.org/10.3390/geosciences12060232






