Active Triclinic Transtension in a Volcanic Arc: A Case of the El Salvador Fault Zone in Central America
Abstract
:1. Introduction
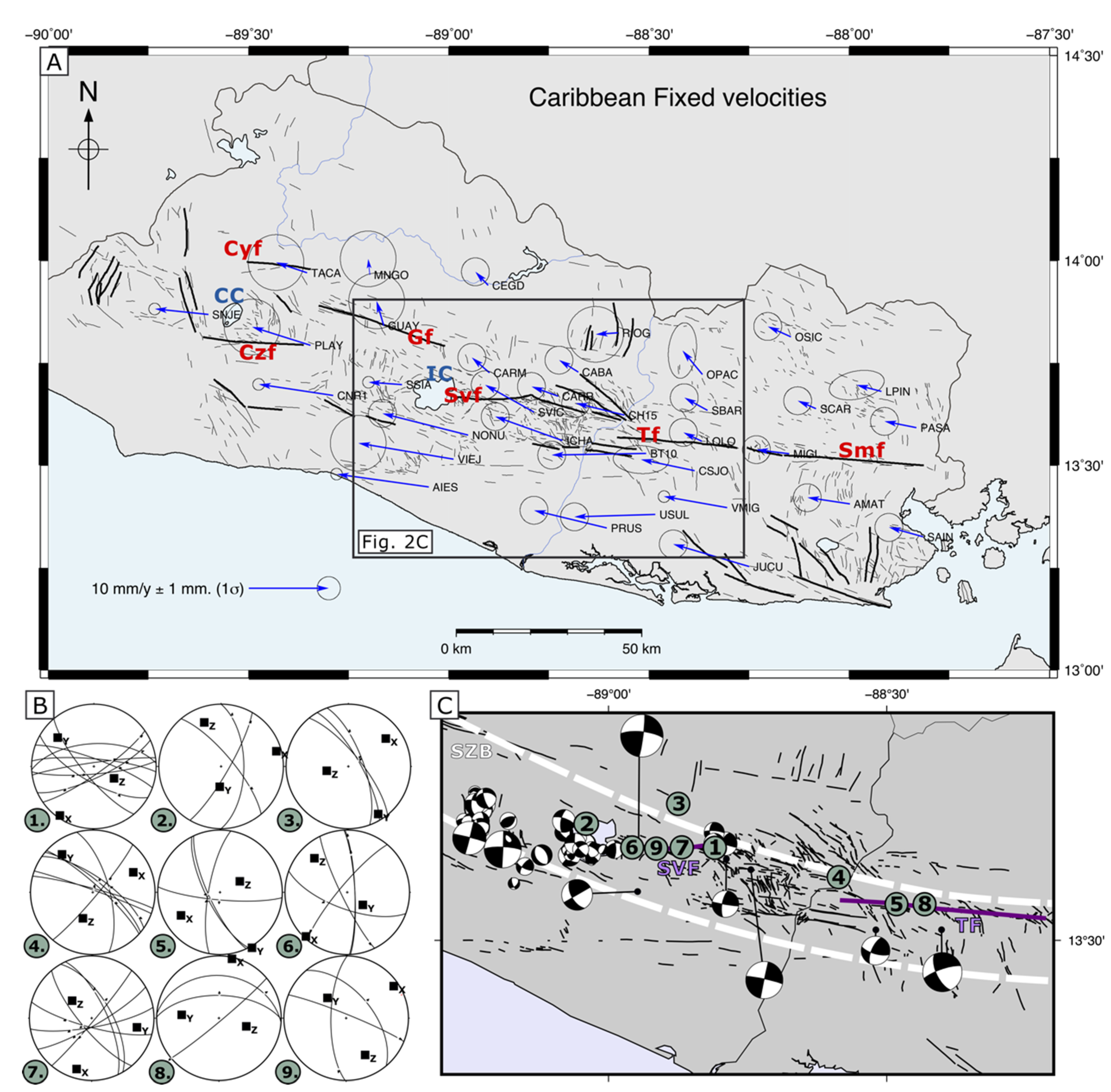
2. Tectonic Frame
3. Methodology
3.1. Incremental Strain Constriction
3.1.1. Infinitesimal Strain Ellipsoid from Fault Slickensides
3.1.2. Incremental Strain Ellipsoid from Earthquake Focal Mechanisms
3.1.3. Incremental Strain Ellipses from GPS Data Sites
Flow Apophyses Constriction
Strain Rate Tensors
3.2. Finite Strain Constriction
3.3. Protocol for Model Application
3.3.1. Data Ranges
3.3.2. Applied Protocol Steps
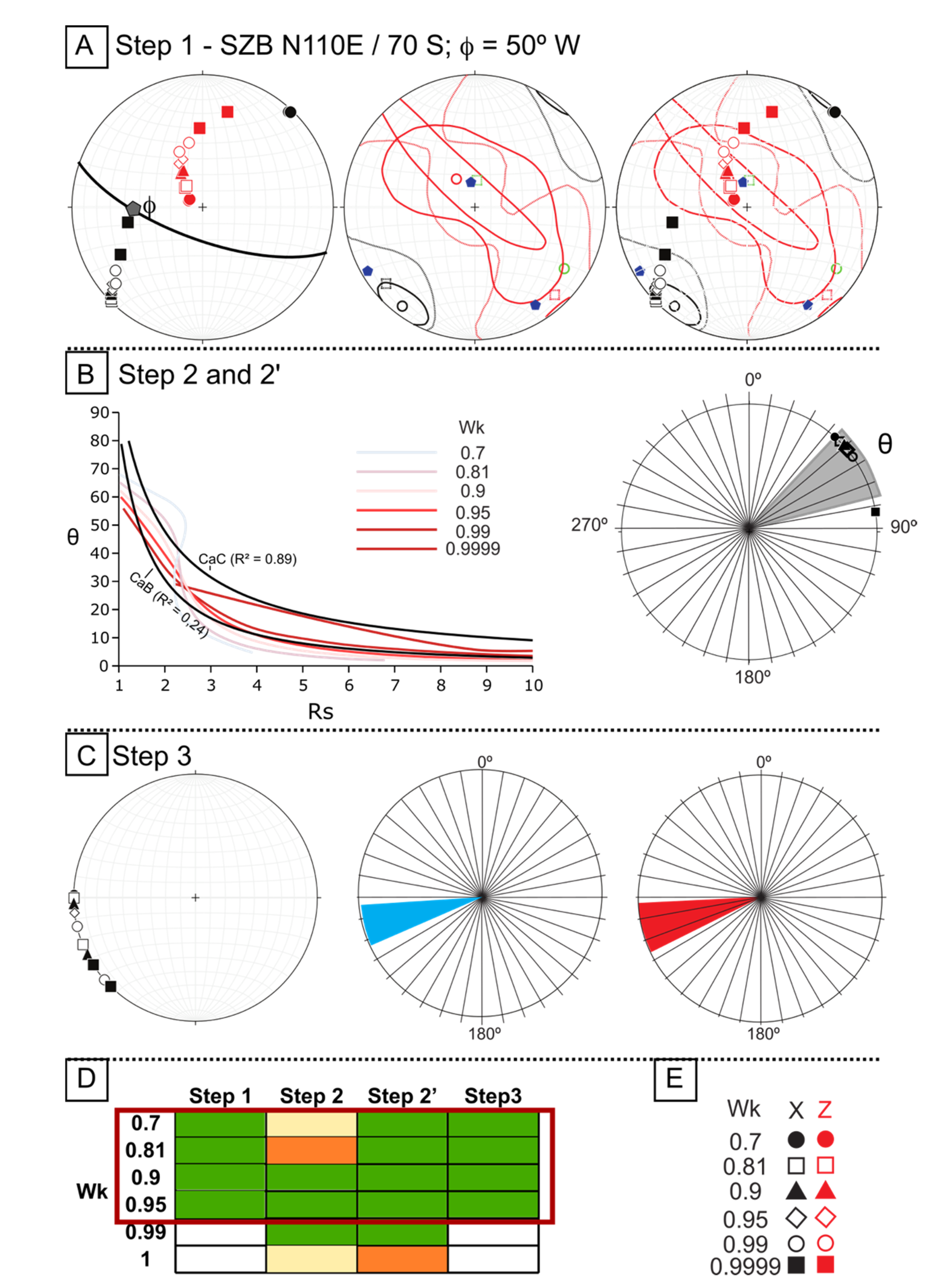
- Step 1: Comparison, in equal area projection, of the X and Z axes of the infinitesimal strain against model predictions for all the considered parameters described above. We consider it to be a good fit when model predictions are projected within the confidence interval both for the faults and focal mechanisms and are close to their mean values. We consider it to be a fair fit in the same situation when the model predictions are not close to the mean values. We consider it to be a poor fit when model predictions are out of the confidence areas of the focal mechanisms or faults. Finally, we consider that there is no fit when the model predictions are out of the confidence areas for both data at the same time (Figure 6A).
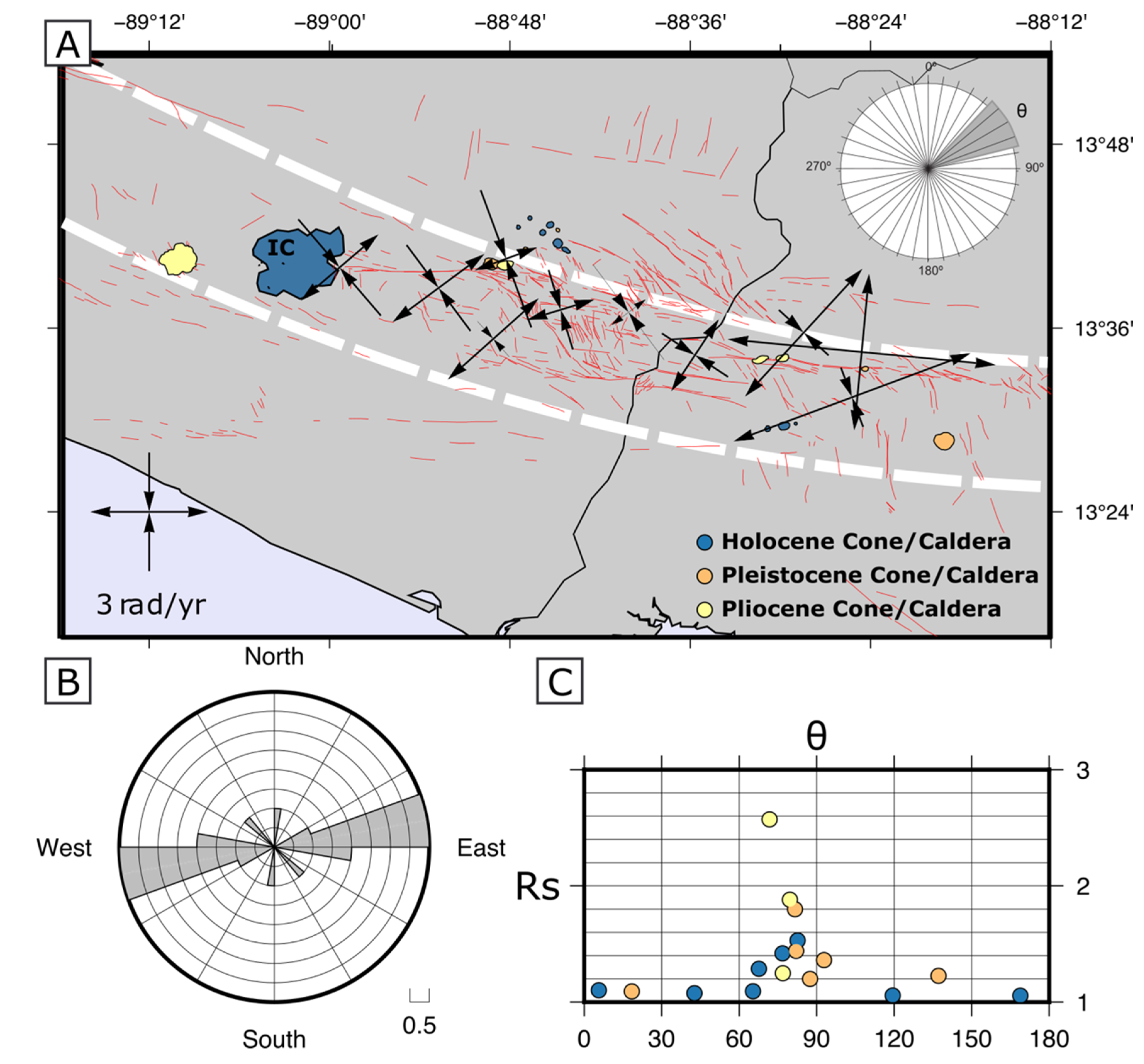
- Step 2: This step was originally designed by [54] to compare the Rs vs. θ curves predicted by the model with the corresponding values obtained from nature. In our case, the volcanic edifices and caldera shapes were used for this purpose. However, the volcanic edifice geometry might not provide discriminating information to constrain the horizontal strain ellipse (as we will discuss below), and, for this reason, we had to adapt the protocol and complement this step with an intermediate step named 2’ focused on incremental strain (and explained further below). We consider it to be a good fit when the model predicted curves are constrained between the ones obtained from the volcanic edifices; fair fit when adapted to the curve geometry inferred from all the edifices against the obtained from Carbonera Caldera (CaC); and no fit when they cross both curves (Figure 6B).
- Step 2’: It is the comparison of the main axes of incremental strain predicted by the model on a horizontal section of the ellipsoid against the strain rate tensors measured by GPS sites obtained within the shear zone from the Delaunay triangulation and the [67] equations, published in [17]. In this study, we use Step 2’ in order to complement the original Step 2 due to the available information. We consider it to be a good fit when the range of values predicted by the model is within the measured and one standard deviation. We consider it to be a fair fit when the range exceeds 5° from one standard deviation, and we have considered it to be no fit when the values predicted by the model are out of this range (Figure 6C).
- Step 3: This step is the comparison of the values of the divergence angle predicted by the model (oblique flow apophyses) for the range of values of the model yielding an acceptable fit in Step 1, with the mean vectors geodetically measured considering the northern block fixed. We have considered them to be good, regular or poor fit when there is a total, partial or null overlap between the model values and the GPS values measured in the closest environment, respectively (Figure 6C).
4. Results
5. Discussion
5.1. On the Data Uncertainty and the Importance of the Incremental Strain
5.2. On the Contraction, Vertical Sink or “Sinkage”
5.3. On the Triclinic Strain Nature and the Tectonic History
6. Conclusions
- The flow type in the CAVA crossing El Salvador is triclinic, located in the simple-shear-dominated strain field or close to the transition between pure and simple shear (Wk ≥ 0.81). Depending on the strike of the shear zone, the simple shear obliquity (φ) varies from low to middle values; that is, a deflection (ζ) angle between 40° and 70°.
- Triclinic transtension is explained if we consider the tectonic evolution of the ESFZ, preceded by an extensional stage that generated south dipping faults, and, as a consequence, the current divergence responsible for the transtension reactivated inclined planes resulting in the triclinic nature of the strain.
- The deformation features in El Salvador make the constrain of very small deformation, nearly infinitesimal, crucial against the rather scarce evidence of finite strain. However, it is probable that the results might be narrowed down if balanced cross sections in several orientations were available or if data were obtained from fault rocks, veins or dikes that recorded progressive strain.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Harland, W.B. Tectonic transpression in Caledonian Spitsbergen. Geol. Mag. 1971, 108, 27–41. [Google Scholar] [CrossRef]
- Sanderson, D.J.; Marchini, W.R.D. Transpression. J. Struct. Geol. 1984, 6, 449–458. [Google Scholar] [CrossRef]
- Fossen, H.; Tikoff, B. The deformation matrix for simultaneous simple shearing, pure shearing and volume change, and its application to transpression-transtension tectonics. J. Struct. Geol. 1993, 15, 413–422. [Google Scholar] [CrossRef]
- Jiang, D.; Williams, P.F. High-strain zones: A unified model. J. Struct. Geol. 1998, 20, 1105–1120. [Google Scholar] [CrossRef]
- Lin, S.; Jiang, D. Using along-strike variation in strain and kinematics to define the movement direction of curved transpressional shear zones: An example from northwestern Superior Province, Manitoba. Geology 2001, 29, 767–770. [Google Scholar] [CrossRef]
- Lin, S.; Jiang, D.; Williams, P.F. Transpression (or transtension) zones of triclinic symmetry: Natural example and theoretical modeling. In Continental Transpression and Transtension Tectonics; Holdsworth, R.E., Strachan, R.A., Dewey, J.F., Eds.; Special Publication; Geological Society: London, UK, 1998; Volume 135, pp. 41–57. [Google Scholar]
- Czeck, D.M.; Hudleston, P.J. Testing models for obliquely plunging lineations in transpression: A natural example and theoretical discussion. J. Struct. Geol. 2003, 25, 959–982. [Google Scholar] [CrossRef]
- Díaz-Azpiroz, M.D.; Fernández, C. Kinematic analysis of the southern Iberian shear zone and tectonic evolution of the Acebuches metabasites (SW Variscan Iberian Massif). Tectonics 2005, 24, TC3010. [Google Scholar] [CrossRef]
- Jones, R.R.; Holdsworth, R.; Clegg, P.; McCaffrey, K.; Tavarnelli, E. Inclined transpression. J. Struct. Geol. 2004, 26, 1531–1548. [Google Scholar] [CrossRef]
- Fernández, C.; Díaz-Azpiroz, M.D. Triclinic transpression zones with inclined extrusion. J. Struct. Geol. 2009, 31, 1255–1269. [Google Scholar] [CrossRef]
- Toy, V.; Norris, R.; Prior, D.; Walrond, M.; Cooper, A. How do lineations reflect the strain history of transpressive shear zones? The example of the active Alpine Fault zone, New Zealand. J. Struct. Geol. 2013, 50, 187–198. [Google Scholar] [CrossRef]
- Díaz-Azpiroz, M.; Barcos, L.; Balanyá, J.C.; Fernández, C.; Expósito, I.; Czeck, D.M. Applying a general triclinic transpression model to highly partitioned brittle-ductile shear zones: A case study from the Torcal de Antequera massif, external Betics, southern Spain. J. Struct. Geol. 2014, 68, 316–336. [Google Scholar] [CrossRef]
- Alonso-Henar, J.; Fernánadez, C.; Martínez-Díaz, J.J. Application of the analytic model of general triclinic trans- pression with oblique extrusion to an active deformation zone: The Alhama de Murcia Fault (SE Iberian Peninsula). J. Struct. Geol. 2020, 130, 103924. [Google Scholar] [CrossRef]
- Yang, R.; Jiang, D.; Lu, L.X. Constrictional strain and linear fabrics as a result of deformation partitioning: A multiscale modeling investigation and tectonic significance. Tectonics 2019, 38, 2829–2849. [Google Scholar] [CrossRef]
- Martínez-Díaz, J.; Álvarez-Gómez, J.; Benito, B.; Hernández, D. Triggering of destructive earthquakes in El Salvador. Geology 2004, 32, 65–68. [Google Scholar] [CrossRef] [Green Version]
- Alonso-Henar, J.; Schreurs, G.; Martínez-Díaz, J.J.; Álvarez-Gómez, J.A.; Villamor, P. Neotectonic development of the El Salvador Fault Zone and implications for deformation in the Central America Volcanic Arc. Insights from 4D analogue modeling experiments. Tectonics 2015, 34, 133–151. [Google Scholar] [CrossRef] [Green Version]
- Staller, A.; Martínez-Díaz, J.J.; Benito, B.; Alonso-Henar, J.; Hernández, D.; Hernández-Rey, R.; Díaz, M. Present-day crustal deformation along the El Salvador Fault Zone from ZFESNet GPS network. Tectonophysics 2016, 670, 66–81. [Google Scholar] [CrossRef] [Green Version]
- Alonso-Henar, J.; Álvarez-Gómez, J.A.; Martínez-Díaz, J.J. Constraints for the recent tectonics of the El Salvador Fault Zone, Central America Volcanic Arc, from morphotectonic analysis. Tectonophysics 2014, 623, 1–13. [Google Scholar] [CrossRef]
- Garibaldi, N.; Tikoff, B.; Hernandez, W. Neotectonic deformation within an extensional stepover in El Salvador magmatic arc, Central America: Implication for the interaction of arc magmatism and deformation. Tectonophysics 2016, 693, 327–339. [Google Scholar] [CrossRef]
- Rogers, R.D.; Mann, P.; Emmet, P.A. Tectonic Terranes of the Chortis Block Based on Integration of Regional Aeromagnetic and Geologic data, en Geologic and Tectonic De-velopment of the Caribbean Plate in Northern Central America; Mann, P.P., Ed.; GSA Special Paper; Geological Society of America: Boulder, CO, USA, 2007; Volume 428, pp. 65–88. [Google Scholar]
- Plafker, G. Tectonic Aspects of the Guatemala Earthquake of 4 February 1976. Science 1976, 193, 1201–1208. [Google Scholar] [CrossRef]
- Guzmán-Speziale, M.; Molina, E. Seismicity and seismically active faulting of Guatemala: A review. J. South Am. Earth Sci. 2022, 115, 103740. [Google Scholar] [CrossRef]
- Garnier, B.; Tikoff, B.; Flores, O.; Jicha, B.; DeMets, C.; Cosenza-Muralles, B.; Hernandez, W.; Greene, D. Deformation in western Guatemala associated with the NAFCA (North America-Central American Forearc-Caribbean) triple junction: Neotectonic strain localization into the Guatemala City graben. Tectonics 2022, 41, e2021TC006739. [Google Scholar] [CrossRef]
- Muehlberger, W.R.; Ritchie, A.W. Caribbean–Americas plate boundary in Guatemala and southern Mexico as seen on Skylab IV orbital photography. Geology 1975, 3, 232–235. [Google Scholar] [CrossRef]
- Gordon, M.B.; Muehlberger, W.R. Rotation of the Chortís block causes dextral slip on the Guayape fault. Tectonics 1994, 13, 858–872. [Google Scholar] [CrossRef]
- Garnier, B.; Tikoff, B.; Flores, O.; Jicha, B.; DeMets, C.; Cosenza-Muralles, B.; Hernandez, D.; Marroquin, G.; Mixco, L.; Hernandez, W. An integrated structural and GPS study of the Jalpatagua fault, southeastern Guatemala. Geosphere 2021, 17, 201–225. [Google Scholar] [CrossRef]
- Corti, G.; Carminati, E.; Mazzarini, F.; Garcia, M.O. Active strike-slip faulting in El Salvador, Central America. Geology 2005, 33, 989–992. [Google Scholar] [CrossRef]
- Canora, C.; Martínez-Díaz, J.J.; Villamor, P.; Berryman, K.; Álvarez-Gómez, J.A.; Pullinger, C.; Capote, R. Geological and seismological analysis of the Mw 6.6 13th February 2001 El Salvador earthquake: Evidence for surface rupture and implications for seismic hazard. Bull. Seismol. Soc. Am. 2010, 100, 2873–2890. [Google Scholar] [CrossRef] [Green Version]
- McBirney, A.R.; Williams, H. Volcanic History of Nicaragua; University of California Publications in Geological Sciences: Berkeley, CA, USA, 1965; Volume 55, p. 73. [Google Scholar]
- Wyk de Vries, B.V. Tectonics and magma evolution of Nicaraguan volcanic systems. Ph.D. Thesis, Open University, Milton Keynes, UK, 1993. [Google Scholar]
- La Femina, P.C.; Dixon, T.H.; Strauch, W. Bookshelf faulting in Nicaragua. Geology 2002, 30, 751–754. [Google Scholar] [CrossRef]
- DeMets, C. A new estimate for present-day Cocos-Caribbean Plate motion: Implications for slip along the Central American Volcanic Arc. Geophys. Res. Lett. 2001, 28, 4043–4046. [Google Scholar] [CrossRef] [Green Version]
- Guzmán-Speziale, M.; Gómez, J.M. Comment on “A new estimate for present-day Cocos-Caribbean plate motion: Implications for slip along the Central American volcanic arc” by Charles DeMets. Geophys. Res. Lett. 2002, 29, 1945. [Google Scholar] [CrossRef]
- Álvarez-Gómez, J.A.; Meijer, P.T.; Martínez-Díaz, J.J.; Capote, R. Constraints from finite element modeling on the active tectonics of northern Central America and the Middle America Trench. Tectonics 2008, 27, TC1008. [Google Scholar] [CrossRef]
- Guzmán-Speziale, M.; Valdés-González, C.; Molina, E.; Gómez, J.M. Seismic activity along the central america volcanic arc: Is it related to subduction of the Cocos plate? Tectonophysics 2005, 400, 241–254. [Google Scholar] [CrossRef]
- Norabuena, E.; Dixon, T.H.; Schwartz, S.; Deshon, H.; Newman, A.; Protti, M.; Gonzalez, V.; Dorman, L.; Flueh, E.R.; Lundgren, P.; et al. Geodetic and seismic constraints on some seismogenic zone processes in Costa Rica. J. Geophys. Res. Earth Surf. 2004, 109. [Google Scholar] [CrossRef]
- LaFemina, P.; Dixon, T.H.; Govers, R.; Norabuena, E.; Turner, H.; Saballos, A.; Mattioli, G.; Protti, M.; Strauch, W. Fore-arc motion and Cocos Ridge collision in Central America. Geochem. Geophys. Geosyst. 2009, 10. [Google Scholar] [CrossRef] [Green Version]
- Alvarez-Gomez, J.; Staller-Vazquez, A.; Martínez-Díaz, J.; Canora, C.; Alonso-Henar, J.; Insúa-Arévalo, J.; Bejar-Pizarro, M. Push-pull Driving of the Central America Forearc in the Context of the Cocos-Caribbean-North America Triple Junction. Sci. Rep. 2019, 9, 11164. [Google Scholar] [CrossRef] [Green Version]
- Rodriguez, M.; DeMets, C.; Rogers, R.; Tenorio, C.; Hernandez, D. A GPS and modelling study of deformation in northern Central America. Geophys. J. Int. 2009, 178, 1733–1754. [Google Scholar] [CrossRef] [Green Version]
- Alvarado, D.; DeMets, C.; Tikoff, B.; Hernández, D.; Wawrzyniec, T.; Pullinger, C.; Mattioli, G.; Turner, H.; Rodriguez, M.; Correa-Mora, F. Forearc motion and deformation between El Salvador and Nicaragua: GPS, seismic, structural, and paleomagnetic observations. Lithosphere 2011, 3, 3–21. [Google Scholar] [CrossRef] [Green Version]
- Correa-Mora, F.; DeMets, C.; Alvarado, D.; Turner, H.L.; Mattioli, G.; Hernandez, D. GPS-derived coupling estimates for Central America subduction zone and volcanic arc faults: El Salvador, Honduras and Nicaragua. Geophys. J. Int. 2009, 179, 1279–1291. [Google Scholar] [CrossRef] [Green Version]
- Franco, A.; Lasserre, C.; Lyon-Caen, H.; Kostoglodov, V.; Molina, E.; Guzman-Speziale, M.; Monterosso, D.; Robles, V.; Figueroa, C.; Amaya, W.; et al. Fault kinematics in northern Central America and coupling along the subduction interface of the Cocos Plate, from GPS data in Chiapas (Mexico), Guatemala and El Salvador. Geophys. J. Int. 2012, 189, 1223–1236. [Google Scholar] [CrossRef] [Green Version]
- DeMets, C.; Gordon, R.G.; Argus, D.F. Geologically current plate motions. Geophys. J. Int. 2010, 181, 1–80. [Google Scholar] [CrossRef] [Green Version]
- Siebert, L.; Simkin, T. 2002–Present. Volcanoes of the World: An Illustrated Catalog of Holocene Volcanoes and Their Eruptions. Smithsonian Institution. Global Volcanism Program Digital Information Series, GVP-3. Available online: http://www.volcano.si.edu (accessed on 27 March 2022).
- Agostini, S.; Corti, G.; Doglioni, C.; Carminati, E.; Innocenti, F.; Tonarini, S.; Manetti, P.; Di Vincenzo, G.; Montanari, D. Tectonic and magmatic evolution of the active volcanic front in El Salvador: Insight into the Berlín and Ahuachapán geothermal areas. Geothermics 2006, 35, 368–408. [Google Scholar] [CrossRef]
- Funk, J.; Mann, P.; McIntosh, K.; Stephens, J. Cenozoic tectonics of the Nicaraguan depression, Nicaragua, and Median Trough, El Salvador, based on seismic-reflection profiling and remote-sensing data. GSA Bull. 2009, 121, 1491–1521. [Google Scholar] [CrossRef]
- Canora, C.; Villamor, P.; Martínez-Díaz, J.J.; Berryman, K.; Álvarez-Gómez, J.A.; Capote, R.; Hernández, W. Paleoseismic analysis of the San Vicente segment of the El Salvador Fault Zone, El Salvador, Central America. Geol. Acta 2012, 10, 103–123. [Google Scholar]
- Canora, C.; Martínez-Díaz, J.; Villamor, P.; Staller, A.; Berryman, K.; Alvarez-Gomez, J.; Capote, R.; Diaz, M. Structural evolution of the El Salvador Fault Zone: An evolving fault system within a volcanic arc. J. Iber. Geol. 2014, 40, 471–488. [Google Scholar] [CrossRef] [Green Version]
- Alonso-Henar, J.; Álvarez-Gómez, J.A.; Martínez-Díaz, J.J. Neogene-quaternary evolution from transpressional to transtensional tectonics in Northern Central America controlled by cocos: Caribbean subduction coupling change. J. Iber. Geol. 2017, 43, 519–538. [Google Scholar] [CrossRef]
- Cepeda, J.M.; Benito, M.B.; Burgos, E.A. Strong-Motion Characteristics of January and February 2001 Earthquakes in El Salvador. In Natural Hazards in El Salvador; Rose, W.I., Bommer, J.J., López, D.L., Carr, M.J., Major, J.J., Eds.; Geological Society of America Special Paper: Boulder, CO, USA, 2014; Volume 375, pp. 405–421. [Google Scholar]
- Alonso-Henar, J.; Benito, B.; Staller, A.; Álvarez-Gómez, J.A.; Martínez-Díaz, J.J.; Canora, C. Large-magnitude crustal seismic sources in El Salvador and deterministic hazard scenarios. Eng. Geol. 2018, 243, 70–83. [Google Scholar] [CrossRef]
- Martínez-Díaz, J.J.; Alvarez-Gomez, J.A.; Staller, A.; Alonso-Henar, J.; Canora, C.; Insúa-Arevalo, J.M.; Tsige, M.; Villamor, P.; Herrero-Barbero, P.; Hernandez-Moreno, C.; et al. Active faults of El Salvador. J. S. Am. Earth Sci. 2021, 105, 103038. [Google Scholar] [CrossRef]
- Ellis, A.; DeMets, C.; McCaffrey, R.; Briole, P.; Cosenza Muralles, B.; Flores, O.; Guzmán-Speziale, M.; Hernández, D.; Kostoglodov, V.; LaFemina, P.; et al. GPS constraints on deformation in northern Central America from 1999 to 2017, Part 2: Block rotations and fault slip rates, fault locking and distributed deformation. Geophys. J. Int. 2019, 218, 729–754. [Google Scholar] [CrossRef] [Green Version]
- Fernández, C.; Czeck, D.M.; Díaz Azpiroz, M. Testing the model of oblique transpression with oblique extrusion in two natural cases: Steps and consequences. J. Struct. Geol. 2013, 54, 85–102. [Google Scholar] [CrossRef]
- Jones, R.R.; Holdsworth, R.E. Oblique simple shear in transpression regimes. In Continental Transpression and Transtension Tectonics; Holdsworth, R.E., Strachan, R.A., Dewey, J.F., Eds.; Special Publication; Geological Society: London, UK, 1998; Volume 135, pp. 35–40. [Google Scholar]
- Dias, R.; Ribeiro, A. Constriction in a transpressive regime: An example in the Iberian branch of the Ibero-Armorican arc. J. Struct. Geol. 1994, 16, 1543–1554. [Google Scholar] [CrossRef]
- Sullivan, W.; Law, R. Deformation path partitioning within the transpressional White Mountain shear zone, California and Nevada. J. Struct. Geol. 2007, 29, 583–598. [Google Scholar] [CrossRef]
- Nabavi, S.T.; Díaz-Azpiroz, M.; Talbot, C. Inclined transpression in the Neka Valley, eastern Alborz, Iran. Geol. Rundsch. 2016, 106, 1815–1840. [Google Scholar] [CrossRef]
- Nabavi, S.T.; Alavi, S.A.; Díaz-Azpiroz, M.; Mohammadi, S.; Ghassemi, M.R.; Fernández, C.; Barcos, L.; Frehner, M. Deformation mechanics in inclined, brittle-ductile transpression zones: Insights from 3D finite element modelling. J. Struct. Geol. 2020, 137, 104082. [Google Scholar] [CrossRef]
- Ramsay, J.G. Folding and Fracturing of Rocks; McGraw-Hill: New York, NY, USA, 1967. [Google Scholar]
- Marrett, R.; Allmendinger, R.W. Kinematic analysis of fault-slip data. J. Struct. Geol. 1990, 12, 973–986. [Google Scholar] [CrossRef]
- Peraldo, G.; Montero, W. Sismología Histórica de América Central; Instituto Panamericano de Geografía e Historia: Mexico City, Mexico, 1999; Volume 513, pp. 1–347. [Google Scholar]
- Álvarez-Gómez, J.A. FMC—Earthquake focal mechanisms data management, cluster and classification. SoftwareX 2019, 9, 299–307. [Google Scholar] [CrossRef]
- Kostrov, V.V. Seismic moment and energy of earthquakes, and seismic flow of rock. Izv. Acad. Sci. USSR Phys. Solid Earth 1974, 1, 23–44. [Google Scholar]
- Watson, D.F. ACORD: Automatic contourning of raw data. Comput. Geosci. 1982, 8, 97–101. [Google Scholar] [CrossRef]
- Wessel, P.; Luis, J.F.; Uieda, L.; Scharroo, R.; Wobbe, F.; Smith, W.H.F.; Tian, D. The Generic Mapping Tools Version 6. Geochem. Geophys. Geosyst. 2019, 20, 5556–5564. [Google Scholar] [CrossRef] [Green Version]
- Feigl, K.L.; King, R.W.; Jordan, T.H. Geodetic measurement of tectonic deformation in the Santa Maria Fold and Thrust Belt, California. J. Geophys. Res. Earth Surf. 1990, 95, 2679–2699. [Google Scholar] [CrossRef]
- Bosse, H.R.; Lorenz, W.; Merino, A.; Mihm, A.; Rode, K.; Schmidt-Thome, M.; Weber, H.S.; Wiesemann, G. Carta Geológica de la República de El Salvador (Centroamérica), vol. 1. 100,000. Maps I to VI; Herausgegeben von der Bunderstalt fur Geowissenschaften und Rohstoffe: Hannover, Germany, 1976. [Google Scholar]
- Jicha, B.R.; Hernández, W. Effusive and explosive eruptive history of the Ilopango caldera complex, El Salvador. J. Volcanol. Geotherm. Res. 2021, 421, 107426. [Google Scholar] [CrossRef]
- Lexa, J.; Šebesta, J.; Alexander, C.J.; Hernández, W.; Pécskay, W. Geology and volcanic evolution in the southern part of the San Salvador Metropolitan Area. J. Geosci. 2010, 56, 105–140. [Google Scholar] [CrossRef] [Green Version]
- Suñe-Puchol, I.; Aguirre-Díaz, G.J.; Dávila-Harris, P.; Miggins, D.P.; Pedrazzi, D.; Costa, A.; Ortega-Obregón, C.; Lacan, P.; Hernández, W.; Gutiérrez, E. The Ilopango caldera complex, El Salvador: Origin and early ignimbrite-forming eruptions of a graben/pull-apart caldera structure. J. Volcanol. Geotherm. Res. 2019, 371, 1–19. [Google Scholar] [CrossRef]
- Truesdell, C.A. The Kinematic of Vorticity; Indiana University Press: Bloomington, IN, USA, 1954. [Google Scholar]
- Schulmann, K.; Thompson, A.B.; Lexa, O.; Jezek, J. Strain distribution and fabric development modeled in active and transient transpressive zones. J. Geophys. Res. 2003, 108, ETG6-1. [Google Scholar]
- Manea, V.C.; Manea, M.; Ferrari, L. A geodynamical perspective on the subduction of Cocos and Rivera plates beneath Mexico and Central America. Tectonophysics 2013, 609, 56–81. [Google Scholar] [CrossRef]
- Reguzzoni, M.; Sampietro, D. Moho estimation using GOCE data: A numerical simulation. In International Association of Geodesy Symposia, “Geodesy for Planet Earth”; Kenyon, S.C., Pacino, M.C., Marti, U.J., Eds.; Springer: Berlin, Germany, 2012; Volume 136. [Google Scholar] [CrossRef]



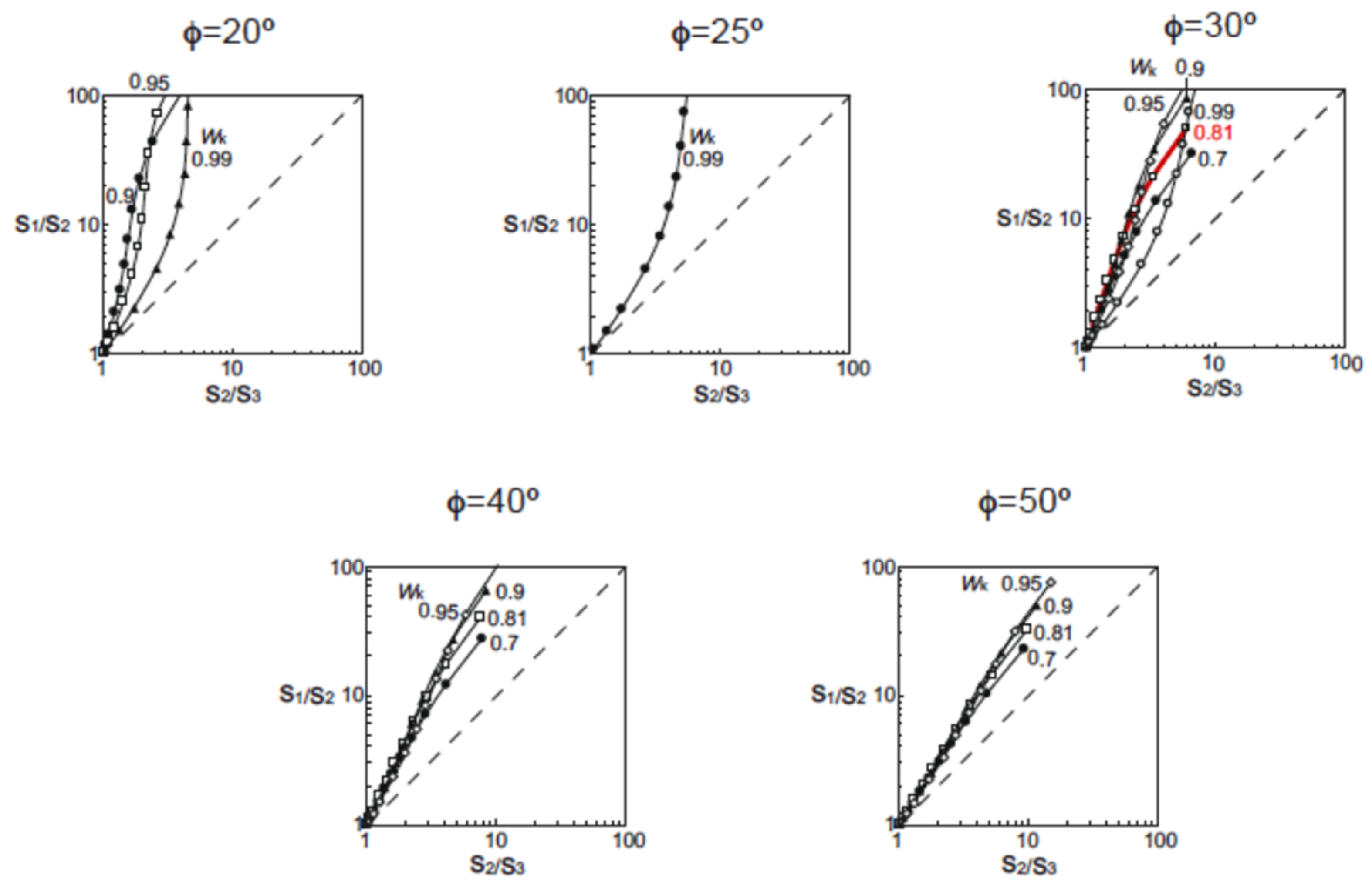


| Orientation | φ (s) | Wk | Reliability |
|---|---|---|---|
| N90° E; 70° S | 20 | 0.99 | Poor |
| 25 | 0.99 | ||
| 0.9999 | |||
| N100° E; 70° S | 25 | 0.99 | Fair |
| 30 | 0.81 | ||
| 0.9 | |||
| 0.95 | |||
| 0.99 | |||
| 40 | 0.9 | Fair | |
| 0.95 | |||
| 0.99 | |||
| 50 | 0.9 | Fair | |
| 0.95 | |||
| 0.99 | |||
| 30 | 0.7 | Poor | |
| 60 | 0.95 | Poor | |
| 0.99 | |||
| N110° E; 70° S | 50 | 0.7 | Good |
| 0.81 | |||
| 0.9 | |||
| 0.95 | |||
| 0.99 | |||
| 40 | 0.7 | Fair | |
| 0.81 | |||
| 0.9 | |||
| 0.95 | |||
| 60 | 0.9 | Fair | |
| 0.95 | |||
| 60 | 0.7 | Poor | |
| 0.81 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alonso-Henar, J.; Fernández, C.; Álvarez-Gómez, J.A.; Canora, C.; Staller, A.; Díaz, M.; Hernández, W.; García, Á.V.; Martínez-Díaz, J.J. Active Triclinic Transtension in a Volcanic Arc: A Case of the El Salvador Fault Zone in Central America. Geosciences 2022, 12, 266. https://doi.org/10.3390/geosciences12070266
Alonso-Henar J, Fernández C, Álvarez-Gómez JA, Canora C, Staller A, Díaz M, Hernández W, García ÁV, Martínez-Díaz JJ. Active Triclinic Transtension in a Volcanic Arc: A Case of the El Salvador Fault Zone in Central America. Geosciences. 2022; 12(7):266. https://doi.org/10.3390/geosciences12070266
Chicago/Turabian StyleAlonso-Henar, Jorge, Carlos Fernández, José Antonio Álvarez-Gómez, Carolina Canora, Alejandra Staller, Manuel Díaz, Walter Hernández, Ángela Valeria García, and José Jesús Martínez-Díaz. 2022. "Active Triclinic Transtension in a Volcanic Arc: A Case of the El Salvador Fault Zone in Central America" Geosciences 12, no. 7: 266. https://doi.org/10.3390/geosciences12070266
APA StyleAlonso-Henar, J., Fernández, C., Álvarez-Gómez, J. A., Canora, C., Staller, A., Díaz, M., Hernández, W., García, Á. V., & Martínez-Díaz, J. J. (2022). Active Triclinic Transtension in a Volcanic Arc: A Case of the El Salvador Fault Zone in Central America. Geosciences, 12(7), 266. https://doi.org/10.3390/geosciences12070266






