Parametric Study of Lateral Loaded Blade Pile in Clay
Abstract
:1. Introduction
2. FEM Simulation of Pile Foundation
2.1. Pile Geometry and Material Parameter
2.2. Soil Material Parameter and Model Geometry
3. Parametrical Study of CHS Pile
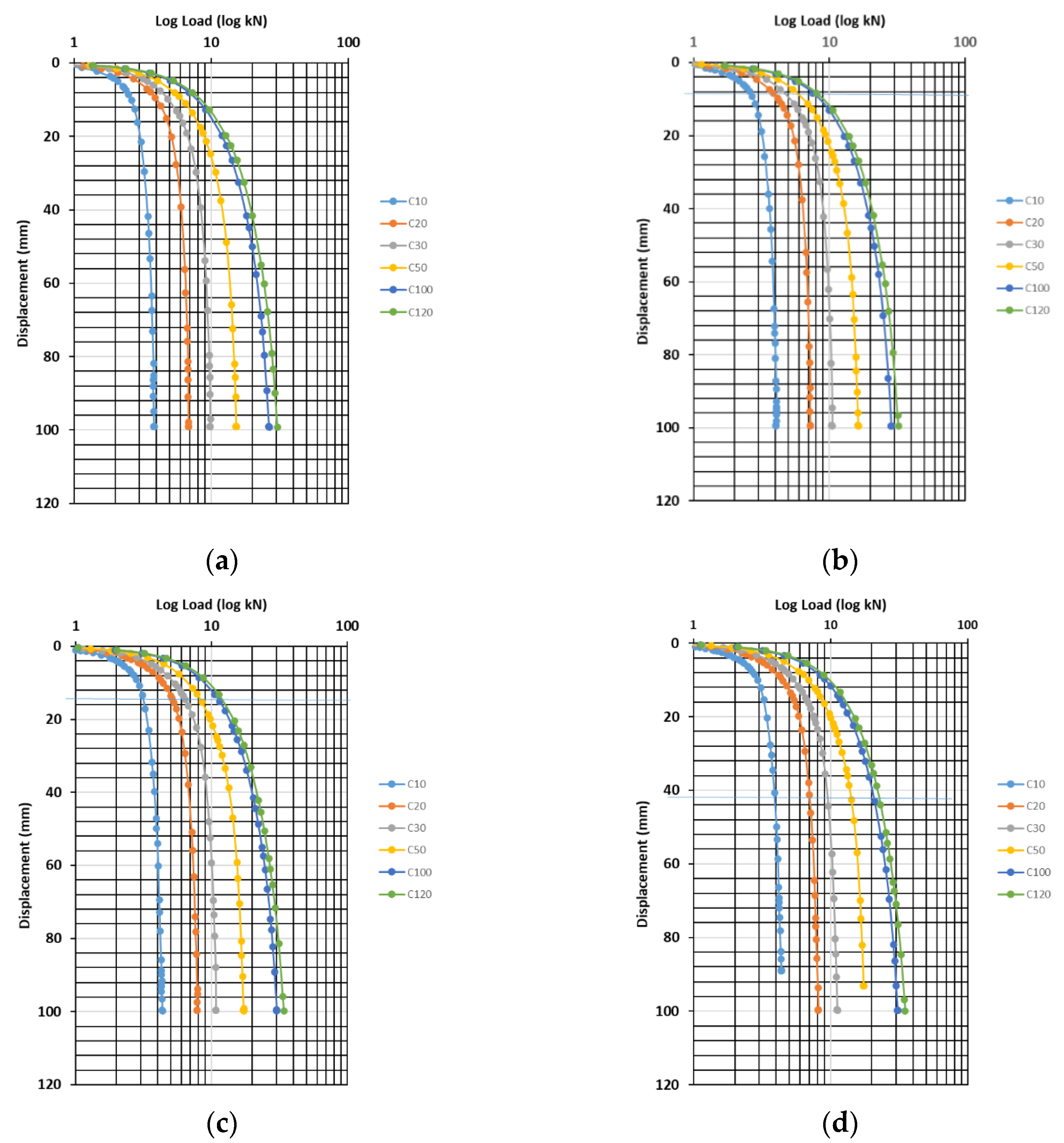
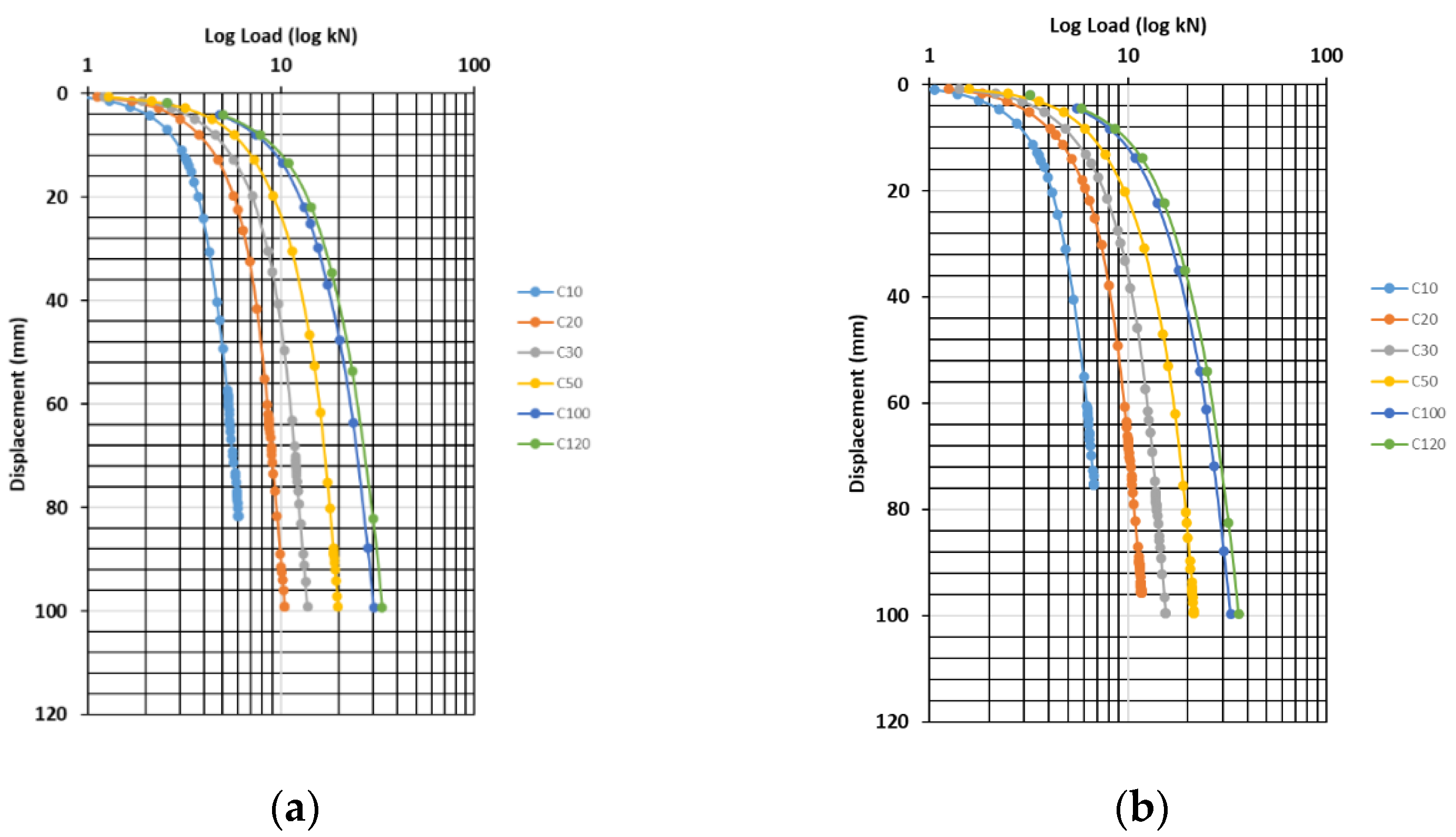
3.1. Study of CHSB0 Pile
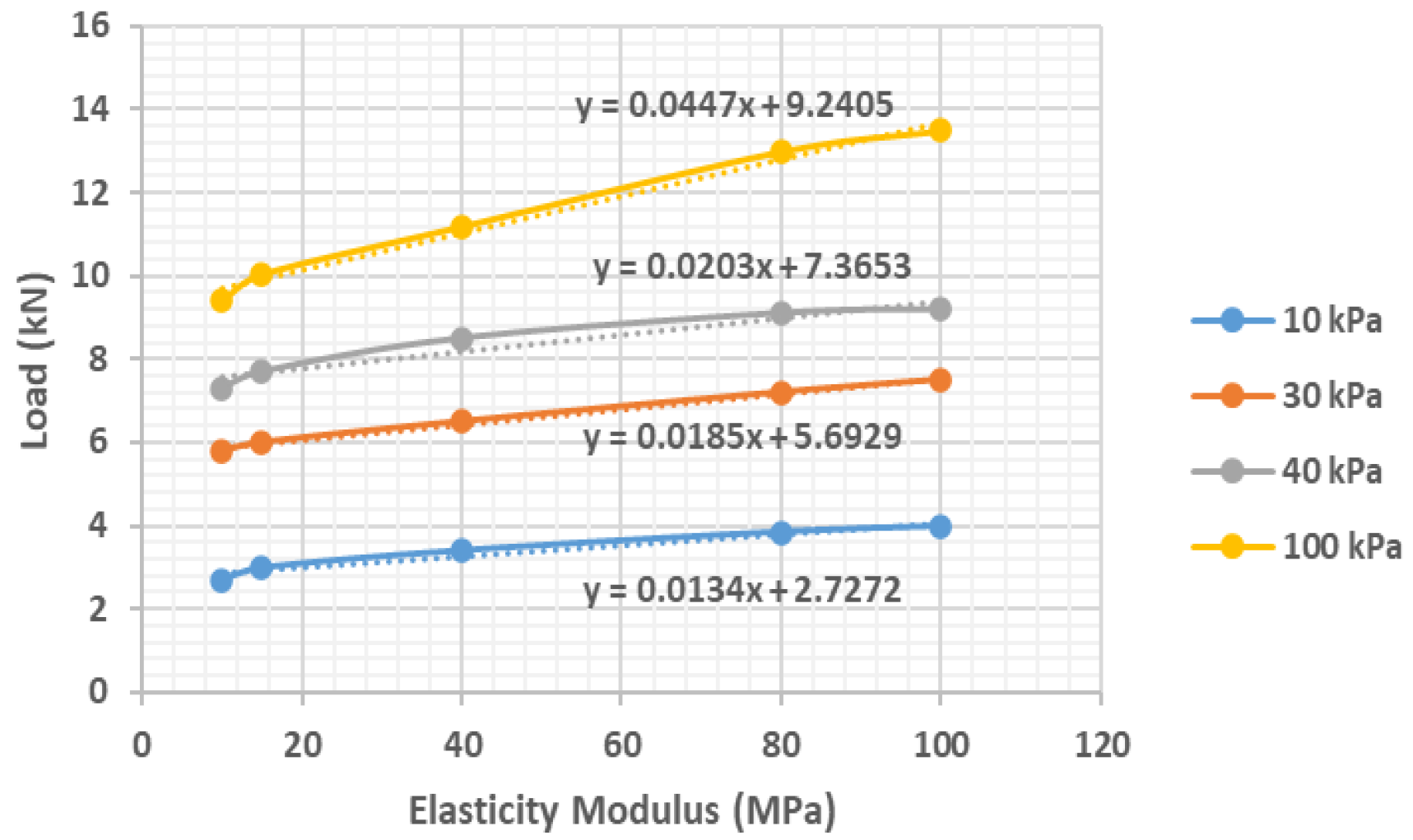
3.1.1. Effect of Modulus of Elasticity
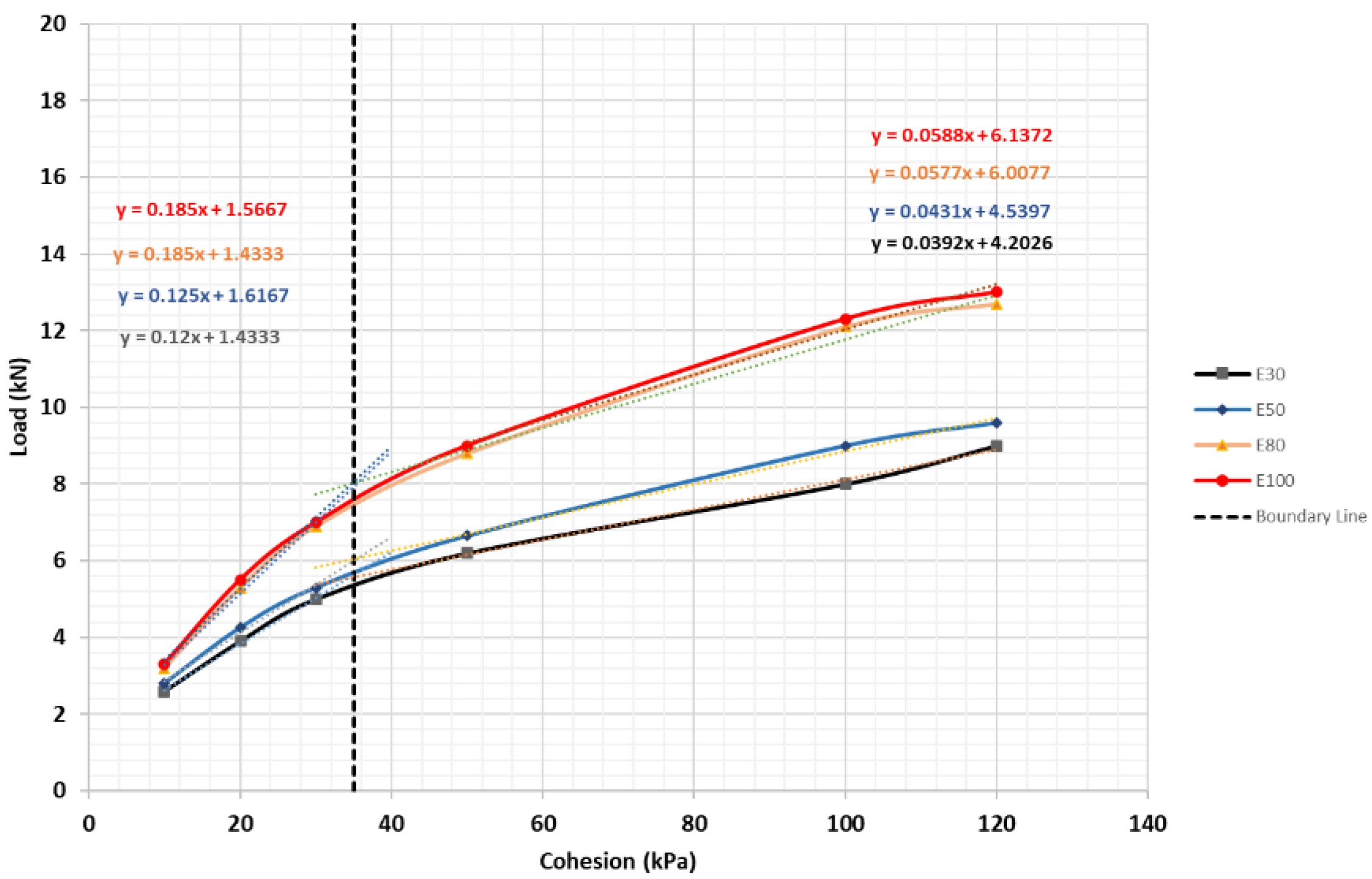
3.1.2. Effect of Cohesion
- = Ultimate bearing capacity of pile foundation in clay.
- C = Cohesion of clay.
- = Increment gradient = 0.15 for C 35; = 0.0497 for 35 C 120.
3.2. Parametrical Study of CHSB1 Pile
3.2.1. Effect of Modulus of Elasticity
3.2.2. Effect of Cohesion
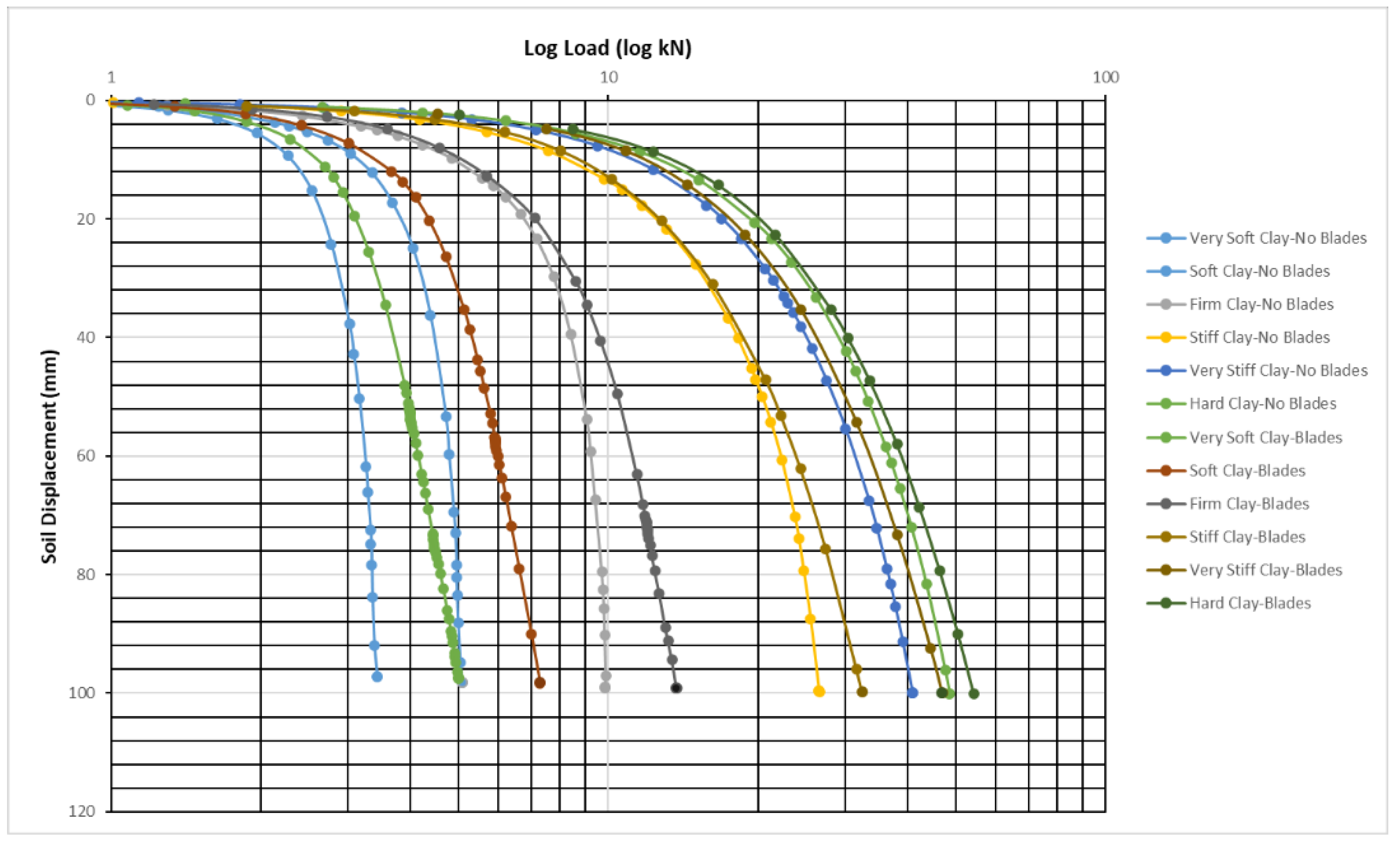
4. Comparison between CHSB0 and CHSB1 Piles
4.1. CHSB0 and CHSB1 Piles in Clay
4.2. Ultimate Bearing Capacity Improvement
5. Conclusions and Recommendation
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhou, J.; Oh, E. Full-Scale Field Tests of Different Types of Piles; Springer: Singapore, 2021. [Google Scholar] [CrossRef]
- Abdel-Rahman, A.H.; Rabie, M.; Awad-Allah, M.F. Comparison between Egyptian code, DIN 4014, and AASHTO methods of predicting ultimate bearing capacity of large diameter bored piles. El-Azher Univ. Eng. J. 2006, 8, 15–26. [Google Scholar]
- Hussein, H.H. Behavior of grouting pile in sandy soil. IOP Conf. Ser. Mater. Sci. Eng. 2020, 737, 12109. [Google Scholar] [CrossRef]
- He, B.; Wang, L.; Hong, Y. Capacity and failure mechanism of laterally loaded jet-grouting reinforced piles: Field and numerical investigation. Sci. China Technol. Sci. 2016, 59, 763–776. [Google Scholar] [CrossRef]
- Al-Baghdadi, T.A.; Brown, M.J.; Knappett, J.A.; Al-Defae, A.H. Effects of vertical loading on lateral screw pile performance. Proc. Inst. Civ. Eng.-Geotech. Eng. 2017, 170, 259–272. [Google Scholar] [CrossRef]
- Soltani-Jigheh, H.; Zahedi, P. Load transfer mechanism of screw piles in sandy soils. Indian Geotech. J. 2020, 50, 871–879. [Google Scholar] [CrossRef]
- Ghaly, A.; Hanna, A.; Hanna, M. Installation torque of screw anchors in dry sand. Soils Found. 1991, 31, 77–92. [Google Scholar] [CrossRef]
- Salhi, L.; Nait-Rabah, O.; Deyrat, C.; Roos, C. Numerical modeling of single helical pile behavior under compressive loading in sand. Electron. J. Geotech. Eng. 2013, 18, 4319–4338. [Google Scholar]
- Rao, S.N.; Prasad, Y.V.S.N.; Shetty, M.D. The behaviour of model screw piles in cohesive soils. Soils Found. 1991, 31, 35–50. [Google Scholar] [CrossRef]
- Perko, H.A. Helical Piles: A Practical Guide to Design and Installation; Wiley: Hoboken, NJ, USA, 2009; pp. 104–118. [Google Scholar] [CrossRef]
- Mitsch, M.P.; Clemence, S.P. Uplift capacity of helix anchors in sand. In Unknown Host Publication Title; Clemence, S.P., Ed.; American Society of Civil Engineers (ASCE): Reston, VA, USA, 1985; pp. 26–47. [Google Scholar]
- Mooney, J.S.; Adamczak, S.; Clemence, S.P. Uplift Capacity of Helical Anchors in Clay and Silt; Clemence, S.P., Ed.; American Society of Civil Engineers: Reston, VA, USA, 1985; pp. 48–72. [Google Scholar]
- Nasr, M.H. Large capacity screw piles. In Proceedings of the International Conference: Future Vision and Challenges for Urban Development, Cairo, Egypt, 20–22 December 2004; pp. 1–15. [Google Scholar]
- Budhu, M. Soil Mechanics and Foundations; Wiley: New York, NY, USA, 2020; No. 1; pp. 1–xvi. [Google Scholar]
- Elkasabgy, M.; Naggar, M.H.E. Dynamic response of vertically loaded helical and driven steel piles. Can. Geotech. J. 2013, 50, 521–535. [Google Scholar] [CrossRef]
- Hoyt, R.M.; Chance, A.; Clemence, S.P. Uplift capacity of helical anchors in soil. In Congrès International de Mécanique des Sols et des Travaux de Fondations; Taylor & Francis: Rio de Janeiro, Brazil, 1989; Volume 12, pp. 1019–1022. [Google Scholar]
- Tsuha, C.D.H.C.; Aoki, N. Relationship between installation torque and uplift capacity of deep helical piles in sand. Can. Geotech. J. 2010, 47, 635–647. [Google Scholar] [CrossRef]
- Das, B.M.; Rozendal, D.B. Ultimate uplift capacity of piles in sand. Transp. Res. Rec. 1983, 945, 40–44. [Google Scholar]
- Feng, S.; Fu, W.; Chen, H.; Li, H.; Xie, Y.; Lv, S.; Li, J. Field tests of micro screw anchor piles under different loading conditions at three soil sites. Bull. Eng. Geol. Environ. 2020, 80, 127–144. [Google Scholar] [CrossRef]
- Dutta, S.C.; Roy, R. A critical review on idealization and modeling for interaction among soil–foundation–structure system. Comput. Struct. 2002, 80, 1579–1594. [Google Scholar]
- Trochanis, A.M.; Bielak, J.; Christiano, P. Three-dimensional nonlinear study of piles. J. Geotech. Eng. 1991, 117, 429–447. [Google Scholar] [CrossRef]
- Zaman, M.M.; Najjar, Y.M.; Muqtadir, A. Effects of cap thickness and pile inclination on the response of a pile group foundation by a three-dimensional nonlinear finite element analysis. Comput. Geotech. 1993, 15, 65–86. [Google Scholar] [CrossRef]
- Ng, C.W.W.; Zhang, L.M. Three-dimensional analysis of performance of laterally loaded sleeved piles in sloping ground. J. Geotech. Geoenvironmental Eng. 2001, 127, 499–509. [Google Scholar] [CrossRef]
- Pan, J.L.; Goh, A.T.C.; Wong, K.S.; Selby, A.R. Three-dimensional analysis of single pile response to lateral soil movements. Int. J. Numer. Anal. Methods Geomech. 2002, 26, 747–758. [Google Scholar]
- Chore, H.S.; Ingle, R.K.; Sawant, V.A. Parametric study of pile groups subjected to lateral load. Struct. Eng. Mech. Int. J. 2010, 36, 243–246. [Google Scholar] [CrossRef]
- Nematzadeh, M.; Fazli, S.; Naghipour, M.; Jalali, J. Experimental study on modulus of elasticity of steel tube-confined concrete stub columns with active and passive confinement. Eng. Struct. 2017, 130, 142–153. [Google Scholar] [CrossRef]
- Zhou, W.; Gao, R.; Zhu, H.; Wei, X.; Cao, Q.; Gao, Z. Behavior of steel casing composite piles under lateral loading and parameter optimization. Eng. Struct. 2020, 220, 110991. [Google Scholar] [CrossRef]
- Look, B.G. Handbook of Geotechnical Investigation and Design Tables; Taylor & Francis: London, UK, 2007; p. 346. [Google Scholar] [CrossRef]
- Nowkandeh, M.J.; Choobbasti, A.J. Numerical study of single helical piles and helical pile groups under compressive loading in cohesive and cohesionless soils. Bull. Eng. Geol. Environ. 2021, 80, 4001–4023. [Google Scholar] [CrossRef]
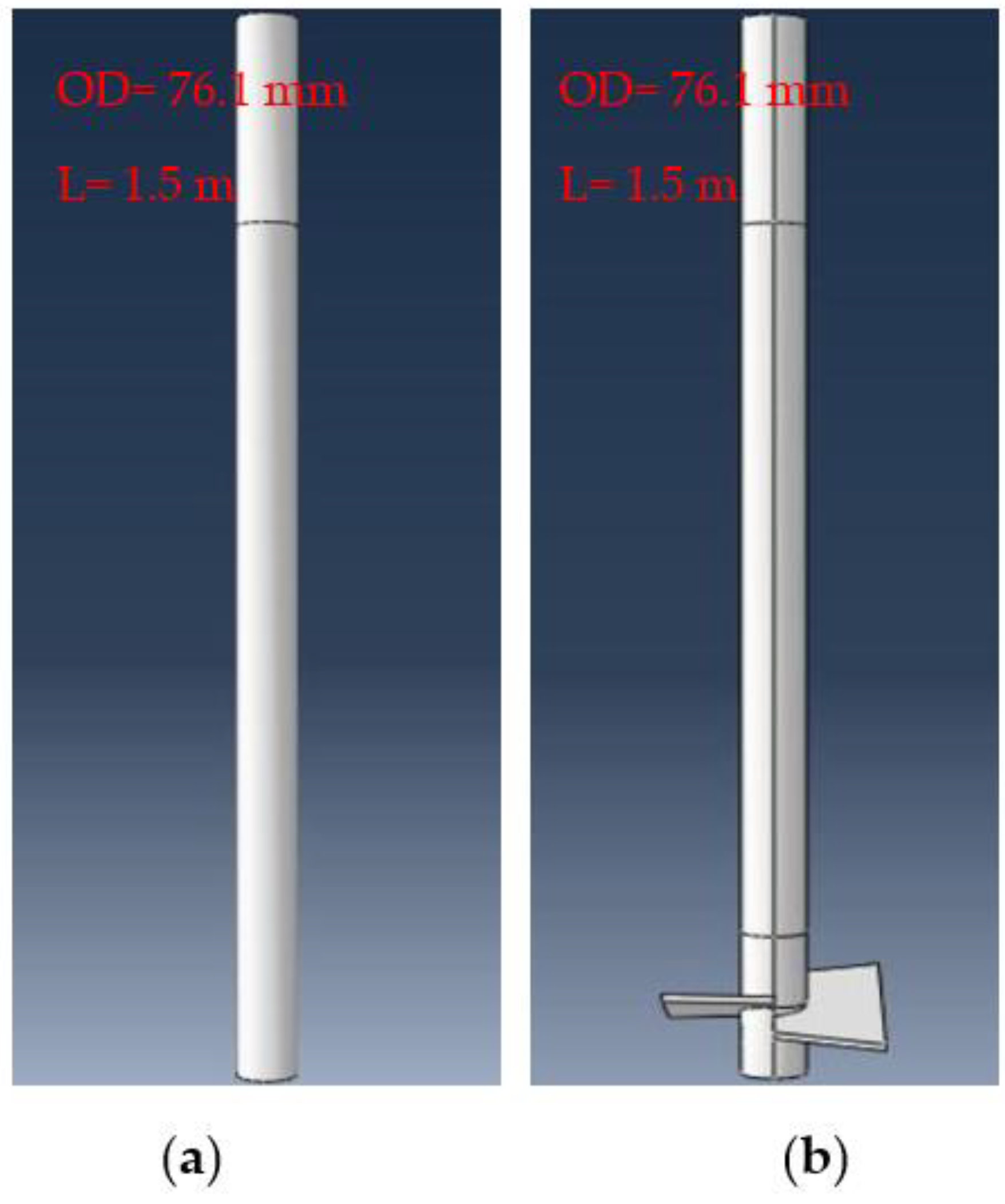





| Type | OD | Wall Thickness | Length | Embedment | Blade No |
|---|---|---|---|---|---|
| mm | mm | m | m | No. | |
| CHSB0P | 76.1 | 4 | 1.5 | 1.2 | 0 |
| CHSB1P | 76.1 | 4 | 1.5 | 1.2 | 2 |
| Type | Wall Thickness | Length | Blade Area |
|---|---|---|---|
| mm | mm | m2 | |
| CHSB0P | 0 | 0 | 0 |
| CHSB1P | 10 | 250 | 0.05375 |
| Type | Modulus | Poisson’s Ratio | Density | CHS Grade | Blade Grade |
|---|---|---|---|---|---|
| MPa | N/A | t/mm3 | MPa | MPa | |
| CHSB0P | 210,000 | 0.3 | 7.8 × 10−9 | 450 | N/A |
| CHSB1P | 210,000 | 0.3 | 7.8 × 10−9 | 450 | 350 |
| Soil Index | Unit Weight, γ | Soil Cohesion, c | Modulus of Elasticity E |
|---|---|---|---|
| kN/m3 | kPa | MPa | |
| Very soft | 16 | 10 | 10 |
| Soft | 17 | 15 | 15 |
| Firm | 18.5 | 30 | 30 |
| Stiff | 20 | 85 | 75 |
| Very stiff | 21 | 150 | 150 |
| Hard | 22.5 | 200 | 180 |
| Controlled | Elastic Modulus (MPa) |
|---|---|
| c = 10 kPa | 10, 15, 40, 80 and 100 |
| c = 30 kPa | 10, 15, 40, 80 and 100 |
| c = 50 kPa | 10, 15, 40, 80 and 100 |
| c = 100 kPa | 10, 15, 40, 80 and 100 |
| Elastic Modulus (MPa) | Pile Foundation Capacity (kN) | |||
|---|---|---|---|---|
| c = 10 kPa | c = 30 kPa | c = 50 kPa | c = 100 kPa | |
| 10 | 2.3 | 4.53 | 5.5 | 9.0 |
| 15 | 2.44 | 4.87 | 6.1 | 9.2 |
| 40 | 2.73 | 5.4 | 6.7 | 11.0 |
| 80 | 2.89 | 5.8 | 7.3 | 12.1 |
| 100 | 2.92 | 6.0 | 7.8 | 12.3 |
| Controlled | Cohesion (kPa) |
|---|---|
| E = 30 MPa | 10, 20, 30, 50, 100 and 120 |
| E = 50 MPa | 10, 20, 30, 50, 100 and 120 |
| E = 80 MPa | 10, 20, 30, 50, 100 and 120 |
| E = 100 MPa | 10, 20, 30, 50, 100 and 120 |
| Cohesion (kPa) | Pile Foundation Capacity (kN) | |||
|---|---|---|---|---|
| E = 30 MPa | E = 50 MPa | E = 80 MPa | E = 100 MPa | |
| 10 | 2.6 | 2.8 | 3.2 | 3.3 |
| 20 | 3.9 | 4.25 | 5.3 | 5.5 |
| 30 | 5.0 | 5.3 | 6.9 | 7.0 |
| 50 | 6.2 | 6.65 | 8.8 | 9.0 |
| 100 | 8.0 | 9.0 | 12.1 | 12.3 |
| 120 | 9.0 | 9.6 | 12.7 | 13.0 |
| Elastic Modulus (MPa) | Pile Foundation Capacity (kN) | |||
|---|---|---|---|---|
| c = 10 kPa | c = 30 kPa | c = 50 kPa | c = 100 kPa | |
| 10 | 2.7 | 5.8 | 7.3 | 9.4 |
| 15 | 2.99 | 6.0 | 7.7 | 10.05 |
| 40 | 3.4 | 6.5 | 8.5 | 11.2 |
| 80 | 3.84 | 7.2 | 9.1 | 13.0 |
| 100 | 3.98 | 7.5 | 9.2 | 13.5 |
| Cohesion (kPa) | Pile Foundation Capacity (kN) | |||
| E = 30 MPa | E = 50 MPa | E = 80 MPa | E = 100 MPa | |
| 10 | 2.9 | 3.2 | 4.1 | 4.35 |
| 20 | 4.2 | 4.65 | 5.9 | 6.0 |
| 30 | 5.05 | 5.4 | 7.2 | 7.35 |
| 50 | 6.4 | 6.95 | 9.0 | 9.15 |
| 100 | 8.9 | 9.3 | 13.0 | 13.5 |
| 120 | 9.2 | 10.0 | 14.0 | 14.8 |
| Pile Label | Ultimate Bearing Capacity (kN) | |||||
| Very Soft | Soft Clay | Firm Clay | Stiff Clay | Very Stiff Clay | Hard Clay | |
| CHSB0 | 2.7 | 3.8 | 6.7 | 12.8 | 16.9 | 19.6 |
| CHSB1 | 3.1 | 4.3 | 7.1 | 12.83 | 17.4 | 20.1 |
| Capacity Improvement (%) | 14.8 | 13.1 | 5.9 | 0.23 | 2.95 | 2.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Sui, G.; Zhou, J.; Oh, E. Parametric Study of Lateral Loaded Blade Pile in Clay. Geosciences 2022, 12, 329. https://doi.org/10.3390/geosciences12090329
Li L, Sui G, Zhou J, Oh E. Parametric Study of Lateral Loaded Blade Pile in Clay. Geosciences. 2022; 12(9):329. https://doi.org/10.3390/geosciences12090329
Chicago/Turabian StyleLi, Lin, Guowei Sui, Jialin Zhou, and Erwin Oh. 2022. "Parametric Study of Lateral Loaded Blade Pile in Clay" Geosciences 12, no. 9: 329. https://doi.org/10.3390/geosciences12090329
APA StyleLi, L., Sui, G., Zhou, J., & Oh, E. (2022). Parametric Study of Lateral Loaded Blade Pile in Clay. Geosciences, 12(9), 329. https://doi.org/10.3390/geosciences12090329








