Stability Analysis of a Multi-Layered Slope in an Open Pit Mine
Abstract
:1. Introduction
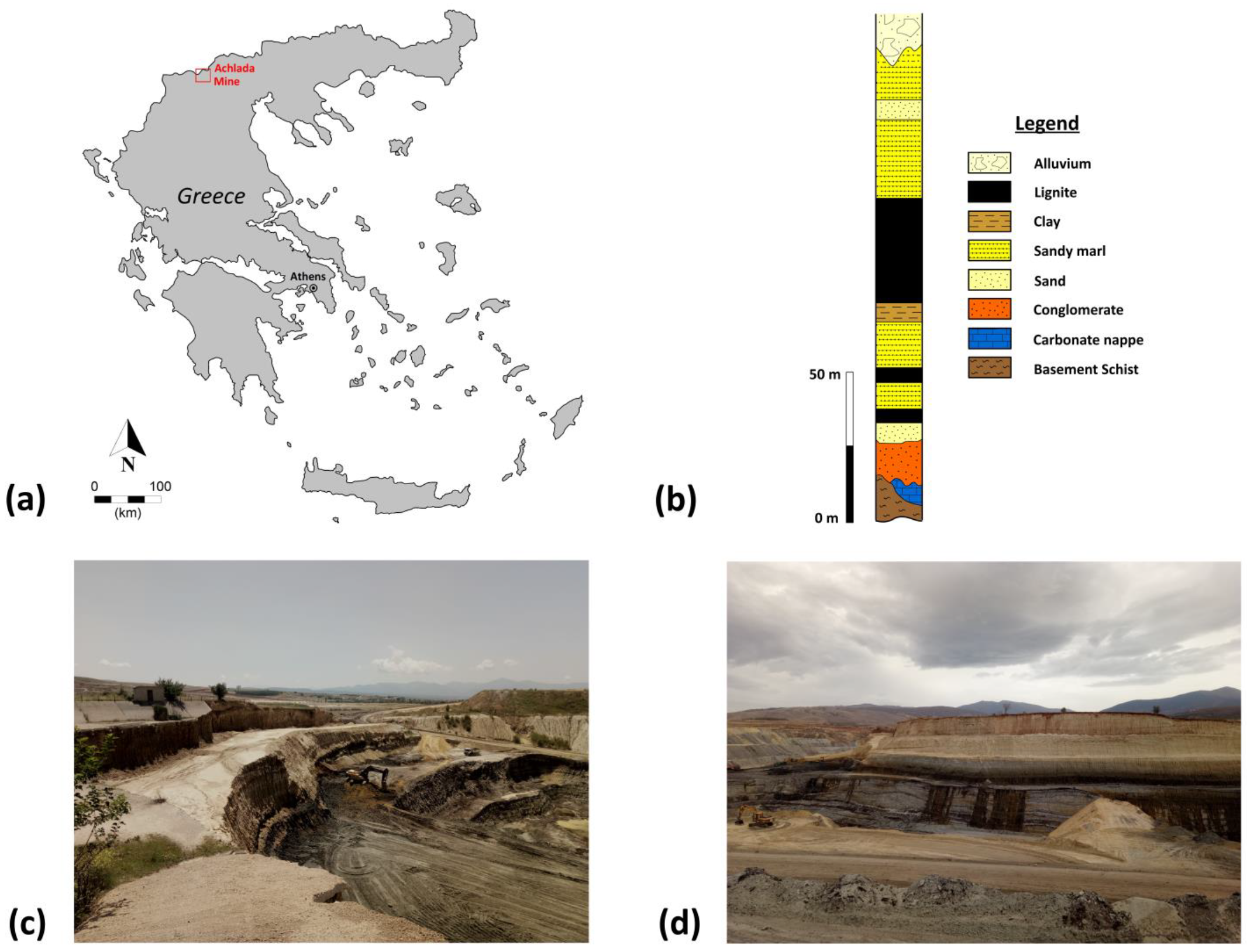
2. Site Location, Regional Geology, Hydrogeology, and Mine Conditions
- (i)
- The lowest consists of conglomerates with a maximum thickness of about 200 m. A transitional passage into marls, sandy marls, sands, clays, and thin lignite horizons is present upwards.
- (ii)
- The middle unit comprises a clayey formation with thick lignite beds, marls, sandy marls, and sands. Conglomerates and marly limestone lenses are also occasionally present [30].
- (iii)
- The upper unit includes alternations in clays, marls, marly breccia, and sandy conglomerates.
3. Evaluation of Slope Stability
3.1. Limit Equilibrium Methods
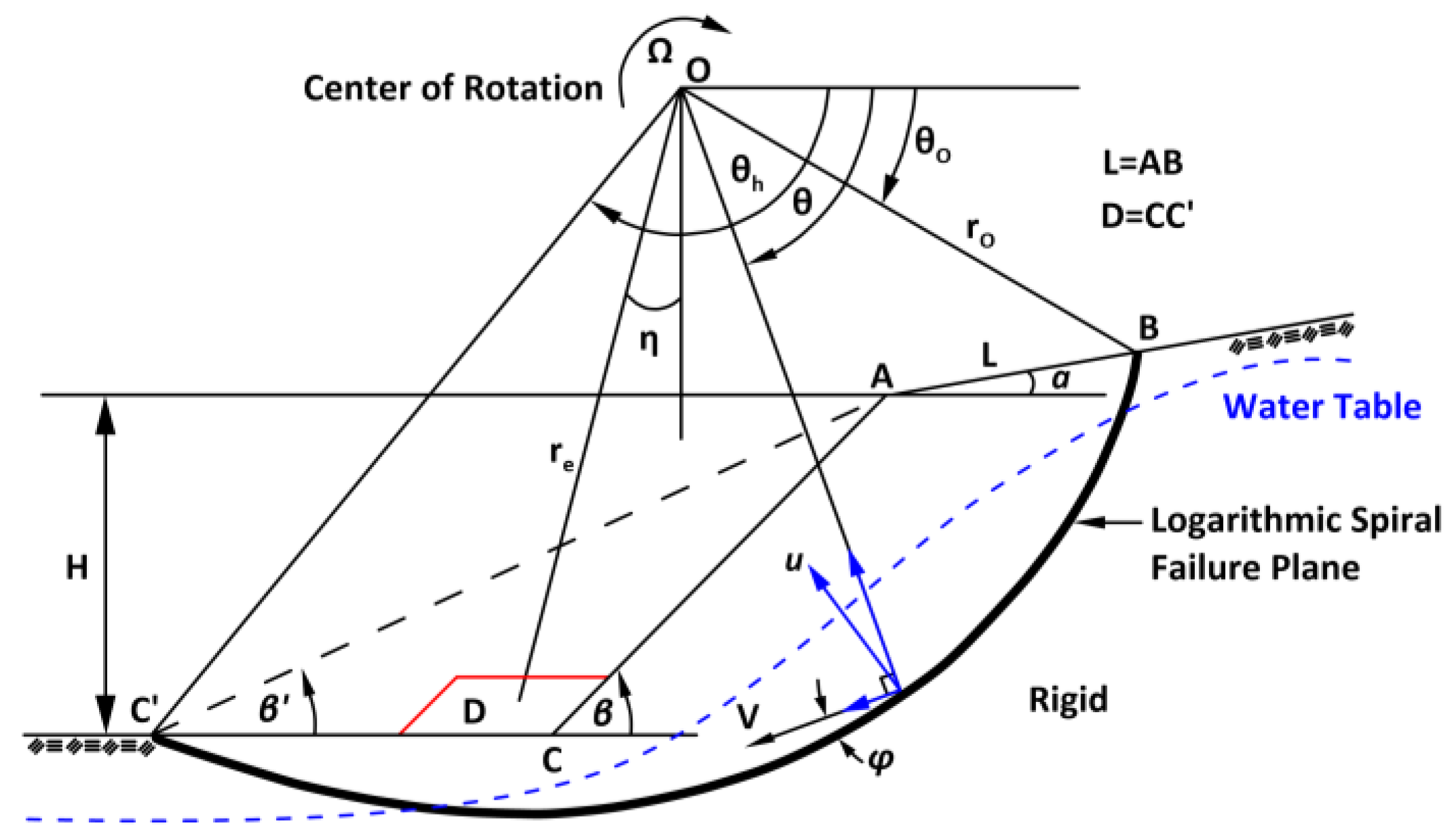
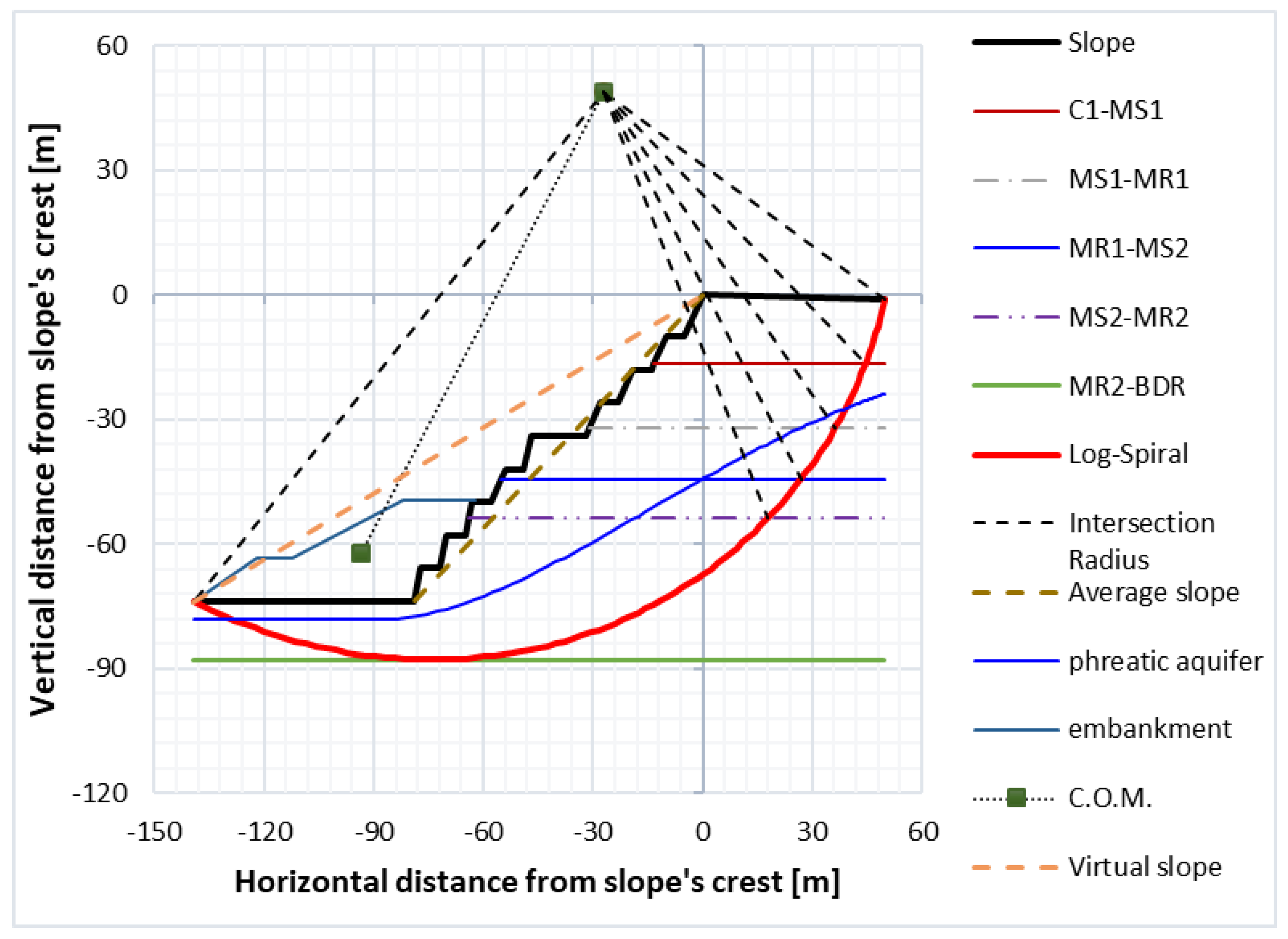
3.2. Limit Analysis and Upper-Bound Theorem
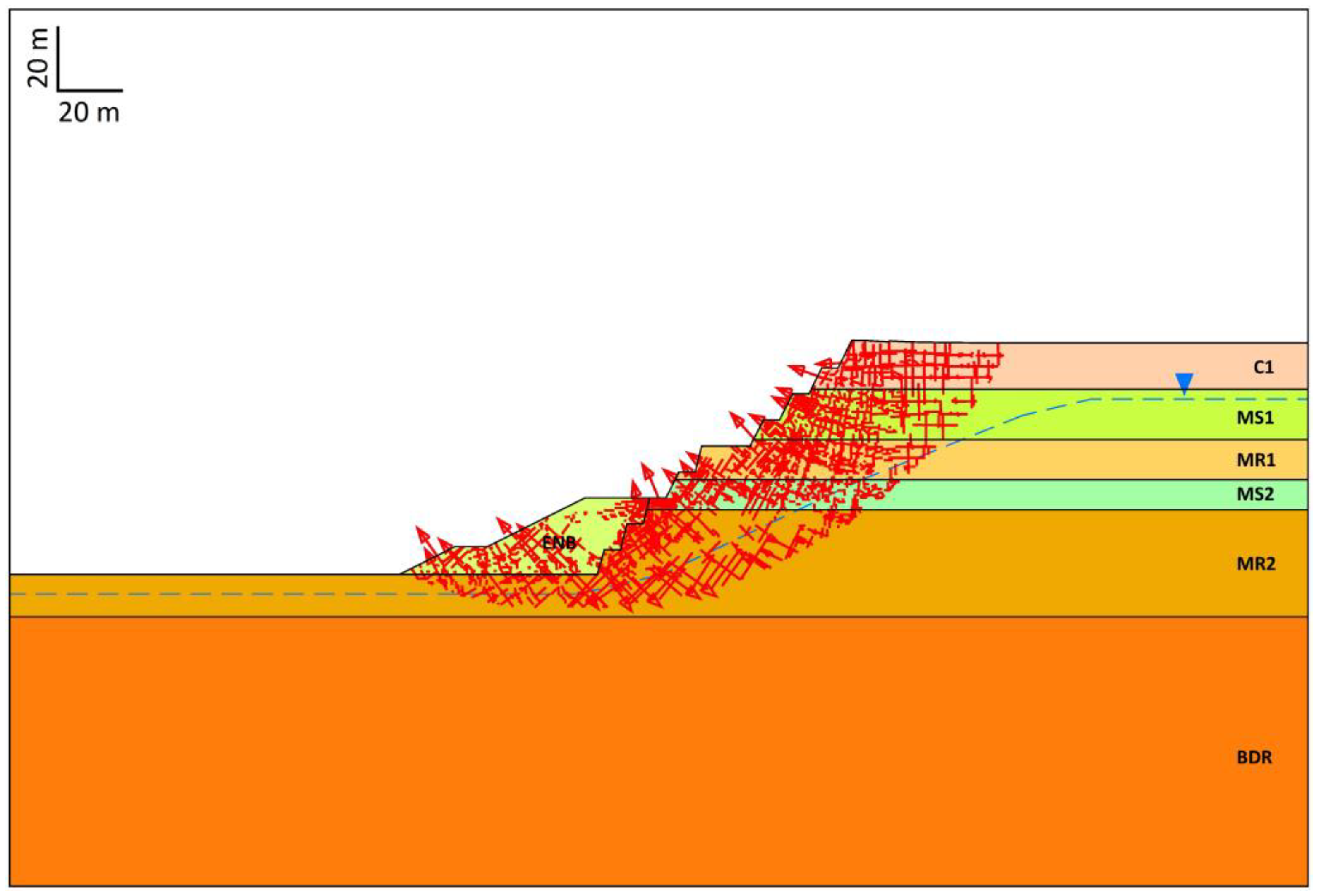
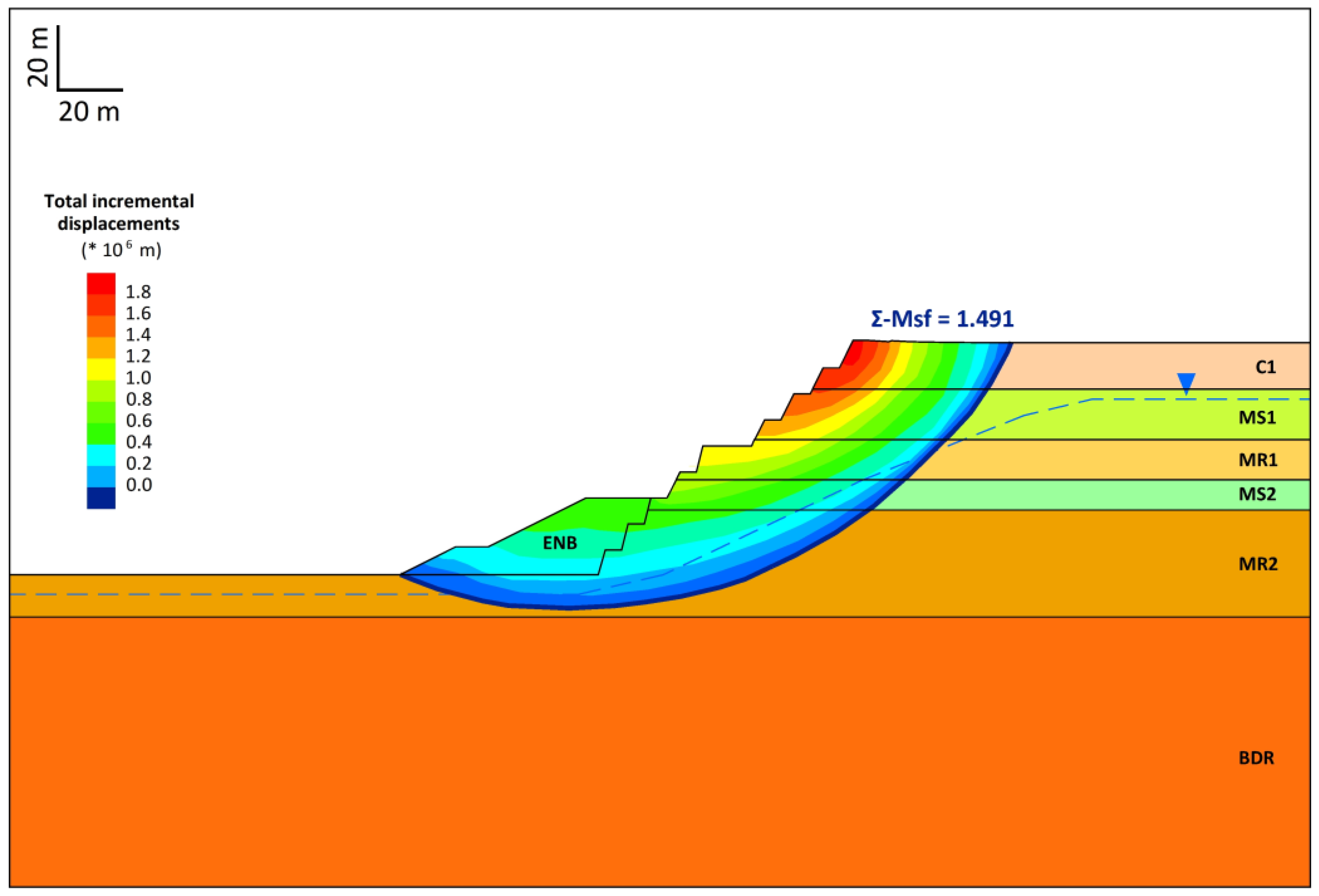
3.3. Finite Element Method
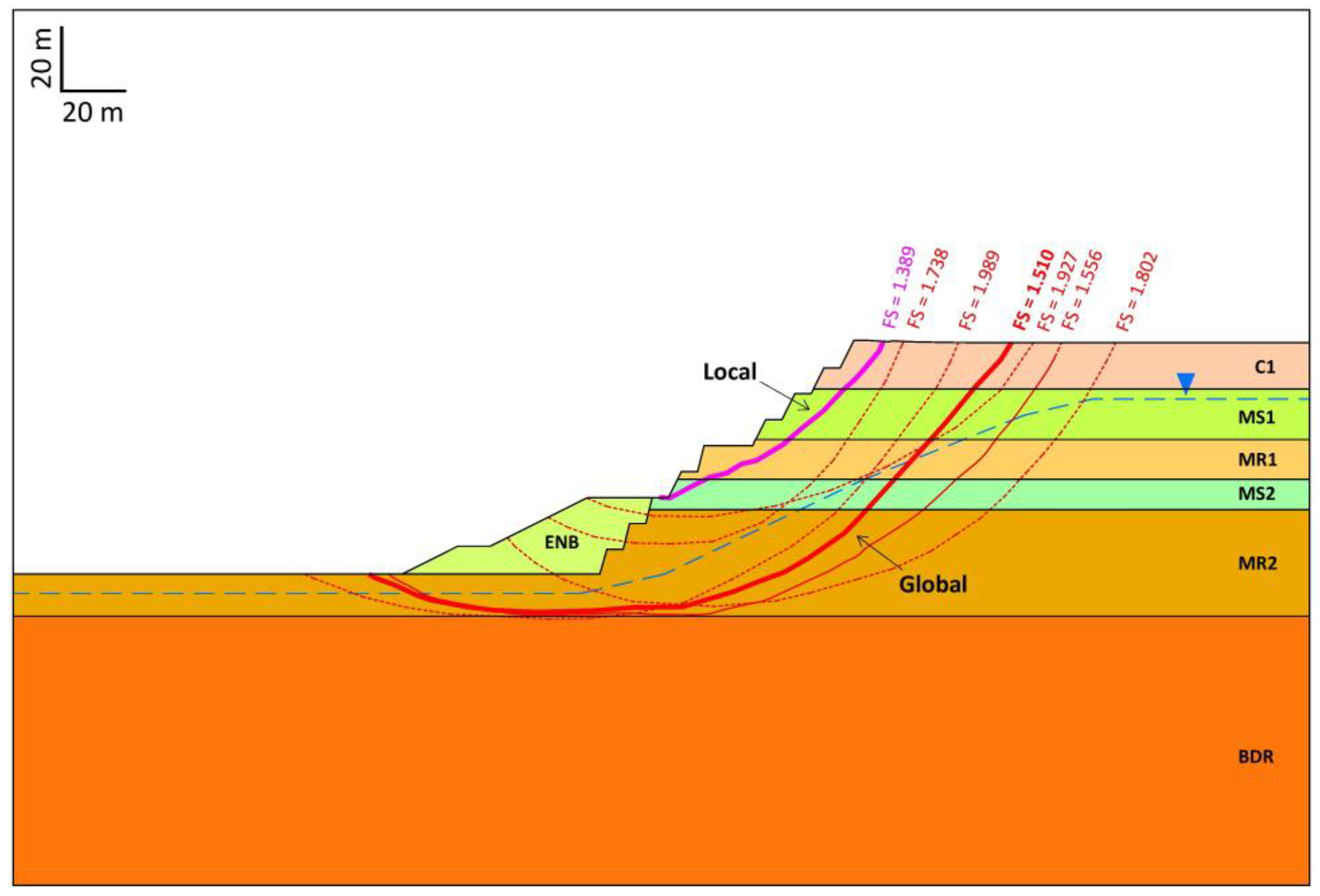
4. Discussion
5. Conclusions
- The solution proposed for the LA (limit analysis) in multi-layered slopes constitutes an innovative and easy assessment of the safety factor.
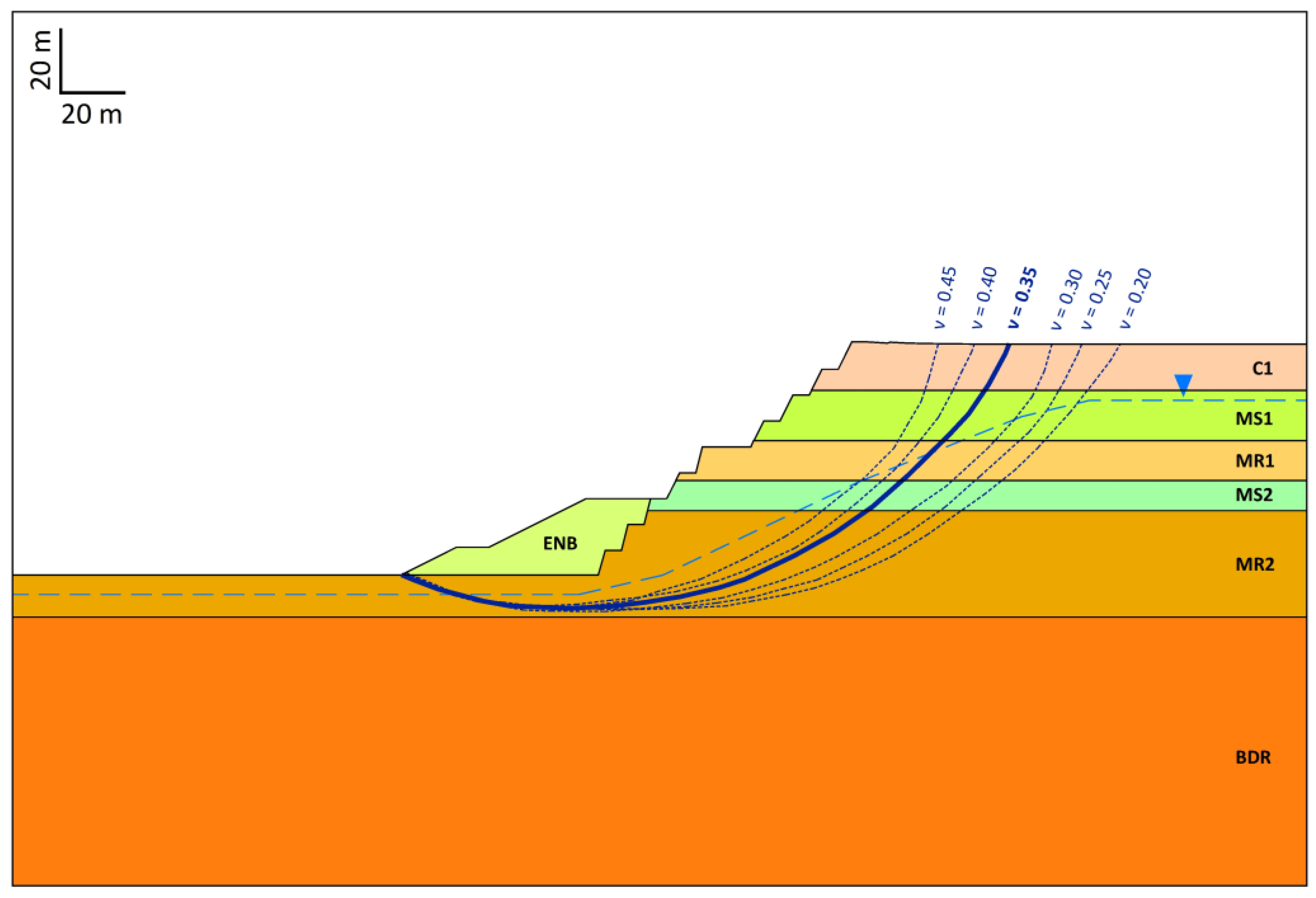
- FEM (finite element method) represents a powerful tool for slope stability analysis in multi-layered formations, provided that quality data concerning the initial conditions and the geotechnical parameters are available. The results indicate that a proper value of Poisson’s ratio (v) is a prerequisite for obtaining reliable results as it affects the size and location (geometry) of the critical slip surfaces.
- The formation of local minima failure surfaces in the LEM is referred to as a major difference between the LEM and the FEM, and the study demonstrates that the implementation of FEM combined with LEM or LA provides the most appropriate tool to analyze the slope stability in a multi-layered formation.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Duncan, J.M. State Of-the-Art Stability and Deformation Analysis. J. Geotech. Eng. ASCE 1996, 122, 557–597. [Google Scholar]
- Fredlund, D.G.; Krahn, J. Comparison of Slope Stability Methods of Analysis. Can. Geotech. J. 1977, 14, 429–439. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Krahn, J.; Pufahl, D.E. The Relationship between Limit Equilibrium Slope Stability Methods. Soil mechanics and foundation engineering. In Proceedings of the 10th International Conference, Stockholm, Sweden, 5–19 June 1981; Volume 3. [Google Scholar] [CrossRef]
- Fang, H.-Y.; Daniels, J.L. Introductory Geotechnical Engineering: An Environmental Perspective; CRC Press: London, UK, 2017; ISBN 9781315274959. [Google Scholar]
- Kim, J.; Salgado, R.; Lee, J. Stability Analysis of Complex Soil Slopes Using Limit Analysis. J. Geotech. Geoenviron. Eng. 2002, 128, 546–557. [Google Scholar] [CrossRef]
- Jiang, G.L.; Magnan, J.P. Stability Analysis of Embankments: Comparison of Limit Analysis with Methods of Slices. Geotechnique 1997, 47, 857–872. [Google Scholar]
- Chuang, P.H. Stability Analysis in Geomechanics by Linear Programming. II: Application. J. Geotech. Eng. 1992, 118, 1716–1726. [Google Scholar] [CrossRef]
- Cheng, Y.M.; Lansivaara, T.; Wei, W.B. Two-Dimensional Slope Stability Analysis by Limit Equilibrium and Strength Reduction Methods. Comput. Geotech. 2007, 34, 137–150. [Google Scholar] [CrossRef]
- Strang, G.; Fix, J. An Analysis of the Finite Element Method; Prentice-Hall: Englewood Cliffs, NJ, USA, 1973. [Google Scholar]
- Hughes, T. Linear Static and Dynamic Finite Element Analysis. In The Finite Element Method; Dover Publications, Inc.: New York, NY, USA, 1987; Volume 65. [Google Scholar]
- Zienkiewicz, O.C.; Taylor, R.L. The Finite Element Method; McGraw-Hill: New York, NY, USA, 1989. [Google Scholar]
- Clough, R.W.; Woodward, R.J. Analysis of Embankment Stresses and Deformations. J. Soil Mech. Found. Div. 1967, 93, 529–549. [Google Scholar] [CrossRef]
- Hammouri, N.A.; Husein Malkawi, A.I.; Yamin, M.M.A. Stability Analysis of Slopes Using the Finite Element Method and Limiting Equilibrium Approach. Bull. Eng. Geol. Environ. 2008, 67, 471–478. [Google Scholar] [CrossRef]
- Wright, S.G.; Kulhawy, F.H.; Duncan, J.M. Accuracy of Equilibrium Slope Stability Analysis. J. Soil Mech. Found. Div. 1973, 99, 783–791. [Google Scholar] [CrossRef]
- Huang, S.L.; Yamasaki, K. Slope Failure Analysis Using Local Minimum Factor-of-Safety Approach. J. Geotech. Eng. 1993, 119, 1974–1989. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Humpheson, C.; Lewis, R.W. Associated and Non-Associated Visco-Plasticity and Plasticity in Soil Mechanics. Géotechnique 1975, 25, 671–689. [Google Scholar] [CrossRef]
- Ugai, K. A Method of Calculation of Total Safety Factor of Slope by Elasto-Plastic FEM. Soils Found. 1989, 29, 190–195. [Google Scholar] [CrossRef] [PubMed]
- Matsui, T.; San, K.-C. Finite Element Slope Stability Analysis by Shear Strength Reduction Technique. Soils Found. 1992, 32, 59–70. [Google Scholar] [CrossRef]
- Ugai, K.; Leshchinsky, D. Three-Dimensional Limit Equilibrium and Finite Element Analyses: A Comparison of Results. Soils Found. 1995, 35, 1–7. [Google Scholar] [CrossRef]
- Dawson, E.M.; Roth, W.H.; Drescher, A. Slope Stability Analysis by Strength Reduction. Géotechnique 1999, 49, 835–840. [Google Scholar] [CrossRef]
- Manzari, M.T.; Nour, M.A. Significance of Soil Dilatancy in Slope Stability Analysis. J. Geotech. Geoenviron. Eng. 2000, 126, 75–80. [Google Scholar] [CrossRef]
- Chang, Y.; Huang, T. Slope Stability Analysis Using Strength Reduction Technique. J. Chin. Inst. Eng. 2005, 28, 231–240. [Google Scholar] [CrossRef]
- Liu, F. Stability Analysis of Geotechnical Slope Based on Strength Reduction Method. Geotech. Geol. Eng. 2020, 38, 3653–3665. [Google Scholar] [CrossRef]
- Griffiths, D.V.; Lane, P.A. Slope Stability Analysis by Finite Elements. Géotechnique 1999, 49, 387–403. [Google Scholar] [CrossRef]
- Song, L.; Yu, X.; Xu, B.; Pang, R.; Zhang, Z. 3D Slope Reliability Analysis Based on the Intelligent Response Surface Methodology. Bull. Eng. Geol. Environ. 2021, 80, 735–749. [Google Scholar] [CrossRef]
- Zheng, H.; Liu, D.F.; Li, C.G. Slope Stability Analysis Based on Elasto-Plastic Finite Element Method. Int. J. Numer. Methods Eng. 2005, 64, 1871–1888. [Google Scholar] [CrossRef]
- Zaki, A. Slope Stability Analysis Overview. Ph.D. Thesis, University of Toronto, Toronto, ON, Canada, 1999. [Google Scholar]
- Pavlides, S.B.; Mountrakis, D.M. Extensional Tectonics of Northwestern Macedonia, Greece, since the Late Miocene. J. Struct. Geol. 1987, 9, 385–392. [Google Scholar] [CrossRef]
- Oikonomopoulos, I.K.; Perraki, M.; Tougiannidis, N.; Perraki, T.; Kasper, H.U.; Gurk, M. Clays from Neogene Achlada Lignite Deposits in Florina Basin (Western Macedonia, N. Greece): A Prospective Resource for the Ceramics Industry. Appl. Clay Sci. 2015, 103, 1–9. [Google Scholar] [CrossRef]
- Koukouzas, N.; Ward, C.R.; Li, Z. Mineralogy of Lignites and Associated Strata in the Mavropigi Field of the Ptolemais Basin, Northern Greece. Int. J. Coal. Geol. 2010, 81, 182–190. [Google Scholar] [CrossRef]
- Metaxas, A.; Karageorgiou, D.E.; Varvarousis, G.; Kotis, T.; Ploumidis, M.; Papanikolaou, G. Geological Evolution—Stratigraphy of Florina, Ptolemaida, Kozani and Saradaporo Graben. Bull. Geol. Soc. Greece 2018, 40, 161–172. [Google Scholar] [CrossRef]
- Geoter, G.; Didaskalou, S.P. Results of Laboratory Tests on Selected Samples of Boreholes NG2/14, NG11/14, NG12/14; Report of geotechnical investigation in Achlada Mine; 2014, unpublished data. (In Greek).
- Steiakakis, E.; Agioutantis, Z.; Monopolis, D. An Investigation of the Kinetic Behavior of a Deep Excavation at an Open Pit Mine Using Finite Elements Analysis. In Proceedings of the AMIREG, Chania, Greece, 7–9 June 2004; pp. 51–56. [Google Scholar]
- Steiakakis, E.; Kavouridis, K.; Monopolis, D. Large Scale Failure of the External Waste Dump at the “South Field” Lignite Mine, Northern Greece. Eng. Geol. 2009, 104, 269–279. [Google Scholar] [CrossRef]
- Arvanitidis, C.; Steiakakis, E.; Agioutantis, Z. Peak Friction Angle of Soils as a Function of Grain Size. Geotech. Geol. Eng. 2019, 37, 1155–1167. [Google Scholar] [CrossRef]
- Ural, S.; Yuksel, F. Geotechnical Characterization of Lignite-Bearing Horizons in the Afsin–Elbistan Lignite Basin, SE Turkey. Eng. Geol. 2004, 75, 129–146. [Google Scholar] [CrossRef]
- Geostudio 2019 R2; Geoslope International Ltd.: Calgary, AB, Canada, 2019.
- Zhang, J.; Li, J. A Comparative Study between Infinite Slope Model and Bishop’s Method for the Shallow Slope Stability Evaluation. Eur. J. Environ. Civ. Eng. 2021, 25, 1503–1520. [Google Scholar] [CrossRef]
- Ouyang, W.; Liu, S.-W.; Yang, Y. An Improved Morgenstern-Price Method Using Gaussian Quadrature. Comput. Geotech. 2022, 148, 104754. [Google Scholar] [CrossRef]
- Morgenstern, N.R.; Price, V.E. The Analysis of the Stability of General Slip Surfaces. Geotechnique 1965, 15, 79–93. [Google Scholar] [CrossRef]
- Atashband, S. Evaluate Reliability of Morgenstern–Price Method in Vertical Excavations. In Numerical Methods for Reliability and Safety Assessment; Springer International Publishing: Cham, Switzerland, 2015; pp. 529–547. [Google Scholar]
- Zhu, D.Y.; Lee, C.F.; Qian, Q.H.; Chen, G.R. A Concise Algorithm for Computing the Factor of Safety Using the Morgenstern– Price Method. Can. Geotech. J. 2005, 42, 272–278. [Google Scholar] [CrossRef]
- Michalowski, R.L.; Nadukuru, S.S. Three-Dimensional Limit Analysis of Slopes with Pore Pressure. J. Geotech. Geoenviron. Eng. 2013, 139, 1604–1610. [Google Scholar] [CrossRef]
- Zhao, L.; Qiao, N.; Zhao, Z.; Zuo, S.; Wang, X. Comparative Study of Material Point Method and Upper Bound Limit Analysis in Slope Stability Analysis. Transp. Saf. Environ. 2020, 2, 44–57. [Google Scholar] [CrossRef]
- Gao, Y.; Song, W.; Zhang, F.; Qin, H. Limit Analysis of Slopes with Cracks: Comparisons of Results. Eng. Geol. 2015, 188, 97–100. [Google Scholar] [CrossRef]
- Chen, W.F. Limit Analysis and Soil Plasticity: Developments in Geotechnical Engineering 7; Elsevier: Amsterdam, The Netherlands, 1975. [Google Scholar]
- Niu, H.; Dong, G.; Ma, X.; Ma, Y. An Analytical Model of a Typhoon Wind Field Based on Spiral Trajectory. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2017, 231, 818–827. [Google Scholar] [CrossRef]
- Plaxis, B.V. Plaxis Finite Element Code for Soil and Rock Analyses; Version 8; RBJ Brinkgreve: Delft, The Netherlands, 2004. [Google Scholar]
- Steiakakis, E.; Agioutantis, Z. A Kinetic Behavior Model at a Surface Lignite Mine, Based on Geotechnical Investigation. Simul. Model Pract. Theory 2010, 18, 558–573. [Google Scholar] [CrossRef]
- Dyson, A.P.; Tolooiyan, A. Prediction and Classification for Finite Element Slope Stability Analysis by Random Field Comparison. Comput. Geotech. 2019, 109, 117–129. [Google Scholar] [CrossRef]
- Liu, S.; Su, Z.; Li, M.; Shao, L. Slope Stability Analysis Using Elastic Finite Element Stress Fields. Eng. Geol. 2020, 273, 105673. [Google Scholar] [CrossRef]
- Gupta, V.; Bhasin, R.K.; Kaynia, A.M.; Kumar, V.; Saini, A.S.; Tandon, R.S.; Pabst, T. Finite Element Analysis of Failed Slope by Shear Strength Reduction Technique: A Case Study for Surabhi Resort Landslide, Mussoorie Township, Garhwal Himalaya. Geomat. Nat. Hazards Risk 2016, 7, 1753. [Google Scholar] [CrossRef]
- Ping, J.; Mengsu, Z. Elastic Parameters Adjusted in Soil Slope Stability and Displacement Analysis. Appl. Mech. Mater. 2013, 303, 2889–2892. [Google Scholar]
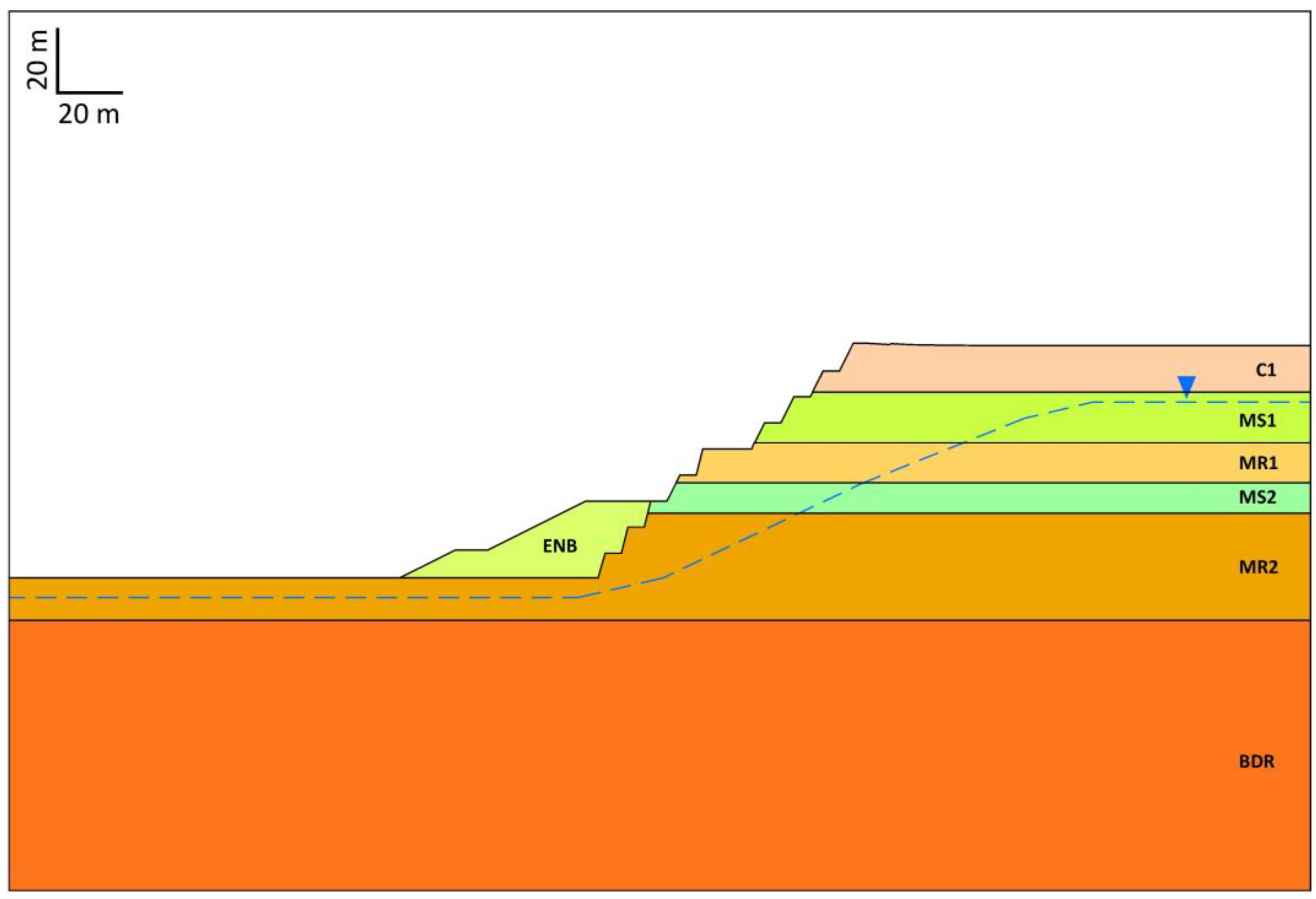



| Soil Name | Unit Weight (kN/m3) | Saturated Unit Weight (kN/m3) | Cohesion (kPa) | Friction Angle (°) | Elastic Modulus (MPa) | Poisson Ratio | Permeability Coefficient (m/s) |
|---|---|---|---|---|---|---|---|
| C1 | 20 | 21 | 35 | 22 | 25 | 0.28 | 1 × 10−7 |
| MS1 | 22 | 23 | 10 | 39 | 60 | 0.30 | 1 × 10−6 |
| MR1 | 20 | 21 | 65 | 26 | 40 | 0.28 | 1 × 10−7 |
| MS2 | 22 | 23 | 12 | 41 | 70 | 0.30 | 1 × 10−6 |
| MR2 | 20 | 21 | 50 | 25 | 35 | 0.35 | 1 × 10−7 |
| BDR | 18 | 19 | 100 | 35 | 100 | 0.30 | 1 × 10−8 |
| ENB | 20 | 21 | 3 | 32 | 50 | 0.25 | 1 × 10−6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Steiakakis, E.; Xiroudakis, G.; Lazos, I.; Vavadakis, D.; Bazdanis, G. Stability Analysis of a Multi-Layered Slope in an Open Pit Mine. Geosciences 2023, 13, 359. https://doi.org/10.3390/geosciences13120359
Steiakakis E, Xiroudakis G, Lazos I, Vavadakis D, Bazdanis G. Stability Analysis of a Multi-Layered Slope in an Open Pit Mine. Geosciences. 2023; 13(12):359. https://doi.org/10.3390/geosciences13120359
Chicago/Turabian StyleSteiakakis, Emmanouil, George Xiroudakis, Ilias Lazos, Dionysios Vavadakis, and George Bazdanis. 2023. "Stability Analysis of a Multi-Layered Slope in an Open Pit Mine" Geosciences 13, no. 12: 359. https://doi.org/10.3390/geosciences13120359
APA StyleSteiakakis, E., Xiroudakis, G., Lazos, I., Vavadakis, D., & Bazdanis, G. (2023). Stability Analysis of a Multi-Layered Slope in an Open Pit Mine. Geosciences, 13(12), 359. https://doi.org/10.3390/geosciences13120359










