Fractal Features in kHz Electromagnetic Observations Preceding Near-Field Earthquakes in Ilia, Greece
Abstract
:1. Introduction
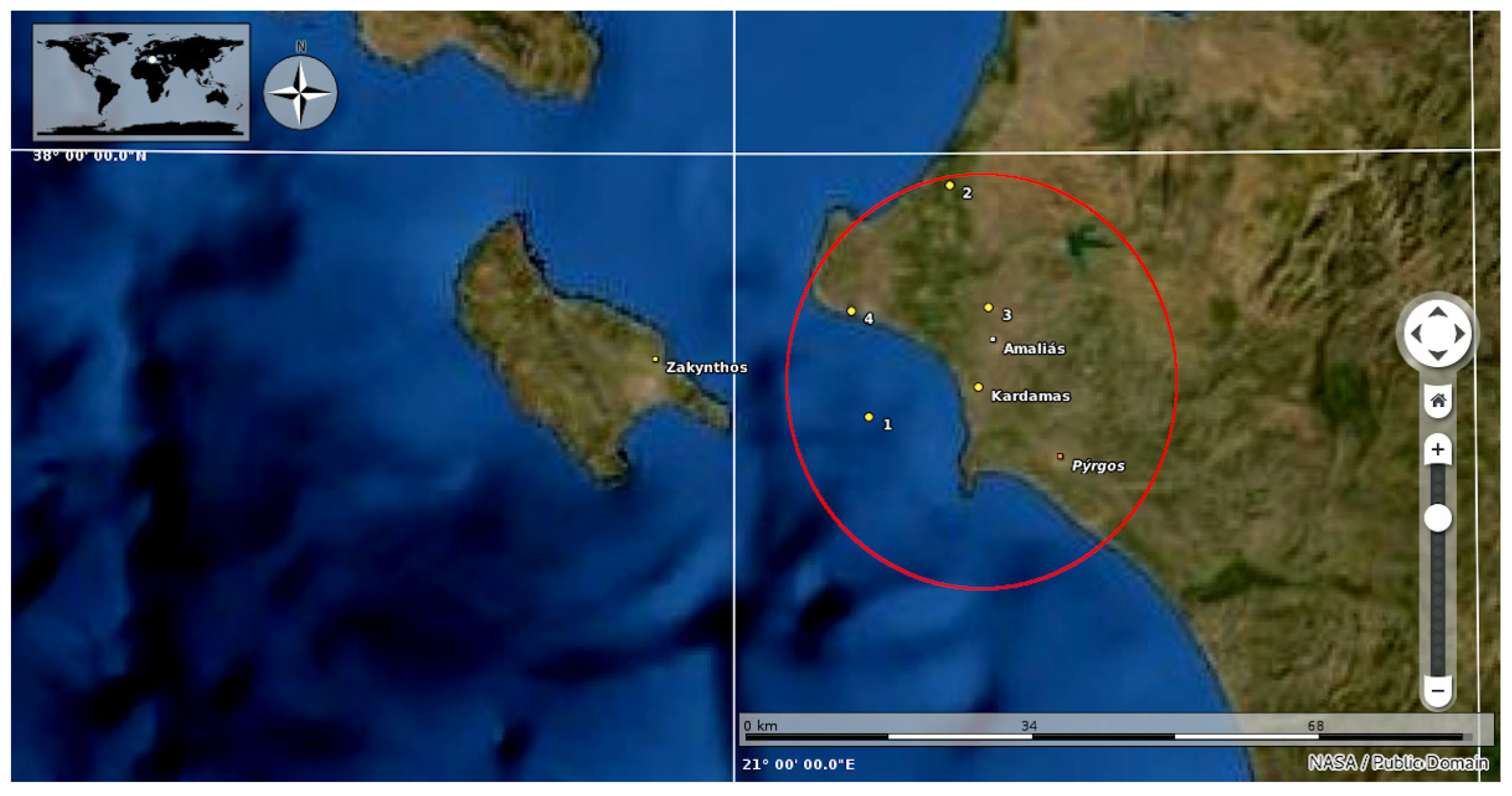
| i | Symbol | Date | GMT | JD | Lt (N) | Lg (E) | Depth (km) | Dist (km) | |
|---|---|---|---|---|---|---|---|---|---|
| 1. | EQ1 | 2019/02/04 | 17:41:09 | 035 | 4.3 | 37.72 | 21.18 | 26.4 | 13.3 |
| 2 | EQ2 | 2018/07/05 | 21:39:05 | 188 | 4.5 | 37.97 | 21.29 | 9.2 | 24.0 |
| 3. | EQ3 | 2015/08/30 | 13:28:02 | 242 | 4.4 | 37.83 | 21.34 | 27.0 | 9.6 |
| 4. | EQ4 | 2015/12/12 | 08:34:09 | 346 | 4.5 | 37.83 | 21.16 | 28.9 | 17.5 |
2. Experimental Aspects
2.1. Geology and Seismic Significance of the Area
2.2. Instrumentation
- (i)
- Circular magnetic field antennas sychronised properly at 3 kHz and at 10 kHz. Two orientations are installed. One at the east-west (EW) orientation and the other to the north-south (NS) orientation.
- (ii)
- Campbell CR-10 data-logger with a 2 h buffer.
- (iii)
- Telemetry equipment continuously sending the measurements to a personal computer at the rate of 1 Hz.
3. Mathematical Aspects
3.1. Power-Law Analysis
3.1.1. Application of Power-Law Analysis
- The EM time-series is divided into segments (windows). In accordance with the previous papers, the segmentation is set to 1024 samples per window.
- The PSD of the EM signal is calculated in each discrete window utilising the CWT with the Morlet base wavelet.
- The PSD is checked for power-law trends of Equation (4), in each segment, by utilising as frequency (f) the central frequency of the Fourier transform of each Morlet wavelet of Equation (3) at the corresponding scale (C). This is implemented via a least square fit to the linear transformation of (4). Accurate fractal segments are considered those with the square of Spearman’s correlation coefficient, of the linear fit.
- Each window advances one sample forward and the steps (1)–(3) are repeated to the end of the time series.
- Plots of power-law b and with time are produced and the partial results were extracted to ASCII files for further use.
3.2. Further Issues
3.2.1. Hurst Exponent
- If 0.5 < 1, the series are persistent. A series’ high value is followed by another high value and a series low value is followed by another low value. The tendencies are long-lasting and occur in the series’ far future.
- If 0 < 0.5, the series are antipersistent. Low series’ values follow high values and vice versa. There is an continuous exchange between low and high values for low H values in the series’ future.
- If , associated series are random.
3.2.2. Class Segmentation
- (a)
- Class I: This class contains the EM segments that exhibit least square log-log fits with Spearman’s coefficient of ≥ and, simultaneously, power-law exponents between 1 ≤ b ≤ 3 (0 ≤ H ≤ 1). These segments are modelled by the fBm category [30,51]. Especially, the Class I EM segments with:
- If b = 2 (H = 0.5), there is no correlation between process increments and the associated geo-system follows random paths driven by non-memory dynamics (random-walk);
- If b = 1.0 (H = 0), the fluctuations of the processes do not grow and the signal is stationary.
- (b)
- Class II: This class contains the EM segments with (A) Spearman’s or (B) and ≤ b < 1 (0 ≤ H < 1), i.e., accurate fractals that follow the fGn category. The Class II EM segments are of low precursory value and low predictability (e.g., [27]).
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cicerone, R.; Ebel, J.; Britton, J. A systematic compilation of earthquake precursors. Tectonophysics 2009, 476, 371–396. [Google Scholar] [CrossRef]
- Hough, S. The Great Quake Debate: The Crusader, the Skeptic, and the Rise of Modern Seismology; University of Washington Press: Seattle, WA, USA, 2020. [Google Scholar]
- Hayakawa, M.; Hobara, Y. Current status of seismo-electromagnetics for short-term earthquake prediction. Geomat. Nat. Hazards Risk 2010, 1, 115–155. [Google Scholar] [CrossRef]
- Molchanov, O.A.; Hayakawa, M. Seismo-Electromagnetics and Related Phenomena: History and Latest Results; Number A8; Terrapub: Tokyo, Japan, 2008; p. 189. [Google Scholar]
- Ouzounov, D.; Pulinets, S.; Hattori, K.; Taylor, P. Pre-Earthquake Processes: A Multidisciplinary Approach to Earthquake Prediction Studies Posters; Wiley John Wiley and Sons: Hoboken, NJ, USA, 2018; p. 384. [Google Scholar]
- Petraki, E.; Nikolopoulos, D.; Nomicos, C.; Stonham, J.; Cantzos, D.; Yannakopoulos, P.; Kottou, S. Electromagnetic Pre-earthquake Precursors: Mechanisms, Data and Models-A Review. J. Earth Sci. Clim. Chang. 2015, 6, 250. [Google Scholar] [CrossRef]
- Petraki, E.; Nikolopoulos, D.; Panagiotaras, D.; Cantzos, D.; Yannakopoulos, P.; Nomicos, C.; Stonham, J. Radon-222: A Potential Short-Term Earthquake Precursor. J. Earth Sci. Clim. Chang. 2015, 6, 282. [Google Scholar] [CrossRef]
- Uyeda, S.; Nagao, T.; Kamogawa, M. Short-term earthquake prediction: Current status of seismo-electromagnetics. Tectonophysics 2009, 470, 205–213. [Google Scholar] [CrossRef]
- Conti, L.; Picozza, P.; Sotgiu, A. A Critical Review of Ground Based Observations of Earthquake Precursors. Front. Earth Sci. 2021, 9, 676766. [Google Scholar] [CrossRef]
- Joshi, S.; Madhusudhanarao, K. Ultra-Low Frequency Geomagnetic Variations before Dholavira Earthquake M = 5.1 on the 20th of June 2012 in Kachchh Region, Gujarat, India. Geotectonics 2021, 55, 633–645. [Google Scholar] [CrossRef]
- Bulusu, J.; Arora, K.; Singh, S.; Edara, A. Simultaneous electric, magnetic and ULF anomalies associated with moderate earthquakes in Kumaun Himalaya. Nat. Hazards 2023, 116, 3925–3955. [Google Scholar] [CrossRef]
- Hayakawa, M.; Itoh, T.; Hattori, K.; Yumoto, K. ULF electromagnetic precursors for an earthquake at Biak, Indonesia on February 17, 1996. Geophys. Res. Lett. 2000, 27, 1531–1534. [Google Scholar] [CrossRef]
- Hayakawa, M. VLF/LF radio sounding of ionospheric perturbations associated with earthquakes. Sensors 2007, 7, 1141–1158. [Google Scholar] [CrossRef]
- Ida, Y.; Yang, D.; Li, Q.; Sun, H.; Hayakawa, M. Fractal analysis of ULF electromagnetic emissions in possible association with earthquakes in China. Nonlin. Processes Geophys. 2012, 19, 577–583. [Google Scholar] [CrossRef]
- Ida, Y.; Hayakawa, M. Fractal analysis for the ULF data during the 1993 Guam earthquake to study prefracture criticality. Nonlin. Processes Geophys. 2012, 13, 409–412. [Google Scholar] [CrossRef]
- Kapiris, P.; Peratzakis, J.P.A.; Nomikos, K.; Eftaxias, K. VHF-electromagnetic evidence of the underlying pre-seismic critical stage. Earth Planets Space 2002, 54, 1237–1246. [Google Scholar] [CrossRef]
- Sarlis, N.; Skordas, E.; Varotsos, P.; Nagao, T.; Kamogawa, M.; Tanaka, H.; Uyeda, S. Minimum of the order parameter fluctuations of seismicity before major earthquakes in Japan. Proc. Natl. Acad. Sci. USA 2013, 110, 13734–13738. [Google Scholar] [CrossRef] [PubMed]
- Skordas, E.S. On the increase of the “non-uniform” scaling of the magnetic field variations before the M(w)9.0 earthquake in Japan in 2011. Chaos 2014, 24, 023131. [Google Scholar] [CrossRef] [PubMed]
- Smirnova, N.A.; Kiyashchenko, D.A.; Troyan, N.V.; Hayakawa, M. Multifractal Approach to Study the Earthquake Precursory Signatures Using the Ground-Based Observations. Rev. Appl. Phys. 2013, 2, 3. [Google Scholar]
- Smirnova, N.; Hayakawa, M. Fractal characteristics of the ground-observed ULF emissions in relation to geomagnetic and seismic activities. J. Atmos. Sol. Ter. Phys. 2007, 69, 1833–1841. [Google Scholar] [CrossRef]
- Varotsos, P.; Alexopoulos, K. Physical properties of the variations of the electric field of the earth preceding earthquakes, I. Tectonophysics 1984, 110, 73–98. [Google Scholar] [CrossRef]
- Varotsos, P.; Alexopoulos, K. Physical properties of the variations of the electric field of the earth preceding earthquakes, II. Tectonophysics 1984, 110, 99–125. [Google Scholar] [CrossRef]
- Varotsos, P.; Sarlis, N.; Skordas, E. Magnetic field variations associated with SES. The instrumentation used for investigating their detectability. Proc. Jpn. Acad. Ser. B 2001, 77, 87–92. [Google Scholar] [CrossRef]
- Varotsos, P.; Sarlis, N.; Skordas, E. Long-range correlations in the electric signals that precede rupture: Further investigations. Phys. Rev. E 2003, 67, 021109. [Google Scholar] [CrossRef]
- Varotsos, P.; Sarlis, N.; Skordas, E.; Lazaridou, M. Electric pulses some minutes before earthquake occurrences. Appl. Phys. Lett. 2007, 90, 064104. [Google Scholar] [CrossRef]
- Eftaxias, K.; Balasis, G.; Contoyiannis, Y.; Papadimitriou, C.; Kalimeri, M. Unfolding the procedure of characterizing recorded ultra low frequency, kHZ and MHz electromagnetic anomalies prior to the L’Aquila earthquake as pre-seismic ones—Part 2. Nat. Hazards Earth Syst. Sci. 2010, 10, 275–294. [Google Scholar] [CrossRef]
- Cantzos, D.; Nikolopoulos, D.; Petraki, E.; Yannakopoulos, P.H.; Nomicos, C. Earthquake precursory signatures in electromagnetic radiation measurements in terms of day-to-day fractal spectral exponent variation: Analysis of the eastern Aegean 13/04/2017–20/07/2017 seismic activity. J. Seismol. 2018, 22, 1499–1513. [Google Scholar] [CrossRef]
- Nikolopoulos, D.; Petraki, E.; Cantzos, D.; Yannakopoulos, P.H.; Panagiotaras, D.; Nomicos, C. Fractal Analysis of Pre-Seismic Electromagnetic and Radon Precursors: A Systematic Approach. J. Earth Sci. Clim. Chang. 2016, 7, 1–11. [Google Scholar]
- Nikolopoulos, D.; Matsoukas, C.; Yannakopoulos, P.H.; Petraki, E.; Cantzos, D.; Nomicos, C. Long-Memory and Fractal Trends in Variations of Environmental Radon in Soil: Results from Measurements in Lesvos Island in Greece. J. Earth Sci. Clim. Chang. 2018, 9, 1–11. [Google Scholar] [CrossRef]
- Nikolopoulos, D.; Yannakopoulos, P.H.; Petraki, E.; Cantzos, D.; Nomicos, C. Long-Memory and Fractal Traces in kHz-MHz Electromagnetic Time Series Prior to the ML = 6.1, 12/6/2007 Lesvos, Greece Earthquake: Investigation through DFA and Time-Evolving Spectral Fractals. J. Earth Sci. Clim. Chang. 2018, 9, 1–15. [Google Scholar]
- Petraki, E. Electromagnetic Radiation and Radon-222 Gas Emissions as Precursors of Seismic Activity. Ph.D. Thesis, Department of Electronic and Computer Engineering, Brunel University, London, UK, 2016. [Google Scholar]
- Petraki, E.; Nikolopoulos, D.; Fotopoulos, A.; Panagiotaras, D.; Koulouras, G.; Zisos, A.; Nomicos, C.; Louizi, A.; Stonham, J. Self-organised critical features in soil radon and MHz electromagnetic disturbances: Results from environmental monitoring in Greece. Appl. Radiat. Isotop. 2013, 72, 39–53. [Google Scholar] [CrossRef]
- Petraki, E.; Nikolopoulos, D.; Fotopoulos, A.; Panagiotaras, D.; Nomicos, C.; Yannakopoulos, P.; Kottou, S.; Zisos, A.; Louizi, A.; Stonham, J. Long-range memory patterns in variations of environmental radon in soil. Anal. Methods 2013, 5, 4010–4020. [Google Scholar] [CrossRef]
- Nikolopoulos, D.; Cantzos, D.; Petraki, E.; Yannakopoulos, P.H.; Nomicos, C. Traces of long-memory in pre-seismic MHz electromagnetic time series-Part1: Investigation through the R/S analysis and time-evolving spectral fractals. J. Earth Sci. Clim. Chang. 2016, 7, 359. [Google Scholar] [CrossRef]
- Nikolopoulos, D.; Petraki, E.; Yannakopoulos, P.H.; Priniotakis, G.; Voyiatzis, I.; Cantzos, D. Long-lasting patterns in 3 kHz electromagnetic time series after the ML = 6.6 earthquake of 2018-10-25 near Zakynthos, Greece. Geosciences 2020, 10, 235. [Google Scholar] [CrossRef]
- Zong, J.; Tao, D.; Shen, X. Possible ELF/VLF Electric Field Disturbances Detected by Satellite CSES before Major Earthquakes. Atmosphere 2022, 13, 1394. [Google Scholar] [CrossRef]
- Yonaiguchi, N.; Ida, Y.; Hayakawa, M.; Masuda, S. Fractal analysis for VHF electromagnetic noises and the identification of preseismic signature of an earthquake. J. Atmos. Sol. Ter. Phys. 2007, 69, 1825–1832. [Google Scholar] [CrossRef]
- Balasis, G.; Daglis, I.; Papadimitriou, C.; Kalimeri, M.; Anastasiadis, A.; Eftaxias, K. Dynamical complexity in Dst time series using non-extensive Tsallis entropy. Geophys. Res. Lett. 2008, 35, 1–6. [Google Scholar] [CrossRef]
- Smirnova, N.; Hayakawa, M.; Gotoh, K. Precursory behavior of fractal characteristics of the ULF electromagnetic fields in seismic active zones before strong earthquakes. Phys. Chem. Earth 2004, 29, 445–451. [Google Scholar] [CrossRef]
- Varotsos, P.; Sarlis, N.; Skordas, E. Scale-specific order parameter fluctuations of seismicity in natural time before mainshocks. Europhys. Lett. 2011, 96, 59002. [Google Scholar] [CrossRef]
- Varotsos, P.; Sarlis, N.; Skordas, E.S.; Christopoulos, G.; Lazaridou, M.S. Identifying the occurrence time of an impending mainshock: A very recent case. Earthq. Sci. 2015, 8, 215–222. [Google Scholar] [CrossRef]
- Varotsos, P.; Sarlis, N.; Skordas, E. Identifying the occurrence time of an impending major earthquake: A review. Earthq. Sci. 2017, 30, 209–218. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Order Parameter and Entropy of Seismicity in Natural Time before Major Earthquakes: Recent Results. Geosciences 2022, 12, 225. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S.; Nagao, T.; Kamogawa, M.; Flores-Márquez, E.L.; Ramírez-Rojas, A.; Perez-Oregon, J. Improving the Estimation of the Occurrence Time of an Impending Major Earthquake Using the Entropy Change of Seismicity in Natural Time Analysis. Geosciences 2023, 13, 222. [Google Scholar] [CrossRef]
- Jiang, F.; Chen, X.; Chen, C.C.; Chen, H.J. Relationship Between Seismic Electric Signals and Tectonics Derived from Dense Geoelectric Observations in Taiwan. Pure Appl. Geophys. 2020, 177, 441–454. [Google Scholar] [CrossRef]
- Argunov, V.V.; Gotovcev, M.R. Study of Ionospheric Effects and Earthquake Precursors Using Radio Engineering Methods. IOP Conf. Ser. Earth Environ. Sci. 2021, 720, 012087. [Google Scholar] [CrossRef]
- Thomas, J.E.; Ekanem, A.M.; George, N.J.; Akpan, A.E. Ionospheric perturbations: A case study of 2007 five major earthquakes using DEMETER data. Acta Geophys. 2023, 71, 1607–1618. [Google Scholar] [CrossRef]
- Vesnin, A.; Yasyukevich, Y.; Perevalova, N.; Şentürk, E. Ionospheric Response to the 6 February 2023 Turkey&-Syria Earthquake. Remote Sens. 2023, 15, 2336. [Google Scholar] [CrossRef]
- Nikolopoulos, D.; Moustris, K.; Petraki, E.; Cantzos, D. Fractal and long-memory traces in PM10 time series in Athens, Greece. Environmnets 2019, 6, 29. [Google Scholar] [CrossRef]
- Nikolopoulos, D.; Moustris, K.; Petraki, E.; Cantzos, D. Long-memory traces in PM _ 10 time series in Athens, Greece: Investigation through DFA and R/S analysis. Meteorol. Atmos. Phys. 2021, 133, 261–279. [Google Scholar] [CrossRef]
- Eftaxias, K.; Balasis, G.; Contoyiannis, Y.; Papadimitriou, C.; Kalimeri, M.; Athanasopoulou, L.; Nikolopoulos, S.; Kopanas, J.; Antonopoulos, G.; Nomicos, C. Unfolding the procedure of characterizing recorded ultra low frequency, kHZ and MHz electromagnetic anomalies prior to the L’Aquila earthquake as pre-seismic ones-Part 1. Nat. Hazard Earth Syst. 2009, 9, 1953–1971. [Google Scholar] [CrossRef]
- Gotoh, K.; Hayakawa, M.; Smirnova, N.; Hattori, K. Fractal analysis of seismogenic ULF emissions. Phys. Chem. Earth 2004, 29, 419–424. [Google Scholar] [CrossRef]
- NOA. Available online: https://www.gein.noa.gr/en/services-products/database-search/ (accessed on 11 August 2023).
- Davis, G.H. Partitioned tectonic shortening, with emphasis on outcrop-scale folding and flattening, Pindos fold-and-thrust belt, Peloponnese, Greece. Can. J. Earth Sci. 2019, 56, 1181–1201. [Google Scholar] [CrossRef]
- Skourlis, K.; Doutsos, T. The Pindos Fold-and-thrust belt (Greece): Inversion kinematics of a passive continental margin. Int. J. Earth Sci. 2003, 92, 891–903. [Google Scholar] [CrossRef]
- Lekas, A.; Fountoulis, I.; Papanikolaou, D. Intensity Distribution and Neotectonic Macrostructure Pyrgos Earthquake Data (26 March 1993, Greece. Nat. Hazards 2000, 21, 19–33. [Google Scholar] [CrossRef]
- USGS. Available online: https://earthquake.usgs.gov/earthquakes/map/?extent=22.41103,91.51611&extent=35.56798,113.57666&range=search&baseLayer=terrain&timeZone=utc&search=%7B%22name%22:%22Search%20Results%22,%22params%22:%7B%22starttime%22:%222008-01-01%2000:00:00%22,%22endtime%22:%222009-01-01%2000:00:00%22,%22maxlatitude%22:36.844,%22minlatitude%22:22.999,%22maxlongitude%22:116.323,%22minlongitude%22:96.504,%22minmagnitude%22:5.5,%22orderby%22:%22time%22%7D%7D (accessed on 26 May 2023).
- Mandelbrot, B.B.; Ness, J.W.V. Fractional Brownian motions, fractional noises and applications. J. Soc. Ind. Appl. Math. 1968, 10, 422–437. [Google Scholar] [CrossRef]
- Morales, I.O.; Landa, O.; Fossion, R.; Frank, A. Scale invariance, self-similarity and critical behaviour in classical and quantum system. J. Phys. Conf. Ser. 2012, 380, 012020. [Google Scholar] [CrossRef]
- Musa, M.; Ibrahim, K. Existence of long memory in ozone time series. Sains Malays. 2012, 41, 1367–1376. [Google Scholar]
- Vadrevu, K.P. Fractal analysis revealed persistent correlations in long-term vegetation fire data in most South and Southeast Asian countries. Environ. Res. Commun. 2023, 5, 011001. [Google Scholar] [CrossRef]
- May, R.M. Simple mathematical models with very complicated dynamics. Nature 1976, 261, 459–467. [Google Scholar] [CrossRef]
- Sugihara, G.; May, R. Nonlinear forecasting as a way of distinguishing chaos from measurement error in time series. Nature 1990, 344, 734–741. [Google Scholar] [CrossRef]
- Liu, C.; Liang, J.; Li, Y.; Shi, K. Fractal analysis of impact of PM2.5 on surface O3 sensitivity regime based on field observations. Sci. Total. Environ. 2023, 858, 160136. [Google Scholar] [CrossRef]
- Pastén, D.; Pavez-Orrego, C. Multifractal time evolution for intraplate earthquakes recorded in southern Norway during 1980–2021. Chaos Solitons Fractals 2023, 167, 113000. [Google Scholar] [CrossRef]
- Chelidze, T.; Matcharashvili, T.; Mepharidze, E.; Dovgal, N. Complexity in Geophysical Time Series of Strain/Fracture at Laboratory and Large Dam Scales: Review. Entropy 2023, 25, 467. [Google Scholar] [CrossRef]
- Kapiris, P.; Eftaxias, K.; Nomikos, K.; Polygiannakis, J.; Dologlou, E.; Balasis, G.; Bogris, N.; Peratzakis, A.; Hadjicontis, V. Evolving towards a critical point: A possible electromagnetic way in which the critical regime is reached as the rupture approaches. Nonlinear Proc. Geoph. 2003, 10, 1–14. [Google Scholar] [CrossRef]
- Eftaxias, K.; Contoyiannis, Y.; Balasis, G.; Karamanos, K.; Kopanas, J.; Antonopoulos, G.; Koulouras, G.; Nomicos, C. Evidence of fractional-Brownian-motion-type asperity model for earthquake generation in candidate pre-seismic electromagnetic emissions. Nat. Hazard Earth Syst. 2008, 8, 657–669. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Attempt to distinguish electric signals of a dichotomous nature. Phys. Rev. E 2003, 68, 031106. [Google Scholar] [CrossRef] [PubMed]
- Hurst, H. Long term storage capacity of reservoirs. Trans. Am. Soc. Civ. Eng. 1951, 116, 770–808. [Google Scholar] [CrossRef]
- Hurst, H.; Black, R.; Simaiki, Y. Long-Term Storage: An Experimental Study; Constable: London, UK, 1965. [Google Scholar]
- Lopez, T.; Martınez-Gonzalez, C.; Manjarrez, J.; Plascencia, N.; Balankin, A. Fractal Analysis of EEG Signals in the Brain of Epileptic Rats, with and without Biocompatible Implanted Neuroreservoirs. Appl. Mech. Mater. 2009, 15, 127–136. [Google Scholar] [CrossRef]
- Kilcik, A.; Anderson, C.; Rozelot, J.; Ye, H.; Sugihara, G.; Ozguc, A. Nonlinear Prediction of Solar Cycle 24. Astrophys. J. 2009, 693, 1173–1177. [Google Scholar] [CrossRef]
- Chattopadhyay, A.; Khondekar, M. An investigation of the relationship between the CME and the Geomagnetic Storm. Astron. Comput. 2023, 43, 100695. [Google Scholar] [CrossRef]
- Dattatreya, G. Hurst Parameter Estimation from Noisy Observations of Data Traffic Traces. In Proceedings of the 4th WSEAS International Conference on Electronics, Control and Signal Processing, Rio de Janeiro, Brazil, 25–27 April 2005; pp. 193–198. [Google Scholar]
- Wang, F.; Wang, H.; Zhou, X.; Fu, R. A Driving Fatigue Feature Detection Method Based on Multifractal Theory. IEEE Sens. J. 2022, 22, 19046–19059. [Google Scholar] [CrossRef]
- Zhou, H.; Chang, F. The long-memory temporal dependence of traffic crash fatality for different types of road users. Phys. A Stat. Mech. Appl. 2022, 607, 128210. [Google Scholar] [CrossRef]
- Rehman, S.; Siddiqi, A. Wavelet based Hurst exponent and fractal dimensional analysis of Saudi climatic dynamics. Chaos Solitons Fractals 2009, 39, 1081–1090. [Google Scholar] [CrossRef]
- Li, X.; Polygiannakis, J.; Kapiris, P.; Peratzakis, A.; Eftaxias, K.; Yao, X. Fractal spectral analysis of pre-epileptic seizures in terms of criticality. J. Neural Eng. 2005, 2, 11–16. [Google Scholar] [CrossRef] [PubMed]
- Escobar-Ipuz, F.; Torres, A.; García-Jiménez, M.; Basar, C.; Cascón, J.; Mateo, J. Prediction of patients with idiopathic generalized epilepsy from healthy controls using machine learning from scalp EEG recordings. Brain Res. 2023, 1798, 148131. [Google Scholar] [CrossRef]
- Wijayanto, I.; Humairani, A.; Hadiyoso, S.; Rizal, A.; Prasanna, D.L.; Tripathi, S.L. Epileptic seizure detection on a compressed EEG signal using energy measurement. Biomed. Signal Process. Control 2023, 85, 104872. [Google Scholar] [CrossRef]
- Granero, M.S.; Segovia, J.T.; Perez, J.G. Some comments on Hurst exponent and the long memory processes on capital Markets. Physica A 2008, 387, 5543–5551. [Google Scholar] [CrossRef]
- Musaev, A.; Makshanov, A.; Grigoriev, D. The Genesis of Uncertainty: Structural Analysis of Stochastic Chaos in Finance Markets. Complexity 2023, 2023, 1302220. [Google Scholar] [CrossRef]
- Pérez-Sienes, L.; Grande, M.; Losada, J.C.; Borondo, J. The Hurst Exponent as an Indicator to Anticipate Agricultural Commodity Prices. Entropy 2023, 25, 579. [Google Scholar] [CrossRef] [PubMed]
- Vogl, M. Hurst exponent dynamics of S&P 500 returns: Implications for market efficiency, long memory, multifractality and financial crises predictability by application of a nonlinear dynamics analysis framework. Chaos Solitons Fractals 2023, 166, 112884. [Google Scholar] [CrossRef]
- Fujinawa, Y.; Takahashi, K. Electromagnetic radiations associated with major earthquakes. Phys. Earth Planet Inter. 1998, 105, 249–259. [Google Scholar] [CrossRef]
- Alam, A.; Wang, N.; Petraki, E.; Barkat, A.; Huang, F.; Shah, M.A.; Cantzos, D.; Priniotakis, G.; Yannakopoulos, P.H.; Papoutsidakis, M.; et al. Fluctuation Dynamics of Radon in Groundwater Prior to the Gansu Earthquake, China (22 July 2013: Ms = 6.6): Investigation with DFA and MFDFA Methods. Pure Appl. Geophys. 2021, 178, 3375–3395. [Google Scholar] [CrossRef]
- Telesca, L.; Lasaponara, R. Vegetational patterns in burned and unburned areas investigated by using the detrended fluctuation analysis. Physica A 2006, 368, 531–535. [Google Scholar] [CrossRef]
- Morgounov, V. Relaxation creep model of impending earthquake. Ann. Geophys. 2001, 44, 369–381. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Self-organized criticality and earthquake predictability: A long-standing question in the light of natural time analysis. Europhys. Lett. 2020, 132, 29001. [Google Scholar] [CrossRef]
- Contoyiannis, Y.; Kapiris, P.; Eftaxias, K. Monitoring of a preseismic phase from its electromagnetic precursors. Phys. Rev. E 2005, 71, 066123. [Google Scholar] [CrossRef] [PubMed]
- Minadakis, G.; Potirakis, S.; Nomicos, C.; Eftaxias, K. Linking electromagnetic precursors with earthquake dynamics: An approach based on nonextensive fragment and self-affine asperity models. Physica A 2012, 391, 2232–2244. [Google Scholar] [CrossRef]
- Papadimitriou, C.; Kalimeri, M.; Eftaxias, K. Nonextensivity and universality in the earthquake preparation process. Phys. Rev. E 2008, 77, 036101. [Google Scholar] [CrossRef]
- Cantzos, D.; Nikolopoulos, D.; Petraki, E.; Nomicos, C.; Yannakopoulos, P.H.; Kottou, S. Identifying Long-Memory Trends in Pre-Seismic MHz Disturbances through Support Vector Machines. J. Earth. Sci. Clim. Chang. 2015, 6, 1–9. [Google Scholar]
- Nikolopoulos, D.; Petraki, E.; Marousaki, A.; Potirakis, S.; Koulouras, G.; Nomicos, C.; Panagiotaras, D.; Stonhamb, J.; Louizi, A. Environmental monitoring of radon in soil during a very seismically active period occurred in South West Greece. J. Environ. Monit. 2012, 14, 564–578. [Google Scholar] [CrossRef]


| Class II | Class I | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| s.fGn | s.fBm | |||||||||||||
| S | A | R | P | A-P | P | |||||||||
| i/i | EQ | Antenna | Class I | Class II | Y | JD | Figure | |||||||
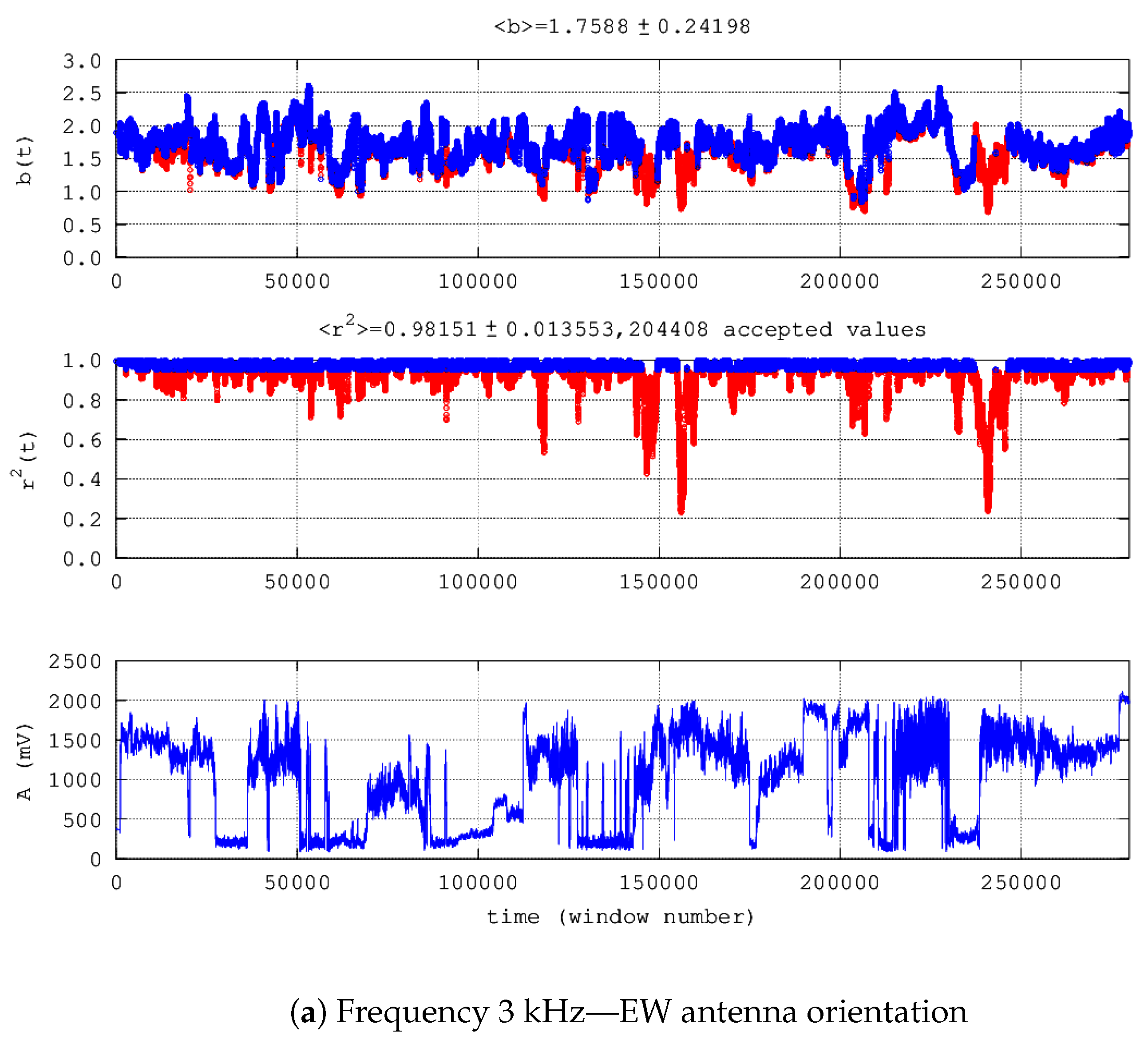
| 1. | EQ1 | 3 kHz EW | 200,813 | 78,055 | 3595 | 0 | 183,584 | 0 | 17,229 | 97,594 | 1490 | 2019 | 031-035 | Figure 3a |
| 2. | 3 kHz NS | 186,757 | 92,111 | 2362 | 0 | 180,131 | 0 | 6626 | 9004 | 30 | 2019 | 031-035 | Figure 3b | |
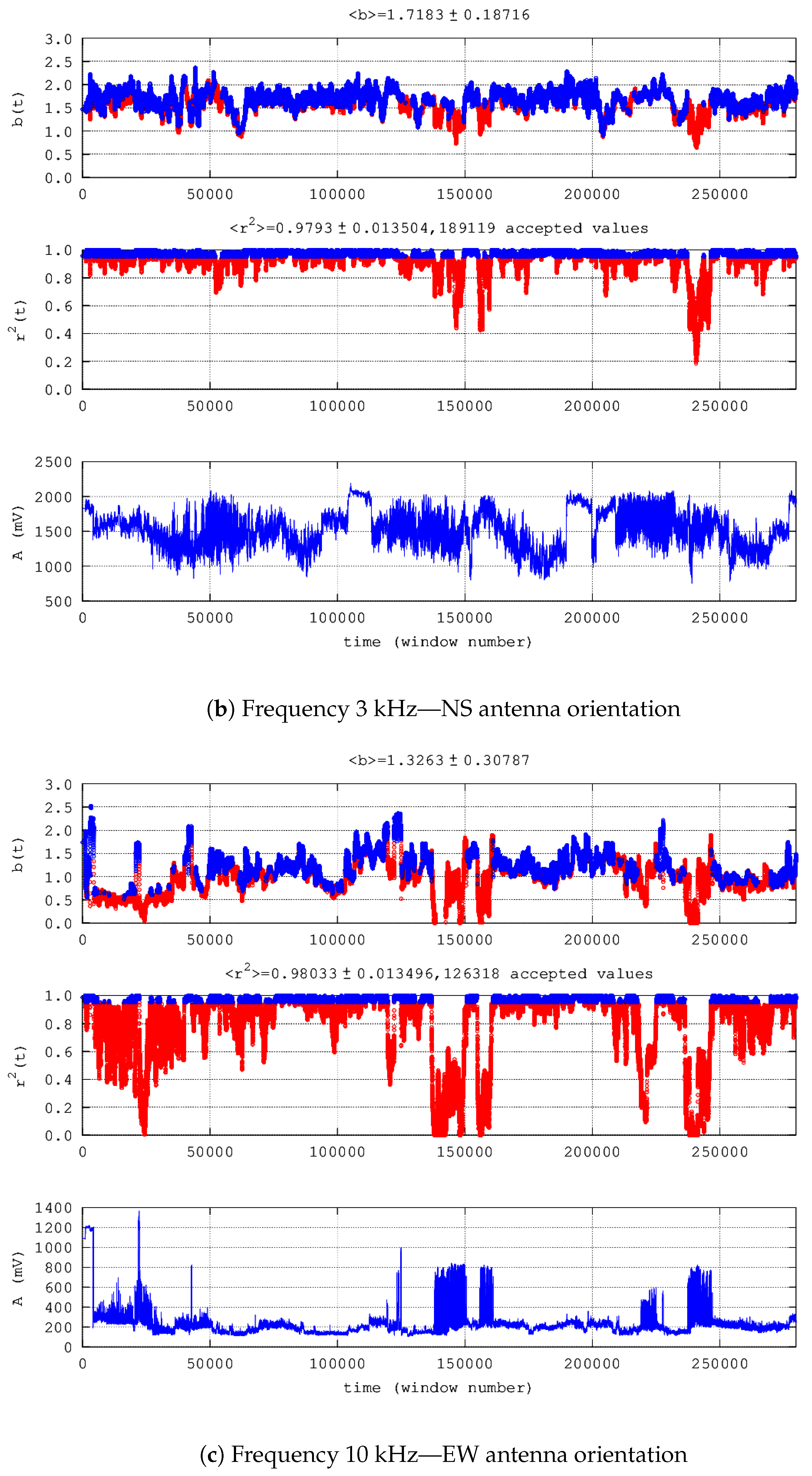
| 3. | 10 kHz EW | 67,124 | 211,744 | 59,194 | 0 | 61,811 | 0 | 5313 | 8774 | 593 | 2019 | 031-035 | Figure 3c | |
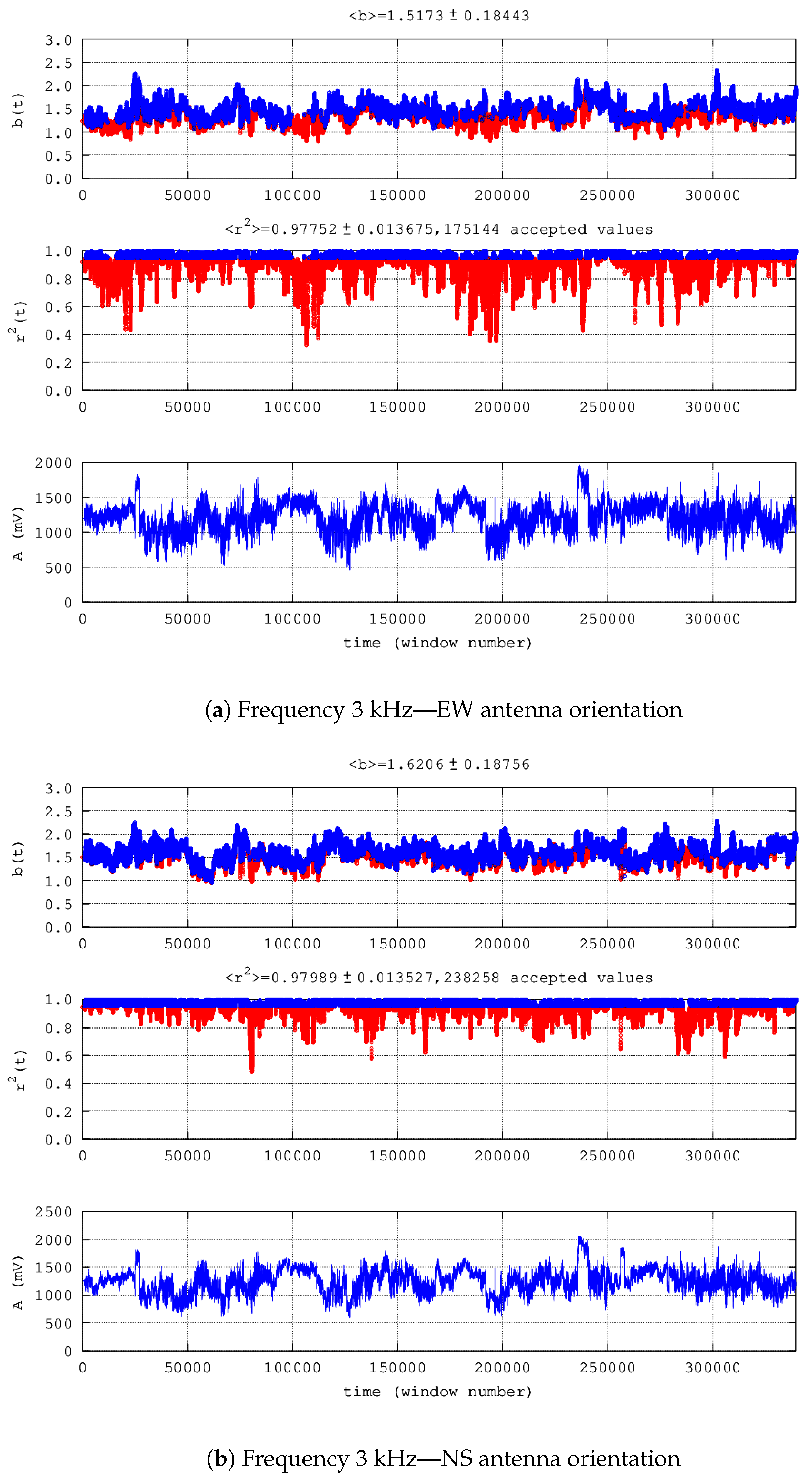
| 4. | EQ2 | 3 kHz EW | 197,361 | 121,569 | 5800 | 0 | 191,726 | 0 | 5635 | 65,278 | 0 | 2018 | 185-188 | Figure 4a |
| 5. | 3 kHz NS | 194,585 | 124,345 | 6254 | 0 | 190,822 | 0 | 3762 | 59,609 | 6 | 2018 | 185-188 | Figure 4b | |
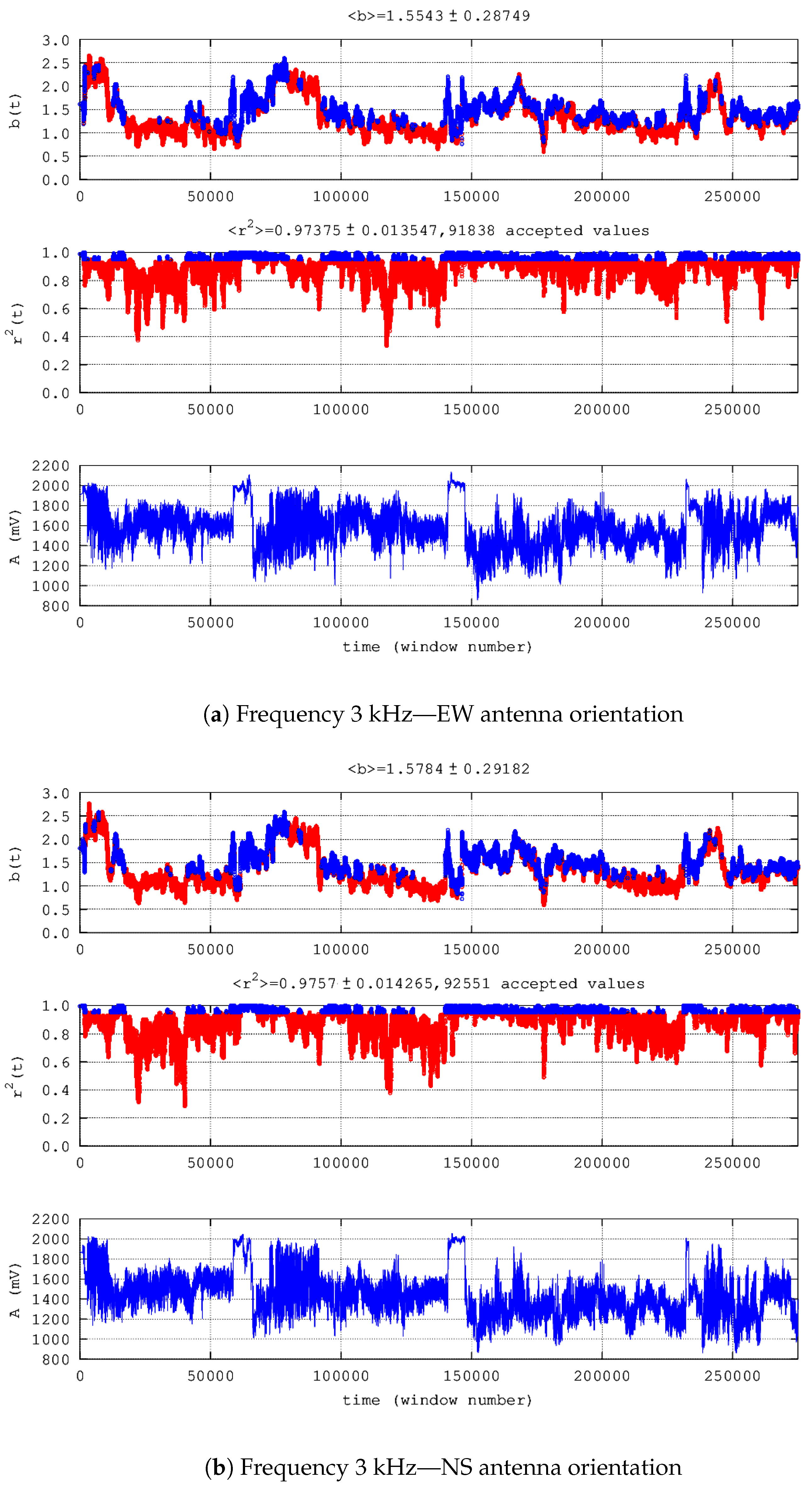
| 6. | EQ3 | 3 kHz EW | 173,415 | 165,282 | 1729 | 1 | 173,061 | 0 | 353 | 10,991 | 0 | 2015 | 239-242 | Figure 5a |
| 7. | 3 kHz NS | 238,076 | 100,621 | 182 | 0 | 235,567 | 0 | 2509 | 53,489 | 0 | 2015 | 239-242 | Figure 5b | |
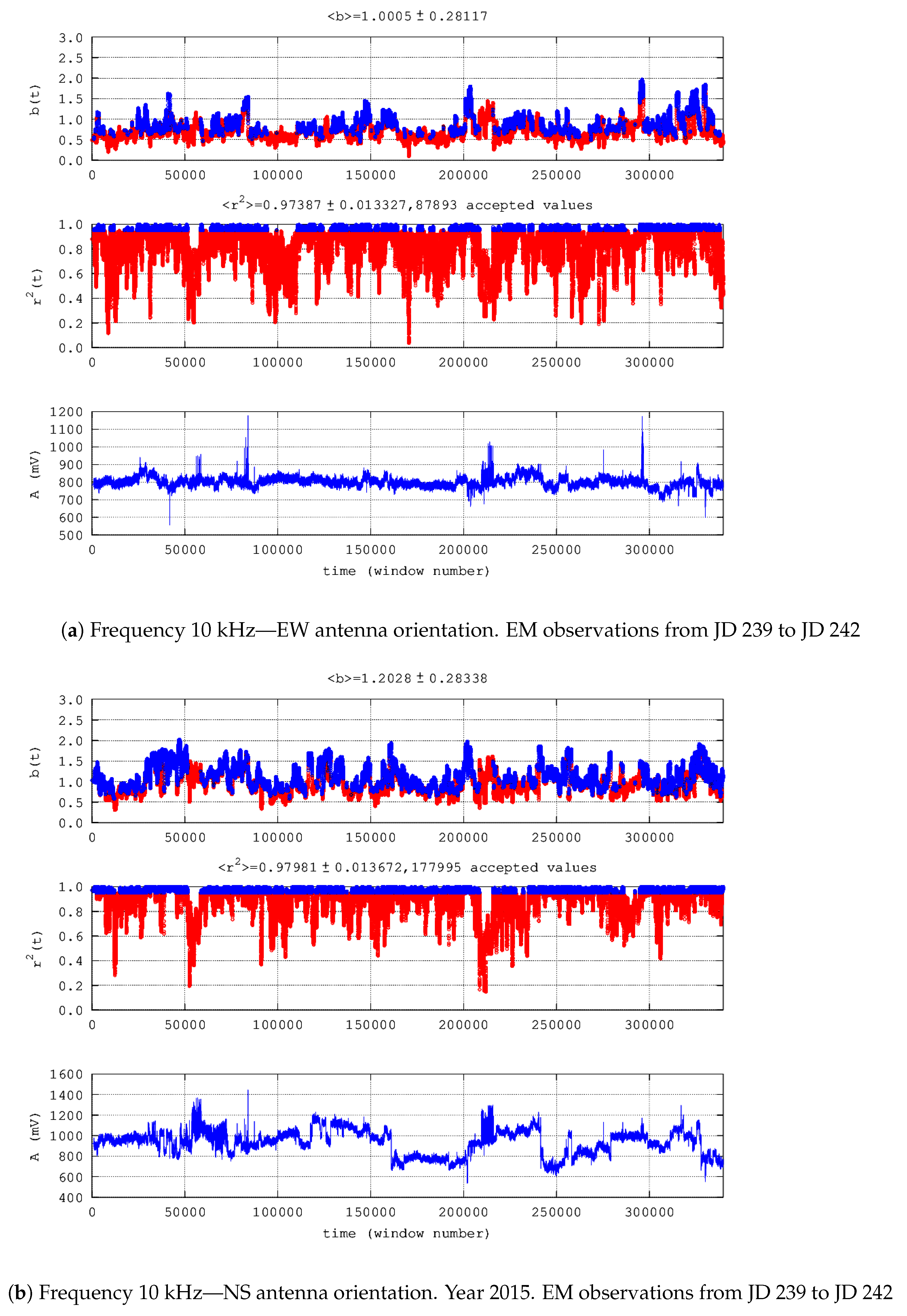
| 8. | 10 kHz EW | 10,479 | 328,218 | 77,414 | 0 | 10,479 | 0 | 0 | 0 | 0 | 2015 | 239-242 | Figure 7a | |
| 9. | 10 kHz NS | 86,099 | 252,598 | 91,896 | 1 | 86,084 | 0 | 14 | 14,502 | 0 | 2015 | 343-346 | Figure 7b | |
| 10. | EQ4 | 3 kHz EW | 78,503 | 195,490 | 13,335 | 0 | 55,423 | 1 | 23,079 | 11,271 | 94,200 | 2015 | 343-346 | Figure 6a |
| 11. | 3 kHz NS | 81,335 | 192,658 | 11,216 | 0 | 56,278 | 0 | 25,057 | 25,995 | 8495 | 2015 | 343-346 | Figure 6b | |
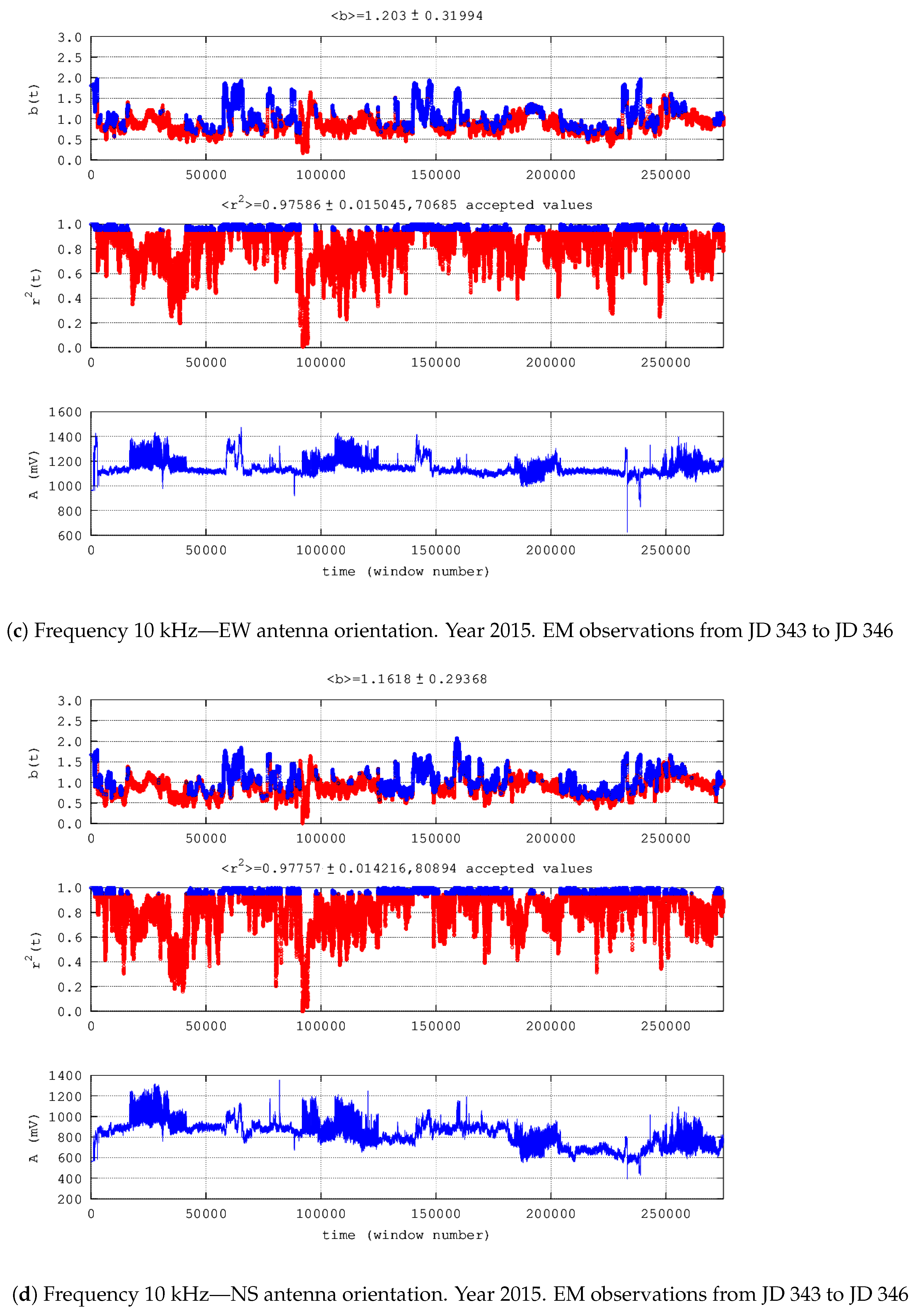
| 12. | 10 kHz EW | 19,176 | 254,817 | 51,509 | 0 | 19,176 | 0 | 0 | 3450 | 0 | 2015 | 343-346 | Figure 7c | |
| 13. | 10 kHz NS | 26,471 | 247,522 | 54,423 | 0 | 126,471 | 0 | 80,891 | 693 | 0 | 2015 | 343-346 | Figure 7d | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nikolopoulos, D.; Petraki, E.; Rafique, M.; Alam, A.; Cantzos, D.; Yannakopoulos, P. Fractal Features in kHz Electromagnetic Observations Preceding Near-Field Earthquakes in Ilia, Greece. Geosciences 2023, 13, 387. https://doi.org/10.3390/geosciences13120387
Nikolopoulos D, Petraki E, Rafique M, Alam A, Cantzos D, Yannakopoulos P. Fractal Features in kHz Electromagnetic Observations Preceding Near-Field Earthquakes in Ilia, Greece. Geosciences. 2023; 13(12):387. https://doi.org/10.3390/geosciences13120387
Chicago/Turabian StyleNikolopoulos, Dimitrios, Ermioni Petraki, Muhammad Rafique, Aftab Alam, Demetrios Cantzos, and Panayiotis Yannakopoulos. 2023. "Fractal Features in kHz Electromagnetic Observations Preceding Near-Field Earthquakes in Ilia, Greece" Geosciences 13, no. 12: 387. https://doi.org/10.3390/geosciences13120387
APA StyleNikolopoulos, D., Petraki, E., Rafique, M., Alam, A., Cantzos, D., & Yannakopoulos, P. (2023). Fractal Features in kHz Electromagnetic Observations Preceding Near-Field Earthquakes in Ilia, Greece. Geosciences, 13(12), 387. https://doi.org/10.3390/geosciences13120387








