Automating the Process for Estimating Tunneling Induced Ground Stability and Settlement
Abstract
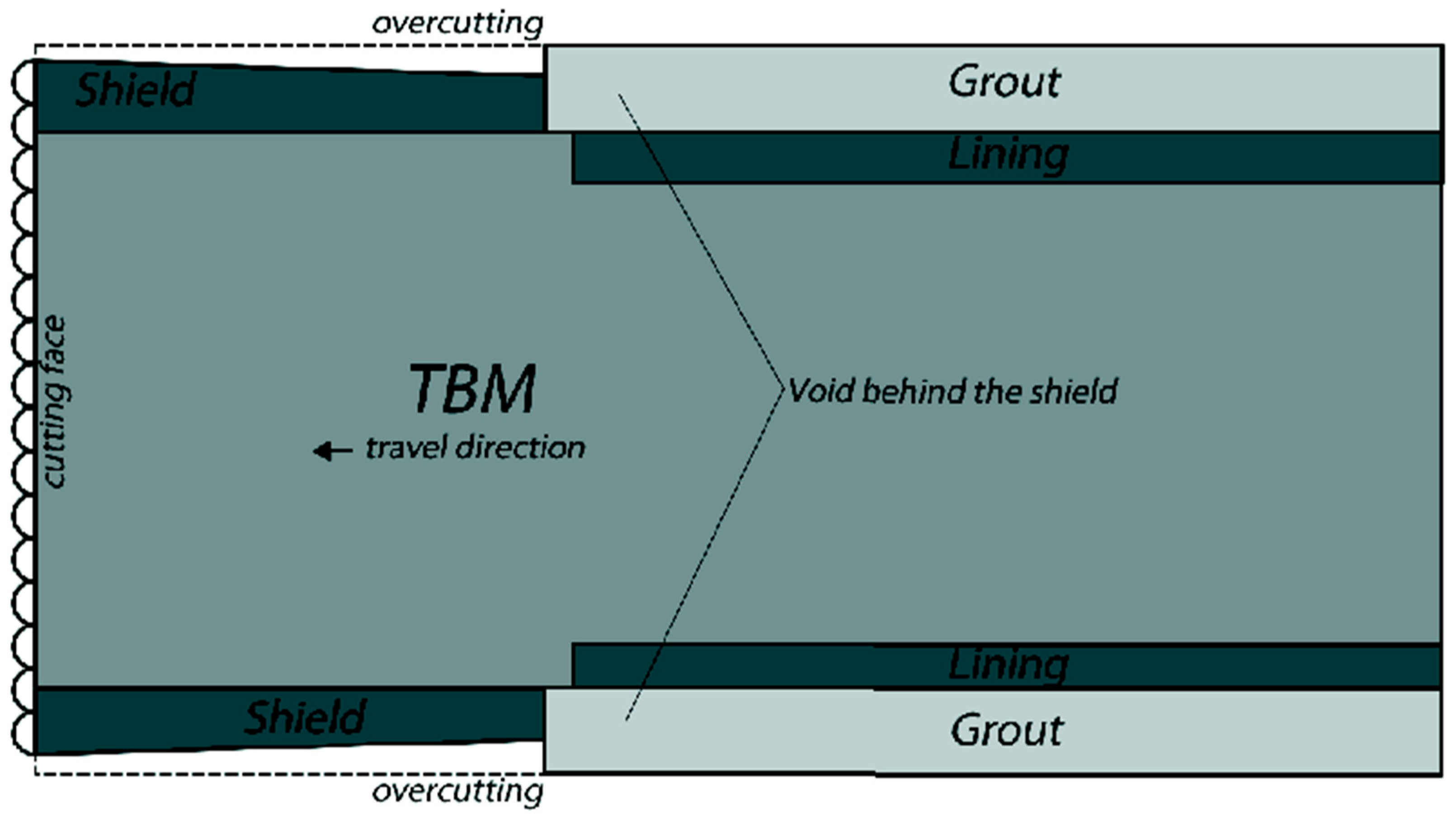
1. Introduction
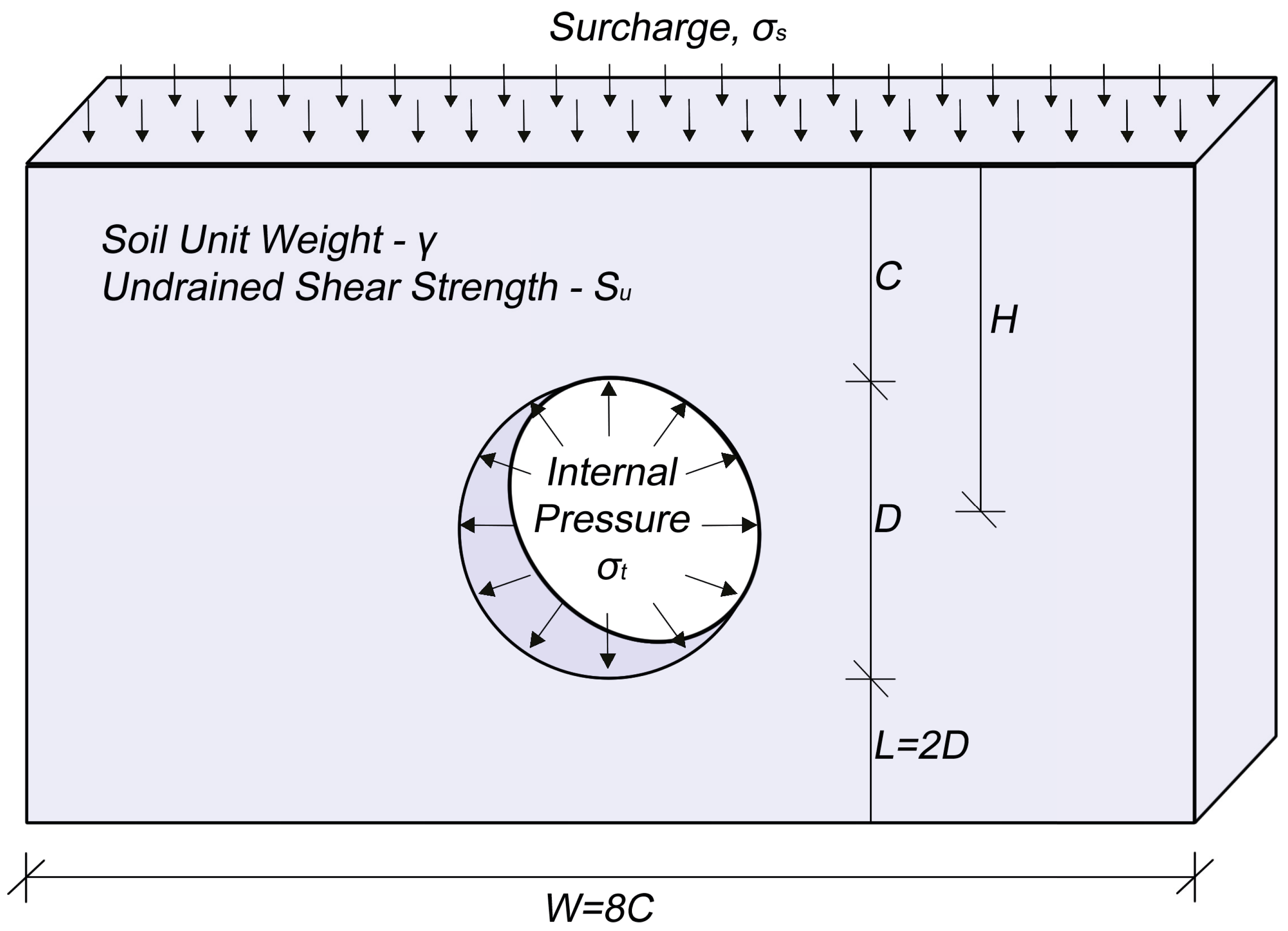
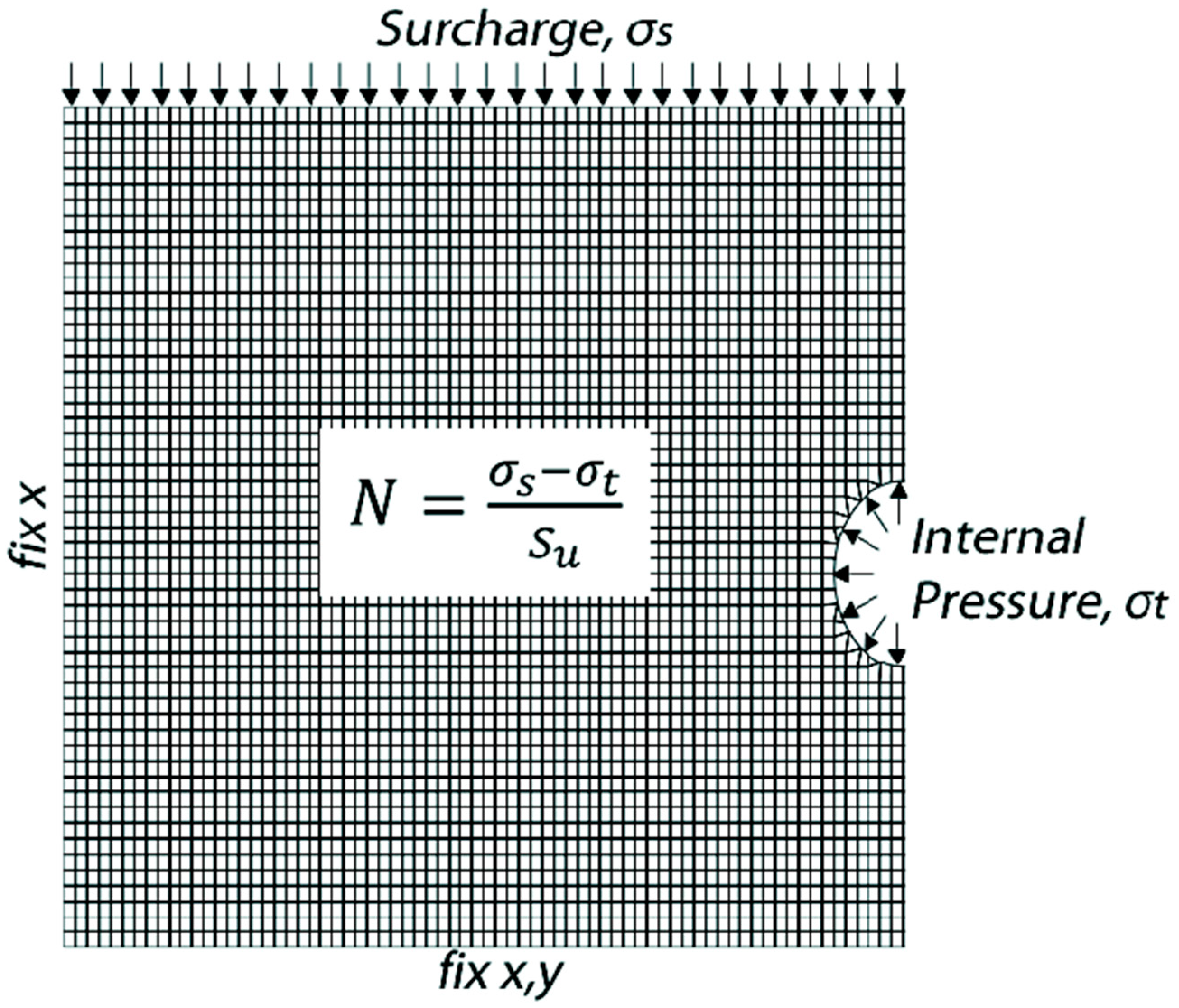
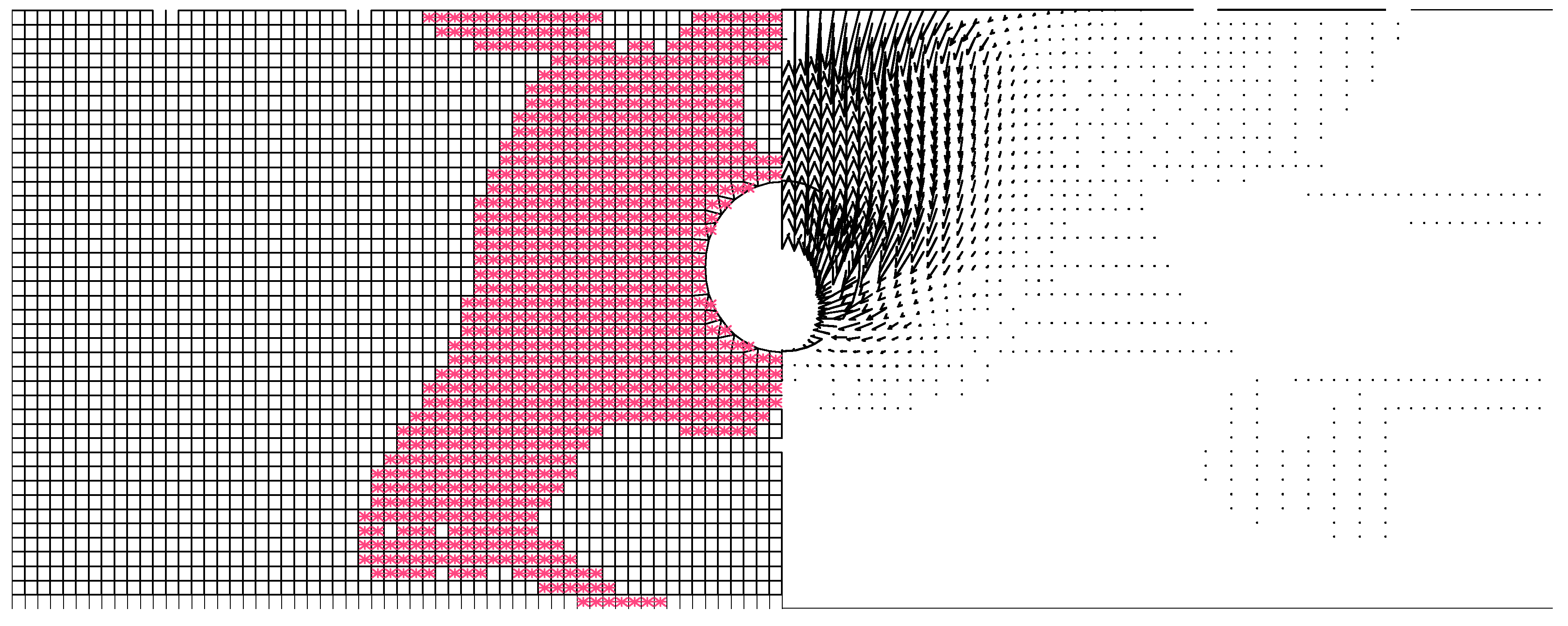
2. Pressure Relaxation Technique
3. Stability Results
3.1. Practical Example 1—Stability in Soft Soil
- Calculate dimensionless ratios from the known data. C/D = 3 and γD/Su = 4.
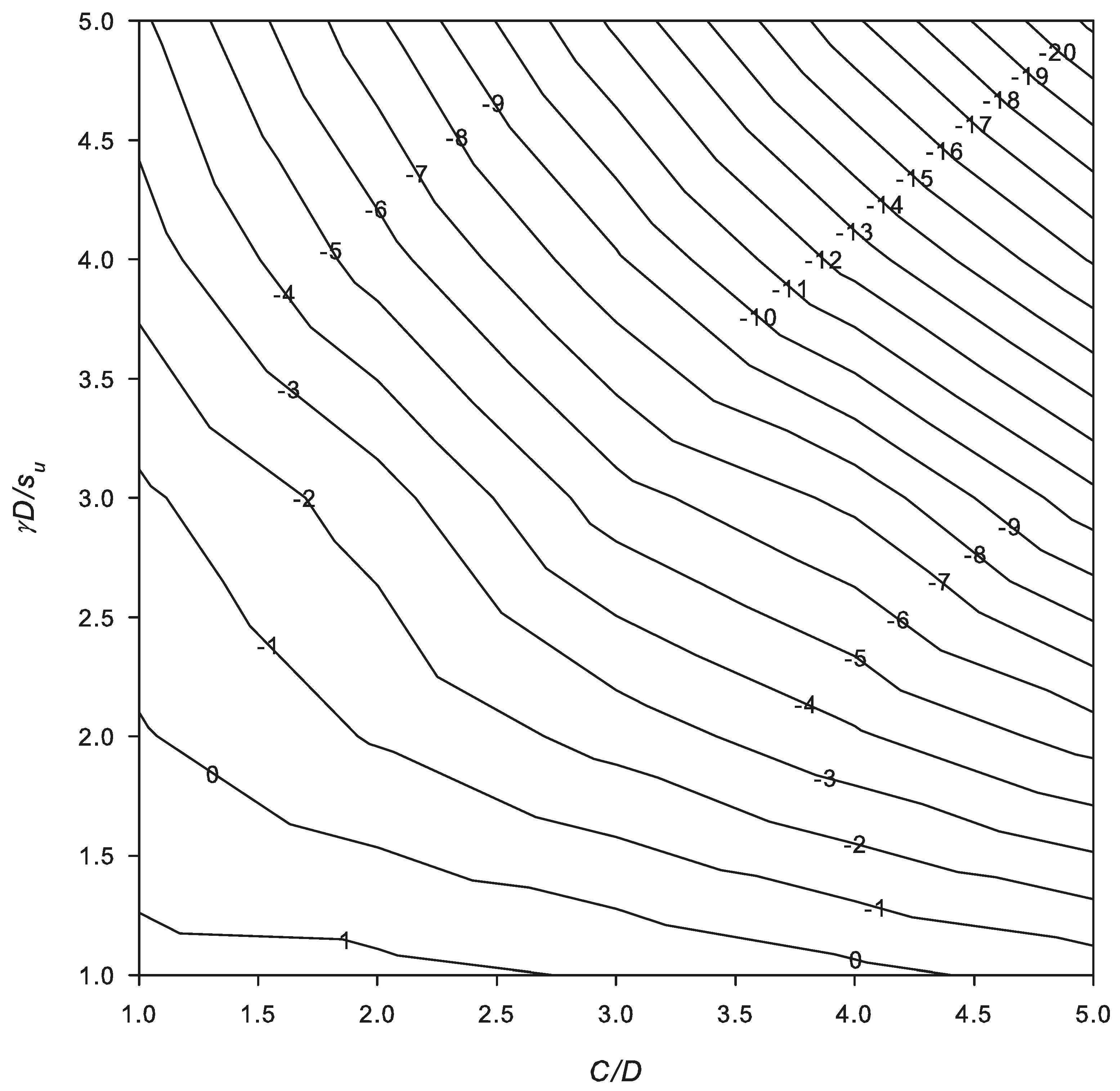
- For a 2D circular tunnel problem with C/D = 3 and γD/Su = 4.0, Figure 8 returns a value of N = –8.1. Equation (9) yields approximately −8.03 for the same problem.
- Using Equation (2) (N = (σs − σt)/Su), σt can then be computed as σt ≈ 0 − (−8.1 × 27) = 219 kPa. A positive value of σt indicates that an internal pushing pressure is required to maintain tunnel stability.
3.2. Practical Example 2—Stability in Stiff Soil
- Calculate dimensionless ratios from the known data. C/D = 2 and γD/Su = 1.35.
- Figure 8 returns a value of N = 0.50.
- Using Equation (2) (N = (σs − σt)/Su), σt can then be computed as σt ≈ 0 − (0.5 × 80) = −40 kPa. A negative value of σt such as this indicates that the tunnel requires a pulling pressure to reach a collapse state. In other words, the tunnel will remain stable without any internal pressure.
3.3. Practical Example 3—Depth Determination
- Calculate dimensionless ratios from the known data. N = (σs − σt)/Su = −5.0 and γD/Su = 2.7.
- Using Figure 8 and these parameters, the maximum allowable depth ratio (C/D) is approximately 3.1. With a specified tunnel diameter of 6 m, this results in a maximum depth of 18.6 m. If the tunnel is placed any deeper than this, a collapse will be induced. Using Equation (9), a C/D value of 3.0 is obtained.
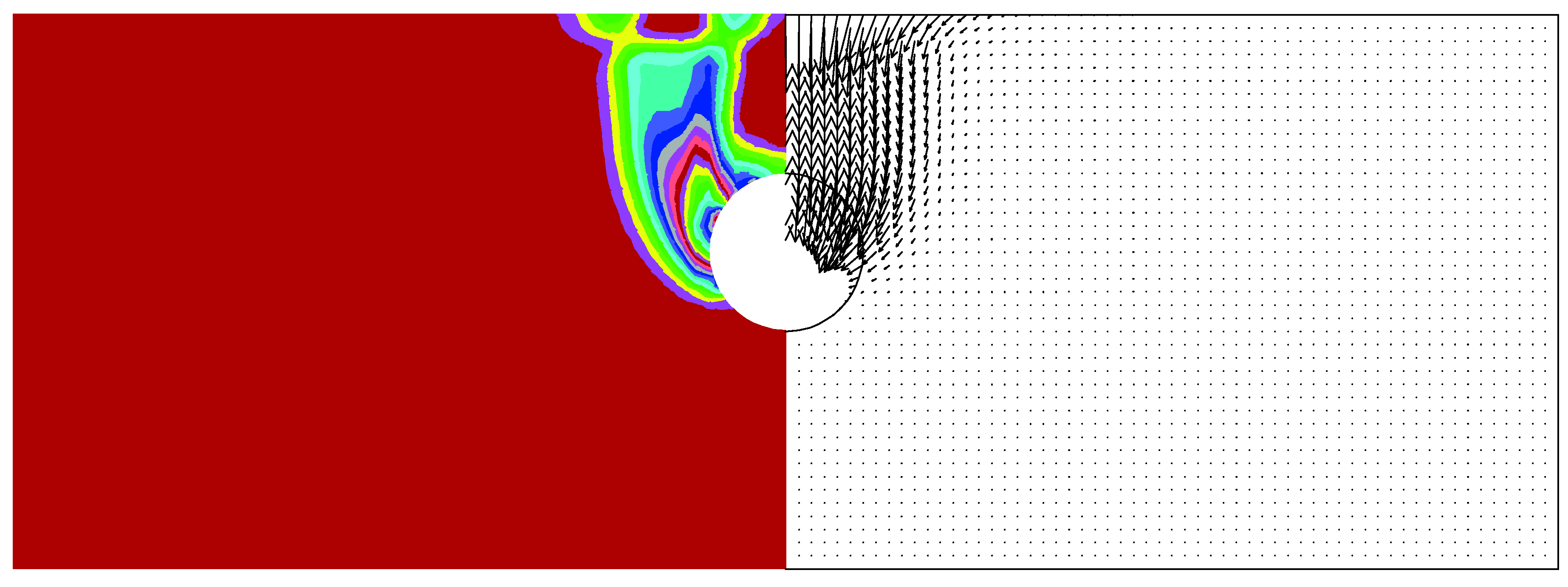
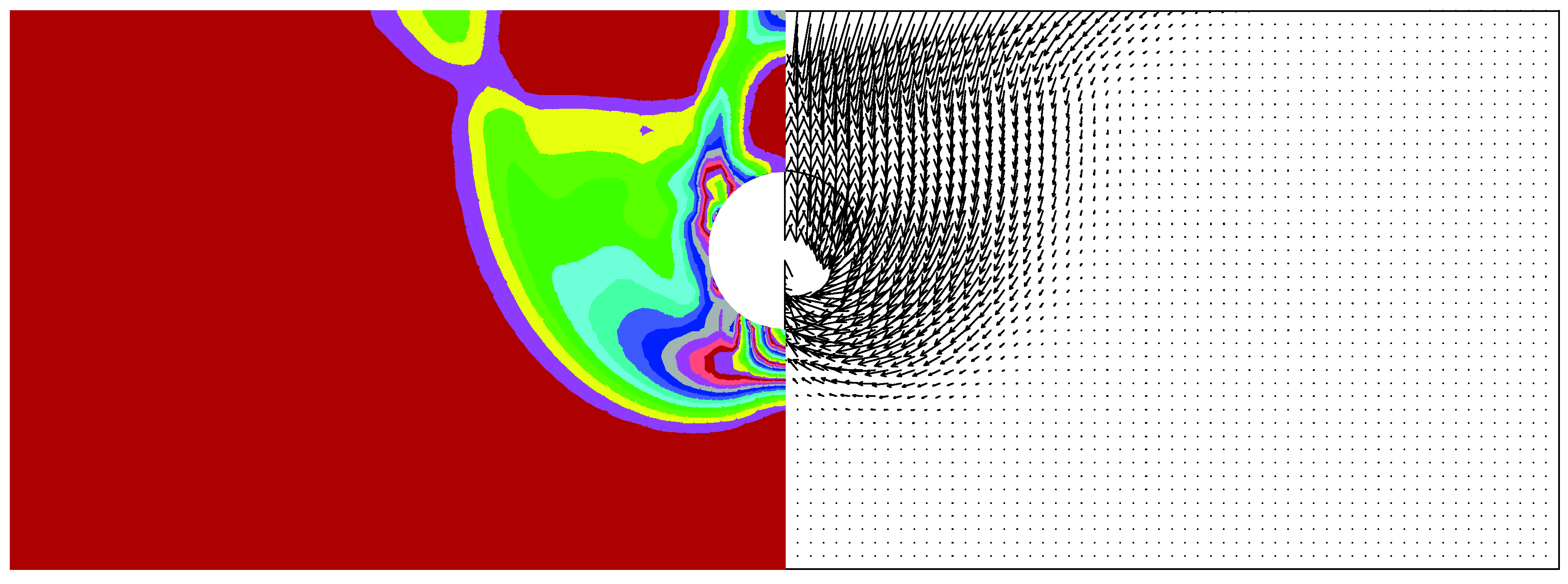
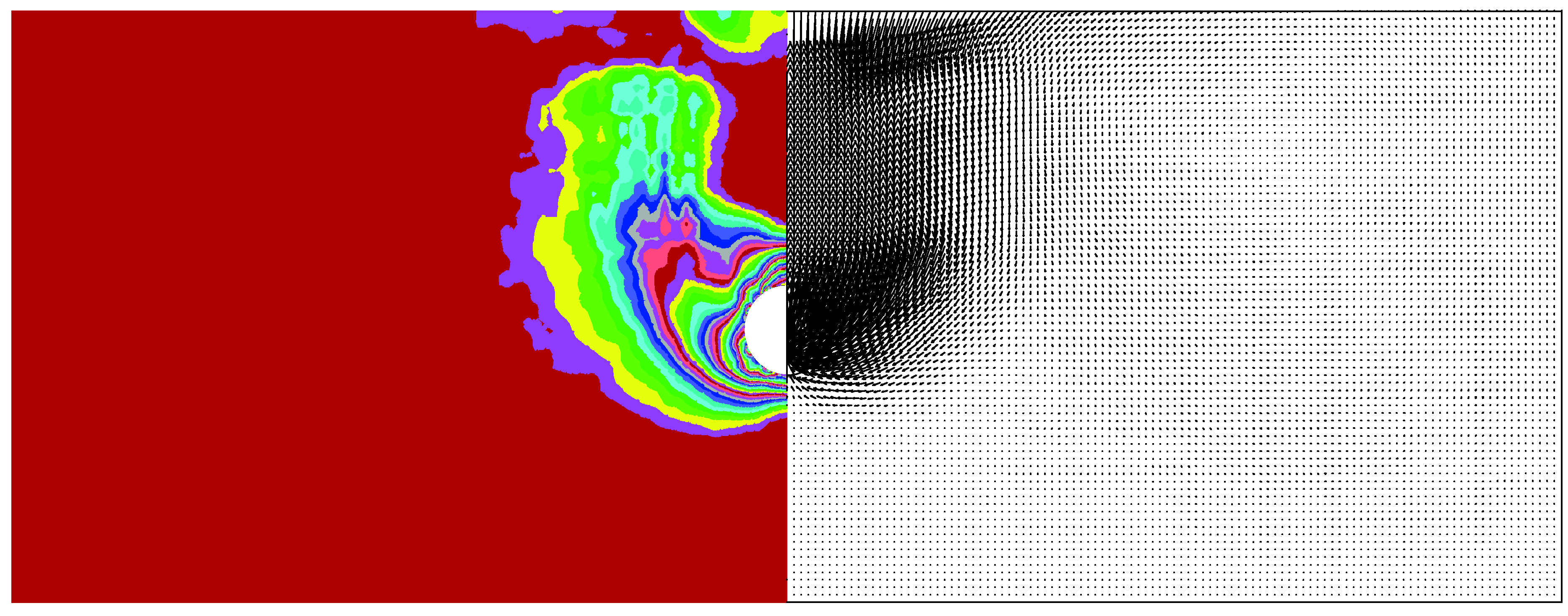
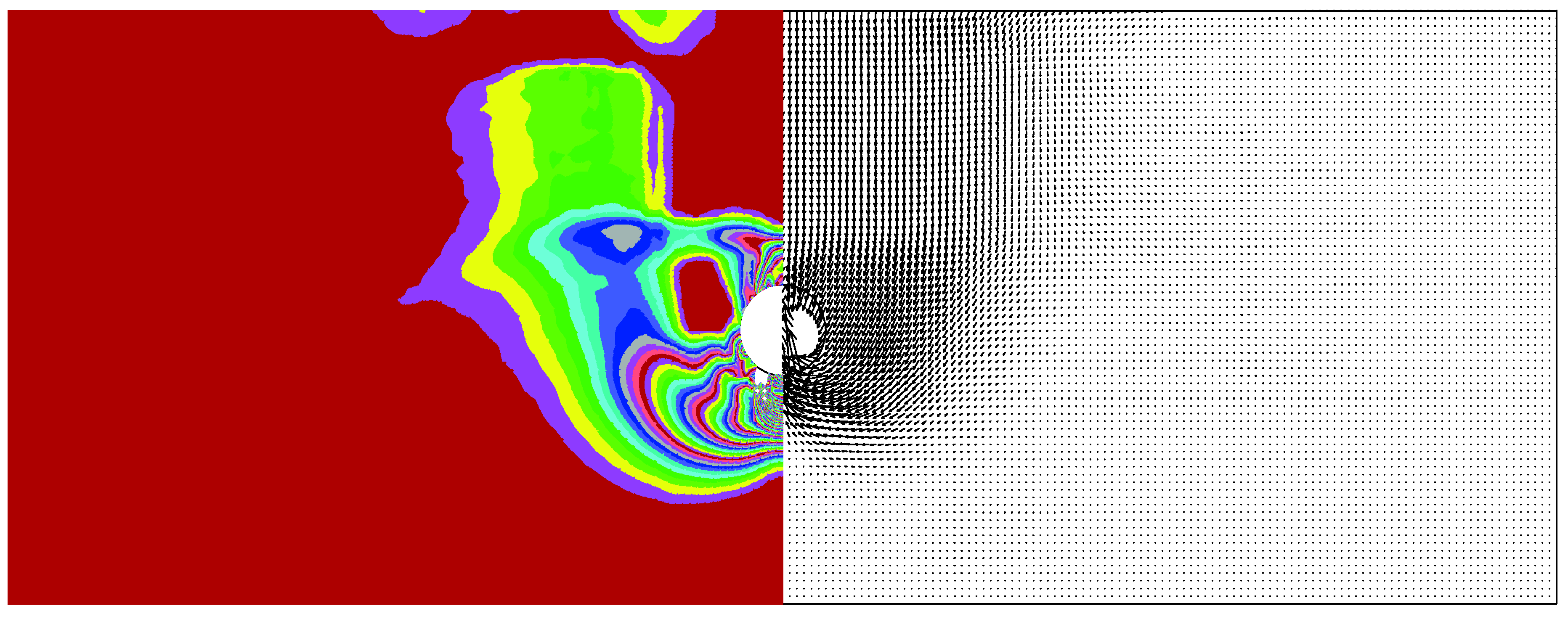
4. Failure Mechanism
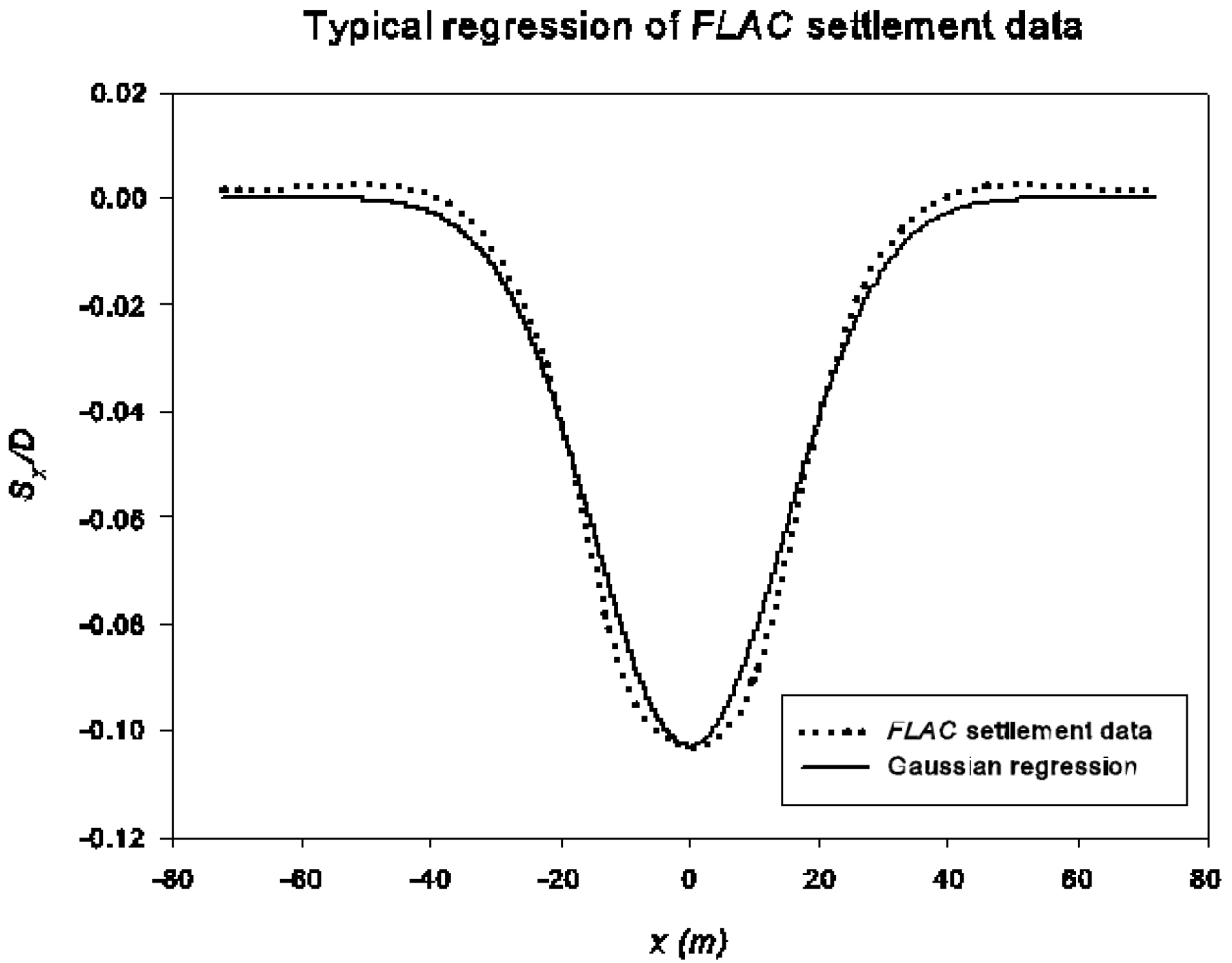
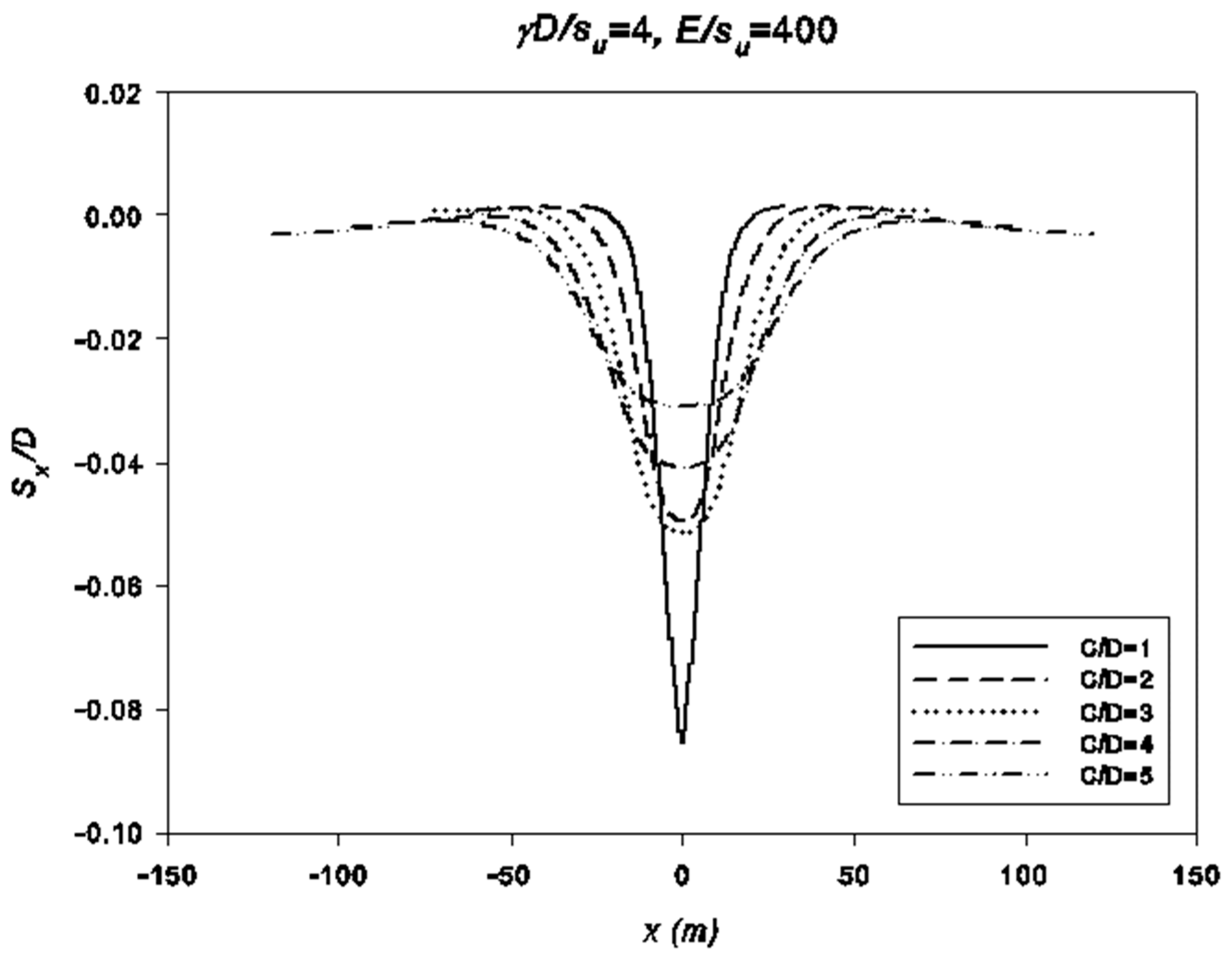
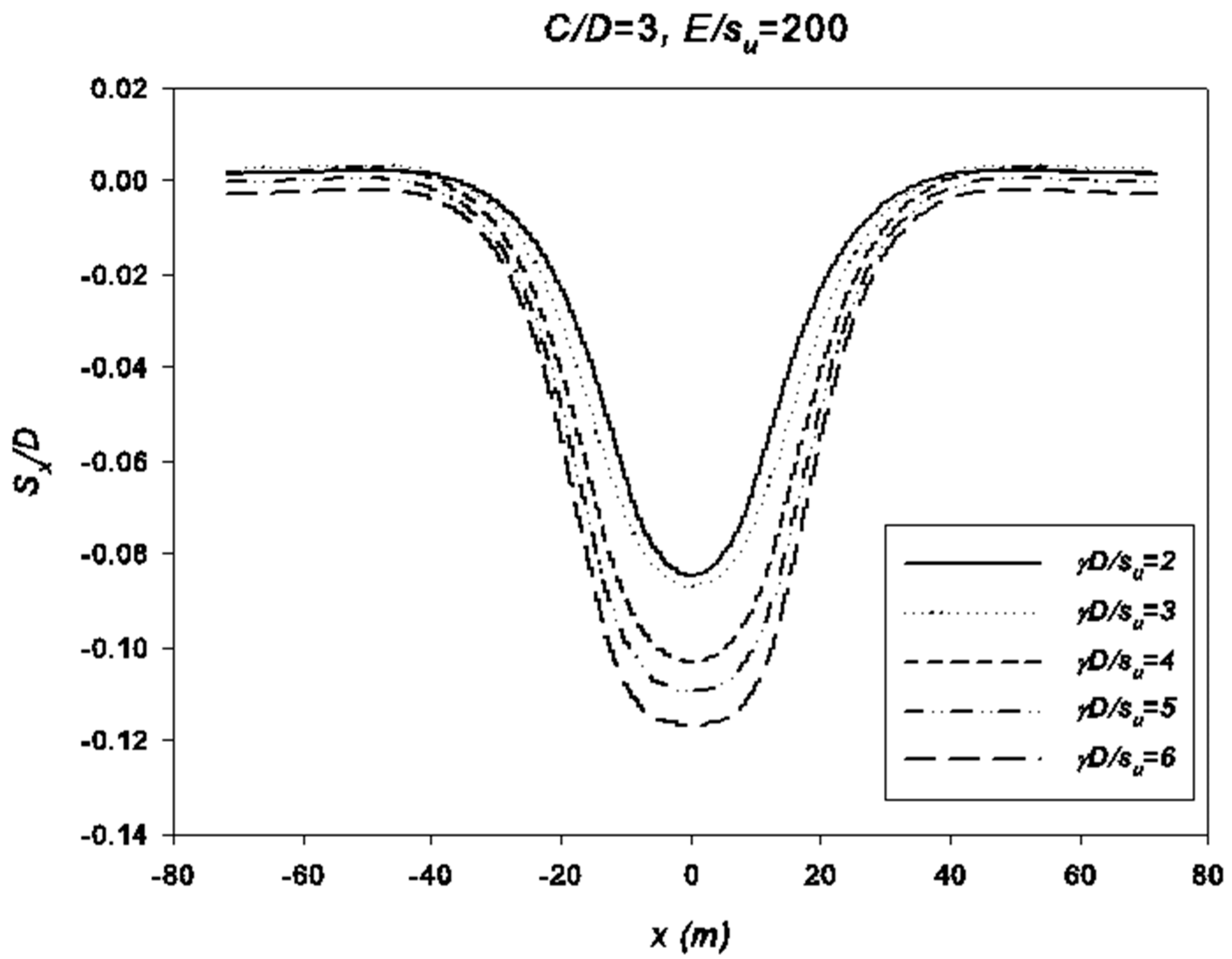
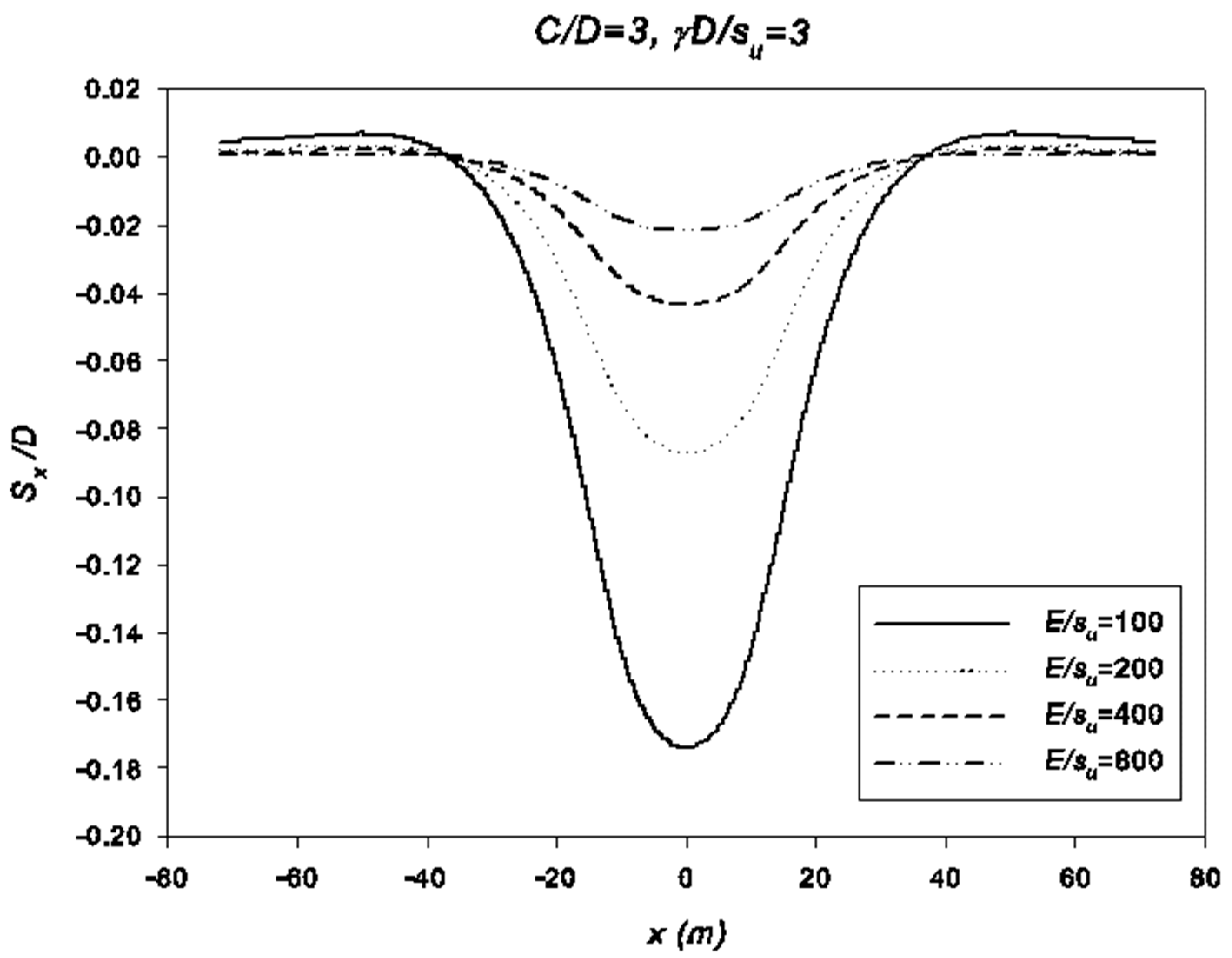
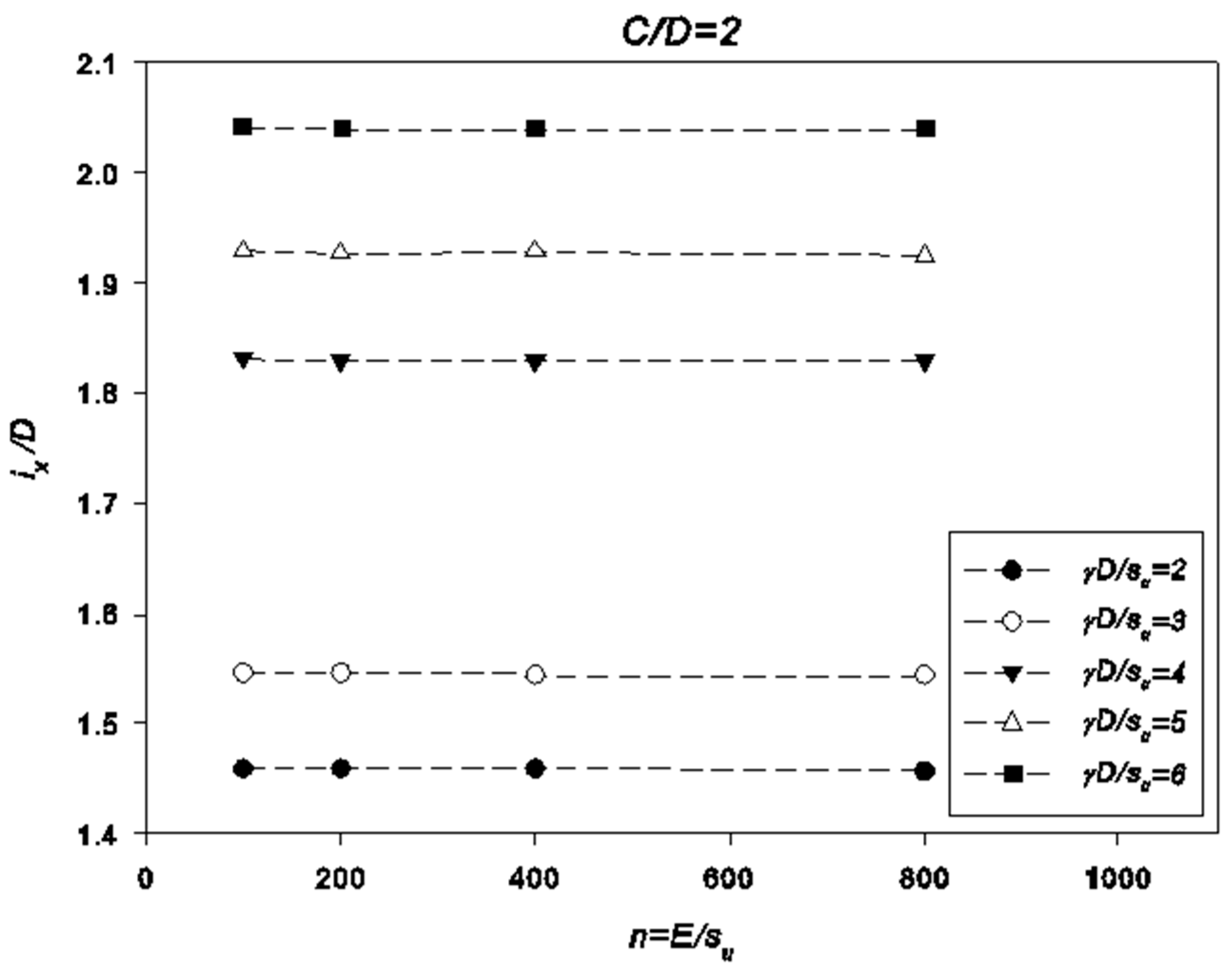
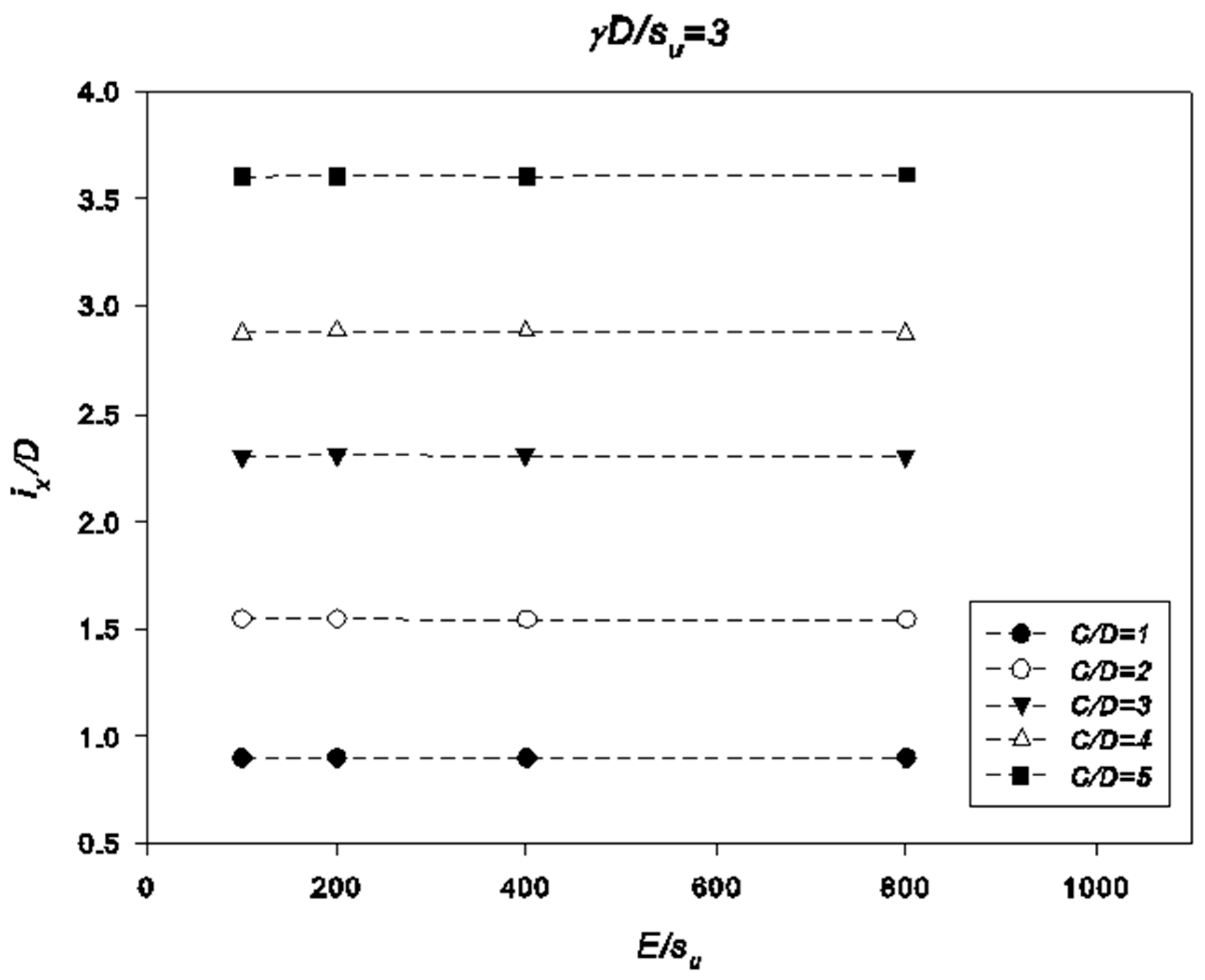
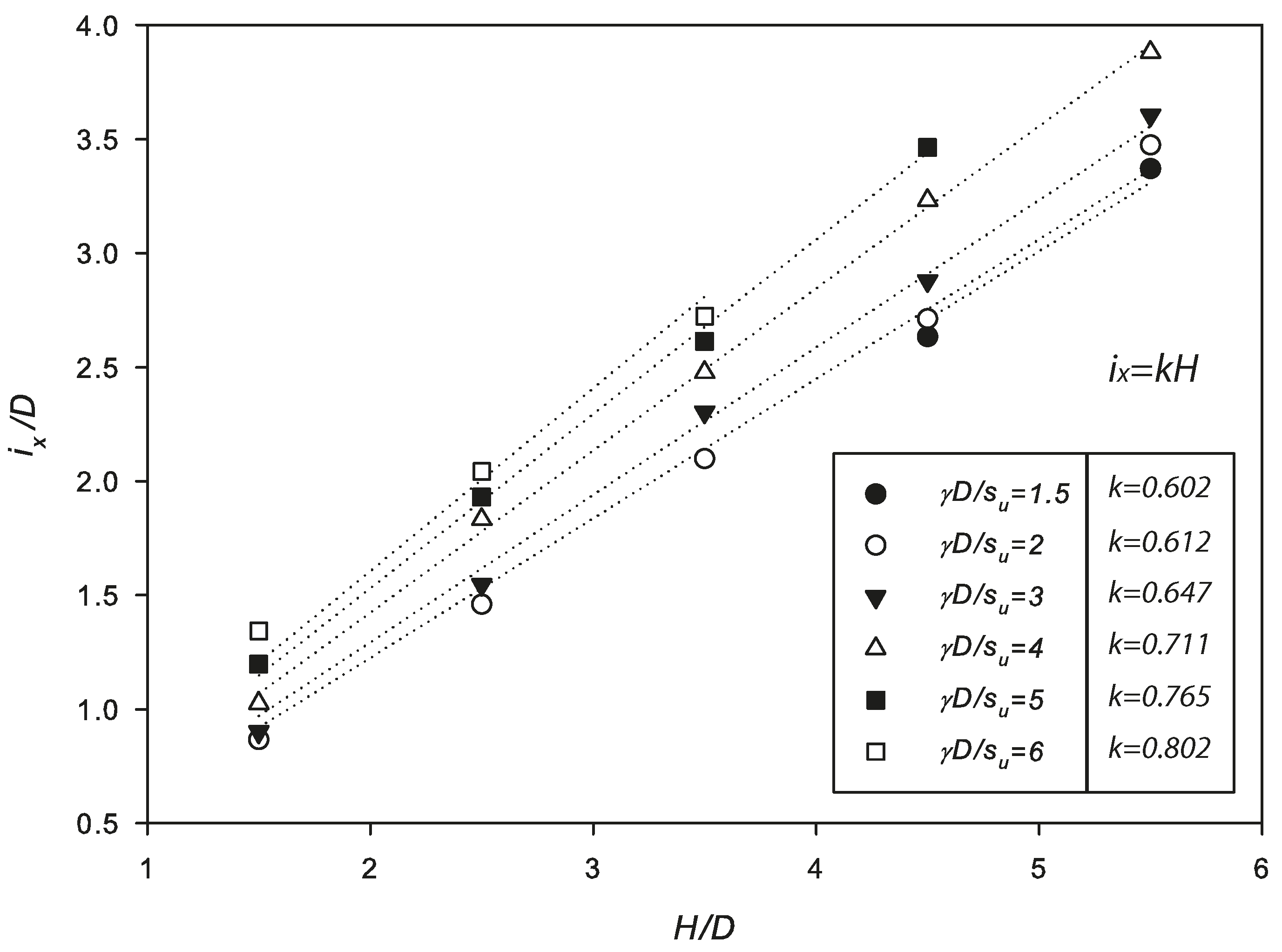
5. Settlement Results
6. Conclusions
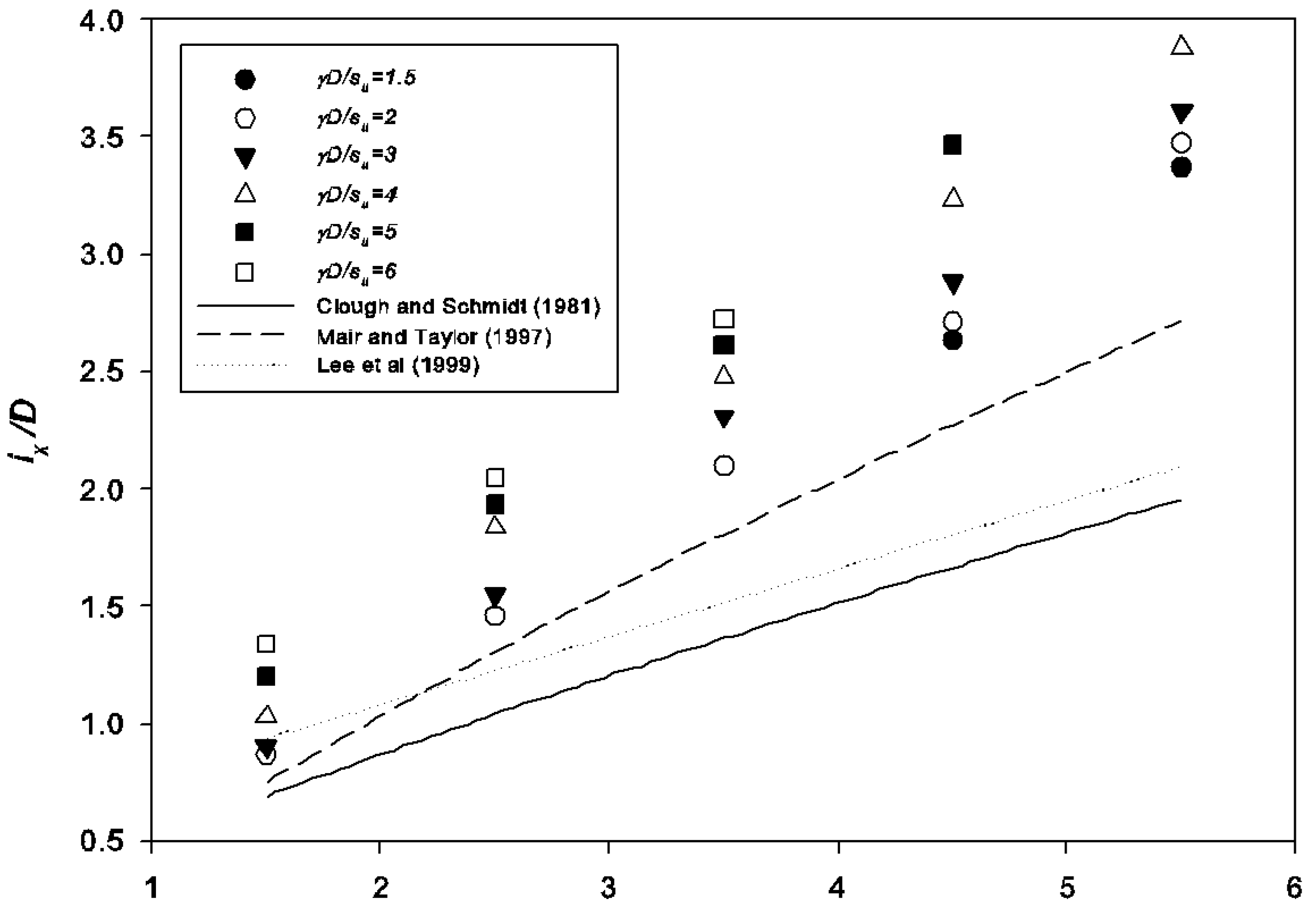
- Validation of the model shows that promising results are obtained using the developed model. Comparison with rigorous upper and lower bound results shows that the results using current pressure relaxation method are accurate and can be used with confidence as a design tool in practice. Based on the parametric study, a design chart is developed, and several practical examples are shown on how to use the design chart.
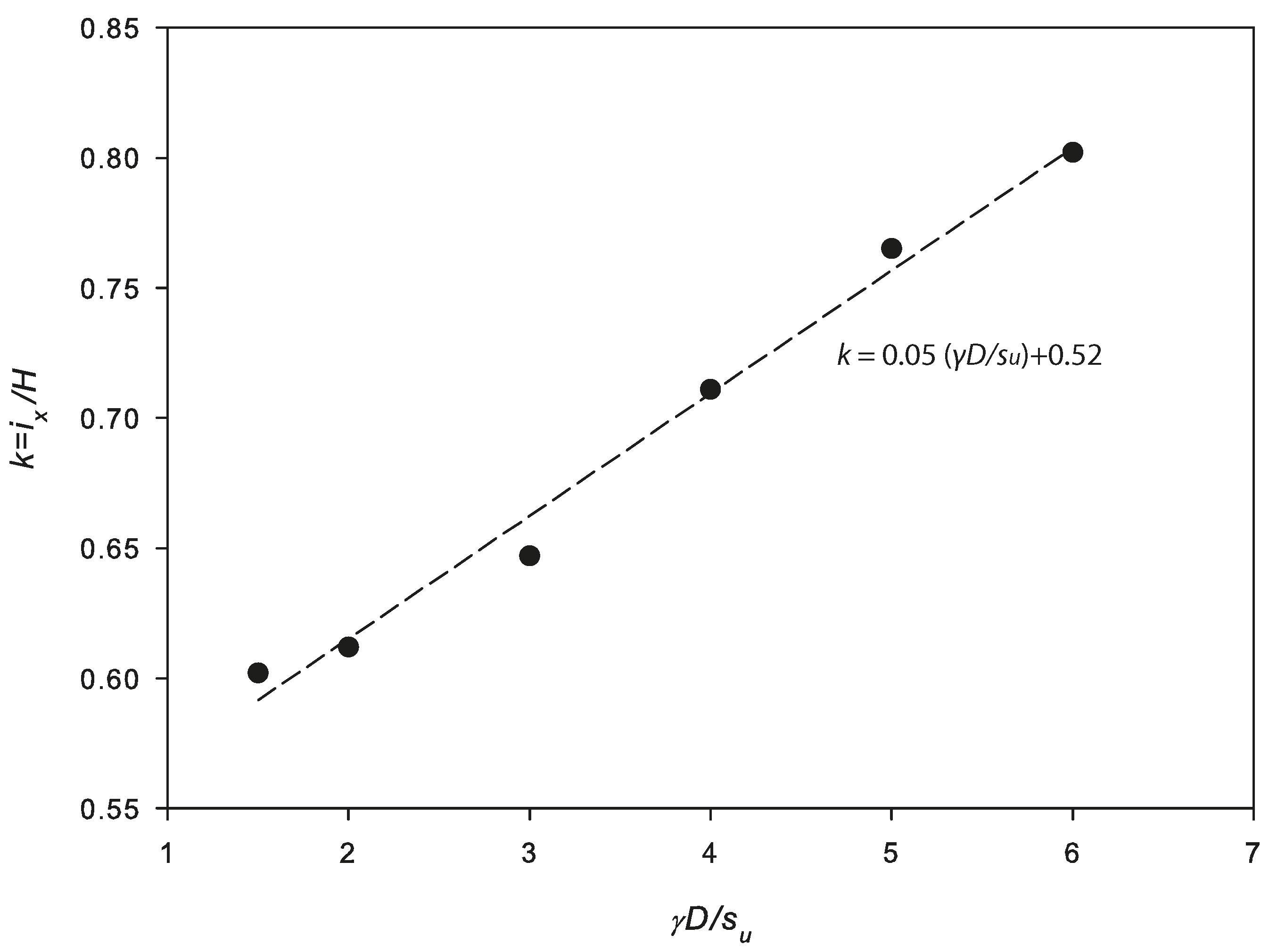
- The great similarity between the obtained settlement and the Gaussian curve indicates that this empirical method is still suitable to be applied in the industry as a preliminary tool. This research suggests that the constant k should be approximately between 0.55–0.75 for undrained clays. A new equation is proposed for estimating the k value based on a linear regression analysis.
- Using a Gaussian distribution curve requires an estimation of Smax, which would likely be estimated by using a volume loss limit. Work in the future needs to be able to estimate k accurately at lower levels of relaxation and with lower volume loss.
- It was concluded that this automated process has many practical significances for industry application. Future work can be attributed to underground mining application.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Peck, R.B. Deep excavations and tunneling in soft ground. In Proceedings of the 7th International Conference on Soil Mechanics and Foundation Engineering, Held in Mexico City, 1969; Sociedad Mexicana de Mecanica: Mexico City, Mexico; Volume 4, pp. 225–290.
- Broms, B.B.; Bennermark, H. Stability of clay at vertical openings. J. Soil Mech. Found. Div. 1967, 193, 71–94. [Google Scholar] [CrossRef]
- Mair, R.J. Centrifugal Modelling of Tunnel Construction in Soft Clay. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 1979. [Google Scholar]
- Davis, E.; Gunn, M.; Mair, R.; Seneviratine, H. The stability of shallow tunnels and underground openings in cohesive material. Geotechnique 1980, 30, 397–416. [Google Scholar] [CrossRef]
- Shiau, J.S.; Lyamin, A.V.; Sloan, S.W. Rigorous solutions of classical lateral earth pressures. In Proceedings of the 6th Australia–New Zealand Young Geotechnical Professionals Conference, Gold Coast, Australia, December 2003; pp. 162–167. [Google Scholar]
- Shiau, J.S.; Lyamin, A.V.; Sloan, S.W. Application of pseudo-static limit analysis in geotechnical earthquake design. In Numerical Methods in Geotechnical Engineering; Schweiger, Ed.; Taylor & Francis Group: London, UK, 2006; pp. 249–255. [Google Scholar]
- Shiau, J.; Al-Asadi, F. Three-dimensional heading stability of twin circular tunnels. Geotech. Geol. Eng. 2020, 38, 2973–2988. [Google Scholar] [CrossRef]
- Shiau, J.; Al-Asadi, F. Stability analysis of twin circular tunnels using shear strength reduction method. Géotech. Lett. 2020, 10, 311–319. [Google Scholar] [CrossRef]
- Shiau, J.; Al-Asadi, F. Twin tunnels stability factors Fc, Fs and Fγ. Geotech. Geol. Eng. 2021, 39, 335–345. [Google Scholar] [CrossRef]
- Shiau, J.; Al-Asadi, F. Revisiting circular tunnel stability using Broms and Bennermarks’ Original Stability Number. Int. J. Geomech. 2021, 21, 06021009. [Google Scholar] [CrossRef]
- Sloan, S. Geotechnical stability analysis. Geotechnique 2013, 63, 531–571. [Google Scholar] [CrossRef]
- Wilson, D.W.; Abbo, A.J.; Sloan, S.W.; Lyamin, A.V. Undrained stability of a circular tunnel where the shear strength increases linearly with depth. Can. Geotech. J. 2011, 48, 1328–1342. [Google Scholar] [CrossRef]
- Loganathan, N.; Poulos, H.G. Analytical prediction for tunneling-induced ground movements in clays. J. Geotech. Geoenviron. Eng. 1998, 124, 846. [Google Scholar] [CrossRef]
- Rankin, W. Ground movements resulting from urban tunnelling: Predictions and effects. Geol. Soc. Lond. Eng. Geol. Spec. Publ. 1988, 5, 79–92. [Google Scholar] [CrossRef]
- Sagaseta, C. Analysis of undraind soil deformation due to ground loss. Geotechnique 1987, 37, 301–320. [Google Scholar] [CrossRef]
- Gunn, M.J. The prediction of surface settlement profiles due to tunneling. In Predictive Soil Mechanics, Proceedings of the Wroth Memorial Symposium, St. Catherines College, Oxford, UK, 27–29 July 1992; Thomas Telford Publishing: London, UK, 1992. [Google Scholar]
- Taylor, R. Modelling of tunnel behaviour. Proc. ICE-Geotech. Eng. 1998, 131, 127–132. [Google Scholar] [CrossRef]
- Martos, F. Concerning an approximate equation of the subsidence trough and its time factors. In Proceedings of the International Strata Control Congress, Leipzig, Germany, 14–16 October 1958; pp. 191–205. [Google Scholar]
- Atkinson, J.; Cairncross, A. Collapse of a shallow tunnel in a Mohr-Coulomb material. In Proceedings of the Symposium on the Role of Plasticity in Soil Mechanics, Cambridge, UK, 13–15 September 1973. [Google Scholar]
- Mair, R.J.; Taylor, R.N. Theme lecture: Bored tunnelling in the urban environment. In Proceedings of the 14th International Conference on Soil Mechanics and Foundation Engineering, Hamburg, Germany, 6–12 September 1997; pp. 2353–2385. [Google Scholar]
- Attewell, P.; Farmer, I. Ground deformations resulting from shield tunnelling in London Clay. Can. Geotech. J. 1974, 11, 380–395. [Google Scholar] [CrossRef]
- Cording, E.J.; Hansmire, W.H. Displacement around soft ground tunnels—General report. In Proceedings of the 5th Pan-American Conference on Soil Mechanics and Foundation Engineering, Buenos Aires, Argentina, 15–19 November 1975. [Google Scholar]
- O’Reilly, M.P.; New, B.M. Settlements above tunnels in the United Kingdom—Their magnitude and prediction. Tunneling 1982, 82, 173–181. [Google Scholar] [CrossRef]
- Phienwej, N. Ground movements in shield tunneling in Bangkok soils. In Proceedings of the 14th International Conference on Soil Mechanics and Foundation Engineering, Hamburg, Germany, 6–12 September 1997; Volume 3, pp. 1469–1472. [Google Scholar]
- Clough, G.W.; Schmidt, B. Design and performance of excavations and tunnels in soft clay. In Soft Clay Engineering; Elsevier: Amsterdam, The Netherlands, 1977; pp. 569–634. [Google Scholar]
- Lee, C.J.; Wu, B.R.; Chiou, S.Y. Soil movements around a tunnel in soft soils. Proc. Natl. Sci. Counc. Part A Phys. Sci. Eng. 1999, 23, 235–247. [Google Scholar]
- Guglielmetti, V.; Grasso, P.; Mahtab, A.; Xu, S. (Eds.) Mechanized Tunnelling in Urban Areas: Design Methodology and Construction Control; Taylor and Francis: Abingdon, UK, 2008; Chapter 5. [Google Scholar]
- Palmer, A.C.; Mair, R.J. Ground movements above tunnels: A method for calculating volume loss. Can. Geotech. J. 2011, 48, 451–457. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shiau, J.; Sams, M.; Arvin, M.R.; Jongpradist, P. Automating the Process for Estimating Tunneling Induced Ground Stability and Settlement. Geosciences 2023, 13, 81. https://doi.org/10.3390/geosciences13030081
Shiau J, Sams M, Arvin MR, Jongpradist P. Automating the Process for Estimating Tunneling Induced Ground Stability and Settlement. Geosciences. 2023; 13(3):81. https://doi.org/10.3390/geosciences13030081
Chicago/Turabian StyleShiau, Jim, Mathew Sams, Mohammad Reza Arvin, and Pornkasem Jongpradist. 2023. "Automating the Process for Estimating Tunneling Induced Ground Stability and Settlement" Geosciences 13, no. 3: 81. https://doi.org/10.3390/geosciences13030081
APA StyleShiau, J., Sams, M., Arvin, M. R., & Jongpradist, P. (2023). Automating the Process for Estimating Tunneling Induced Ground Stability and Settlement. Geosciences, 13(3), 81. https://doi.org/10.3390/geosciences13030081







