Towards a Hybrid Design Approach of Anchored Drapery Systems
Abstract
:1. Introduction
2. Methodology
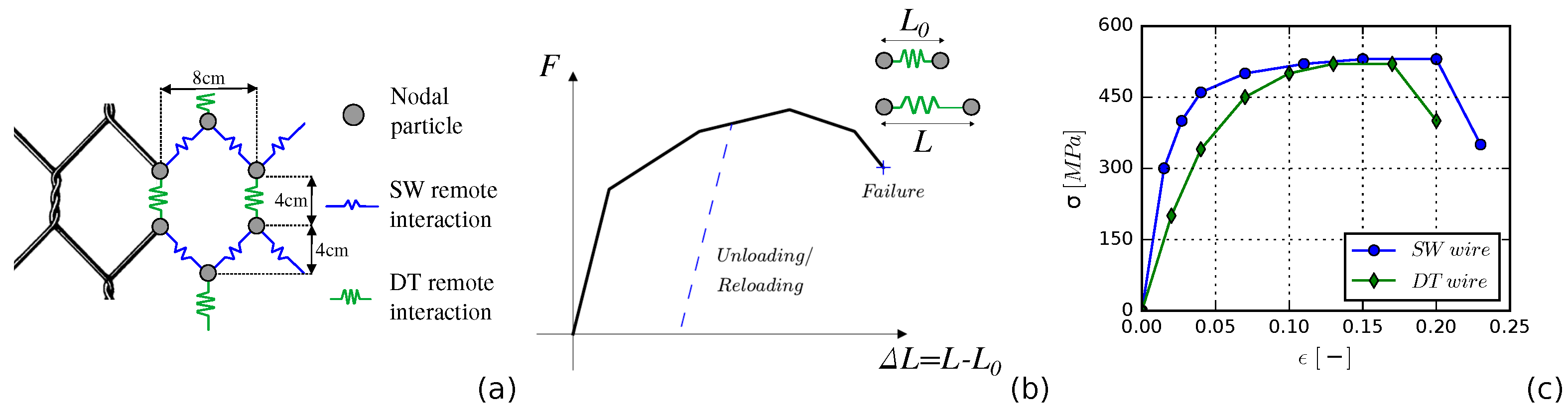
2.1. Discrete Element Modeling of the Wire Mesh
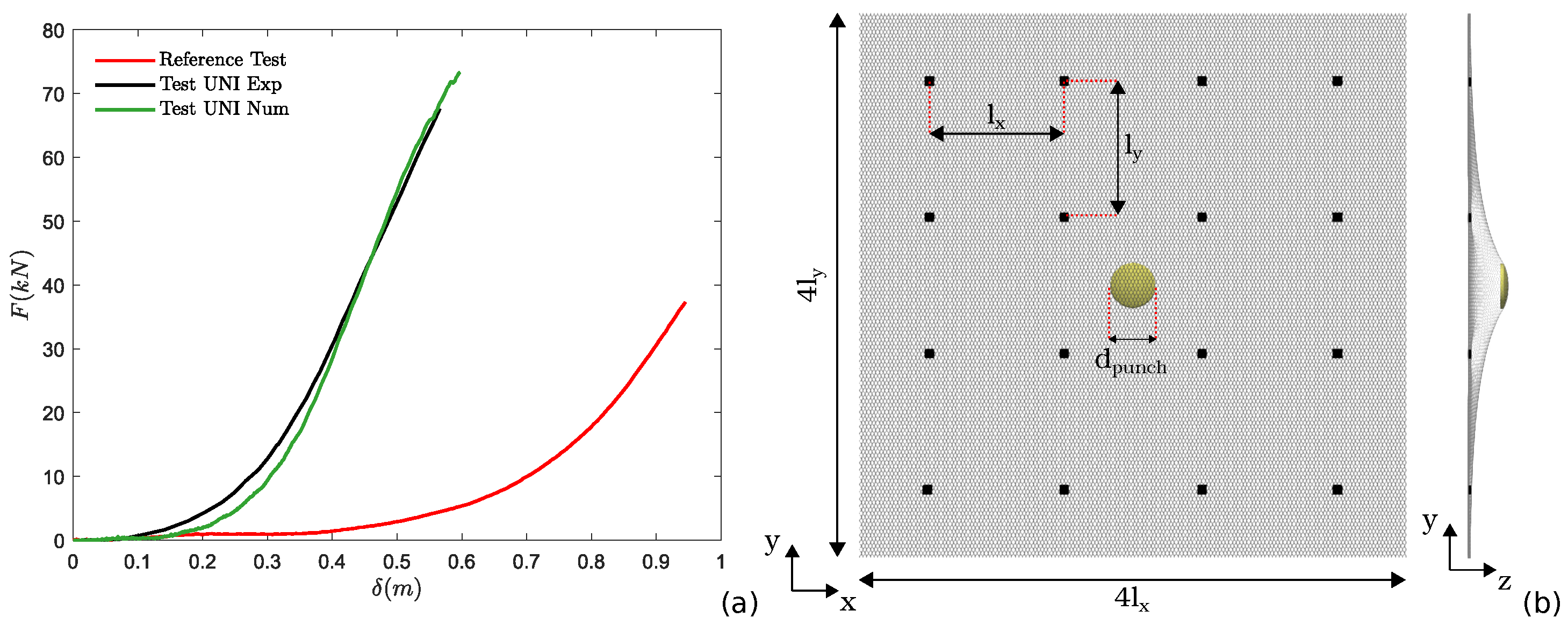
2.2. Standardized Laboratory Tests
2.3. Large-Scale Model of a Pinned Mesh System
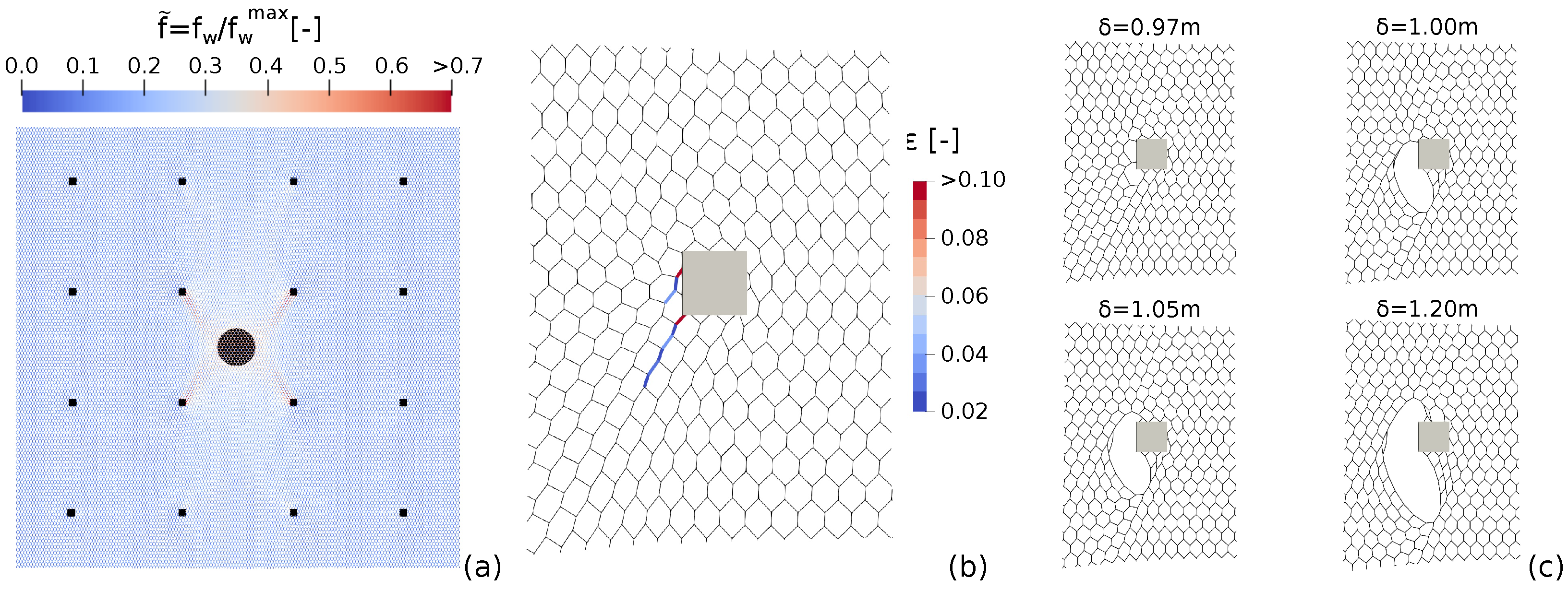
3. Parametric Analysis
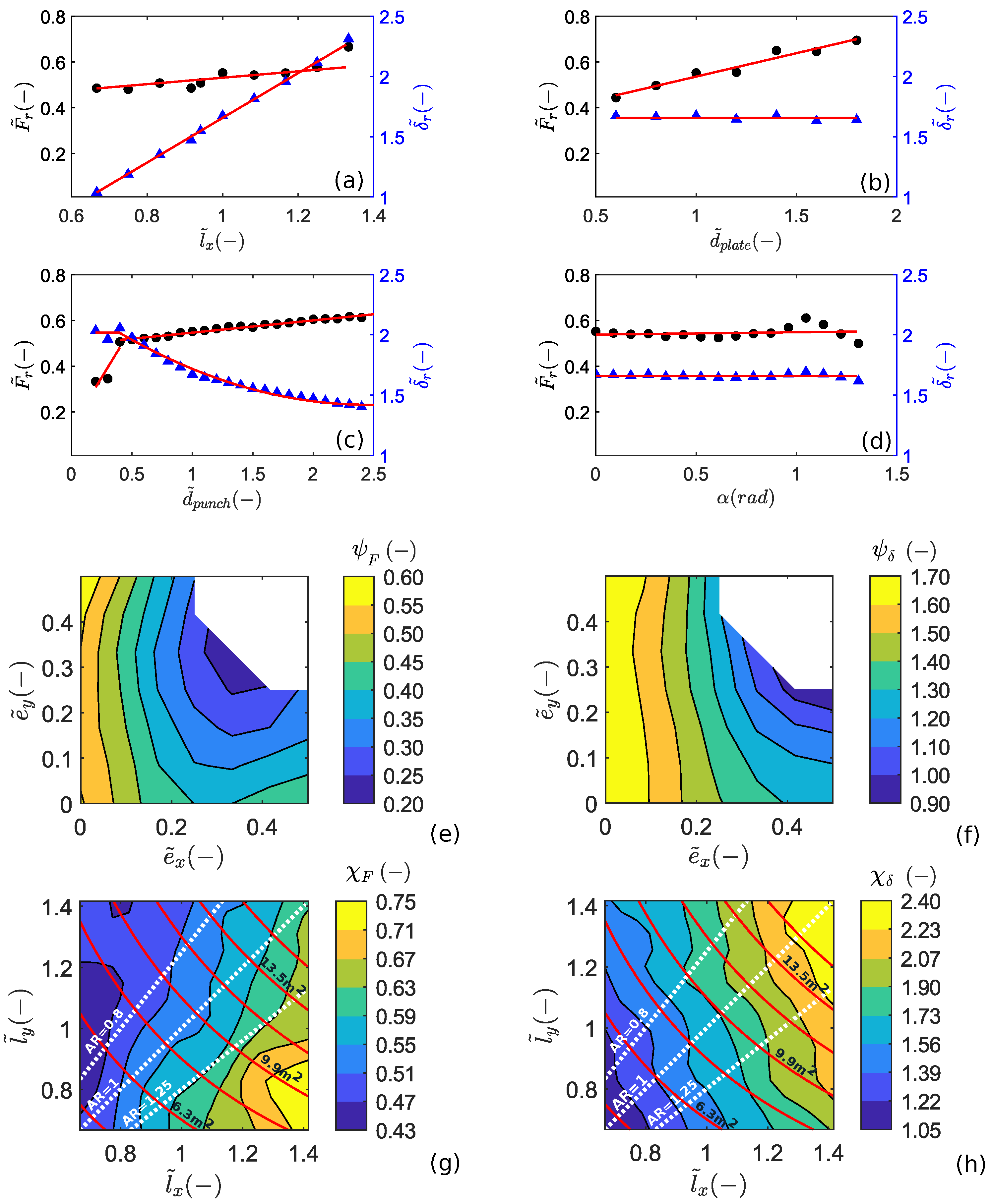
3.1. Anchor Plate Size
3.2. Punching Element Position
3.3. Punching Element Size
3.4. Mesh Panel Geometry
3.4.1. Anchor Spacing
3.4.2. Aspect Ratio
4. Extension to Field Conditions
4.1. Estimation of the Mesh System Characteristic Values
4.2. Master Curve
- The master curve (Equation (10)) is rescaled with the computed and values;
- The curve is obtained by rescaling the normalized curve with the characteristic values of the standard UNI punch test ( and ).
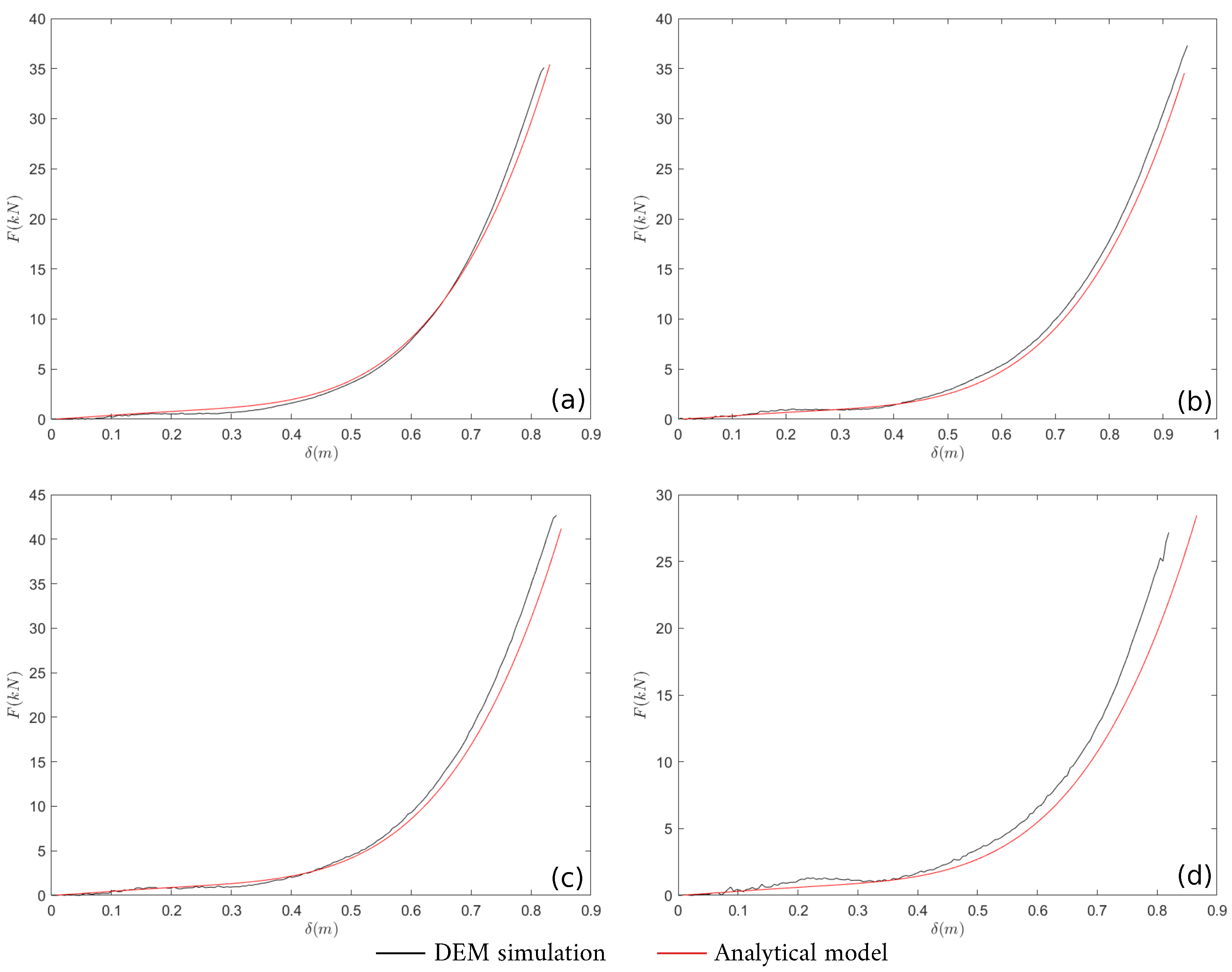
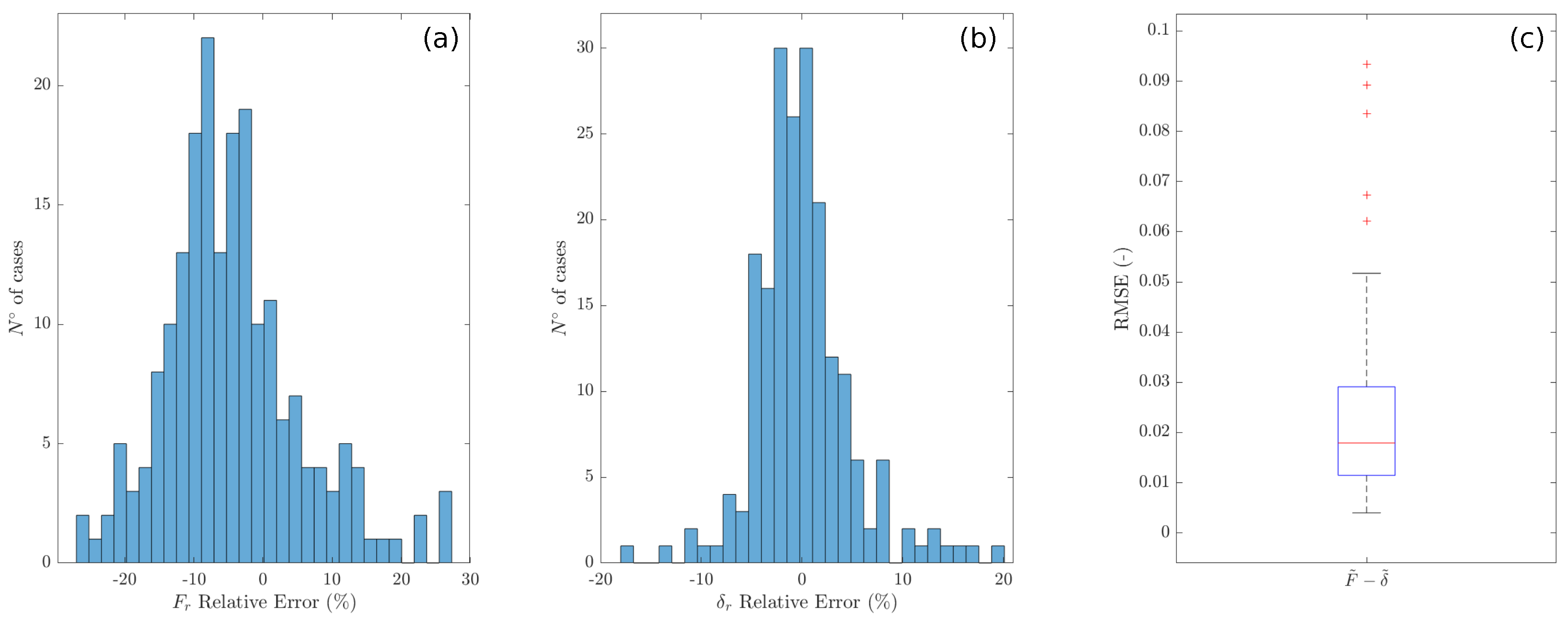
4.3. Accuracy of the Analytical Model
4.4. Towards a Hybrid Design Approach
5. Conclusions
- Increasing the anchor spacing results in an increment of the panel’s out-of-plane deformability as well as the deflection at failure. A slight but systematic increment of the maximum force supported by the panel is observed, possibly related to a better redistribution of the stresses on the wires for larger mesh panels.
- Increasing the anchor plate dimension is reflected in an increment of the force at failure. This shows that the available resistance at the mesh–anchor connection is mainly controlled by the anchor plate size. The deflection at failure is instead mostly unaffected by the anchor plate dimension.
- The eccentricity along the x-axis affects the mechanical response of the mesh system, reducing both the force and the deflection at failure with respect to a centered case. Conversely, the influence of eccentricity along the y-axis is negligible.
- For relatively large punching elements (larger than the anchor plate), the mechanical response of the mesh is improved both in terms of mechanical resistance and out-of-plane deformability. A strong variation is observed for the threshold value = 0.4 m when the failure modality changes from a “block-punching” to an “anchor-punching” type.
- The inclination of the thrust imposed by the punching element has a negligible influence on the force–displacement response of the mesh system.
- The adoption of a panel geometry in which the vertical spacing between the anchors is reduced compared with the horizontal spacing enhances the redistribution of the punching load on the neighboring panels. An opposite trend of the maximum force is observed in the case of a “periodic” loading condition [19], i.e., when each mesh panel is equally loaded.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shu, S.; Muhunthan, B.; Badger, T.C. Snow loads on wire mesh and cable net rockfall slope protection systems. Eng. Geol. 2005, 81, 15–31. [Google Scholar] [CrossRef]
- Muhunthan, B.; Shu, S.; Sasiharan, N.; Hattamleh, O.; Badger, T.; Lowell, S.; Duffy, J. Analysis and Design of Wire/Mesh Cable Net Slope Protection; Technical Report; U.S. Department of Transportation—Federal Highway Administration: Washington, DC, USA, 2005. [Google Scholar]
- Savi, S.; Comiti, F.; Strecker, M.R. Pronounced increase in slope instability linked to global warming: A case study from the eastern European Alps. Earth Surf. Process. Landforms 2021, 46, 1328–1347. [Google Scholar] [CrossRef]
- Da Costa, A.; Sagaseta, C. Analysis of shallow instabilities in soil slopes reinforced with nailed steel wire meshes. Eng. Geol. 2010, 113, 53–61. [Google Scholar] [CrossRef]
- Blanco-Fernandez, E.; Castro-Fresno, D.; Díaz, J.D.C.; Lopez-Quijada, L. Flexible systems anchored to the ground for slope stabilisation: Critical review of existing design methods. Eng. Geol. 2011, 122, 129–145. [Google Scholar] [CrossRef]
- Giacchetti, G.; Grimod, A. Superficial consolidation of rock slope: Design at the ultimate and seriviceability limit state. In Engineering Geology for Society and Territory; Springer: Berlin/Heidelberg, Germany, 2015; Volume 2, pp. 1885–1888. [Google Scholar]
- Marchelli, M.; Giacchetti, G. Reinforced Drapery Meshes: A Design Method Accounting for Retaining Ropes Contribution. Appl. Sci. 2021, 11, 11176. [Google Scholar] [CrossRef]
- Bertolo, P.; Oggeri, C.; Peila, D. Full-scale testing of draped nets for rockfall protection. Can. Geotech. J. 2009, 46, 306–316. [Google Scholar] [CrossRef]
- Cala, M.; Stolz, M.; Baraniak, P.; Rist, A.; Roduner, A. Large scale field tests for slope stabilizations made with flexible facings. In Proceedings of the ISRM International Symposium-EUROCK 2013, Wroclaw, Poland, 23–26 October 2013; OnePetro: Richardson, TX, USA, 2013. [Google Scholar]
- Bucher, R.; Wendeler, C.; Baraniak, P. New results of large-scale testing of high-tensile steel meshes and soil nails for slope stabilisation and validation of modelling software. In Proceedings of the First Asia Pacific Slope Stability in Mining Conference. Australian Centre for Geomechanics, Perth, Australia, 14–16 November 2016; pp. 709–720. [Google Scholar]
- Gratchev, I.; Kim, D.H.; Chung, M. Study of the interface friction between mesh and rock surface in drapery systems for rock fall hazard control. Eng. Geol. 2015, 199, 12–18. [Google Scholar] [CrossRef]
- ASTM A975:2021; Standard Specification for Double-Twisted Hexagonal Mesh Gabions and Revet Mattresses (Metallic-Coated Steel Wire or Metallic-Coated Steel Wire With Poly(Vinyl Chloride) (PVC) Coating). ASTM: West Conshohocken, PA, USA, 2021.
- EN 15381:2008; Geotextiles and Geotextile-Related Products. Characteristics Required for Use in Pavements and Asphalt Overlays. European Standard: Brussels, Belgium, 2008.
- ISO 17745:2016; Steel Wire Ring Net Panels—Definitions and Specifications. ISO: Geneva, Switzerland, 2016.
- ISO 17746; Steel Wire Rope Net Panels and Rolls—Definitions and Specifications. ISO: Geneva, Switzerland, 2016.
- EN 10223-3:2013; Hexagonal Steel Wire Mesh Products for Civil Engineering Purposes. ISO: Geneva, Switzerland, 2013.
- UNI 11437; Opere di difesa dalla caduta massi—Prove su reti per rivestimento di versanti. UNI: Milano, Italy, 2012.
- Pol, A. Discrete Element Modelling of Wire Meshes for Secured Drapery Applications. Ph.D. Thesis, Università degli Studi di Padova, Padova, Italy, 2020. [Google Scholar]
- Pol, A.; Gabrieli, F.; Brezzi, L. Discrete element analysis of the punching behavior of a secured drapery system: From laboratory characterization to idealized in situ conditions. Acta Geotech. 2021, 16, 2553–2573. [Google Scholar] [CrossRef]
- Cazzani, A.; Mongioví, L.; Frenez, T. Dynamic finite element analysis of interceptive devices for falling rocks. Int. J. Rock Mech. Min. Sci. 2002, 39, 303–321. [Google Scholar] [CrossRef]
- Volkwein, A. Numerical simulation of flexible rockfall protection systems. In Proceedings of the Computing in Civil Engineering, ASCE, Cancun, Mexico, 12–15 July 2005. [Google Scholar]
- Sasiharan, N.; Muhunthan, B.; Badger, T.; Shu, S.; Carradine, D. Numerical analysis of the performance of wire mesh and cable net rockfall protection systems. Eng. Geol. 2006, 88, 121–132. [Google Scholar] [CrossRef]
- Govoni, L.; de Miranda, S.; Gentilini, C.; Gottardi, G.; Ubertini, F. Modelling of falling rock protection barriers. Int. J. Phys. Model. Geotech. 2011, 11, 126–137. [Google Scholar] [CrossRef]
- Gentilini, C.; Govoni, L.; de Miranda, S.; Gottardi, G.; Ubertini, F. Three-dimensional numerical modelling of falling rock protection barriers. Comput. Geotech. 2012, 44, 58–72. [Google Scholar] [CrossRef]
- Mentani, A.; Giacomini, A.; Buzzi, O.; Govoni, L.; Gottardi, G.; Fityus, S. Numerical modelling of a low-energy rockfall barrier: New insight into the bullet effect. Rock Mech. Rock Eng. 2016, 49, 1247–1262. [Google Scholar] [CrossRef]
- Giacomini, A.; Thoeni, K.; Lambert, C.; Booth, S.; Sloan, S. Experimental study on rockfall drapery systems for open pit highwalls. Int. J. Rock Mech. Min. Sci. 2012, 56, 171–181. [Google Scholar] [CrossRef]
- Bertrand, D.; Nicot, F.; Gotteland, P.; Lambert, S. Modelling a geo-composite cell using discrete analysis. Comput. Geotech. 2005, 32, 564–577. [Google Scholar] [CrossRef]
- Thoeni, K.; Giacomini, A.; Lambert, C.; Sloan, S.W.; Carter, J.P. A 3D discrete element modelling approach for rockfall analysis with drapery systems. Int. J. Rock Mech. Min. Sci. 2014, 68, 107–119. [Google Scholar] [CrossRef]
- Albaba, A.; Lambert, S.; Kneib, F.; Chareyre, B.; Nicot, F. DEM modeling of a flexible barrier impacted by a dry granular flow. Rock Mech. Rock Eng. 2017, 50, 3029–3048. [Google Scholar] [CrossRef]
- Coulibaly, J.B.; Chanut, M.A.; Lambert, S.; Nicot, F. Nonlinear discrete mechanical model of steel rings. J. Eng. Mech. 2017, 143, 04017087. [Google Scholar] [CrossRef]
- Gabrieli, F.; Pol, A.; Thoeni, K. Comparison of two DEM strategies for modelling cortical meshes. In Proceedings of the PARTICLES V International Conference on Particle-Based Methods: Fundamentals and Applications, Hannover, Germany, 26–28 October 2017; CIMNE: Barcelona, Spain, 2017; pp. 489–496. [Google Scholar]
- Xu, C.; Tannant, D.D.; Zheng, W. Discrete element analysis of the influence of bolt pattern and spacing on the force-displacement response of bolted steel mesh. Int. J. Numer. Anal. Methods Geomech. 2019, 43, 2106–2125. [Google Scholar] [CrossRef]
- Xu, C.; Tannant, D.D.; Zheng, W.; Liu, K. Discrete element method and support vector machine applied to the analysis of steel mesh pinned by rockbolts. Int. J. Rock Mech. Min. Sci. 2020, 125, 104163. [Google Scholar] [CrossRef]
- Pol, A.; Gabrieli, F.; Bost, M. A simple tool for forecasting the mechanical response of anchored wire mesh panels. IOP Conf. Ser. Earth Environ. Sci. 2021, 833, 012104. [Google Scholar] [CrossRef]
- Gabrieli, F.; Pol, A.; Thoeni, K.; Mazzon, N. Particle-based modelling of cortical meshes for soil retaining applications. In Numerical Methods in Geotechnical Engineering IX; CRC Press: Boca Raton, FL, USA, 2018; pp. 391–397. [Google Scholar]
- Pol, A.; Gabrieli, F.; Mazzon, N. Enhancement of design methodologies of anchored mesh systems using the discrete element method. In Geotechnical Research for Land Protection and Development: Proceedings of CNRIG 2019 7; Springer: Berlin/Heidelberg, Germany, 2020; pp. 500–508. [Google Scholar]
- Pol, A.; Gabrieli, F. Discrete element simulation of wire-mesh retaining systems: An insight into the mechanical behavior. Comput. Geotech. 2021, 134, 104076. [Google Scholar] [CrossRef]
- Pol, A.; Gabrieli, F. Anchor plate bearing capacity in flexible mesh facings. Soils Found. 2022, 62, 101222. [Google Scholar] [CrossRef]
- Gabrieli, F.; Pol, A.; Bost, M.; Brezzi, L. Design Tool for Pinned Drapery Meshes. Available online: https://geotechlab.dicea.unipd.it/codes/design-tool-for-drapery-mesh/ (accessed on 15 January 2023).
- Nicot, F.; Cambou, B.; Mazzoleni, G. Design of rockfall restraining nets from a discrete element modelling. Rock Mech. Rock Eng. 2001, 34, 99–118. [Google Scholar] [CrossRef]
- Pol, A.; Gabrieli, F.; Thoeni, K.; Mazzon. Discrete element modelling of punch tests with a double-twist hexagonal wire mesh. In Proceedings of the 6th Interdisciplinary Workshop on Rockfall Protection, Barcelona, Spain, 22–24 May 2017; pp. 22–24. [Google Scholar]
- Gabrieli, F.; Pol, A.; Mazzon, N.; Deana, M. Discrete element simulations of punch tests for the mechanical characterization of cortical meshes. In Proceedings of the 14th ISRM Congress, Foz do Iguassu, Brazil, 13–18 September 2019; OnePetro: Richardson, TX, USA, 2019. [Google Scholar]
- Effeindzourou, A.; Chareyre, B.; Thoeni, K.; Giacomini, A.; Kneib, F. Modelling of deformable structures in the general framework of the discrete element method. Geotext. Geomembr. 2016, 44, 143–156. [Google Scholar] [CrossRef]
- Effeindzourou, A.; Thoeni, K.; Giacomini, A.; Wendeler, C. Efficient discrete modelling of composite structures for rockfall protection. Comput. Geotech. 2017, 87, 99–114. [Google Scholar] [CrossRef]
- Marigo, N.; Gabrieli, F.; Pol, A.; Bisson, A.; Brezzi, L. A Discrete Element Framework for the modelling of rock-filled gabions. IOP Conf. Ser. Earth Environ. Sci. 2021, 833, 012102. [Google Scholar] [CrossRef]
- Thoeni, K.; Lambert, C.; PGiacomini, A.; Sloan, S.W. Discrete modelling of hexagonal wire meshes with a stochastically distorted contact model. Comput. Geotech. 2013, 49, 158–169. [Google Scholar] [CrossRef]
- Marchelli, M.; De Biagi, V.; Peila, D. A quick-assessment procedure to evaluate the degree of conservation of rockfall drapery meshes. Frat. Integrità Strutt. 2019, 13, 437–450. [Google Scholar] [CrossRef]
- Galli, A.; Maiorano, R.M.S.; di Prisco, C.; Aversa, S. Design of slope-stabilizing piles: From ultimate limit state approaches to displacement based methods. Riv. Ital. Geotec. 2017, 51, 77–93. [Google Scholar]
- Galli, A.; Deana, M.; Mazzon, N. Application of a hybrid approach to the design of anchored wire meshes on steep slopes. In Proceedings of the Slope Stability 2020 International Symposium on Slope Stability in Open Pit Mining and Civil Engineering, Perth, Australia, 12–14 May 2020; Australian Centre for Geomechanics: Crawley, Australia, 2020; pp. 823–830. [Google Scholar]



| Parameter | Range | Normalized Range | Reference Value |
|---|---|---|---|
| Length side (m) | (step 0.25 m) | 3 m | |
| Anchor plate size (cm) | (step 2 cm) | 20 cm | |
| Eccentricity , (cm) | (step 25 cm) | 0 cm | |
| Punching element size (m) | (step 0.1 m) | 1 m | |
| Punching element loading direction () | (step 5) | - | |
| Aspect ratio (-) | (step for of 0.25 m) | - | 1 |
| Equation (8) | Equation (9) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| (m) | (-) | (cm) | (m) | (m) | (m) | (kN) | (m) | (kN) | (m) | |
| a | 2.5 | 1 | 24 | 0.8 | 0 | 0 | 35.0 (∼0%) | 0.83 (+1%) | 35.0 | 0.82 |
| b | 3 | 1 | 20 | 1 | 0 | 0 | 34.2 (−8%) | 0.94 (−1%) | 37.3 | 0.95 |
| c | 3 | 1.25 | 24 | 1.2 | 0 | 0 | 40.8 (−4%) | 0.85 (+1%) | 42.7 | 0.84 |
| d | 3.5 | 1 | 32 | 1.2 | 1 | 0.3 | 28.2 (+4%) | 0.87 (+6%) | 27.2 | 0.82 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marchelli, M.; Pol, A.; Peila, D.; Gabrieli, F. Towards a Hybrid Design Approach of Anchored Drapery Systems. Geosciences 2023, 13, 147. https://doi.org/10.3390/geosciences13050147
Marchelli M, Pol A, Peila D, Gabrieli F. Towards a Hybrid Design Approach of Anchored Drapery Systems. Geosciences. 2023; 13(5):147. https://doi.org/10.3390/geosciences13050147
Chicago/Turabian StyleMarchelli, Maddalena, Antonio Pol, Daniele Peila, and Fabio Gabrieli. 2023. "Towards a Hybrid Design Approach of Anchored Drapery Systems" Geosciences 13, no. 5: 147. https://doi.org/10.3390/geosciences13050147
APA StyleMarchelli, M., Pol, A., Peila, D., & Gabrieli, F. (2023). Towards a Hybrid Design Approach of Anchored Drapery Systems. Geosciences, 13(5), 147. https://doi.org/10.3390/geosciences13050147







