Integrated Schumann Resonance Intensity as an Indicator of the Global Thunderstorm Activity
Abstract
:1. Introduction
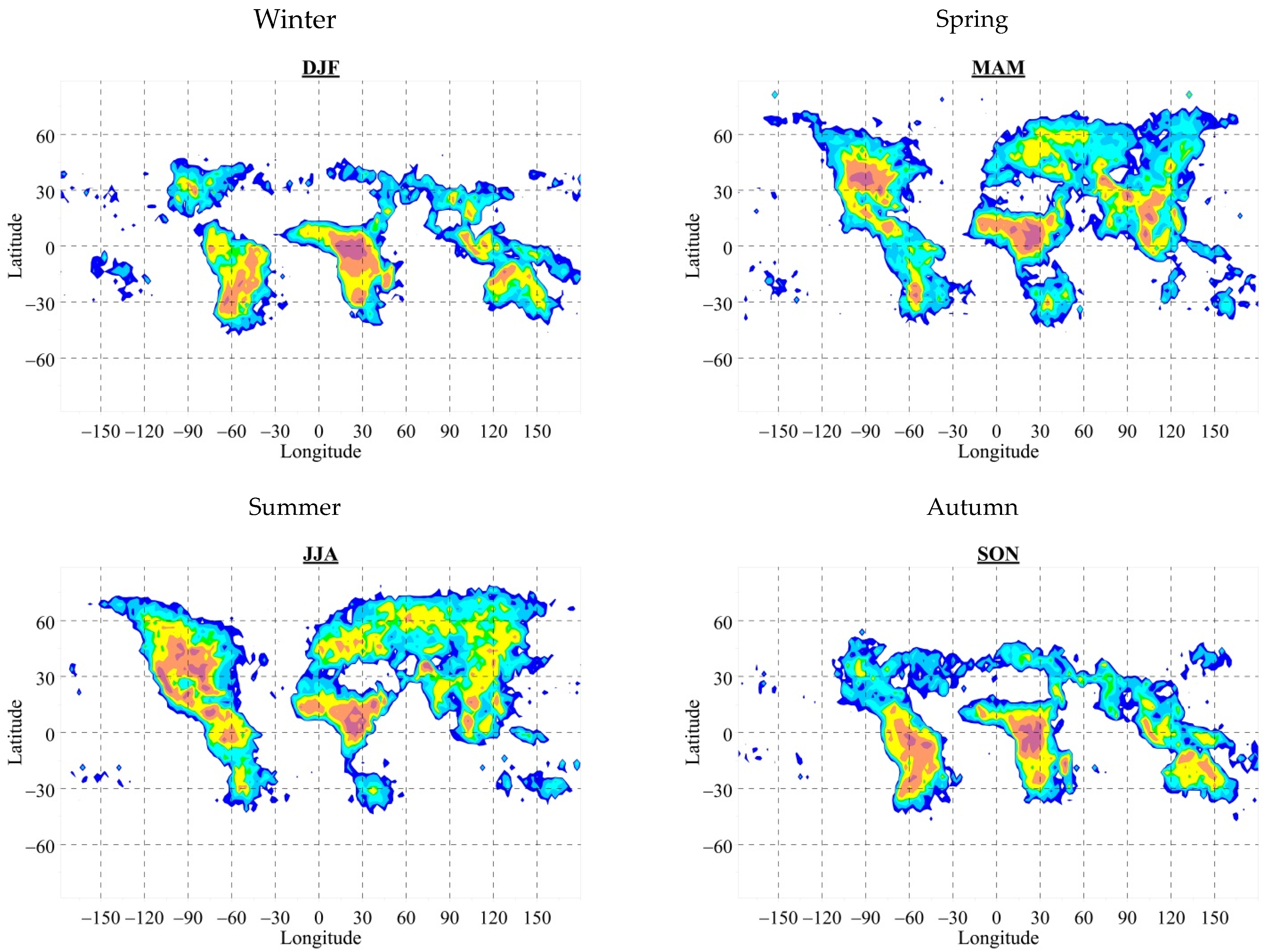
2. Formulation of the Problem
3. Model Daily Variations
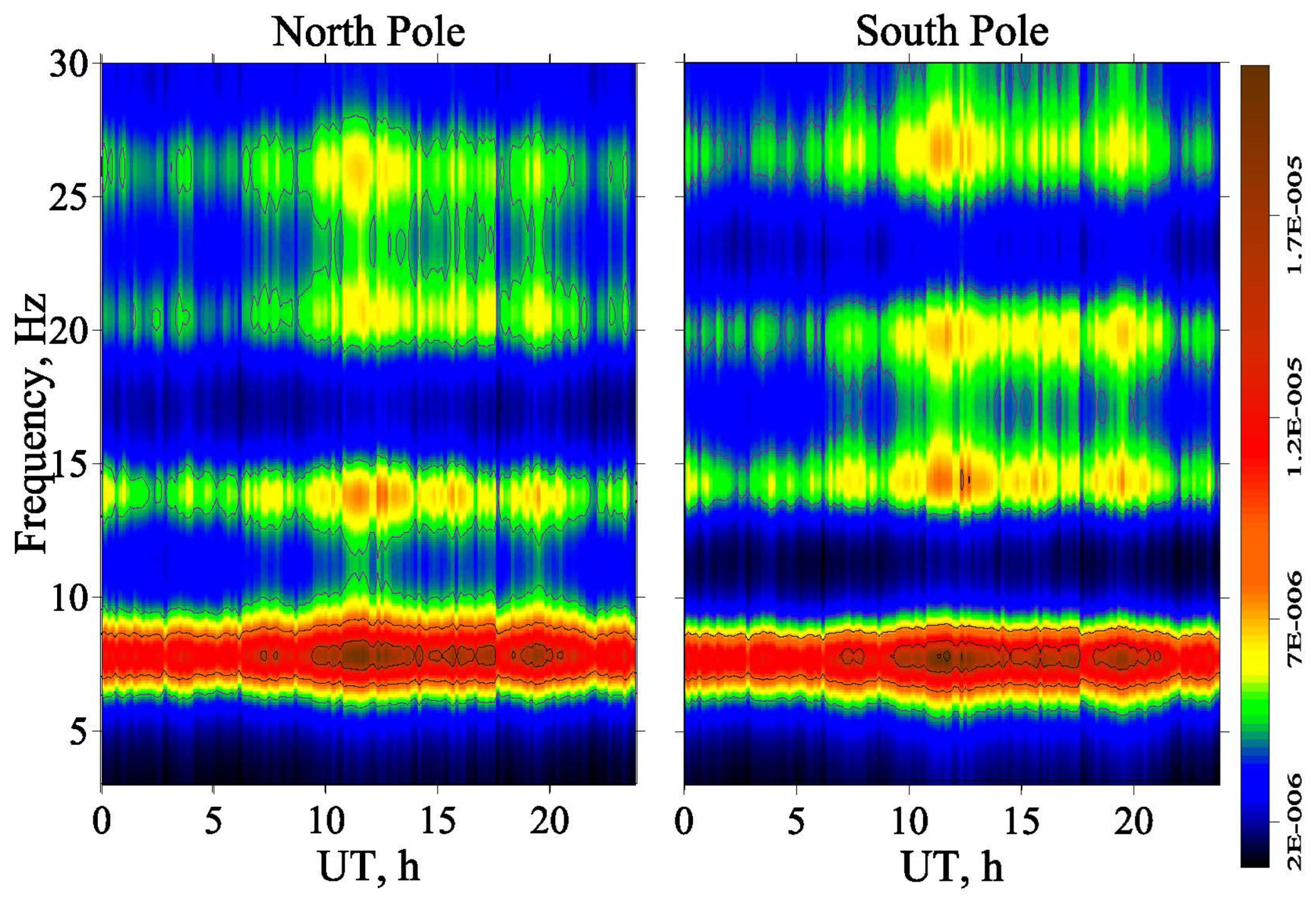
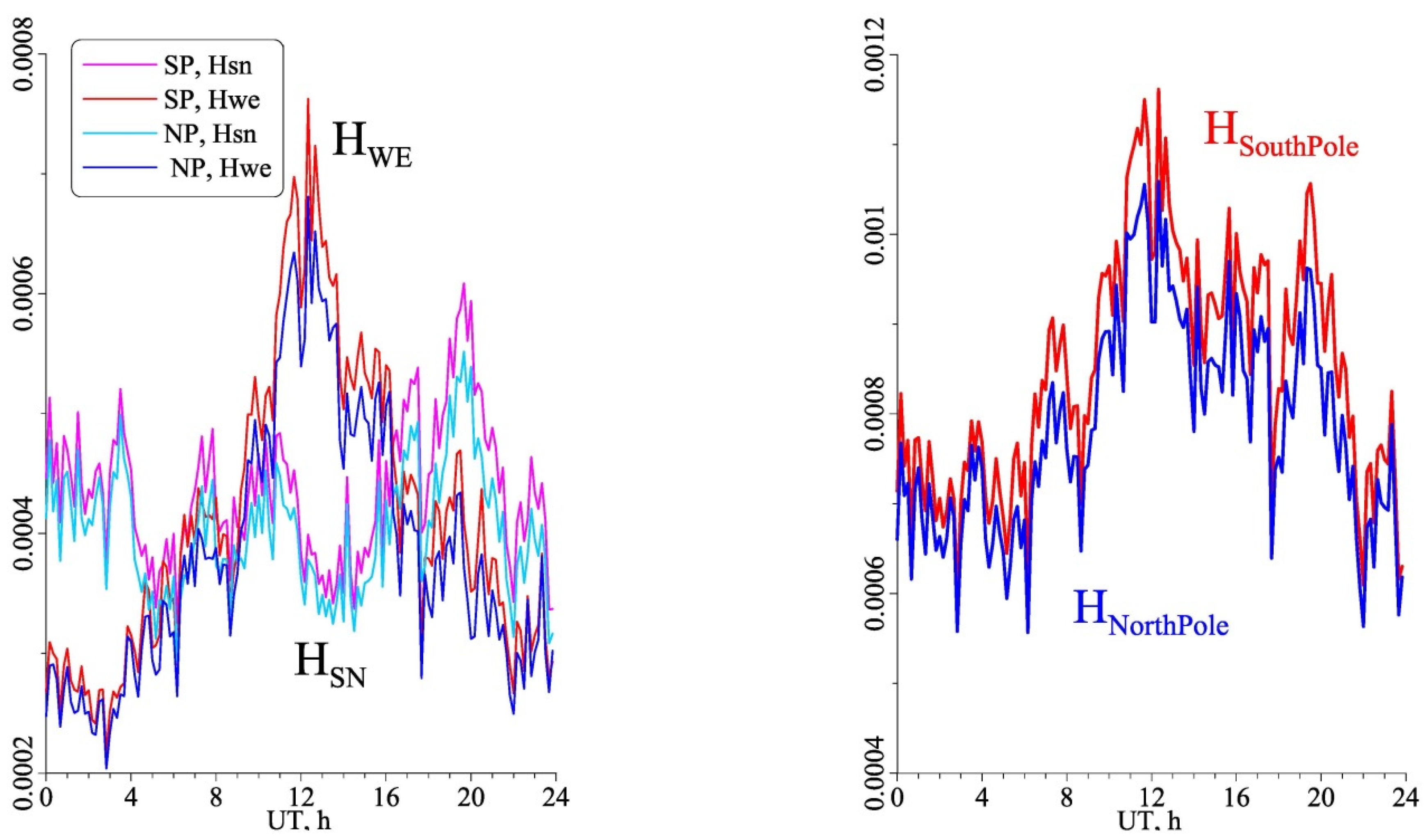
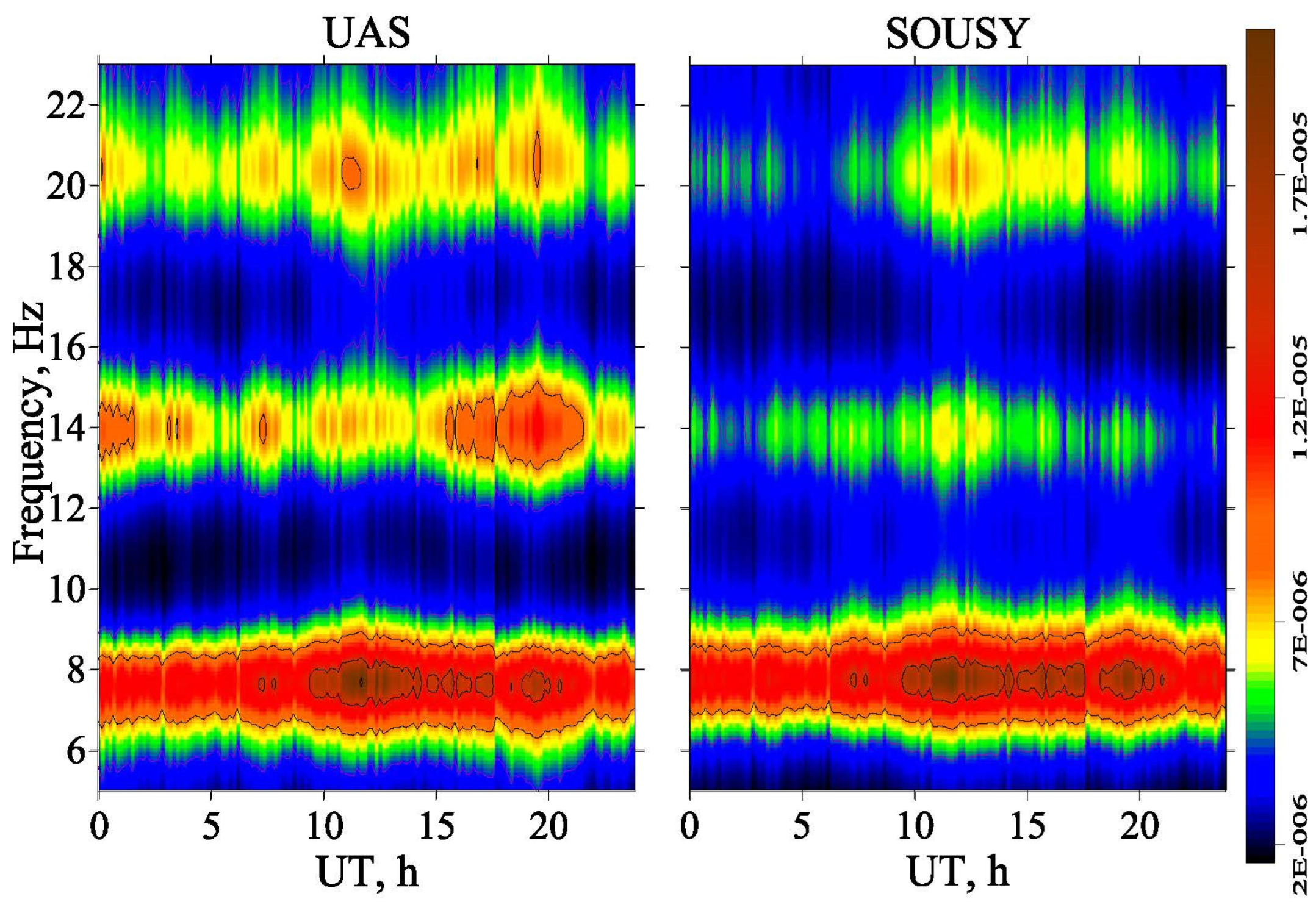
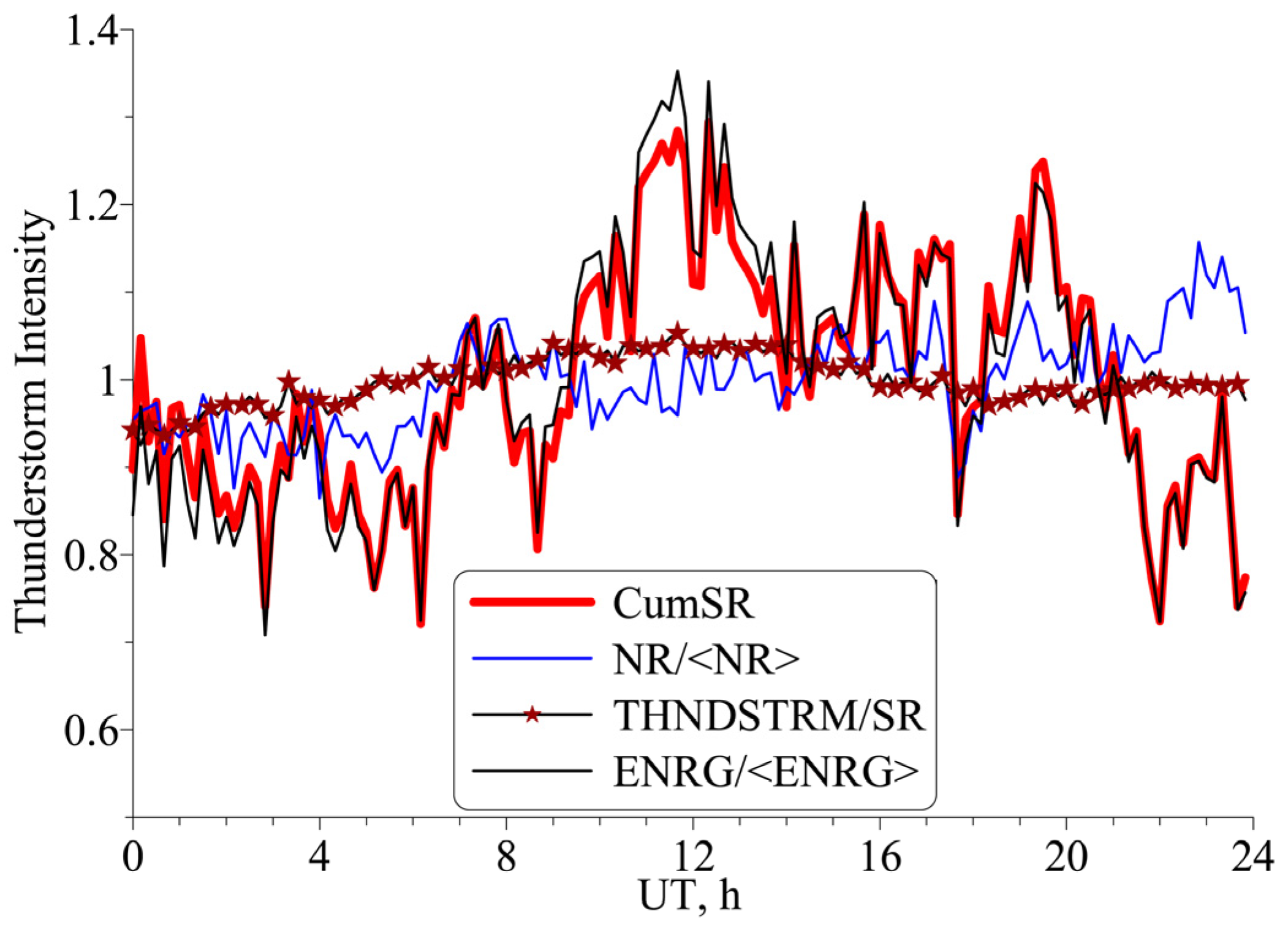
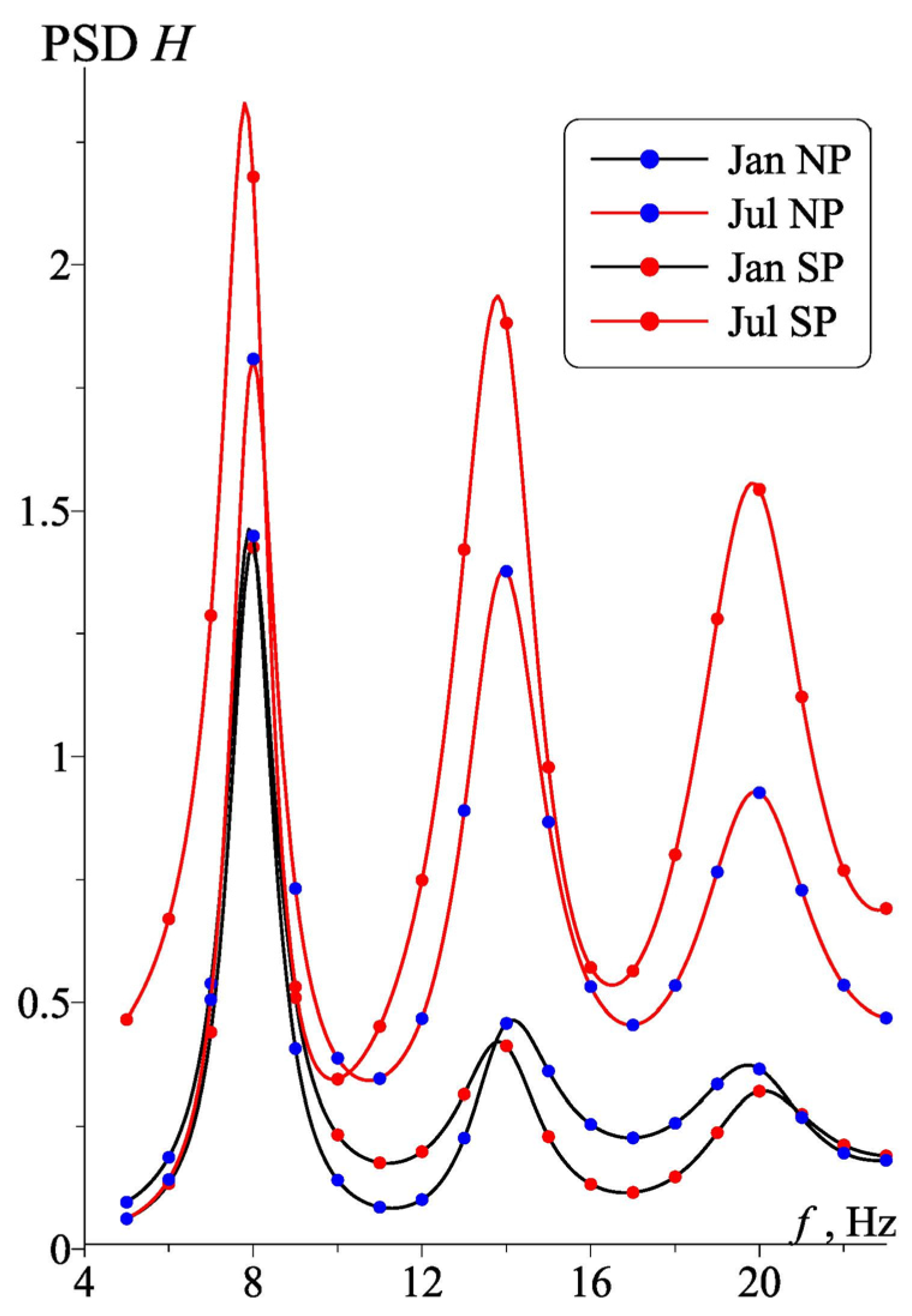
3.1. Polar Observers
3.2. Diurnal Variations for High-Latitude Observers
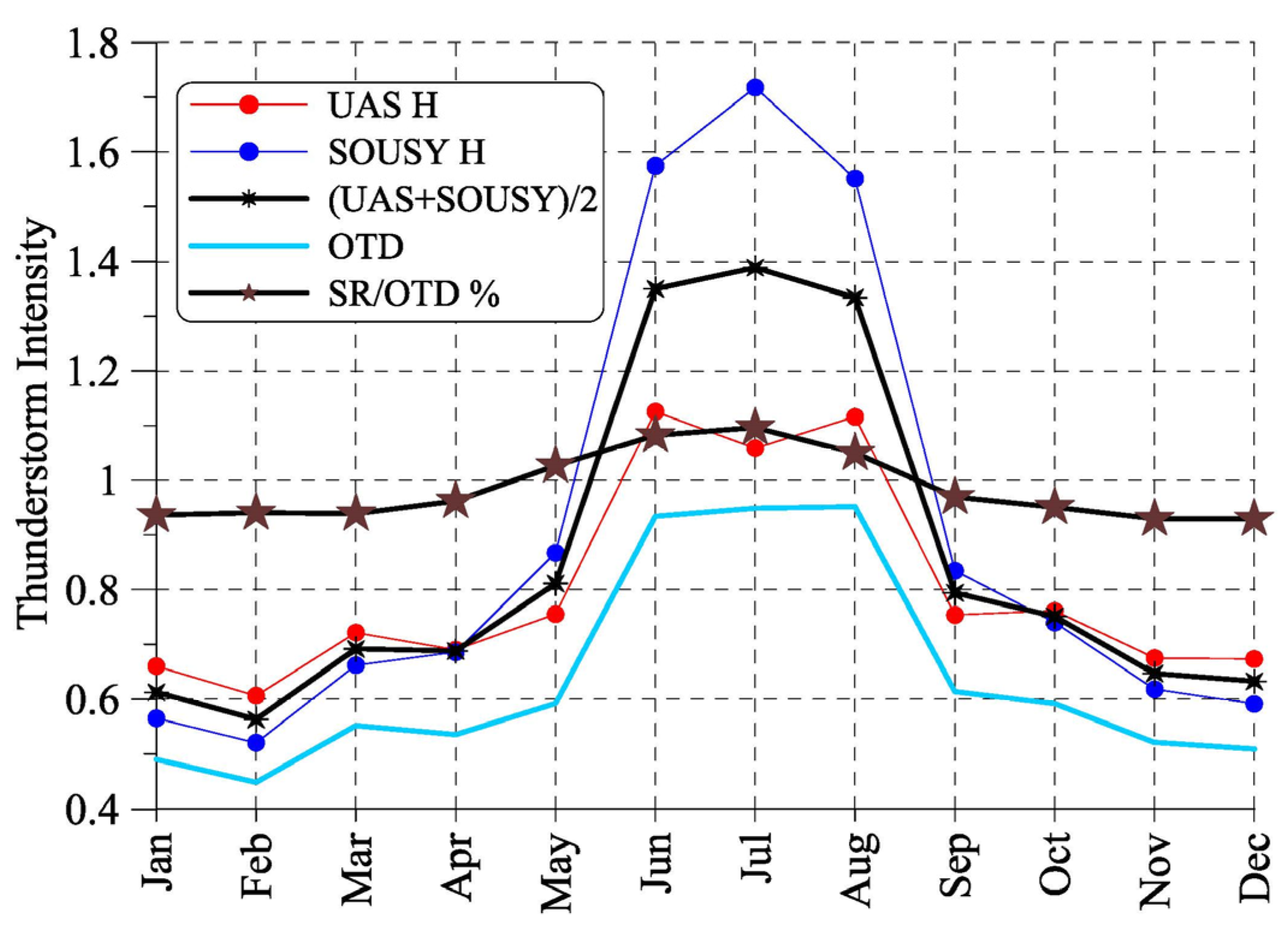
4. Model Seasonal Variations
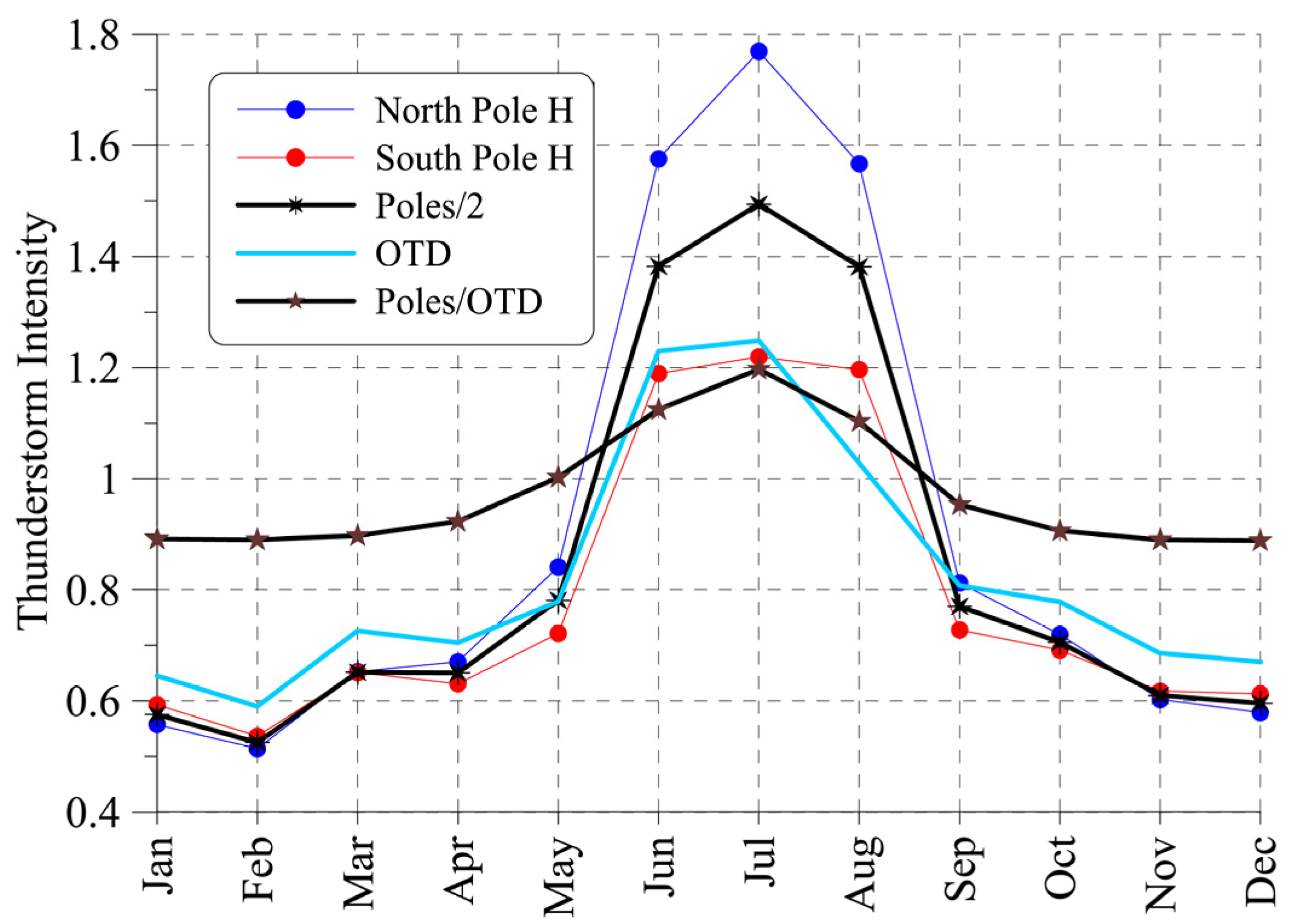
4.1. Polar Observers
4.2. High-Latitude Observers in the Northern and Southern Hemispheres
5. Summary
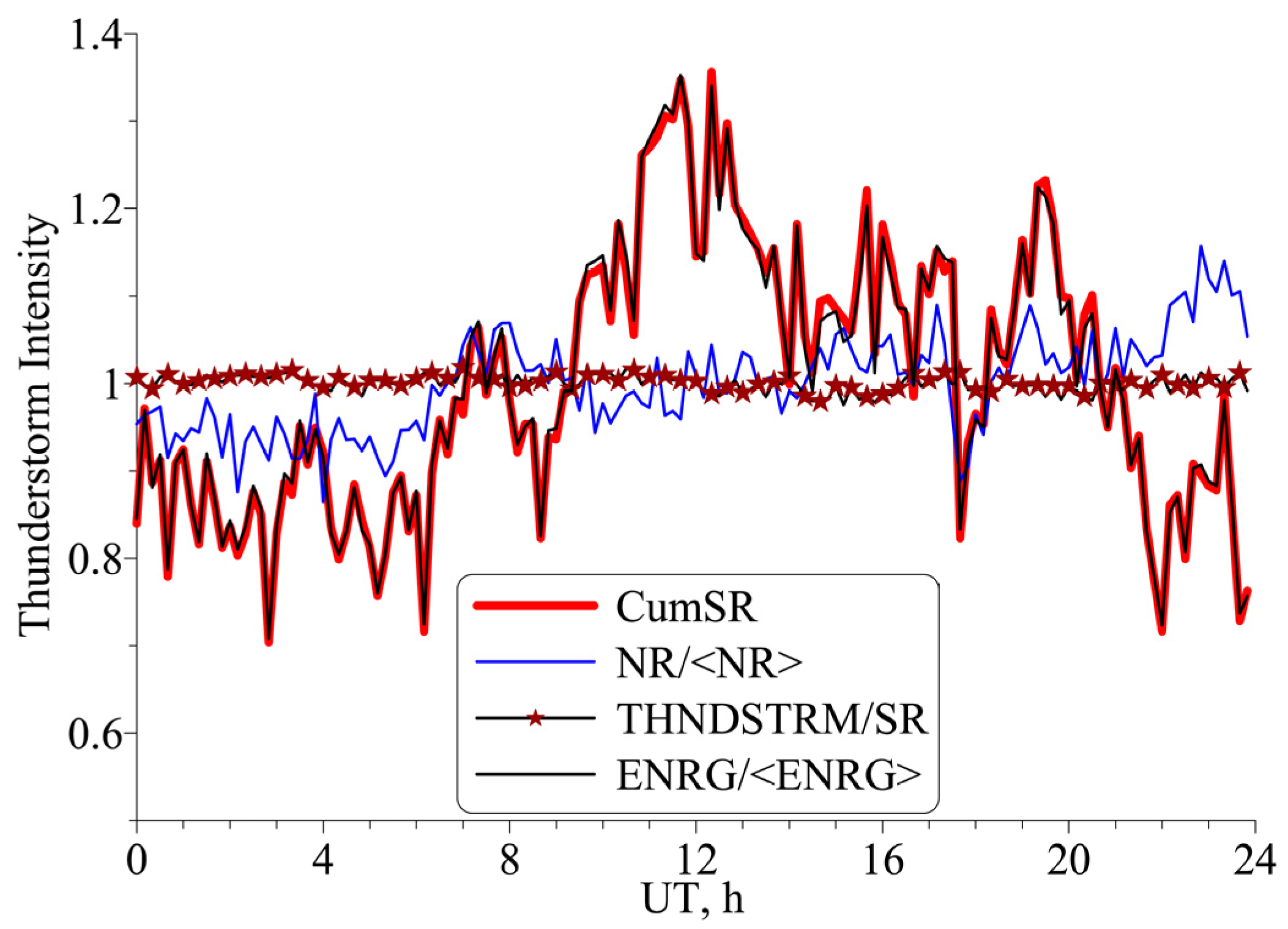
- The numerical simulations showed a rather high accuracy of the estimates for the diurnal variations in the level of global thunderstorm activity by using the concurrent records of the integrated SR intensity at two high-latitude observatories, UAS and SOUSY. The relative error does not exceed 3% for the daily time resolution of 10 min or more;
- Alterations in the relative intensity of global thunderstorms on the seasonal time-scale are estimated from the SR data with an error of about 10%;
- Since the rate of changes in the level of global thunderstorm activity on the considered time-scales is approximately one octave (the factor of two), the above errors indicate an acceptable overall accuracy of the estimates acquired using simultaneous SR monitoring at the high-latitude observatories in the Arctic and Antarctic.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Polk, C. Relation of ELF noise and Schumann resonances to thunderstorm activity. In Planetary Electrodynamics; Coronoti, S.C., Hughes, J., Eds.; Gordon and Breach: New York, NY, USA, 1969; Volume 2, pp. 55–83. [Google Scholar]
- Polk, C. Schumann resonances. In Handbook of Atmospherics; Volland, H., Ed.; CRC Press: Boca Raton, FL, USA, 1982; Volume 1, pp. 111–178. [Google Scholar]
- Bliokh, P.V.; Nickolaenko, A.P.; Filippov, Y.F. Schumann Resonances in the Earth-Ionosphere Cavity; Peter Perigrinus: New York, NY, USA; London, UK; Paris, France, 1980; p. 168. [Google Scholar]
- Sentman, D.D. Schumann Resonances. In Handbook of Atmospheric Electrodynamics; Volland, H., Ed.; CRC Press: Boca Raton, FL, USA; London, UK; Tokyo, Japan, 1995; Volume 1, pp. 267–298. [Google Scholar]
- Nickolaenko, A.P.; Hayakawa, M. Resonances in the Earth-Ionosphere Cavity; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2002; p. 388. [Google Scholar]
- Nickolaenko, A.; Hayakawa, M. Schumann Resonance for Tyros; Springer: Tokyo, Japan; Heidelberg, Germany; New York, NY, USA; Dordrecht, The Netherlands; London, UK, 2014; p. 348. [Google Scholar] [CrossRef]
- Price, C. ELF electromagnetic waves from lightning: The Schumann resonances. Review. Atmosphere 2016, 7, 116. [Google Scholar] [CrossRef] [Green Version]
- Nickolaenko, A.P.; Shvets, A.V.; Hayakawa, M. Propagation at Extremely Low-Frequency Radio Waves. In Wiley Encyclopedia of Electrical and Electronics Engineering; Webster, J., Ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2016; pp. 1–20. [Google Scholar] [CrossRef]
- Sentman, D.D.; Fraser, B.J. Simultaneous observation of Schumann resonances in California and Australia: Evidence for intensity modulation by local height of D. region. J. Geophys. Res. 1991, 96, 15973–15984. [Google Scholar] [CrossRef]
- Nickolaenko, A.P. Modern aspects of the Schumann resonance studies. J. Atmos. Solar-Terr. Phys. 1997, 59, 805–816. [Google Scholar] [CrossRef]
- Nickolaenko, A.P.; Hayakawa, M.; Sekiguchi, M. Variations in global thunderstorm activity inferred from the OTD records. Geophys. Res. Lett. 2006, 33, L06823. [Google Scholar] [CrossRef]
- Sekiguchi, M.; Hayakawa, M.; Nickolaenko, A.P.; Hobara, Y. Evidence of a link between the intensity of Schumann resonance and global surface temperature. Ann. Geophys. 2006, 24, 1809–1817. [Google Scholar] [CrossRef] [Green Version]
- Bozóki, T.; Sátori, G.; Williams, E.; Guha, A.; Liu, Y.; Steinbach, P.; Leal, A.; Atkinson, M.; Beggan, C.D.; DiGangi, E.; et al. A Schumann Resonance-based quantity for characterizing day-to-day changes in global lightning activity. J. Geophys. Res. Atmos. 2023; in press. [Google Scholar] [CrossRef]
- Kudintseva, I.G.; Nickolaenko, A.P.; Rycroft, M.J.; Odzimek, A. AC and DC global electric circuit properties and the height profile of atmospheric conductivity. Ann. Geophys. 2016, 59, A0545. [Google Scholar] [CrossRef]
- Hynninen, E.M.; Galuk, Y.P. The field of vertical electric dipole source over the spherical Earth with non-uniform along the height ionosphere. In Problems of Radio Wave Diffraction and Propagation; LSU Publ.: St. Petersburg, Russia, 1972; pp. 109–120. [Google Scholar]
- Galuk, Y.P.; Ivanov, V.I. Propagation characteristics of VLF fields in the waveguide Earth–vertically non-uniform anisotropic ionosphere. In Problems of Radio Wave Diffraction and Propagation; LSU Publ.: St. Petersburg, Russia, 1978; pp. 148–153. [Google Scholar]
- Galuk, Y.P. Schumann resonance in the model of global thunderstorm activity uniformly distributed over the Earth. Radio-Phys. Electron. 2015, 6, 3–9. [Google Scholar]
- Lay, E.H.; Rodger, C.J.; Holzworth, R.H.; Dowden, R.L. Introduction to the World Wide Lightning Location Network (WWLLN). Geophys. Res. Abstr. 2005, 7, 02875, 2005 SRef-ID: 1607-7962/gra/EGU05-A-02875. [Google Scholar]
- Rodger, C.J.; Werner, S.; Brundell, J.B.; Lay, E.H.; Thomson, N.R.; Holzworth, R.H.; Dowden, R.L. Detection efficiency of the VLF World-Wide Lightning Location Network (WWLLN): Initial case study. Ann. Geophys. 2006, 24, pp. 3197–3214. Available online: www.ann-geophys.net/24/3197/2006 (accessed on 10 January 2023).
- Hutchins, M.L.; Holzworth, R.H.; Brundell, J.B.; Rodger, C.J. Relative detection efficiency of the World Wide Lightning Location Network. Radio Sci. 2012, 47, RS6005. [Google Scholar] [CrossRef]
- Rodger, C.J.; Brundell1, J.B.; Hutchins, M.; Holzworth, R.H. The world wide lightning location network (WWLLN): Update of status and applications. In Proceedings of the 2014 XXXIth URSI General Assembly and Scientific Symposium (URSI GASS), Beijing, China, 16–23 August 2014. [Google Scholar] [CrossRef]
- Holzworth, R.H.; Brundell, J.B.; McCarthy, M.P.; Jacobson, A.R.; Rodger, C.J.; Anderson, T.S. Lightning in the Arctic. Geophys. Res. Lett. 2021, 48, e2020GL091366. [Google Scholar] [CrossRef]
- Koloskov, A.V.; Bezrodny, V.G.; Budanov, O.V.; Yampolski, Y.M. Polarization monitoring of the Schumann resonances in the Antarctic and recognition of the world thunderstorm activity characteristics. Radiofiz. I Radioastron. 2005, 10, 11–29. [Google Scholar]
- Koloskov, O.V.; Nickolaenko, A.P.; Yampolski, Y.M.; Budanov, O.V. Electromagnetic seasons in Schumann resonance records. J. Geophys. Res. Atmos. 2022, 127, e2022JD036582. [Google Scholar] [CrossRef]
- Christian, H.J.; Blakeslee, R.J.; Boccippio, D.J.; Boeck, W.L.; Buechler, D.E.; Driscoll, E.T.; Goodman, S.J.; Hall, J.M.; Koshak, W.J.; Mach, D.M.; et al. Global frequency and distribution of lightning as observed from space by the Optical Transient Detector. J. Geophys. Res. 2003, 108, 4005. [Google Scholar] [CrossRef] [Green Version]
- Ogawa, T.; Murakami, Y. Schumann resonance frequencies and conductivity profiles in the atmosphere. Contr. Geophys. Inst. Kyoto Univ. 1973, 13, 13–20. [Google Scholar]
- Israel, H. Atmospherische Elekrizitat; Akademische Verlaggeseltschaft: Leipzig, Germany, 1961; Volume 2, 503p. [Google Scholar]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hayakawa, M.; Galuk, Y.P.; Nickolaenko, A.P. Integrated Schumann Resonance Intensity as an Indicator of the Global Thunderstorm Activity. Geosciences 2023, 13, 177. https://doi.org/10.3390/geosciences13060177
Hayakawa M, Galuk YP, Nickolaenko AP. Integrated Schumann Resonance Intensity as an Indicator of the Global Thunderstorm Activity. Geosciences. 2023; 13(6):177. https://doi.org/10.3390/geosciences13060177
Chicago/Turabian StyleHayakawa, Masashi, Yuriy P. Galuk, and Alexander P. Nickolaenko. 2023. "Integrated Schumann Resonance Intensity as an Indicator of the Global Thunderstorm Activity" Geosciences 13, no. 6: 177. https://doi.org/10.3390/geosciences13060177
APA StyleHayakawa, M., Galuk, Y. P., & Nickolaenko, A. P. (2023). Integrated Schumann Resonance Intensity as an Indicator of the Global Thunderstorm Activity. Geosciences, 13(6), 177. https://doi.org/10.3390/geosciences13060177






