Internal Friction Angle of Cohesionless Binary Mixture Sand–Granular Rubber Using Experimental Study and Machine Learning †
Abstract
:1. Introduction
2. Materials and Experimental Methodology
2.1. Materials
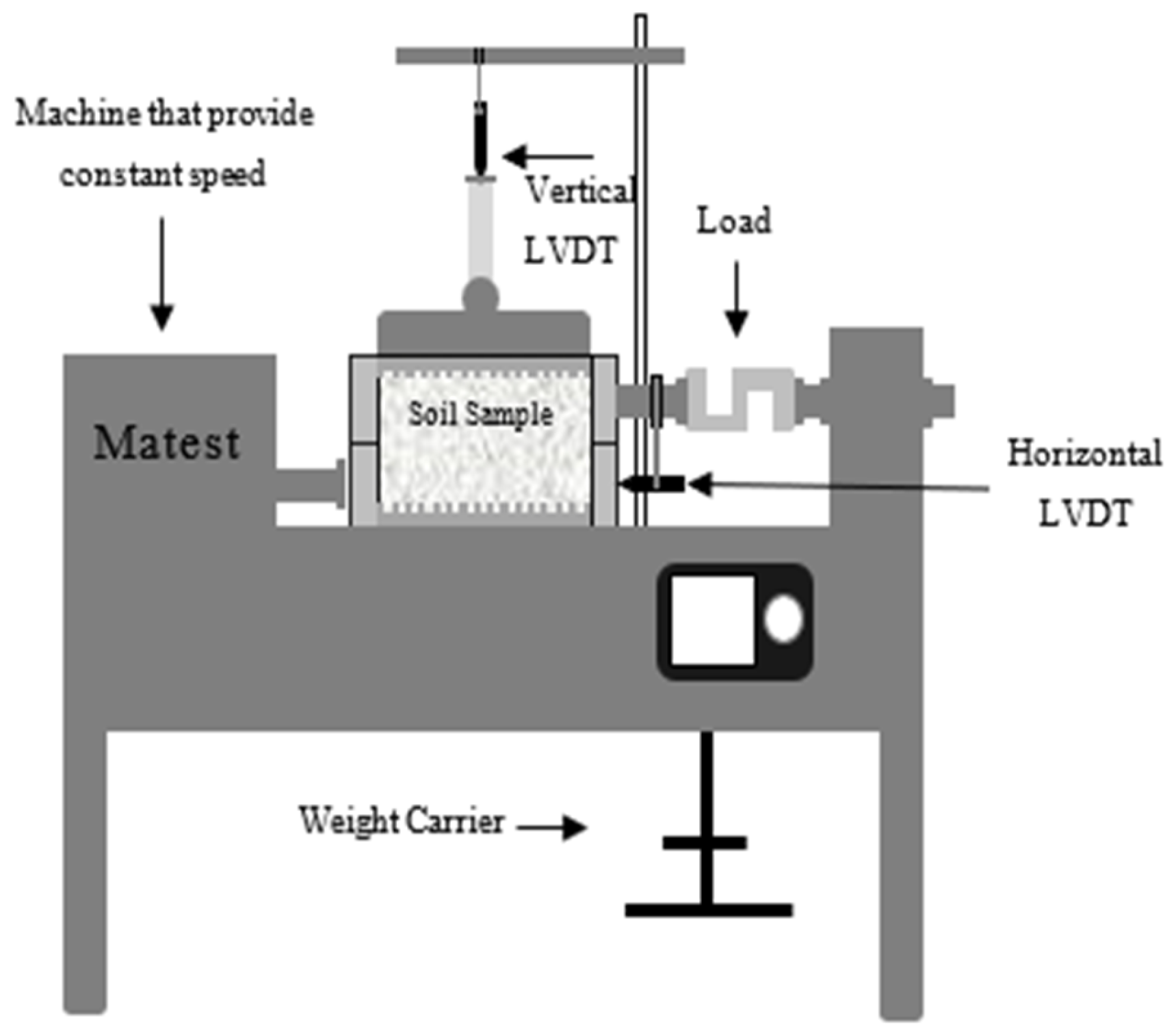
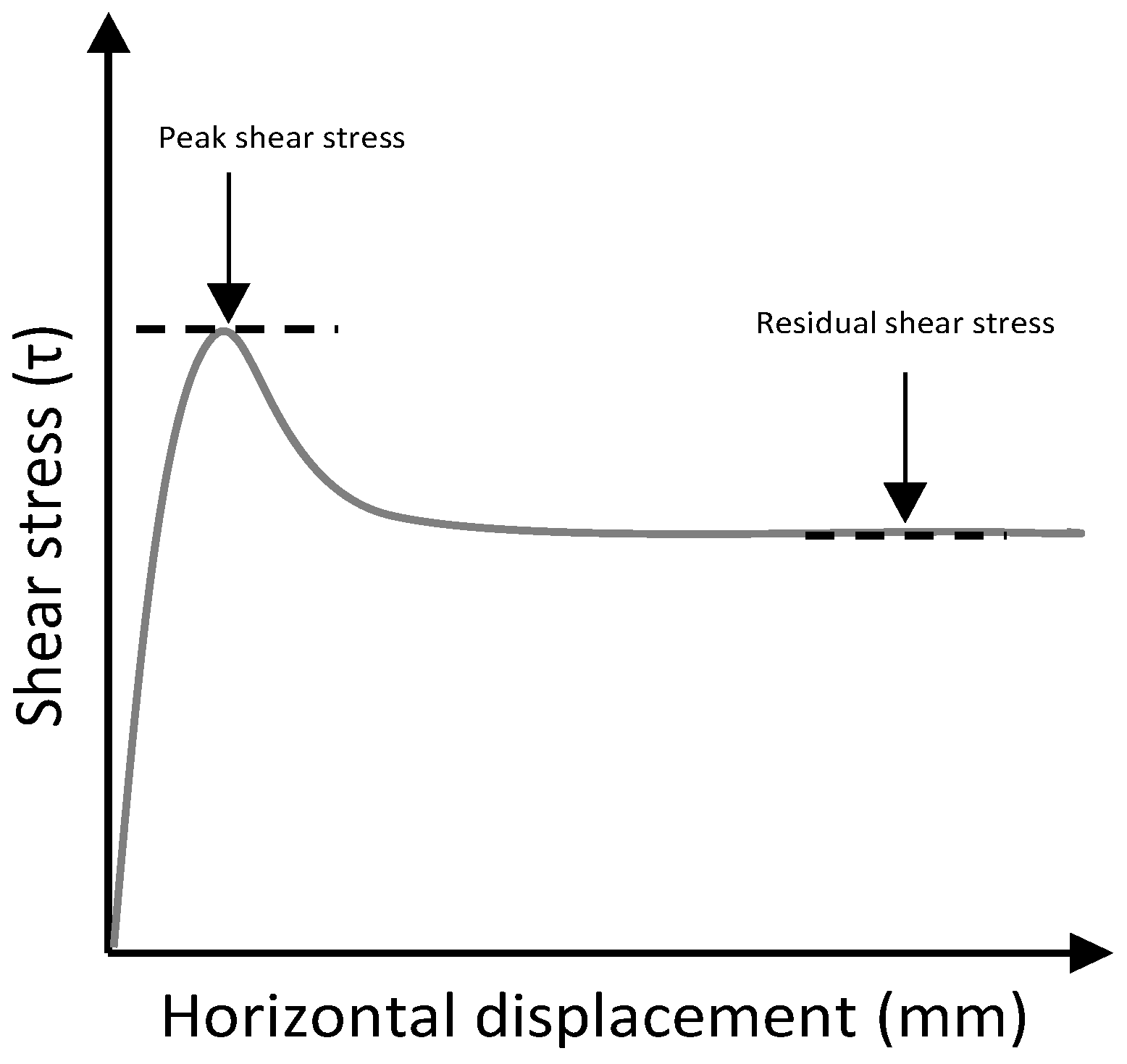
2.2. Direct Shear Test
2.3. Sample Preparation
2.4. Test Procedure
3. Mathematical Models
3.1. Multiple Linear Regression (MLR)
3.2. Classification and Regression Random Forests (CRRF)
3.3. Genetic Programing (GP)
4. Results
4.1. Experimental
4.1.1. Unit Weight, and Void Ratio
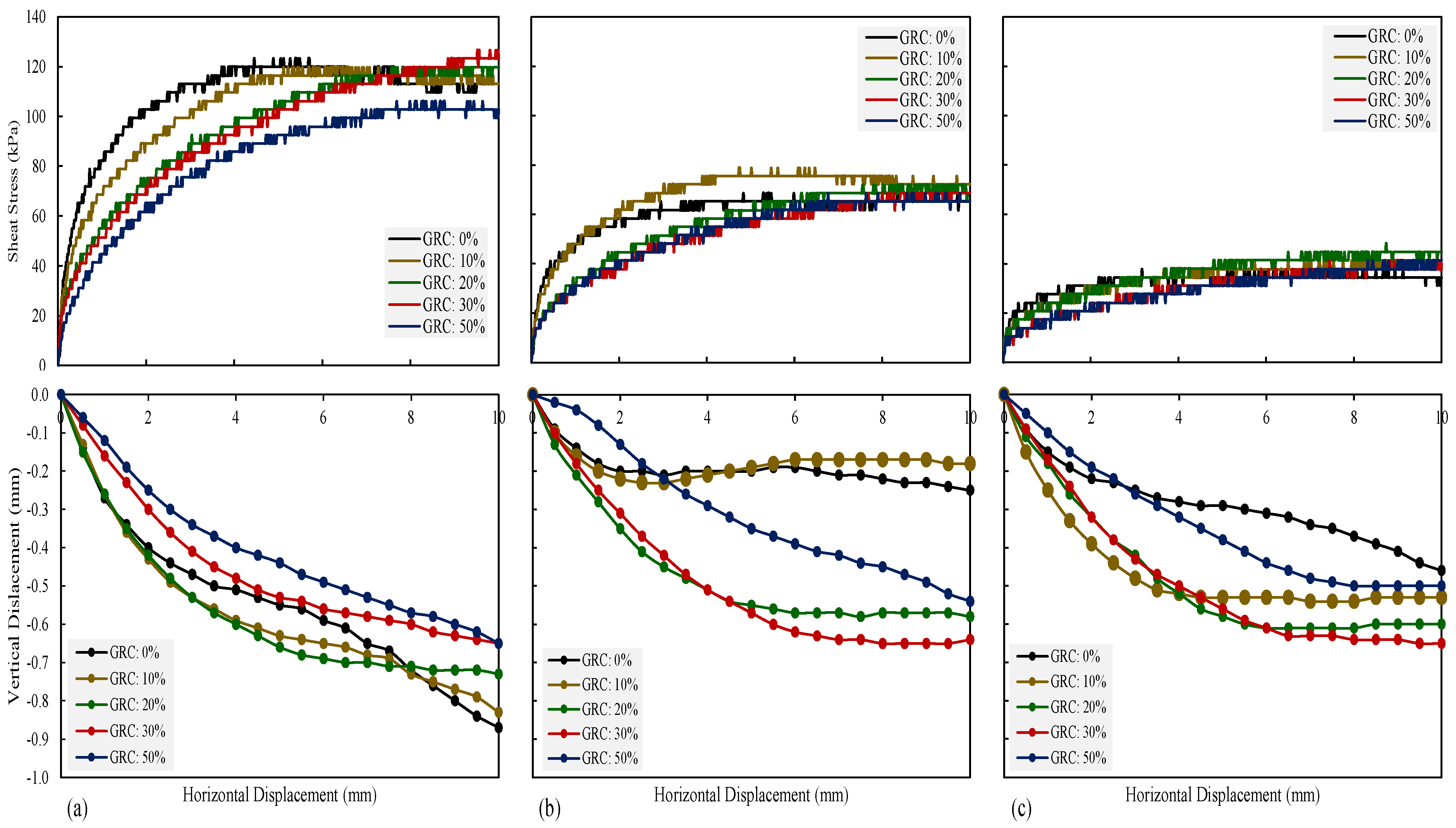
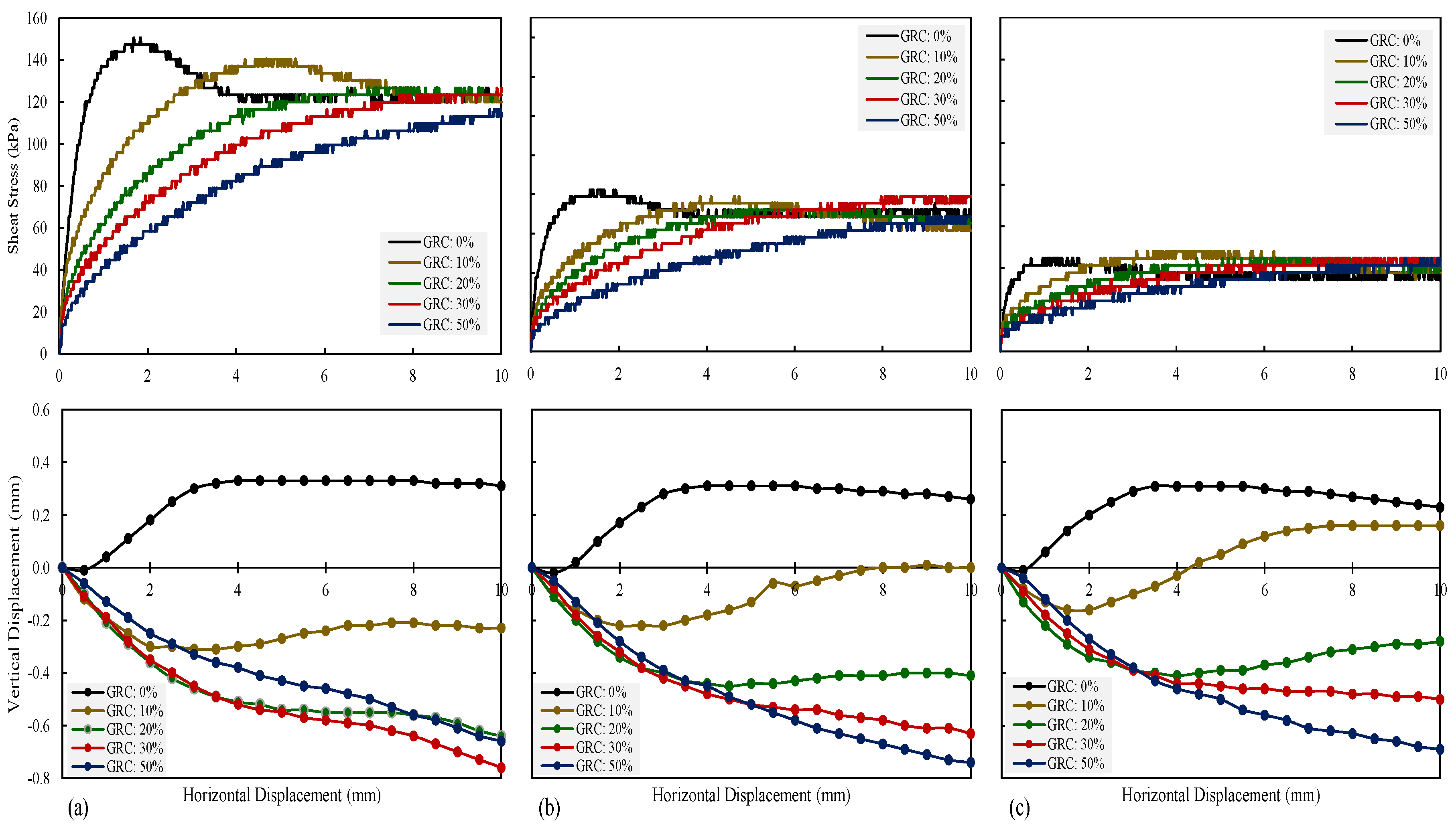
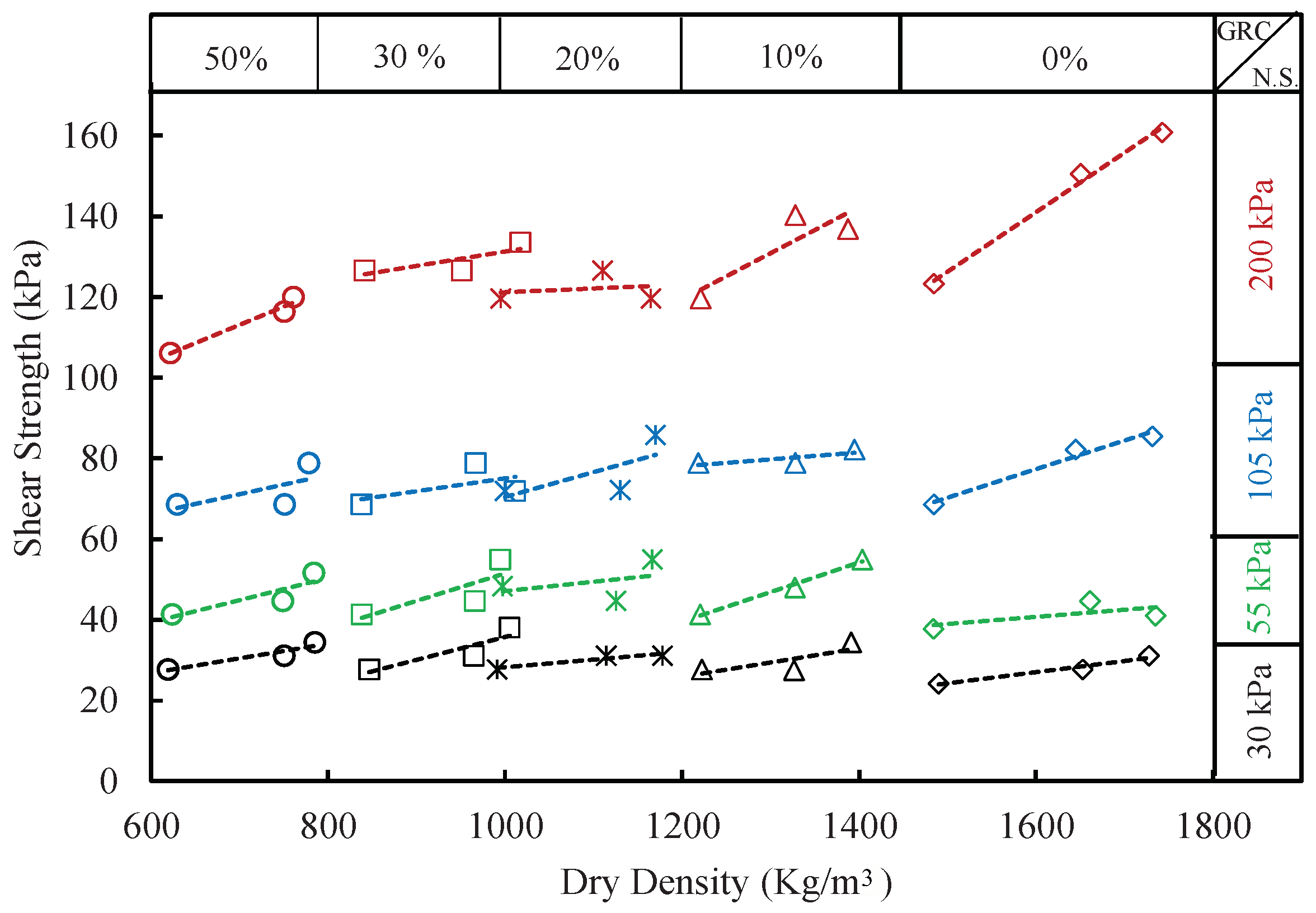
4.1.2. Shear Strength
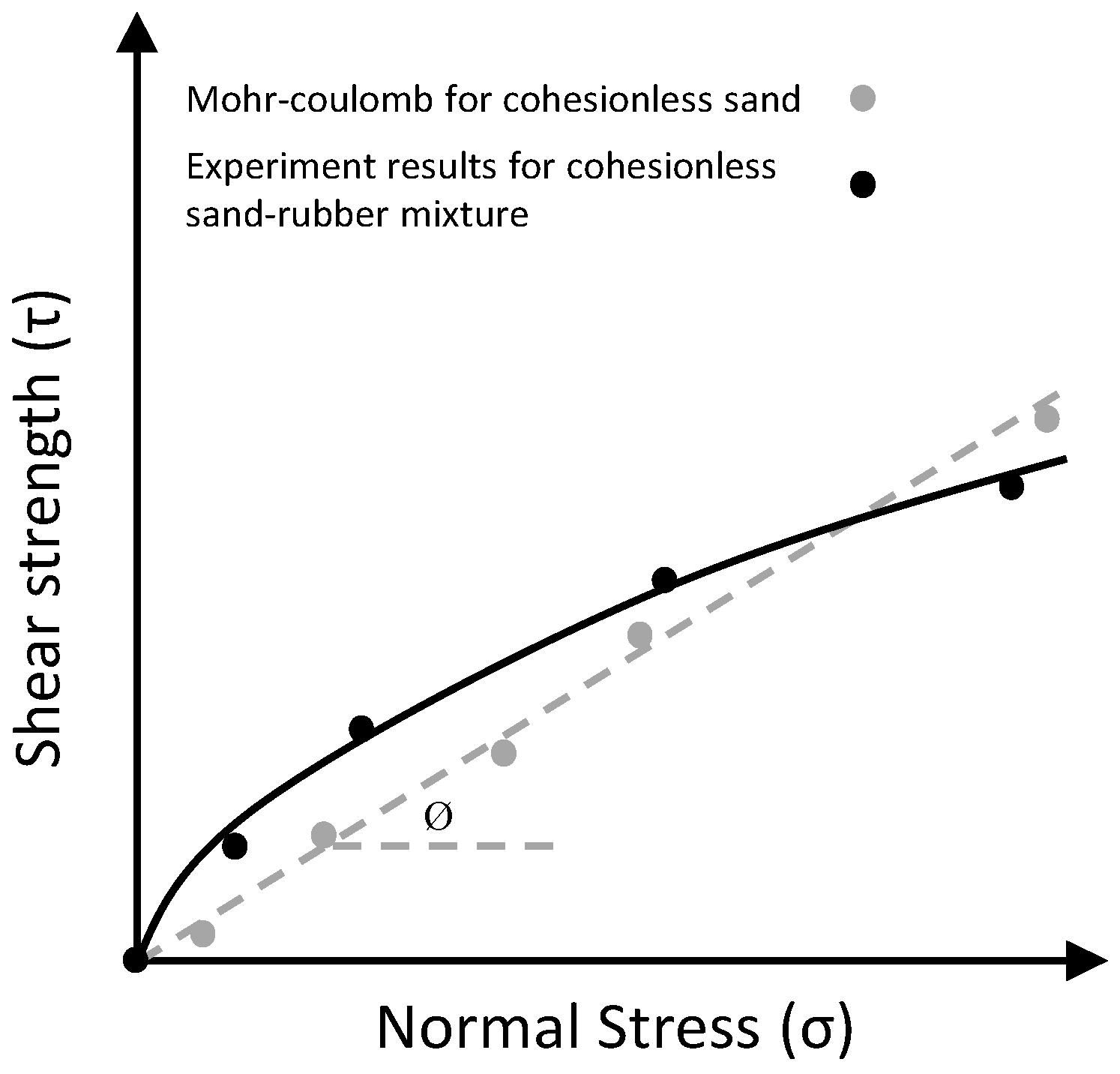
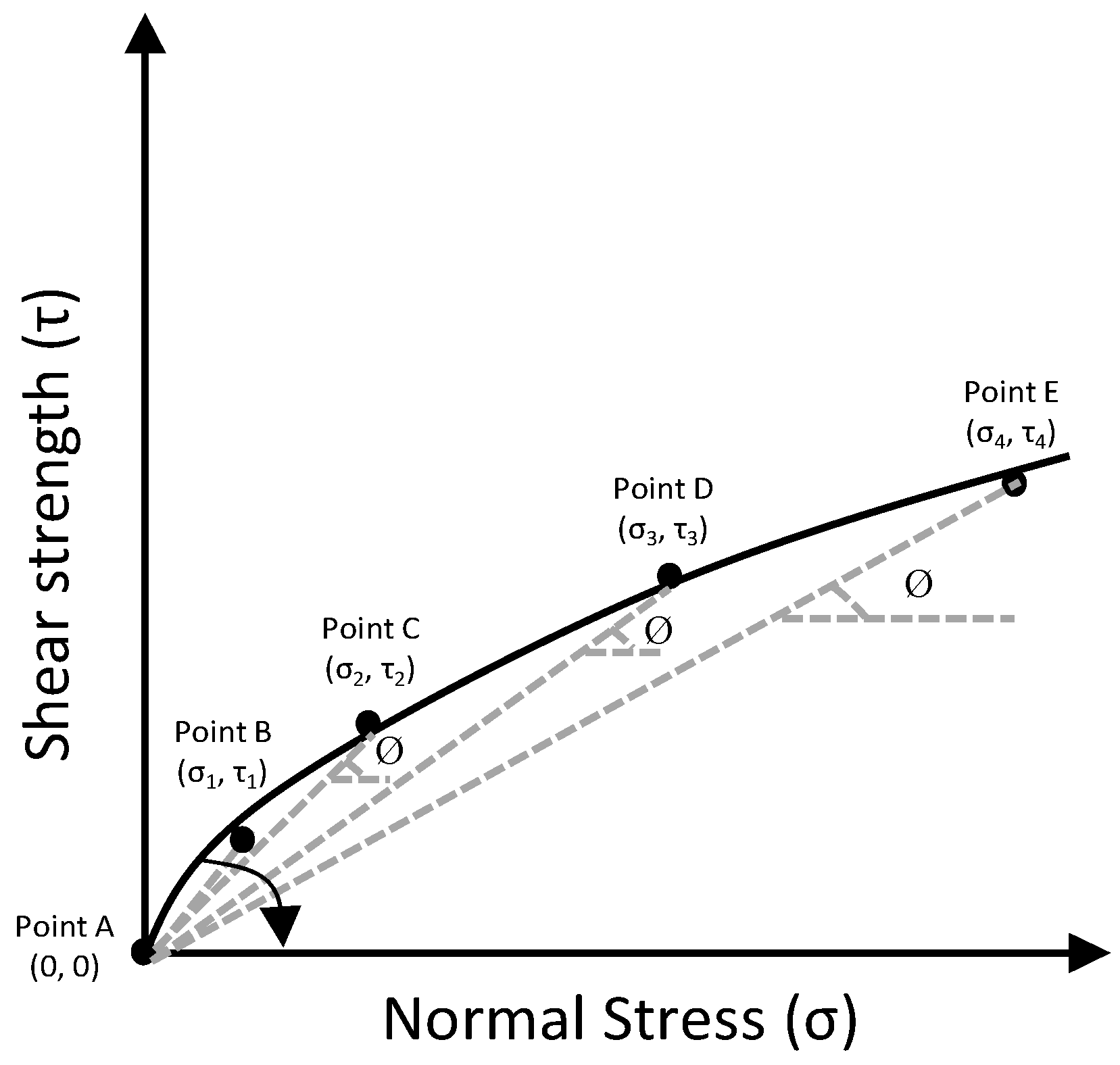
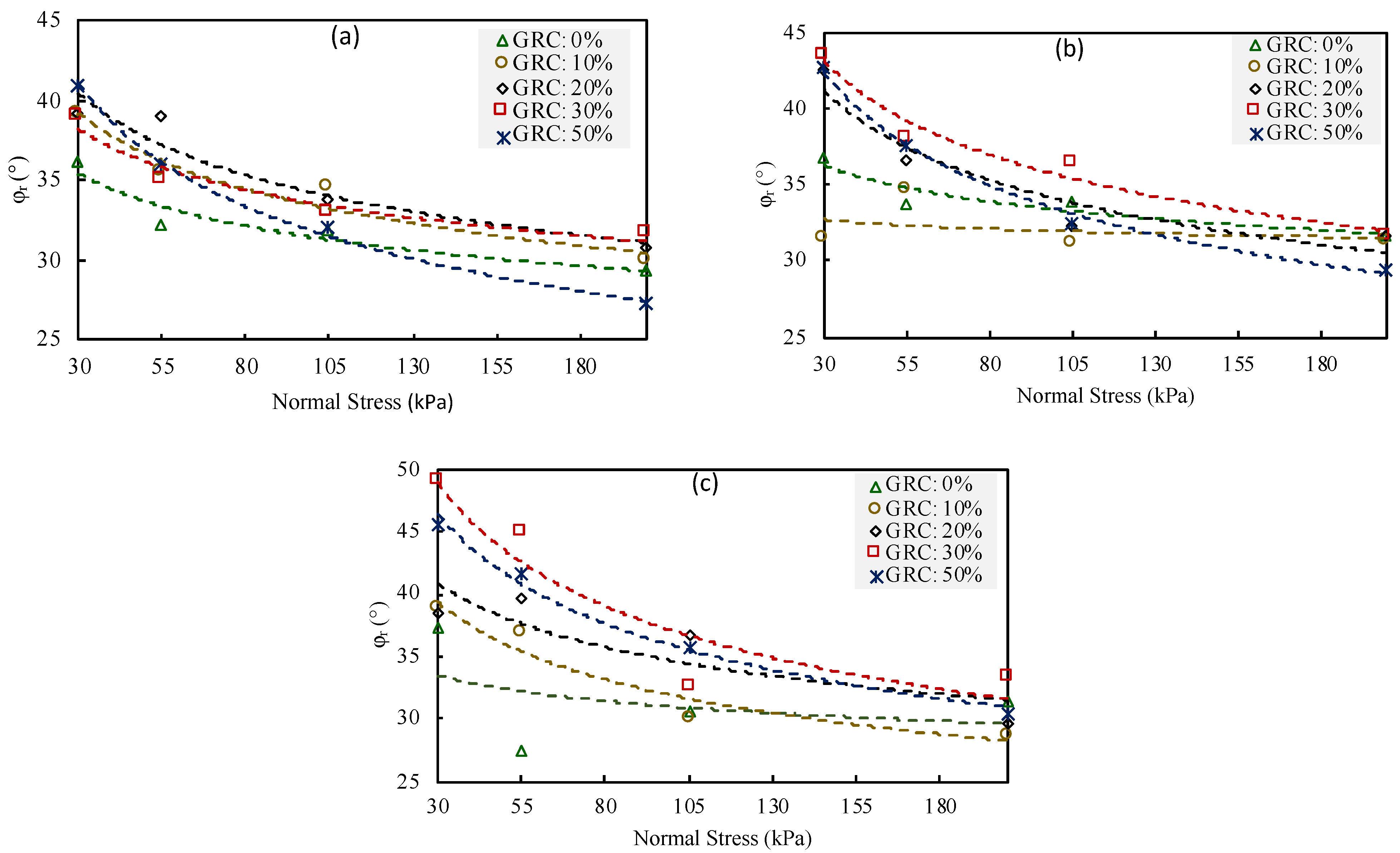
4.1.3. Internal Friction Angle
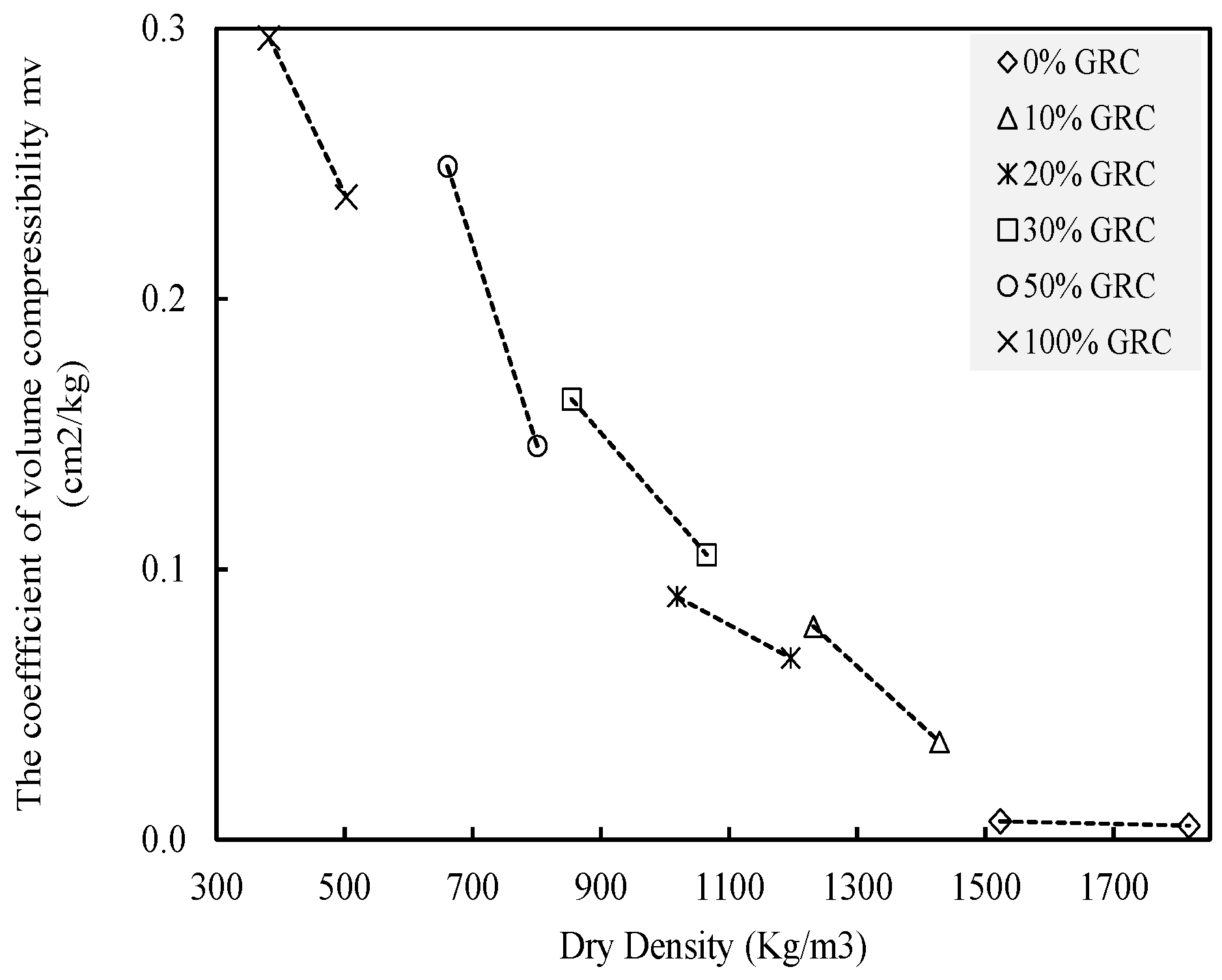
4.1.4. Volume Compressibility
4.2. AI Modelling
4.2.1. Database Preparation
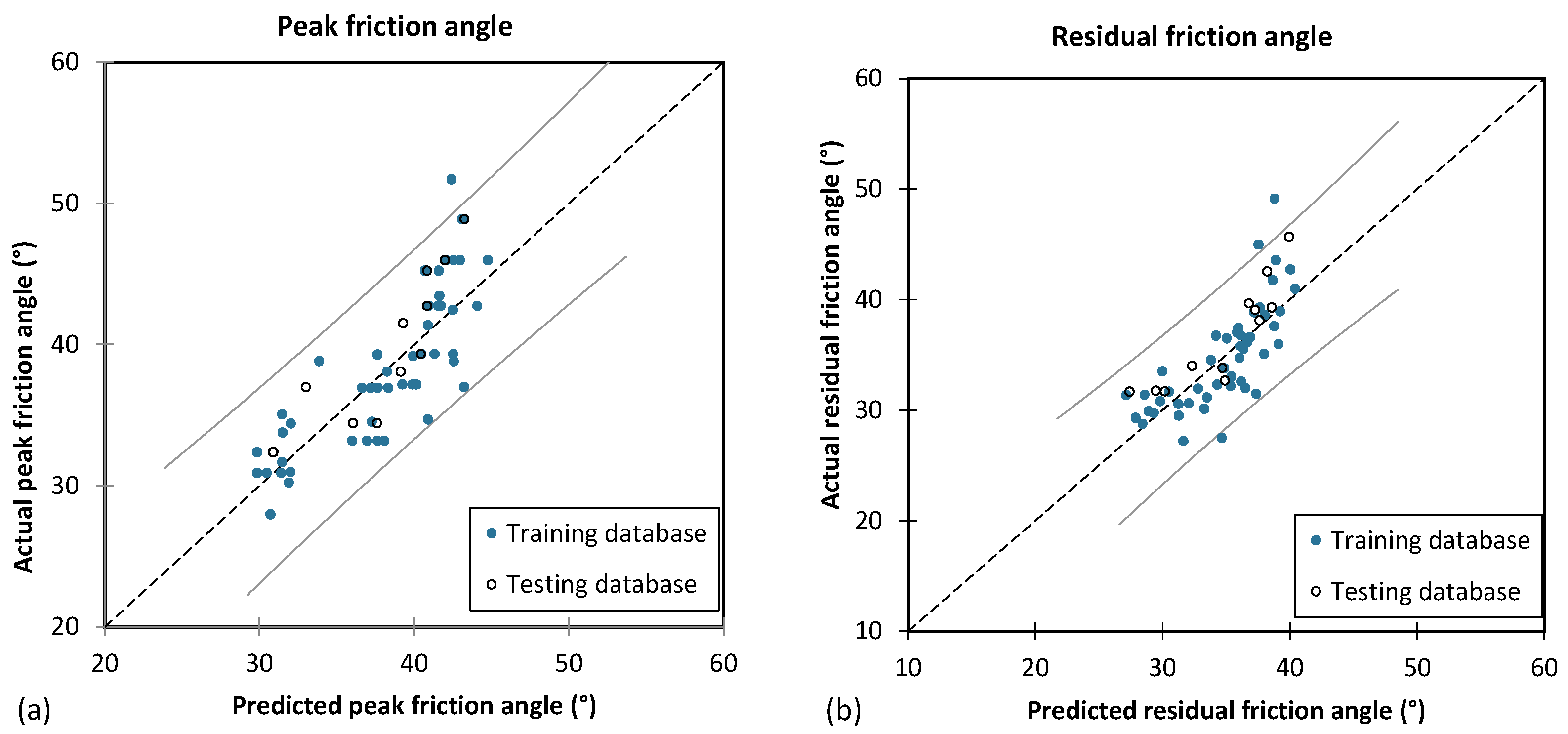
4.2.2. Multiple Linear Regression
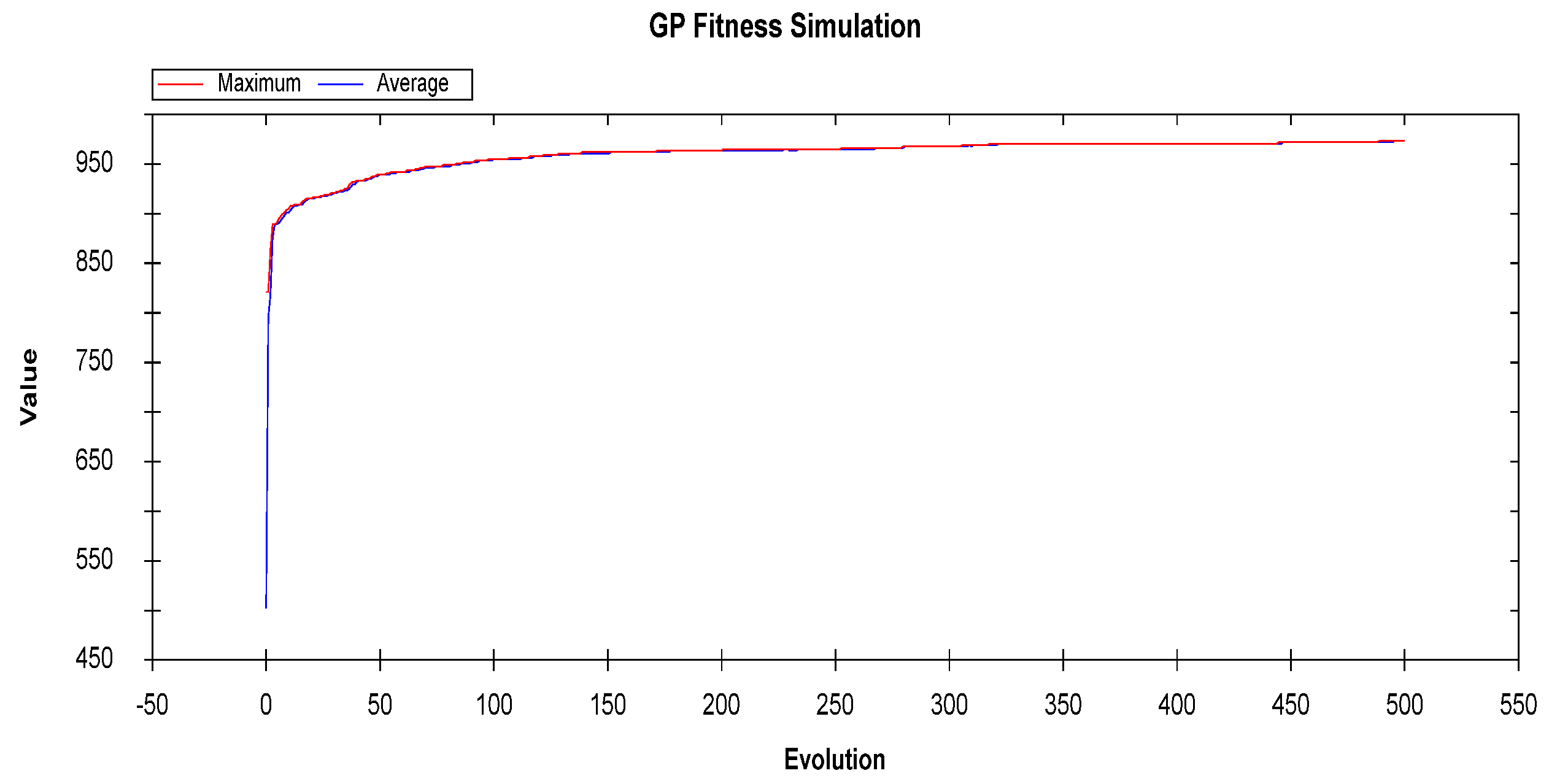
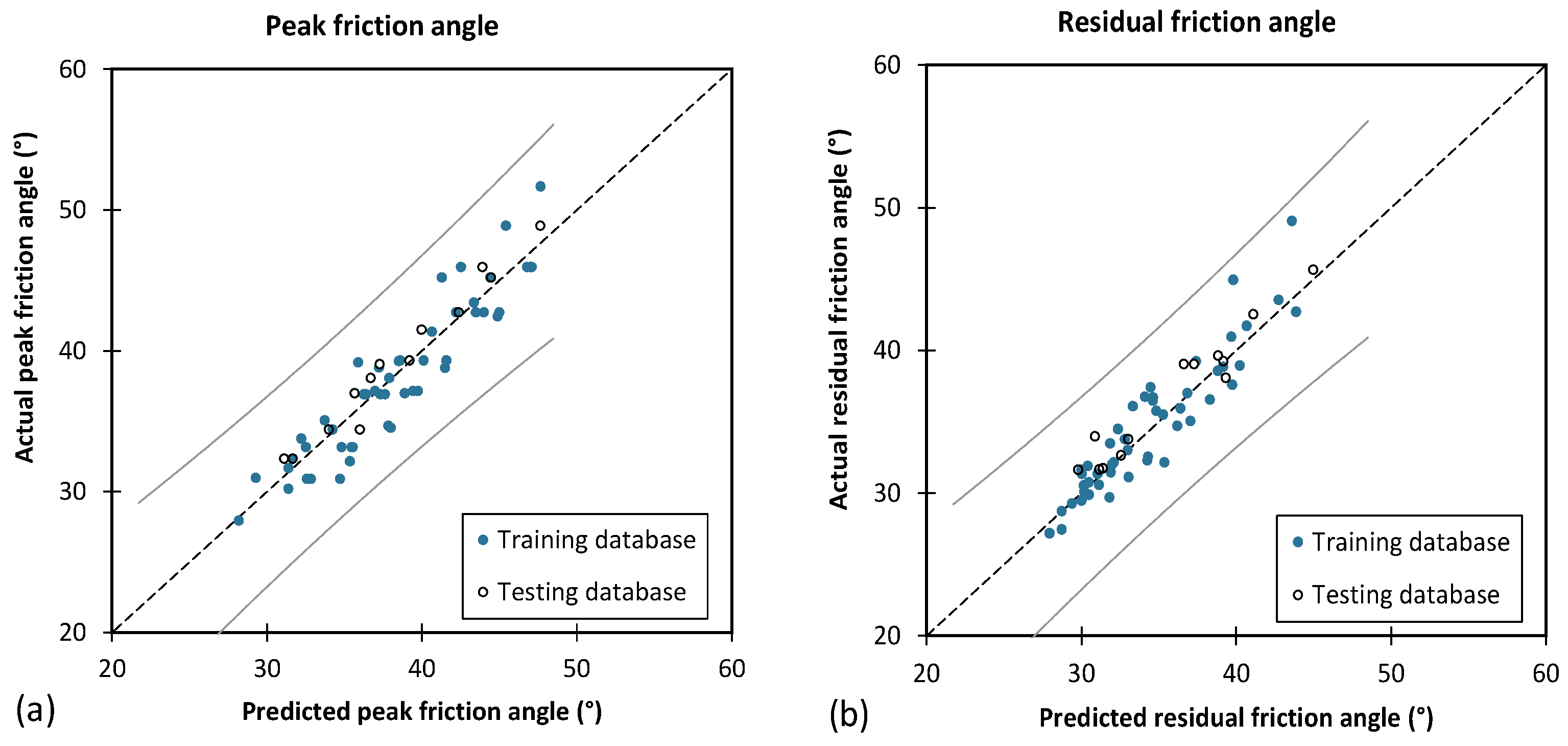
4.2.3. Genetic Programming
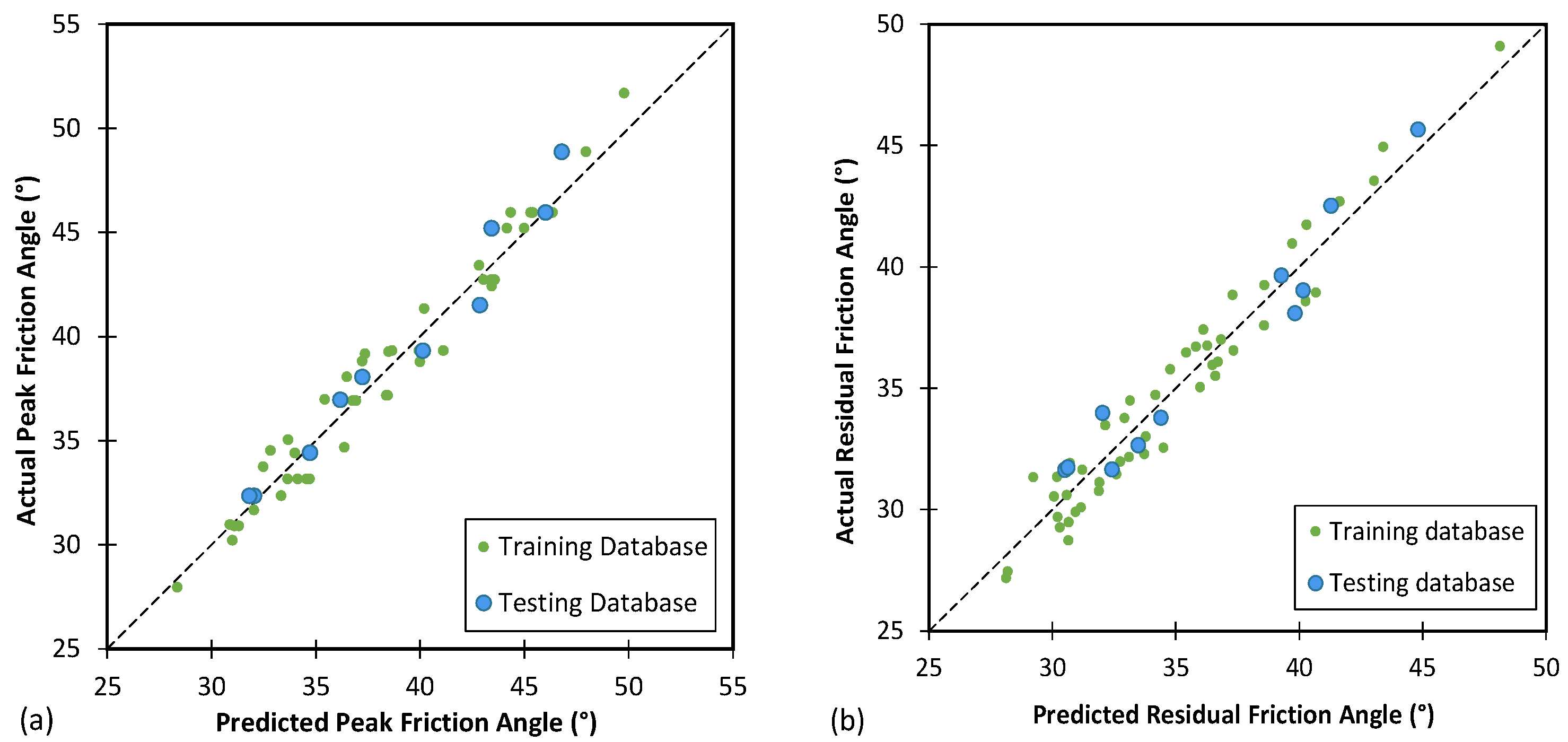
4.2.4. Classification and Regression Random Forest
5. Discussion
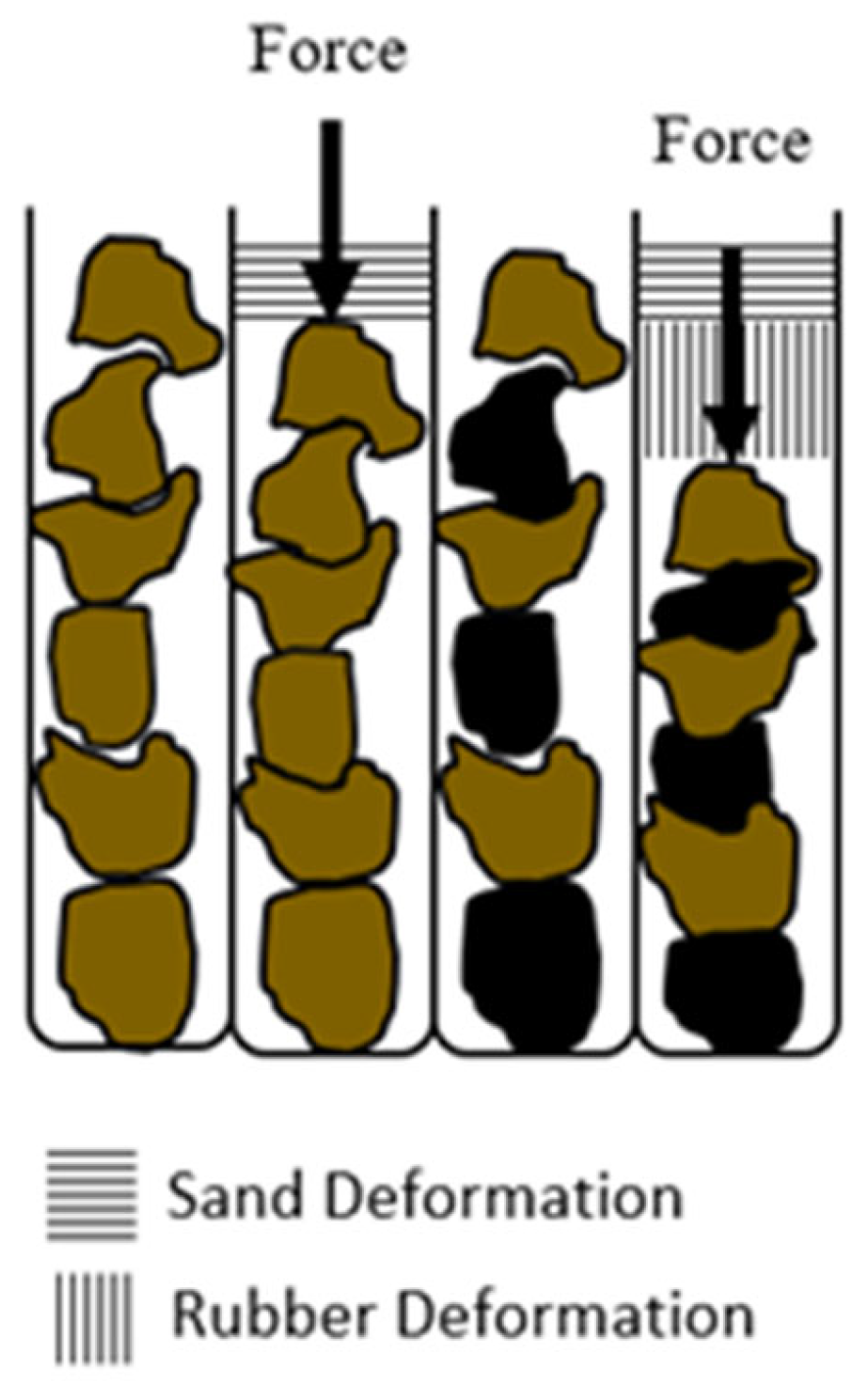
5.1. Particle Morphology
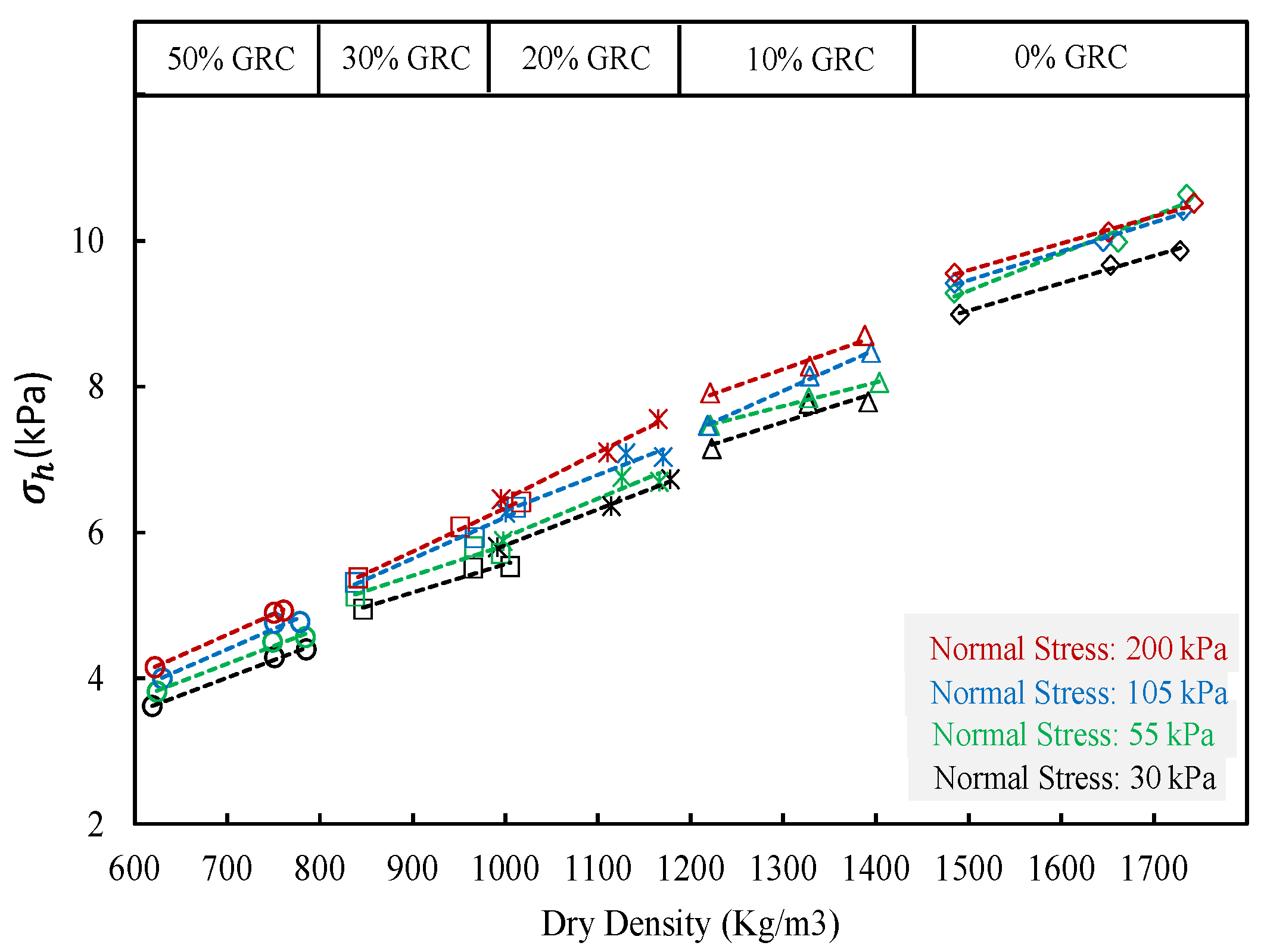
5.2. Active Lateral Pressure
5.3. Comparison of AI Models
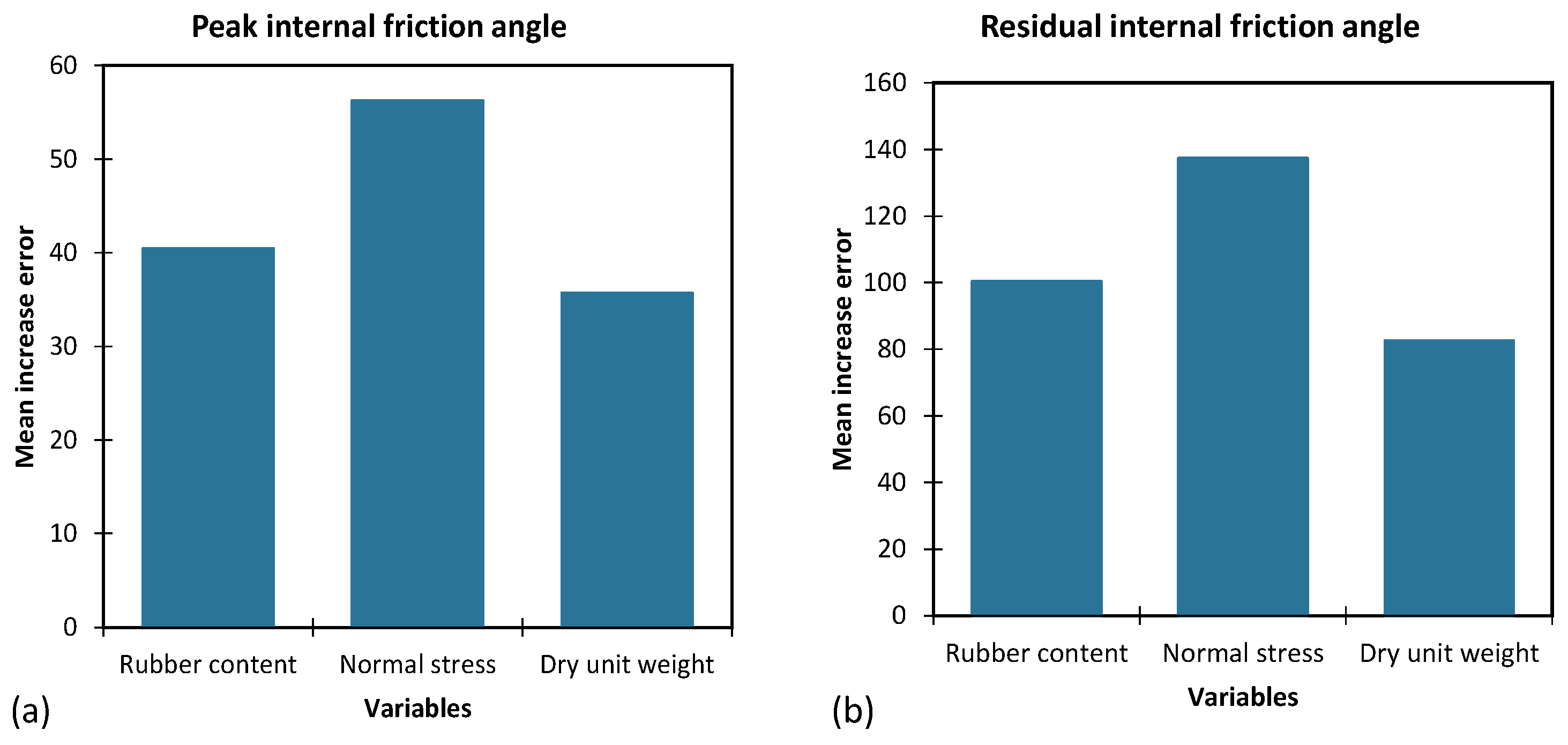
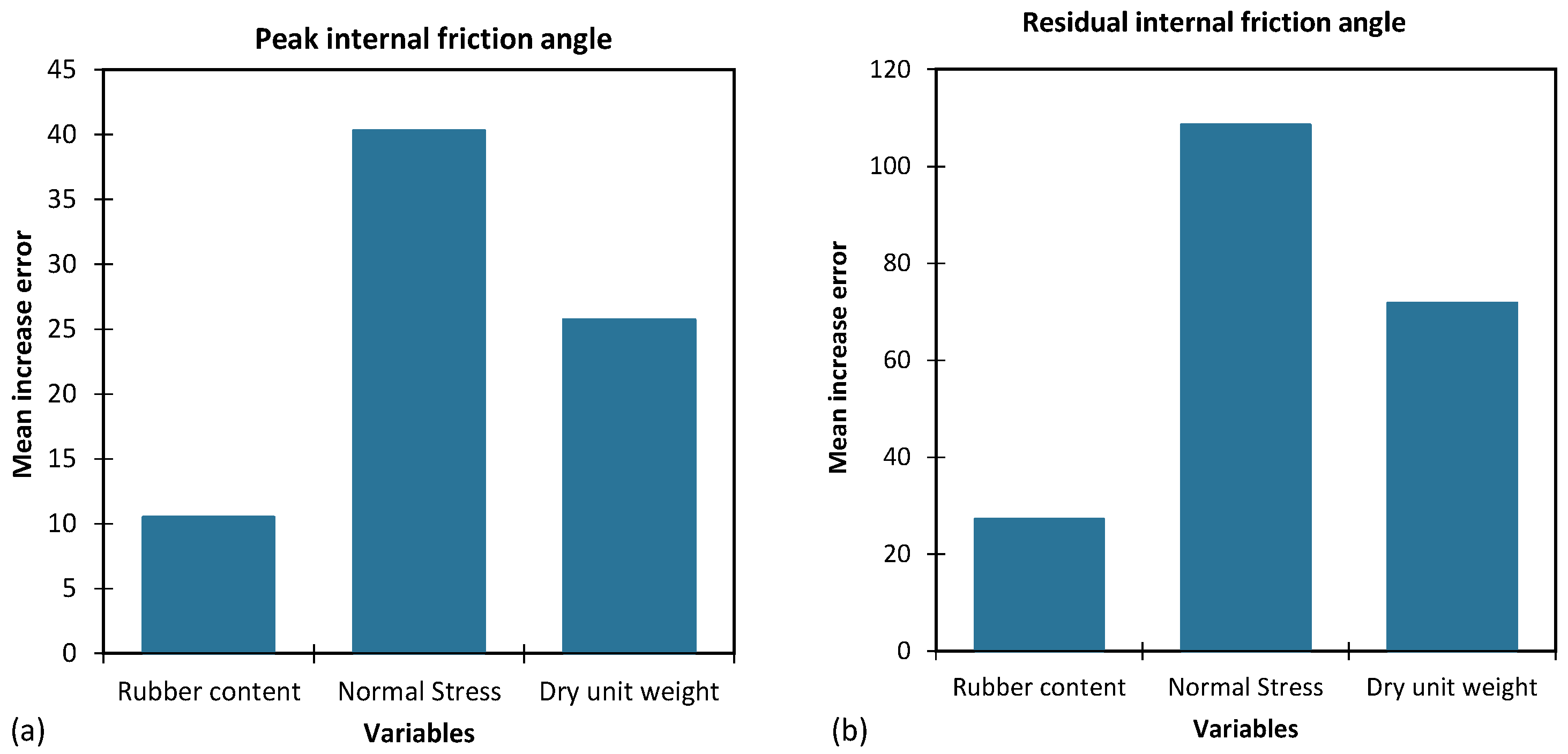
5.4. The Importance of Input Parameters
6. Conclusions
- The Mohr–Coulomb criteria cannot be effectively applied to sand–rubber mixtures as rubbers are compressible and the friction angle depends on normal stress, unlike incompressible soils where the friction angle remains constant with increases in normal stress;
- A high rubber content results in a high-volume compression coefficient, while a low rubber content results in a low-volume compression coefficient. Dense mixtures have lower compressibility, while loose mixtures have higher compressibility;
- The MLR model had low accuracy in predicting both φp and φr, with RMSE and R2 values of 3.151 and 0.664 for the training database, and 3.025 and 0.676 for the testing database for the φp, and 2.844 and 0.604 for the φr for the testing database;
- Using the GP model, two equations to calculate φp and φr were proposed. The GP model achieved an RMSE of 1.958 and R2 of 0.870 for the φp and an RMSE of 1.747 and R2 of 0.863 for the φr based on the training database. The model also exhibited high accuracy in predicting the φp, with an RMSE of 1.186 and R2 of 0.950, and the φr, with an RMSE of 1.433 and R2 of 0.899 based on the testing database. These results demonstrate the exceptional predictive capability of the GP model for both the φp and φr;
- The CRRF model accurately predicted φp with low RMSE and high R2 values for both the training (RMSE 1.046, R2 0.963) and testing (RMSE 1.121, R2 0.955) databases. The results showed high accuracy for φr predictions as well (training RMSE 1.116, R2 0.944, testing RMSE 1.193, R2 0.93);
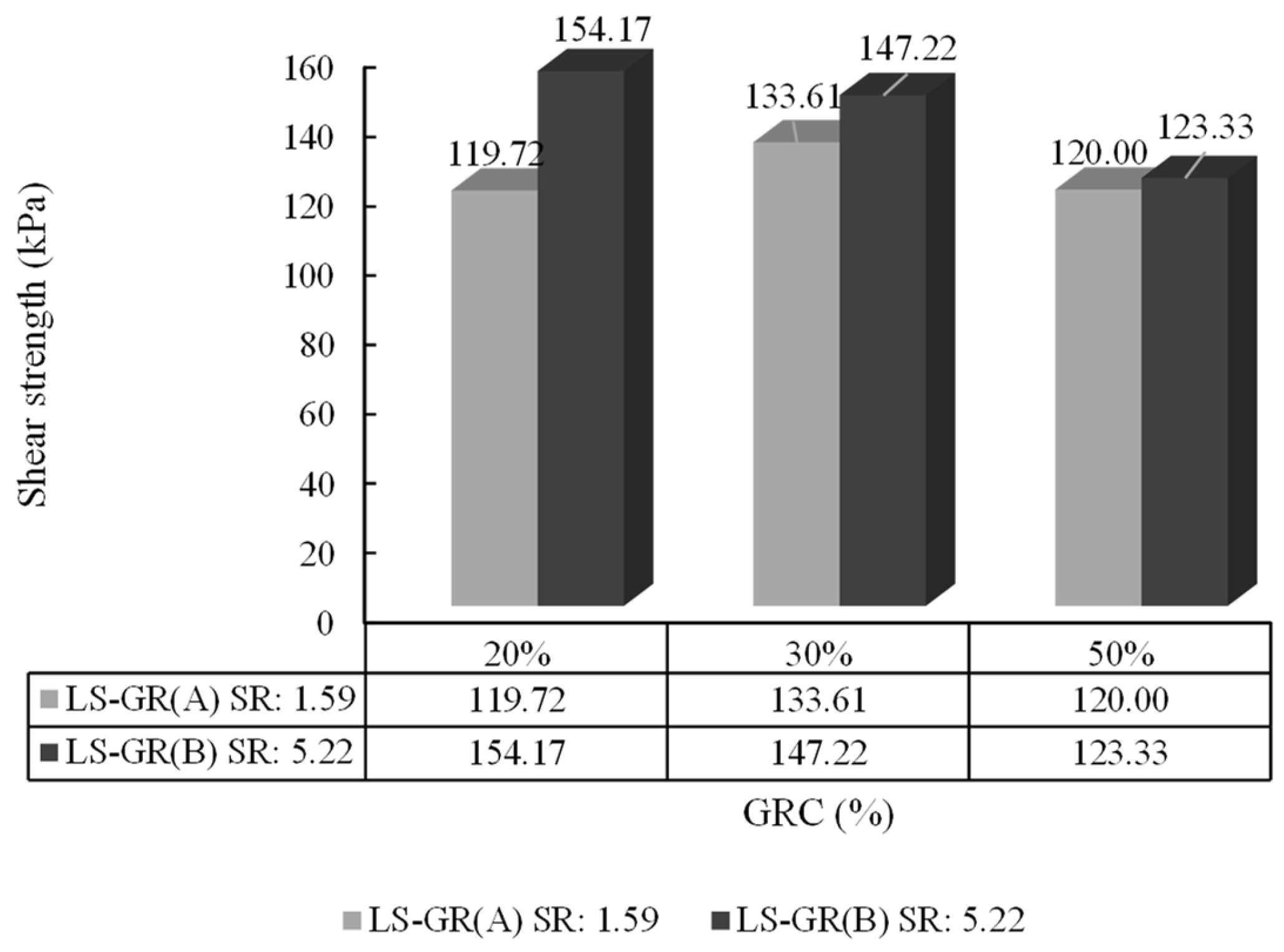
- The mixture with a size ratio of 5.22 had higher shear strength compared with the mixture with a size ratio of 1.59 under normal stresses of 200 kPa in a dense state;
- An increase in rubber content in the mixture decreased lateral earth pressure, confirming that the sand–rubber mixture can be used as a lightweight material in retaining walls, thereby reducing costs;
- The importance of parameters in AI models is determined by individually increasing/decreasing the values of input parameters and calculating the resulting error in the model. Results showed that normal stress had the highest error for both output parameters, indicating that the models are highly sensitive to changes in this parameter, making it the most important.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mohajerani, A.; Burnett, L.; Smith, J.V.; Markovski, S.; Rodwell, G.; Rahman, M.T.; Kurmus, H.; Mirzababaei, M.; Arulrajah, A.; Horpibulsuk, S. Recycling waste rubber tyres in construction materials and associated environmental considerations: A review. Resour. Conserv. Recycl. 2020, 155, 104679. [Google Scholar] [CrossRef]
- Qaidi, S.M.; Mohammed, A.S.; Ahmed, H.U.; Faraj, R.H.; Emad, W.; Tayeh, B.A.; Althoey, F.; Zaid, O.; Sor, N.H. Rubberized geopolymer composites: A comprehensive review. Ceram. Int. 2022, 48, 24234–24259. [Google Scholar] [CrossRef]
- Kole, P.J.; Löhr, A.J.; Van Belleghem, F.G.; Ragas, A.M. Wear and tear of tyres: A stealthy source of microplastics in the environment. Int. J. Environ. Res. Public Health 2017, 14, 1265. [Google Scholar] [CrossRef] [Green Version]
- Department of the Environment, Australian Government. Factsheet-Product Stewardship for End-of-Life Tyres. Available online: https://www.dcceew.gov.au/sites/default/files/documents/35159-fs-tps.pdf (accessed on 30 March 2023).
- Weldeslassie, T.; Naz, H.; Singh, B.; Oves, M. Chemical contaminants for soil, air and aquatic ecosystem. In Modern Age Environmental Problems and Their Remediation; Springer: Cham, Switzerland, 2018; pp. 1–22. [Google Scholar]
- Thomas, B.S.; Gupta, R.C. A comprehensive review on the applications of waste tire rubber in cement concrete. Renew. Sustain. Energy Rev. 2016, 54, 1323–1333. [Google Scholar] [CrossRef]
- Authority, E.P. Storage of Waste Tyres—Regulatory Impact Statement (RIS); EPA Victoria: Brisbane, Australia, 2014. [Google Scholar]
- Daghistani, F.; Naga, H.A. Shear Strength Characteristics of Sand-Particulate Rubber Mixture. Int. J. Geotech. Geol. Eng. 2023, 17, 36–41. [Google Scholar]
- Humphrey, D.N. Civil engineering applications of tire shreds. In Proceedings of the Tire Industry Conference, Hilton Head Island, SC, USA, 1–3 March 1999; pp. 1–16. [Google Scholar]
- Baghbani, A.; Daghistani, F.; Naga, H.A.; Costa, S. Development of a Support Vector Machine (SVM) and a Classification and Regression Tree (CART) to Predict the Shear Strength of Sand Rubber Mixtures. In Proceedings of the 8th International Symposium on Geotechnical Safety and Risk (ISGSR), Newcastle, Australia, 14 December 2022. [Google Scholar]
- Sahebzadeh, S.; Heidari, A.; Kamelnia, H.; Baghbani, A. Sustainability features of Iran’s vernacular architecture: A comparative study between the architecture of hot–arid and hot–arid–windy regions. Sustainability 2017, 9, 749. [Google Scholar] [CrossRef] [Green Version]
- Anvari, S.M.; Shooshpasha, I.; Kutanaei, S.S. Effect of granulated rubber on shear strength of fine-grained sand. J. Rock Mech. Geotech. Eng. 2017, 9, 936–944. [Google Scholar] [CrossRef]
- Baghbani, A.; Costa, S.; O’Kelly, B.C.; Soltani, A.; Barzegar, M. Experimental study on cyclic simple shear behaviour of predominantly dilative silica sand. Int. J. Geotech. Eng. 2023, 17, 91–105. [Google Scholar] [CrossRef]
- Zhang, T.; Cai, G.; Duan, W. Strength and microstructure characteristics of the recycled rubber tire-sand mixtures as lightweight backfill. Environ. Sci. Pollut. Res. 2018, 25, 3872–3883. [Google Scholar] [CrossRef]
- Lim, S.K.; Tan, C.S.; Li, B.; Ling, T.-C.; Hossain, M.U.; Poon, C.S. Utilizing high volumes quarry wastes in the production of lightweight foamed concrete. Constr. Build. Mater. 2017, 151, 441–448. [Google Scholar] [CrossRef]
- Bosscher, P.J.; Edil, T.B.; Kuraoka, S. Design of highway embankments using tire chips. J. Geotech. Geoenviron. Eng. 1997, 123, 295–304. [Google Scholar] [CrossRef]
- Lee, J.; Salgado, R.; Bernal, A.; Lovell, C. Shredded tires and rubber-sand as lightweight backfill. J. Geotech. Geoenviron. Eng. 1999, 125, 132–141. [Google Scholar] [CrossRef]
- O’Shaughnessy, V.; Garga, V.K. Tire-reinforced earthfill. Part 2: Pull-out behaviour and reinforced slope design. Can. Geotech. J. 2000, 37, 97–116. [Google Scholar] [CrossRef]
- Siddique, R.; Naik, T.R. Properties of concrete containing scrap-tire rubber—An overview. Waste Manag. 2004, 24, 563–569. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.; Shin, H.; Lee, J.S. Behavior of sand–rubber particle mixtures: Experimental observations and numerical simulations. Int. J. Numer. Anal. Methods Geomech. 2014, 38, 1651–1663. [Google Scholar] [CrossRef]
- Heimdahl, T.C.; Drescher, A. Elastic anisotropy of tire shreds. J. Geotech. Geoenviron. Eng. 1999, 125, 383–389. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, Q.; Shi, W.; Lv, J.; Lu, Z.; Ling, X. Advances in properties of rubber reinforced soil. Adv. Civ. Eng. 2020, 2020, 6629757. [Google Scholar] [CrossRef]
- Meddah, A.; Merzoug, K. Feasibility of using rubber waste fibers as reinforcements for sandy soils. Innov. Infrastruct. Solut. 2017, 2, 5. [Google Scholar] [CrossRef]
- Feng, Z.-Y.; Sutter, K.G. Dynamic properties of granulated rubber/sand mixtures. Geotech. Test. J. 2000, 23, 338–344. [Google Scholar]
- Mahmoud, G. Shear strength characteristics of sand-mixed with granular rubber. Geotech. Geol. Eng. 2004, 22, 401–416. [Google Scholar]
- Poh, P.S.; Broms, B.B. Slope stabilization using old rubber tires and geotextiles. J. Perform. Constr. Facil. 1995, 9, 76–79. [Google Scholar] [CrossRef]
- Foose, G.J.; Benson, C.H.; Bosscher, P.J. Sand reinforced with shredded waste tires. J. Geotech. Eng. 1996, 122, 760–767. [Google Scholar] [CrossRef]
- Downs, L.A.; Humphrey, D.N.; Katz, L.E.; Rock, C.A. Water quality effects of using tire chips below the groundwater table. In Civil Engineering; University of Maine: Orono, ME, USA, 1996. [Google Scholar]
- Eldin, N.N.; Senouci, A.B. Rubber-tire particles as concrete aggregate. J. Mater. Civ. Eng. 1993, 5, 478–496. [Google Scholar] [CrossRef]
- ASTM. Standard Test Methods for Maximum Index Density and Unit Weight of Soils Using a Vibratory Table; ASTM: West Conshohocken, PA, USA, 2006. [Google Scholar]
- ASTM. Standard Terminology Relating to Rubber; ASTM: West Conshohocken, PA, USA, 2020. [Google Scholar]
- ASTM. Standard Practice for Use of Scrap Tires in Civil Engineering Applications; ASTM: West Conshohocken, PA, USA, 2020. [Google Scholar]
- Ahmed, I. Laboratory Study on Properties of Rubber-Soils; Purdue University: West Lafayette, IN, USA, 1993. [Google Scholar]
- Zornberg, J.G.; Cabral, A.R.; Viratjandr, C. Behaviour of tire shred sand mixtures. Can. Geotech. J. 2004, 41, 227–241. [Google Scholar] [CrossRef]
- Yoon, Y.W.; Heo, S.B.; Kim, K.S. Geotechnical performance of waste tires for soil reinforcement from chamber tests. Geotext. Geomembr. 2008, 26, 100–107. [Google Scholar] [CrossRef]
- Anbazhagan, P.; Manohar, D.; Rohit, D. Influence of size of granulated rubber and tyre chips on the shear strength characteristics of sand–rubber mix. Geomech. Geoeng. 2017, 12, 266–278. [Google Scholar] [CrossRef]
- Tian, Y.; Kasyap, S.S.; Senetakis, K. Influence of loading history and soil type on the normal contact behavior of natural sand grain-elastomer composite interfaces. Polymers 2021, 13, 1830. [Google Scholar] [CrossRef]
- Lee, J.-S.; Dodds, J.; Santamarina, J.C. Behavior of rigid-soft particle mixtures. J. Mater. Civ. Eng. 2007, 19, 179–184. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Kwok, C.Y.; Senetakis, K. Effects of inclusion of granulated rubber tires on the mechanical behaviour of a compressive sand. Can. Geotech. J. 2020, 57, 763–769. [Google Scholar] [CrossRef]
- Perez, J.L.; Kwok, C.; Senetakis, K. Micromechanical analyses of the effect of rubber size and content on sand-rubber mixtures at the critical state. Geotext. Geomembr. 2017, 45, 81–97. [Google Scholar] [CrossRef]
- Takano, D.; Chevalier, B.; Otani, J. Experimental and numerical simulation of shear behavior on sand and tire chips. In Proceedings of the 14th International Conference on Computer Methods and Recent Advances in Geomechanics, Kyoto, Japan, 22–25 September 2015; pp. 1545–1550. [Google Scholar]
- Noorzad, R.; Raveshi, M. Mechanical behavior of waste tire crumbs–sand mixtures determined by triaxial tests. Geotech. Geol. Eng. 2017, 35, 1793–1802. [Google Scholar] [CrossRef]
- Fakhimi, A.; Hosseinpour, H. The role of oversize particles on the shear strength and deformational behavior of rock pile material. In Proceedings of the 42nd US Rock Mechanics Symposium (USRMS), San Francisco, CA, USA, 29 June–2 July 2008. [Google Scholar]
- Ghazavi, M.; Ghaffari, J.; Farshadfar, A. Experimental determination of waste tire chip-sand-geogrid interface parameters using large direct shear tests. In Proceedings of the 5th Symposium on Advances in Science and Technology, Mashhad, Iran, 12–17 May 2011; pp. 12–17. [Google Scholar]
- Baghbani, A.; Choudhury, T.; Costa, S.; Reiner, J. Application of artificial intelligence in geotechnical engineering: A state-of-the-art review. Earth-Sci. Rev. 2022, 228, 103991. [Google Scholar] [CrossRef]
- Baghbani, A.; Nguyen, M.D.; Alnedawi, A.; Milne, N.; Baumgartl, T.; Abuel-Naga, H. Improving soil stability with alum sludge: An AI-enabled approach for accurate prediction of California Bearing Ratio. Appl. Sci. 2023, 13, 4934. [Google Scholar] [CrossRef]
- Essam, Y.; Kumar, P.; Ahmed, A.N.; Murti, M.A.; El-Shafie, A. Exploring the reliability of different artificial intelligence techniques in predicting earthquake for Malaysia. Soil Dyn. Earthq. Eng. 2021, 147, 106826. [Google Scholar] [CrossRef]
- Baghbani, A.; Choudhury, T.; Samui, P.; Costa, S. Prediction of secant shear modulus and damping ratio for an extremely dilative silica sand based on machine learning techniques. Soil Dyn. Earthq. Eng. 2023, 165, 107708. [Google Scholar] [CrossRef]
- Suman, S.; Khan, S.; Das, S.; Chand, S. Slope stability analysis using artificial intelligence techniques. Nat. Hazards 2016, 84, 727–748. [Google Scholar] [CrossRef]
- Baghbani, A.; Abuel-Naga, H.; Shirani Faradonbeh, R.; Costa, S.; Almasoudi, R. Ultrasonic Characterization of Compacted Salty Kaolin–Sand Mixtures Under Nearly Zero Vertical Stress Using Experimental Study and Machine Learning. Geotech. Geol. Eng. 2023, 41, 2987–3012. [Google Scholar] [CrossRef]
- Baghbani, A.; Costa, S.; Choudhury, T. Developing Mathematical Models for Predicting Cracks and Shrinkage Intensity Factor during Clay Soil Desiccation. 2023. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4408164 (accessed on 30 March 2023).
- Nguyen, M.D.; Baghbani, A.; Alnedawi, A.; Ullah, S.; Kafle, B.; Thomas, M.; Moon, E.M.; Milne, N.A. Experimental Study on the Suitability of Aluminium-Based Water Treatment Sludge as a Next Generation Sustainable Soil Replacement for Road Construction. 2023. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4331275 (accessed on 30 March 2023).
- Hoang, N.-D.; Pham, A.-D. Hybrid artificial intelligence approach based on metaheuristic and machine learning for slope stability assessment: A multinational data analysis. Expert Syst. Appl. 2016, 46, 60–68. [Google Scholar] [CrossRef]
- Baghbani, A.; Costa, S.; Faradonbeh, R.S.; Soltani, A.; Baghbani, H. Modeling the effects of particle shape on damping ratio of dry sand by simple shear testing and artificial intelligence. Appl. Sci. 2023, 13, 4363. [Google Scholar] [CrossRef]
- Baghbani, A.; Costa, S.; Faradonbeh, R.S.; Soltani, A.; Baghbani, H. Experimental-AI investigation of the effect of particle shape on the damping ratio of dry sand under simple shear test loading. Appl. Sci. 2023, 13, 4363. [Google Scholar] [CrossRef]
- Baghbani, A.; Daghistani, F.; Baghbani, H.; Kiany, K. Predicting the Strength of Recycled Glass Powder-Based Geopolymers for Improving Mechanical Behavior of Clay Soils Using Artificial Intelligence; EasyChair: Manchester, UK, 2023. [Google Scholar]
- Baghbani, A.; Daghistani, F.; Baghbani, H.; Kiany, K.; Bazaz, J.B. Artificial Intelligence-Based Prediction of Geotechnical Impacts of Polyethylene Bottles and Polypropylene on Clayey Soil; EasyChair: Manchester, UK, 2023. [Google Scholar]
- Baghbani, A.; Daghistani, F.; Kiany, K.; Shalchiyan, M.M. AI-Based Prediction of Strength and Tensile Properties of Expansive Soil Stabilized with Recycled Ash and Natural Fibers; EasyChair: Manchester, UK, 2023. [Google Scholar]
- Choudhury, T.; Costa, S. Prediction of parallel clay cracks using neural networks–a feasibility study. In Contemporary Issues in Soil Mechanics: Proceedings of the 2nd GeoMEast International Congress and Exhibition on Sustainable Civil Infrastructures, Egypt 2018—The Official International Congress of the Soil-Structure Interaction Group in Egypt (SSIGE); Springer International Publishing: Cham, Switzerland, 2019; pp. 214–224. [Google Scholar]
- Baghbani, A.; Costa, S.; Choundhury, T.; Faradonbeh, R.S. Prediction of Parallel Desiccation Cracks of Clays Using a Classification and Regression Tree (CART) Technique. In Proceedings of the 8th International Symposium on Geotechnical Safety and Risk (ISGSR), Newcastle, Australia, 14 December 2022. [Google Scholar]
- Lawal, A.I.; Kwon, S. Application of artificial intelligence to rock mechanics: An overview. J. Rock Mech. Geotech. Eng. 2021, 13, 248–266. [Google Scholar] [CrossRef]
- Baghbani, A.; Baghbani, H.; Shalchiyan, M.M.; Kiany, K. Utilizing artificial intelligence and finite element method to simulate the effects of new tunnels on existing tunnel deformation. J. Comput. Cogn. Eng. 2022. [Google Scholar] [CrossRef]
- Tasalloti, A.; Chiaro, G.; Banasiak, L.; Palermo, A. Experimental investigation of the mechanical behaviour of gravel-granulated tyre rubber mixtures. Constr. Build. Mater. 2021, 273, 121749. [Google Scholar] [CrossRef]
- AS1289.6.2.2; Determination of Shear Strength of a Soil—Direct Shear Test Using a Shear Box. Standards Australia: Sydney, Australia, 2020.
- Senthen Amuthan, M.; Boominathan, A.; Banerjee, S. Density and shear strength of particulate rubber mixed with sand and fly ash. J. Mater. Civ. Eng. 2018, 30, 04018136. [Google Scholar] [CrossRef]
- Dai, B.B.; Yang, J.; Zhou, C.Y. Observed effects of interparticle friction and particle size on shear behavior of granular materials. Int. J. Geomech. 2016, 16, 04015011. [Google Scholar] [CrossRef]
- Skinner, A. A note on the influence of interparticle friction on the shearing strength of a random assembly of spherical particles. Geotechnique 1969, 19, 150–157. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Pan, W. Shrinking classification trees for bootstrap aggregation. Pattern Recognit. Lett. 1999, 20, 961–965. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef] [Green Version]
- Cramer, N.L. A representation for the adaptive generation of simple sequential programs. In Proceedings of the First International Conference on Genetic Algorithms and Their Applications; Psychology Press: London, UK, 2014; pp. 183–187. [Google Scholar]
- Koza, J.R. Evolution of subsumption using genetic programming. In Proceedings of the First European conference on Artificial Life; MIT Press: Cambridge, MA, USA, 1992; pp. 110–119. [Google Scholar]
- Koza, J.R. Genetic Programming: On the Programming of Computers by Means of Natural Selection (Complex Adaptive Systems); A Bradford Book: Denver, CO, USA, 1993; Volume 1, p. 18. [Google Scholar]
- Koza, J.R. Genetic programming as a means for programming computers by natural selection. Stat. Comput. 1994, 4, 87–112. [Google Scholar] [CrossRef]
- Pour, A.F.; Faradonbeh, R.S.; Gholampour, A.; Ngo, T.D. Predicting ultimate condition and transition point on axial stress–strain curve of FRP-confined concrete using a meta-heuristic algorithm. Compos. Struct. 2023, 304, 116387. [Google Scholar] [CrossRef]
- Gholampour, A.; Gandomi, A.H.; Ozbakkaloglu, T. New formulations for mechanical properties of recycled aggregate concrete using gene expression programming. Constr. Build. Mater. 2017, 130, 122–145. [Google Scholar] [CrossRef]
- Rouhanifar, S.; Afrazi, M.; Fakhimi, A.; Yazdani, M. Strength and deformation behaviour of sand-rubber mixture. Int. J. Geotech. Eng. 2021, 15, 1078–1092. [Google Scholar] [CrossRef]
- Wang, C.; Deng, A.; Taheri, A. Three-dimensional discrete element modeling of direct shear test for granular rubber–sand. Comput. Geotech. 2018, 97, 204–216. [Google Scholar] [CrossRef]
- Neaz Sheikh, M.; Mashiri, M.; Vinod, J.; Tsang, H.-H. Shear and compressibility behavior of sand–tire crumb mixtures. J. Mater. Civ. Eng. 2013, 25, 1366–1374. [Google Scholar] [CrossRef]
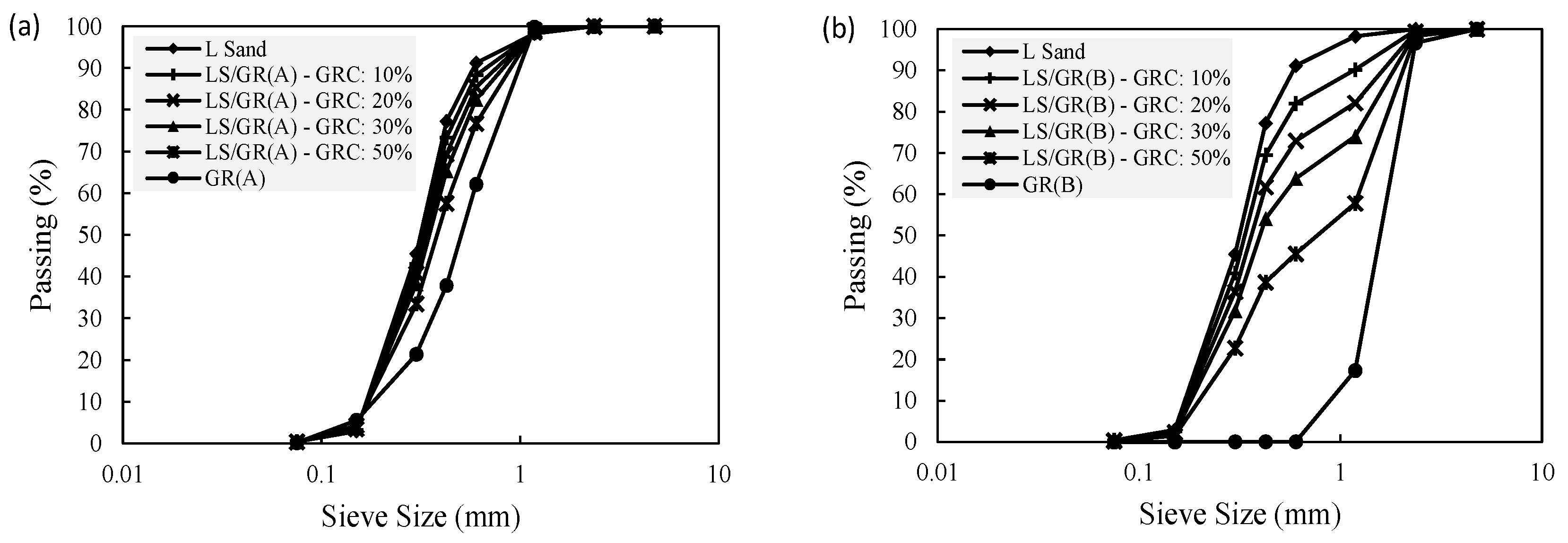






| L Sand | GR-A | LS-GR(A) 10% | LS-GR(A) 20% | LS-GR(A) 30% | LS-GR(A) 50% | GR-B | LS-GR(B) 10% | LS-GR(B) 20% | LS-GR(B) 30% | LS-GR(B) 50% | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| D10 (mm) | 0.17 | 0.19 | 0.18 | 0.18 | 0.18 | 0.18 | 0.93 | 0.18 | 0.18 | 0.19 | 0.21 |
| D30 (mm) | 0.25 | 0.37 | 0.25 | 0.26 | 0.26 | 0.28 | 1.37 | 0.26 | 0.27 | 0.29 | 0.36 |
| D50 (mm) | 0.32 | 0.51 | 0.33 | 0.34 | 0.35 | 0.39 | 1.67 | 0.34 | 0.37 | 0.40 | 0.81 |
| D60 (mm) | 0.36 | 0.58 | 0.37 | 0.38 | 0.40 | 0.45 | 1.81 | 0.38 | 0.42 | 0.53 | 1.24 |
| CU (mm) | 2.04 | 3.04 | 2.11 | 2.18 | 2.26 | 2.49 | 1.94 | 2.14 | 2.27 | 2.80 | 5.92 |
| CC (mm) | 0.96 | 1.19 | 0.97 | 0.97 | 0.98 | 0.99 | 1.10 | 0.96 | 0.97 | 0.84 | 0.49 |
| Gs | 2.57 | 0.99 | 2.41 | 2.25 | 2.10 | 1.78 | 1.08 | 2.42 | 2.27 | 2.12 | 1.83 |
| SR | - | 1.59 | 1.59 | 1.59 | 1.59 | 1.59 | 5.22 | 5.22 | 5.22 | 5.22 | 5.22 |
| HCF * | 1.10 | 1.38 | - | - | - | - | - | - | - | - | - |
| Type of Mixtures | Density State | Total Energy (kJ) | |||||
|---|---|---|---|---|---|---|---|
| L-Sand/GR (A) | 1 | 3 | 0.026 | 0.30 | 0.00013896 | Slightly dense | 165 |
| 5 | 3 | 0.026 | 0.30 | Dense | 825 |
| Variable | Observations | Minimum | Maximum | Mean | Std. Deviation |
|---|---|---|---|---|---|
| Dry unit weight, (kN/m3) | 48 | 618.960 | 1742.730 | 1142.927 | 339.775 |
| Rubber percentage (%) | 48 | 0.000 | 0.500 | 0.221 | 0.183 |
| Normal stress (kPa) | 48 | 30.000 | 200.000 | 97.500 | 65.736 |
| Peak friction angle (°) | 48 | 27.950 | 51.680 | 38.165 | 5.495 |
| Residual friction angle (°) | 48 | 27.186 | 49.096 | 34.721 | 4.768 |
| Variable | Observations | Minimum | Maximum | Mean | Std. Deviation |
|---|---|---|---|---|---|
| Dry unit weight, (kN/m3) | 12 | 785.120 | 1650.910 | 1115.758 | 266.606 |
| Rubber percentage (%) | 12 | 0.000 | 0.500 | 0.217 | 0.134 |
| Normal stress (kPa) | 12 | 30.000 | 200.000 | 97.500 | 67.940 |
| Peak friction angle (°) | 12 | 32.350 | 48.870 | 39.347 | 5.548 |
| Residual friction angle (°) | 12 | 31.638 | 45.665 | 36.642 | 4.718 |
| Dry Unit Weight | Rubber Content | Normal Stress | Peak Friction Angle | Residual Friction Angle | |
|---|---|---|---|---|---|
| Dry unit weight | 1 | 0.063 | −0.451 | −0.111 | −0.221 |
| Rubber content | 0.063 | 1 | −0.080 | −0.593 | 0.526 |
| Normal stress | −0.451 | −0.080 | 1 | 0.176 | 0.340 |
| Peak friction angle | −0.111 | −0.593 | 0.176 | 1 | 0.672 |
| Residual friction angle | −0.221 | 0.426 | 0.340 | 0.672 | 1 |
| Performance Metrics | Training Database | Testing Database |
|---|---|---|
| MAE | 2.502 | 2.661 |
| MSE | 9.929 | 9.150 |
| RMSE | 3.151 | 3.025 |
| MSLE | 0.006 | 0.005 |
| RMSLE | 0.078 | 0.073 |
| R2 | 0.664 | 0.676 |
| Performance Metrics | Training Database | Testing Database |
|---|---|---|
| MAE | 2.329 | 2.382 |
| MSE | 9.740 | 8.087 |
| RMSE | 3.121 | 2.844 |
| MSLE | 0.007 | 0.006 |
| RMSLE | 0.085 | 0.076 |
| R2 | 0.562 | 0.604 |
| Population | Probability of GP Operations | Selection | Tree Structure Level | Random Constants | GP Imp. Parameters | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Size | Initialization | Crossover | Mutation | Reproduction | Elitism | Method | Tour Size | Max. Initial | Max. Operation | From-to | Count | Brood Size |
| 200 | HalfHalf | 0.9 | 0.99 | 0.2 | 1 | Tournament Selection | 2 | 4 | 4 | 0–1 | 10 | 2 |
| Constants | In Equation (16) to Calculate | In Equation (17) to Calculate |
|---|---|---|
| r1 | 0.18021 | 0.91961 |
| r2 | 0.2066 | 0.34778 |
| r3 | 0.98255 | 0.28656 |
| r4 | - | 0.30767 |
| Performance Metrics | Training Database | Testing Database |
|---|---|---|
| MAE | 1.591 | 1.048 |
| MSE | 3.834 | 1.406 |
| RMSE | 1.958 | 1.186 |
| MSLE | 0.002 | 0.001 |
| RMSLE | 0.049 | 0.030 |
| R2 | 0.870 | 0.950 |
| Performance Metrics | Training Database | Testing Database |
|---|---|---|
| MAE | 1.300 | 1.114 |
| MSE | 3.051 | 2.054 |
| RMSE | 1.747 | 1.433 |
| MSLE | 0.002 | 0.002 |
| RMSLE | 0.045 | 0.040 |
| R2 | 0.863 | 0.899 |
| Trees Parameters | Forest Parameters | ||||||
|---|---|---|---|---|---|---|---|
| Min. Node Size | Min. Son Size | Max Depth | Mtry | CP | Sampling | Sample Size | Number of Trees |
| 2 | 1 | 7 | 2 | 0.00001 | Random with replacement | 48 | 100 |
| Performance Metrics | Training Database | Testing Database |
|---|---|---|
| MAE | 0.893 | 0.910 |
| MSE | 1.093 | 1.256 |
| RMSE | 1.046 | 1.121 |
| MSLE | 0.001 | 0.001 |
| RMSLE | 0.027 | 0.025 |
| R2 | 0.963 | 0.955 |
| Performance Metrics | Training Database | Testing Database |
|---|---|---|
| MAE | 1.023 | 1.106 |
| MSE | 1.245 | 1.423 |
| RMSE | 1.116 | 1.193 |
| MSLE | 0.001 | 0.001 |
| RMSLE | 0.032 | 0.032 |
| R2 | 0.944 | 0.930 |
| Performance Metrics | Peak Friction Angle (φp) | Residual Friction Angle (φr) | ||||
|---|---|---|---|---|---|---|
| MLR | CRRF | GP | MLR | CRRF | GP | |
| MAE | 2.661 | 0.910 | 1.048 | 2.382 | 1.106 | 1.114 |
| MSE | 9.150 | 1.256 | 1.406 | 8.087 | 1.423 | 2.054 |
| RMSE | 3.025 | 1.121 | 1.186 | 2.844 | 1.193 | 1.433 |
| MSLE | 0.005 | 0.001 | 0.001 | 0.006 | 0.001 | 0.002 |
| RMSLE | 0.073 | 0.025 | 0.030 | 0.076 | 0.032 | 0.040 |
| R2 | 0.676 | 0.955 | 0.950 | 0.604 | 0.930 | 0.899 |
| Rubber Content | Normal Stress | Dry Unit Weight | ||||
|---|---|---|---|---|---|---|
| GP | CRRF | GP | CRRF | GP | CRRF | |
| 2 | 3 | 1 | 1 | 3 | 2 | |
| 2 | 3 | 1 | 1 | 3 | 2 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Daghistani, F.; Baghbani, A.; Abuel Naga, H.; Faradonbeh, R.S. Internal Friction Angle of Cohesionless Binary Mixture Sand–Granular Rubber Using Experimental Study and Machine Learning. Geosciences 2023, 13, 197. https://doi.org/10.3390/geosciences13070197
Daghistani F, Baghbani A, Abuel Naga H, Faradonbeh RS. Internal Friction Angle of Cohesionless Binary Mixture Sand–Granular Rubber Using Experimental Study and Machine Learning. Geosciences. 2023; 13(7):197. https://doi.org/10.3390/geosciences13070197
Chicago/Turabian StyleDaghistani, Firas, Abolfazl Baghbani, Hossam Abuel Naga, and Roohollah Shirani Faradonbeh. 2023. "Internal Friction Angle of Cohesionless Binary Mixture Sand–Granular Rubber Using Experimental Study and Machine Learning" Geosciences 13, no. 7: 197. https://doi.org/10.3390/geosciences13070197
APA StyleDaghistani, F., Baghbani, A., Abuel Naga, H., & Faradonbeh, R. S. (2023). Internal Friction Angle of Cohesionless Binary Mixture Sand–Granular Rubber Using Experimental Study and Machine Learning. Geosciences, 13(7), 197. https://doi.org/10.3390/geosciences13070197










