Is the Earth’s Magnetic Field a Constant? A Legacy of Poisson
Abstract
:1. Introduction
2. On the Constancy of the Magnetic Field
2.1. Some Consequences of Maxwell’s Equations
2.2. The Electrostatic Field
2.3. The Magnetostatic Field
3. Some Further Remarks on Section 2
- The position term of each moving particle fluctuates with time so that the Legendre–Laplace condition (5a) is not satisfied any more, that is, the inverse distance is no more a natural solution of the Laplacian. One would need to introduce time but then the Laplacian would have to be replaced by a Dalembertian, i.e., a different problem.
- It is the number and/or quality of the charges that would change with time. But then the nature of the core would change with time, and one would need to find a physical mechanism that would explain how the field intensity could decrease (as is the case at present), yet could have increased and even reversed in the past.
4. Reconciling Modern Observations with Poisson’s Theory
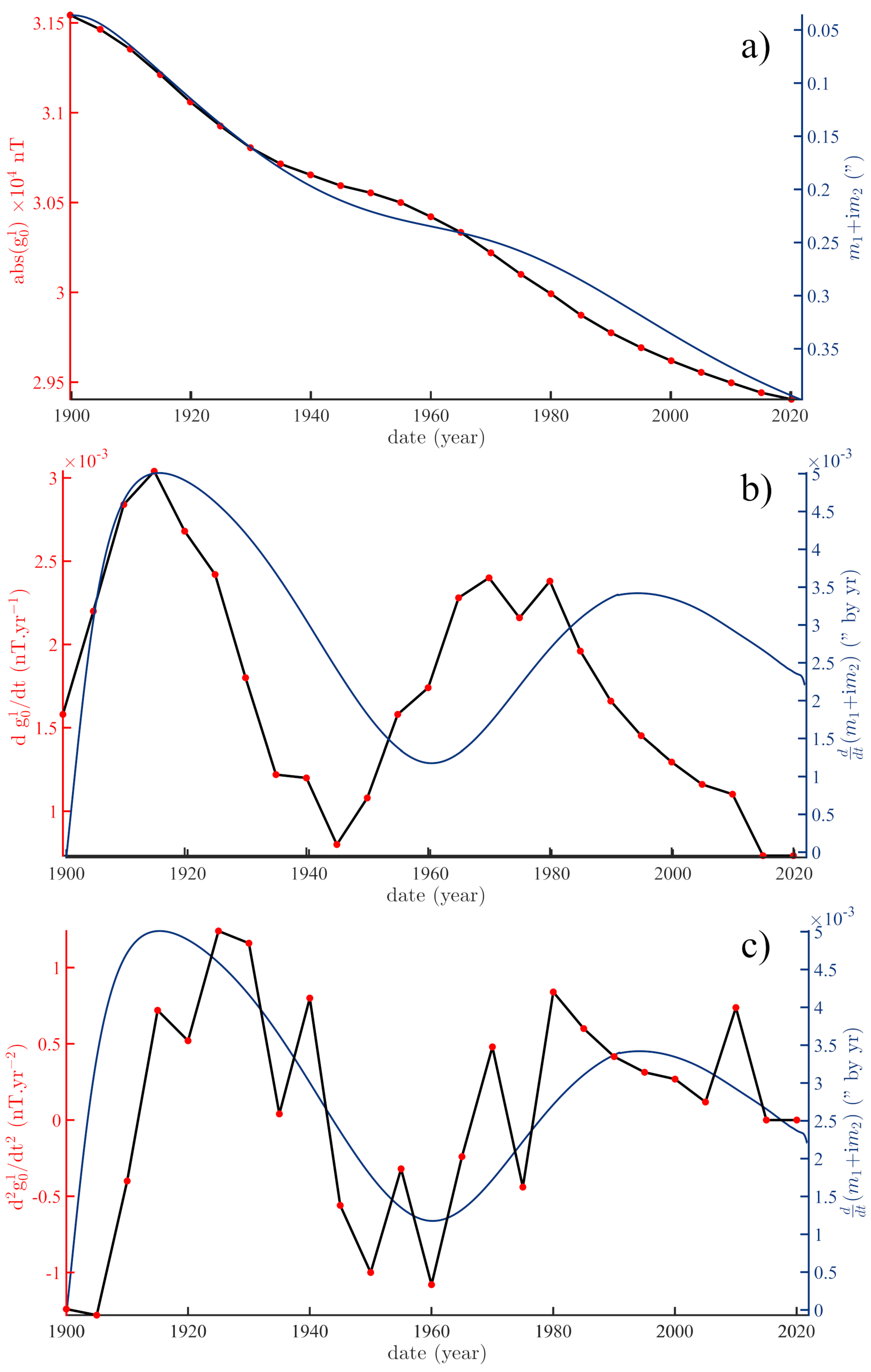
4.1. On the Drift of the Magnetic Dipole
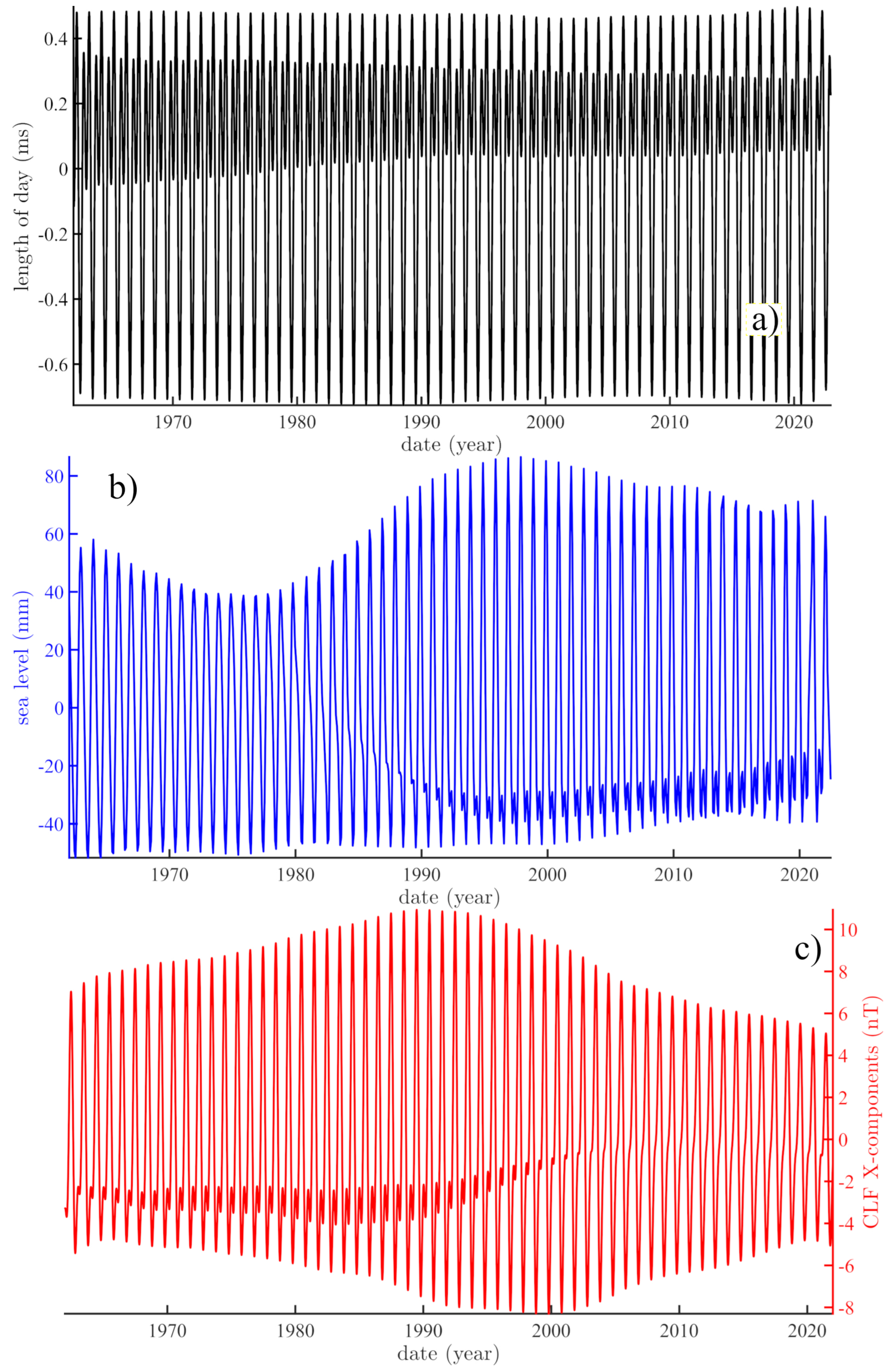
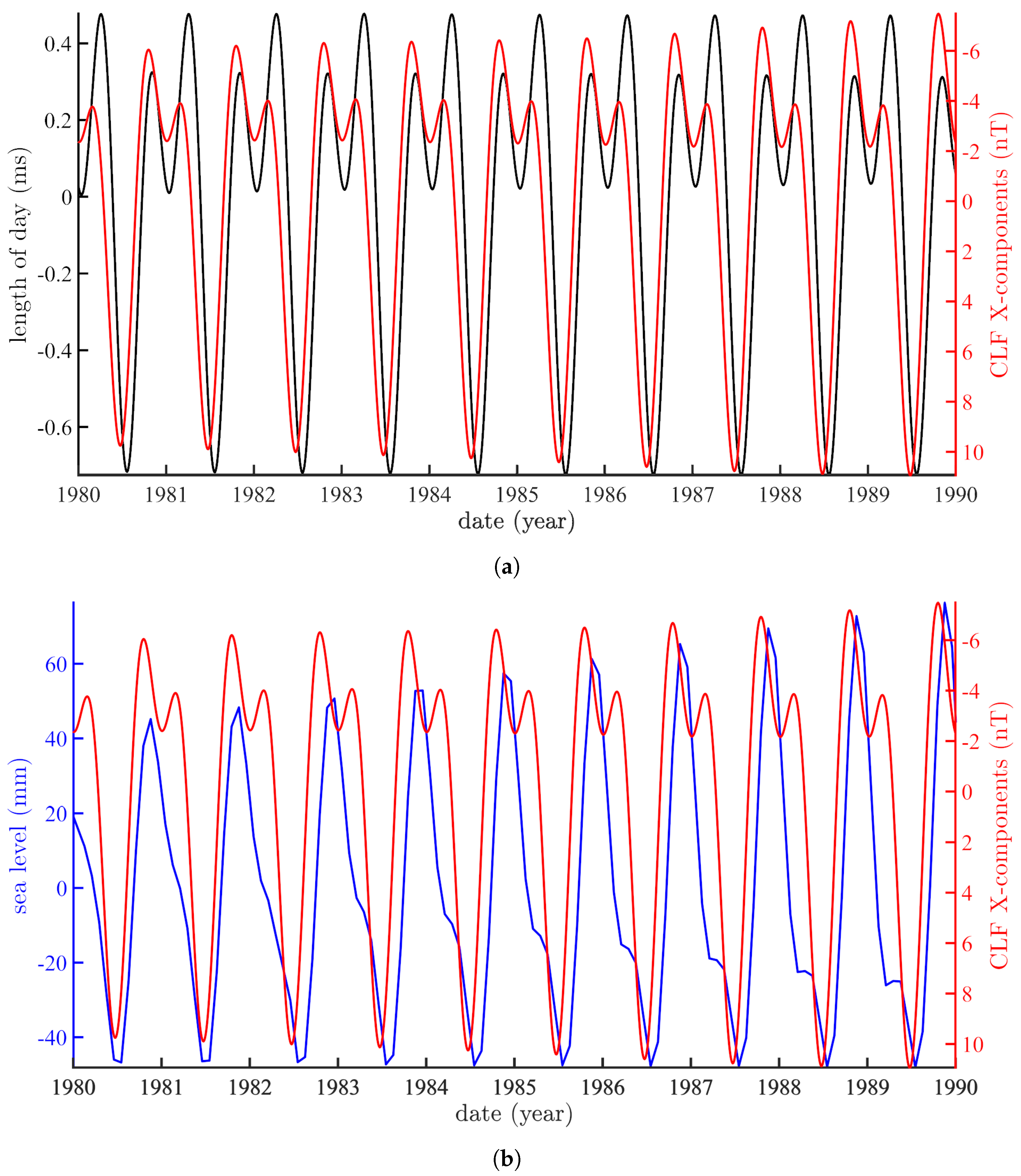
4.2. On the Forced Quasi-Cycles of the Magnetic Field
4.3. On the 11 yr Cycle and the Magnetic Field
4.4. On the International Geomagnetic Reference Field
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. The Polar Motion


References
- Peregrinus, P. De Magnete, seu Rota Perpetui Motus, Libellus nunc Primum Promulgatus; Translated in English by Brother Arnold, M. Sc “The letters of Petrus Peregrinus, on the Magnet, A.D. 1269”; McGraw-Hill: New York, NY, USA, 1917. [Google Scholar]
- Courtillot, V.; Le Mouël, J.L. The study of Earth’s magnetism (1269–1950): A foundation by Peregrinus and subsequent development of geomagnetism and paleomagnetism. Rev. Geophys. 2007, 45. [Google Scholar] [CrossRef] [Green Version]
- Gilbert, W. De Magnete; Courier Corporation: Washington, DC, USA, 1600. [Google Scholar]
- Mayaud, P.N. The aa indices: A 100-year series characterizing the magnetic activity. J. Geophys. Res. 1972, 77, 6870–6874. [Google Scholar] [CrossRef]
- Courtillot, V.; Le Mouel, J.; Mayaud, P. Maximum entropy spectral analysis of the geomagnetic activity index aa over a 107-year interval. J. Geophys. Res. 1977, 82, 2641–2649. [Google Scholar] [CrossRef]
- Le Mouël, J.; Lopes, F.; Courtillot, V. Singular spectral analysis of the aa and Dst geomagnetic indices. J. Geophys. Res. Space Phys. 2019, 124, 6403–6417. [Google Scholar] [CrossRef]
- Ducruix, J.; Courtillot, V.; Le Mouël, J.L. The late 1960s secular variation impulse, the eleven year magnetic variation and the electrical conductivity of the deep mantle. Geophys. J. Int. 1980, 61, 73–94. [Google Scholar] [CrossRef] [Green Version]
- Le Mouel, J.L.; Courtillot, V. Core motions, electromagnetic core-mantle coupling and variations in the Earth’s rotation: New constraints from geomagnetic secular variation impulses. Phys. Earth Planet. Inter. 1981, 24, 236–241. [Google Scholar] [CrossRef]
- Courtillot, V.; Le Mouël, J. Geomagnetic secular variation impulses. Nature 1984, 311, 709–716. [Google Scholar] [CrossRef]
- Bartels, J. Terrestrial-magnetic activity and its relations to solar phenomena. Terr. Magn. Atmos. Electr. 1932, 37, 1–52. [Google Scholar] [CrossRef] [Green Version]
- Bartels, J.; Heck, N.; Johnston, H. The three-hour-range index measuring geomagnetic activity. Terr. Magn. Atmos. Electr. 1939, 44, 411–454. [Google Scholar] [CrossRef]
- Chapman, S.; Bartels, J. Geomagnetism, vol. II: Analysis of the Data, and Physical Theories; Oxford Univ. Press: London, UK, 1940. [Google Scholar]
- Mayaud, P.N. Indices Kn, Ks et Km: 1964–1967; Editions du Centre National de la Recherche Scientifique: Paris, France, 1968. [Google Scholar]
- Mayaud, P. Une mesure planétaire d’activité magnétique basée sur deux observatoires antipodaux. Ann. Geophys 1971, 27, 67–70. [Google Scholar]
- Mayaud, P. The annual and daily variations of the Dst index. Geophys. J. Int. 1978, 55, 193–201. [Google Scholar] [CrossRef] [Green Version]
- Mayaud, P. Derivation, Meaning and Use of Geomagnetic Indices; American Geophysical Union: Washington, DC, USA, 1980; Volume 22. [Google Scholar]
- Le Mouël, J.L.; Blanter, E.; Chulliat, A.; Shnirman, M. On the semiannual and annual variations of geomagnetic activity and components. In Proceedings of the Ann Geophys; Copernicus Publications: Göttingen, Germany, 2004; Volume 22, pp. 3583–3588. [Google Scholar]
- Le Mouël, J.; Lopes, F.; Courtillot, V. Solar turbulence from sunspot records. Mon. Not. R. Astron. Soc. 2020, 492, 1416–1420. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. The local structure of turbulence in incompressible viscous fluid for very large Reynolds number. Ann. Sov. Acad. 1941, 30, 301–303. [Google Scholar]
- Le Mouël, J. Outer-core geostrophic flow and secular variation of Earth’s geomagnetic field. Nature 1984, 311, 734–735. [Google Scholar] [CrossRef]
- Jault, D.; Gire, C.; Le Mouël, J. Westward drift, core motions and exchanges of angular momentum between core and mantle. Nature 1988, 333, 353–356. [Google Scholar] [CrossRef]
- Jault, D.; Le Mouël, J.L. The topographic torque associated with a tangentially geostrophic motion at the core surface and inferences on the flow inside the core. Geophys. Astrophys. Fluid Dyn. 1989, 48, 273–295. [Google Scholar] [CrossRef]
- Jault, D.; Le Mouël, J.L. Core-mantle boundary shape: Constraints inferred from the pressure torque acting between the core and the mantle. Geophys. J. Int. 1990, 101, 233–241. [Google Scholar] [CrossRef] [Green Version]
- Jault, D.; Le Mouël, J. Exchange of angular momentum between the core and the mantle. J. Geomag. Geoelec. 1991, 43, 111–129. [Google Scholar] [CrossRef]
- Landau, L.; Lifshitz, E. Fluid Mechanics, V. 6 of Course of Theoretical Physics, 2nd ed.; Pergamon Press: Oxford, UK; New York, NY, USA; Beijing, China; Frankfurt, Germany; San Paulo, Brazil; Sydney, Australia; Tokyo, Japan; Toronto, ON, Canada, 1987. [Google Scholar]
- Proudman, J. On the dynamical theory of tides. Part II. Flat seas. Proc. London Math. 2nd Ser. 1916, 18, 21–50. [Google Scholar]
- Poisson, S.D. Mémoire Sur la Théorie du Magnétisme en Mouvement; L’Académie des Sciences: Paris, France, 1826. [Google Scholar]
- Gauss, C.F.; Weber, W.E. Resultate aus den Beobachtungen des Magnetischen Vereins: im Jahre 1836; im Verlage der Dieterischen Buchhandlung: Göttingen, Germany, 1837; Volume 2. [Google Scholar]
- Poisson, S.D. Solution D’un Problème Relatif au Magnétisme Terrestre; L’Académie des Sciences: Paris, France, 1825. [Google Scholar]
- Leprêtre, B.; Le Mouël, J.L. Sur la mesure de l’intensité du champ magnétique terrestre et la distribution du magnétisme dans les aimants. CR Geosci. 2005, 337, 1384–1391. [Google Scholar] [CrossRef]
- Gauss, C.F. Intensitas vis Magneticae Terrestris ad Mensuram Absolutam Revocata; Reprinted in: Werke, tome 5, Göttingen, Allemagne, 1877; Springer: Berlin/Heidelberg, Germany, 1832. [Google Scholar]
- Legendre, A.M. Recherches Sur L’attraction des Spheroides Homogenes; Bibliothèque Nationale de France: Paris, France, 1785. [Google Scholar]
- Laplace, P.S. Traité de Mécanique Céleste; de l’Imprimerie de Crapelet: Paris, France, 1799; Volume 1. [Google Scholar]
- Maupertuis, P.L.M. Essai de Cosmologie; de l’imprimerie d’Elie Luzac et fils: Paris, France, 1750. [Google Scholar]
- Lopes, F.; Courtillot, V.; Gibert, D.; Mouël, J.L.L.; Boulé, J.B. On power-law distributions of planetary rotations and revolutions as a function of aphelia, following Lagrange’s formulation. arXiv 2023, arXiv:2209.07213. [Google Scholar] [CrossRef]
- Lagrange, J.L. Mécanique Analytique; Mallet-Bachelier: Paris, France, 1788. [Google Scholar]
- Landau, L.; Lifshitz, E. The Classical Theroy of Fields, V. 2 of Course of Theoretical Physics, 4th ed.; Pergamon Press: Oxford, UK; New York, NY, USA; Beijing, China; Frankfurt, Germany; San Paulo, Brazil; Sydney, Australia; Tokyo, Japan; Toronto, ON, Canada, 1994. [Google Scholar]
- Coulomb, J.; Jobert, G. Traité de Géophysique Interne; Sismologie et pesanteur; Masson: Paris, France, 1973; Volume 1. [Google Scholar]
- Lorentz, H.A. Simplified theory of electrical and optical phenomena in moving systems. K. Ned. Akad. Van Wet. Proc. Ser. B Phys. Sci. 1898, 1, 427–442. [Google Scholar]
- Larmor, J. Aether and Matter: A Development of the Dynamical Relations of the Aether to Material Systems on the Basis of the Atomic Constitution of Matter, Including a Discussion of the Influence of the Earth’s Motion on Optical Phenomena, Being an Adams Prize Essay in the University of Cambridge; University Press: Cambridge, UK, 1900. [Google Scholar]
- Brillouin, L. A theorem of Larmor and its importance for electrons in magnetic fields. Phys. Rev. 1945, 67, 260. [Google Scholar] [CrossRef]
- Heaviside, O. A gravitational and electromagnetic analogy. Electrician 1893, 31, 281–282. [Google Scholar]
- Talwani, M.; Worzel, J.L.; Landisman, M. Rapid gravity computations for two-dimensional bodies with application to the Mendocino submarine fracture zone. J. Geophys. Res. 1959, 64, 49–59. [Google Scholar] [CrossRef] [Green Version]
- Talwani, M. Computation with the help of a digital computer of magnetic anomalies caused by bodies of arbitrary shape. Geophysics 1965, 30, 797–817. [Google Scholar] [CrossRef]
- Markowitz, W. Concurrent astronomical observations for studying continental drift, polar motion, and the rotation of the Earth. In Proceedings of the Symposium-International Astronomical Union; Cambridge University Press: Cambridge, UK, 1968; Volume 32, pp. 25–32. [Google Scholar]
- Stoyko, A. Mouvement seculaire du pole et la variation des latitudes des stations du SIL. In Proceedings of the Symposium-International Astronomical Union; Cambridge University Press: Cambridge, UK, 1968; Volume 32, pp. 52–56. [Google Scholar]
- Milanković, M. Théorie Mathématique des Phénomènes Thermiques Poduits Par la Radiation Solaire; Gauthier-Villars: Paris, France, 1920. [Google Scholar]
- Laskar, J.; Fienga, A.; Gastineau, M.; Manche, H. La2010: A new orbital solution for the long-term motion of the Earth. Astron. Astrophys. 2011, 532, A89. [Google Scholar] [CrossRef] [Green Version]
- Lopes, F.; Le Mouël, J.; Courtillot, V.; Gibert, D. On the shoulders of Laplace. Phys. Earth Planet. Inter. 2021, 316, 106693. [Google Scholar] [CrossRef]
- Bank, M.J.; Scafetta, N. Scaling, mirror symmetries and musical consonances among the distances of the planets of the solar system. Front. Astron. Space Sci. 2022, 8, 758184. [Google Scholar] [CrossRef]
- Lopes, F.; Courtillot, V.; Gibert, D.; Le Mouël, J.L. Extending the Range of Milankovic Cycles and Resulting Global Temperature Variations to Shorter Periods (1–100 Year Range). Geosciences 2022, 12, 448. [Google Scholar] [CrossRef]
- Mörth, H.; Schlamminger, L. Planetary motion, sunspots and climate. In Solar-Terrestrial Influences on Weather and Climate: Proceedings of a Symposium/Workshop Held at the Fawcett Center for Tomorrow, The Ohio State University, Columbus, OH, USA, 24–28 August 1978; Springer: Dordrecht, The Netherlands, 1979; pp. 193–207. [Google Scholar]
- Scafetta, N. Does the Sun work as a nuclear fusion amplifier of planetary tidal forcing? A proposal for a physical mechanism based on the mass-luminosity relation. J. Atmos. Sol. Terr. Phys. 2012, 81, 27–40. [Google Scholar] [CrossRef] [Green Version]
- Stefani, F.; Giesecke, A.; Weber, N.; Weier, T. Synchronized helicity oscillations: A link between planetary tides and the solar cycle? Sol. Phys. 2016, 291, 2197–2212. [Google Scholar] [CrossRef] [Green Version]
- Courtillot, V.; Lopes, F.; Le Mouël, J. On the prediction of solar cycles. Sol. Phys. 2021, 296, 1–23. [Google Scholar] [CrossRef]
- Lambeck, K. The Earth’s Variable Rotation: Geophysical Causes and Consequences; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Poincaré, H. Sur l’équilibre d’une masse fluide animée d’un mouvement de rotation. Bull. Astron. Obs. Paris 1885, 2, 109–118. [Google Scholar]
- Courtillot, V.; Le Mouël, J.L.; Lopes, F.; Gibert, D. On Sea-Level Change in Coastal Areas. J. Mar. Sci. 2022, 10, 1871. [Google Scholar] [CrossRef]
- Lopes, F.; Courtillot, V.; Le Mouël, J.L. Triskeles and Symmetries of Mean Global Sea-Level Pressure. Atmosphere 2022, 13, 1354. [Google Scholar] [CrossRef]
- Alexandrescu, M.; Courtillot, V.; Le Mouël, J.L. Geomagnetic field direction in Paris since the mid-sixteenth century. Phys. Earth Planet. Inter. 1996, 98, 321–360. [Google Scholar] [CrossRef]
- Alexandrescu, M.; Courtillot, V.; Le Mouël, J.L. High-resolution secular variation of the geomagnetic field in western Europe over the last 4 centuries: Comparison and integration of historical data from Paris and London. J. Geophys. Res. Solid Earth 1997, 102, 20245–20258. [Google Scholar] [CrossRef]
- Golyandina, N.; Zhigljavsky, A. Singular Spectrum Analysis with R; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Lemmerling, P.; Van Huffel, S. Analysis of the structured total least squares problem for Hankel/Toeplitz matrices. Num. Algorithms 2001, 27, 89–114. [Google Scholar] [CrossRef]
- Golub, G.H.; Reinsch, C. Singular value decomposition and least squares solutions. Linear Algebra 1971, 2, 134–151. [Google Scholar]
- Le Mouël, J.L.; Lopes, F.; Courtillot, V. Sea-Level Change at the Brest (France) Tide Gauge and the Markowitz Component of Earth’s Rotation. J. Coast. Res. 2021, 37, 683–690. [Google Scholar] [CrossRef]
- Lopes, F.; Le Mouël, J.L.; Gibert, D. The mantle rotation pole position. A solar component. CR Geosci. 2017, 349, 159–164. [Google Scholar] [CrossRef]
- Lopes, F.; Courtillot, V.; Gibert, D.; Mouël, J.L.L. On two formulations of polar motion and identification of its sources. Geosciences 2022, 12, 398. [Google Scholar] [CrossRef]
- Stephenson, F.R.; Morrison, L.V. Long-term changes in the rotation of the Earth: 700 BC to AD 1980. Philos. Trans. R. Soc. A 1984, 313, 47–70. [Google Scholar]
- Gross, R.S. A combined length-of-day series spanning 1832–1997: LUNAR97. Phys. Earth Planet. Inter. 2001, 123, 65–76. [Google Scholar] [CrossRef]
- Stewart, B. Terrestrial Magnetism; Encyclopedia Brittanica: Chicago, IL, USA, 1882. [Google Scholar]
- Stewart, B. On the cause of the solar-diurnal variations of terrestrial magnetism. Philos. Trans. R. Soc. A 1886, 8, 38. [Google Scholar]
- Russell, C.; McPherron, R. Semiannual variation of geomagnetic activity. J. Geophys. Res. 1973, 78, 92–108. [Google Scholar] [CrossRef]
- Lockwood, M.; Owens, M.J.; Barnard, L.A.; Haines, C.; Scott, C.J.; McWilliams, K.A.; Coxon, J.C. Semi-annual, annual and Universal Time variations in the magnetosphere and in geomagnetic activity: 1. Geomagnetic data. J. Space Weather. Space Clim. 2020, 10, 23. [Google Scholar] [CrossRef]
- Lockwood, M.; Haines, C.; Barnard, L.A.; Owens, M.J.; Scott, C.J.; Chambodut, A.; McWilliams, K.A. Semi-annual, annual and Universal Time variations in the magnetosphere and in geomagnetic activity: 4. Polar Cap motions and origins of the Universal Time effect. J. Space Weather. Space Clim. 2021, 11, 15. [Google Scholar] [CrossRef]
- Schwabe, H. Sonnenbeobachtungen im jahre 1843. von herrn hofrath schwabe in dessau. Astron. Nachrichten 1844, 21, 233. [Google Scholar]
- Courtillot, V.; Le Mouel, J.L. Time variations of the Earth’s magnetic field: From daily to secular. Annu. Rev. Earth Planet Sci. 1988, 16, 389–476. [Google Scholar] [CrossRef]
- Le Mouël, J.; Lopes, F.; Courtillot, V.; Gibert, D. On forcings of length of day changes: From 9-day to 18.6-year oscillations. Phys. Earth Planet. Inter. 2019, 292, 1–11. [Google Scholar] [CrossRef]
- Alken, P.; Thébault, E.; Beggan, C.D.; Amit, H.; Aubert, J.; Baerenzung, J.; Bondar, T.; Brown, W.; Califf, S.; Chambodut, A.; et al. International geomagnetic reference field: The thirteenth generation. Earth Planets Space 2021, 73, 1–25. [Google Scholar] [CrossRef]

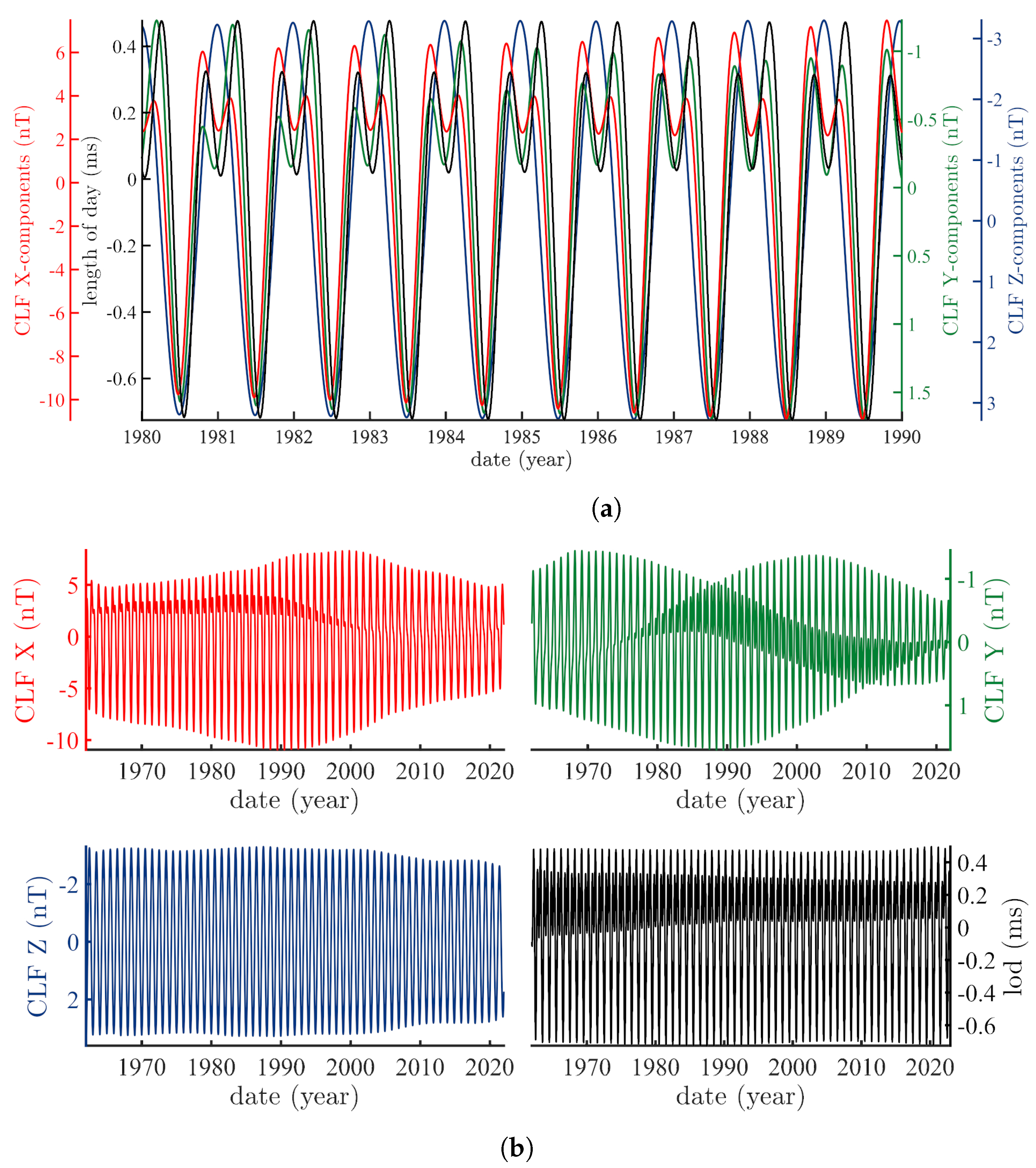
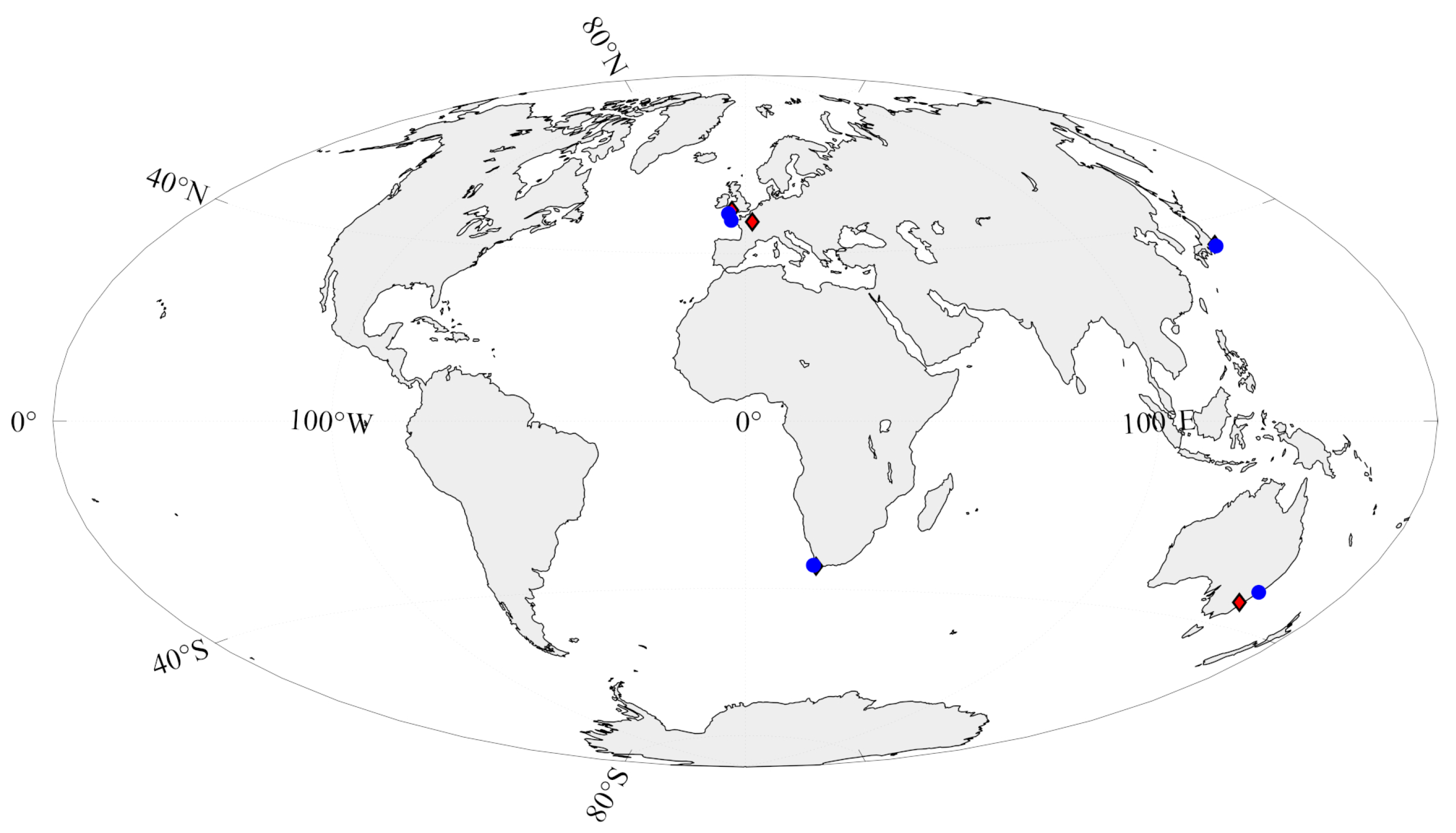
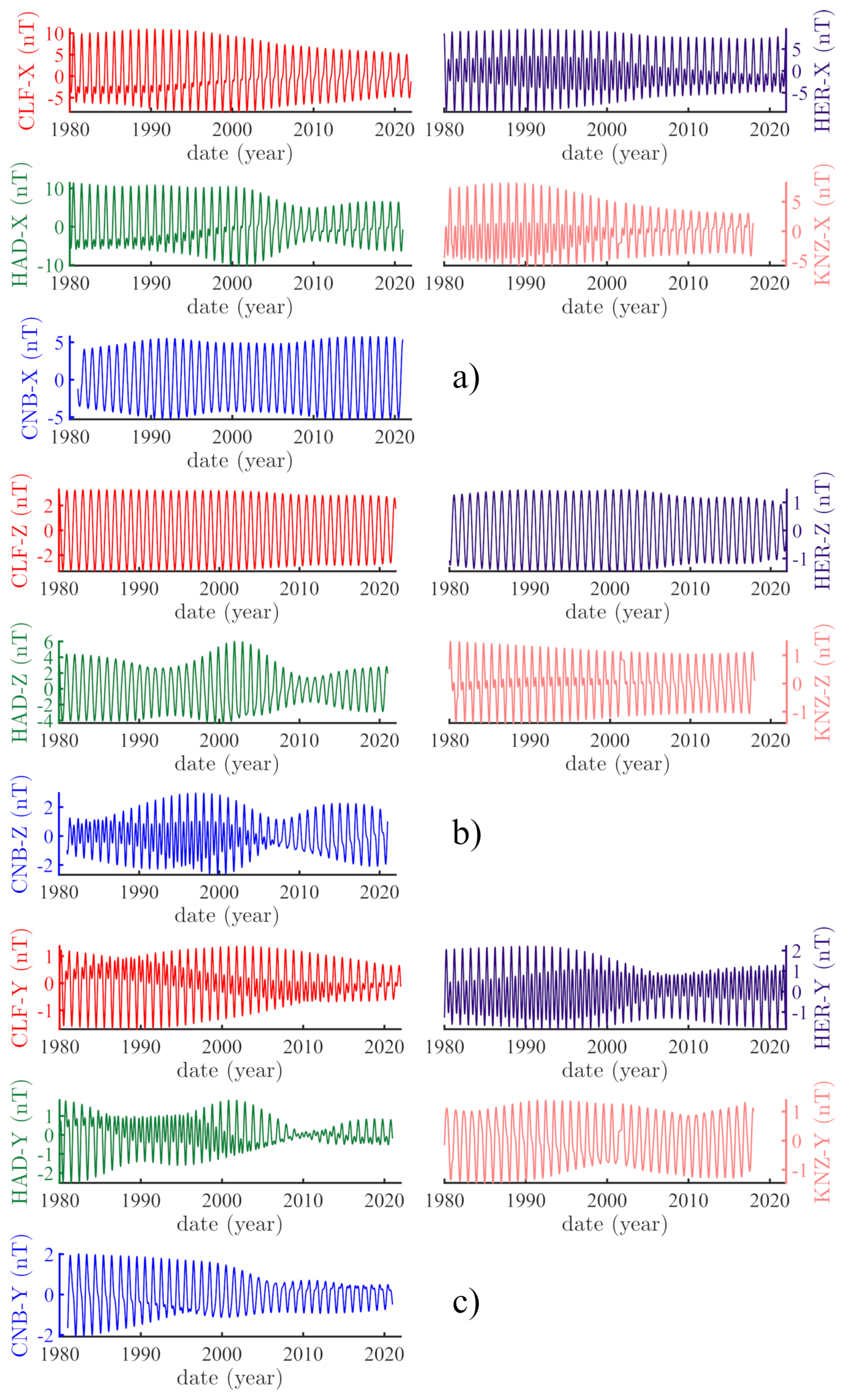
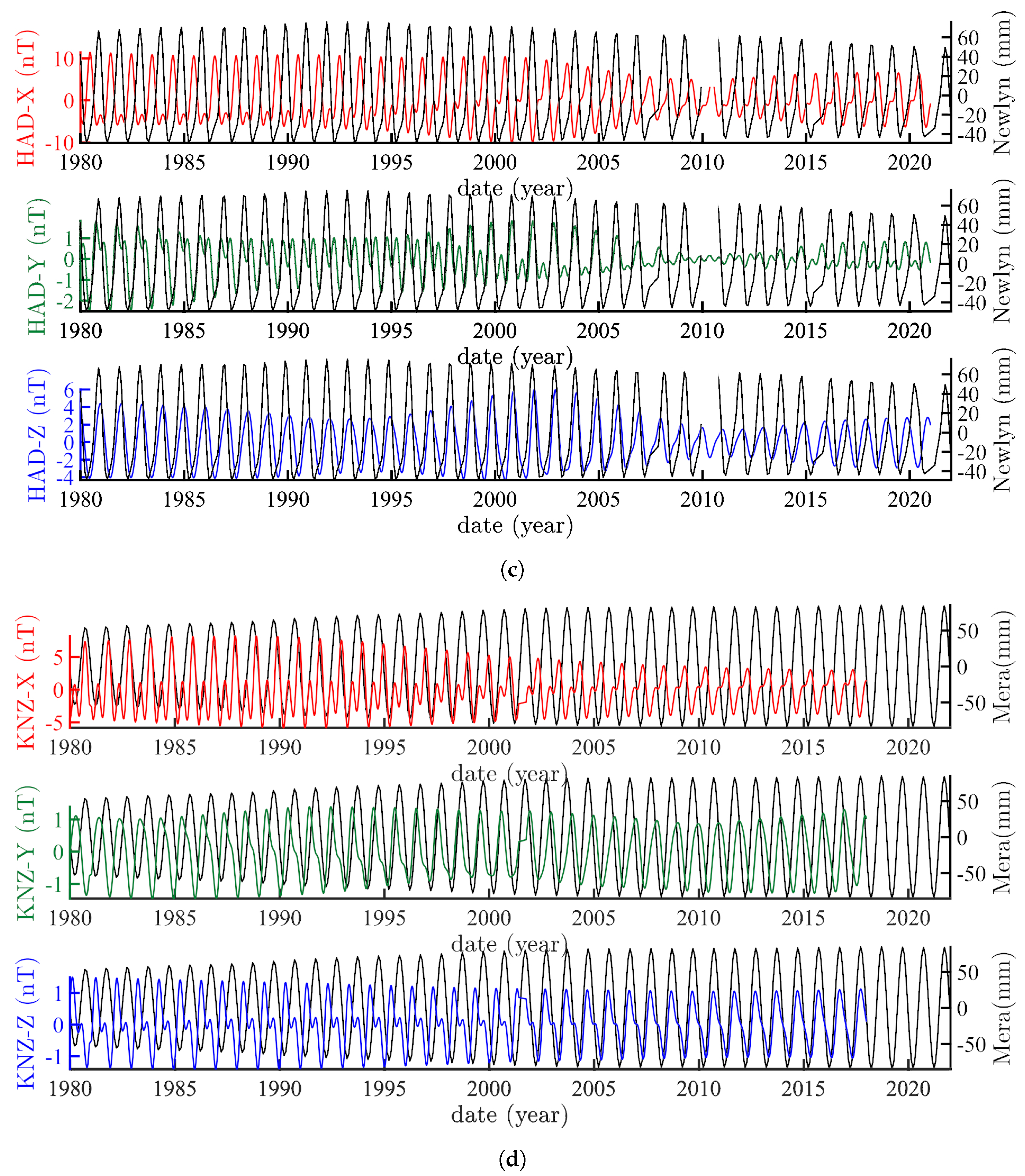
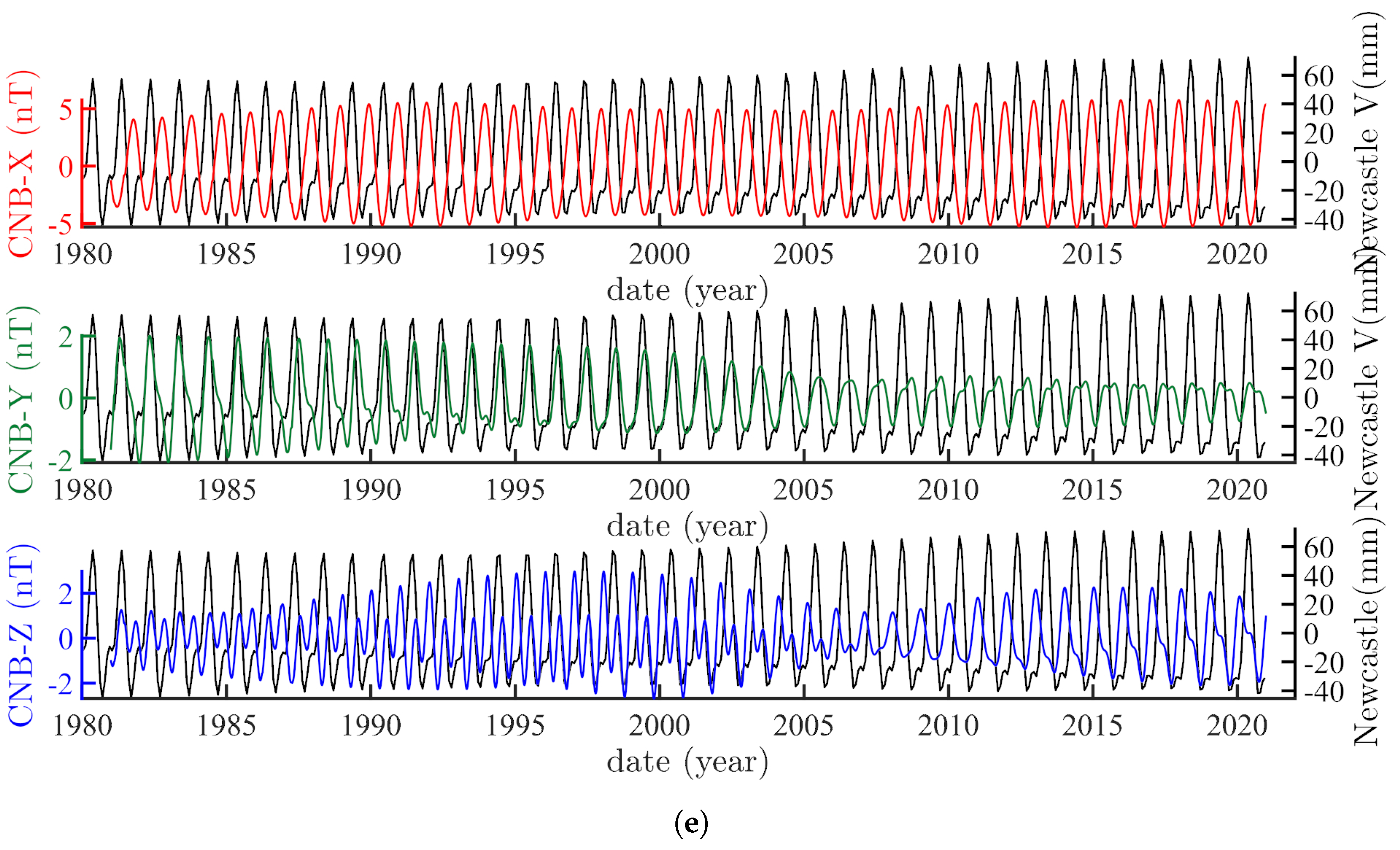

| Magnetic Observatory | Tide Gauge |
|---|---|
| Chambon-La-Forêt (CLF, 2.26 E, 48.02 N) | Brest (4.49 W, 48.38 N) |
| Hartland (HAD, 4.48 W, 51 N) | Newlyn (5.54 W, 50.10 N) |
| Canberra (CNB, 149.36 E, 35.32 S) | Newcaslte V (151.78 E, 32.92 S) |
| Hermanus (HER, 19.23 W, 34.43 S) | Simons Bay (18.44 E, 34.18 S) |
| Kanozan (KNZ, 139.95 E, 35.25 N) | Mera (139.82° E, 34.91 N) |
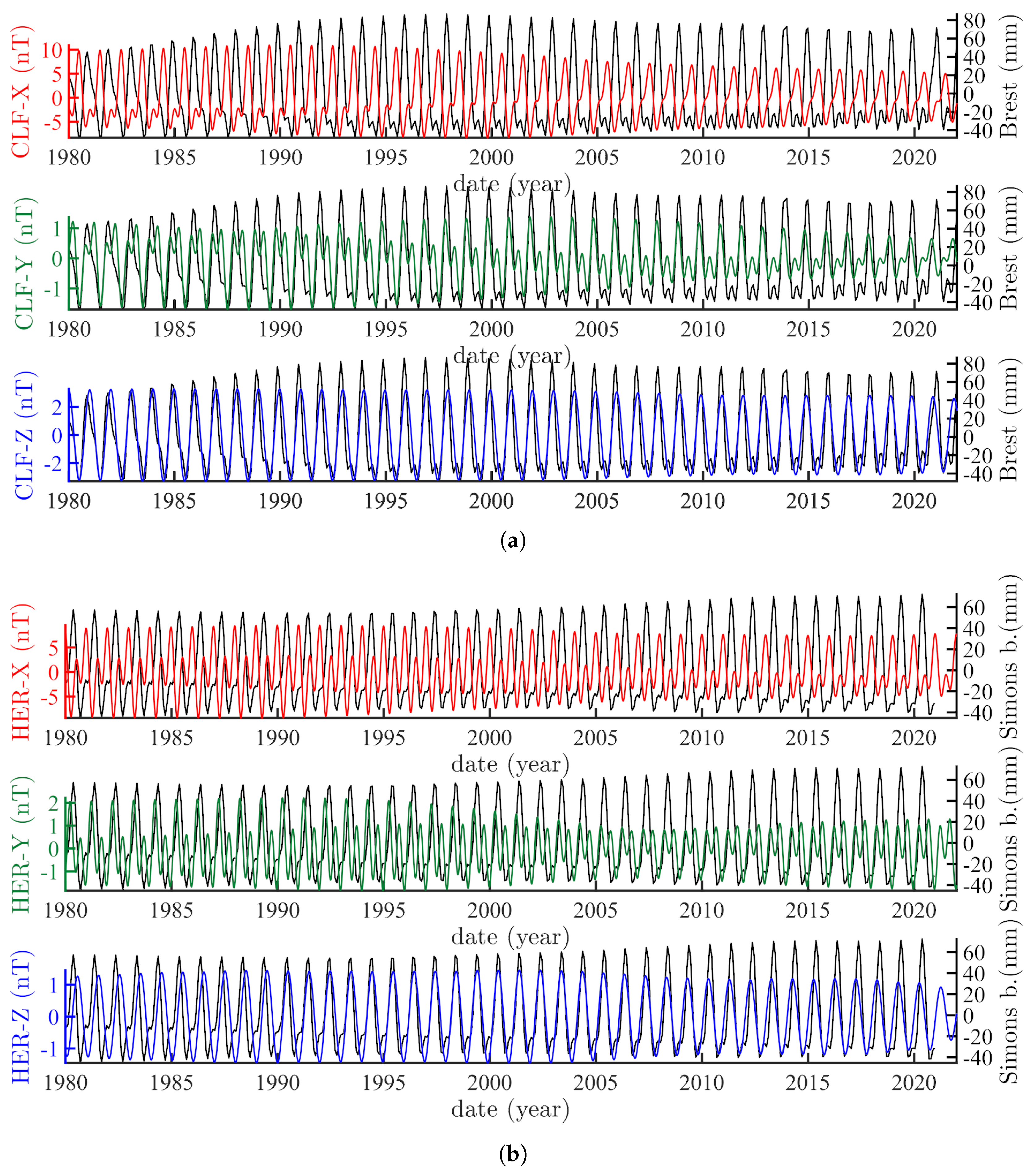
| Couple Observatory–Tide Gauge | Ratio Sea Level/Magnetic Component | Order of Magnitude |
|---|---|---|
| CLF/Brest, between 1980 and 2000 | ∼100 mm/15 nT | ∼7 mm/nT |
| HAD/Newlyn, between 1980 and 2005 | ∼100 mm/15 nT | ∼7 mm/nT |
| CNB/Newcaste V, between 1980 and 2022 | ∼ 80 mm/10 nT | ∼8 mm/nT |
| HER/Simons bay, between 1980 and 2000 | ∼100 mm/14 nT | ∼7 mm/nT |
| KNZ/Mera, between 1980 and 1995 | ∼140 mm/14 nT | ∼10 mm/nT |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Le Mouël, J.-L.; Lopes, F.; Courtillot, V.; Gibert, D.; Boulé, J.-B. Is the Earth’s Magnetic Field a Constant? A Legacy of Poisson. Geosciences 2023, 13, 202. https://doi.org/10.3390/geosciences13070202
Le Mouël J-L, Lopes F, Courtillot V, Gibert D, Boulé J-B. Is the Earth’s Magnetic Field a Constant? A Legacy of Poisson. Geosciences. 2023; 13(7):202. https://doi.org/10.3390/geosciences13070202
Chicago/Turabian StyleLe Mouël, Jean-Louis, Fernando Lopes, Vincent Courtillot, Dominique Gibert, and Jean-Baptiste Boulé. 2023. "Is the Earth’s Magnetic Field a Constant? A Legacy of Poisson" Geosciences 13, no. 7: 202. https://doi.org/10.3390/geosciences13070202
APA StyleLe Mouël, J.-L., Lopes, F., Courtillot, V., Gibert, D., & Boulé, J.-B. (2023). Is the Earth’s Magnetic Field a Constant? A Legacy of Poisson. Geosciences, 13(7), 202. https://doi.org/10.3390/geosciences13070202







