Multi-Parameter Statistical Analysis of K, Th, and U Concentrations in Eastern Senegal: Implications for the Interpretation of Airborne Radiometrics
Abstract
:1. Introduction
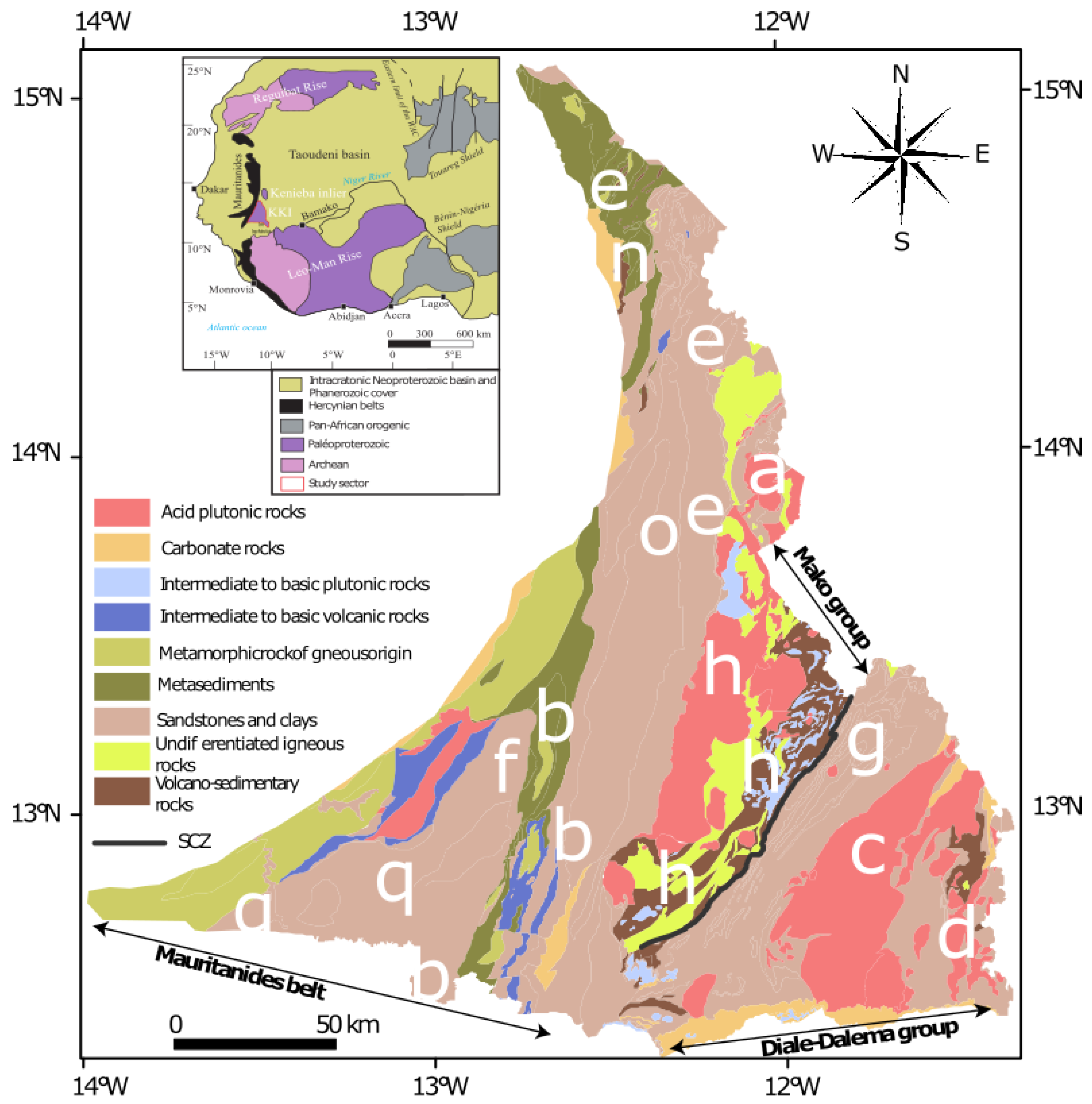
2. Geological Context
3. Data and Methods
3.1. Airborne Radiometric Data
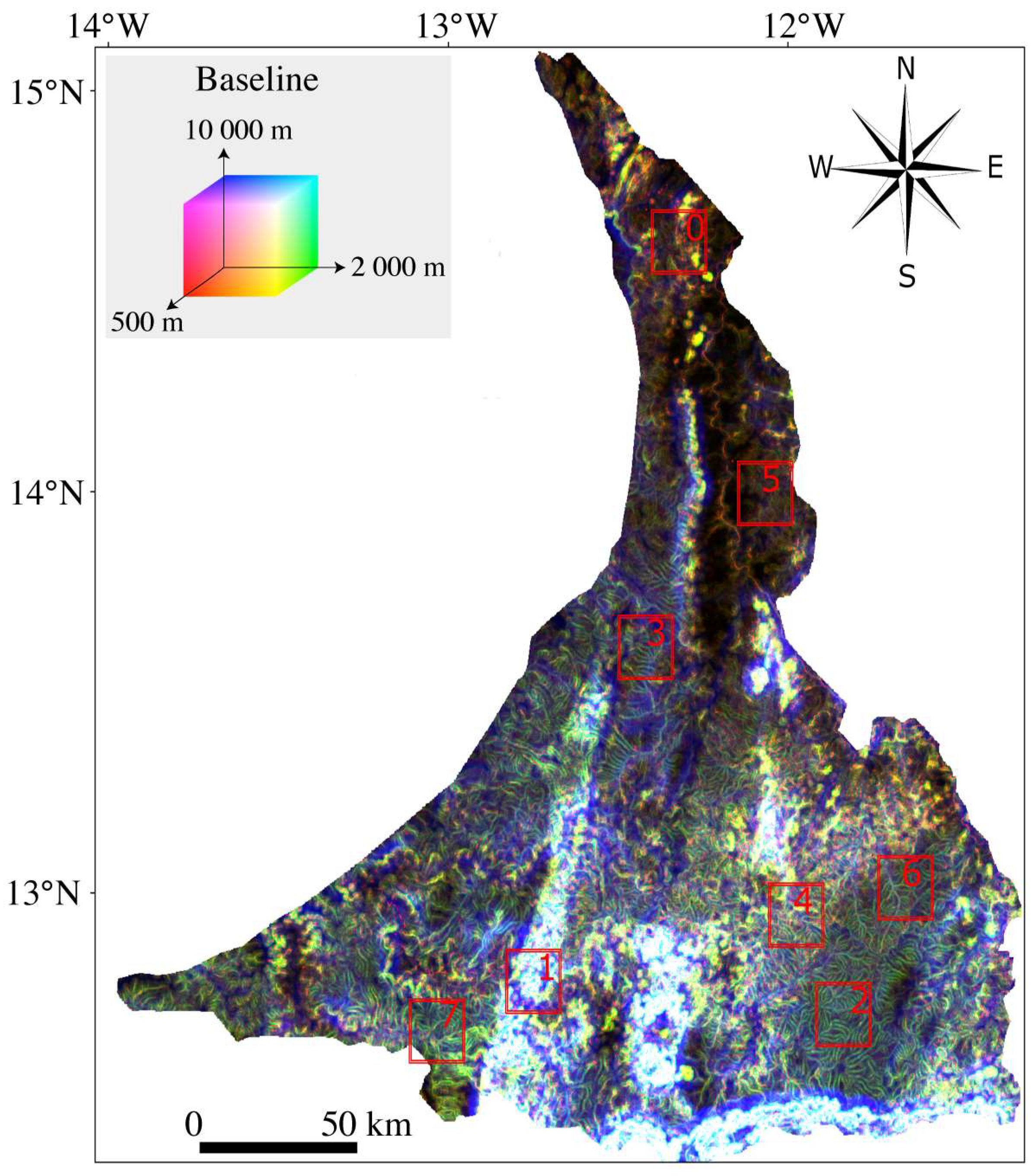
3.2. Topographic Information
3.3. Roughness Calculation
3.4. Calculation of the Statistical Parameters of K, Th, and U Concentration Distribution
3.5. Classification
3.5.1. UMAP
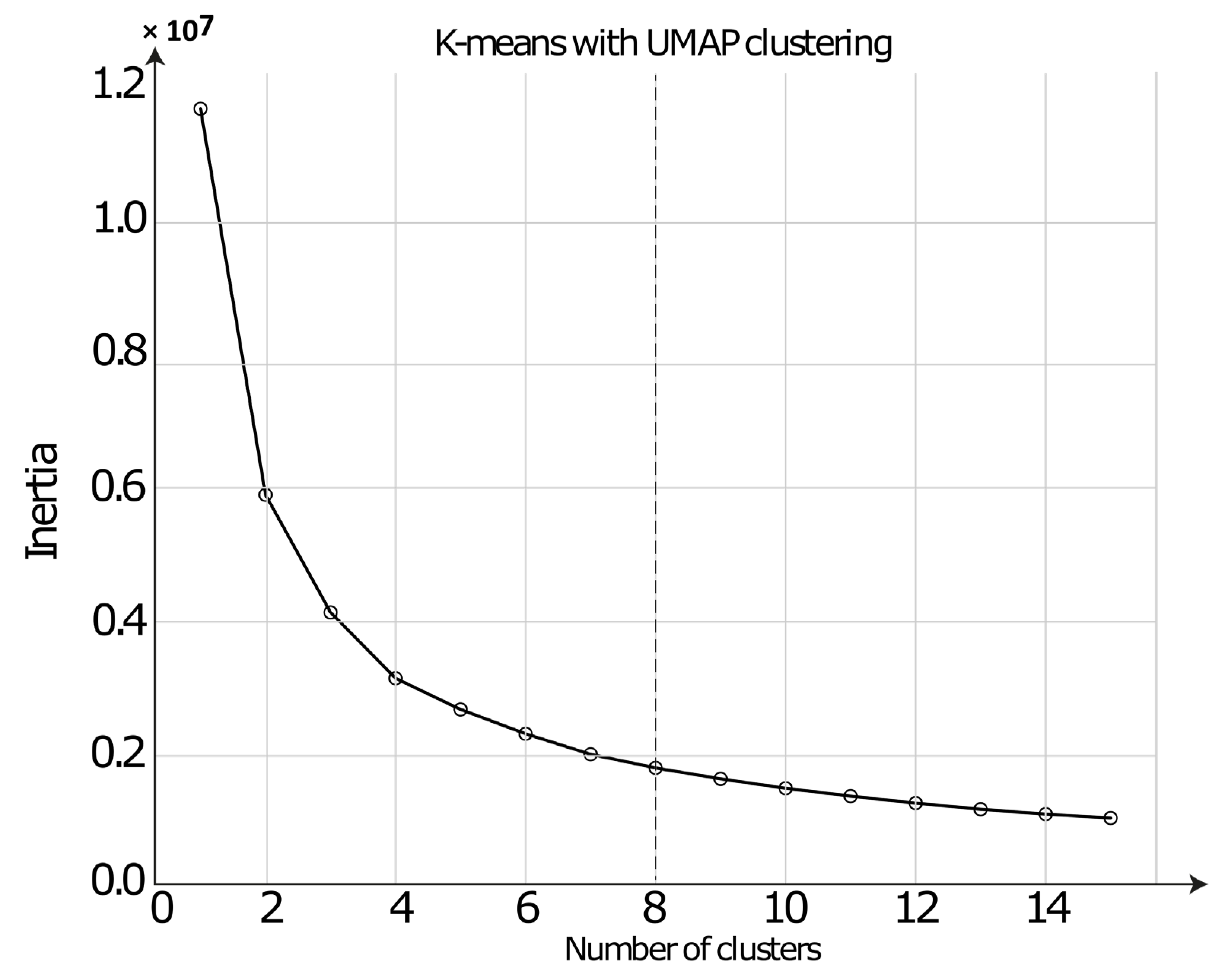
3.5.2. K-Means Clustering
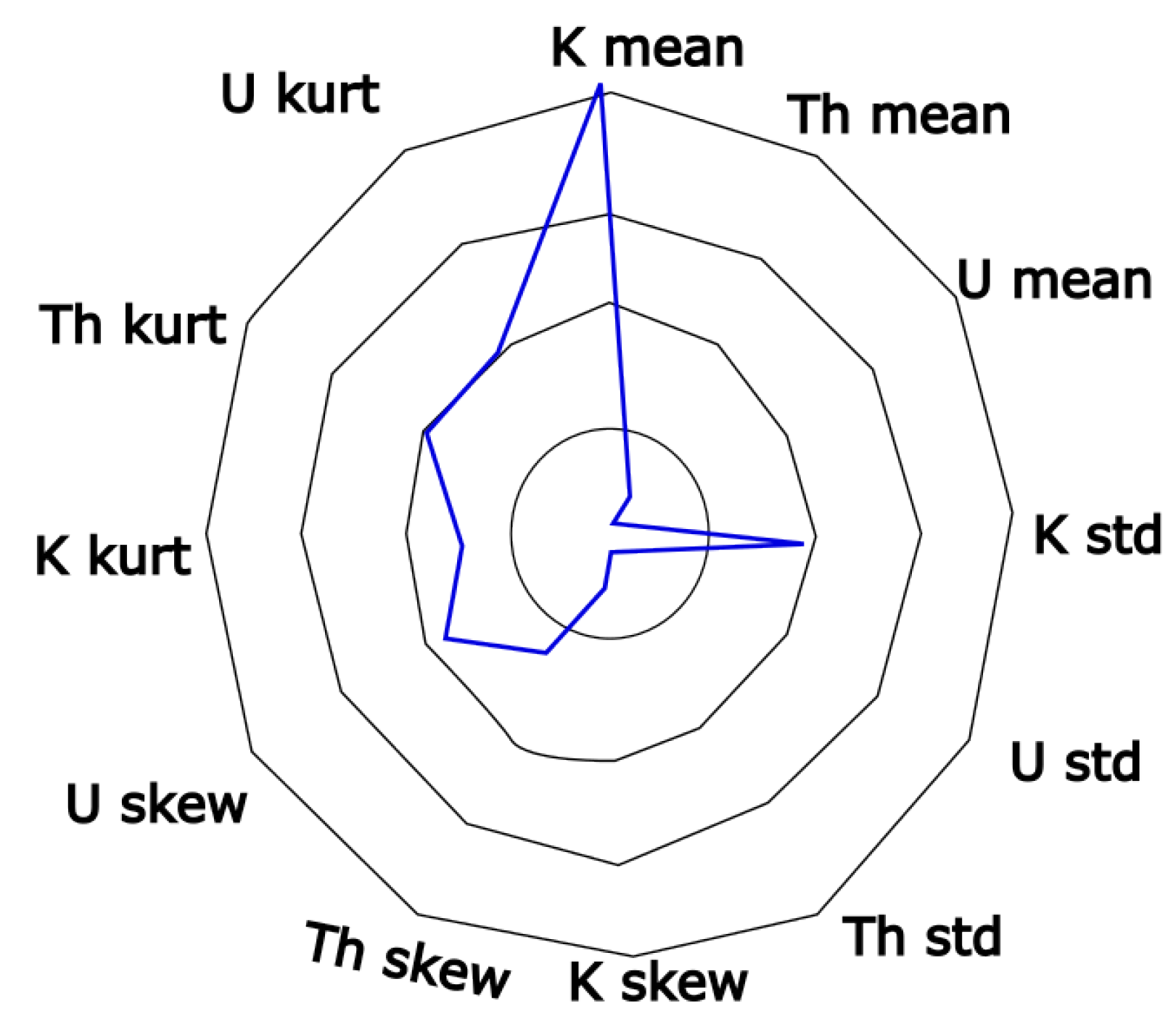
3.5.3. Plotting Statistical Signatures of Clusters with the Radar Plot
4. Results
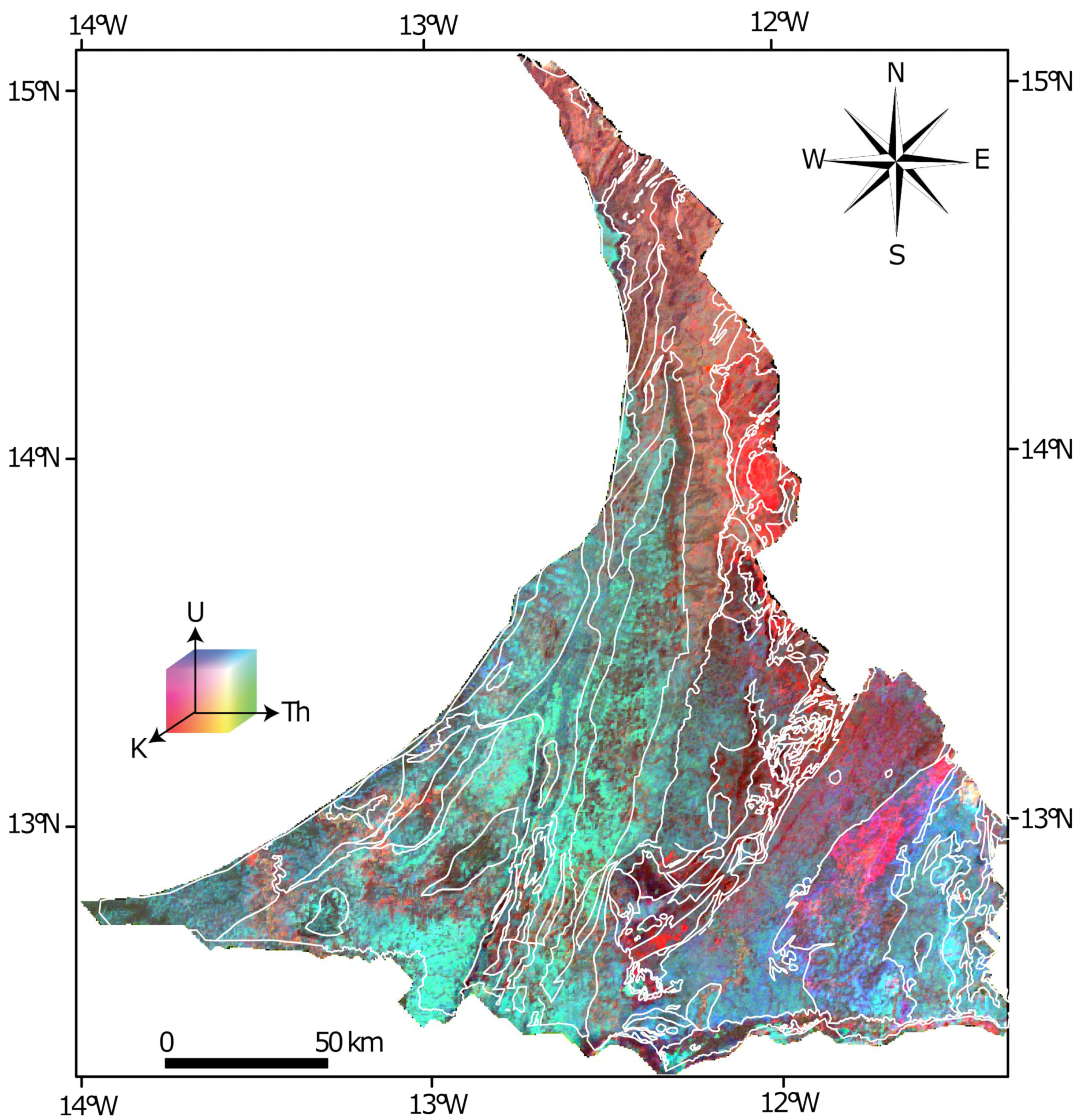
4.1. Maps of the Statistical Parameters of K, Th, and U Concentrations
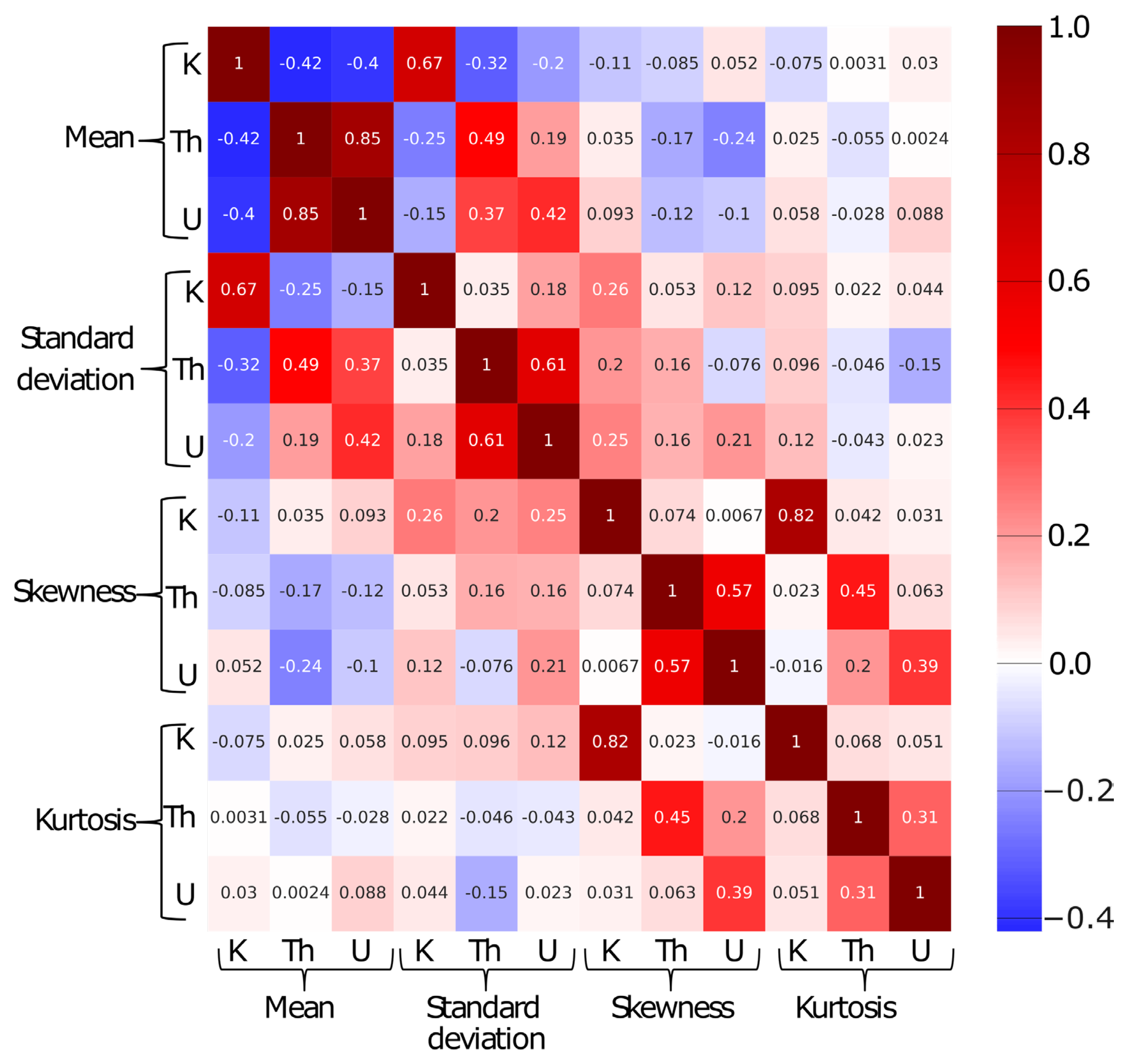
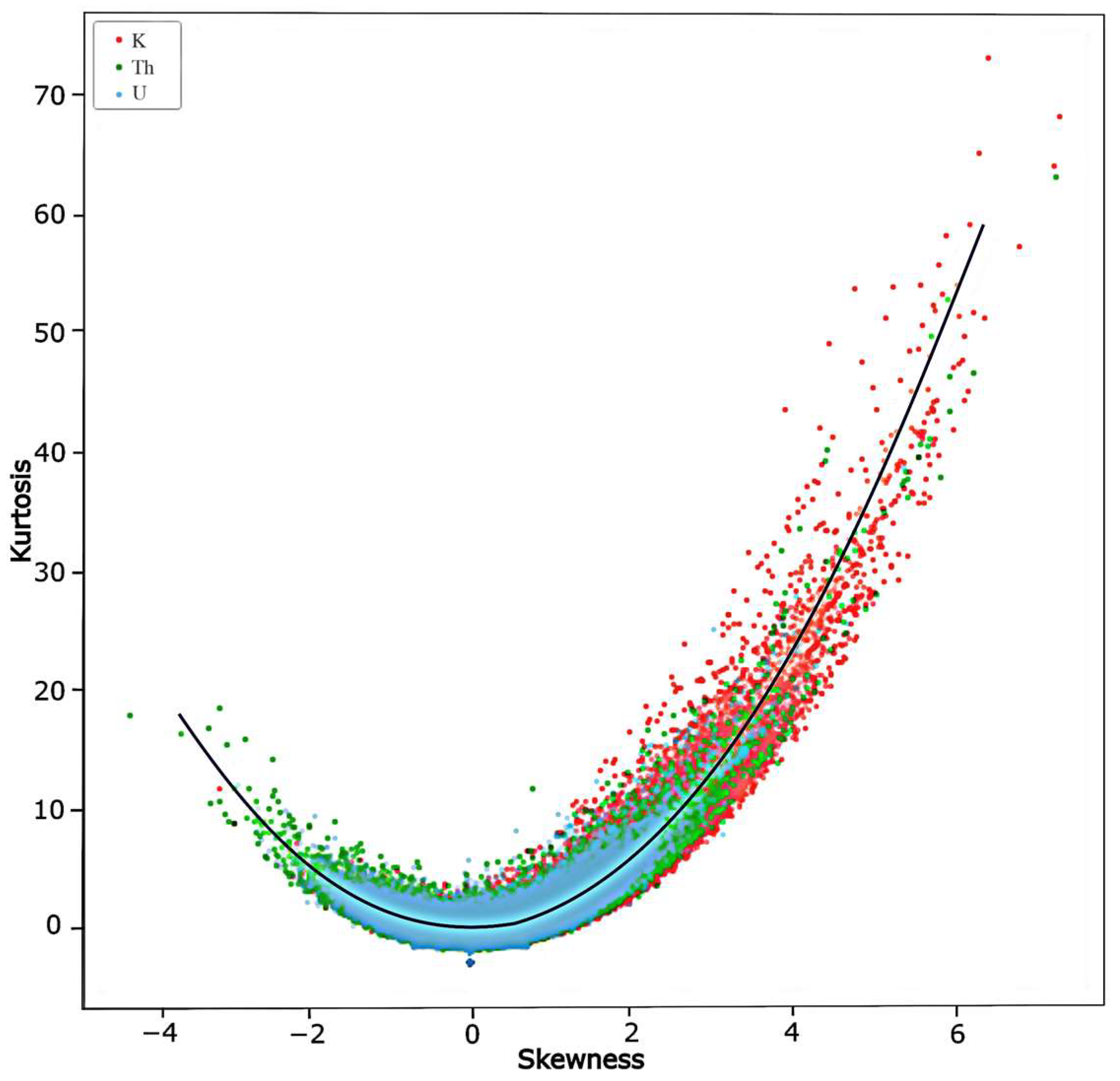
4.2. Correlation between the Statistical Parameters
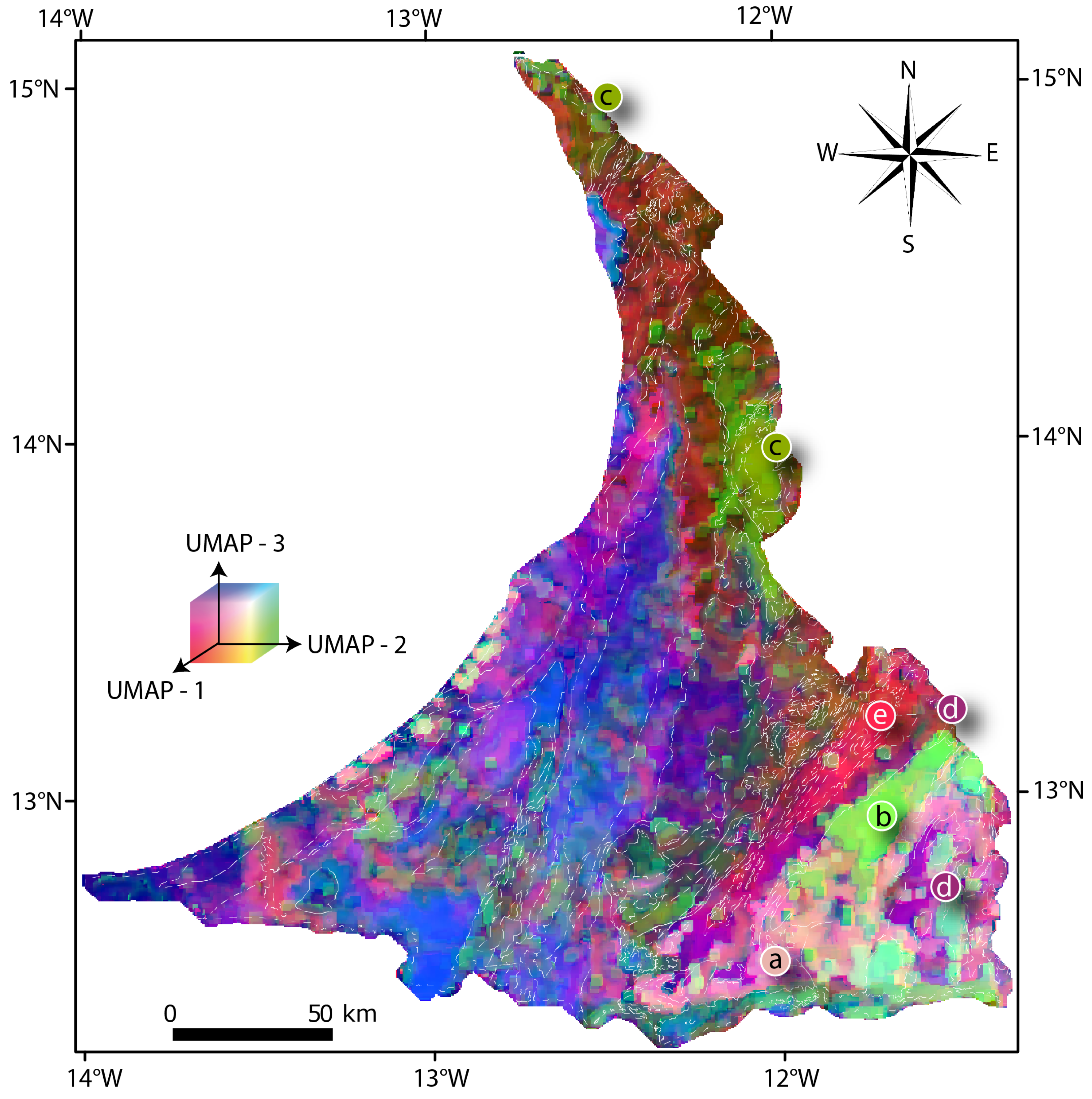
4.3. Statistical Map Visualization after Dimensionality Reduction
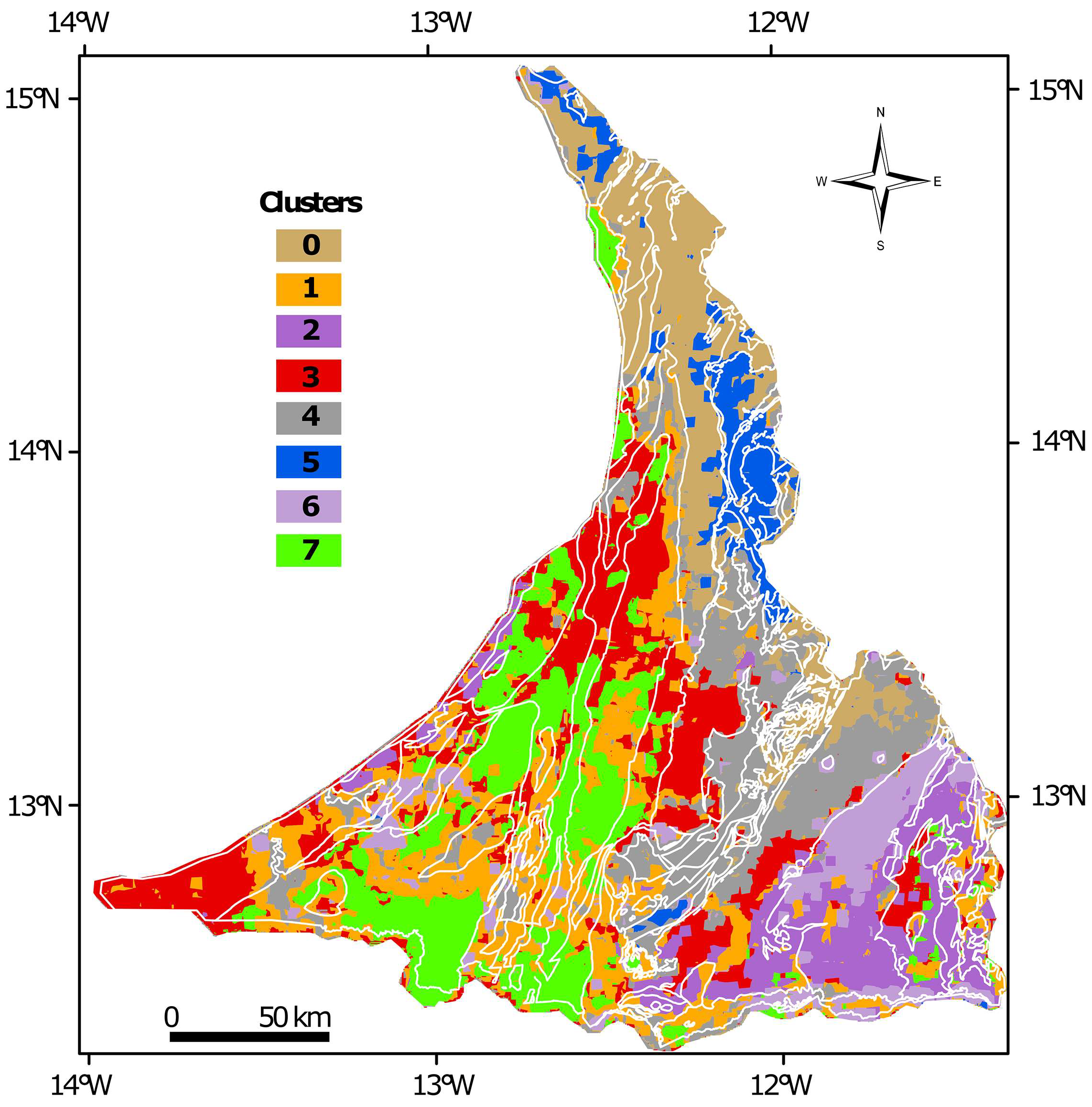
4.4. Clustering and Clusters Characteristic
5. Discussion
5.1. Interpretations of the Scales of Variations of the Statistical Parameters
5.2. Interpretations of Correlations between Statistical Parameters
5.3. Relations between Clusters and Geological Units, Topography, and Roughness
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dentith, M.; Mudge, S.T. Geophysics for the Mineral Exploration Geoscientist; Cambridge University Press: Cambridge, UK, 2014; ISBN 978-0-521-80951-1. [Google Scholar]
- Essa, K.S.; Munschy, M.; Youssef, M.A.S.; Khalaf, E.E.D.A.H. Aeromagnetic and Radiometric Data Interpretation to Delineate the Structural Elements and Probable Precambrian Mineralization Zones: A Case Study, Egypt. Min. Metall. Explor. 2022, 39, 2461–2475. [Google Scholar] [CrossRef]
- Eppelbaum, L.V.; Mishne, A.R. Unmanned Airborne Magnetic and VLF investigations: Effective Geophysical Methodology of the Near Future. Positioning 2011, 2, 112–133. [Google Scholar] [CrossRef]
- Amestoy, J.; Meslin, P.-Y.; Richon, P.; Delpuech, A.; Derrien, S.; Raynal, H.; Pique, É.; Baratoux, D.; Chotard, P.; Van Beek, P.; et al. Effects of environmental factors on the monitoring of environmental radioactivity by airborne gamma-ray spectrometry. J. Environ. Radioact. 2021, 237, 106695. [Google Scholar] [CrossRef] [PubMed]
- Minty, B.R.S. Fundamentals of airborne gamma-ray spectrometry. AGSO J. Aust. Geol. Geophys. 1997, 17, 39–50. [Google Scholar]
- Minty, B.R.S.; Luyendyk, A.P.J.; Brodie, R.C. Calibration and data processing for airborne gamma-ray spectrometry. AGSO J. Aust. Geol. Geophys. 1997, 17, 51–62. [Google Scholar]
- Berning, J. The Rossing uranium deposit. In Mineral Deposits of South Africa; Anhaeusser, C.R., Maske, S., Eds.; Geological Society of South Africa: Johannesburg, South Africa, 1986; pp. 1819–1832. [Google Scholar]
- Smith, R.J. Geophysics in Australian mineral exploration. Geophysics 1985, 50, 2637–2665. [Google Scholar] [CrossRef]
- Forman, J.M.A.; Angeiras, A.G. Poços de Calderas and Itataia: Two Case Histories of Uranium Exploration in Brazil; International Atomic Energy Agency: Vienna, Austria, 1981; pp. 99–139. [Google Scholar]
- Dentith, M.C.; Frankcombe, K.F.; Trench, A. Geophysical signatures of Western Australia mineral deposits: An overview. In Geophysical Signatures of Western Australian Mineral Deposits; Dentith, M.C., Frankcombe, K.F., Ho, S.E., Shepherd, J.M., Groves, D.I., Trench, A., Eds.; Publication 26, and Australian Society of Exploration Geophysicists, Special Publication; The University of Western Australia: Crawley, Australia, 1994; Volume 7, pp. 29–84. [Google Scholar]
- Bucher, B.; Rybach, L.; Schwarz, G. Search for long-term radiation trends in the environs of Swiss nuclear power plants. J. Environ. Radioact. 2008, 99, 1311–1318. [Google Scholar] [CrossRef]
- Paridaens, J. Development of a low cost, GPS-based upgrade to a standard handheld gamma detector for mapping environmental radioactive contamination. Appl. Radiat. Isot. 2006, 64, 264–271. [Google Scholar] [CrossRef]
- Rybach, L.; Bucher, B.; Schwarz, G. Airborne surveys of Swiss nuclear facility sites. J. Environ. Radioact. 2001, 53, 291–300. [Google Scholar] [CrossRef]
- Sanderson, D.C.W.; Cresswell, A.J.; Hardeman, F.; Debauche, A. An airborne gamma-ray spectrometry survey of nuclear sites in Belgium. J. Environ. Radioact. 2004, 72, 213–224. [Google Scholar] [CrossRef]
- Elkhateeb, S.O.; Abdellatif, M.A.G. Delineation potential gold mineralization zones in a part of Central Eastern Desert, Egypt using Airborne Magnetic and Radiometric data. NRIAG J. Astron. Geophys. 2018, 7, 361–376. [Google Scholar] [CrossRef]
- Metelka, V.; Baratoux, L.; Naba, S.; Jessell, M.W. A geophysically constrained litho-structural analysis of the Eburnean greenstone belts and associated granitoid domains, Burkina Faso, West Africa. Precambrian Res. 2011, 190, 48–69. [Google Scholar] [CrossRef]
- Morris, P.A.; Pirajno, F.; Shevchenko, S. Proterozoic mineralization identified by integrated regional regolith geochemistry, geophysics and bedrock mapping in Western Australia. Geochem. Explor. Environ. Anal. 2003, 3, 13–28. [Google Scholar] [CrossRef]
- Scott, K.M.; Pain, C. Regolith Science; Springer: Dordrecht, The Netherlands, 2008; ISBN 978-1-4020-8859-9. [Google Scholar]
- Metelka, V.; Baratoux, L.; Jessell, M.W.; Barth, A.; Ježek, J.; Naba, S. Automated regolith landform mapping using airborne geophysics and remote sensing data, Burkina Faso, West Africa. Remote Sens. Environ. 2018, 204, 964–978. [Google Scholar] [CrossRef]
- Dickson, B.; Scott, K. Interpretation of aerial gamma-ray surveys—Adding the geochemical factors. AGSO J. Aust. Geol. Geophys. 1997, 17, 187–199. [Google Scholar]
- Ahrens, L.H. The lognormal distribution of the elements (A fundamental law of geochemistry and its subsidiary). Geochim. Cosmochim. Acta 1954, 5, 49–73. [Google Scholar] [CrossRef]
- Wijs, H.J. Statistics of ore distribution: (2) Theory of binomial distribution applied to sampling and engineering problems. Geol. Mijnb. 1953, 15, 12–24. [Google Scholar]
- Allegre, C.J.; Lewin, E. Scaling laws and geochemical distributions. Earth Planet. Sci. Lett. 1995, 132, 1–13. [Google Scholar] [CrossRef]
- Turcotte, D.L. A fractal approach to the relationship between ore grade and tonnage. Econ. Geol. 1986, 81, 1528–1532. [Google Scholar] [CrossRef]
- Fall, M.; Baratoux, D.; Ndiaye, P.M.; Jessell, M.; Baratoux, L. Multi-scale distribution of Potassium. Thorium and Uranium in Paleoproterozoic granites from eastern Senegal. J. Afr. Earth Sci. 2018, 148, 30–51. [Google Scholar] [CrossRef]
- Fall, M.; Baratoux, D.; Jessell, M.; Ndiaye, P.M.; Vanderhaeghe, O.; Moyen, J.F.; Baratoux, L.; Bonzi, W.M.-E. The redistribution of thorium, uranium, potassium by magmatic and hydrothermal processes versus surface processes in the Saraya Batholith (Eastern Senegal): Insights from airborne radiometrics data and topographic roughness. J. Geochem. Explor. 2020, 219, 106633. [Google Scholar] [CrossRef]
- Moyen, J.-F.; Cuney, M.; Baratoux, D.; Sardini, P.; Carrouée, S. Multi-scale spatial distribution of K, Th and U in an Archaean potassic granite: A case study from the Heerenveen batholith, Barberton Granite-Greenstone Terrain, South Africa. S. Afr. J. Geol. 2021, 124, 53–86. [Google Scholar] [CrossRef]
- Baratoux, D.; Fall, M.; Meslin, P.-Y.; Jessell, M.W.; Vanderhaeghe, O.; Moyen, J.-F.; Ndiaye, P.M.; Boamah, K.; Baratoux, L.; André-Mayer, A.-S. The Impact of Measurement Scale on the Univariate Statistics of K, Th, and U in the Earth Crust. Earth Space Sci. 2021, 8, e2021EA001786. [Google Scholar] [CrossRef]
- Abouchami, W.; Boher, M.; Michard, A.; Albarede, F. A major 2.1 Ga event of mafic magmatism in west Africa: An Early stage of crustal accretion. J. Geophys. Res. 1990, 95, 17605. [Google Scholar] [CrossRef]
- Boher, M.; Abouchami, W.; Michard, A.; Albarede, F.; Arndt, N.T. Crustal growth in West Africa at 2.1 Ga. J. Geophys. Res. 1992, 97, 345. [Google Scholar] [CrossRef]
- Lemoine, S.; Tempier, P.; Bassot, J.P.; Caen-Vachette, M.; Vialette, Y.; Wenmenga, U.; Touré, S. The Burkinian, an orogenic cycle, precursor of the Eburnean of West Africa. Coll. Afr. Geol. 13th 1985, 27. [Google Scholar]
- Bassot, J.P.; Bonhomme, M.; Roques, M.; Vachette, M. Mesures d’âges absolus sur les séries précambriennes et paléozoïques du Sénégal oriental. Bull. Société Géologique Fr. 1963, S7-V, 401–405. [Google Scholar] [CrossRef]
- Bassot, J.P.; Caen-Vachette, M. Données géochronologiques et géochimiques nouvelles sur les granitoïdes de l’est Sénégal: Implications sur l’histoire géologique du birimien de cette région. In Géologie Africaine; Klerkx, J., Michot, J., Eds.; Musée Royal de l’Afrique Centrale: Tervuren, Belgium, 1983. [Google Scholar]
- Feybesse, J.L.; Milési, J.P.; Johan, Y.; Dommanget, A.; Calvez, J.-Y.; Boher, M.; Abauchami, W. La limite Archéen-Protérozoïque d’Afrique de l’Ouest: Une zone de chevauchement antérieure à l’accident de Sanssandra, l’exemple de la région de d’Odienne et de Touba (Cote d’Ivoire). C.R. Acad. Sci. Paris 1989, 309, 1847–1853. [Google Scholar]
- Liégeois, J.P.; Claessens, W.; Camara, D.; Klerkx, J. Short-lived Eburnian orogeny in southern Mali. Geology, tectonics, U-Pb and Rb-Sr geochronology. Precambrian Res. 1991, 50, 111–136. [Google Scholar] [CrossRef]
- Bassot, J.P. Le complexe volcano-plutonique calco-alcali de la rivière daléma (Est Sénégal): Discussion de sa signification géodynamique dans le cadre de l’orogénie eburnéenne (protérozoïque inférieur). J. Afr. Earth Sci. 1983 1987, 6, 505–519. [Google Scholar] [CrossRef]
- Milési, J.-P.; Ledru, P.; Feybesse, J.-L.; Dommanget, A.; Marcoux, E. Early proterozoic ore deposits and tectonics of the Birimian orogenic belt, West Africa. Precambrian Res. 1992, 58, 305–344. [Google Scholar] [CrossRef]
- Niang, I. Traitement de Données Topographiques srtm pour L’établissement d’une Carte de Rugosité sur l’Afrique de l’Ouest. Master’s Thesis, University Cheikh Anta Diop, Institut des Sciences de la Terre, Dakar, Senegal, 2018. [Google Scholar]
- Yamazaki, D.; Ikeshima, D.; Tawatari, R.; Yamaguchi, T.; O’Loughlin, F.; Neal, J.C.; Sampson, C.C.; Kanae, S.; Bates, P.D. A high-accuracy map of global terrain elevations: Accurate Global Terrain Elevation map. Geophys. Res. Lett. 2017, 44, 5844–5853. [Google Scholar] [CrossRef]
- Shepard, M.K.; Campbell, B.A.; Bulmer, M.H.; Farr, T.G.; Gaddis, L.R.; Plaut, J.J. The roughness of natural terrain: A planetary and remote sensing perspective. J. Geophys. Res. Planets 2001, 106, 32777–32795. [Google Scholar] [CrossRef]
- Smith, M.W. Roughness in the Earth Sciences. Earth-Sci. Rev. 2014, 136, 202–225. [Google Scholar] [CrossRef]
- Cord, A.; Baratoux, D.; Mangold, N.; Martin, P.; Pinet, P.; Greeley, R.; Costard, F.; Masson, P.; Foing, B.; Neukum, G. Surface roughness and geological mapping at subhectometer scale from the High Resolution Stereo Camera onboard Mars Express. Icarus 2007, 191, 38–51. [Google Scholar] [CrossRef]
- Kreslavsky, M.A.; Head, J.W. Kilometer-scale roughness of Mars: Results from MOLA data analysis. J. Geophys. Res. Planets 2000, 105, 26695–26711. [Google Scholar] [CrossRef]
- Kreslavsky, M.A.; Head, J.W.; Neumann, G.A.; Rosenburg, M.A.; Aharonson, O.; Smith, D.E.; Zuber, M.T. Lunar topographic roughness maps from Lunar Orbiter Laser Altimeter (LOLA) data: Scale dependence and correlation with geologic features and units. Icarus 2013, 226, 52–66. [Google Scholar] [CrossRef]
- Lemelin, M.; Daly, M.G.; Deliège, A. Analysis of the Topographic Roughness of the Moon Using the Wavelet Leaders Method and the Lunar Digital Elevation Model From the Lunar Orbiter Laser Altimeter and SELENE Terrain Camera. J. Geophys. Res. Planets 2020, 125, e2019JE006105. [Google Scholar] [CrossRef]
- Pommerol, A.; Chakraborty, S.; Thomas, N. Comparative study of the surface roughness of the Moon, Mars and Mercury. Planet. Space Sci. 2012, 73, 287–293. [Google Scholar] [CrossRef]
- Rosenburg, M.A.; Aharonson, O.; Head, J.W.; Kreslavsky, M.A.; Mazarico, E.; Neumann, G.A.; Smith, D.E.; Torrence, M.H.; Zuber, M.T. Global surface slopes and roughness of the Moon from the Lunar Orbiter Laser Altimeter. J. Geophys. Res. 2011, 116, E02001. [Google Scholar] [CrossRef]
- Aharonson, O.; Zuber, M.T.; Rothman, D.H. Statistics of Mars’ topography from the Mars Orbiter Laser Altimeter: Slopes, correlations, and physical Models. J. Geophys. Res. Planets 2001, 106, 23723–23735. [Google Scholar] [CrossRef]
- Van der Maaten, L.; Hinton, G. Viualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- McInnes, L.; Healy, J.; Melville, J. UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction. arXiv 2018, arXiv:1802.03426. [Google Scholar]


| Lithology | Statistical Signature | Roughness | Physical Meaning | |
|---|---|---|---|---|
| Cluster 0 | Metamorphic and detrital rocks | 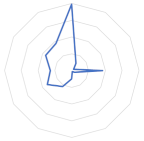 | 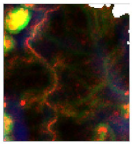 | K-rich detrital formation deposit zone |
| Cluster 1 | Detrital, metamorphic and basic rocks | 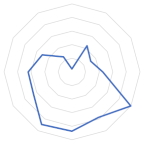 | 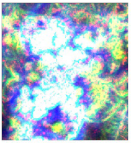 | Active erosion area over various lithologies |
| Cluster 2 | Southern part of the Saraya granite |  |  | Sedimentation zone, lateritic surface on top of granitoid rocks |
| Cluster 3 | Detrital and metamorphic rocks |  |  | Sedimentation area, lateritic surface on top of metamorphic rocks |
| Cluster 4 | Intermediate to mafic rocks, volcano-sedimentary |  | 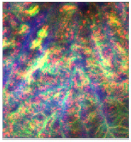 | Follows drainage networks |
| Cluster 5 | Biotite granite, metasediments | 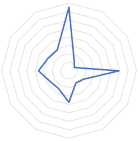 |  | Active erosion area over granite and metasediments |
| Cluster 6 | Northern part of the Saraya granite |  |  | Active erosion area over granitoids rocks |
| Cluster 7 | Detrital rocks and carbonates |  |  | Sedimentation area, lateritic surface over clasts and carbonates |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thiam, A.; Baratoux, D.; Fall, M.; Faye, G.; Ouattara, G. Multi-Parameter Statistical Analysis of K, Th, and U Concentrations in Eastern Senegal: Implications for the Interpretation of Airborne Radiometrics. Geosciences 2023, 13, 263. https://doi.org/10.3390/geosciences13090263
Thiam A, Baratoux D, Fall M, Faye G, Ouattara G. Multi-Parameter Statistical Analysis of K, Th, and U Concentrations in Eastern Senegal: Implications for the Interpretation of Airborne Radiometrics. Geosciences. 2023; 13(9):263. https://doi.org/10.3390/geosciences13090263
Chicago/Turabian StyleThiam, Aïssata, David Baratoux, Makhoudia Fall, Gayane Faye, and Gbele Ouattara. 2023. "Multi-Parameter Statistical Analysis of K, Th, and U Concentrations in Eastern Senegal: Implications for the Interpretation of Airborne Radiometrics" Geosciences 13, no. 9: 263. https://doi.org/10.3390/geosciences13090263
APA StyleThiam, A., Baratoux, D., Fall, M., Faye, G., & Ouattara, G. (2023). Multi-Parameter Statistical Analysis of K, Th, and U Concentrations in Eastern Senegal: Implications for the Interpretation of Airborne Radiometrics. Geosciences, 13(9), 263. https://doi.org/10.3390/geosciences13090263







