Spectral Investigation of the Relationship between Seismicity and Water Level in the Enguri High Dam Area (Georgia)
Abstract
:1. Introduction
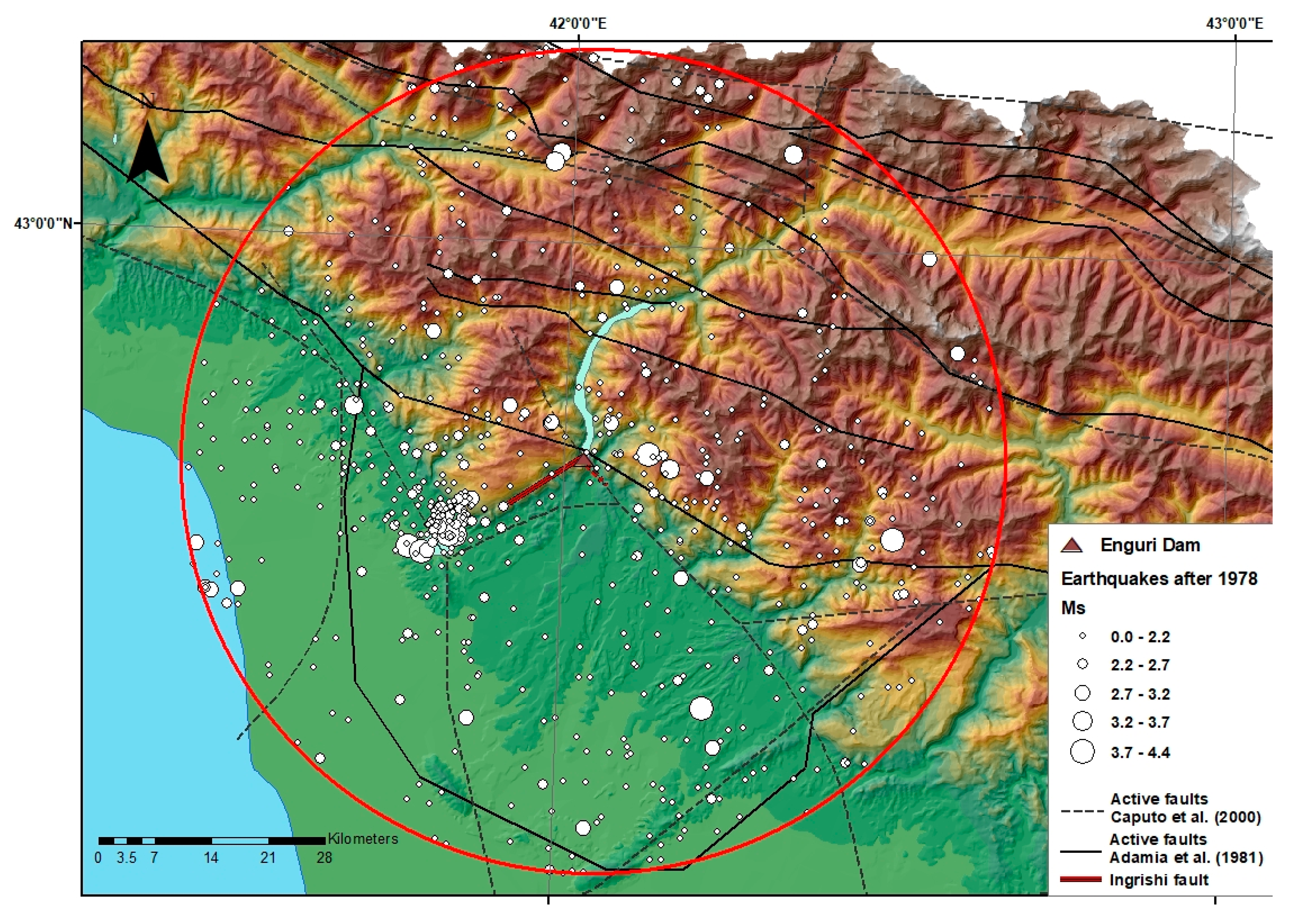
2. Seismo-Tectonic Settings
3. Seismicity Data
4. Methods
4.1. The Periodogram Analysis
4.2. Schuster’s Spectrum
4.3. Empirical Mode Decomposition
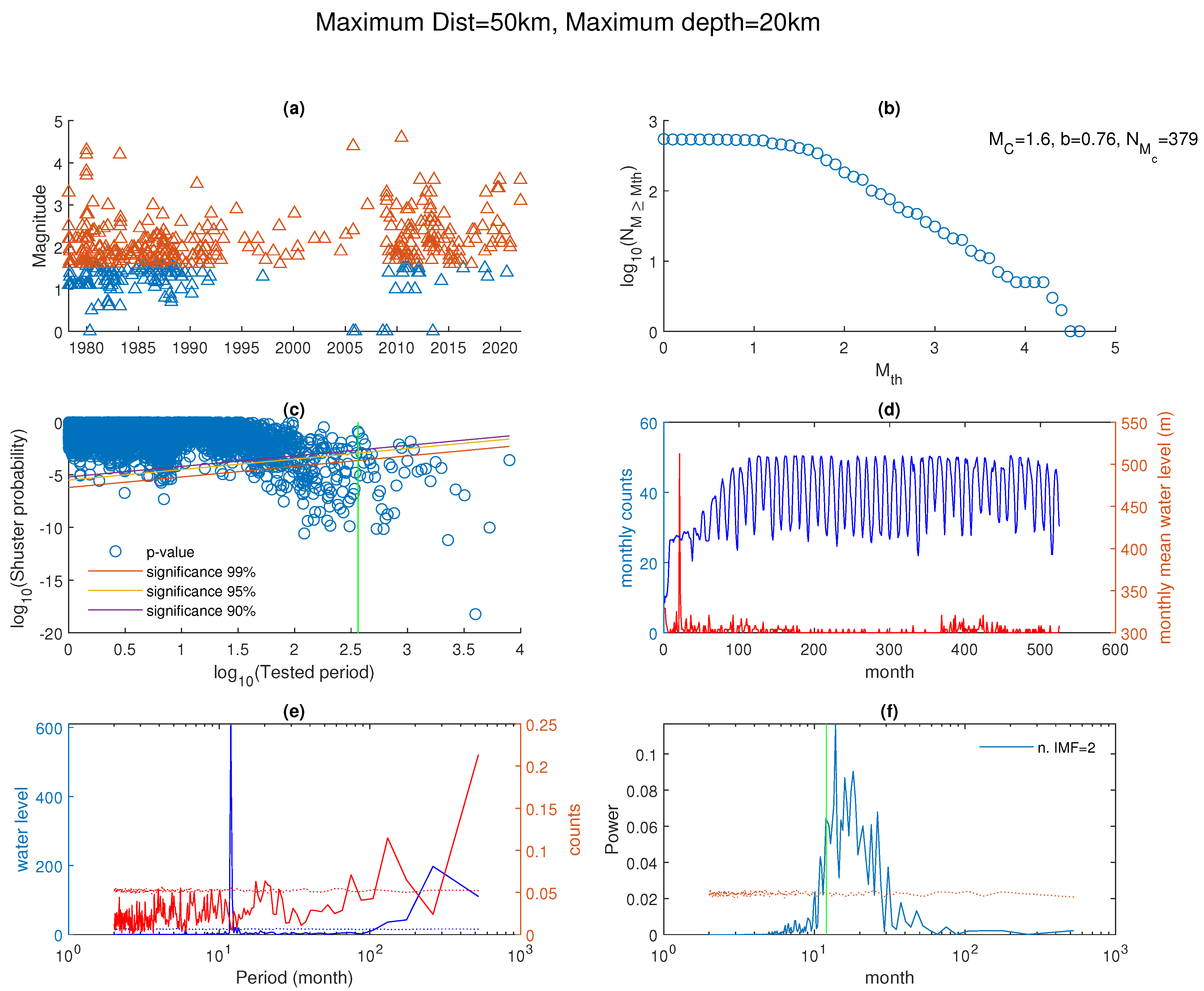
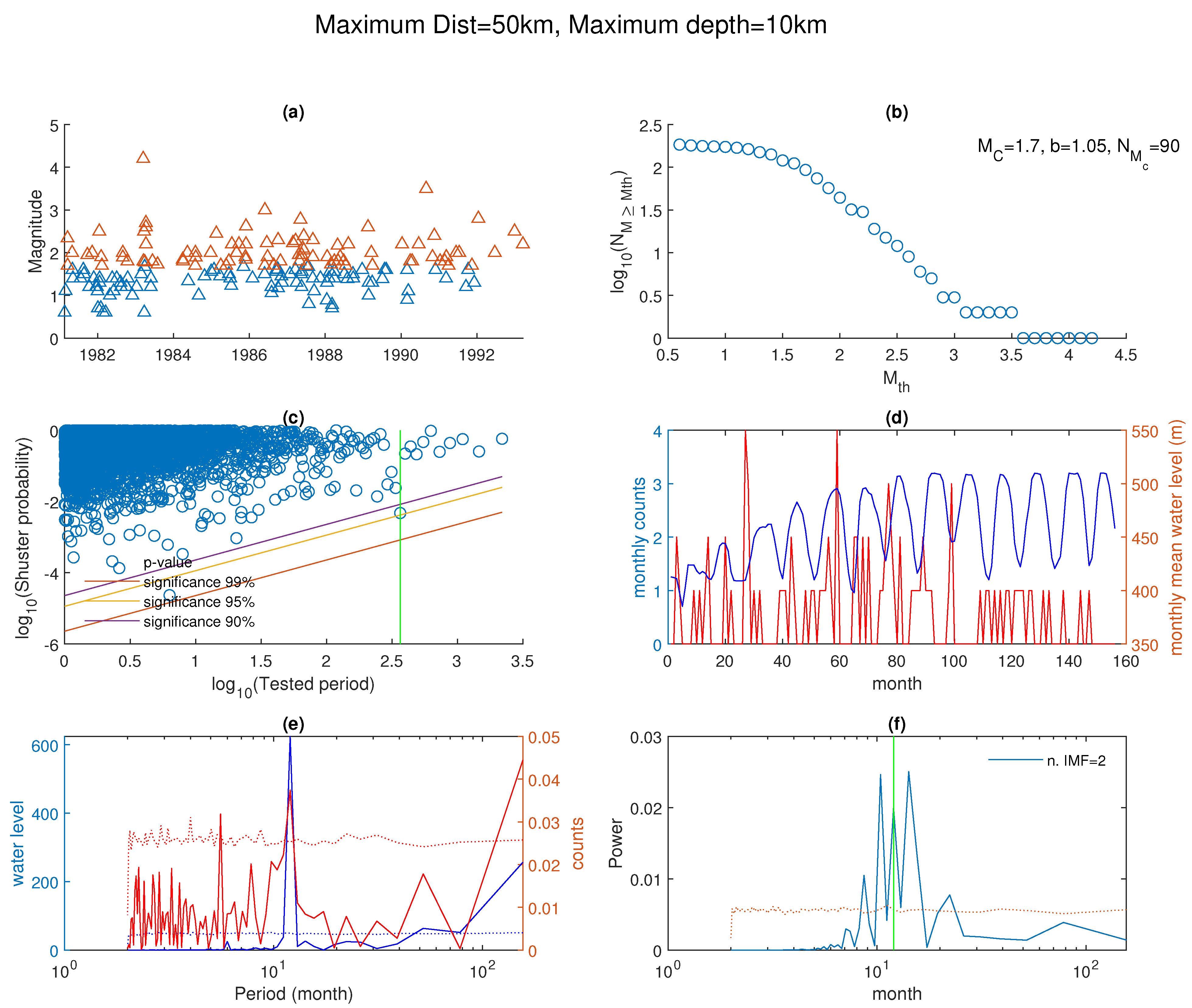
5. Results
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gupta, H.K. A review of recent studies of triggered earthquakes by artificial water reservoirs with special emphasis on earthquakes in Koyna, India. Earth Sci. Rev. 2002, 58, 279–310. [Google Scholar] [CrossRef]
- Bhaskara Rao, V.; Satyanarayana Murty, B.; Satyanarayana Murty, A. Some geological and geophysical aspects of the Koyna (India) earthquake, December 1967. Tectonophysics 1969, 7, 265–271. [Google Scholar]
- Gupta, H.K.; Rastogi, B.K.; Narain, H. The Koyna earthquake of December 10, 1967: A multiple seismic event. Bull. Seismol. Soc. Am. 1971, 61, 167–176. [Google Scholar] [CrossRef]
- Agrawal, P.N. December 11, 1967 Koyna earthquake and reservoir filling. Bull. Seismol. Soc. Am. 1972, 62, 661–662. [Google Scholar] [CrossRef]
- Talwani, P. Seismotectonics of the Koyna-Warna area, India. Pure Appl. Geophys. 1997, 150, 511–550. [Google Scholar] [CrossRef]
- Telesca, L. Analysis of the cross-correlation between seismicity and water level in Koyna area (India). Bull. Seismol. Soc. Am. 2010, 100, 2317–2321. [Google Scholar] [CrossRef]
- Simpson, D.W.; Negmatullaev, S.K. Induced seismicity at Nurek Reservoir, Tadjikistan, USSR. Bull. Seismol. Soc. Am. 1981, 71, 1561–1586. [Google Scholar]
- Leblanc, G.; Anglin, F. Induced seismicity at the Manic 3 reservoir, Quebec. Bull. Seismol. Soc. Am. 1978, 68, 1469–1485. [Google Scholar] [CrossRef]
- Gahalaut, K.; Gahalaut, V.; Pandey, M. A new case of reservoir-triggered seismicity: Govind Ballav Pant reservoir (Rihand dam), central India. Tectonophysics 2007, 439, 171–178. [Google Scholar] [CrossRef]
- Gough, D.; Gough, W. Load-induced earthquakes at Lake Kariba, 2. Geophys. J. 1970, 79, 101. [Google Scholar] [CrossRef]
- Gupta, H.; Rastogi, B. Dams and Earthquakes; Elsevier: Amsterdam, The Netherlands, 1976; p. 229. [Google Scholar]
- Gupta, H. Preface. In Reservoir-Induced Earthquakes; Elsevier: New York, NY, USA, 1992; Volume 64. [Google Scholar]
- Liu, S.; Xu, L.; Talwani, P. Reservoir-induced seismicity in the Danjiangkou Reservoir: A quantitative analysis. Geophys. J. Int. 2011, 185, 514–528. [Google Scholar] [CrossRef]
- Rajendran, K.; Harish, C.; Kumaraswamy, S. Re-Evaluation of Earthquake Data from Koyna—Warna Region: Phase I; Technical Report; Department of Science and Technology: Trivandrum, India, 1996. [Google Scholar]
- Rajendran, K.; Harish, C. Mechanism of triggered seismicity at Koyna: An assessment based on relocated earthquakes during 1983–1993. Curr. Sci. 2000, 79, 358–363. [Google Scholar]
- Nascimento, A.; Cowie, P.; Lunn, R.; Pearce, R. Spatio-temporal evolution of induced seismicity at Acu reservoir, NE Brazil. Geophys. J. Int. 2004, 158, 1041–1052. [Google Scholar] [CrossRef]
- Gupta, H.; Shashidhar, D.; Pereira, M.; Purnachandra Rao, N.; Kousalya, M.; Satyanarayana, H.; Saha, S.; Babu Naik, R.; Dimri, V. A new zone of seismic activity at Koyna, India. J. Geol. Soc. India 2007, 69, 1136–1137. [Google Scholar]
- Gupta, H.; Rao, N.; Roy, S.; Arora, K.; Tiwari, V.; Patro, P.; Satyanarayana, H.; Shashidhar, D.; Mallika, K.; Akkiraju, V. Investigations related to scientific deep drilling to study reservoir-triggered earthquakes at Koyna, India. Int. J. Earth Sci. 2015, 10, 1511–1522. [Google Scholar] [CrossRef]
- Mikhailov, V.; Arora, K.; Ponomarev, A.; Srinagesh, D.; Smirnov, V.; Chadha, R. Reservoir-induced seismicity in the Koyna–Warna region, India: Overview of the recent results and hypotheses. Izv. Phys. Solid Earth 2017, 53, 518–529. [Google Scholar] [CrossRef]
- Valoroso, L.; Improta, L.; Chiaraluce, L.; Di Stefano, R.; Ferranti, L.; Govoni, A.; Chiarabba, C. Active faults and induced seismicity in the Val d’Agri area (Southern Apennines, Italy). Geophys. J. Int. 2009, 178, 488–502. [Google Scholar] [CrossRef]
- Telesca, L.; Kadirov, F.; Yetirmishli, G.; Safarov, R.; Babayev, G.; Islamova, S.; Kazimova, S. Analysis of the relationship between water level temporal changes and seismicity in the Mingechevir reservoir (Azerbaijan). J. Seismol. 2020, 24, 937–952. [Google Scholar] [CrossRef]
- Telesca, L.; Thai, A.T.; Cao, D.T.; Ha, T.G. Spectral evidence for reservoir triggered seismicity at Song Tranh 2 Reservoir (Vietnam). Pure Appl. Geophys. 2021, 178, 3817–3828. [Google Scholar] [CrossRef]
- Gupta, H.; Rastogi, B.; Narain, H. Common features of the reservoir-associated seismic activities. Bull. Seismol. Soc. Am. 1972, 62, 481–492. [Google Scholar] [CrossRef]
- Adamia, S.A.; Chkhotua, T.; Kekelia, M.; Lordkipanidze, M.; Shavishvili, I.; Zakariadze, G. Tectonics of the Caucasus and adjoining regions: Implications for the evolution of the Tethys ocean. J. Struct. Geol. 1981, 3, 437–447. [Google Scholar] [CrossRef]
- Adamia, S.; Alania, V.; Chabukiani, A.; Chichua, G.; Enukidze, O.; Sadradze, N. Evolution of the late Cenozoic basins of Georgia (SW Caucasus): A review. Geol. Soc. Lond. Spec. Publ. 2010, 340, 239–259. [Google Scholar] [CrossRef]
- Jackson, J.; Ambraseys, N.; Giardini, D.; Balassanian, S. Convergence between Eurasia and Arabia in eastern Turkey and the Caucasus. Hist. Prehist. Earthquakes Cauc. 1997, 28, 79–90. [Google Scholar]
- Banks, C.J.; Robinson, A.G.; Williams, M.P. Structure and Regional Tectonics of the Achara-Trialet Fold Belt and the Adjacent Rioni and Kartli Foreland Basins, Republic of Georgia; American Association of Petroleum Geologists: Tulsa, OK, USA, 1997; pp. 331–346. [Google Scholar]
- Smith, A.G. Alpine deformation and the oceanic areas of the Tethys, Mediterranean, and Atlantic. Geol. Soc. Am. Bull. 1971, 82, 2039–2070. [Google Scholar] [CrossRef]
- Dewey, J.F.; Pitaman, W.C.; Ryan, W.B.; Bonnin, J. Plate tectonics and the evolution of the Alpine system. Geol. Soc. Am. Bull. 1973, 84, 3137–3180. [Google Scholar] [CrossRef]
- Khain, V. Structure and main stages in the tectonomagmatic development of the Caucasus: An attempt at geodynamic interpretation. Am. J. Sci. 1975, 275, 131–156. [Google Scholar]
- Pearce, J.A.; Bender, J.; De Long, S.; Kidd, W.; Low, P.; Güner, Y.; Saroglu, F.; Yilmaz, Y.; Moorbath, S.; Mitchell, J. Genesis of collision volcanism in Eastern Anatolia, Turkey. J. Volcanol. Geotherm. Res. 1990, 44, 189–229. [Google Scholar] [CrossRef]
- Mosar, J.; Kangarli, T.; Bochud, M.; Glasmacher, U.A.; Rast, A.; Brunet, M.F.; Sosson, M. Cenozoic-recent tectonics and uplift in the greater Caucasus: A perspective from Azerbaijan. Geol. Soc. Spec. Publ. 2010, 340, 261–280. [Google Scholar] [CrossRef]
- Sosson, M.; Rolland, Y.; Müller, C.; Danelian, T.; Melkonyan, R.; Kekelia, S.; Adamia, S.; Babazadeh, V.; Kangarli, T.; Avagyan, A.; et al. Subductions, obduction and collision in the lesser Caucasus (Armenia, Azerbaijan, Georgia), new insights. Geol. Soc. Spec. Publ. 2010, 340, 329–352. [Google Scholar] [CrossRef]
- Martin, R.J.; Gulen, L.; Sun, Y.; Toksoz, M. The Crustal and Mantle Velocity Structure in Central Asia from 3D Travel Time Tomography; Technical Report; New England Research Inc. (Veterans Affairs): White River Junction, VT, USA, 2010. [Google Scholar]
- Mcclusky, S.; Balassanian, S.; Barka, A.; Demir, C.; Ergintav, S.; Georgiev, I.; Gurkan, O.; Hamburger, M.; Hurst, K.; Kahle, H.; et al. Global positioning system constraints on plate kinematics and dynamics in the eastern Mediterranean and Caucasus. J. Geophys. Res. Solid Earth 2000, 105, 5695–5719. [Google Scholar] [CrossRef]
- Allen, M.; Jackson, J.; Walker, R. Late Cenozoic reorganization of the Arabia-Eurasia collision and the comparison of short-term and long-term deformation rates. Tectonics 2004, 23, TC2008. [Google Scholar] [CrossRef]
- Reilinger, R.; McClusky, S.; Vernant, P.; Lawrence, S.; Ergintav, S.; Cakmak, R.; Ozener, H.; Kadirov, F.; Guliev, I.; Stepanyan, R.; et al. GPS constraints on continental deformation in the Africa-Arabia-Eurasia continental collision zone and implications for the dynamics of plate interactions. J. Geophys. Res. Solid Earth 2006, 11, B05411. [Google Scholar] [CrossRef]
- Tan, O.; Taymaz, T. Active tectonics of the Caucasus: Earthquake source mechanisms and rupture histories obtained from inversion of teleseismic body waveforms. Spec. Pap. Geol. Soc. Am. 2006, 409, 531. [Google Scholar]
- Kadirov, F.; Mammadov, S.; Reilinger, R.; McClusky, S. Some new data on modern tectonic deformation and active faulting in Azerbaijan (according to Global Positioning System measurements). Proc. Azerbaijan Natl. Acad. Sci. Proc. Sci. Earth 2008, 1, 82–88. [Google Scholar]
- Kadirov, F.; Gadirov, A.; Abdullayev, N. Gravity modelling of the regional profile across South Caspian basin and tectonic implications. In The Modern Problems of Geology and Geophysics of Eastern Caucasus and the South Caspian Depression; Nafta-Press: Bonn, Germany, 2012. [Google Scholar]
- Pasquarè, F.; Tormey, D.; Vezzoli, L.; Okrostsvaridze, A.; Tutberidze, B. Mitigating the consequences of extreme events on strategic facilities: Evaluation of volcanic and seismic risk affecting the Caspian oil and gas pipelines in the Republic of Georgia. J. Environ. Manag. 2011, 92, 1774–1782. [Google Scholar] [CrossRef]
- Tibaldi, A.; Alania, V.; Bonali, F.; Enukidze, O.; Tsereteli, N.; Kvavadze, N.; Varazanashvili, O. Active inversion tectonics, simple shear folding and back-thrusting at Rioni Basin, Georgia. J. Struct. Geol. 2017, 96, 35–53. [Google Scholar] [CrossRef]
- Tibaldi, A.; Russo, E.; Bonali, F.; Alania, V.; Chabukiani, A.; Enukidze, O.; Tsereteli, N. 3-d anatomy of an active fault-propagation fold: A multidisciplinary case study from Tsaishi, western Caucasus (Georgia). Tectonophysics 2017, 717, 253–269. [Google Scholar] [CrossRef]
- Tibaldi, A.; Bonali, F.; Russo, E.; Mariotto, F.P. Structural development and stress evolution of an arcuate fold-and-thrust system, southwestern greater Caucasus, republic of Georgia. J. Asian Earth Sci. 2018, 156, 226–245. [Google Scholar] [CrossRef]
- Tibaldi, A.; Tsereteli, N.; Varazanashvili, O.; Babayev, G.; Barth, A.; Mumladze, T.; Bonali, F.; Russo, E.; Kadirov, F.; Yetirmishli, G.; et al. Active stress field and fault kinematics of the greater Caucasus. J. Asian Earth Sci. 2020, 188, 104108. [Google Scholar] [CrossRef]
- DeMets, C.; Gordon, R.; Argus, D.; Stein, S. Current plate motions. Geophys. J. Int. 1990, 101, 425–478. [Google Scholar] [CrossRef]
- DeMets, C.; Gordon, R.; Argus, D.; Stein, S. Effect of recent revisions to the geomagnetic reversal time scale on estimates of current plate motions. Geophys. Res. Lett. 1994, 21, 2191–2194. [Google Scholar] [CrossRef]
- Triep, E.; Abers, G.; Lerner-Lam, A.; Mishatkin, V.; Zakharchenko, N.; Starovoit, O. Active thrust front of the greater Caucasus: The April 29, 1991, Racha earthquake sequence and its tectonic implications. J. Geophys. Res. Solid Earth 1995, 100, 4011–4033. [Google Scholar] [CrossRef]
- Sokhadze, G.; Floyd, M.; Godoladze, T.; King, R.; Cowgill, E.; Javakhishvili, Z.; Hahubia, G.; Reilinger, R. Active convergence between the lesser and greater Caucasus in Georgia: Constraints on the tectonic evolution of the lesser-greater Caucasus continental collision. Earth Planet. Sci. Lett. 2018, 481, 154–161. [Google Scholar] [CrossRef]
- Reilinger, R.; McClusky, S.; Oral, M.; King, R.; Toksoz, M.; Barka, A.; Kinik, I.; Lenk, O.; Sanli, I. Global positioning system measurements of present-day crustal movements in the Arabia-Africa-Eurasia plate collision zone. J. Geophys. Res. Solid Earth 1997, 102, 9983–9999. [Google Scholar] [CrossRef]
- Shevchenko, V.; Guseva, T.; Lukk, A.; Mishin, A.; Prilepin, M.; Reilinger, R.; Hamburger, M.; Shempelev, A.; Yunga, S. Recent geodynamics of the Caucasus mountains from GPS and seismological evidence. Izv. Phys. Solid Earth 1999, 35, 691–704. [Google Scholar]
- Guliev, I.; Kadirov, F.; Reilinger, R.; Gasanov, R.; Mamedov, A. Active tectonics in Azerbaijan based on geodetic, gravimetric, and seismic data. Dokl. Earth Sci. 2002, 383, 174–177. [Google Scholar]
- Aktuğ, B.; Meherremov, E.; Kurt, M.; Özdemir, S.; Esedov, N.; Lenk, O. GPS constraints on the deformation of Azerbaijan and surrounding regions. J. Geodyn. 2013, 67, 40–45. [Google Scholar] [CrossRef]
- Karamzadeh, N.; Tsereteli, N.; Gaucher, E.; Tugushi, N.; Shubladze, T.; Varazanashvili, O.; Rietbrock, A. Seismological study around the Enguri dam reservoir (Georgia) based on old catalogs and ongoing monitoring. J. Seismol. 2023, 27, 953–977. [Google Scholar] [CrossRef]
- Caputo, M.; Gamkrelidze, I.; Malvezzi, V.; Sgrigna, V.; Shengelaia, G.; Zilpimiani, D. Geostructural basis and geophysical investigations for the seismic hazard assessment and prediction in the Caucasus. Il Nuovo Cimento C 2000, 23, 191–216. [Google Scholar]
- Tsereteli, N.; Danciu, L.; Varazanashvili, O.; Sesetyan, K.; Qajaia, L.; Sharia, T.; Svanadze, D.; Khvedelidze, I. The 2020 national seismic hazard model for Georgia (Sakartvelo). In Building Knowledge for Geohazard Assess Management in the Caucasus and other Orogenic Regions; Springer: Dordrecht, The Netherlands, 2021; pp. 131–168. [Google Scholar]
- Kondorskaya, N.V.; Shebalin, N.V. New Catalog of Strong Earthquakes in the USSR from Ancient Times through 1977; World Data Center A for Solid Earth Geophysics; EDIS: Boulder, CO, USA, 1982; p. 608. [Google Scholar]
- Vanek, I.; Zatopek, A.; Karnik, V.; Kondorskaya, N.V.; Riznichenko, Y.V.; Savarensky, E.F.; Solovyev, S.L.; Shebalin, N.V. Standardization of Magnitude Scales. IZV. AN SSSR Ser. Geophys. 1962, 1, 153–158. [Google Scholar]
- Rautian, T.G.; Khalturin, V.I.; Fujita, K.; Mackey, K.G.; Kendall, A.D. Origins and Methodology of the Russian Energy K-Class System and Its Relationship to Magnitude Scales. Seismol. Res. Lett. 2007, 78, 579–590. [Google Scholar] [CrossRef]
- Tsereteli, N.; Tibaldi, A.; Alania, V.; Gventsadse, A.; Enukidze, O.; Varazanashvili, O.; Müller, B. Active tectonics of central-western Caucasus, Georgia. Tectonophysics 2016, 691, 328–344. [Google Scholar] [CrossRef]
- Onur, T.; Gok, R.; Godoladze, T.; Gunia, I.; Boichenko, G.; Buzaladze, A.; Tumanova, N.; Dzmanashvili, M.; Sukhishvili, L.; Javakishvili, Z.; et al. Probabilistic Seismic Hazard Assessment Using Legacy Data in Georgia. Seismol. Res. Lett. 2020, 91, 1500–1517. [Google Scholar] [CrossRef]
- Zare, M.; Amini, H.; Yazdi, P.; Sesetyan, K.; Demircioglu, M.B.; Kalafat, D.; Erdik, M.; Giardini, D.; Khan, M.A.; Tsereteli, N. Recent developments of the Middle East catalog. J. Seismol. 2014, 18, 749–772. [Google Scholar] [CrossRef]
- Rautian, T. Determination of earthquake energy at a distance to 3000 km. Eksp Seismika Trudy IFZ AN SSSR 1964, 32, 199. [Google Scholar]
- Varazanashvili, O.; Tsereteli, N.; Bonali, F.; Arabidze, V.; Russo, E.; Pasquaré Mariotto, F.; Gogoladze, Z.; Tibaldi, A.; Kvavadze, N.; Oppizzi, P. GeoInt: The first macroseismic intensity database for the Republic of Georgia. J. Seismol. 2018, 22, 625–667. [Google Scholar] [CrossRef]
- Gutenberg, R.; Richter, C.F. Frequency of earthquakes in California. Bull. Seismol. Soc. Am. 1944, 34, 185–188. [Google Scholar] [CrossRef]
- Scholz, C.H. The frequency-magnitude relation of microfracturing in rock and its relation to earthquakes. Bull. Seismol. Soc. Am. 1968, 58, 399–415. [Google Scholar] [CrossRef]
- Wyss, M. Towards a physical understanding of the earthquake frequency distribution. Geophys. J. R. Astron. Soc. 1973, 31, 341–359. [Google Scholar] [CrossRef]
- Aki, K. Maximum likelihood estimate of b in the formula log(N)=a-bM and its confidence limits. Bull. Earthq. Res. Inst. Univ. Tokyo 1965, 43, 237–239. [Google Scholar]
- Utsu, T. Representation and analysis of the earthquake size distribution: A historical review and some new approaches. Pageoph 1999, 155, 509–535. [Google Scholar] [CrossRef]
- Wiemer, S.; Wyss, M. Minimum magnitude of completeness in earthquake catalogs: Examples from Alaska, the Western United States, and Japan. Bull. Seismol. Soc. Am. 2000, 90, 859–869. [Google Scholar] [CrossRef]
- Tanaka, S.; Sato, H.; Matsumura, S.; Ohtake, M. Tidal triggering of earthquakes in the subducting Philippine Sea plate beneath the locked zone of the plate interface in the Tokai region, Japan. Tectonophysics 2006, 417, 69–80. [Google Scholar] [CrossRef]
- Ader, T.J.; Avouac, J.P. Detecting periodicities and declustering in earthquake catalogs using the Schuster spectrum, application to Himalayan seismicity. Earth Planet. Sci. Lett. 2013, 377–378, 97–105. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.L.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. Roy. Soc. Lond. A 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Colominas, M.A.; Schlotthauer, G.; Torres, M.E. Improved complete ensemble EMD: A suitable tool for biomedical signal processing. Biomed. Signal Process. Control. 2014, 14, 19–29. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Telesca, L.; Tsereteli, N.; Chelidze, T.; Lapenna, V. Spectral Investigation of the Relationship between Seismicity and Water Level in the Enguri High Dam Area (Georgia). Geosciences 2024, 14, 22. https://doi.org/10.3390/geosciences14010022
Telesca L, Tsereteli N, Chelidze T, Lapenna V. Spectral Investigation of the Relationship between Seismicity and Water Level in the Enguri High Dam Area (Georgia). Geosciences. 2024; 14(1):22. https://doi.org/10.3390/geosciences14010022
Chicago/Turabian StyleTelesca, Luciano, Nino Tsereteli, Tamaz Chelidze, and Vincenzo Lapenna. 2024. "Spectral Investigation of the Relationship between Seismicity and Water Level in the Enguri High Dam Area (Georgia)" Geosciences 14, no. 1: 22. https://doi.org/10.3390/geosciences14010022
APA StyleTelesca, L., Tsereteli, N., Chelidze, T., & Lapenna, V. (2024). Spectral Investigation of the Relationship between Seismicity and Water Level in the Enguri High Dam Area (Georgia). Geosciences, 14(1), 22. https://doi.org/10.3390/geosciences14010022








