Abstract
Today, we have satellite images of Mars with a resolution of up to 24 cm per pixel. The planet has a thin atmosphere compared to Earth’s, but its surface is revealing itself to be active and complex. The use of images is an increasingly precise means of investigation for the study of transient phenomena that occur on the surface of the planet. We have developed a dating code that could be useful in the study of such phenomena. Thanks to this dating code, it is possible to immediately understand what season is in progress in the observed area starting from the terrestrial reference date of the photos taken by the orbiters. Some intermediate parameters of this calculation, such as the Martian year and the day of the year, can be equally useful for similar investigations. Satellite study of transient phenomena observable on the surface of Mars can range from geology (wind erosion and sedimentation) to meteorology (wind and phase transitions) to indigenous or non-indigenous biology.
1. Introduction
The High-Resolution Imaging Science Experiment (HiRISE) camera on board the Mars Reconnaissance Orbiter (MRO) provides photographic images with a maximum resolution of 24.1 cm per pixel. The details visible at this resolution allow us to observe transient phenomena on the surface of the planet, such as wind erosion and transport, the activity of gullies [1,2,3], but also physico-chemical phenomena such as freezing and the color variations affecting some areas. As a matter of fact, it can be assumed that the erosion of the gullies is still ongoing today and that the most significant morphological changes are linked to the seasonal cycle [4,5]. The abundance of images that the MRO has provided since 2006 now allows for transient or seasonal change monitoring.
Some tools already exist to estimate the seasonality of Mars. One example is the online converter of “The Mars Climate Database Projects” (see “Data Availability Statement”). This calculates solar longitude (Ls) and a hypothetical “Martian month”. In our studies, we preferred to avoid the use of months that show some artifacts also on Earth and are not so easy to manage (e.g., leap years). On Mars, we believe it makes even less sense to adopt this complexity. In addition, Earth months, if used on Mars, would have to be almost doubled in the length of days. This makes the position of a date with respect to the elapsed season and to the time remaining until its conclusion unintuitive. On the other hand, we needed a seasonal reference with a much higher resolution than 1/12. As for the Ls angle, this would have the required resolution but does not offer the intuitive sense of seasonality that months have.
Most works use solar longitude (Ls), which is provided along with the data for each mission. However, this is an angle measured in the orbital plane. Over the same year, Ls takes the same value for opposite seasons in opposite hemispheres. Therefore, it is not possible to compare this parameter at different sites or to use it in a planetary-scale graph except by separating the two hemispheres. Another useful reference that each space agency provides for any mission is the on-board clock, which starts from a reference date (e.g., mission. start). It may take different names, but it is ultimately a “mission time” expressed in seconds. This offers optimal resolution but no immediate perception with respect to seasonal cycles. Different agencies offer different software tools to employ this resource in various ways. Nasa also offers a Navigation and Ancillary Information Facility (NAIF), which is certainly an effective tool but whose SPICE kernels are not always easy to use and implement in user-developed codes and applications.
The solar year (or tropical year) on Mars has a duration of 687 Earth days (1.88 Earth years). In addition, the duration of the average solar day on Mars (called a sol) exceeds that of the Earth’s solar day by 39 min and 35.244 s. All of this makes the conception of time passed on the planet non-intuitive. In addition, several transient phenomena seem to be associated with the seasonal cycles of the planet [4,6,7]. This gives rise to the need for a measure of Martian time able to provide an immediate and intuitive estimate of local time and seasonal cycles.
These things considered, the tilt of the Earth’s axis on the orbital plane is 23°27′ while the tilt of the Martian axis is 25°10′ and that planet has a seasonal cycle partly similar to that of the Earth but is more marked. The differences between Earth and Mars seasons are also enhanced by the smaller eccentricity of the Earth’s orbit (0.017) compared to that of Mars (0.093). As a result, on Earth the four alternating seasons on opposite hemispheres have almost the same duration, with the maximum difference being 5 days (summer vs. winter). Instead, Mars, having a more pronounced elliptical orbit, is characterized by a greater difference duration between the four seasons. Not only do the seasons last longer than the Earth’s, but they have a maximum difference of 51 Martian days between the lengths of spring and autumn (see Table 1). The consequence of all this is that it is not immediate to assess how many days or years have passed locally between one Martian photo and another. Even more difficult is extrapolating what season was in progress in the study area starting from the terrestrial date on which the Martian photo was taken.

Table 1.
Season duration in Martian days (dd). Data from [8].
To solve this problem, we propose a Martian dating system that immediately expresses the Martian year, the season and the percentage of the season elapsed at a given time instant. Our dating system is designed in such a way that the code can be mapped univocally and monotonically (but not linearly) on natural numbers and can therefore be used as a time scale for a graph. The idea for this code came from the needs of studying erosive phenomena related to the phase transition of water ongoing at our research institute. For this reason, we named it INGV Martian Dating (IMD). The calculation that leads to IMD passes through several intermediate values, namely the Martian year (MY) and the current day of the year on Mars (Md), which are useful too.
We therefore preferred to deal directly with astronomical seasons, calculating their elapsed percentage. IMD dating, differently from a “Julian-like approach”, intuitively and versatilely offers the opportunity to compare years and seasons accurately. At the same time, being a single numerical entity, it can be immediately adopted in quantitative tasks (e.g., plot scales, etc.).
2. Computing Details
Although there is no definitive standard, the years on Mars are often numbered as proposed by the Planetary Society, starting from the spring equinox (Ls = 0°) occurring in the Northern Hemisphere on Earth on 11 April 1955. This is the first year on Mars. This convention was adopted for the first time in [9]. We therefore define the Martian year as the tropical year, that is, the year that elapses between two homologous solstices or equinoxes.
We attach to this paper examples of applications of the same algorithm in three different computational environments, including Excel. Excel spreadsheets are dependent on the operating system and may be affected by the millennium bug. In particular, Excel cannot operate properly on dates prior to 1900. However, according to the Planetary Society standard, the current year on Mars is 0037. To simplify the calculations, but also to avoid problems related to the millennium bug, the terrestrial date in the Gregorian calendar is immediately converted to the Julian day. Subsequently, we will also define a “Martian Julian day” on which all Martian calculations will be based. In the exposition of the formulas, the square bracket “[]” is used to indicate the integer part of a decimal number. Example: for [x.y], it means “the integer part of x.y″ = x.
2.1. Julian Day (JD)
To compute the JD, we use a simplified formula that is valid only for a Gregorian date (GD) > 15 October 1582. Since the Martian calendar begins on GD 11 April 1955, this limitation will be perfectly compatible with the Martian date of interest. We therefore use the following expression to convert the GD in “YYYY/MM/DD” format to the JD: a decimal number in the format “######0.0”.
where
JD = [365.25 × (A + 4716)] + [30.6001 × (B + 1)] + DD + 2 − [A/100] + [A/400] − 1524.5
A = IF (MM > 2) THEN (A = YYYY) ELSE (A = YYYY − 1)
B = IF (MM > 2) THEN (B = MM) ELSE (B = MM + 12)
Example: input GD = 1968/08/12 → output: JD = 2,440,080.5
2.2. Martian Julian Day (MJD)
Of course, there is no such thing as a “Martian Julian day” in a strict sense. By the MJD, we mean the Martian solar days (sols) elapsed from the terrestrial Julian day corresponding to the first Martian New Year. For consistency, we call GD0 the date of 11 April 1955. In this calculation, we use two constants. The first is derived from the calculation made according to Equation (1) on the date GD0. The JD corresponding to GD0 is JD0 = 2,435,208.5. But in JD0, the decimal 0.5 corresponds to the terrestrial time 00 (the choice was made to facilitate astronomical applications: the date would no longer change at night but during the day). Since we usually observe photos taken near local noon and change day at 00, this choice is inconvenient for us and it also introduces a systematic error. Moreover, we note that at 00:00 on the first day of the first Martian year (the time of the Martian spring equinox), it was not necessarily 12:00 or 00:00 on Earth (indeed, it very likely was not). We empirically estimated that the maximum calculation accuracy is obtained with an alternative value JDC = 2,435,208.21, which corresponds to 17:02:24 UTC on 10 April 1955 on Earth. To convert the number of terrestrial days derived from the JD into Martian solar days (sols), we use the value CC = 1.02749125 suggested by [10].
where
MJD = (JD − JDC)/CC
JDC = 2,435,208.21
CC = 1.02749125
Example: input JD = 2,440,080.5 → output MJD = 4741.9
2.3. Martian Year (MY)
To convert the MJD into Martian years, we define a value “Martian Year” (MY) in the format “###Y.000” that expresses as ###Y the tropical years passed since the first Martian New Year (the Earth year 1955 or GD0) until the Gregorian date used for the JD to calculate the MJD. The decimal part of the MY is the elapsed fraction of the ###Y year. The precision to the third decimal place is necessary so that the resolution is at worst the Earth day, thus avoiding having the same MY value for two consecutive Gregorian dates. The approximation introduced with JDC ensures correct values only if the MY value is rounded up to the third decimal place, so the MY format must be “#.000”. For the duration of the Martian tropical year (Mty) expressed in Martian days, we have adopted the updated value from [10].
where
MY = 1 + (MJD/Mty)
- Mty = 668.5921
- Example: input MJD = 4741.9 → output MY = 8.092
2.4. INGV Martian Date (IMD)
We define the Martian time notation as a succession of numerical values expressing the following: (1) the Martian year as an integer value (YYYY); (2) the current season in the northern Martian hemisphere coded with digits from 1 to 4 starting from spring (S); and (3) the time percentage of the current season elapsed expressed with one decimal place (Sp) (one decimal place is sufficient in this case to resolve the difference between two consecutive Gregorian dates in the corresponding terrestrial dating). Then, we compose in a single figure the succession of the results of this using three separate calculations: YYYY; S; Sp.
YYYY = [MY.000]
In Equation (6), the integer part of the MY value must be taken after rounding it to the third decimal place. Example: for MY = 2.9995, [MY] = 3 is obtained.
From the decimal part of MY.000 (again MY rounded to the third decimal place), we obtain the number (Md) of Martian days (Sol) already passed in the current Martian year:
Md = [1 + (MY.000-[MY.000]) × Mty]
The identification of the current season (S) implies a coding according to Table 2. The value of the Md has to be compared to season durations expressed in Table 1 using a conditional expression:
S = IF (Md < 194) THEN (1) ELSEIF (Md < 194 + 178) THEN (2) ELSEIF (Md < 194 + 178 + 143) THEN (3) ELSE (4)

Table 2.
Season code in IMD notation.
The calculation of the elapsed percentage of the season (Sp) again requires the values of Table 1. The numeric value must be formatted as “00.0” even for the integer or <10 numbers.
Sp = { IF (S = 1) THEN (100 × Md/193) ELSEIF (S = 2) THEN (100 × (Md − 193)/178) ELSEIF (S = 3) THEN
(100 × (Md – 193 − 178)/143) ELSE (100 × (Md − 193 – 178 − 143)/154) } − 0.5
(100 × (Md – 193 − 178)/143) ELSE (100 × (Md − 193 – 178 − 143)/154) } − 0.5
The concatenation of the values (YYYY; S; Sp) in a single numeric value in the format “###0000.0” represent the IMD coding of Martian time (Figure 1).
Example: input MY = 8.092 → output Md = 62; IMD = 8131.6

Figure 1.
Screenshot of Excel graphic interface for IMD computation (algorithm in Supplementary Materials).
Table 3 shows all the numerical examples. Table 4 reports all the numerical constants. The conversion constant (CC) from the Earth solar day to the Martian solar day and the duration of the Martian tropical year (Mty) are critical values that can affect the robustness and accuracy of the results. We have adopted the estimates published by [10] that correct previously estimated values. More and more precise values of these constants could in the future further increase the accuracy of our calculations. Even a more precise value of the decimals of JDC could improve the calculations, if necessary.

Table 3.
Numeric example.

Table 4.
Summary of numerical constants used in IMD computations.
All the formulas presented here have been tested on the web-published calendar by “The Planetary Society”, where the dates of the equinoxes and solstices are reported for 40 Martian years. On this matrix of 160 dates, a possibility of a small error was found only for the value of the seasonal percentage (Sp). This error is cyclical and has a maximum relative amplitude of 0.008. It is a type of error that cannot affect the functionality of the presented algorithms and does not at all compromise the effectiveness of the discrimination of seasonality in the investigated events since the IMD does not intend to enter the realm of the hours of the day. The decimal digit of the IMD actually is needed only to prevent two consecutive Earth dates corresponding to the same IMD code.
3. Products and Application Examples
Attached to this paper, we also provide three scripts, developed in Excel, Python and MatLab environments, to directly compute the IMD and all the parameters involved starting from the Gregorian Earth date (GD) as the only input (Figure 1).
IMD dating can be useful in monitoring the changing surface of Mars, especially when phenomena are linked to seasonal cycles. Some examples may be the appearance of new gullies [2] or the mutations in their path, in some cases attributed to the periodic melting of the permafrost [7] and in other cases to the sliding of ice in spring [11]. Important processes also affect the circumpolar and polar regions: seasonal frosting/defrosting and clear albedo changes [12] and dark albedo changes on polar dunes [13].
Next, we present an example of an application on the transient phenomena observable on the sand dunes that are located inside the Russel Crater (southern hemisphere). The reference date of the HiRISE satellite photos is the input of the calculation. Figure 2 shows some apparently seasonal phenomena that can be observed on these dunes [7,14]. Sometimes, a white blanket (presumably frost) is observed on the surface, or the traces left by the passage of Dust Devils are engraved. Such changing surface ice formations and later sublimation might be connected to ephemeral nighttime liquid water emergence on a microscopic surfeces [15]. Thanks to the IMD, we are immediately able to understand that these three photos were taken in different Martian years and, more importantly, in different seasons. The frost appeared in winter and the dust devils passed in summer. The time elapsed between the first two photos is half a solar year: the entire spring and summer seasons. Between the last two photos, almost three solar years (bar a full summer) passed.

Figure 2.
Three images of the same dune taken in different years. Zooming highlights the following from the left: the frost-covered surface, the “clean” surface and the typical dark, sinuous tracks left by the passage of dust devils. IMD dating code immediately highlights how many Martian years occurred between the images (respectively less than one and about two) and the current seasons. Images: HiRISE, south hemisphere, north up.
Figure 3 shows some transient phenomena observable in HiRISE photos in the Martian year 31 (2012–2013). By comparing MY and IMD time scales, the seasonal distribution of the phenomena is clearly highlighted. The top graph projects the phenomena on a temporal scale calculated as MY, i.e., the elapsed percentage Martian year 31 is evidenced. The cadence of the seasons was marked with overlaid blue lines since it is not intuitive. It is clear that dividing the solar year (tropic) into four equal parts would result in roughly approximate seasonal cycles due to the significant difference in the duration of Martian seasons compared to what we are used to on Earth. The IMD dating is a progressive number that can be expressed on this graph. The lower diagram projects the same phenomena in a non-linear time scale, grouping them proportionally to the duration of the seasons. On the IMD scale, the seasons are immediately recognizable and coded according to Table 2. In both cases, the seasonal cycle begins with autumn since the Russel Crater is located in the southern hemisphere. The gray squares highlight the actual photographic coverage throughout the year.
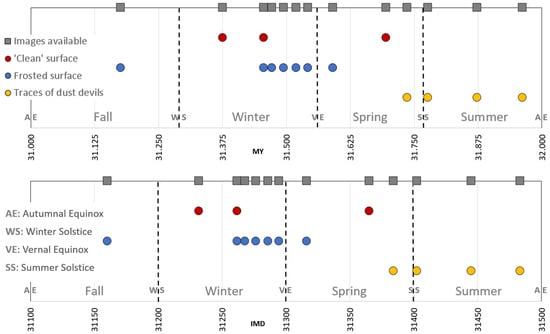
Figure 3.
MYIMD. Transient phenomena observed on the surface of the Russel Crater sand dunes during Martian year 31. Top: time scale in MY with the cadence of the seasons marked by the blue lines. Bottom: IMD time scale. The cadence of the seasons is immediately recognizable because it is equally spaced by a value of 100. (Russel Crater, south hemisphere, observations on HiRISE photos).
For the study of the seasonality of these phenomena, the Martian day (Md), derived from Equation (7) and also called “sol”, is far from an intermediate parameter useful only for the calculation of the IMD. In Figure 4, the observations of the same phenomena over a period of 16 Earth years (2006–2022) are reported on a single graph, or in the Martian years 28.4 to 36.6. The temporal scale is in the Md and the seasonal cadence is marked by the blue lines. The photographic coverage of the temporal scale is now wider and the transient phenomena confirm their presumed seasonal dependence. Dust devils are distributed from mid-spring to almost all summer. Frost can appear in autumn episodes but is mostly observed between winter and spring with a particular concentration around the spring equinox.

Figure 4.
Annual recurrence on Md scale. Phenomena observed over a period of approximately 7 Martian years are here projected on the same time scale representing the day of the Martian year. The photographic coverage is wider throughout the year and the seasonal distribution of the phenomena seems to be confirmed. (Russel Crater, south hemisphere, observations on HiRISE images).
We also present, in Table 5 an easier example of the application of IMD on the landing/deployment dates of all landers/rovers that have operated on the surface of Mars to date. The landing latitude was also given because the seasonality is relative to the hemisphere. Through the simple coding in Table 2, IMD dating highlights the season as a function of the north or south latitude of the landing site. We can see that the first five missions (1976 to 2004) always started in the Martian summer period. After that, the missions began to diversify seasons but only the rovers targeting near-equatorial areas started operations in winter.

Table 5.
Comparison of mission starting dates of all exploration vehicles that have operated on the surface of Mars to date.
4. Conclusions
The IMD is a dating code designed to provide direct information on the seasonality of Martian phenomena. Starting from the Earth reference date of the photos of the Martian orbiters, the IMD code indicates the following: the Martian year (with thousands), the season code (with hundreds, see Table 2) and the percentage of season elapsed in the area observed at the time of the shot (with tens). With respect to existing calendars (e.g., that of “The Mars Climate Database Projects”), IMD has the advantage of giving multiple types of relevant information in just one number that, being a monotonically increasing number, can also be immediately used as a time scale in numerical graphs. Beyond this, it gives prompt and precise information about the seasonal tracking of investigated events. Some intermediate parameters of the IMD calculation, such as the Martian solar year (MY) and the current year day (Md), are also useful in the study of Martian transients. The IMD has been successfully tested on all equinoxes and solstices of the first 40 years of the Martian calendar proposed by “The Planetary Society”. The periodicity found in the decimal approximation suggests that the IMD can be applied without problems even for the years after 40.
Incidentally, we report that testing IMD on all the equinoxes and solstices reported on “The Planetary Society” online calendar allowed us to likely find a typo in the column “Autumnal equinox” year 17 of that calendar: “Jun Jan 1986” should actually be 1 Jun 1986 according to IMD computations.
Supplementary Materials
To facilitate the application of IMD and promote its diffusion, we have developed a suitable algorithm in three versions (Excel, Python, and Matlab) which we make available to the scientific community through this link: http://hdl.handle.net/2122/16819 (Earth-prints Repository) (accessed on 18 April 2024).
Author Contributions
Conceptualization, A.N.; methodology, A.N.; software, A.N., P.B. and A.P.; validation, A.N., P.B. and A.P.; formal analysis, A.N. and A.P.; investigation, A.N.; resources, A.N.; data curation, A.N., P.B. and A.P.; writing—original draft preparation, A.N. and A.P.; writing—review and editing, A.N. and A.P.; visualization, A.N.; supervision, A.N. and A.P.; project administration, A.N.; funding acquisition, A.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available on request from the author. All photos used in this work are from the HiRISE Image Gallery by High-Resolution Imaging Science Experiment (Mars Reconnaissance mission) archive. Archive: https://www.uahirise.org (accessed on 18 April 2024). The dates of the equinoxes and solstices over the first 40 Martian years published on the web by The Planetary Society were used to test the algorithms: https://www.planetary.org/articles/mars-calendar (accessed on 18 April 2024). The web page “Earth Date to Martian Solar Longitude Conversion” by The Mars Climate Database Projects see [16] offers an alternative conversion tool. Here, you can estimate seasonality through solar longitude (Ls) or a hypothetical “Martian month”: https://www-mars.lmd.jussieu.fr/mars/time/martian_time.html (accessed on 18 April 2024). The NAIF resource provided by NASA is available through this link: https://naif.jpl.nasa.gov/naif/ (accessed on 18 April 2024).
Conflicts of Interest
The author declares no conflicts of interest.
References
- Dundas, C.M.; McEwen, A.S.; Diniega, S.; Hansen, C.J.; Byrne, S.; McElwaine, J.N. The formation of gullies on Mars today. Geol. Soc. Lond. Spéc. Publ. 2017, 467, 67–94. [Google Scholar] [CrossRef]
- Motazedian, T. Currently flowing water on Mars. In Proceedings of the 34th Annual Lunar and Planetary Science Conference, League City, TX, USA, 17–21 March 2003. [Google Scholar]
- Changela, H.G.; Chatzitheodoridis, E.; Antunes, A.; Beaty, D.; Bouw, K.; Bridges, J.C.; Capova, K.A.; Cockell, C.S.; Conley, C.A.; Dadachova, E.; et al. Mars: New insights and unresolved questions. Int. J. Astrobiol. 2021, 20, 394–426. [Google Scholar] [CrossRef]
- Nardi, A.; Piersanti, A. Geomorphologic observations and physical hypothesis on Martian gullies. Ital. J. Geosci. 2022, 141, 245–258. [Google Scholar] [CrossRef]
- Dundas, C.M.; Diniega, S.; Hansen, C.J.; Byrne, S.; McEwen, A.S. Seasonal activity and morphological changes in martian gullies. Icarus 2012, 220, 124–143. [Google Scholar] [CrossRef]
- Diniega, S.; Byrne, S.; Bridges, N.T.; Dundas, C.M.; McEwen, A.S. Seasonality of present-day Martian dune-gully activity. Geology 2010, 38, 1047–1050. [Google Scholar] [CrossRef]
- Kossacki, K.J.; Markiewicz, W.J. Seasonal melting of surface water ice condensing in martian gullies. Icarus 2004, 171, 272–283. [Google Scholar] [CrossRef]
- Appelbaum, J.; Flood, D.J. Solar radiation on Mars. Sol. Energy 1990, 45, 353–363. [Google Scholar] [CrossRef]
- Clancy, R.T.; Sandor, B.J.; Wolff, M.J.; Christensen, P.R.; Smith, M.D.; Pearl, J.C.; Conrath, B.J.; Wilson, R.J. An intercomparison of ground-based millimeter, MGS TES, and Viking atmospheric temperature measurements: Seasonal and interannual variability of temperatures and dust loading in the global Mars atmosphere. J. Geophys. Res. 2000, 105, 9553–9571. [Google Scholar] [CrossRef]
- Allison, M.; McEwen, M. A post-Pathfinder evaluation of areocentric solar coordinates with improved timing recipes for Mars seasonal/diurnal climate studies. Planet. Space Sci. 2000, 48, 215–235. [Google Scholar] [CrossRef]
- Diniega, S.; Hansen, C.; McElwaine, J.; Hugenholtz, C.; Dundas, C.; McEwen, A.; Bourke, M. A new dry hypothesis for the formation of martian linear gullies. Icarus 2013, 225, 526–537. [Google Scholar] [CrossRef]
- Cartwright, S.F.A.; Cartwright, S.F.A.; Calvin, W.M.; Calvin, W.M.; Seelos, F.P.; Seelos, F.P.; Seelos, K.D.; Seelos, K.D. Spatial and Temporal Variation of Mars South Polar Ice Composition From Spectral Endmember Classification of CRISM Mapping Data. J. Geophys. Res. Planets 2023, 128, 19. [Google Scholar] [CrossRef]
- Horváth, A.; Kereszturi, Á.; Bérczi, S.; Sik, A.; Pócs, T.; Gánti, T.; Szathmáry, E. Analysis of Dark Albedo Features on a Southern Polar Dune Field of Mars. Astrobiology 2009, 9, 90–103. [Google Scholar] [CrossRef] [PubMed]
- Reiss, D.; Erkeling, G.; Bauch, K.E.; Hiesinger, H. Evidence for present day gully activity on the Russell crater dune field, Mars. Geophys. Res. Lett. 2010, 37, 7. [Google Scholar] [CrossRef]
- Pál, B.; Kereszturi, Á.; Forget, F.; Smith, M.D. Global seasonal variations of the near-surface relative humidity levels on present-day Mars. Icarus 2019, 333, 481–495. [Google Scholar] [CrossRef]
- Read, P.; Collins, M.; Forget, F.; Fournier, R.; Hourdin, F.; Lewis, S.; Talagrand, O.; Taylor, F.; Thomas, N. A GCM climate database for Mars: For mission planning and for scientific studies. Adv. Space Res. 1997, 19, 1213–1222. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).