Possible Interrelations of Space Weather and Seismic Activity: An Implication for Earthquake Forecast
Abstract
:1. Introduction
2. Methods of Verification of Hypothesis of Electromagnetic Earthquake Triggering by Strong X-Class SFs
2.1. Testable Hypothesis of Earthquake Triggering by Strong SFs
2.2. Analysis of Geomagnetic Field Variations and Seismic Activity during Strong X-Class SFs
3. Results of Verification of Hypothesis of Earthquake Triggering by Strong Solar Flares
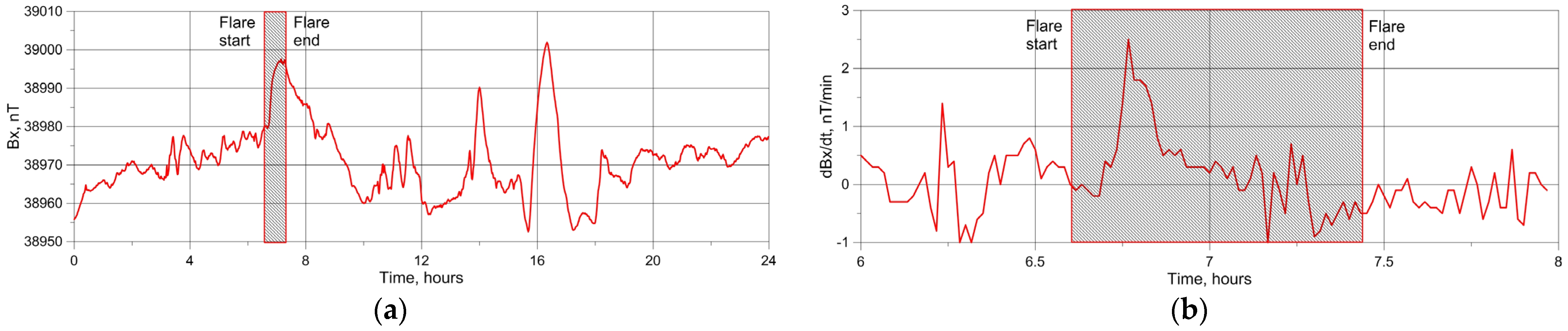
3.1. Response of Geomagnetic Field to Strong Solar Flare: The Case Study of Solar Flare X5.01 of 31 December 2023
3.2. Seismic Activity before and after Strong X-Class SFs
4. Discussion
- (1)
- Pulsations in the geomagnetic field predicted by the model [12] due to the interaction of X-ray radiation from SFs with the ionosphere were observed during the SF on the illuminated part of the globe. The maximal Bx and dBx/dt pulsations were observed in an area of 5000 km around the SSP at the time of SF occurrence. With an increasing area radius, Bx and dBx/dt pulsations decreased and practically disappeared at the border of the illuminated part. Such pulsations were not observed on the non-illuminated part of the globe. These results are consistent with those obtained earlier and presented in a review by Curto [28] and a study by Grodji et al. [29].
- (2)
- The observed sharp variations in the geomagnetic field were capable of generating GICs in the conductive elements of the lithosphere, including seismogenic faults. According to the model [12], these GICs are comparable to a splash of telluric currents generated by artificial pulsed power systems, which resulted in the EQ triggering and spatiotemporal redistribution of seismicity in the northern Tien Shan and Pamir [13]. Our analysis of seismicity after strong SFs supported the hypothesis of Sorokin et al. [12] of the EM triggering of EQs by SFs (Table 2). For the illuminated part, within 10 days after an X-class SF, the seismicity increased in comparison with 10 days before the SF by ~11 to ~33%, depending on the distance from the SSP. It significantly exceeded the Earth’s overall seismic response. This result positively estimates the hypothesis proposed in Sorokin et al. [12] on EQ triggering by the X-ray radiation of SFs and indicates the incorrectness of a purely statistical approach to the study of the interrelationship of solar and seismic activities without any physical model, explaining a possible relationship between the processes on the Sun and within the Earth. For further study, it is reasonable to consider the solar–terrestrial relations based on the physical model [12], or any models considering another physical mechanism of these relations, provided that a refined approach is used to select the data for statistical analysis. In other words, “Physics should be ahead of Statistics”.
- (3)
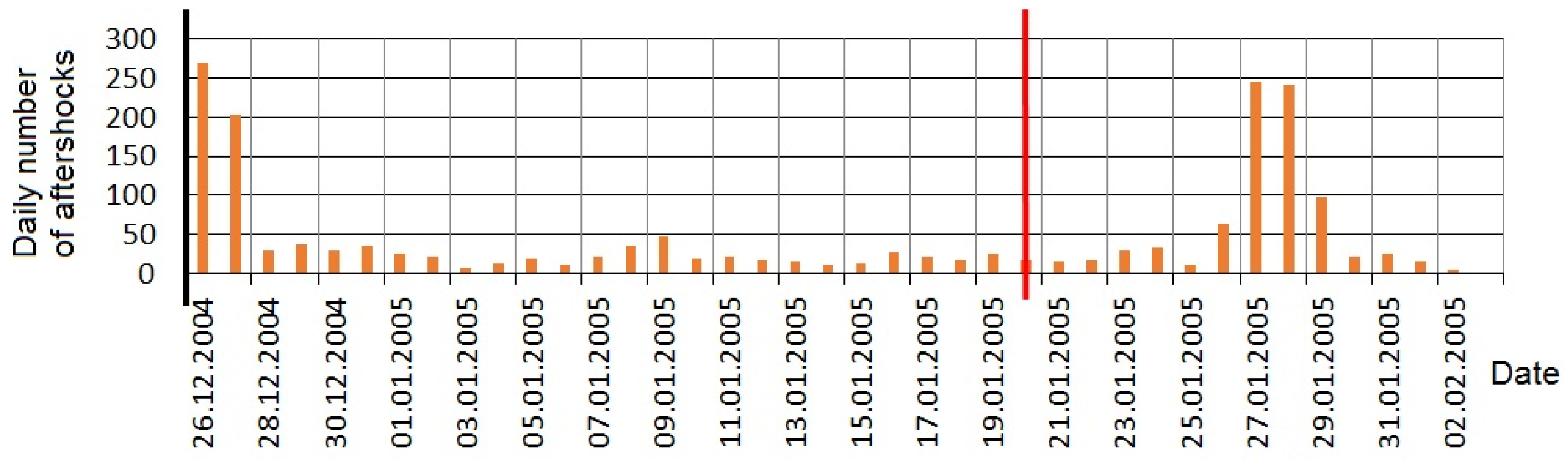
- The next finding of the presented analysis was the response of the aftershock area of a strong EQ to the impact of a SF, where areas with a subcritical stress–strain state appeared constantly due to the redistribution of the stresses in the crust after the main shock. Based on two case studies of the aftershock zones of a strong magnitude Mw = 7.1 EQ in New Zealand and a strong Mw = 9.1 EQ in Indonesia, a clear response of the aftershock sequences to X-class SFs was discovered (Figure 6). The general feature of this response is a delay of 6 to 8 days, which may indicate a multi-stage physical mechanism triggering processes in the crust fault, including fluid migration under EM impact, that require some time for fluid diffusion into the fault, reducing its frictional properties and strength.
- (a)
- determination of an unstable area (a fault section in the Earth’s crust), where strong EQs are expected based on existing mid-term methods for selecting seismic-prone regions [31];
- (b)
- selection of crustal faults in the regions identified in step (a) that are the most sensitive to EM impact in terms of their orientation and close to the direction of the GIC density vector, as well as based on their electrical conductivity;
- (c)
- selection of EQs that occurred in the faults identified in step from regional seismic catalogs (b);
- (d)
- correlation analysis of EQ occurrence times and variations in space weather parameters to determine the delay time of EQ triggering and the threshold values of space weather parameters that resulted in the triggering effect in the EQ preparation zone.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| No. | SF Date | SF Class | Time of Max X-ray Flux (UT) | SSP LAT | SSP LONG | ΣR=5000 | ΣR=10,000 | Σglobal | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| a | b | a | b | a | b | ||||||
| 1 | 6 November 1997 | X12.97 | 11:55 | 16°04′ S | 2°35′ W | 7 | 0 | 35 | 50 | 151 | 136 |
| 2 | 6 May 1998 | X3.81 | 8:09 | 16°31′ N | 57°10′ E | 13 | 13 | 66 | 61 | 121 | 96 |
| 3 | 18 August 1998 | X7.03 | 22:19 | 12°56′ N | 153°33′ W | 15 | 14 | 85 | 71 | 114 | 106 |
| 4 | 18 August 1998 | X4.03 | 8:24 | 13°07′ N | 54°59′ E | 11 | 18 | 52 | 57 | 112 | 106 |
| 5 | 19 August 1998 | X5.57 | 21:45 | 12°37′ N | 145°06′ W | 7 | 11 | 88 | 67 | 116 | 100 |
| 6 | 22 November 1998 | X5.37 | 6:42 | 20°06′ S | 76°01′ E | 8 | 7 | 72 | 68 | 121 | 100 |
| 7 | 28 November 1998 | X4.77 | 5:52 | 21°16′ S | 88°58′ E | 36 | 17 | 94 | 84 | 129 | 108 |
| 8 | 14 July 2000 | X8.21 | 10:24 | 21°36′ N | 25°28′ E | 9 | 6 | 44 | 52 | 183 | 202 |
| 9 | 26 November 2000 | X5.83 | 16:48 | 21°05′ S | 75°07′ W | 14 | 12 | 26 | 19 | 133 | 376 |
| 10 | 2 April 2001 | X28.57+ | 21:51 | 5°13′ N | 146°38′ W | 13 | 9 | 82 | 82 | 117 | 115 |
| 11 | 6 April 2001 | X8.08 | 19:21 | 6°42′ N | 109°25′ W | 12 | 13 | 46 | 61 | 109 | 132 |
| 12 | 15 April 2001 | X20.67+ | 13:50 | 9°55′ N | 27°30′ W | 1 | 8 | 27 | 40 | 134 | 115 |
| 13 | 25 August 2001 | X7.7 | 16:45 | 10°34′ N | 70°30′ W | 9 | 18 | 19 | 24 | 148 | 173 |
| 14 | 11 December 2001 | X4.02 | 8:08 | 23°01′ S | 56°19′ E | 8 | 3 | 59 | 61 | 113 | 109 |
| 15 | 13 December 2001 | X8.9 | 14:30 | 23°11′ S | 38°55′ W | 14 | 17 | 31 | 29 | 106 | 119 |
| 16 | 28 December 2001 | X4.99 | 20:45 | 23°15′ S | 130°33′ W | 12 | 10 | 85 | 54 | 143 | 108 |
| 17 | 15 July 2002 | X4.39 | 20:08 | 21°27′ N | 120°30′ W | 1 | 3 | 46 | 45 | 108 | 116 |
| 18 | 20 July 2002 | X4.74 | 21:30 | 20°34′ N | 140°54′ W | 1 | 1 | 58 | 75 | 97 | 122 |
| 19 | 23 July 2002 | X6.98 | 0:35 | 20°09′ N | 173°07′ E | 37 | 43 | 74 | 85 | 102 | 110 |
| 20 | 24 August 2002 | X4.54 | 1:12 | 11°13′ N | 162°38′ E | 82 | 91 | 105 | 118 | 141 | 135 |
| 21 | 28 May 2003 | X5.17 | 0:27 | 21°22′ N | 172°47′ E | 56 | 45 | 124 | 120 | 154 | 160 |
| 22 | 23 October 2003 | X7.77 | 8:35 | 11°18′ S | 47°36′ E | 2 | 5 | 45 | 47 | 132 | 130 |
| 23 | 28 October 2003 | X24.57+ | 11:10 | 13°04′ S | 8°28′ E | 1 | 1 | 24 | 24 | 152 | 129 |
| 24 | 29 October 2003 | X14.36 | 20:49 | 13°32′ S | 136°04′ W | 25 | 15 | 77 | 78 | 163 | 121 |
| 25 | 2 November 2003 | X11.96 | 17:25 | 14°47′ S | 30°08′ E | 4 | 1 | 35 | 30 | 160 | 134 |
| 26 | 3 November 2003 | X5.61 | 9:55 | 14°60′ S | 27°24′ E | 4 | 1 | 41 | 28 | 164 | 135 |
| 27 | 3 November 2003 | X3.88 | 1:30 | 14°53′ S | 153°24′ E | 82 | 66 | 125 | 109 | 162 | 133 |
| 28 | 4 November 2003 | X40+ | 19:53 | 15°26′ S | 122°06′ W | 6 | 5 | 64 | 62 | 174 | 139 |
| 29 | 16 July 2004 | X5.24 | 13:55 | 21°15′ N | 26°58′ W | 5 | 4 | 37 | 27 | 117 | 120 |
| 30 | 17 January 2005 | X5.52 | 9:52 | 20°41′ S | 34°33′ E | 2 | 6 | 239 | 164 | 376 | 265 |
| 31 | 20 January 2005 | X10.16 | 7:01 | 20°05′ S | 77°46′ E | 524 | 127 | 621 | 223 | 679 | 275 |
| 32 | 7 September 2005 | X24.42+ | 17:40 | 5°50′ N | 85°32′ W | 14 | 19 | 31 | 37 | 164 | 184 |
| 33 | 8 September 2005 | X7.77 | 21:06 | 5°24′ N | 137°07′ W | 2 | 11 | 97 | 102 | 158 | 192 |
| 34 | 9 September 2005 | X8.87 | 20:04 | 5°02′ N | 121°42′ W | 11 | 13 | 77 | 79 | 147 | 204 |
| 35 | 9 September 2005 | X5.17 | 9:59 | 5°12′ N | 29°50′ E | 5 | 6 | 40 | 72 | 144 | 207 |
| 36 | 5 December 2006 | X12.95 | 10:35 | 22°23′ S | 19°08′ E | 3 | 3 | 25 | 35 | 152 | 210 |
| 37 | 6 December 2006 | X9.4 | 18:47 | 22°32′ S | 103°43′ W | 13 | 22 | 40 | 73 | 149 | 208 |
| 38 | 13 December 2006 | X4.88 | 2:40 | 23°08′ S | 138°29′ E | 61 | 66 | 123 | 131 | 150 | 157 |
| 39 | 9 August 2011 | X9.96 | 8:05 | 15°55′ N | 60°24′ E | 15 | 20 | 101 | 109 | 176 | 191 |
| 40 | 7 March 2012 | X7.79 | 0:24 | 5°12′ S | 176°46′ E | 70 | 87 | 187 | 217 | 249 | 265 |
| 41 | 13 May 2013 | X4.11 | 16:05 | 18°32′ N | 61°55′ W | 18 | 16 | 39 | 36 | 263 | 163 |
| 42 | 14 May 2013 | X4.64 | 1:11 | 18°38′ N | 161°35′ E | 172 | 77 | 211 | 101 | 266 | 162 |
| 43 | 5 November 2013 | X4.93 | 22:12 | 15°56′ S | 157°05′ W | 51 | 52 | 147 | 151 | 196 | 199 |
| 44 | 25 February 2014 | X7.13 | 0:49 | 9°11′ S | 171°17′ E | 49 | 60 | 101 | 110 | 174 | 159 |
| 45 | 24 October 2014 | X4.58 | 21:41 | 11°58′ S | 148°57′ W | 34 | 38 | 120 | 157 | 200 | 256 |
| 46 | 5 May 2015 | X3.93 | 22:11 | 16°22′ N | 153°20′ W | 19 | 11 | 222 | 139 | 285 | 202 |
| 47 | 6 September 2017 | X13.37 | 12:02 | 6°15′ N | 0°55′ W | 4 | 9 | 43 | 59 | 231 | 170 |
| 48 | 10 September 2017 | X11.88 | 16:06 | 4°41′ N | 62°17′ W | 68 | 104 | 100 | 140 | 206 | 229 |
| 49 | 31 December 2023 | X5.01 | 21:55 | 23°04′ S | 147°44′ W | 31 | 49 | 122 | 148 | 216 | 204 |
| 50 | 22 February 2024 | X6.3 | 22:34 | 10°07′ S | 155°08′ W | 35 | 23 | 113 | 102 | 172 | 173 |
| Total EQs after and before 50 SFs | 1696 | 1276 | 4565 | 4113 | 8629 | 7987 | |||||
| Total difference in EQ amount after and before 50 SFs, ΔEQ = ∑a − ∑b | 420 | 452 | 642 | ||||||||
| Total variation in EQs amount after 50 SFs, ΔEQ, % | 32.92 | 10.99 | 8.04 | ||||||||
References
- Sobolev, G.A. The effect of strong magnetic storms on the occurrence of large earthquakes. Izv. Phys. Solid Earth 2021, 57, 20–36. [Google Scholar] [CrossRef]
- Rabeh, T.; Miranda, M.; Hvozdara, M. Strong earthquakes associated with high amplitude daily geomagnetic variations. Nat. Hazards 2010, 53, 561–574. [Google Scholar] [CrossRef]
- Tavares, M.; Azevedo, A. Influence of solar cycles on earthquakes. Nat. Sci. 2011, 3, 436–443. [Google Scholar] [CrossRef]
- Urata, N.; Duma, G.; Freund, F. Geomagnetic Kp Index and Earthquakes. Open J. Earthq. Res. 2018, 7, 39–52. [Google Scholar] [CrossRef]
- Sorokin, V.M.; Yashchenko, A.K.; Novikov, V.A. A possible mechanism of stimulation of seismic activity by ionizing radiation of solar flares. Earthq. Sci. 2019, 32, 26–34. [Google Scholar] [CrossRef]
- Marchitelli, V.; Harabaglia, P.; Troise, C.; De Natale, G. On the Correlation between Solar Activity and Large Earthquakes Worldwide. Sci. Rep. 2020, 10, 11495. [Google Scholar] [CrossRef] [PubMed]
- Novikov, V.; Ruzhin, Y.; Sorokin, V.; Yaschenko, A. Space weather and earthquakes: Possible triggering of seismic activity by strong solar flares. Ann. Geophys. 2020, 63, PA554. [Google Scholar] [CrossRef]
- Tarasov, N.T. Effect of Solar Activity on Electromagnetic Fields and Seismicity of the Earth. IOP Conf. Ser. Earth Environ. Sci. 2021, 929, 012019. [Google Scholar] [CrossRef]
- Anagnostopoulos, G.; Spyroglou, I.; Rigas, A.; Preka-Papadema, P.; Mavromichalaki, H.; Kiosses, I. The sun as a significant agent provoking earthquakes. Eur. Phys. J. Spec. Top. 2021, 230, 287–333. [Google Scholar] [CrossRef]
- Love, J.J.; Thomas, J.N. Insignificant solar-terrestrial triggering of earthquakes. Geophys. Res. Lett. 2013, 40, 1165–1170. [Google Scholar] [CrossRef]
- Akhoondzadeh, M.; De Santis, A. Is the Apparent Correlation between Solar-Geomagnetic Activity and Occurrence of Powerful Earthquakes a Casual Artifact? Atmosphere 2022, 13, 1131. [Google Scholar] [CrossRef]
- Sorokin, V.; Yaschenko, A.; Mushkarev, G.; Novikov, V. Telluric Currents Generated by Solar Flare Radiation: Physical Model and Numerical Estimations. Atmosphere 2023, 14, 458. [Google Scholar] [CrossRef]
- Zeigarnik, V.A.; Bogomolov, L.M.; Novikov, V.A. Electromagnetic Earthquake Triggering: Field Observations, Laboratory Experiments, and Physical Mechanisms—A Review. Izv. Phys. Solid Earth 2022, 58, 30–58. [Google Scholar] [CrossRef]
- Helman, D.S. Earth electricity: A review of mechanisms which cause telluric currents in the lithosphere. Ann. Geophys. 2014, 56, G0564. [Google Scholar] [CrossRef]
- Han, Y.; Guo, Z.; Wu, J.; Ma, L. Possible triggering of solar activity to big earthquakes (Ms≥8) in faults with near west-east strike in China. Sci. China Ser. G Phys. Mech. Astron. 2004, 47, 173–181. [Google Scholar] [CrossRef]
- Scoville, J.; Heraud, J.; Freund, F. Pre-earthquake magnetic pulses. Nat. Hazards Earth Syst. Sci. 2015, 15, 1873–1880. [Google Scholar] [CrossRef]
- Guglielmi, A.V.; Zotov, O.D. Magnetic perturbations before the strong earthquakes. Izv. Phys. Solid Earth 2012, 48, 171–173. [Google Scholar] [CrossRef]
- INTERMAGNET Data Viewer. Available online: https://imag-data.bgs.ac.uk/GIN_V1/GINForms2 (accessed on 10 April 2024).
- Day and Night World Map. Available online: https://www.timeanddate.com/worldclock/sunearth.html (accessed on 10 April 2024).
- Search Earthquake Catalog. Available online: https://earthquake.usgs.gov/earthquakes/search/ (accessed on 10 April 2024).
- Real-Time Data and Plots Auroral Activity. Available online: https://www.spaceweatherlive.com/en/solar-activity/top-50-solar-flares.html (accessed on 1 February 2024).
- Thomson, A.W.P.; McKay, A.J.; Viljanen, A. A Review of Progress in Modelling of Induced Geoelectric and Geomagnetic Fields with Special Regard to Induced Currents. Acta Geophys. 2009, 57, 209–219. [Google Scholar] [CrossRef]
- Zavialov, A.D.; Morozov, A.N.; Aleshin, I.M.; Ivanov, S.D.; Kholodkov, K.I.; Pavlenko, V.A. Medium-term Earthquake Forecast Method Map of Expected Earthquakes: Results and Prospects. Izv. Atmos. Ocean. Phys. 2022, 58, 908–924. [Google Scholar] [CrossRef]
- Sedghizadeh, M.; Shcherbakov, R. The Analysis of the Aftershock Sequences of the Recent Mainshocks in Alaska. Appl. Sci. 2022, 12, 1809. [Google Scholar] [CrossRef]
- Araki, E.; Shinohara, M.; Obana, K.; Yamada, T.; Kaneda, Y.; Kanazawa, T.; Suyehiro, K. Aftershock distribution of the 26 December 2004 Sumatra-Andaman earthquake from ocean bottom seismographic observation. Earth Planets Space 2006, 58, 113–119. [Google Scholar] [CrossRef]
- Potter, S.H.; Becker, J.S.; Johnston, D.M.; Rossiter, K.P. An overview of the impacts of the 2010–2011 Canterbury earthquakes. Int. J. Disaster Risk Reduct. 2015, 14, 6–14. [Google Scholar] [CrossRef]
- New Zealand Active Faults Database. Available online: https://data.gns.cri.nz/af/ (accessed on 10 April 2024).
- Curto, J.J. Geomagnetic solar flare effects: A review. J. Space Weather. Space Clim. 2020, 10, 27. [Google Scholar] [CrossRef]
- Grodji, O.D.F.; Doumbia, V.; Amaechi, P.O.; Amory-Mazaudier, C.; N’guessan, K.; Diaby, K.A.A.; Zie, T.; Boka, K. A Study of Solar Flare Effects on the Geomagnetic Field Components during Solar Cycles 23 and 24. Atmosphere 2022, 13, 69. [Google Scholar] [CrossRef]
- Sobolev, G.A. Seismicity dynamics and earthquake predictability. Nat. Hazards Earth Syst. Sci. 2011, 11, 445–458. [Google Scholar] [CrossRef]
- Dzeboev, B.A.; Gvishiani, A.D.; Agayan, S.M.; Belov, I.O.; Karapetyan, J.K.; Dzeranov, B.V.; Barykina, Y.V. System-Analytical Method of Earthquake-Prone Areas Recognition. Appl. Sci. 2021, 11, 7972. [Google Scholar] [CrossRef]
- Ledo, J.; Jones, A.G.; Ferguson, I.J. Electromagnetic images of a strike-slip fault: The Tintina fault-Northern Canadian. Geophys. Res. Lett. 2002, 29, 1225. [Google Scholar] [CrossRef]
- Unsworth, M.J.; Malin, P.E.; Egbert, G.D.; Booker, J.R. Internal Structure of the San Andreas Fault Zone at Parkfield, California. Geology 1997, 25, 359–362. [Google Scholar]
- Ingham, M.; Brown, C. A magnetotelluric study of the Alpine Fault, New Zealand. Geophys. J. Int. 1998, 2, 542–552. [Google Scholar] [CrossRef]
- Jones, A.G.; Kurtz, R.D.; Boerner, D.E.; Craven, J.A.; McNeice, G.W.; Gough, D.I.; DeLaurier, J.M.; Ellis, R.G. Electromagnetic constraints on strike-slip fault geometry—The Fraser River fault system. Geology 1992, 20, 561–564. [Google Scholar]
- Stanley, W.D.; Labson, V.F.; Nokleberg, W.J.; Csejtey, B.; Fisher, M.A. The Denali fault system and Alaska Range of Alaska: Evidence for underplated Mesozoic flysch from magnetotelluric surveys. Geol. Soc. Am. Bull. 1990, 102, 160–173. [Google Scholar]
- Mackie, R.L.; Livelybrooks, D.W.; Madden, T.R.; Larsen, J.C. A magnetotelluric investigation of the San Andreas Fault at Carrizo Plain, California. Geoph. Res. Lett. 1997, 24, 1847–1850. [Google Scholar] [CrossRef]
- Sorokin, V.M.; Chmyrev, V.M.; Hayakawa, M. A Review on Electrodynamic Influence of Atmospheric Processes to the Ionosphere. Open J. Earthq. Res. 2020, 9, 113–141. [Google Scholar] [CrossRef]
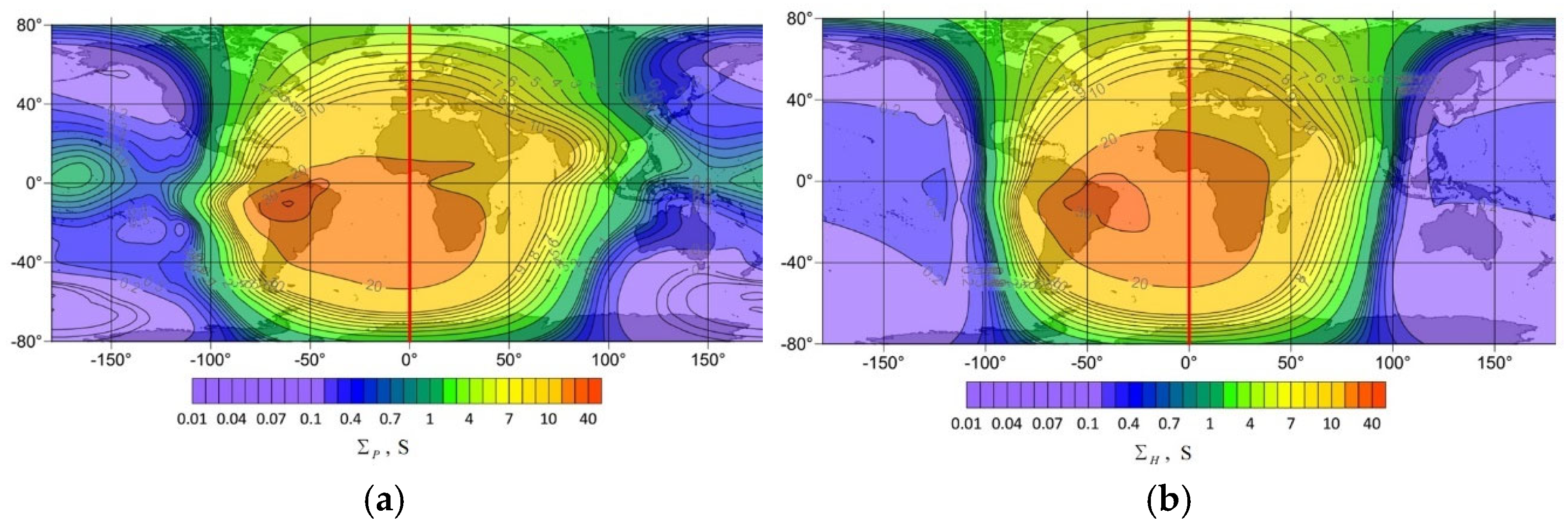
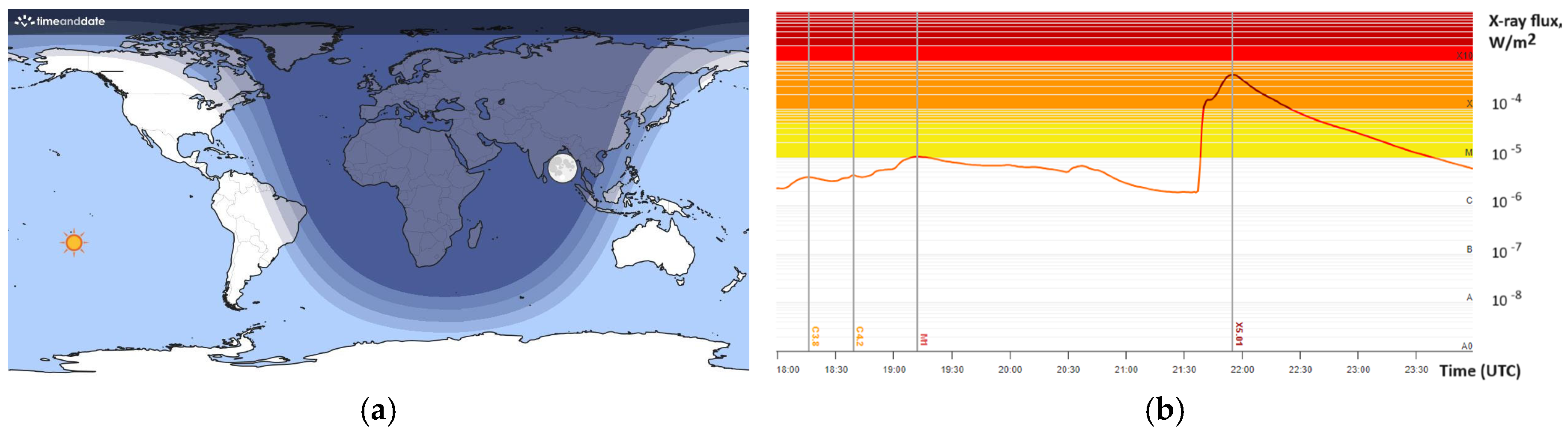
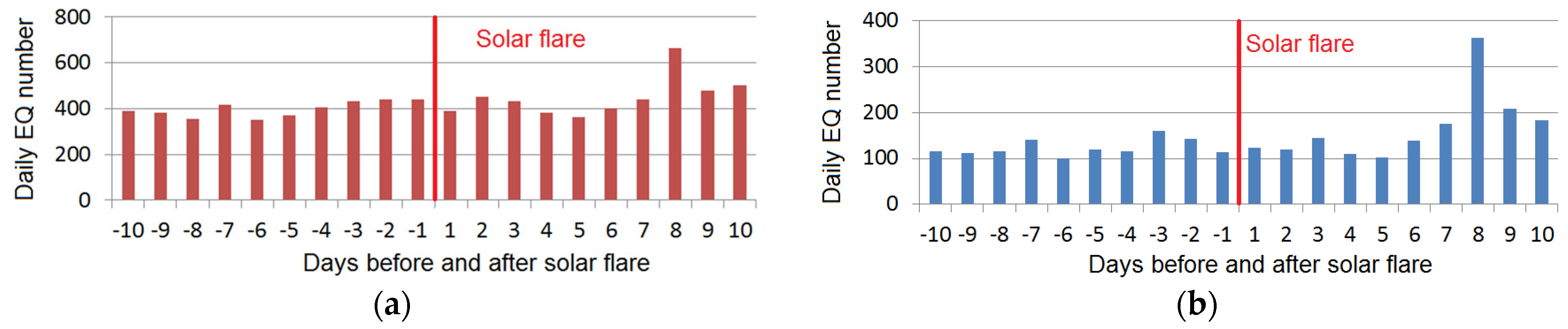
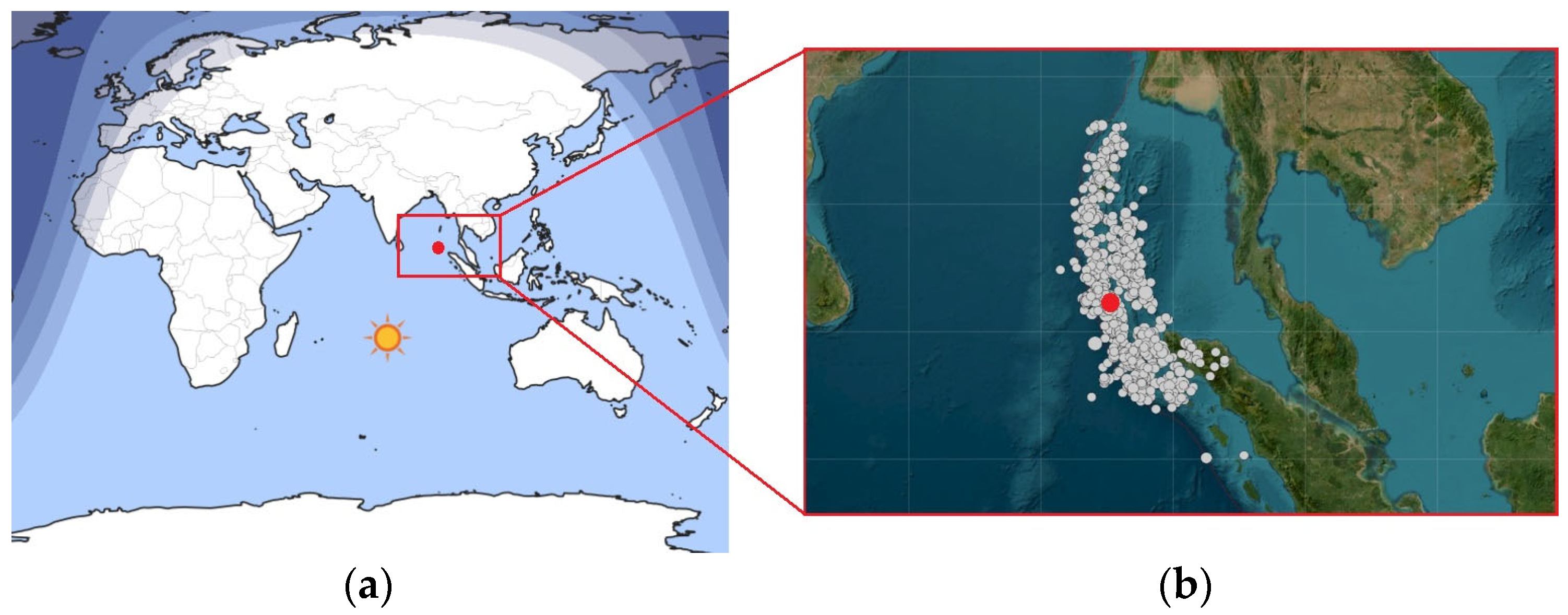
| IAGA Code | Latitude | Longitude | Distance to Subsolar Point R, km |
|---|---|---|---|
| PPT | −17.567 | 210.426 | 640.92 |
| EYR | −43.474 | 172.393 | 4287.45 |
| HON | 21.320 | 202.000 | 5059.38 |
| CTA | −20.090 | 146.264 | 6774.29 |
| AIA | −65.245 | 295.742 | 7388.67 |
| FRD | 38.210 | 282.633 | 10,003.97 |
| ABG | 18.638 | 72.872 | 15,780.24 |
| ΣR=5000 | ΣR=10,000 | Σglobal | ||||
|---|---|---|---|---|---|---|
| a | b | a | b | a | b | |
| 1696 | 1276 | 4565 | 4113 | 8629 | 7987 | |
| ΔEQ, % | 32.92 | 10.99 | 8.04 | |||
| SF Date | SF Class | Time of Max X-ray Flux (UT) | SSP Latitude | SSP Longitude | Distance to Sumatra–Andaman EQ Epicenter, km |
|---|---|---|---|---|---|
| 1 January 2005 | 2.49 | 0:31 | 23°01′ S | 172°52′ E | 8815.447 |
| 15 January 2005 | 1.79 | 0:43 | 21°08′ S | 171°20′ E | 8628.460 |
| 15 January 2005 | 1.21 | 4:26 | 21°07′ S | 115°51′ E | 3471.743 |
| 15 January 2005 | 1.24 | 5:54 | 21°06′ S | 93°52′ E | 2722.371 |
| 15 January 2005 | 3.79 | 23:02 | 20°58′ S | 163°05′ W | 7782.587 |
| 17 January 2005 | 5.51 | 9:52 | 20°41′ S | 34°33′ E | 7201.479 |
| 19 January 2005 | 2.00 | 8:22 | 20°17′ S | 57°12′ E | 4977.074 |
| 20 January 2005 | 10.16 | 7:02 | 20°05′ S | 77°16′ E | 3306.360 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sorokin, V.; Novikov, V. Possible Interrelations of Space Weather and Seismic Activity: An Implication for Earthquake Forecast. Geosciences 2024, 14, 116. https://doi.org/10.3390/geosciences14050116
Sorokin V, Novikov V. Possible Interrelations of Space Weather and Seismic Activity: An Implication for Earthquake Forecast. Geosciences. 2024; 14(5):116. https://doi.org/10.3390/geosciences14050116
Chicago/Turabian StyleSorokin, Valery, and Victor Novikov. 2024. "Possible Interrelations of Space Weather and Seismic Activity: An Implication for Earthquake Forecast" Geosciences 14, no. 5: 116. https://doi.org/10.3390/geosciences14050116
APA StyleSorokin, V., & Novikov, V. (2024). Possible Interrelations of Space Weather and Seismic Activity: An Implication for Earthquake Forecast. Geosciences, 14(5), 116. https://doi.org/10.3390/geosciences14050116







