Correction Factors to Account for Seismic Directionality Effects: Case Study of the Costa Rican Strong Motion Database
Abstract
:1. Introduction
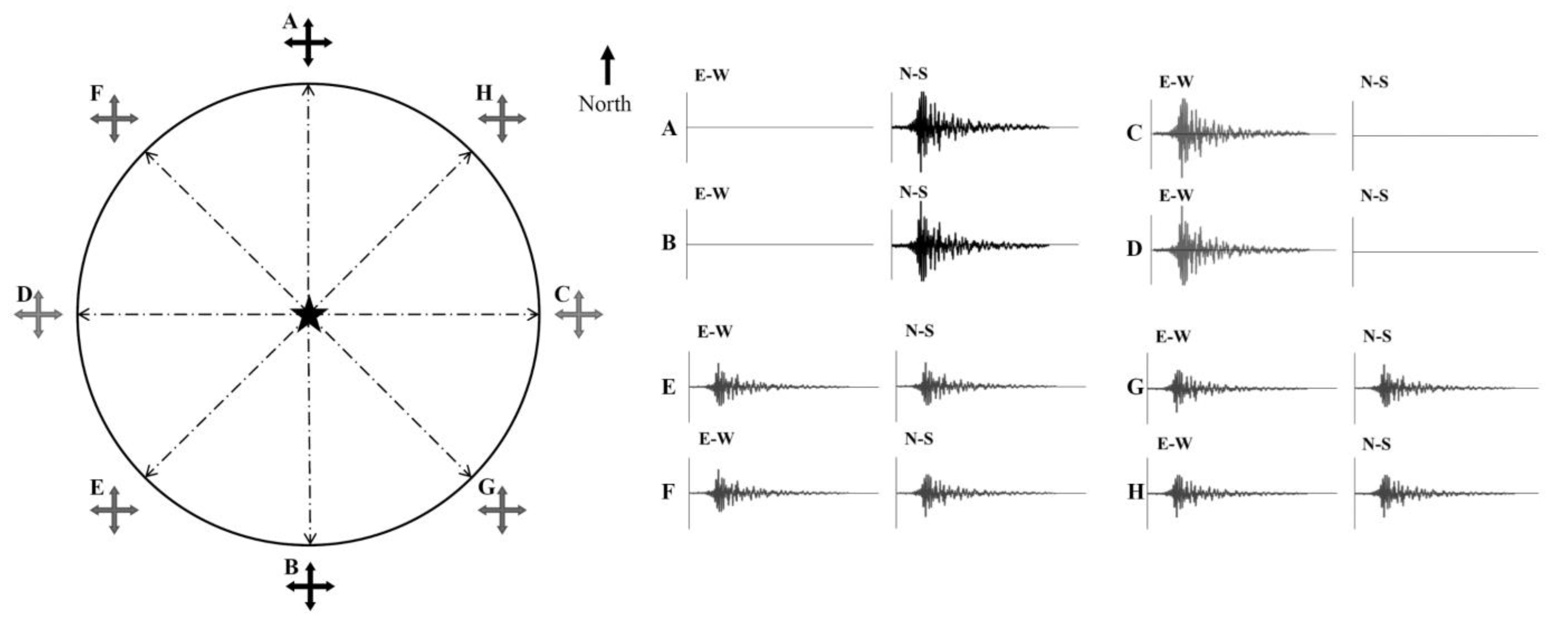
2. Directionality Effects on Ground Motions
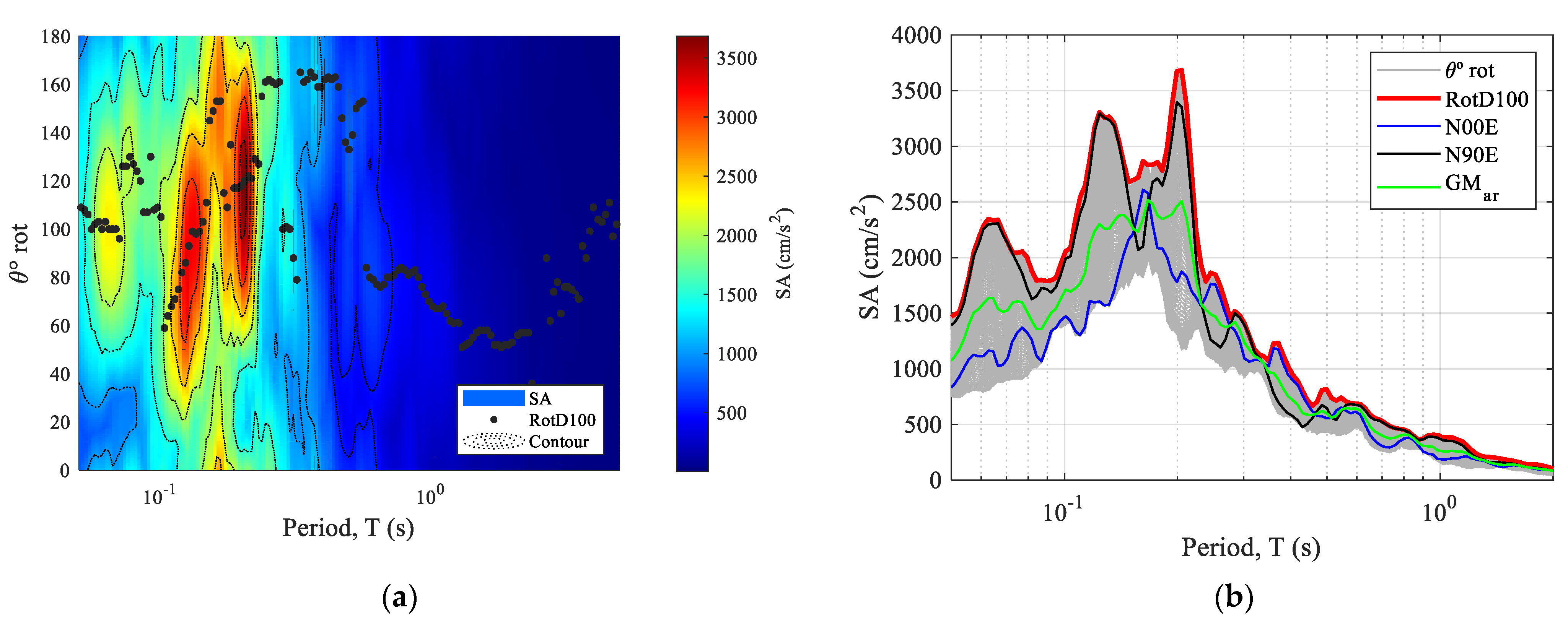
3. Comprehensive Analysis
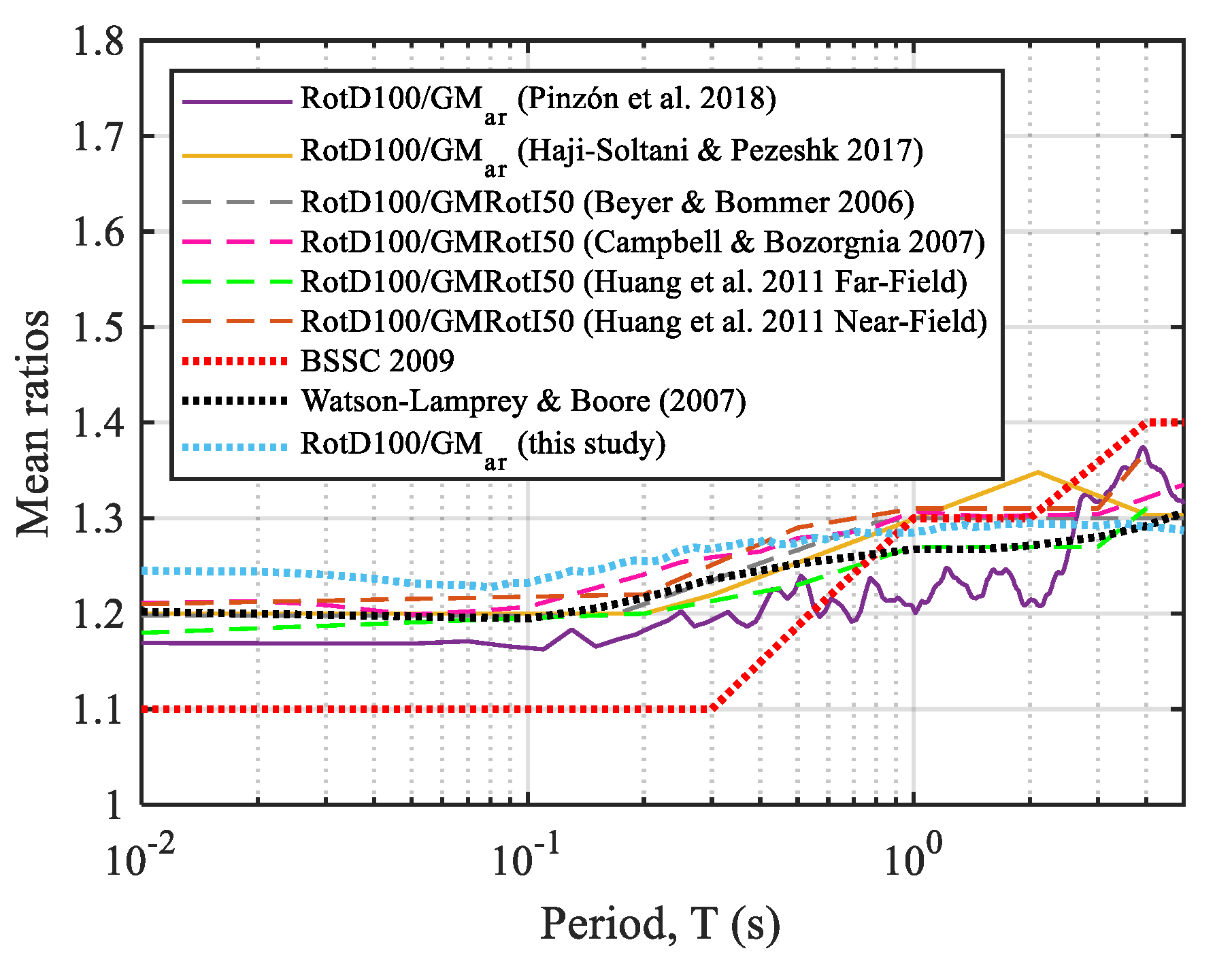
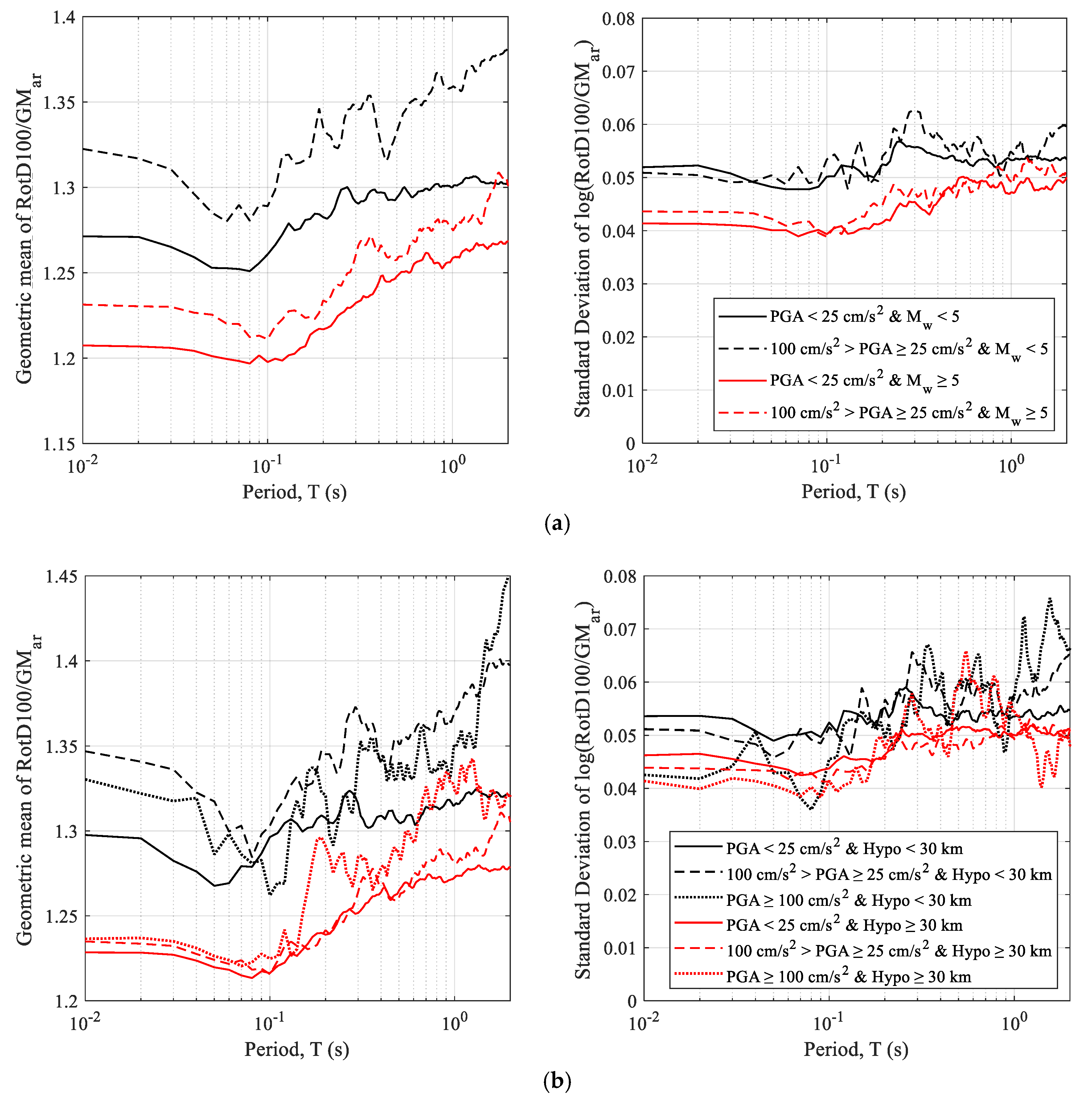
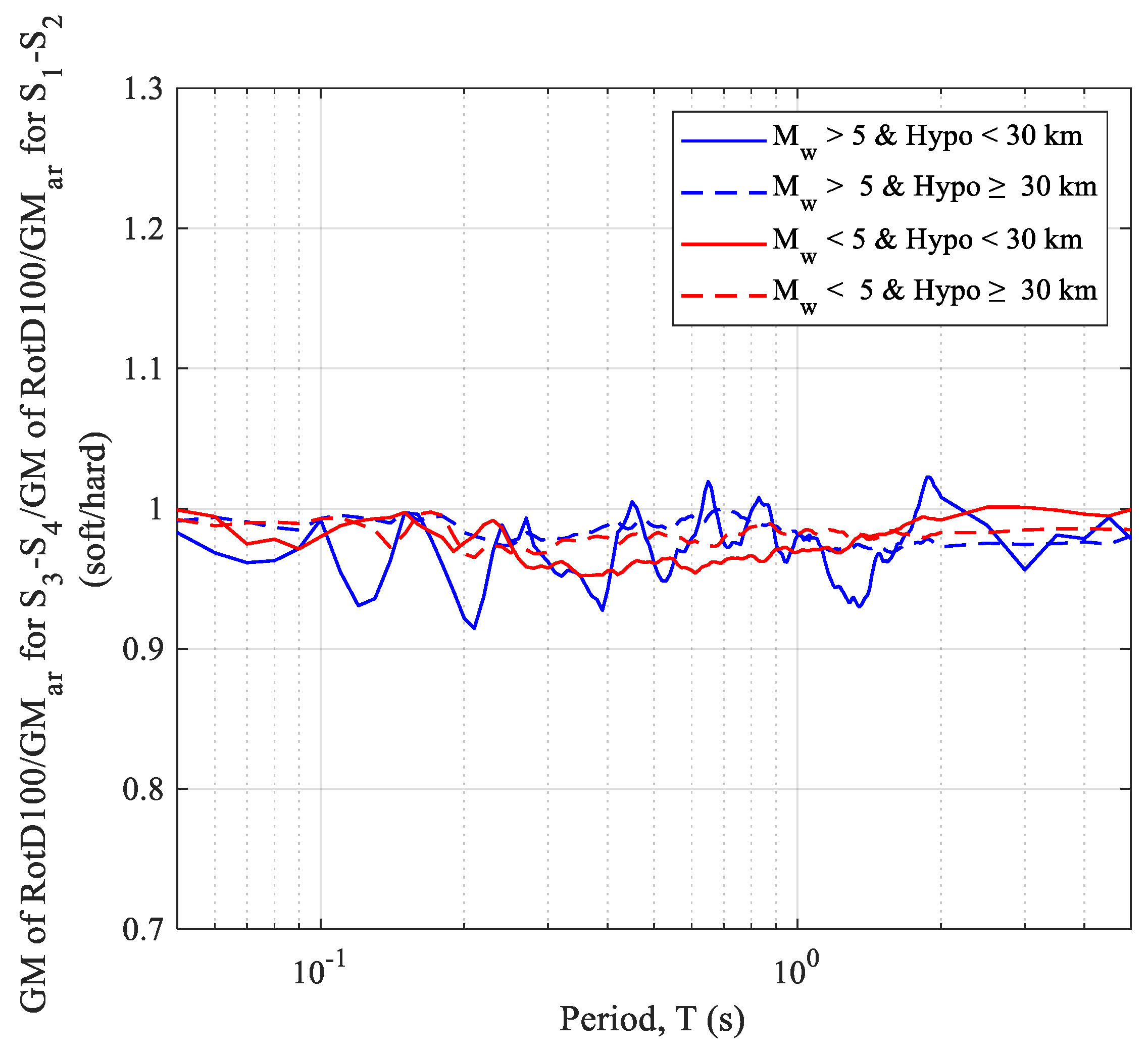
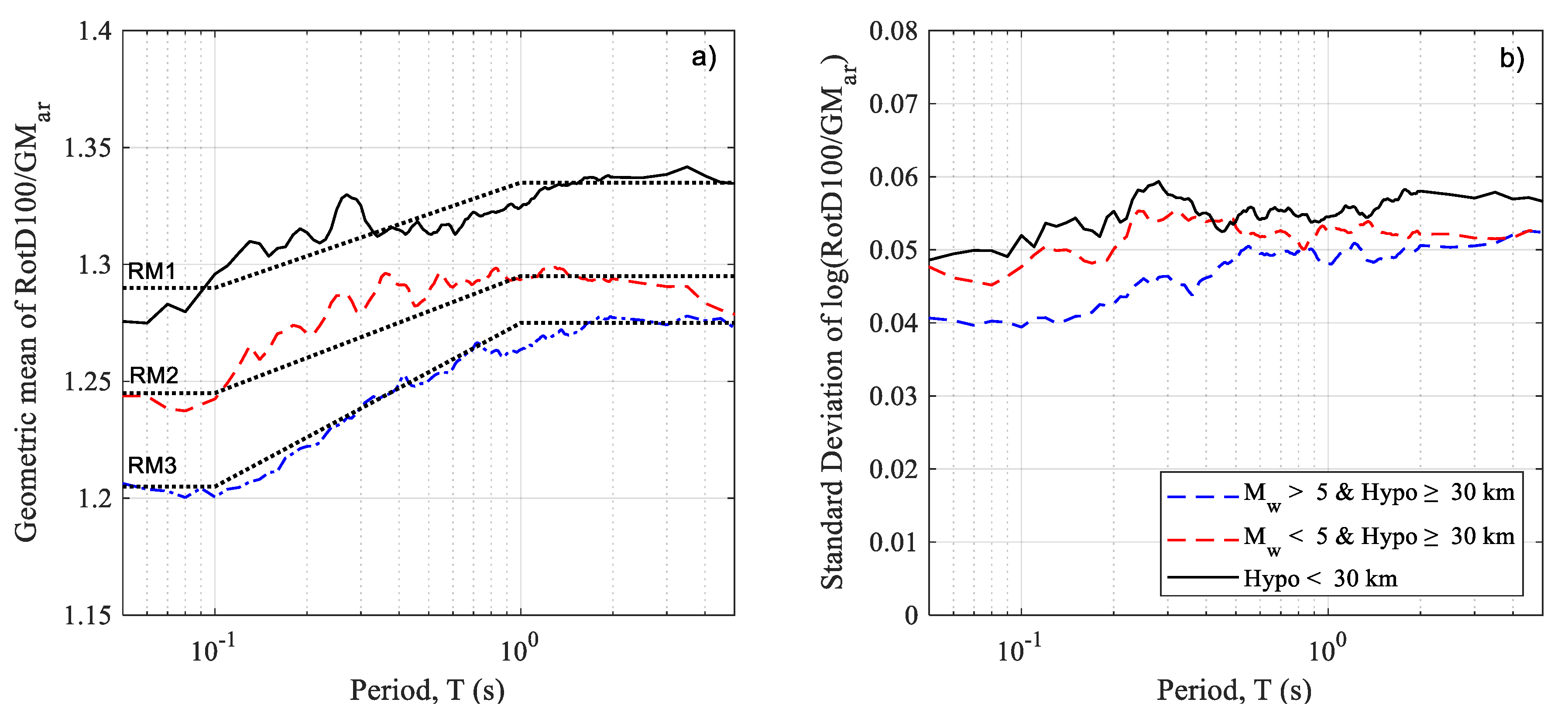
4. Correction Factors
Maximum-Direction Ground Motion Correction Factor (RotD100/GMar)
5. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Boore, D.M.; Watson-Lamprey, J.; Abrahamson, N.A. Orientation-Independent Measures of Ground Motion. Bull. Seismol. Soc. Am. 2006, 96, 1502–1511. [Google Scholar] [CrossRef]
- Bradley, B.A.; Baker, J.W. Ground Motion Directionality in the 2010–2011 Canterbury Earthquakes. Earthq. Eng. Struct. Dyn. 2015, 44, 371–384. [Google Scholar] [CrossRef]
- Boore, D.M. Orientation-Independent, Nongeometric-Mean Measures of Seismic Intensity from Two Horizontal Components of Motion. Bull. Seismol. Soc. Am. 2010, 100, 1830–1835. [Google Scholar] [CrossRef]
- Shahi, S.K.; Baker, J.W. NGA-West2 Models for Ground Motion Directionality. Earthq. Spectra 2014, 30, 1285–1300. [Google Scholar] [CrossRef]
- Beyer, K.; Bommer, J.J. Relationships between Median Values and between Aleatory Variabilities for Different Definitions of the Horizontal Component of Motion. Bull. Seismol. Soc. Am. 2006, 96, 1512–1522. [Google Scholar] [CrossRef]
- Pinzón, L.A.; Pujades, L.G.; Hidalgo-Leiva, D.A.; Díaz, S.A. Directionality Models from Ground Motions of Italy. Ing. Sismica 2018, 35, 43–63. [Google Scholar]
- Lagaros, N.D. The Impact of the Earthquake Incident Angle on the Seismic Loss Estimation. Eng. Struct. 2010, 32, 1577–1589. [Google Scholar] [CrossRef]
- Rigato, A.B.; Medina, R.A. Influence of Angle of Incidence on Seismic Demands for Inelastic Single-Storey Structures Subjected to Bi-Directional Ground Motions. Eng. Struct. 2007, 29, 2593–2601. [Google Scholar] [CrossRef]
- Torbol, M.; Shinozuka, M. The Directionality Effect in the Seismic Risk Assessment of Highway Networks. Struct. Infrastruct. Eng. 2014, 10, 175–188. [Google Scholar] [CrossRef]
- Soltanieh, S.; Memarpour, M.M.; Kilanehei, F. Performance Assessment of Bridge-Soil-Foundation System with Irregular Configuration Considering Ground Motion Directionality Effects. Soil Dyn. Earthq. Eng. 2019, 118, 19–34. [Google Scholar] [CrossRef]
- Athanatopoulou, A.M. Critical Orientation of Three Correlated Seismic Components. Eng. Struct. 2005, 27, 301–312. [Google Scholar] [CrossRef]
- Matsushima, S.; Kosaka, H.; Kawase, H. Directionally Dependent Horizontal-to-Vertical Spectral Ratios of Microtremors at Onahama, Fukushima, Japan. Earth Planets Space 2017, 69, 96. [Google Scholar] [CrossRef]
- Vargas-Alzate, Y.F.; Pujades, L.G.; Barbat, A.H.; Hurtado, J.E.; Diaz, S.A.; Hidalgo-Leiva, D.A. Probabilistic Seismic Damage Assessment of Reinforced Concrete Buildings Considering Direccionality Effects. Struct. Infrastruct. Eng. 2017, 16, 817–829. [Google Scholar]
- Pinzón, L.A.; Pujades, L.G.; Diaz, S.A.; Alva, R.E. Do Directionality Effects Influence Expected Damage? A Case Study of the 2017 Central Mexico Earthquake. Bull. Seismol. Soc. Am. 2018, 108, 2543–2555. [Google Scholar] [CrossRef]
- Moya-Fernández, A.; Pinzón, L.A.; Schmidt-Díaz, V.; Hidalgo-Leiva, D.A.; Pujades, L.G. A Strong-Motion Database of Costa Rica: 20 Yr of Digital Records. Seismol. Res. Lett. 2020, 91, 3407–3416. [Google Scholar] [CrossRef]
- Hidalgo-Leiva, D.A.; Linkimer, L.; Arroyo, I.G.; Arroyo-Solórzano, M.; Piedra, R.; Climent, A.; Schmidt Díaz, V.; Esquivel, L.C.; Alvarado, G.E.; Castillo, R.; et al. The 2022 Seismic Hazard Model for Costa Rica. Bull. Seismol. Soc. Am. 2023, 113, 23–40. [Google Scholar] [CrossRef]
- Pinzón, L.A.; Leiva, D.A.H.; Moya-Fernández, A.; Schmidt-Díaz, V.; Pujades, L.G. Seismic Site Classification of the Costa Rican Strong-Motion Network Based on VS30 Measurements and Site Fundamental Period. Earth Sci. Res. J. 2021, 25, 383–389. [Google Scholar] [CrossRef]
- Nigam, N.C.; Jennings, P.C. Calculation of Response Spectra From Strong-Motion Earthquake Records. Bull. Seismol. Soc. Am. 1969, 59, 909–922. [Google Scholar] [CrossRef]
- Boore, D.M.; Kishida, T. Relations Between Some Horizontal-Component Ground-Motion Intensity Measures Used In Practice. Bull. Seismol. Soc. Am. 2016, 107, 334–343. [Google Scholar] [CrossRef]
- Douglas, J. Earthquake Ground Motion Estimation Using Strong-Motion Records: A Review of Equations for the Estimation of Peak Ground Acceleration and Response Spectral Ordinates. Earth-Sci. Rev. 2003, 61, 43–104. [Google Scholar] [CrossRef]
- Poulos, A.; Miranda, E. Relations between MaxRotD50 and Some Horizontal Components of Ground-Motion Intensity Used in Practice. Bull. Seismol. Soc. Am. 2021, 111, 2167–2176. [Google Scholar] [CrossRef]
- Pinzón, L.A.; Pujades, L.G.; Medranda, I.; Alva, R.E. Case Study of a Heavily Damaged Building during the 2016 MW 7.8 Ecuador Earthquake: Directionality Effects in Seismic Actions and Damage Assessment. Geosciences 2021, 11, 74. [Google Scholar] [CrossRef]
- Haji-Soltani, A.; Pezeshk, S. Relationships among Various Definitions of Horizontal Spectral Accelerations in Central and Eastern North America. Bull. Seismol. Soc. Am. 2017, 108, 409–417. [Google Scholar] [CrossRef]
- Campbell, K.W.; Bozorgnia, Y. Campbell-Bozorgnia NGA Ground Motion Relations for the Geometric Mean Horizontal Component of Peak and Spectral Ground Motion Parameters; PEER Rep. 2007/02; Pacific Earthquake Engineering Research Center: Berkeley, CA, USA, 2007; Volume 238. [Google Scholar]
- Huang, Y.; Whittaker, A.S.; Luco, N. Establishing Maximum Spectral Demand for Performance-Based Earthquake Engineering: Collaborative Research with the University at Buffalo and the USGS; United States Geological Survey: Reston, VA, USA, 2011; Volume 80401. [Google Scholar]
- Building Seismic Safety Council. NEHRP Recommended Seismic Provisions for New Buildings Abd Other Structures; FEMA P-750; Federal Emergency Management Agency: Washington, DC, USA, 2009; Volume 388. [Google Scholar]
- Watson-Lamprey, J.A.; Boore, D.M. Beyond SaGMRotI: Conversion to SaArb, SaSN, and SaMaxRot. Bull. Seismol. Soc. Am. 2007, 97, 1511–1524. [Google Scholar] [CrossRef]
- Huang, Y.N.; Whittaker, A.S.; Luco, N. Maximum Spectral Demands in the Near-Fault Region. Earthq. Spectra 2008, 24, 319–341. [Google Scholar] [CrossRef]
- Aki, K.; Richards, P.G. Quantitative Seismology, 2nd ed.; University Science Books: Sausalito, CA, USA, 2002; ISBN 1891389637. [Google Scholar]
- Stein, S.; Wysession, M. An Introduction to Seismology, Earthquakes, and Earth Structure; Wiley: Hoboken, NJ, USA, 2009; ISBN 9781444311310. [Google Scholar]
- Boore, D.M. Simulation of Ground Motion Using the Stochastic Method. Pure Appl. Geophys. 2003, 160, 635–676. [Google Scholar] [CrossRef]
- CFIA Código Sísmico de Costa Rica 2010 (Revisión 2014); Editorial Tecnológica de Costa Rica: Cartago, Costa Rica, 2016; ISBN 9789977662343.






| IM | Definition |
|---|---|
| GMar | Geometric mean of the response spectra of the two as-recorded horizontal components [2,5,6,19]. |
| Larger | Envelope of the response spectra of the two as-recorded horizontal components [2,6,19,20]. |
| GMRotD50 | 50th percentile of a set of geometric means of the response spectra of the two as-recorded horizontal components rotated onto all nonredundant azimuths (GMRot) [1,19]. |
| GMRotI50 | GMRot response spectrum from the rotation angle best matching the GMRotD50 [1,19]. |
| RotD50 | 50th percentile of a set of response spectra of the two as-recorded horizontal components rotated onto all nonredundant azimuths [3,6]. |
| RotD100 | 100th percentile of a set of response spectra of the two as-recorded horizontal components rotated onto all nonredundant azimuths [3,6]. |
| LRotD50 | 50th percentile of a set of envelopes of the response spectra of the two as-recorded horizontal components rotated onto all nonredundant azimuths [6], also referred to as MaxRotD50 [21]. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pinzón, L.A.; Hidalgo-Leiva, D.A.; Pujades, L.G. Correction Factors to Account for Seismic Directionality Effects: Case Study of the Costa Rican Strong Motion Database. Geosciences 2024, 14, 139. https://doi.org/10.3390/geosciences14050139
Pinzón LA, Hidalgo-Leiva DA, Pujades LG. Correction Factors to Account for Seismic Directionality Effects: Case Study of the Costa Rican Strong Motion Database. Geosciences. 2024; 14(5):139. https://doi.org/10.3390/geosciences14050139
Chicago/Turabian StylePinzón, Luis A., Diego A. Hidalgo-Leiva, and Luis G. Pujades. 2024. "Correction Factors to Account for Seismic Directionality Effects: Case Study of the Costa Rican Strong Motion Database" Geosciences 14, no. 5: 139. https://doi.org/10.3390/geosciences14050139
APA StylePinzón, L. A., Hidalgo-Leiva, D. A., & Pujades, L. G. (2024). Correction Factors to Account for Seismic Directionality Effects: Case Study of the Costa Rican Strong Motion Database. Geosciences, 14(5), 139. https://doi.org/10.3390/geosciences14050139










