Research on High-Density Discrete Seismic Signal Denoising Processing Method Based on the SFOA-VMD Algorithm
Abstract
1. Introduction
2. Materials and Methods
2.1. Variational Mode Decomposition (VMD)
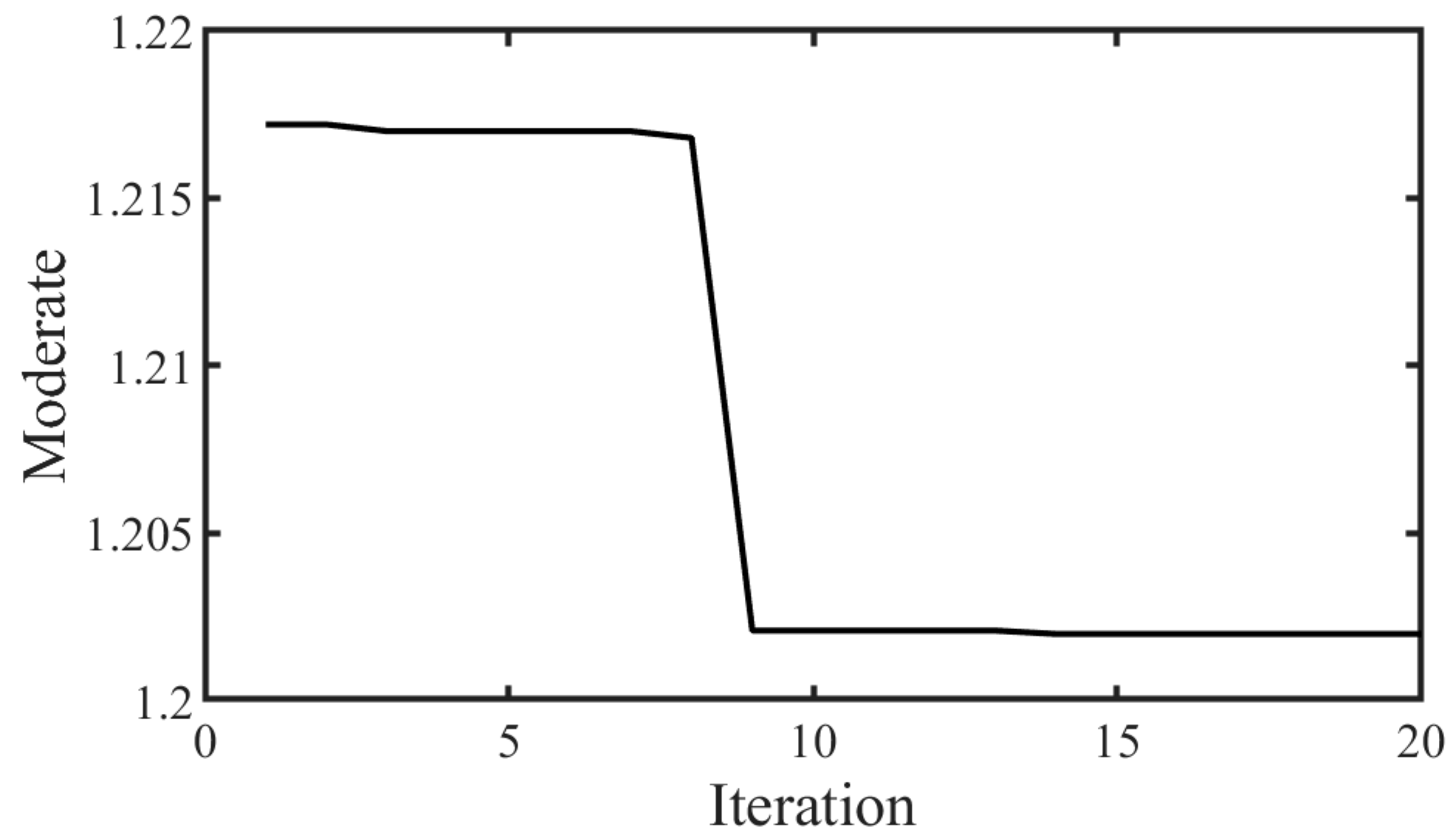
2.2. The Starfish Optimization Algorithm (SFOA)
2.2.1. Initialization
2.2.2. Exploration Phase
2.2.3. Exploitation Phase
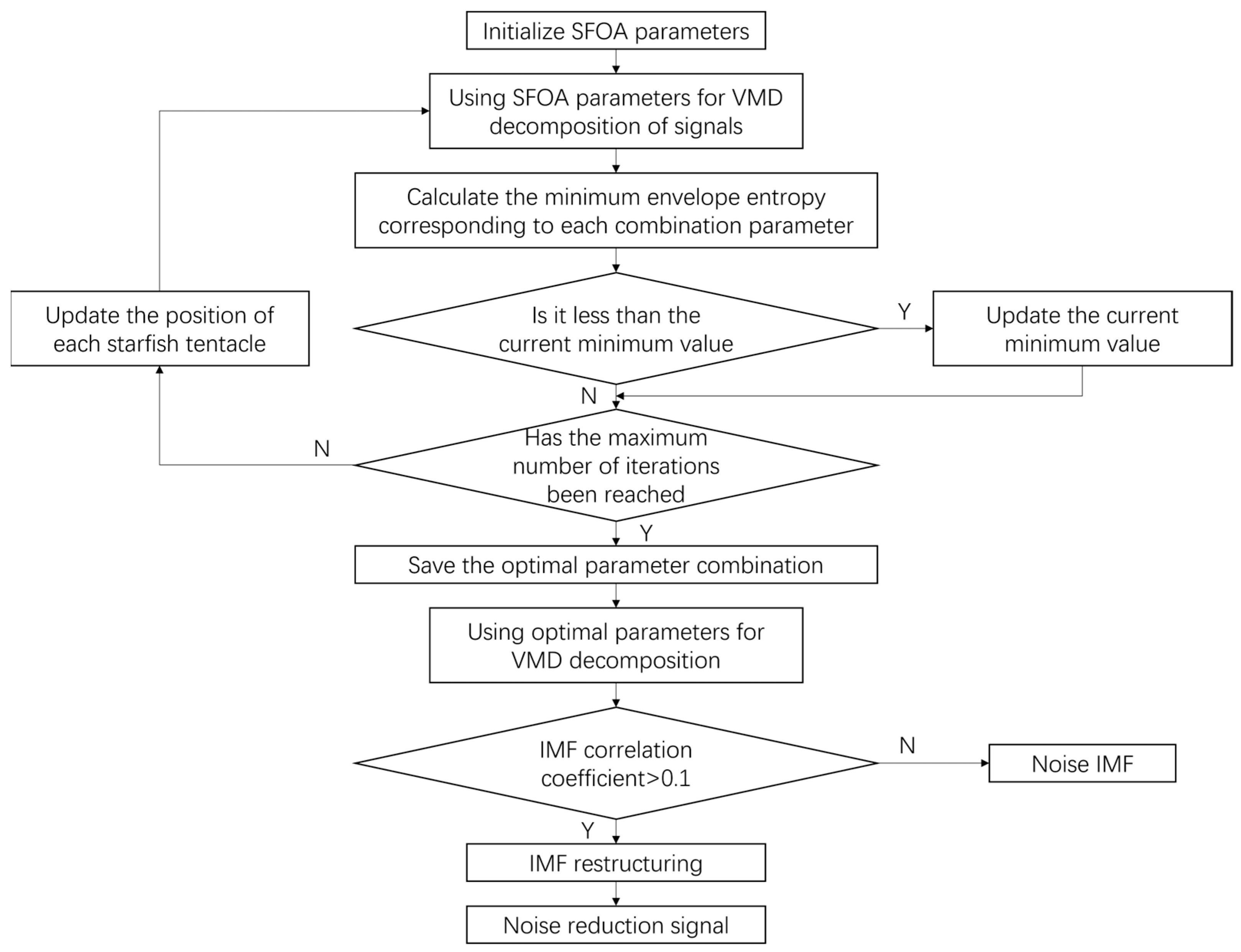
3. Denoising Principle and Evaluation Parameters
3.1. Denoising Principle
3.2. Denoising Performance Evaluation Methods
4. Denoising Application
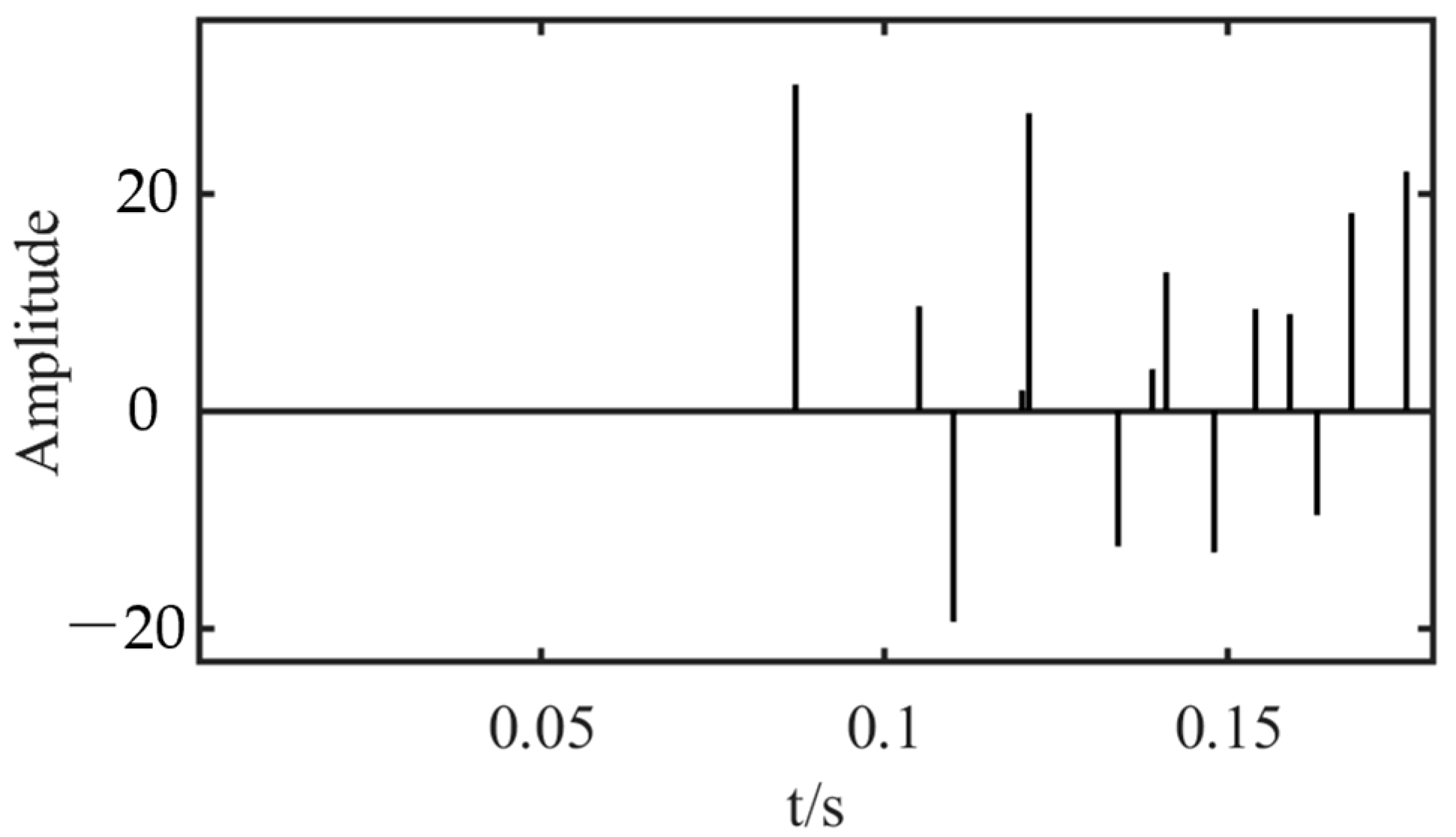
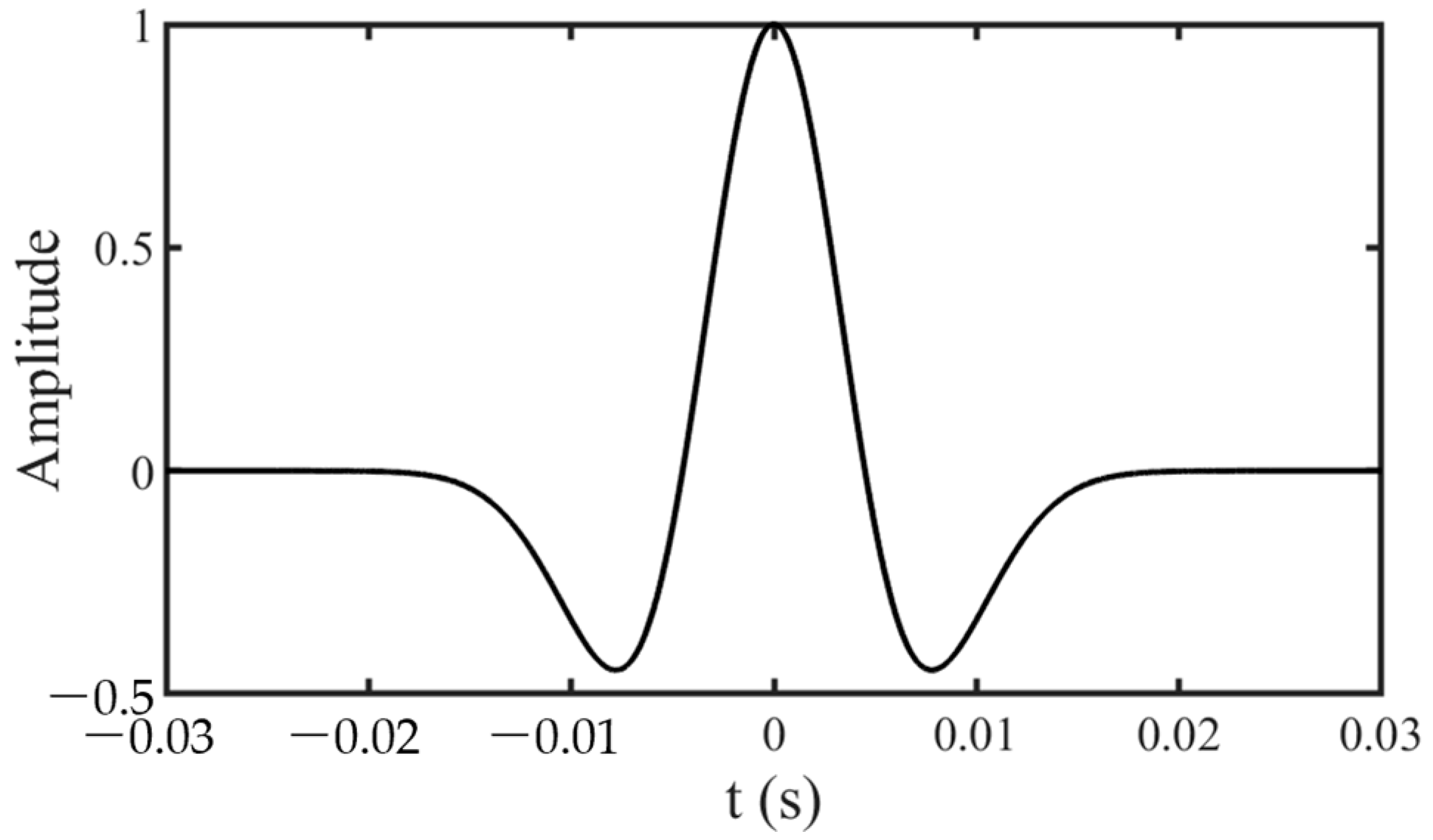
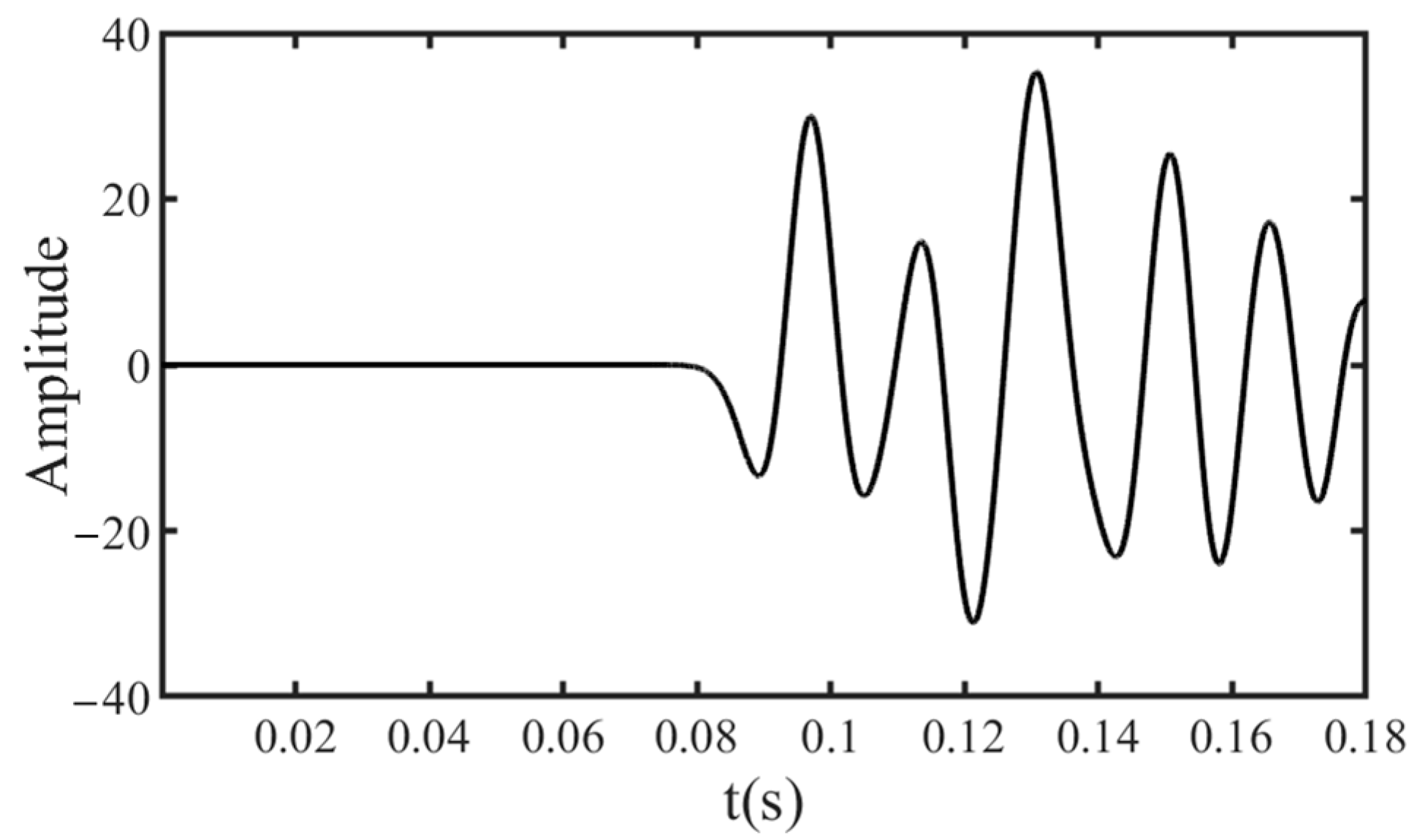
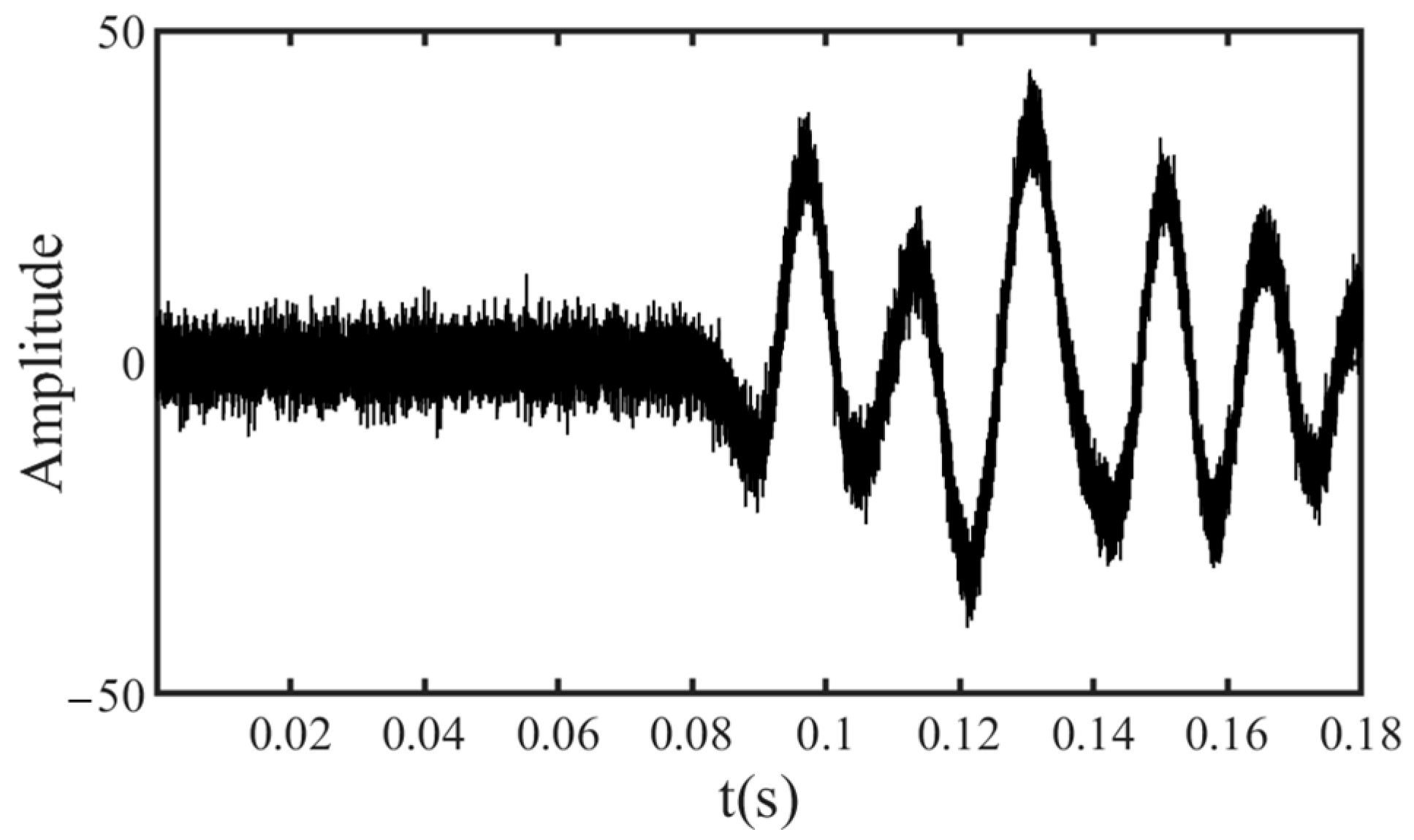
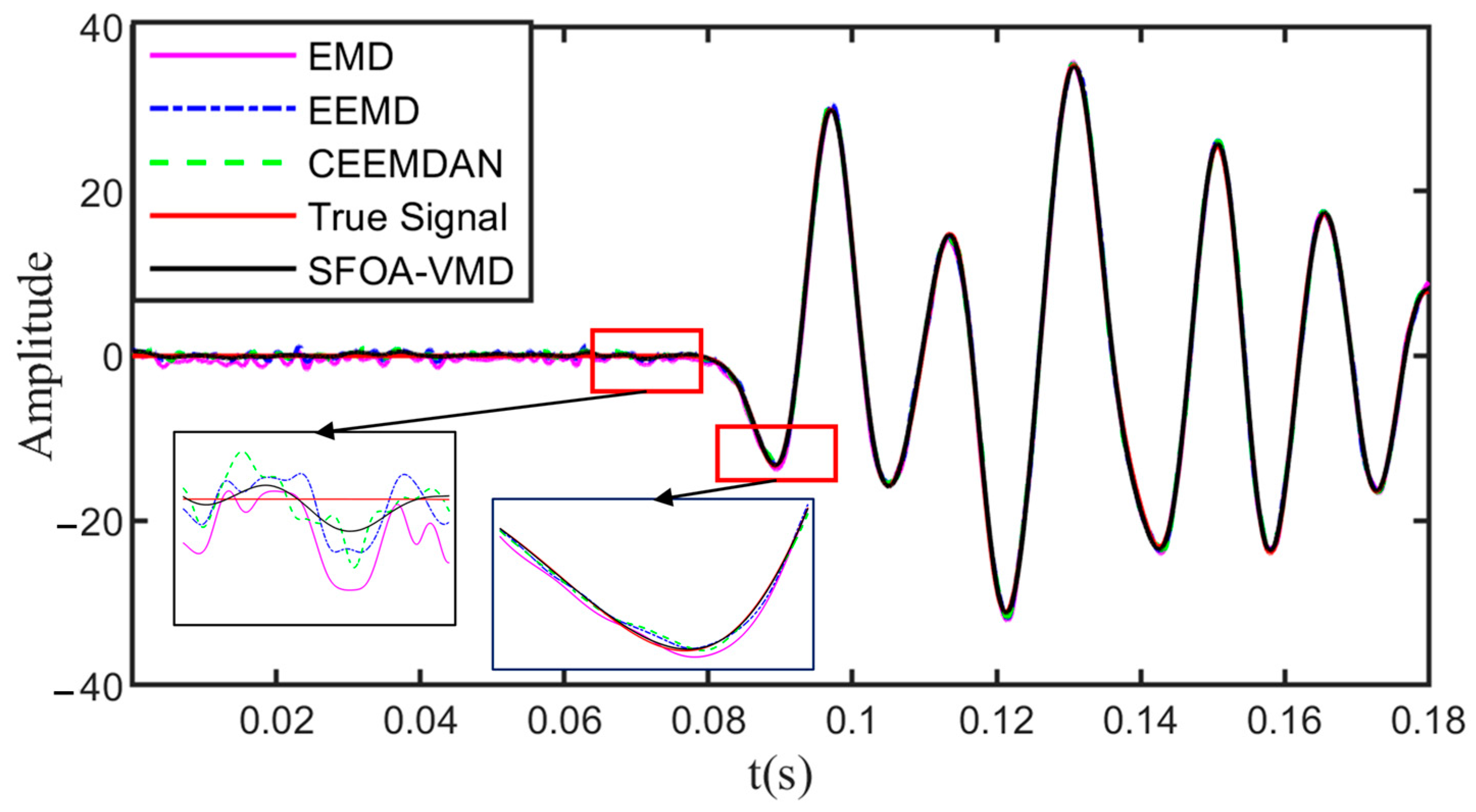
4.1. Synthetic Signal Test
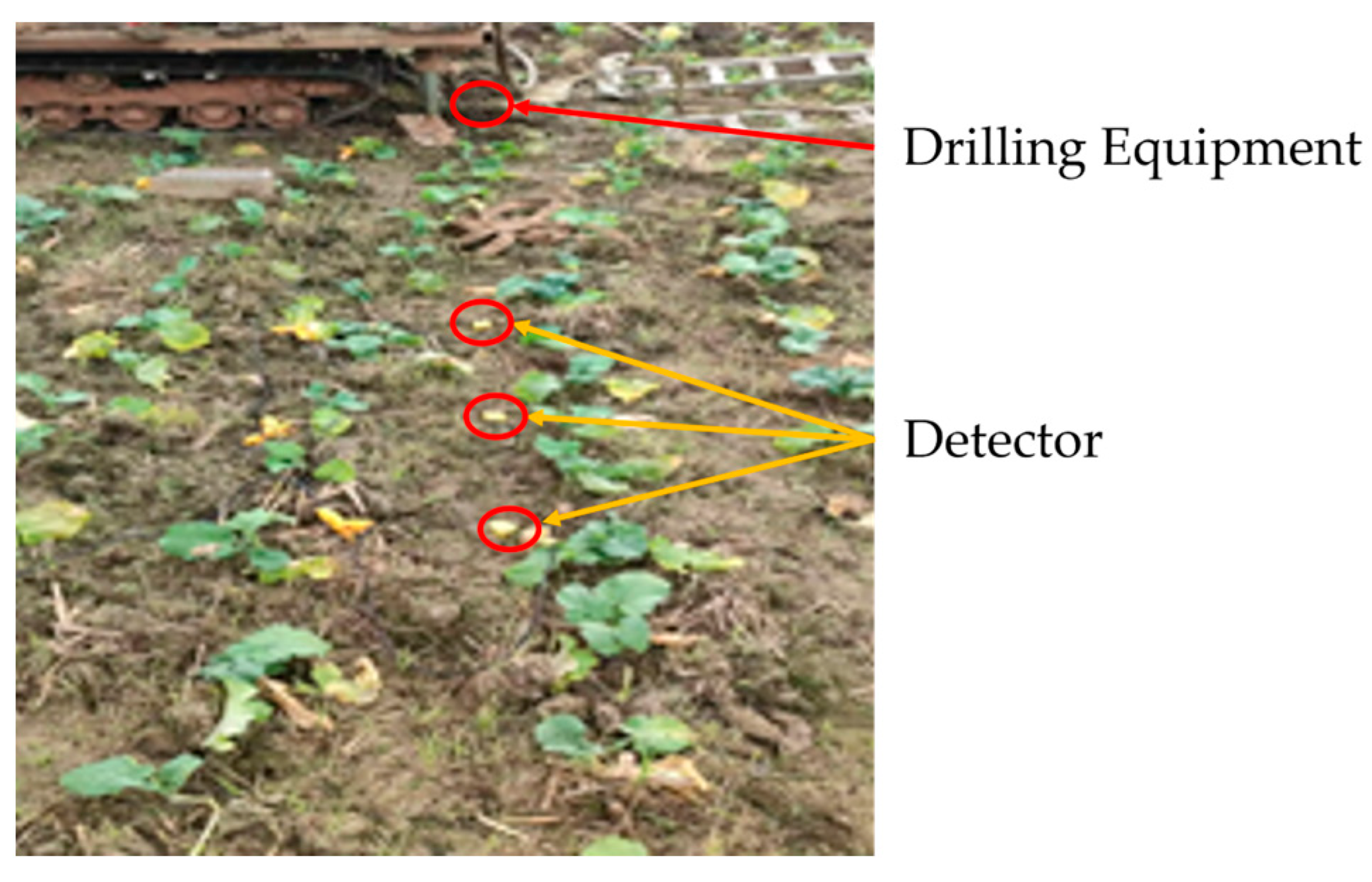
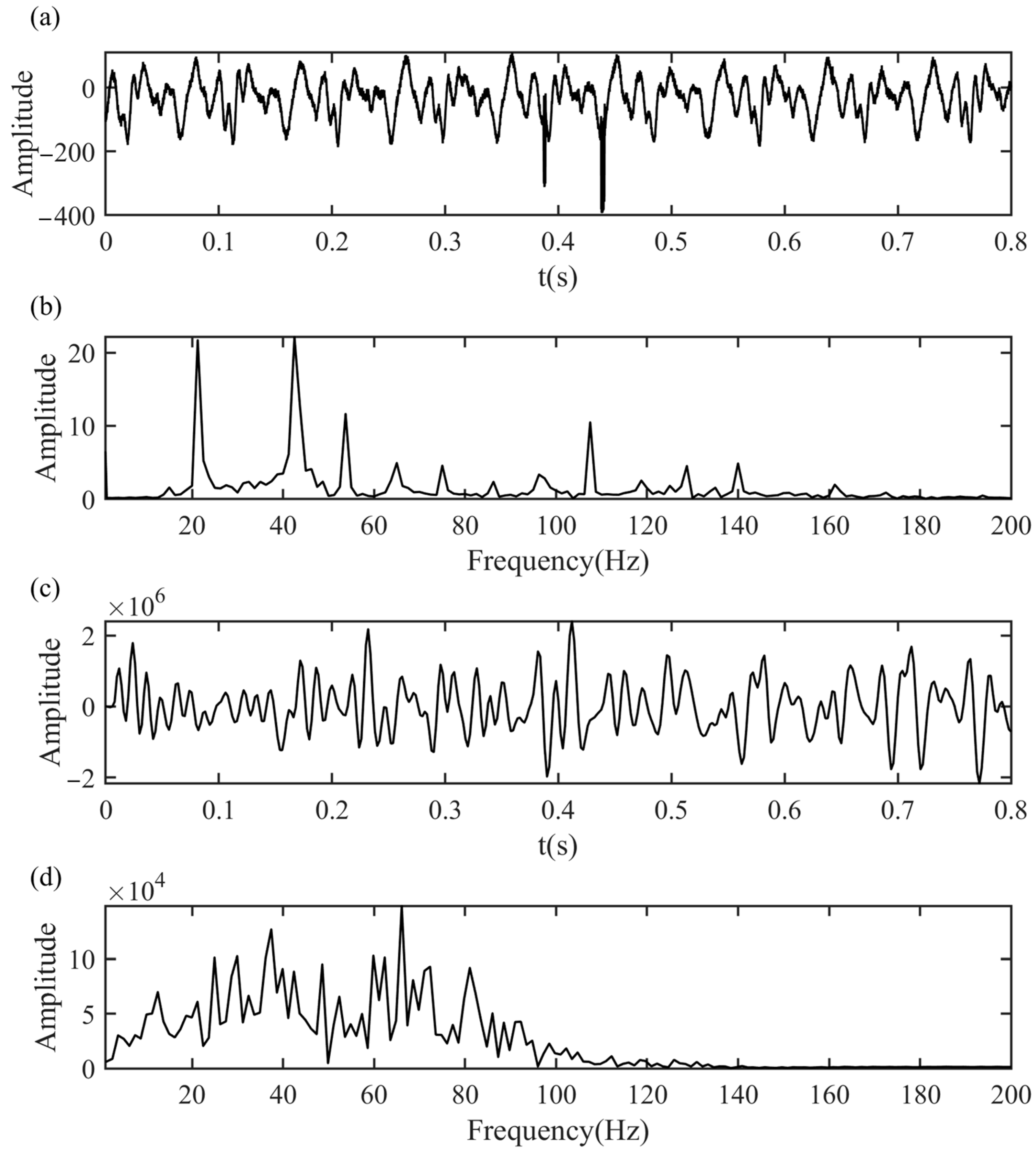
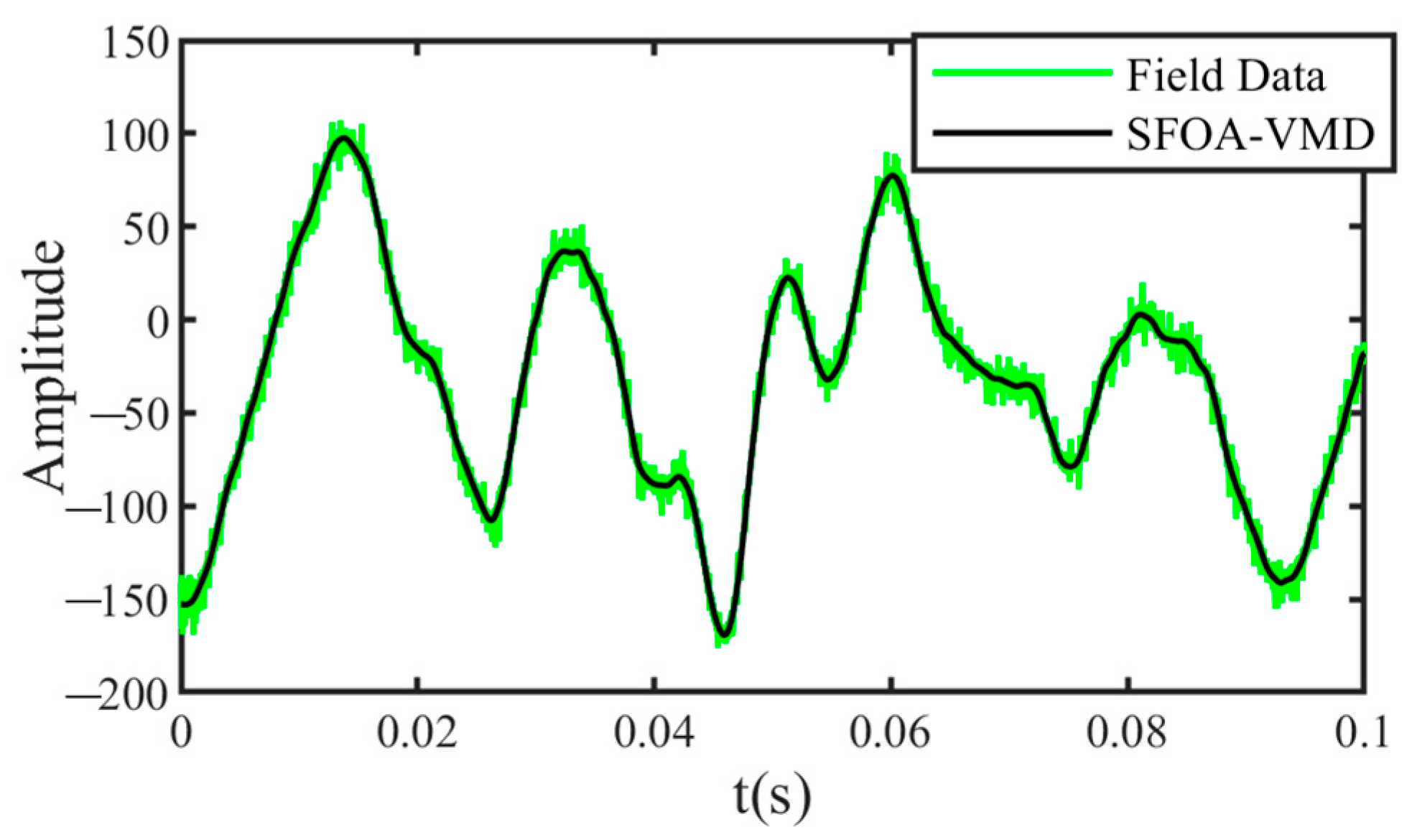
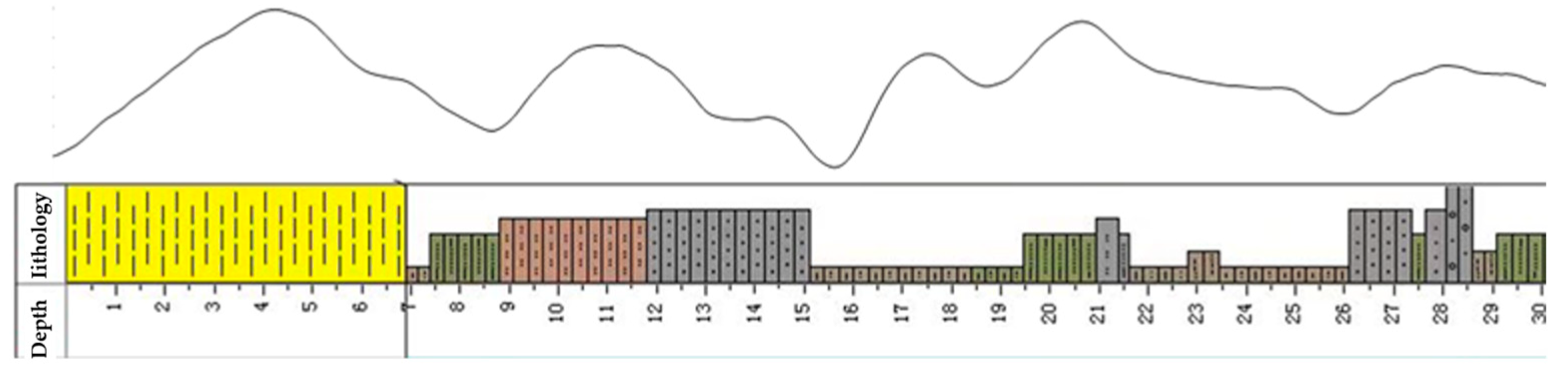
4.2. Field Data Test
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Luo, B. Research and Application Effect of Logging While Drilling Seismic Technology. Ph.D. Thesis, China University of Geosciences, Beijing, China, 2005. [Google Scholar]
- Liu, J.; Zhang, P.; Liu, S.; Hu, X.; Zhang, W.; Liu, H.; Cao, Y. Research on Lithology Identification Technology of Logging While Drilling Seismic Based on EEMD and DE-PNN [J/OL]. J. China Coal Soc. 2025, 1–12. [Google Scholar] [CrossRef]
- Cao, L. Microseismic Signal Denoising Research Based on Wavelet Threshold and Autoencoder. Master’s Thesis, Dalian University of Technology, Dalian, China, 2022. [Google Scholar] [CrossRef]
- Wang, L. Research on Key Technologies of Logging While Drilling Seismic Exploration. Ph.D. Thesis, Ocean University of China, Qingdao, China, 2009. [Google Scholar]
- Wu, M. Research and Application of Time-Frequency Analysis of Seismic Data Based on Empirical Mode Decomposition (EMD). Master’s Thesis, Chengdu University of Technology, Chengdu, China, 2020. [Google Scholar] [CrossRef]
- Wang, P. Numerical Simulation Study of Logging While Drilling Seismic Wavefield. Master’s Thesis, Institute of Geophysics, China Earthquake Administration, Beijing, China, 2009. [Google Scholar]
- Liu, W.; Liu, Y.; Li, S.; Chen, Y. A Review of Variational Mode Decomposition in Seismic Data Analysis. Surv. Geophys. 2022, 44, 323–355. [Google Scholar] [CrossRef]
- Xue, Y.J.; Cao, J.X.; Wang, X.J.; Li, Y.X.; Du, J. Recent Developments in Local Wave Decomposition Methods for Understanding Seismic Data: Application to Seismic Interpretation. Surv. Geophys. 2019, 40, 1185–1210. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shin, Q.; Zheng, H.H.; Yen, N.C.; Tung, C.C.; Liu, H.H. The Empirical Mode Decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. Royal Soc. Lond. A 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Smith, J.S. The Local Mean Decomposition and Its Application to EEG Perception Data. J. R. Soc. Interface 2005, 2, 443–454. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.; Huang, N.E. Ensemble Empirical Mode Decomposition: A Noise-assisted Data Analysis Method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Yeh, J.R.; Shieh, J.S.; Huang, N.E. Complementary ensemble empirical mode decomposition: A novel noise enhanced data analysis method. Adv. Adapt. Data Anal. 2010, 2, 135–156. [Google Scholar] [CrossRef]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A complete ensemble empirical mode decomposition with adaptive noise. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 4144–4147. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Huang, Y.; Bao, H.; Qi, X. Seismic Random Noise Attenuation Method Based on Variational Mode Decomposition and Correlation Coefficients. Electronics 2018, 7, 280. [Google Scholar] [CrossRef]
- Wang, Z.; Chang, X.; Wang, J.; Du, W.; Duan, N. Dang changying. Gearbox fault diagnosis based on permutation entropy optimized variational mode decomposition. Trans. Chin. Soc. Agric. Eng. (Trans. CSAE) 2018, 34, 59–66. [Google Scholar] [CrossRef]
- Yang, K.; Kwak, G.; Cho, K.; Huh, J. Wind farm layout optimization for wake effect uniformity. Energy 2019, 183, 983–995. [Google Scholar] [CrossRef]
- Miao, Y.; Zhao, M.; Lin, J. Identification of mechanical compound-fault based on the improved parameter-adaptive variational mode decomposition. ISA Trans. 2019, 84, 82–95. [Google Scholar] [CrossRef]
- Shi, J.; Zhu, M.; Shen, H.; Bian, Y.X.; Cui, K.; Zhu, R.H. Denoising Method of Hydrophone Signals Based on VMD and Wavelet Threshold. J. Sens. Technol. 2020, 33, 1003–1012. [Google Scholar]
- Lin, Z.; Chengbo, Y.; Yong, T. A Method for Pulse Signal Denoising Based on VMD Parameter Optimization and Grey Wolf Optimizer. J. Phys. Conf. Ser. 2021, 1920, 012100. [Google Scholar]
- Li, Q.; Li, M.; Fu, C.; Wang, J. Fault Diagnosis of Wind Turbine Component Based on an Improved Dung Beetle Optimization Algorithm to Optimize Support Vector Machine. Electronics 2024, 13, 3621. [Google Scholar] [CrossRef]
- Li, S.; Zhao, Q.; Liu, J.; Zhang, X.; Hou, J. Noise Reduction of Steam Trap Based on SSA-VMD Improved Wavelet Threshold Function. Sensors 2025, 25, 1573. [Google Scholar] [CrossRef]
- Wang, H.; Wang, H.; Chen, P.; Wu, S.; Ma, Y. Bearing Small Sample Fault Diagnosis Model Based on IVYA-FMD and EELM-Yager. Mech. Electr. Eng. 2025, 42, 1093–1101. [Google Scholar]
- Liang, T.; Lu, H.; Sun, H. Application of Parameter Optimized Variational Mode Decomposition Method in Fault Feature Extraction of Rolling Bearing. Entropy 2021, 23, 520. [Google Scholar] [CrossRef]
- Ma, Z.; Zhang, Y. A study on rolling bearing fault diagnosis using RIME-VMD. Sci. Rep. 2025, 15, 4712. [Google Scholar] [CrossRef] [PubMed]
- Ying, L.; Peng, W.; Wu, S.; Peng, B. Fault Feature Extraction Method of Reciprocating Compressor Based on AO-VMD. Mech. Electr. Eng. 2023, 40, 673–681. [Google Scholar]
- Wang, X.-B.; Yang, Z.-X.; Yan, X.-A. Novel Particle Swarm Optimization-Based Variational Mode Decomposition Method for the Fault Diagnosis of Complex Rotating Machinery. IEEE/ASME Trans. Mechatron. 2018, 23, 68–79. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, W.; Zou, Y. Fault Diagnosis Method of Rolling Bearing Based on Optimized VMD Combined with BP Neural Network. J. Jilin Eng. Norm. Univ. 2023, 39, 91–96. [Google Scholar]
- Jiang, T.; Yu, C.; Huang, K.; Zhao, J.; Wang, L. Bridge Signal Denoising Method Based on AO Algorithm Optimized VMD Parameters Combined with Wavelet Threshold. China J. Highw. Transp. 2023, 36, 158–168. [Google Scholar] [CrossRef]
- Huang, L.; Fu, J.; Yuan, C.; Lv, Q.; Gao, J. Millimeter-Wave Radar Heart Rate Detection Based on GWO-VMD [J/OL]. J. Univ. Electron. Sci. Technol. China 2025, 54, 1–7. Available online: http://kns.cnki.net/kcms/detail/51.1207.TN.20250115.1401.004.html (accessed on 26 June 2025).
- Li, X.; Ni, R.; Ji, Z. ICG signal denoising based on ICEEMDAN and PSO-VMD methods. Phys. Eng. Sci. Med. 2024, 47, 1547–1556. [Google Scholar] [CrossRef]
- Bai, Y.; Chen, Z.; Zhang, X.; Liu, B.; Chen, G. Denoising Method of Partial Discharge Ultrasonic Signals of Oil-Immersed Transformers Based on Improved VMD-WT. J. Electron. Meas. Instrum. 2024, 38, 237–249. [Google Scholar] [CrossRef]
- Zhong, C.; Li, G.; Meng, Z.; Li, H.; Yildiz, A.R.; Mirjalili, S. Starfish optimization algorithm (SFOA): A bio-inspired metaheuristic algorithm for global optimization compared with 100 optimizers. Neural Comput. Appl. 2024, 37, 3641–3683. [Google Scholar] [CrossRef]
- Chen, L.; Bai, X.; He, Y.; Jia, D.; Li, Y.; Li, Z. Multi-fault diagnosis and damage assessment of rolling bearings based on IDBO-VMD and CNN-BiLSTM. Sci. Rep. 2025, 15, 31121. [Google Scholar] [CrossRef] [PubMed]
- Xiong, L.; Fan, K.; Huang, J.; Liu, Z.; Fan, A. Adaptive filtering of UAV acoustic signals based on MFDE-LOF fundamental frequency filtering and PSO-VMD harmonic reconstruction. Appl. Acoust. 2025, 240, 110923. [Google Scholar] [CrossRef]
- Li, H.; Li, S.; Sun, J.; Huang, B.; Zhang, J.; Gao, M. Ultrasound signal processing based on joint GWO-VMD wavelet threshold functions. Measurement 2024, 226, 114143. [Google Scholar] [CrossRef]
- Lay, T. Quantitative Seismology, Second Edition. Eos Trans. Am. Geophys. Union 2003, 84, 202. [Google Scholar] [CrossRef]
- Gardner, G.H.F.; Gardner, L.W.; Gregory, A.R. Formation Velocity and Density—The Diagnostic Basics for Stratigraphic Traps. Geophysics 1974, 39, 770–780. [Google Scholar] [CrossRef]
- Ricker, N.H. Transient Waves in Visco-Clastic Media; Elsevier: New York, NY, USA, 1977; Volume 45. [Google Scholar] [CrossRef]
- Yilmaz, O. Seismic Data Analysis: Processing, Inversion, and Interpretation of Seismic Data; Society of Exploration Geophysicists: Tulsa, OK, USA, 2001; 1028p. [Google Scholar]
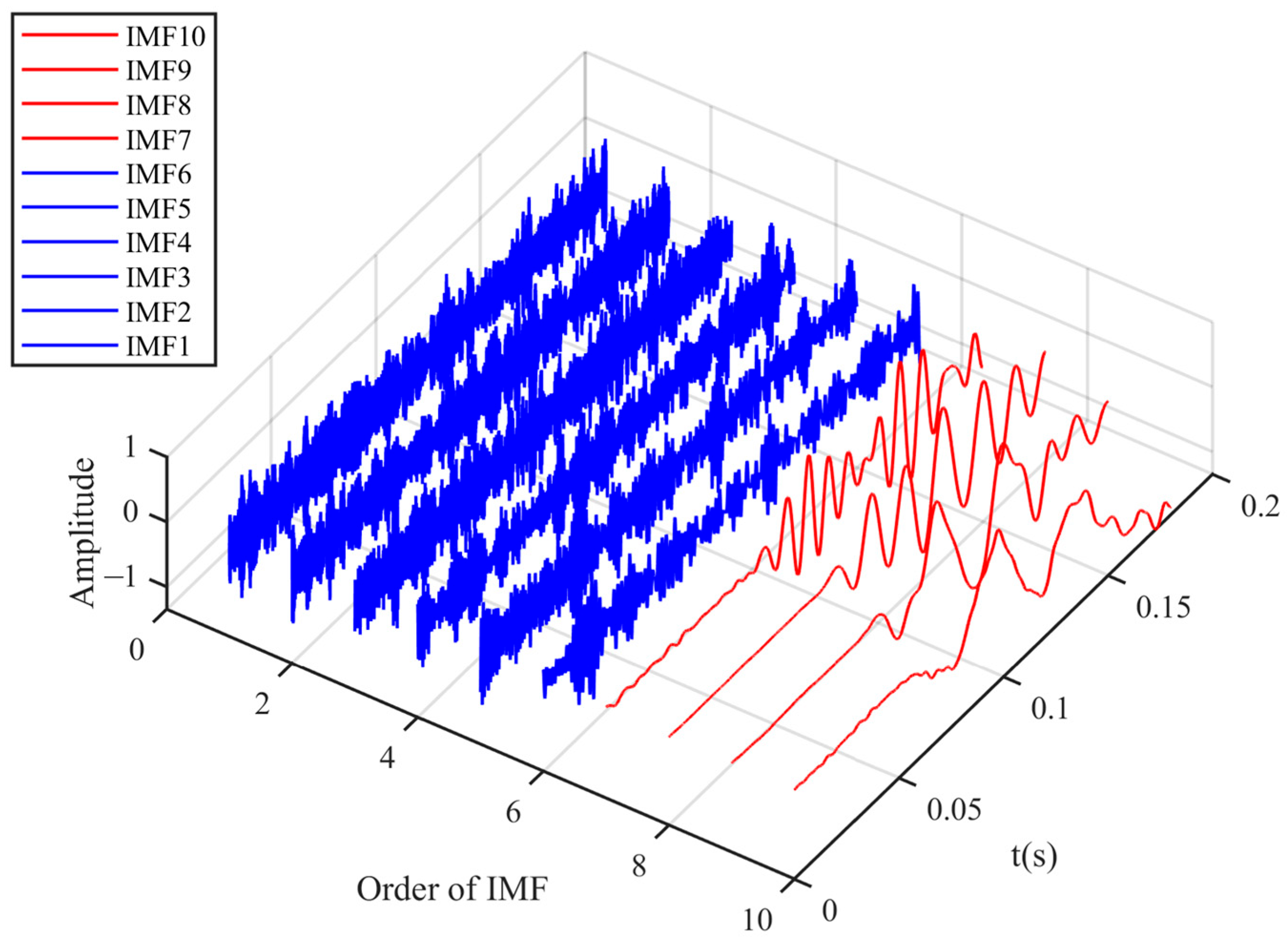


| IMF | Correlation Coefficient |
|---|---|
| IMF1 | 0.0348 |
| IMF2 | 0.0291 |
| IMF3 | 0.0280 |
| IMF4 | 0.0298 |
| IMF5 | 0.0312 |
| IMF6 | 0.0393 |
| IMF7 | 0.0952 |
| IMF8 | 0.5002 |
| IMF9 | 0.9622 |
| IMF10 | 0.3379 |
| Methods | SNR | RMSE | RRMSE | NCC |
|---|---|---|---|---|
| EMD | 28.2443 | 4.691 × 10−4 | 0.0387 | 0.99925 |
| EEMD | 30.6813 | 3.543 × 10−4 | 0.0292 | 0.99957 |
| CEEMDAN | 31.4108 | 3.258 × 10−4 | 0.0269 | 0.99964 |
| SFOA-VMD | 34.2514 | 2.349 × 10−4 | 0.0194 | 0.99981 |
| IMF | Correlation Coefficient |
|---|---|
| IMF 1 | 0.0071 |
| IMF2 | 0.0038 |
| IMF3 | 0.0045 |
| IMF4 | 0.0038 |
| IMF5 | 0.0050 |
| IMF6 | 0.0075 |
| IMF7 | 0.0355 |
| IMF8 | 0.3650 |
| IMF9 | 0.4778 |
| IMF10 | 0.9987 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Lin, K.; Guo, G.; Wen, X.; Chen, D. Research on High-Density Discrete Seismic Signal Denoising Processing Method Based on the SFOA-VMD Algorithm. Geosciences 2025, 15, 409. https://doi.org/10.3390/geosciences15110409
Wang X, Lin K, Guo G, Wen X, Chen D. Research on High-Density Discrete Seismic Signal Denoising Processing Method Based on the SFOA-VMD Algorithm. Geosciences. 2025; 15(11):409. https://doi.org/10.3390/geosciences15110409
Chicago/Turabian StyleWang, Xiaoji, Kai Lin, Guangzhao Guo, Xiaotao Wen, and Dan Chen. 2025. "Research on High-Density Discrete Seismic Signal Denoising Processing Method Based on the SFOA-VMD Algorithm" Geosciences 15, no. 11: 409. https://doi.org/10.3390/geosciences15110409
APA StyleWang, X., Lin, K., Guo, G., Wen, X., & Chen, D. (2025). Research on High-Density Discrete Seismic Signal Denoising Processing Method Based on the SFOA-VMD Algorithm. Geosciences, 15(11), 409. https://doi.org/10.3390/geosciences15110409





