Soil Water Potential in Geosciences: An Overview
Abstract
:1. Introduction
2. Abnormal Behavior of Absorbed Soil Water
3. Definition of Soil Water Potential
4. Mathematical Formulation
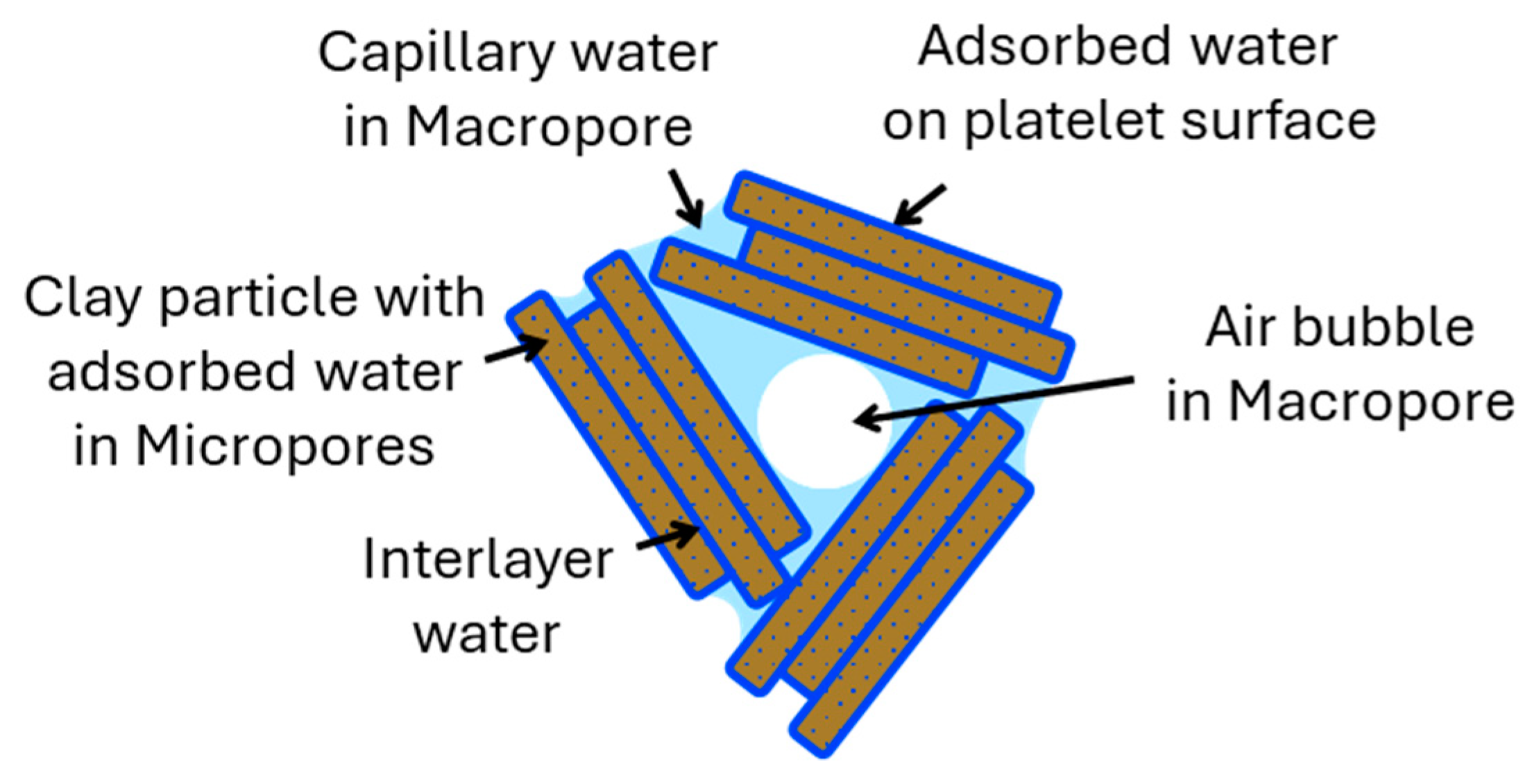
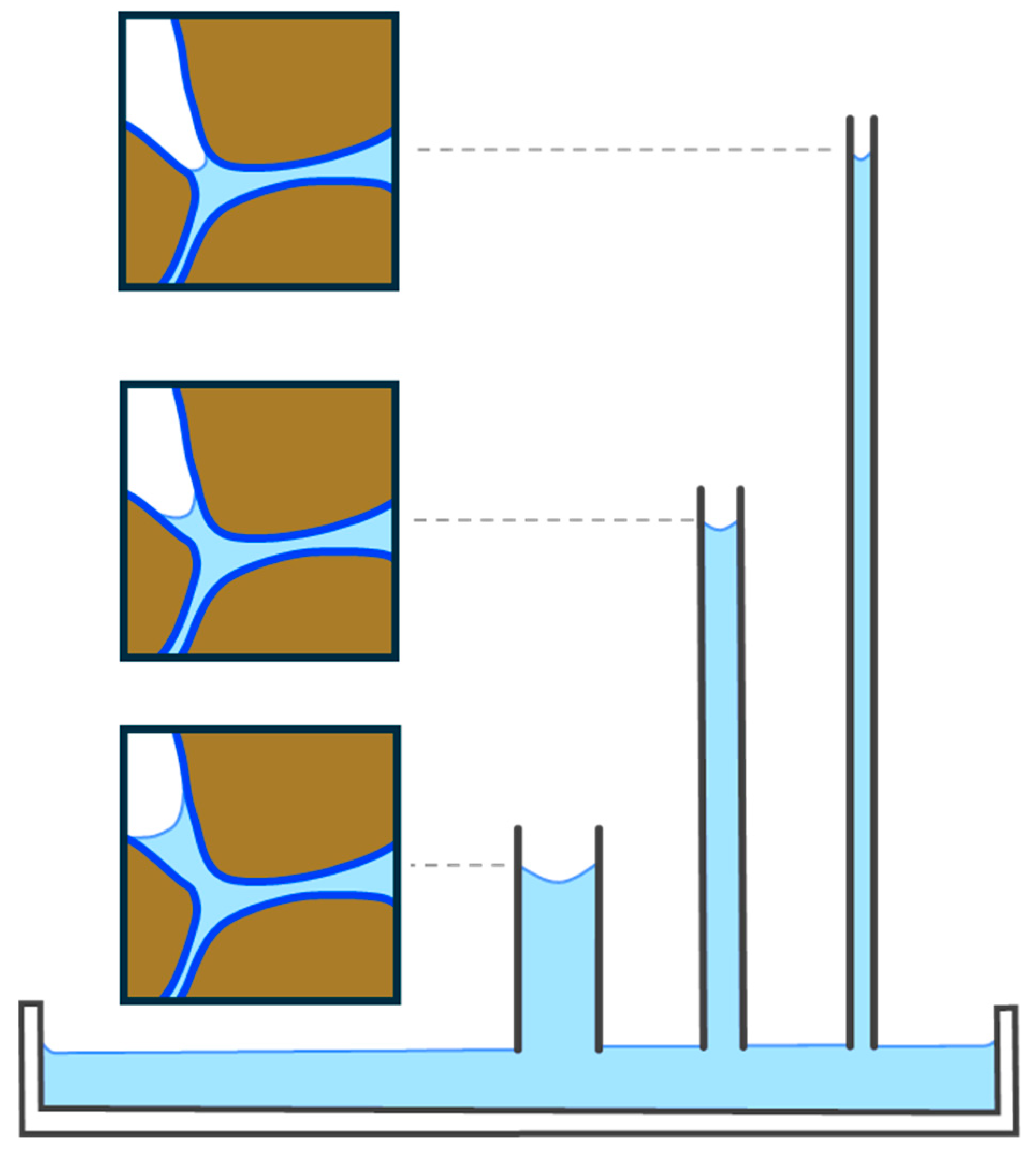
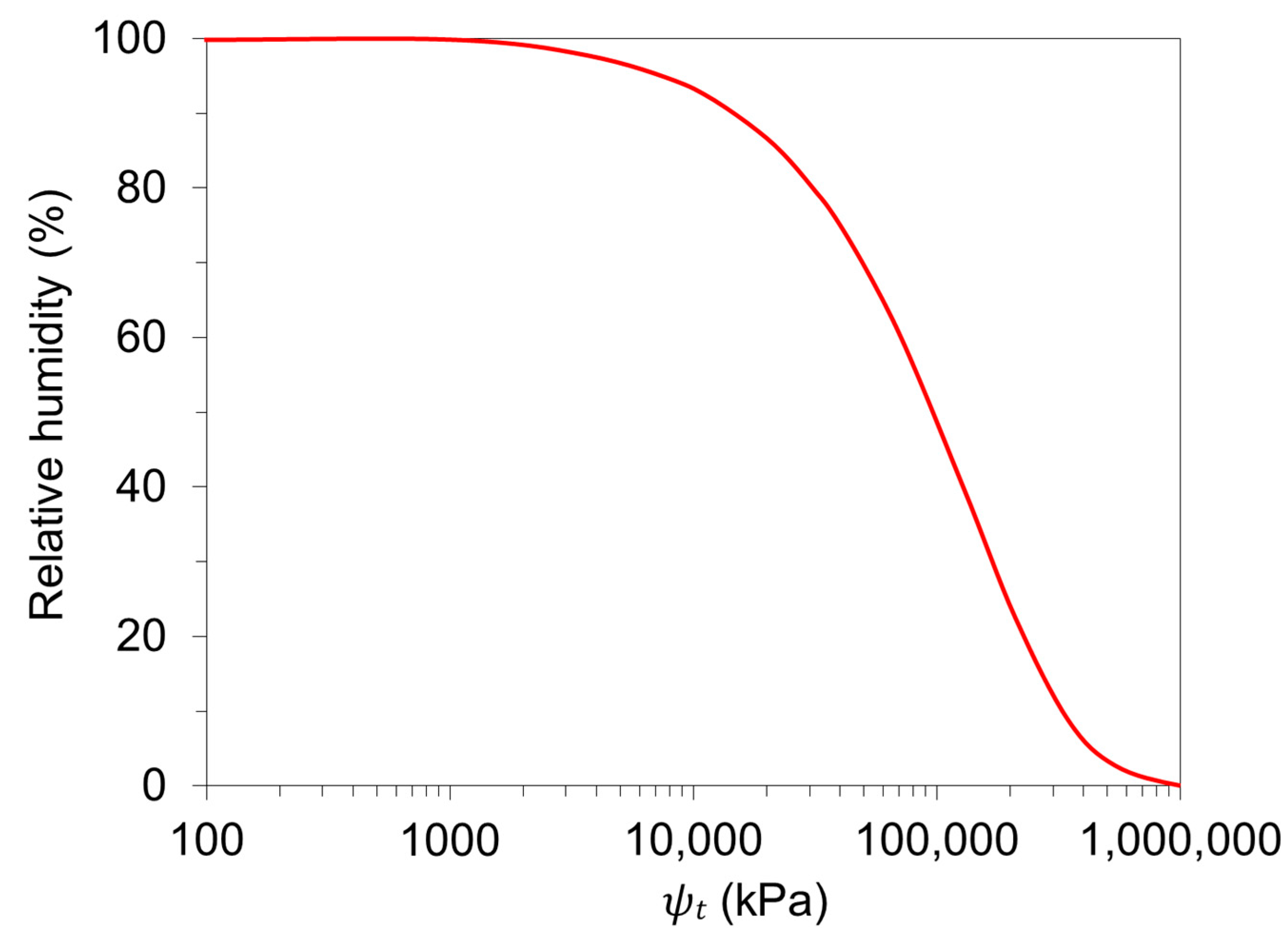
5. Matric Potential—Capillarity and Adsorption
6. Soil Water Potential Measurements
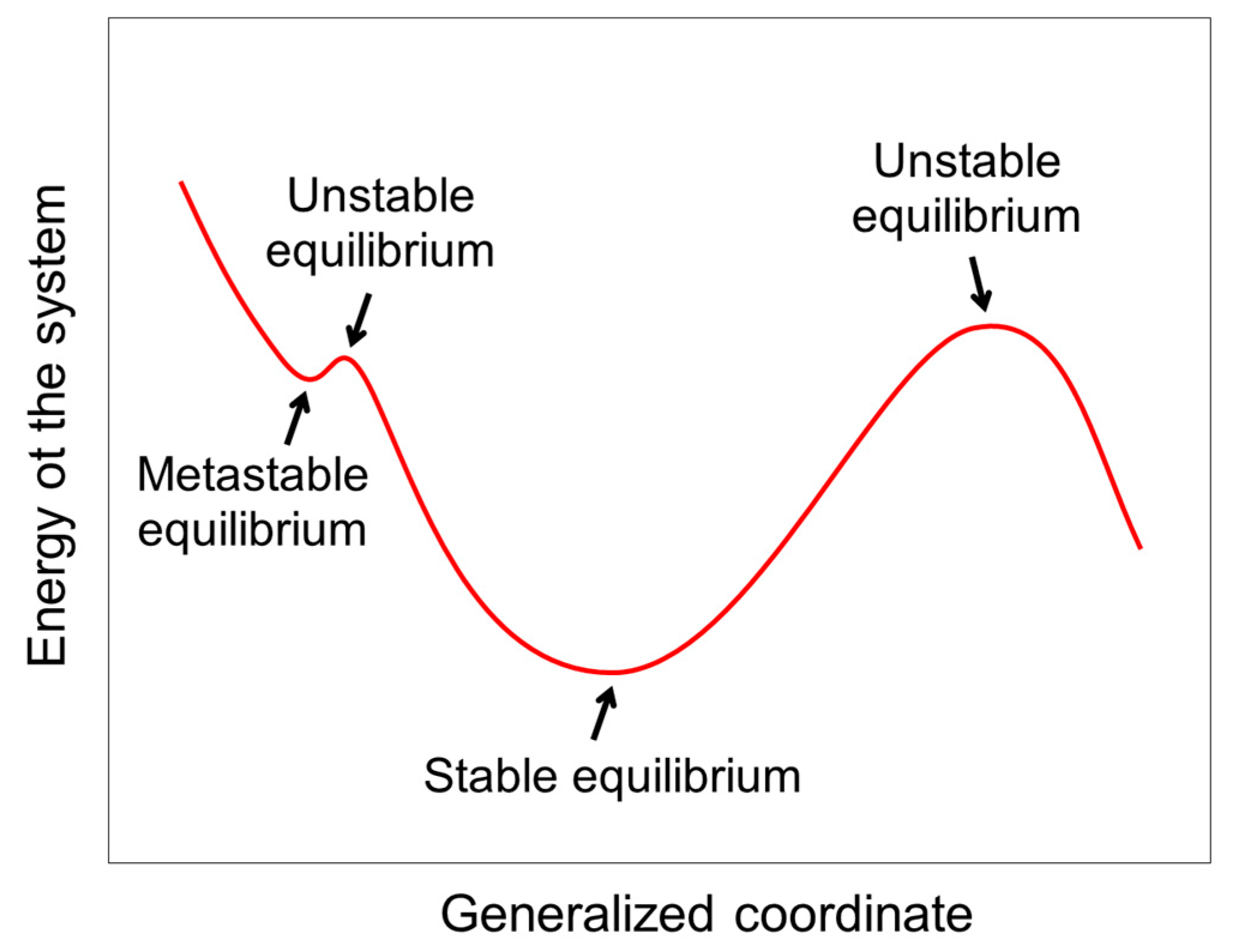
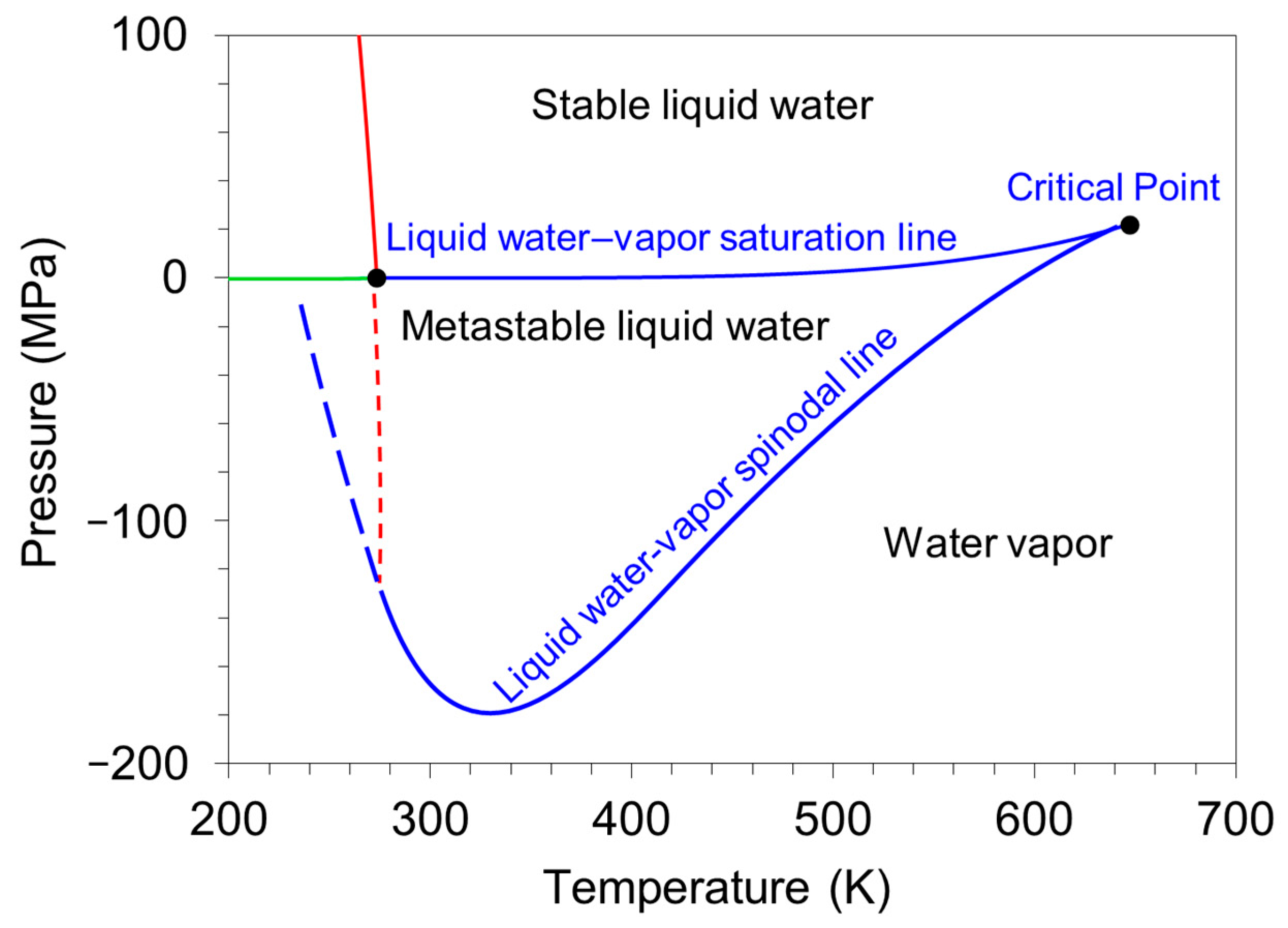
7. Cavitation
8. Flow in Unsaturated Soil
- Retention curves are based on equilibrium states rather than flow states and therefore must be altered to match non-equilibrium conditions (e.g., [85]). In addition, the retention curve is affected by the soil properties (density and void ratio) [86] and confined stress history [55,87,88], parameters that are not taken into account in the majority of cases. Moreover, in some cases, the hysteresis between wetting and drying cycles is not taken into account. Pitfalls in the interpretation of the gravimetric water content-based soil water characteristic curve for deformable porous media were reviewed by [89].
- There are some limitations to Darcy’s law, primarily for macroscopic and multi-phase fluid flow [90]. In particular, experiments [91,92,93] indicated that Darcy’s law is not valid for describing water flow in clayey soils due to highly non-linear relationships between water flux and the hydraulic gradient. Moreover, assumptions built into the law [90] need to be considered. These limitations are not taken into account in many cases.
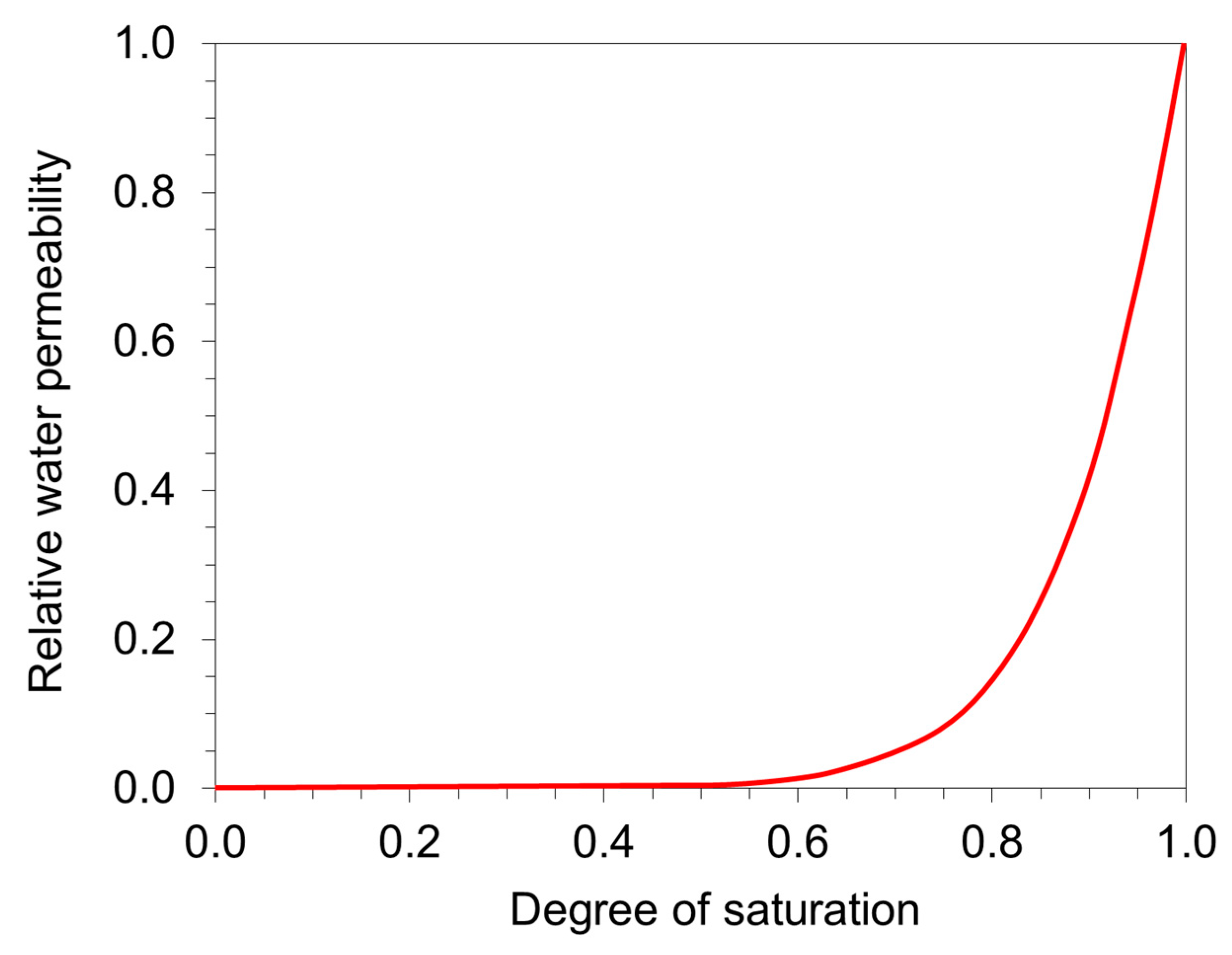
- As soil saturation decreases, water potential can reach thousands of kPa (especially in clayey soils). A water potential with an extremely high value is accompanied by a high value derivative ( in Equation (6)); therefore, in order to obtain a reasonable water flux, it is necessary to multiply the enormous water potential by a nearly zero permeability (e.g., [43,94,95]). For example, Figure 12 shows the relative water permeability, which is the permeability in unsaturated conditions relative to saturated conditions for Boom clay (after [43]). However, multiple different magnitudes are problematic from a mathematical perspective, especially when applied to numerical analysis [96,97].
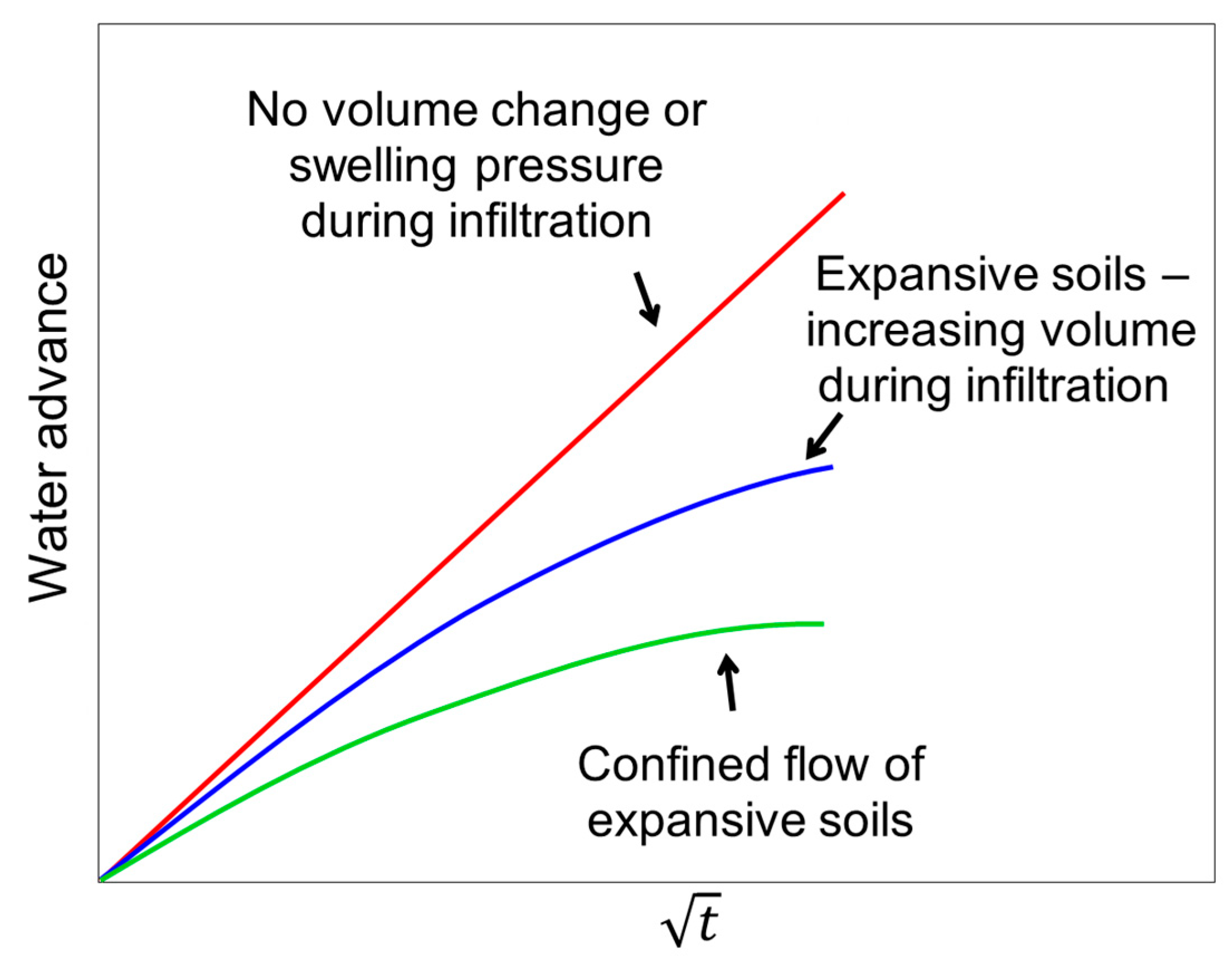
9. Flow in Swelling Soil
10. Soil Water Potential in the Geomechanics Field
11. Numerical Methods of Unsaturated Soil Problems
12. The Effect of Gravity Potential
13. Summary and Conclusions
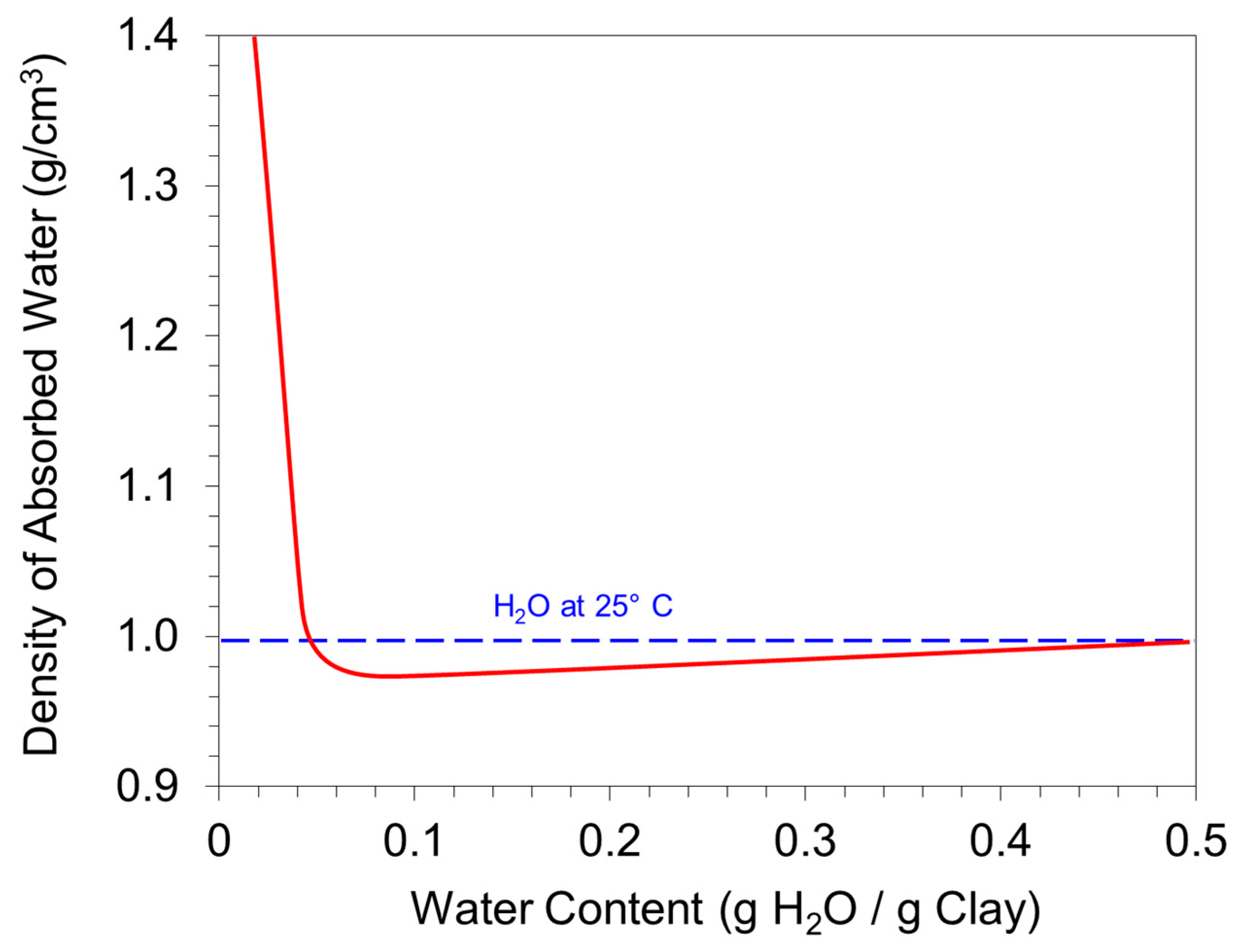
- Interactions between water and soil particles differentiate the physical properties of soil water from that of free water; water in soil pores does not freeze at 0 °C and can reach significantly higher density values than 1 g/cm3. Therefore, analyzing absorbed soil water may require different approaches and techniques than analyzing free water based on how the water interacts with soils.
- Soil water potential is typically defined as the sum of three independent potential functions: gravitational, osmotic, and matric, where three independent state variables are assumed to create the three independent potentials. This definition is questionable because osmotic and matric potentials exhibit substantial coupling effects. Furthermore, from a mathematical perspective, the matric potential dominates the total potential because of its high values, and the gravitational potential may appear to be negligible. Gravitational potential may, however, lead to different flow mechanisms that may alter the soil’s mechanical behavior. Therefore, calculating the total water potential as the algebraic sum of the different potentials may be not valid.
- By definition, soil water potential is an energy variable rather than a mechanical stress. It may not be an error to sum the matric potential with the gravity potential if the potential is a stress variable; however, since it is not a stress variable, it might be an error.
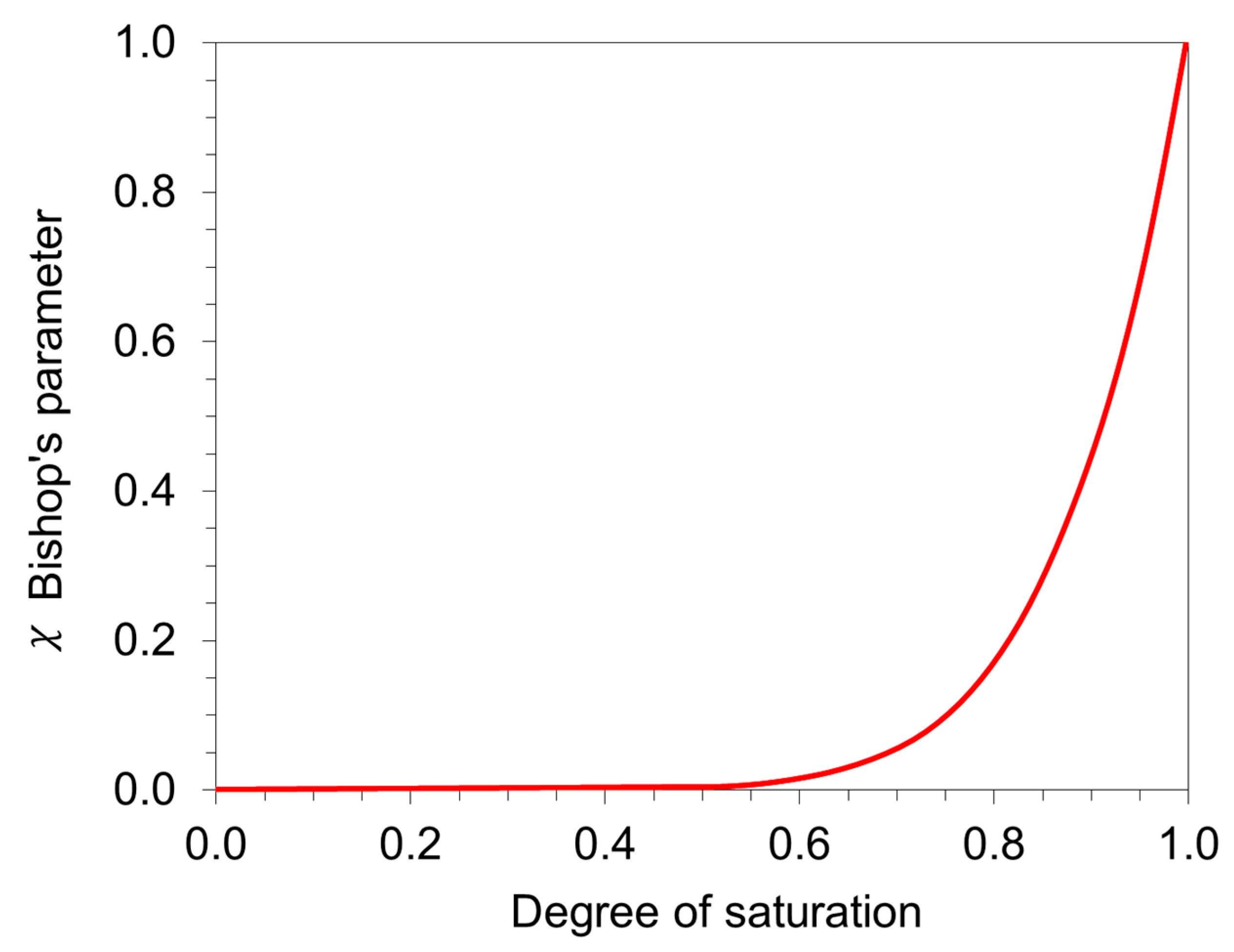
- In clayey soils, water potential can reach thousands of kPa as saturation decreases. When these conditions are considered in the flow equations, the potential of the water is multiplied by a permeability that is almost zero. Additionally, in constitutive laws in geomechanics, the water potential is multiplied by a coefficient with an almost zero value, such as Bishop’s parameter. However, multiple different magnitudes may be problematic from a mathematical perspective, especially when applied to numerical analysis.
- It is often suggested that the matric potential be defined analogously to the capillary potential (i.e., the difference between air pressure and water pressure) by comparing pores in soil to capillary tubes with small radiuses. In this definition, all the physicochemical mechanisms associated with water adsorption are ignored, i.e., the energy contribution from adsorption is not considered.
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bhattacharya, A. Soil Water Deficit and Physiological Issues in Plants; Springer: Singapore, 2021; pp. 393–488. [Google Scholar]
- Boyer, J.S. Relationship of water potential to growth of leaves. Plant Physiol. 1968, 43, 1056–1062. [Google Scholar] [PubMed]
- Jordan, W.R.; Ritchie, J.T. Influence of soil water stress on evaporation, root absorption, and internal water status of cotton. Plant Physiol. 1971, 48, 783–788. [Google Scholar]
- Lafolie, F.; Bruckler, L.; Tardieu, F. Modeling root water potential and soil-root water transport: I. Model presentation. Soil Sci. Soc. Am. J. 1991, 55, 1203–1212. [Google Scholar]
- Ma, Y.; Liu, H.; Yu, Y.; Guo, L.; Zhao, W.; Yetemen, O. Revisiting Soil Water Potential: Towards a Better Understanding of Soil and Plant Interactions. Water 2022, 14, 3721. [Google Scholar] [CrossRef]
- Bittelli, M. Measuring soil water potential for water management in agriculture: A review. Sustainability 2010, 2, 1226–1251. [Google Scholar] [CrossRef]
- Bianchi, A.; Masseroni, D.; Thalheimer, M.; Medici, L.D.; Facchi, A. Field irrigation management through soil water potential measurements: A review. Ital. J. Agrometeorol. 2017, 22, 25–38. [Google Scholar]
- Yang, J.; Liu, K.; Wang, Z.; Du, Y.; Zhang, J. Water-saving and high-yielding irrigation for lowland rice by controlling limiting values of soil water potential. J. Integr. Plant Biol. 2007, 49, 1445–1454. [Google Scholar]
- Thamir, F.; McBride, C.M. Measurements of Matric and Water Potentials in Unsaturated Tuff at Yucca Mountain, Nevada (No. CONF-8511172-7); Goodson and Associates, Inc.: Denver, CO, USA; Western State Coll. of Colorado: Gunnison, CO, USA, 1985. [Google Scholar]
- Ringler, J.W. Monitoring the Hydrology of Soils for On-Site Wastewater Treatment Systems Using Matric Potential Sensors. Master’s Thesis, The Ohio State University, Columbus, OH, USA, 2009. [Google Scholar]
- Buckingham, E. Studies on the Movement of Soil Moisture (Bull. 38); USDA Bureau of Soils: Washington, DC, USA, 1907.
- Corey, A.T.; Kemper, W.D. Concept of total potential in water and its limitations. Soil Sci. 1961, 91, 299–302. [Google Scholar]
- Richardson, J.L.; Wilding, L.P.; Daniels, R.B. Recharge and discharge of groundwater in aquic conditions illustrated with flow net analysis. Geoderma 1992, 53, 65–78. [Google Scholar]
- Williams, J.; Prebble, R.E.; Williams, W.T.; Hignett, C.T. The influence of texture, structure and clay mineralogy on the soil moisture characteristic. Soil Res. 1983, 21, 15–32. [Google Scholar]
- Nachum, S.; Talesnick, M.; Weisberg, E.; Zaidenberg, R. Development of swelling induced shear and slickensides in Vertisols. Geoderma 2022, 409, 115629. [Google Scholar]
- Raats, P.A. Developments in soil–water physics since the mid 1960s. Geoderma 2001, 100, 355–387. [Google Scholar]
- Alonso, E.E.; Gens, A.; Josa, A. A constitutive model for partially saturated soils. Géotechnique 1990, 40, 405–430. [Google Scholar]
- Loret, B.; Khalili, N. An effective stress elastic–plastic model for unsaturated porous media. Mech. Mater 2002, 34, 97–116. [Google Scholar]
- Tarantino, A. A water retention model for deformable soils. Géotechnique 2009, 59, 751–762. [Google Scholar] [CrossRef]
- Vanapalli, S.; Lu, L. A State-of-the Art Review of 1-D Heave Prediction Methods for Expansive Soils. Int. J. Geotech. Eng 2012, 6, 15–41. [Google Scholar]
- Rahardjo, H.; Kim, Y.; Satyanaga, A. Role of unsaturated soil mechanics in geotechnical engineering. Int. J. Geo-Eng. 2019, 10, 8. [Google Scholar]
- Tarantino, A.; Roberts-Self, E. Transpiration in the water-limited regime: Soil-plant-atmosphere interactions. In Proceedings of the 8th International Conference on Unsaturated Soils (UNSAT 2023), Milos Island, Greece, 3–5 May 2023; Volume 382. [Google Scholar]
- Mohamed, A.M.; Yong, R.N.; Cheung, S.C. Temperature dependence of soil water potential. Geotech. Test. J. 1992, 15, 330–339. [Google Scholar]
- Vanderborght, J.; Fetzer, T.; Mosthaf, K.; Smits, K.M.; Helmig, R. Heat and water transport in soils and across the soil-atmosphere interface: 1. Theory and different model concepts. Water Resour. Res. 2017, 53, 1057–1079. [Google Scholar] [CrossRef]
- Cardoso, R.; Dias, A.S. Study of the electrical resistivity of compacted kaolin based on water potential. Eng. Geol. 2017, 226, 1–11. [Google Scholar]
- Hansson, K.; Simunek, J.; Mizoguchi, M.; Lundin, L.C.; Van Genuchten, M.T. Water flow and heat transport in frozen soil: Numerical solution and freeze–thaw applications. Vadose Zone J. 2004, 3, 693–704. [Google Scholar]
- Martin, R.T. Adsorbed water on clay: A review. Clays Clay Miner. 1962, 9, 28–70. [Google Scholar]
- Jacinto, A.C.; Villar, M.V.; Ledesma, A. Influence of water density on the water-retention curve of expansive clays. Géotechnique 2012, 62, 657–667. [Google Scholar] [CrossRef]
- Zhang, C.; Lu, N. What is the range of soil water density? Critical reviews with a unified model. Rev. Geophys. 2018, 56, 532–562. [Google Scholar] [CrossRef]
- Guggenheim, S.; Brady, J.; Mogk, D.; Perkins, D. Introduction to the properties of clay minerals. In Teaching Mineralogy; Brady, J.B., Mogk, D.W., Perkins, D., Eds.; Mineralogical Society of America: Washington, DC, USA, 1997; pp. 371–388. [Google Scholar]
- Tournassat, C.; Bourg, I.C.; Steefel, C.I.; Bergaya, F. Surface properties of clay minerals. In Natural and Engineered Clay Barriers; Elsevier: Amsterdam, The Netherlands, 2015; Volume 6, pp. 5–31. [Google Scholar]
- Kassif, G.; Livneh, M.; Wiseman, G. Pavements on Expansive Clays; Academic Press: Jerusalem, Israel, 1969. [Google Scholar]
- Briggs, L.J. The Mechanics of Soil Moisture (Bull. 10); USDA Bureau of Soils: Washington, DC, USA, 1897.
- Aslyng, H.C.; Bolt, G.H.; Miller, R.D.; Gardner, W.R.; Rode, A.A.; Holmes, J.W.; Youngs, E.G. Soil Physics Terminology; International Society of Soil Science: Vienna, Austria, 1963; Volume 22. [Google Scholar]
- Iwata, S. On the definition of soil water potentials as proposed by the I.S.S.S. in 1963. Soil Sci. 1972, 114, 88–92. [Google Scholar] [CrossRef]
- Bolt, G.H.; Iwata, S.; Peck, A.J.; Raats, P.A.C.; Rode, A.A.; Vachaud, G.; Voronin, A.D. Soil physics terminology. Int. Soc. Soil Sci. 1976, 49, 26–36. [Google Scholar]
- Bolt, G.H.; Miller, R.D. Calculation of total and component potentials of water in soil. Eos Trans. Am. Geophys. Union 1958, 39, 917–928. [Google Scholar]
- Campbell, G.S. Soil water potential measurement: An overview. Irrig. Sci. 1988, 9, 265–273. [Google Scholar]
- Luo, S.; Lu, N.; Zhang, C.; Likos, W. Soil water potential: A historical perspective and recent breakthroughs. Vadose Zone J. 2022, 21, e20203. [Google Scholar]
- Sugden, S. CLXXV.—The determination of surface tension from the rise in capillary tubes. J. Chem. Soc. Trans. 1921, 119, 1483–1492. [Google Scholar] [CrossRef]
- Gens, A.; Alonso, E.E.; Suriol, J.; Lloret, A. Effect of structure on the volumetric behavior of a compacted soil. In Proceedings of the First International Conference on Unsaturated Soils, Paris, France, 6–8 September 1995; pp. 83–88. [Google Scholar]
- Delage, P.; Audiguier, M.; Cui, Y.J.; Howat, D. Microstructure of a compacted silt. Can. Geotech. J 1996, 33, 150–158. [Google Scholar]
- Romero, E.; Gens, A.; Lloret, A. Water permeability, water retention and microstructure of unsaturated compacted Boom clay. Eng. Geol. 1999, 54, 117–127. [Google Scholar] [CrossRef]
- Beven, K.; Germann, P. Macropores and water flow in soils. Water Resour. Res. 1982, 18, 1311–1325. [Google Scholar] [CrossRef]
- Gerke, H.H.; Van Genuchten, M.T. A dual-porosity model for simulating the preferential movement of water and solutes in structured porous media. Water Resour. Res. 1993, 29, 305–319. [Google Scholar] [CrossRef]
- Tarantino, A. Unsaturated soils: Compacted versus reconstituted states. In Proceedings of the 5th International Conference on Unsaturated Soil, Barcelona, Spain, 6–8 September 2010; pp. 113–136. [Google Scholar]
- Alonso, E.E.; Pinyol, N.M.; Gens, A. Compacted soil behaviour: Initial state and constitutive modelling. Géotechnique 2013, 63, 463–478. [Google Scholar] [CrossRef]
- Wen, T.; Luo, Y.; Tang, M.; Chen, X.; Shao, L. Effects of representative elementary volume size on three-dimensional pore characteristics for modified granite residual soil. J. Hydrol. 2024, 643, 132006. [Google Scholar] [CrossRef]
- Baker, R.; Frydman, S. Unsaturated soil mechanics; critical review of physical foundations. Eng. Geol. 2009, 106, 26–39. [Google Scholar] [CrossRef]
- Frydman, S.; Baker, R. Theoretical soil-water characteristic curves based on adsorption, cavitation, and a double porosity model. Int. J. Geomech. 2009, 9, 250–257. [Google Scholar] [CrossRef]
- Pedrotti, M.; Tarantino, A. A conceptual constitutive model unifying slurried (saturated), compacted (unsaturated) and dry states. Géotechnique 2019, 69, 217–233. [Google Scholar] [CrossRef]
- Janssen, D.J.; Dempsey, B.J. Soil-moisture properties of subgrade soils. Transp. Res. Rec. 1981, 790, 61–66. [Google Scholar]
- Tuller, M.; Or, D. Water retention and characteristic curve. In Encyclopedia of Soils in the Environment, 4; Hillel, D., Ed.; Elsevier Ltd.: Oxford, UK, 2004; pp. 278–289. [Google Scholar]
- De Rooij, G.H. Averaged water potentials in soil water and groundwater, and their connection to menisci in soil pores, field-scale flow phenomena, and simple groundwater flows. Hydrol. Earth Syst. Sci. 2011, 15, 1601–1614. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Rahardjo, H.; Fredlund, M.D. Unsaturated Soil Mechanics in Engineering Practice; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Holmes, J.W.; Taylor, S.A.; Richards, S.J. Measurement of soil water. Irrig. Agric. Lands 1967, 11, 275–303. [Google Scholar]
- Papendick, R.I.; Campbell, G.S. Theory and measurement of water potential. In Water Potential Relations in Soil Microbiology; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1981; Volume 9, pp. 1–22. [Google Scholar]
- Tarantino, A.; Ridley, A.M.; Toll, D.G. Field measurement of suction, water content, and water permeability. Geotech. Geol. Eng. 2008, 26, 751–782. [Google Scholar]
- ASTM D5298-16; Standard Test Method for Measurement of Soil Potential (Suction) Using Filter Paper. ASTM International: West Conshohocken, PA, USA, 2014.
- Ridley, A.M.; Burland, J.B. A new instrument for the measurement of soil moisture suction. Géotechnique 1993, 43, 321–324. [Google Scholar]
- Tarantino, A.; Mongiovì, L. Calibration of tensiometer for direct measurements of matric suction. Géotechnique 2003, 53, 137–141. [Google Scholar]
- Take, W.A.; Bolton, M.D. Tensiometer saturation and the reliable measurement of matric suction. Géotechnique 2003, 53, 159–172. [Google Scholar]
- Hilf, J.W. An Investigation of Pore-Water Pressure in Compacted Cohesive Soils. Ph.D. Thesis, University of Colorado at Boulder, Boulder, CO, USA, 1956. [Google Scholar]
- Ng, C.W.; Cui, Y.; Chen, R.U.I.; Delage, P. The axis-translation and osmotic techniques in shear testing of unsaturated soils: A comparison. Soils Found. 2007, 47, 675–684. [Google Scholar] [CrossRef]
- Wang, Y.; Hu, L.; Luo, S.; Lu, N. Soil water isotherm model for particle surface sorption and interlamellar sorption. Vadose Zone J. 2022, 21, e20221. [Google Scholar]
- Arthur, E.; Tuller, M.; Moldrup, P.; Wollesen de Jonge, L. Rapid and fully automated measurement of water vapor sorption isotherms: New opportunities for vadose zone research. Vadose Zone J. 2014, 13, vzj2013-10. [Google Scholar]
- Murray, E.J.; Sivakumar, V. Unsaturated Soils: A Fundamental Interpretation of Soil Behaviour; Wiley-Blackwell: Hoboken, NJ, USA, 2010. [Google Scholar]
- Polen, M.; Brubaker, T.; Somers, J.; Sullivan, R.C. Cleaning up our water: Reducing interferences from nonhomogeneous freezing of “pure” water in droplet freezing assays of ice-nucleating particles. Atmos. Meas. Tech. 2018, 11, 5315–5334. [Google Scholar]
- Caupin, F.; Stroock, A.D. The Stability Limit and other Open Questions on Water at Negative Pressure. In Liquid Polymorphism: Advances in Chemical Physics, 1st ed.; Wiley & Sons, Inc.: Hoboken, NJ, USA, 2013; Volume 152. [Google Scholar]
- Ridley, A.M.; Burland, J.B. Measurement of suction in materials which swell. Appl. Mech. Rev. 1995, 48, 727–732. [Google Scholar]
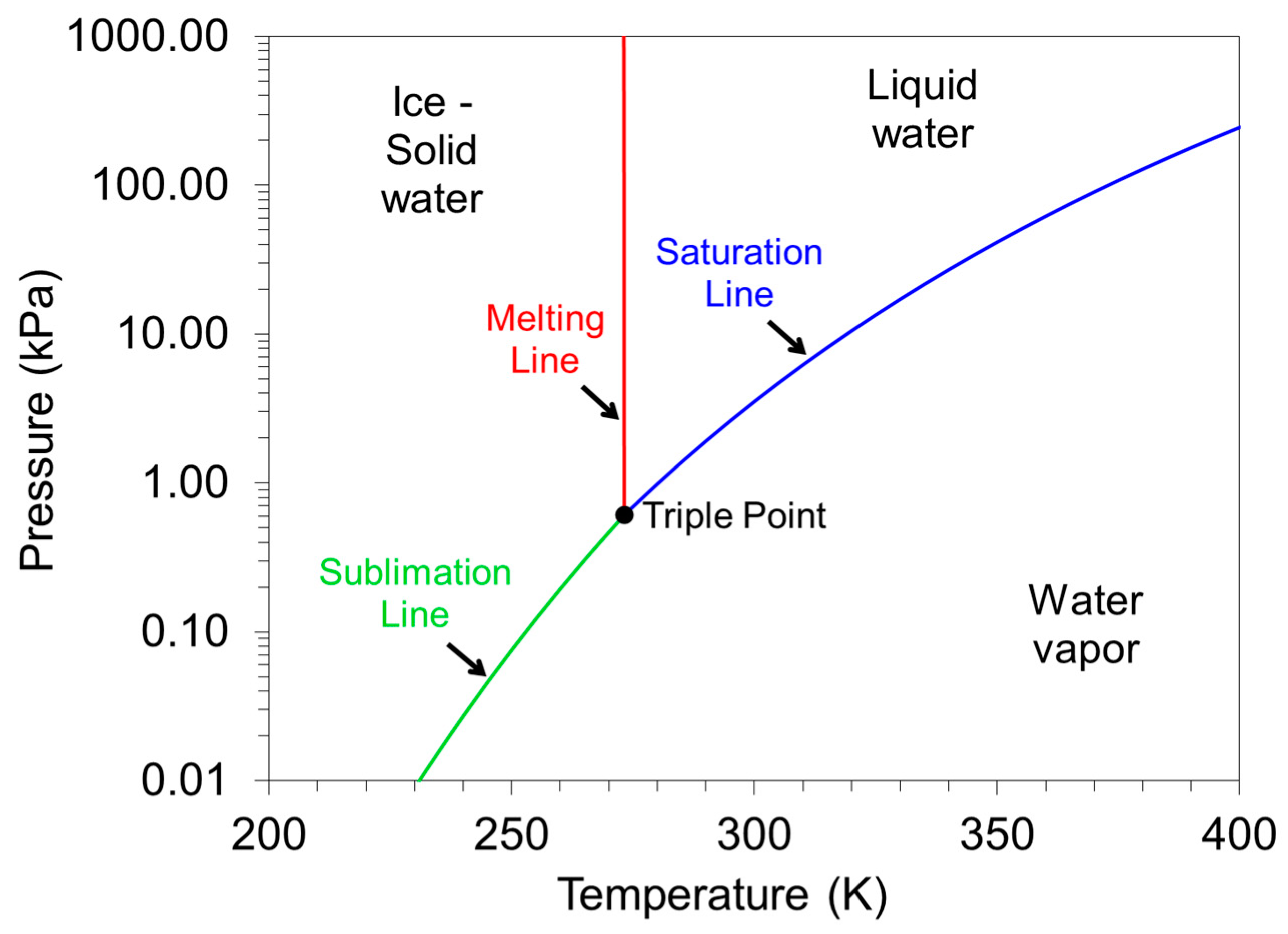
- Nosonovsky, M.; Bhushan, B. Phase behavior of capillary bridges: Towards nanoscale water phase diagram. Phys. Chem. Chem. Phys. 2008, 10, 2137–2144. [Google Scholar] [CrossRef] [PubMed]
- Lassin, A.; Azaroual, M.; Mercury, L. Geochemistry of unsaturated soil systems: Aqueous speciation and solubility of minerals and gases in capillary solutions. Geochim. Cosmochim. Acta 2005, 69, 5187–5201. [Google Scholar]
- Zheng, Q.; Durben, D.J.; Wolf, G.H.; Angell, C.A. Liquids at large negative pressures: Water at the homogeneous nucleation limit. Science 1991, 254, 829–832. [Google Scholar] [PubMed]
- Speedy, R.J. Stability-limit conjecture: An interpretation of the properties of water. J. Phys. Chem. 1982, 86, 982–991. [Google Scholar]
- Karapetyants, M.K. Chemical Thermodynamics; Leib, G., Translator; Mir Publishers: Moscow, Russia, 1978. [Google Scholar]
- Glasser, L. Water, water, everywhere: Phase diagrams of ordinary water substance. J. Chem. Educ. 2004, 81, 414. [Google Scholar]
- Richards, L.A. Capillary conduction of liquids through porous mediums. Physics 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Darcy, H. Les Fontaines Publiques de La Ville de Dijon; Dalmont: Paris, France, 1856. [Google Scholar]
- Brooks, R.H.; Corey, A.T. Hydraulic Properties of Porous Media; Hydrology Paper; Colorado State University: Fort Collins, CO, USA, 1964; Volume 3. [Google Scholar]
- Smiles, D.E.; Rosenthal, M.J. The movement of water in swelling materials. Soil Res. 1968, 6, 237–248. [Google Scholar]
- Zaslavsky, D. Saturated and unsaturated flow equation in an unstable porous medium. Soil Sci. 1964, 98, 317–321. [Google Scholar]
- Smiles, D.E. Hydrology of swelling soils: A review. Soil Res. 2000, 38, 501–521. [Google Scholar]
- Leong, E.C.; Rahardjo, H. Permeability functions for unsaturated soils. J. Geotech. Geoenvironmental Eng. 1997, 123, 1118–1126. [Google Scholar]
- Assouline, S.; Selker, J. Introduction and evaluation of a Weibull hydraulic conductivity-pressure head relationship for unsaturated soils. Water Resour. Res. 2017, 53, 4956–4964. [Google Scholar]
- Schultze, B.; Ippisch, O.; Huwe, B.; Durner, W.; van Genuchten, M.T. Dynamic nonequilibrium during unsaturated water flow. In Characterization and Measurement of the Hydraulic Properties of Unsaturated Porous Media; University of California: Riverside, CA, USA, 1999; pp. 877–892. [Google Scholar]
- Rojas, E.; Chávez, O.; Arroyo, H.; López-Lara, T.; Hernández, J.B.; Horta, J. Modeling the dependency of soil-water retention curve on volumetric deformation. Int. J. Geomech. 2017, 17, 04016039. [Google Scholar]
- Bannour, H.; Stoltz, G.; Delage, P.; Touze-Foltz, N. Effect of stress on water retention of needlepunched geosynthetic clay liners. Geotext. Geomembr. 2014, 42, 629–640. [Google Scholar]
- Gallipoli, D.; Wheeler, S.J.; Karstunen, M. Modelling the variation of degree of saturation in a deformable unsaturated soil. Géotechnique 2003, 53, 105–112. [Google Scholar]
- Pasha, A.Y.; Khoshghalb, A.; Khalili, N. Pitfalls in interpretation of gravimetric water content–based soil-water characteristic curve for deformable porous media. Int. J. Geomech. 2016, 16, D4015004. [Google Scholar]
- Govindarajan, S.K. An overview on extension and limitations of macroscopic Darcy’s law for a single and multi-phase fluid flow through a porous medium. Int. J. Min. Sci 2019, 5, 1–21. [Google Scholar]
- Liu, H.H.; Birkholzer, J. On the relationship between water flux and hydraulic gradient for unsaturated and saturated clay. J. Hydrol. 2012, 475, 242–247. [Google Scholar]
- Liu, H.H.; Li, L.; Birkholzer, J. Unsaturated properties for non-Darcian water flow in clay. J. Hydrol. 2012, 430, 173–178. [Google Scholar]
- Teng, Y.; Li, Z.; Chen, C. Pre-Darcy flows in low-permeability porous media. Hydrogeol. J. 2024, 32, 957–1977. [Google Scholar]
- Zhang, F.; Fredlund, D.G. Examination of the estimation of relative permeability for unsaturated soils. Can. Geotech. J. 2015, 52, 2077–2087. [Google Scholar]
- Cai, G.; Zhou, A.; Sheng, D. Permeability function for unsaturated soils with different initial densities. Can. Geotech. J. 2014, 51, 1456–1467. [Google Scholar]
- Forsythe, G.E. Pitfalls in computation, or why a math book isn’t enough. Am. Math. Mon. 1970, 77, 931–956. [Google Scholar] [CrossRef]
- Burden, R.L.; Faires, J.D. Numerical Analysis, 9th ed.; Cengage Learning Brooks/Cole: Boston, MA, USA, 2010. [Google Scholar]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar]
- Assouline, S.; Or, D. Conceptual and parametric representation of soil hydraulic properties: A review. Vadose Zone J. 2013, 12, vzj2013-07. [Google Scholar]
- Assouline, S.; Tessier, D.; Bruand, A. A conceptual model of the soil water retention curve. Water Resour. Res. 1998, 34, 223–231. [Google Scholar]
- Al Majou, H.; Bruand, A.; Duval, O.; Le Bas, C.; Vautier, A. Prediction of soil water retention properties after stratification by combining texture, bulk density and the type of horizon. Soil Use Manag. 2008, 24, 383–391. [Google Scholar]
- Wang, X.; Gao, Y.; Hou, J.; Yang, J.; Smits, K.; He, H. Machine learning facilitates connections between soil thermal conductivity, soil water content, and soil matric potential. J. Hydrol. 2024, 633, 130950. [Google Scholar]
- Warrick, A.W. Soil Water Dynamics; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Holtzman, R. Effects of pore-scale disorder on fluid displacement in partially-wettable porous media. Sci. Rep. 2016, 6, 36221. [Google Scholar]
- Zhao, B.; MacMinn, C.W.; Primkulov, B.K.; Chen, Y.; Valocchi, A.J.; Zhao, J.; Kang, Q.; Bruning, K.; McClure, J.E.; Miller, C.T.; et al. Comprehensive comparison of pore-scale models for multiphase flow in porous media. Proc. Natl. Acad. Sci. USA 2019, 116, 13799–13806. [Google Scholar]
- Philip, J.R. Kinetics of sorption and volume change in clay-colloid pastes. Soil Res. 1968, 6, 249–267. [Google Scholar]
- Kim, J.; Jaramillo, R.A.; Vauclin, M. Modeling of soil deformation and water flow in a swelling soil. Geoderma 1999, 92, 217–238. [Google Scholar]
- Philip, J.R. Flow in porous media. Annu. Rev. Fluid Mech. 1970, 2, 177–204. [Google Scholar]
- Keissar, I. The Development of a Model for the Prediction of Flow, Strains and Stresses in Expansive Soils. Ph.D. Thesis, Technion-Israel Institute of Technology, Haifa, Israel, 1989. [Google Scholar]
- Philip, J.R. Theory of infiltration. Adv. Hydrosci. 1969, 5, 215–296. [Google Scholar]
- Yong, R.N.; Warkentin, B.P. Soil Properties and Behaviour; Elsevier: Amsterdam, The Netherlands, 1975. [Google Scholar]
- Vardhan, H.; Garg, A.; Li, J.; Garg, A. Measurement of stress dependent permeability of unsaturated clay. Measurement 2016, 91, 371–376. [Google Scholar]
- Jha, B.; Juanes, R. A locally conservative finite element framework for the simulation of coupled flow and reservoir geomechanics. Acta Geotech. 2007, 2, 139–153. [Google Scholar]
- Kim, J.; Tchelepi, H.A.; Juanes, R. Stability, accuracy and efficiency of sequential methods for coupled flow and geomechanics. In SPE reservoir simulation symposium. SPE J. 2009, 16, 249–262. [Google Scholar]
- Khalili, N.; Loret, B. An elasto-plastic model for non-isothermal analysis of flow and deformation in unsaturated porous media: Formulation. Int. J. Solids Struct. 2001, 38, 8305–8330. [Google Scholar]
- Jones, L.D.; Jefferson, I. ICE Manual; ICE Publishing: London, UK, 2015; Ch. C5. [Google Scholar]
- Wang, J.X. Characterization of Expansive Soils in Northern Louisiana. In Proceedings of the Louisiana Transportation Conference, Baton Rouge, LA, USA, 28 February–2 March 2016. [Google Scholar]
- Bishop, A.W. The principle of effective stress. Tek. Ukebl. 1959, 106, 859–863. [Google Scholar]
- Vaunat, J.; Casini, F. A procedure for the direct determination of Bishop’s χ parameter from changes in pore size distribution. Géotechnique 2017, 67, 631–636. [Google Scholar]
- Pereira, J.M.; Coussy, O.; Alonso, E.E.; Vaunat, J.; Olivella, S. Is the degree of saturation a good candidate for Bishop’s X parameter? arXiv 2010, arXiv:1010.2608. [Google Scholar]
- Ofoegbu, G.I.; Dasgupta, B.; Manepally, C.; Stothoff, S.A.; Fedors, R. Modeling the mechanical behavior of unsaturated expansive soils based on Bishop principle of effective stress. Environ. Earth Sci. 2017, 76, 555. [Google Scholar] [CrossRef]
- Einav, I.; Liu, M. Hydrodynamics of non-equilibrium soil water retention. Water Resour. Res. 2023, 59, e2022WR033409. [Google Scholar] [CrossRef]
- Hosseini, R.; Kumar, K. Measuring the effective stress parameter using the multiphase lattice Boltzmann method and investigating the source of its hysteresis. arXiv 2024, arXiv:2501.00661. [Google Scholar]
- Asadi, R.; Zamani Aliabadi, Z. Comparison of numerical methods for the solution of Richards’ equation in layered porous media. Numer. Methods Civ. Eng. 2025, 9, 1–10. [Google Scholar]
- Cheng, X.; Tan, M.; Vanapalli, S. Simple approaches for the design of shallow and deep foundations for unsaturated soils II: Numerical techniques. Indian Geotech. J. 2021, 51, 115–126. [Google Scholar] [CrossRef]
- Nogueira, G.E.; Gonçalves, R.D. Groundwater recharge in phreatic aquifers, a case study: Modeling unsaturated zone and recharge rates of the Rio Claro Aquifer using Hydrus-1D. Holos Environ. 2021, 21, 402–422. [Google Scholar] [CrossRef]
- Romashchenko, M.I.; Bohaienko, V.O.; Matiash, T.V.; Kovalchuk, V.P.; Krucheniuk, A.V. Numerical simulation of irrigation scheduling using fractional Richards equation. Irrig. Sci. 2021, 39, 385–396. [Google Scholar] [CrossRef]
- Banaei, S.M.A.; Javid, A.H.; Hassani, A.H. Numerical simulation of groundwater contaminant transport in porous media. Int. J. Environ. Sci. Technol. 2021, 18, 151–162. [Google Scholar] [CrossRef]
- Simunek, J.; Sejna, M.; Van Genuchten, M.T.; Šimůnek, J.; Šejna, M.; Jacques, D.; Sakai, M. HYDRUS-1D. In Simulating the One-Dimensional Movement of Water, Heat, and Multiple Solutes in Variably-Saturated Media, Version 2; University of California Riverside: Riverside, CA, USA, 1998. [Google Scholar]
- Ijaz, N.; Ye, W.; ur Rehman, Z.; Dai, F.; Ijaz, Z. Numerical study on stability of lignosulphonate-based stabilized surficial layer of unsaturated expansive soil slope considering hydro-mechanical effect. Transp. Geotech. 2022, 32, 100697. [Google Scholar] [CrossRef]
- Lo, W.; Chang, J.; Borja, R.I.; Deng, J.H.; Lee, J.W. Mathematical modeling of consolidation in unsaturated poroelastic soils under fluid flux boundary conditions. J. Hydrol. 2021, 595, 125671. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, L. A critical state constitutive model for unsaturated structured soils. Comput. Geotech. 2022, 140, 104361. [Google Scholar] [CrossRef]
- Amri, A.; Saâdi, Z.; Ababou, R. Modeling two-phase flow with hysteresis: Comparative study of hysteresis models and application. Rock Mech. Rock Eng. 2024, 57, 4333–4354. [Google Scholar]
- Shwan, B. Effect of hydro-mechanical hysteresis on active earth pressure for unsaturated soils. In Proceedings of the UNSAT 2023, Milos Island, Greece, 3–5 May 2023; Volume 382, p. 02006. [Google Scholar]
- Liu, X.; Zhou, A.; Shen, S.L.; Li, J.; Arulrajah, A. Modelling unsaturated soil-structure interfacial behavior by using DEM. Comput. Geotech. 2021, 137, 104305. [Google Scholar]
- Barreto, D.; Leak, J. A guide to modeling the geotechnical behavior of soils using the discrete element method. In Modeling in Geotechnical Engineering; Elsevier: Amsterdam, The Netherlands, 2021; pp. 79–100. [Google Scholar]
- Walunj, A.; Chen, Y.; Tian, Y.; Zeng, Z. Modeling soil–plant–machine dynamics using discrete element method: A review. Agronomy 2023, 13, 1260. [Google Scholar] [CrossRef]
- Alnmr, A.; Hosamo, H.H.; Lyu, C.; Ray, R.P.; Alzawi, M.O. Novel insights in soil mechanics: Integrating experimental investigation with machine learning for unconfined compression parameter prediction of expansive soil. Appl. Sci. 2024, 14, 4819. [Google Scholar] [CrossRef]
- Zhang, Z.; Song, X. Nanoscale soil-water retention mechanism of unsaturated clay via MD and machine learning. Comput. Geotech. 2023, 163, 105678. [Google Scholar]
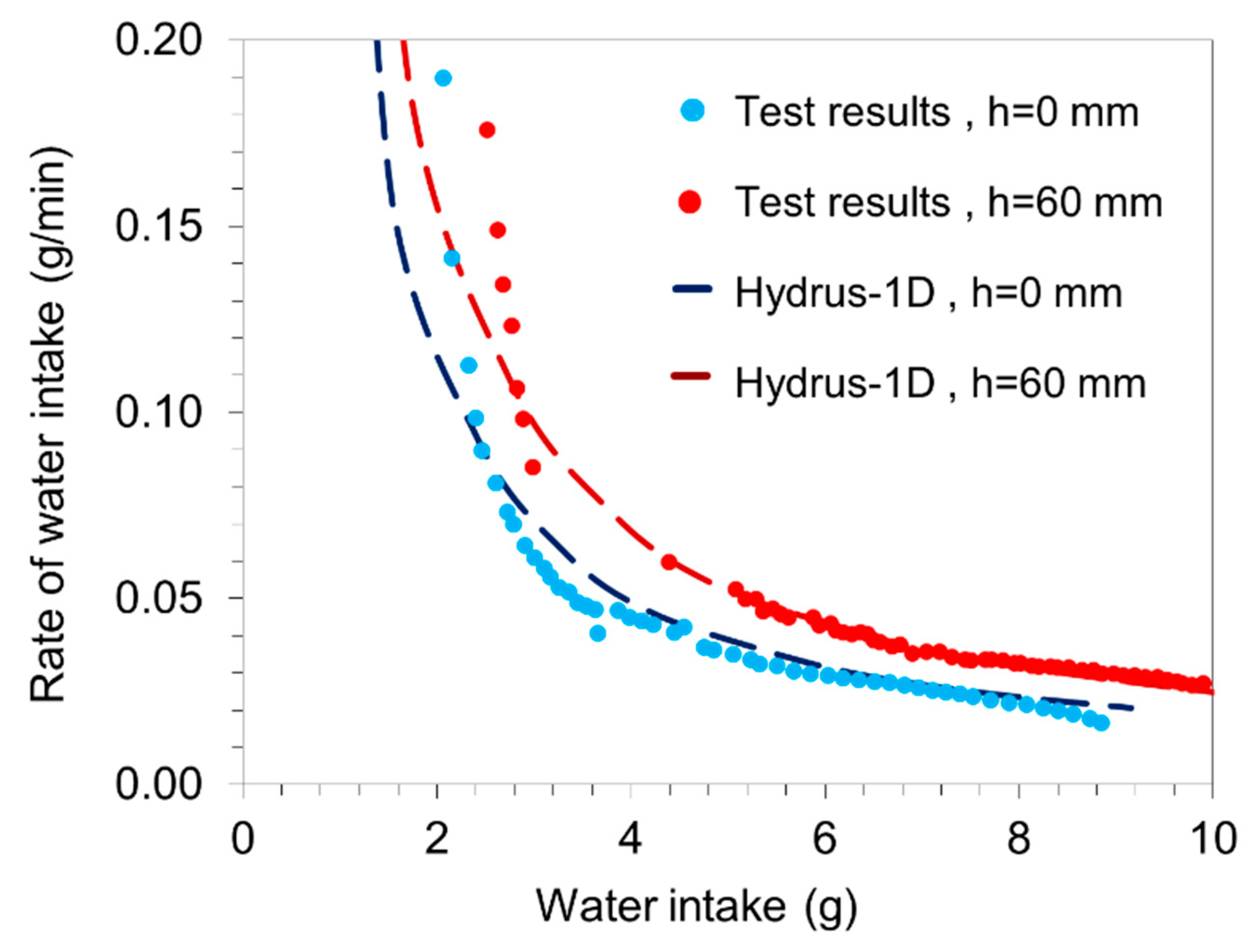
- Nachum, S.; Talesnick, M.; Frydman, S. Effect of external hydraulic head on swelling of unsaturated clay. In Proceedings of the 4th European Conference on Unsaturated Soils; Lisbon, Portugal, 24–26 June 2020; Volume 195. [Google Scholar]
- Nachum, S.; Talesnick, M.; Frydman, S. Swelling of compacted clay as affected by quantity of water intake and soil structure. Geotech. Geol. Eng. 2022, 40, 4961–4974. [Google Scholar]
- Buzzi, O. On the use of dimensional analysis to predict swelling strain. Eng. Geol. 2010, 116, 149–156. [Google Scholar] [CrossRef]
- Nachum, S.; Talesnick, M.; Frydman, S. A new apparatus for studying laterally restrained swell of compacted clay with lateral pressure measurement. Geotech. Test. J 2021, 44, 547–563. [Google Scholar] [CrossRef]
- Corapcioglu, M.Y.; Haridas, A. Transport and fate of microorganisms in porous media: A theoretical investigation. J. Hydrol. 1984, 72, 149–169. [Google Scholar]
- Nachum, S. Swell Magnitude of Unsaturated Clay as Affected by Different Wetting Conditions. Standards 2025, 5, 1. [Google Scholar] [CrossRef]
- Perkins, T.K.; Johnston, O. A review of diffusion and dispersion in porous media. SPE J. 1963, 3, 70–84. [Google Scholar]
- Snethen, D.R.; Johnson, L.D.; Patrick, D.M. An Evaluation of Expedient Methodology for Identification of Potentially Expansive Soils; No. FHWA-RD-77-94; Office of Research and Development, Federal Highway Administration: Washington, DC, USA, 1977.



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nachum, S. Soil Water Potential in Geosciences: An Overview. Geosciences 2025, 15, 123. https://doi.org/10.3390/geosciences15040123
Nachum S. Soil Water Potential in Geosciences: An Overview. Geosciences. 2025; 15(4):123. https://doi.org/10.3390/geosciences15040123
Chicago/Turabian StyleNachum, Shay. 2025. "Soil Water Potential in Geosciences: An Overview" Geosciences 15, no. 4: 123. https://doi.org/10.3390/geosciences15040123
APA StyleNachum, S. (2025). Soil Water Potential in Geosciences: An Overview. Geosciences, 15(4), 123. https://doi.org/10.3390/geosciences15040123





