A Review of Parameters and Methods for Seismic Site Response
Abstract
1. Introduction
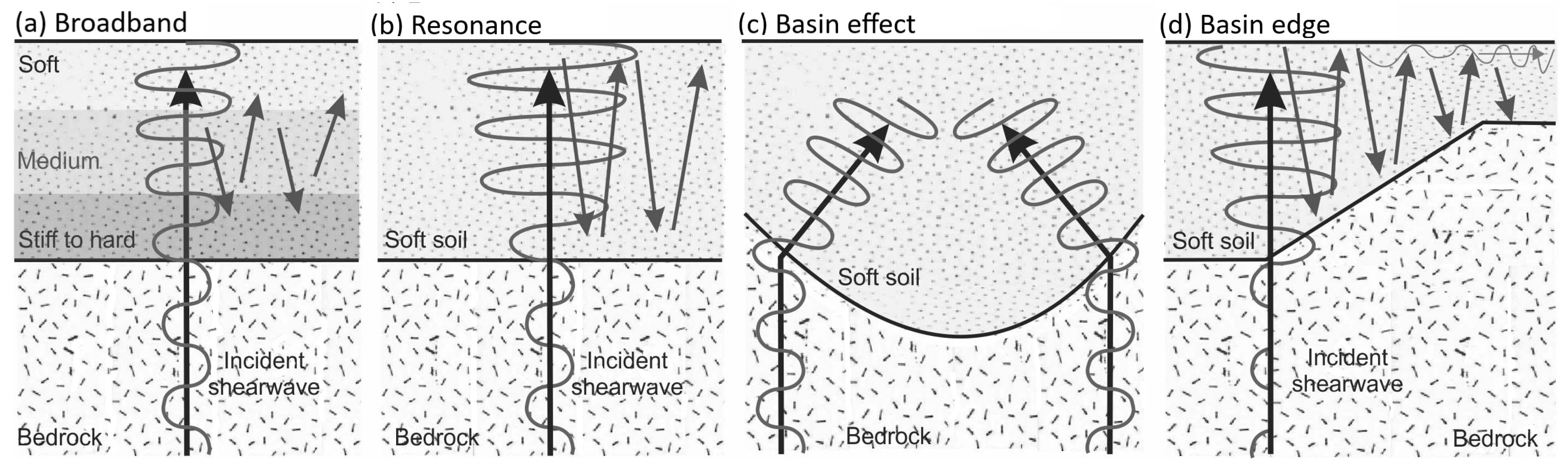
2. Site Effects
2.1. Resonance Amplification
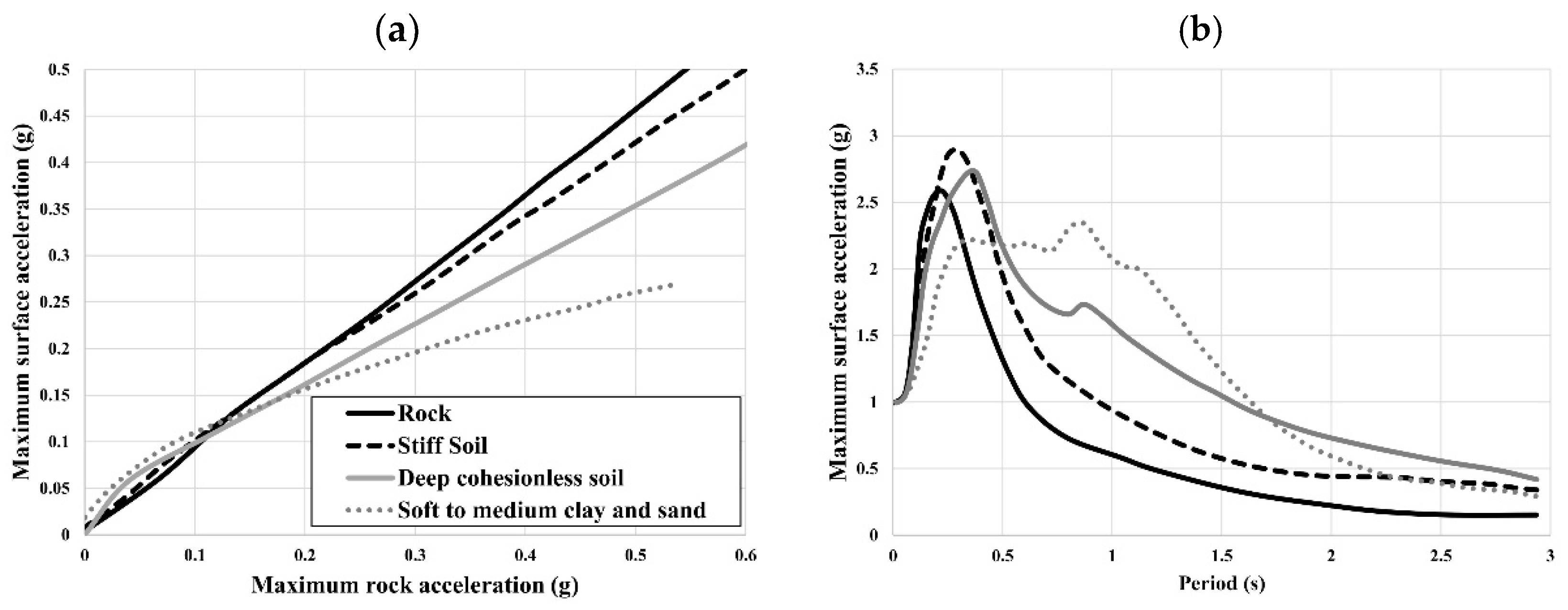
2.2. Broadband Amplification
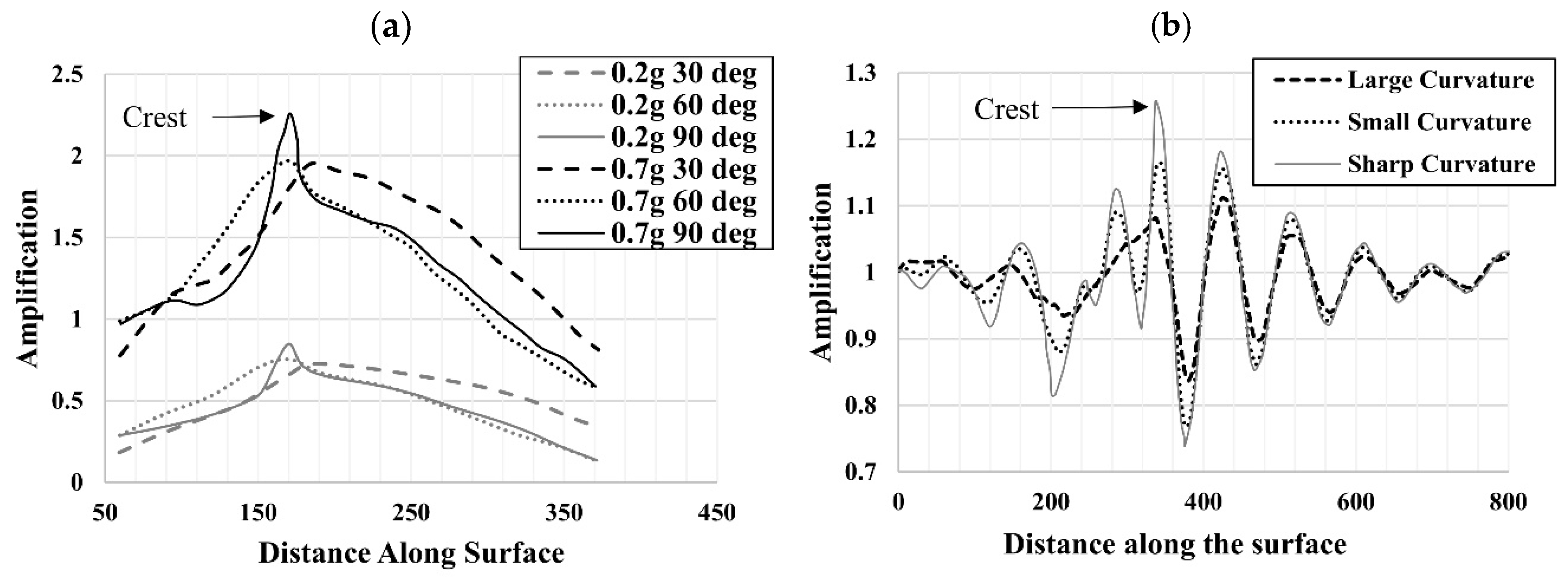
2.3. Topographic Effect
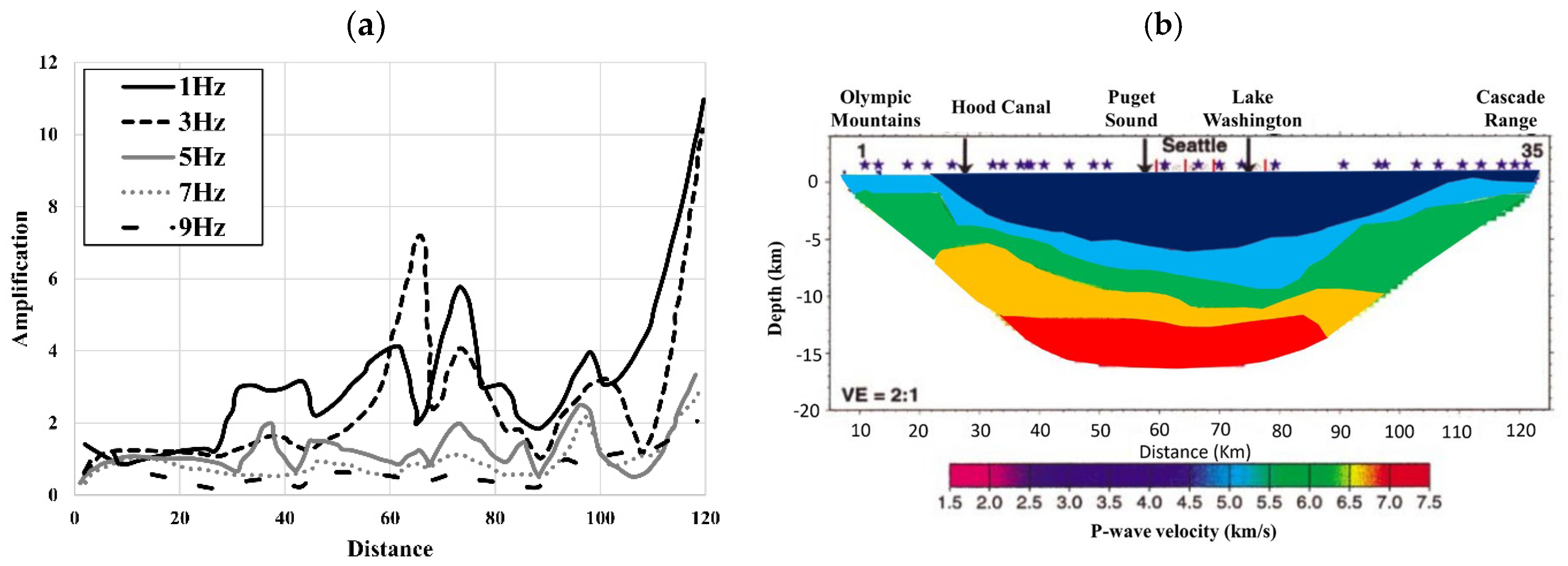
2.4. Basin Effect
3. Soil Parameters
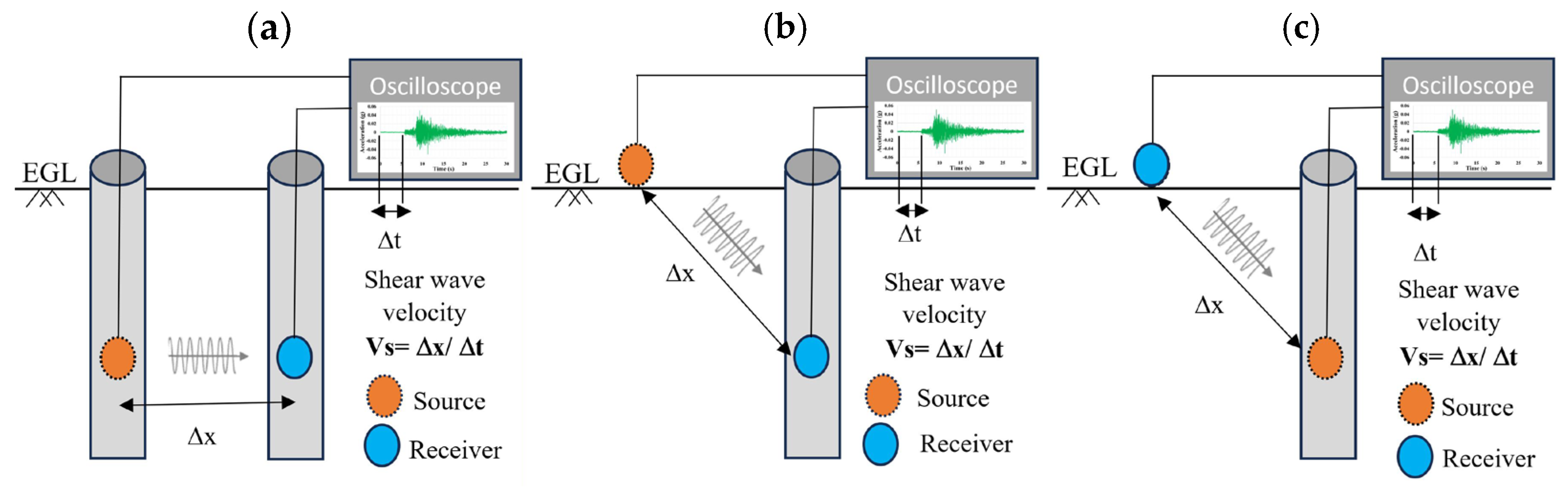
3.1. Shear-Wave Velocity (VS)
3.1.1. In-Situ Measurements
3.1.2. Laboratory Measurements
3.2. Shear Modulus and Damping Ratio
3.2.1. Measurement of SM and DR
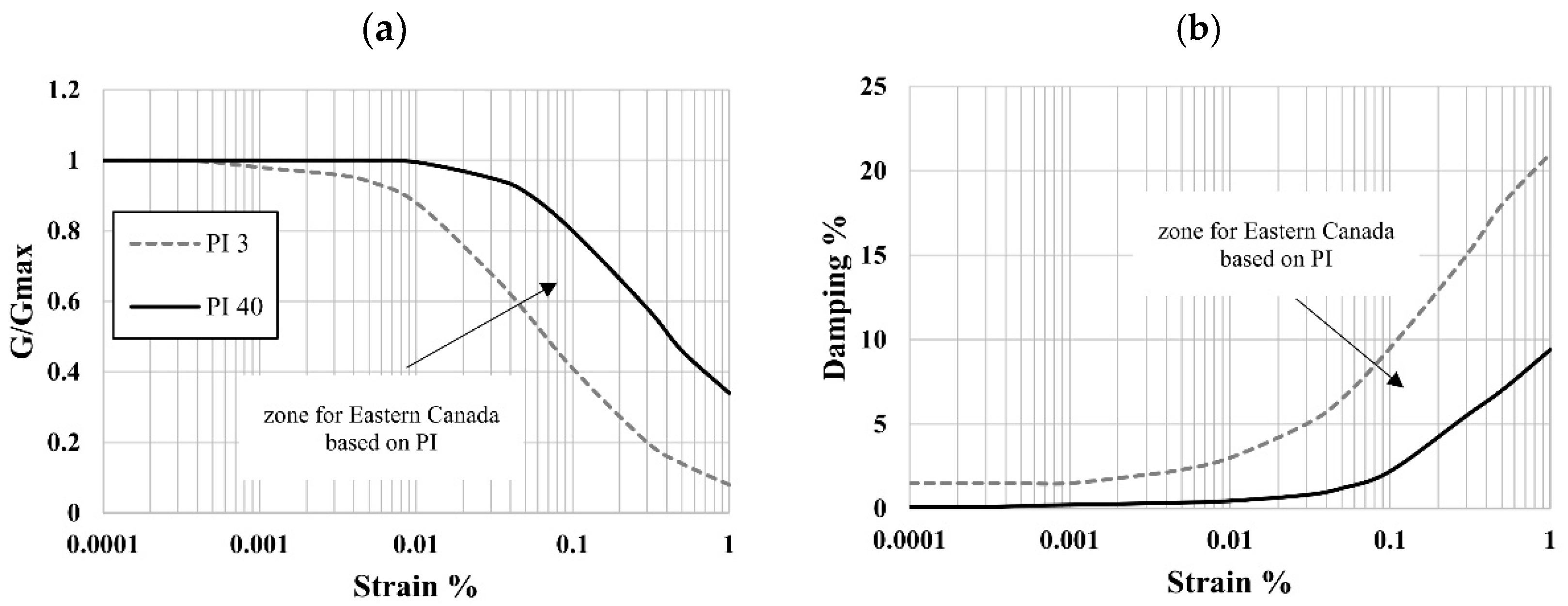
3.2.2. Factors Affecting Shear Modulus Reduction and Damping Ratio Curves
Cohesionless Soil
Cohesive Soil
Sensitive Clay
3.2.3. Nonlinear Effects in Dynamic Loading
4. Seismic Parameters
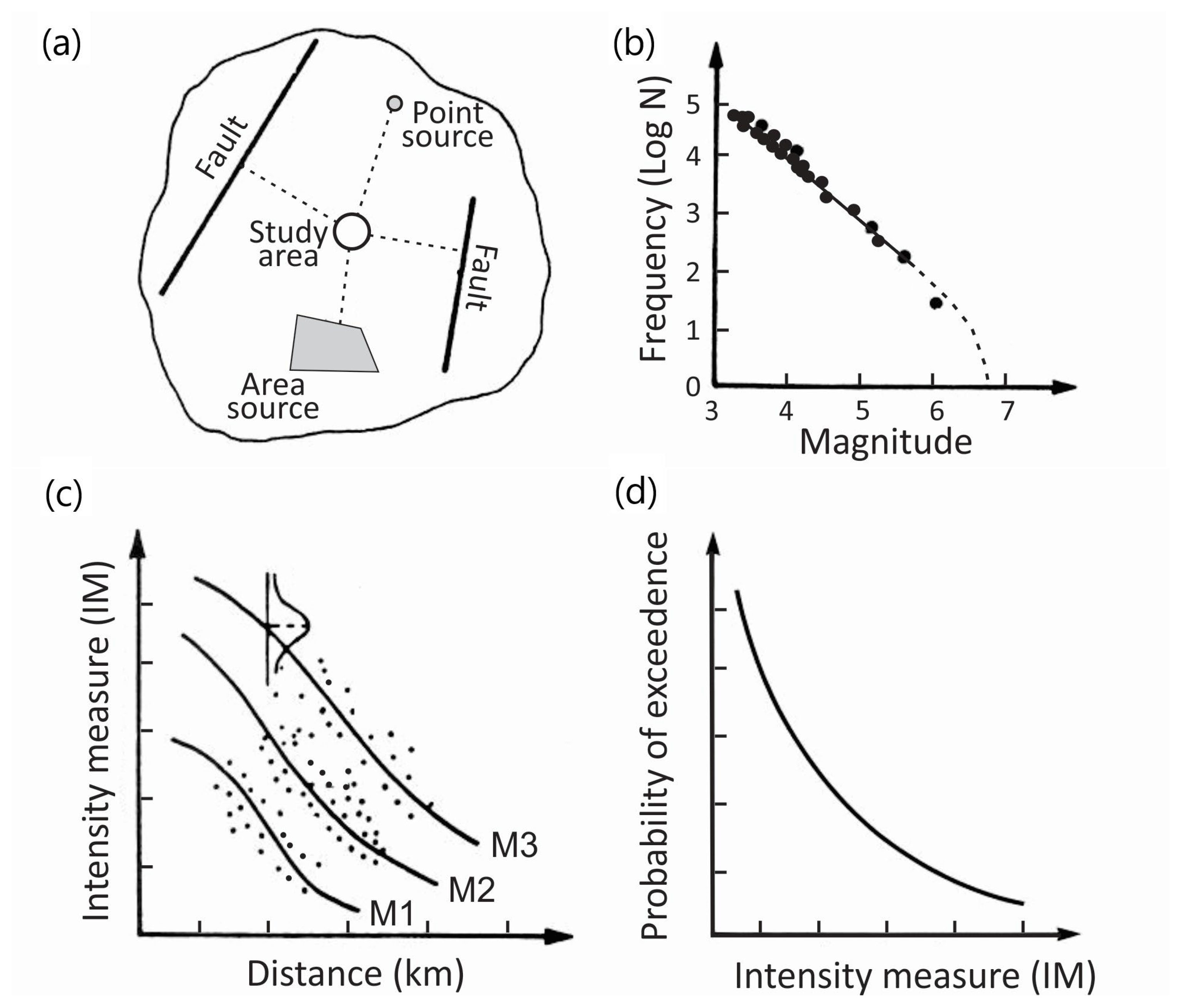
4.1. Seismic Hazard
4.2. Input Ground Motions
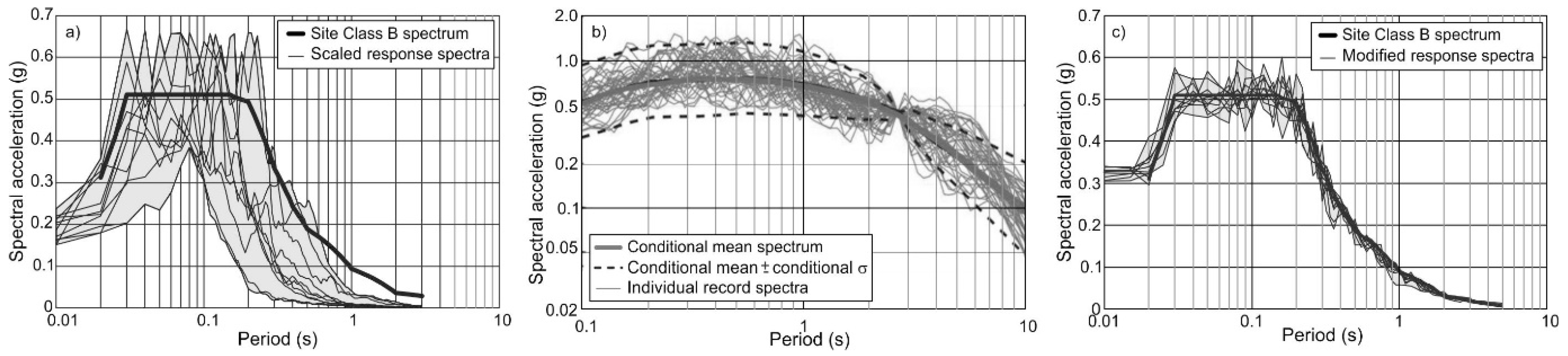
4.2.1. Selection of Real Accelerogram
4.2.2. Synthetic Accelerograms
4.2.3. Spectral Matching in the Time Domain
4.2.4. Spectral Matching in Frequency Domain
4.2.5. Baseline Correction
5. Evaluation of Site Effect Through Site Response Proxies
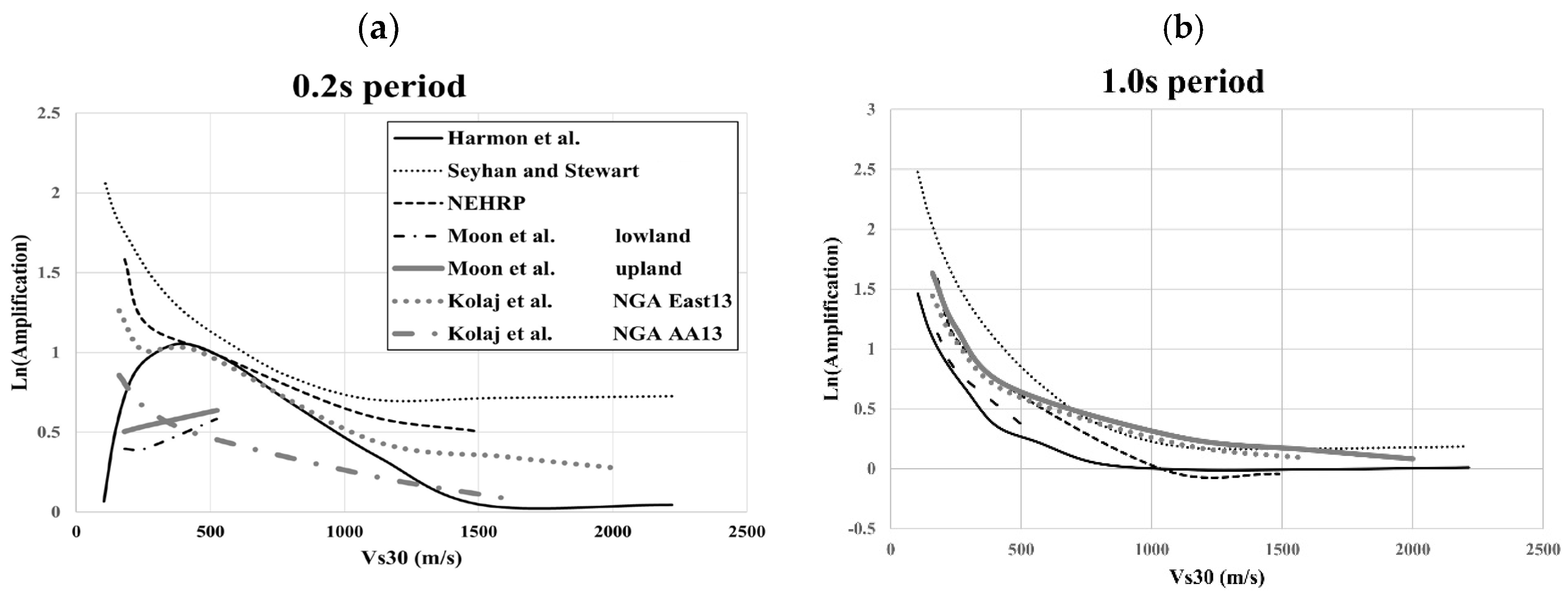
5.1. Average Shear-Wave Velocity in the Top 30 m (VS30)
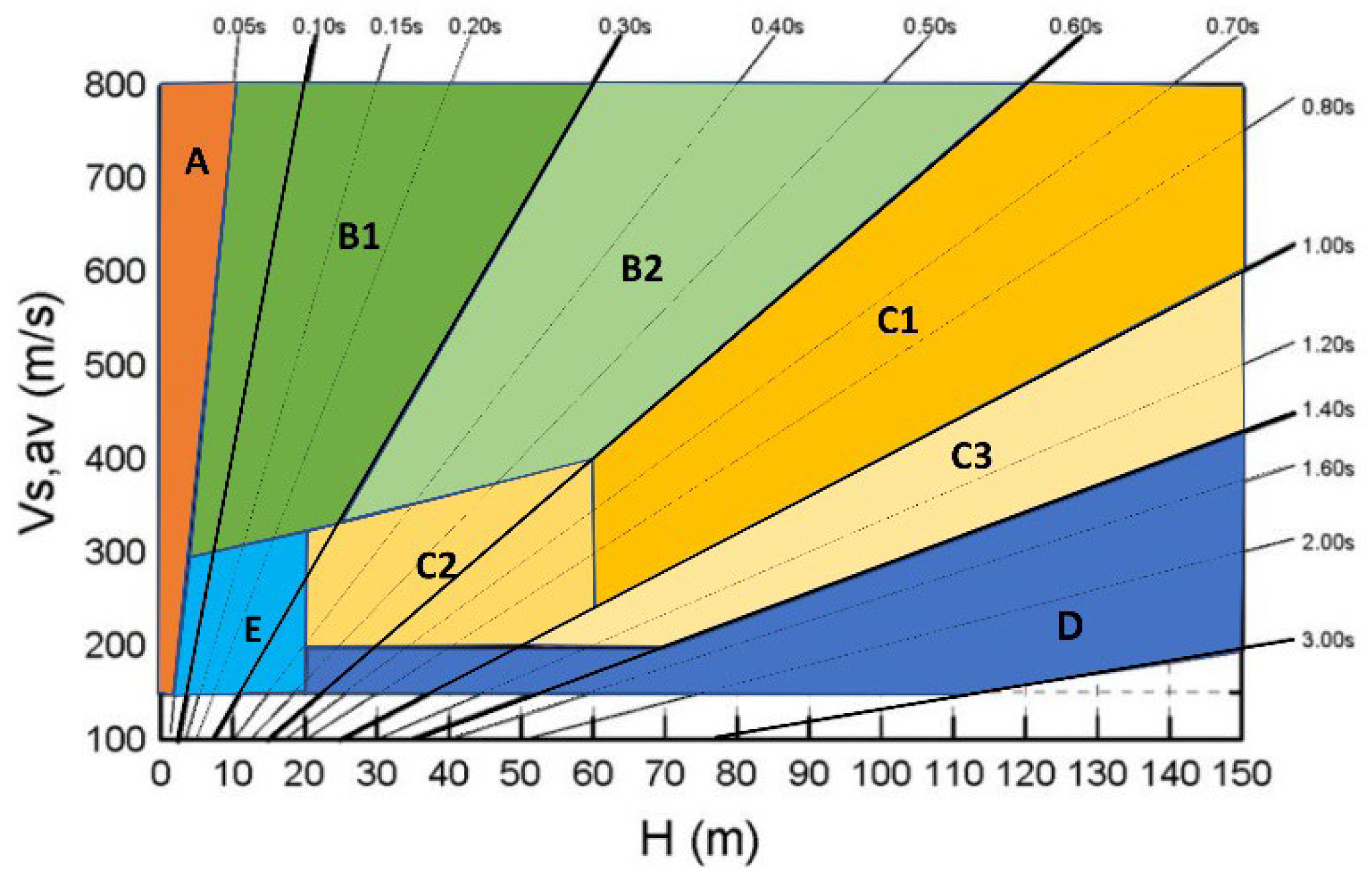
5.2. Fundamental Site Period
5.2.1. Field Measurements
5.2.2. Analytical Approach
6. Evaluation of Site Effect Through Experimental Analysis
7. Evaluation of Site Effect Through Numerical Analysis
7.1. Linear Site Response (L)
7.2. Equivalent Linear Site Response (EL)
7.3. Nonlinear Site Response (NL)
7.4. Comparison Between the Numerical Methods
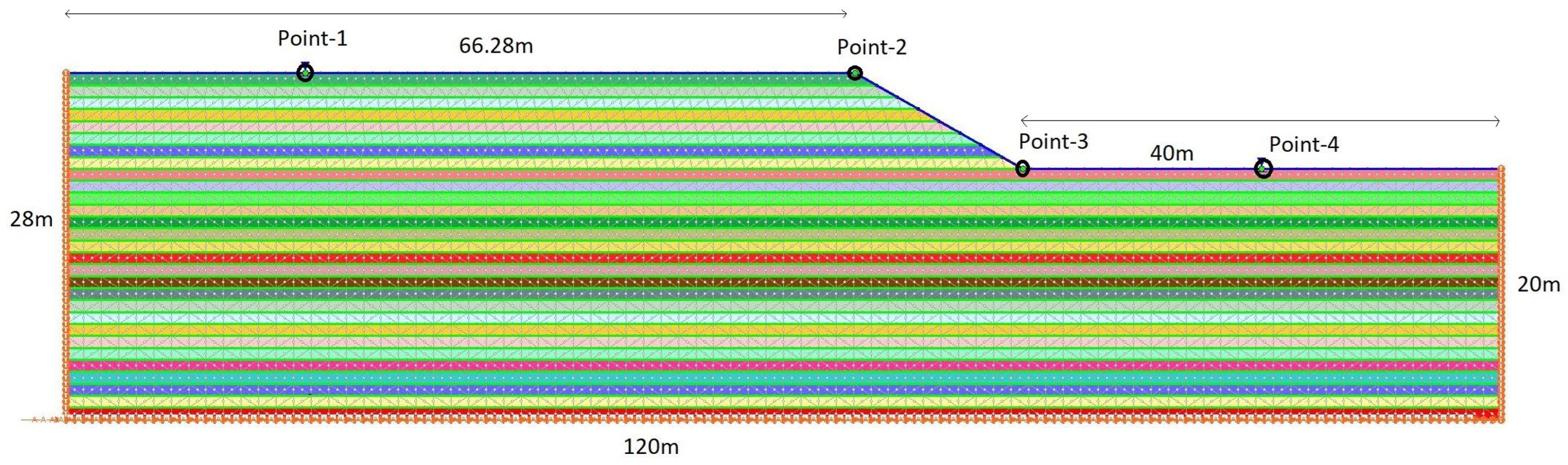
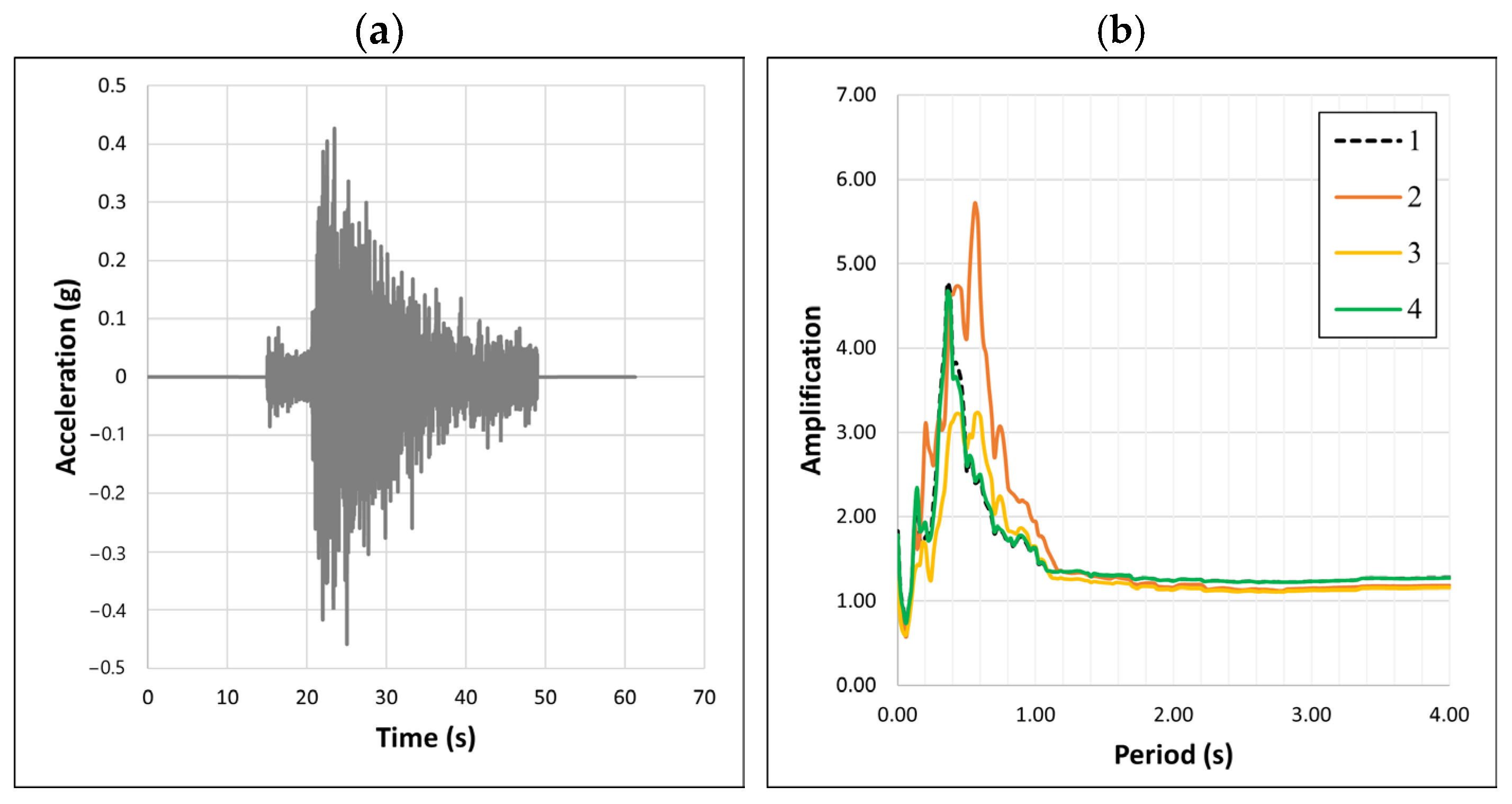
7.5. Illustrative Example: 2D FEM-Based Dynamic Analysis for Site Effect Estimation
8. Conclusions and Discussion
- (i)
- Site Effects
- (ii)
- Soil Parameters
- ▪
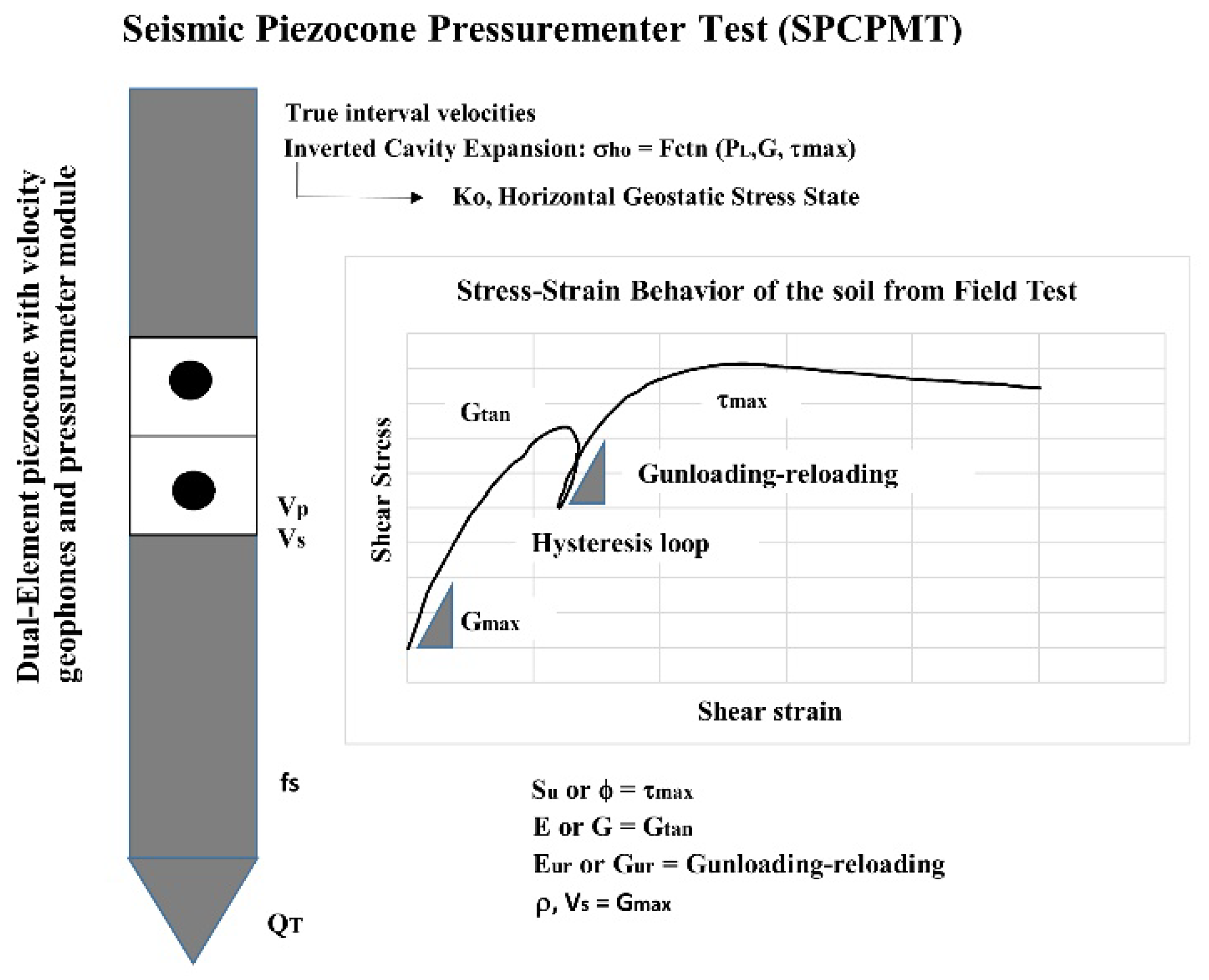
- Among the existing field tests, the seismic cone penetration test (SCPT) or suspension logging yields highly accurate shear-wave velocity (VS) results. However, it is often costly and challenging to perform in gravelly soil. On the other hand, non-invasive geophysical methods are more applicable in various soil conditions and can provide a broader range of VS profiles. The setback is that they must be validated against results from at least one invasive investigation at similar/nearby sites to ensure accuracy. In addition, empirical correlations developed between different SCPT parameters can be combined with numerous CPT results when readily available for the study area.
- ▪
- Shear modulus and damping ratio curves are critical for the characterization of the soil’s nonlinear behavior during earthquake shaking. They define how the soil stiffness (shear modulus) and energy dissipation (damping ratio) vary with strain levels. These parameters are essential for realistic seismic site response analyses as they directly influence ground motion amplification and deformation. Both curves are obtained through laboratory tests tailored to the specific application and soil type, such as resonant column, cyclic triaxial tests, or cyclic direct, simple shear tests. The factors influencing these parameters must be carefully considered for cohesive and cohesionless soils. For example, plasticity, water content, and over-consolidation ratio significantly impact cohesive soils’ modulus reduction and damping behavior. In contrast, more critical factors in cohesionless soils are the particle size distribution, relative density, and adequate confining pressure. Proper evaluation of these factors ensures reliable selection or development of shear modulus and damping ratio curves for dynamic analyses.
- (iii)
- Seismic parameters
- ▪
- The impacts of the complex medium, through which seismic waves propagate from the source fault, can be divided into two parts: the source-to-site propagation part, commonly determined with the ground motions from semi-empirical ground motion prediction equations, GMPEs, and the amplification part approximated with horizontal shear waves propagating vertically from the reference rock conditions. This interface is commonly defined as VS30 = 760∼800 m/s (B/C boundary) and measured with geophysical surveys or geotechnical investigations for engineering purposes.
- ▪
- The seismic hazard at reference rock conditions is determined based on the seismic sources affecting the studied location, respective magnitude–frequency relationships, and applicable GMPEs. Probabilistic seismic hazard analysis yields the uniform hazard spectrum (UHS) with spectral accelerations (Sa) as the common ground motion output with the same exceedance probability. UHS is the maximum possible Sa value generated from different earthquake events in each period. Less conservative options are the conditional mean response spectrum (CMS) and conditional response spectrum (CS), which consider the intercorrelations between Sa at different periods.
- ▪
- To evaluate the potential amplification with numerical analyses, a suite of at least seven acceleration representative time histories is commonly recommended. When the number of strong earthquake records collected is insufficient, synthetic or ground motions from other regions with similar seismotectonic settings (magnitude, fault rupture mechanisms, source-to-site distance, and reference site conditions) may be used. Regarding the amplitude–frequency content, time histories are typically scaled to match the hazard spectrum at periods of interest in the time domain. Frequency-matching techniques can reproduce spectral accelerations across all periods; however, it would be highly unlikely to expect a single earthquake event to reach the maximum Sa values of the UHS. When there is a baseline drift, baseline correction is mandatory before the dynamic analyses.
- (iv)
- Site parameters
- ▪
- VS30 is undoubtedly the most frequently used proxy recommended in the building codes. A standard site classification scheme according to VS30 ranges includes site categories with similar amplification potential, such as hard rock, moderately fractured and weathered rock, stiff and dense soil, loose sandy soil, and soft clayey soil. For each site category, a respective amplification factor is provided. More recent building codes provide an amplification factor concerning VS30 as a continual function. However, the VS30 concept was developed based mainly on studies in California, where soft surficial soils gradually transform to regolith and rock without distinct impedance contrast. As such, it is not always correlated with the amplification observed in regions with high impedance contrast at the bedrock interface.
- ▪
- On the other hand, T0 reflects the vibration period at which the seismic waves are expected to be most amplified. It is measured relatively easily using horizontal-to-vertical spectral ratio (HVSR) field measurements, which provide direct and practical insights into the resonance characteristics of the site. However, since the ambient noise does not induce significant strain, HVSR cannot account for the nonlinear behavior of soil during strong ground motion, thus overestimating the actual amplification. Alternatively, T0 can be calculated analytically if the soil thickness and in-depth shear-wave velocity are known. While the commonly used quarter wavelength equation (T = 4H/Vs) is simple and widely applied, it appears limited to relatively shallow soil layers. To improve accuracy, other analytical approaches that account for complex soil stratification, varying velocity profiles, and impedance contrasts should be considered, offering more precise estimations of the fundamental site period depending on site-specific conditions.
- (v)
- Experimental and Numerical evaluation
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Method | Layer | Name of Method | References |
|---|---|---|---|
| Basic | Single | Constant distribution of shear-wave velocity with depth | [142] |
| Method-1 | Single | π times the travel time of the shear-wave velocity method | [144] |
| Method-2 | Single | Power-law distribution of the shear-wave method | [82] |
| Method-3 | Single | Linear distribution of shear modulus with depth method | [141,142] |
| Method-4 | Double | Constant distribution of shear-wave velocity with depth | [142] |
| Method-5 | Double | Simplified Rayleigh’s method | [145] |
| Method-6 | Double | Linear fundamental mode shape | [145] |
| H (m) | Vsavg (m/s) | Basic (s) | M1 (s) | M2 (s) | M3 (s) | M4 (s) | M5 (s) | M6 (s) | Deviation M1 | Deviation M2 | Deviation M3 | Deviation M4 | Deviation M5 | Deviation M6 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| M1 | 10 | 150 | 0.27 | 0.21 | 0.23 | 0.23 | 0.34 | 0.17 | 0.26 | −21.46 | −13.90 | −13.81 | 29.15 | −37.65 | −1.23 |
| M2 | 20 | 160 | 0.50 | 0.39 | 0.41 | 0.41 | 0.61 | 0.30 | 0.47 | −21.46 | −18.30 | −18.22 | 22.54 | −40.84 | −6.28 |
| M3 | 30 | 180 | 0.67 | 0.52 | 0.50 | 0.50 | 0.75 | 0.36 | 0.58 | −21.46 | −24.73 | −24.65 | 12.91 | −45.49 | −13.65 |
| M4 | 40 | 190 | 0.84 | 0.66 | 0.61 | 0.61 | 0.92 | 0.44 | 0.70 | −21.46 | −27.14 | −27.06 | 9.30 | −47.24 | −16.42 |
| M5 | 60 | 200 | 1.20 | 0.94 | 0.85 | 0.85 | 1.27 | 0.62 | 0.97 | −21.46 | −29.18 | −29.11 | 6.23 | −48.72 | −18.76 |
| M6 | 80 | 210 | 1.52 | 1.20 | 1.05 | 1.05 | 1.58 | 0.76 | 1.21 | −21.46 | −30.93 | −30.86 | 3.61 | −49.99 | −20.77 |
| M7 | 100 | 220 | 1.82 | 1.43 | 1.23 | 1.23 | 1.84 | 0.89 | 1.41 | −21.46 | −32.45 | −32.38 | 1.33 | −51.09 | −22.51 |
| M8 | 150 | 250 | 2.40 | 1.88 | 1.54 | 1.54 | 2.30 | 1.11 | 1.76 | −21.46 | −35.99 | −35.93 | −3.99 | −53.65 | −26.58 |
| M9 | 200 | 290 | 2.76 | 2.17 | 1.68 | 1.68 | 2.51 | 1.21 | 1.92 | −21.46 | −39.22 | −39.16 | −8.83 | −55.99 | −30.28 |
| M10 | 250 | 320 | 3.13 | 2.45 | 1.84 | 1.85 | 2.77 | 1.34 | 2.12 | −21.46 | −40.97 | −40.91 | −11.45 | −57.25 | −32.28 |
| M11 | 300 | 350 | 3.43 | 2.69 | 1.98 | 1.98 | 2.97 | 1.43 | 2.27 | −21.46 | −42.34 | −42.28 | −13.50 | −58.25 | −33.85 |
| M12 | 350 | 380 | 3.68 | 2.89 | 2.08 | 2.09 | 3.13 | 1.51 | 2.39 | −21.46 | −43.44 | −43.39 | −15.16 | −59.05 | −35.12 |
| M13 | 400 | 410 | 3.90 | 3.06 | 2.17 | 2.17 | 3.26 | 1.57 | 2.49 | −21.46 | −44.35 | −44.30 | −16.53 | −59.71 | −36.17 |
| M14 | 450 | 420 | 4.29 | 3.37 | 2.37 | 2.38 | 3.56 | 1.72 | 2.72 | −21.46 | −44.62 | −44.57 | −16.93 | −59.90 | −36.47 |
| M15 | 500 | 430 | 4.65 | 3.65 | 2.56 | 2.57 | 3.85 | 1.86 | 2.94 | −21.46 | −44.88 | −44.82 | −17.32 | −60.09 | −36.77 |
| M16 | 600 | 440 | 5.45 | 4.28 | 2.99 | 3.00 | 4.49 | 2.17 | 3.43 | −21.46 | −45.12 | −45.06 | −17.68 | −60.26 | −37.04 |
| M17 | 700 | 450 | 6.22 | 4.89 | 3.40 | 3.40 | 5.10 | 2.46 | 3.90 | −21.46 | −45.35 | −45.29 | −18.02 | −60.42 | −37.30 |
| M18 | 800 | 460 | 6.96 | 5.46 | 3.79 | 3.79 | 5.68 | 2.74 | 4.34 | −21.46 | −45.56 | −45.51 | −18.34 | −60.58 | −37.55 |
| M19 | 900 | 470 | 7.66 | 6.02 | 4.15 | 4.16 | 6.23 | 3.01 | 4.77 | −21.46 | −45.77 | −45.71 | −18.65 | −60.73 | −37.79 |
| M20 | 1000 | 475 | 8.42 | 6.61 | 4.56 | 4.56 | 6.84 | 3.30 | 5.23 | −21.46 | −45.87 | −45.81 | −18.80 | −60.80 | −37.90 |
| M21 | 1100 | 480 | 9.17 | 7.20 | 4.95 | 4.96 | 7.43 | 3.59 | 5.68 | −21.46 | −45.96 | −45.91 | −18.94 | −60.87 | −38.01 |
| M22 | 1200 | 485 | 9.90 | 7.77 | 5.34 | 5.34 | 8.01 | 3.87 | 6.12 | −21.46 | −46.06 | −46.00 | −19.08 | −60.94 | −38.12 |
| M23 | 1300 | 490 | 10.61 | 8.33 | 5.71 | 5.72 | 8.57 | 4.14 | 6.56 | −21.46 | −46.15 | −46.09 | −19.22 | −61.01 | −38.22 |
| M24 | 1400 | 495 | 11.31 | 8.89 | 6.08 | 6.09 | 9.12 | 4.40 | 6.98 | −21.46 | −46.24 | −46.18 | −19.36 | −61.07 | −38.33 |
| M25 | 1500 | 500 | 12.00 | 9.42 | 6.44 | 6.45 | 9.66 | 4.66 | 7.39 | −21.46 | −46.33 | −46.27 | −19.49 | −61.13 | −38.43 |
Appendix B
| Type | Unit Weight | |
|---|---|---|
| Clay | 18.17 | kN/m3 |
| Rock | 28 | kN/m3 |
| Depth | VS (m/s) | Gmax (Mpa) | E (Mpa) | Su (kPa) |
|---|---|---|---|---|
| 1 | 124 | 28 | 77 | 58 |
| 2 | 130 | 32 | 85 | 64 |
| 3 | 136 | 34 | 93 | 70 |
| 4 | 141 | 37 | 100 | 76 |
| 5 | 146 | 40 | 107 | 81 |
| 6 | 151 | 42 | 114 | 87 |
| 7 | 156 | 45 | 121 | 92 |
| 8 | 160 | 48 | 128 | 98 |
| 9 | 164 | 50 | 135 | 103 |
| 10 | 169 | 53 | 142 | 109 |
| 11 | 173 | 55 | 149 | 114 |
| 12 | 177 | 58 | 156 | 119 |
| 13 | 181 | 60 | 163 | 125 |
| 14 | 184 | 63 | 170 | 130 |
| 15 | 188 | 66 | 177 | 136 |
| 16 | 192 | 68 | 184 | 141 |
| 17 | 195 | 71 | 191 | 147 |
| 18 | 199 | 73 | 198 | 153 |
| 19 | 203 | 76 | 205 | 158 |
| 20 | 206 | 79 | 212 | 164 |
| 21 | 210 | 81 | 220 | 170 |
| 22 | 213 | 84 | 227 | 175 |
| 23 | 216 | 87 | 234 | 181 |
| 24 | 220 | 89 | 241 | 187 |
| 25 | 223 | 92 | 249 | 193 |
| 26 | 226 | 95 | 256 | 199 |
| 27 | 230 | 98 | 264 | 205 |
| 28 | 233 | 100 | 271 | 211 |
| Rock | 1875 | 6512 | 17,582 | 15,266 |
References
- Kramer, S.L. Geotechnical Earthquake Engineering; Pearson Education: Hoboken, NJ, USA, 1996. [Google Scholar]
- Hunter, J.A.M.; Crow, H.L. Shear Wave Velocity Measurement Guidelines for Canadian Seismic Site Characterization in Soil and Rock; Natural Resources Canada: Gatineau, QC, Canada, 2015. [Google Scholar]
- Naggar, E. Geotechnical Earthquake Engineering; CRC Press: Toronto, ON, Canada, 2010. [Google Scholar]
- Nastev, M.; Parent, M.; Ross, M.; Howlett, D.; Benoit, N. Geospatial modelling of shear-wave velocity and fundamental site period of Quaternary marine and glacial sediments in the Ottawa and St. Lawrence Valleys, Canada. Soil Dyn. Earthq. Eng. 2016, 85, 103–116. [Google Scholar] [CrossRef]
- Kwon, O.-S.; Elnashai, A.S. Distributed analysis of interacting soil and structural systems under dynamic loading. Innov. Infrastruct. Solut. 2017, 2, 30. [Google Scholar] [CrossRef]
- Dobry, R. Dynamic properties and seismic response of soft clay deposits. Proc. Int. Symp. Geotech. Engrg. Soft Soils 1987, 2, 51–87. [Google Scholar]
- Clayton, C. Stiffness at small strain: Research and practice. Géotechnique 2011, 61, 5–37. [Google Scholar] [CrossRef]
- Luna, R.; Jadi, H. Determination of dynamic soil properties using geophysical methods. In Proceedings of the First International Conference on the Application of Geophysical and NDT Methodologies to Transportation Facilities and Infrastructure, St. Louis, MO, USA, 11–15 December 2000; pp. 1–15. [Google Scholar]
- John, A.; Stephen, H.; Trevor, A.; Garry, R. Canada’s 6th Generation Seismic Hazard Model, as Prepared for the 2020 National Building Code of Canada. In Proceedings of the 12th Canadian Conference on Earthquake Engineering, Quebec City, QC, Canada, 17–20 June 2015. [Google Scholar]
- Tremblay, R.; Atkinson, G.M.; Bouaanani, N.; Daneshvar, P.; Léger, P.; Koboevic, S. Selection and scaling of ground motion time histories for seismic analysis using NBCC 2015. In Proceedings of the 11th Canadian Conference on Earthquake Engineering (11CCEE), Victoria, BC, Canada, 21–24 July 2015; p. 69. [Google Scholar]
- Motazedian, D. Stochastic Finite-Fault Modeling Based on a Dynamic Corner Frequency. Bull. Seism. Soc. Am. 2005, 95, 995–1010. [Google Scholar] [CrossRef]
- Seed, H.B.; Idriss, I.M. Ground Motions and Soil Liquefaction During Earthquakes; Earthquake Engineering Research Insititue: Berkeley, CA, USA, 1982. [Google Scholar]
- Foulon, T.; Saeidi, A.; Chesnaux, R.; Nastev, M.; Rouleau, A. Spatial distribution of soil shear-wave velocity and the fundamental period of vibration—A case study of the Saguenay region, Canada. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2018, 12, 74–86. [Google Scholar] [CrossRef]
- Stone, W.C.; Yokel, F.Y.; Celebi, M. Engineering Aspects of the September 19, 1985 Mexico; Earthquake Engineering Research: Hyogo, Japan, 1987. [Google Scholar]
- Mayoral, J.; Asimaki, D.; Tepalcapa, S.; Wood, C.; la Sancha, A.R.-D.; Hutchinson, T.; Franke, K.; Montalva, G. Site effects in Mexico City basin: Past and present. Soil Dyn. Earthq. Eng. 2019, 121, 369–382. [Google Scholar] [CrossRef]
- Hossain, A.S.M.F.; Adhikari, T.L.; Ansary, M.A.; Bari, Q.H. Characteristics and Consequence of Nepal Earthquake 2015: A Review. Geotech. Eng. J. SEAGS AGSSEA 2015, 46, 114–120. [Google Scholar]
- Molnar, S.; Cassidy, J.F. A Comparison of Site Response Techniques Using Weak-Motion Earthquakes and Microtremors. Earthq. Spectra 2006, 22, 169–188. [Google Scholar] [CrossRef]
- Bouchon, M.; Barker, J.S. Seismic response of a hill: The example of Tarzana, California. Bull. Seism. Soc. Am. 1996, 86, 66–72. [Google Scholar] [CrossRef]
- Spudich, P.; Hellweg, M.; Lee, W.H.K. Directional topographic site response at Tarzana observed in aftershocks of the 1994 Northridge, California, earthquake: Implications for mainshock motions. Bull. Seism. Soc. Am. 1996, 86, S193–S208. [Google Scholar] [CrossRef]
- Abrahamson, N.A.; Somerville, P.G. Effects of the hanging wall and footwall on ground motions recorded during the Northridge earthquake. Bull. Seism. Soc. Am. 1996, 86, S93–S99. [Google Scholar] [CrossRef]
- Molnar, S.; Sirohey, A.; Assaf, J.; Bard, P.-Y.; Castellaro, S.; Cornou, C.; Cox, B.; Guillier, B.; Hassani, B.; Kawase, H.; et al. A review of the microtremor horizontal-to-vertical spectral ratio (MHVSR) method. J. Seism. 2022, 26, 653–685. [Google Scholar] [CrossRef]
- Graves, R.W.; Pitarka, A.; Somerville, P.G. Ground-motion amplification in the Santa Monica area: Effects of shallow basin-edge structure. Bull. Seism. Soc. Am. 1998, 88, 1224–1242. [Google Scholar] [CrossRef]
- Hossain, A.F.; Salsabili, M.; Saeidi, A.; Suescun, J.R.; Nastev, M. Effects of Shear Wave Velocity and Thickness of Soil Layers on 1D Dynamic Response in the Saguenay Region, Quebec. In Rocscience International Conference (RIC 2023); Atlantis Press: Toronto, ON, Canada, 2023; pp. 165–173. [Google Scholar] [CrossRef]
- Hossain, A.F.; Saeidi, A.; Salsabili, M.; Nastev, M.; Suescun, J.R. Soil Dynamic Response and Site Amplification Parameters for Saguenay, Eastern Canada. Jpn. Geotech. Soc. Spéc. Publ. 2024, 10, 1952–1957. [Google Scholar] [CrossRef]
- Hossain, A.F.; Saeidi, A.; Salsabili, M.; Nastev, M.; Suescun, J.R. Analytical and numerical investigation of the site response period in the Saguenay region, Eastern Canada. In Proceedings of the 3rd Croatian Conference on Earthquake Engineering (3CroCEE), Split, Croatia, 19–22 March 2025. [Google Scholar]
- Seed, H.B.; Romo, M.P.; Sun, J.I.; Jaime, A.; Lysmer, J. The Mexico Earthquake of September 19, 1985—Relationships Between Soil Conditions and Earthquake Ground Motions. Earthq. Spectra 1988, 4, 687–729. [Google Scholar] [CrossRef]
- Jackson, F.; Molnar, S.; Ghofrani, H.; Atkinson, G.M.; Cassidy, J.F.; Assatourians, K. Ground Motions of the December 2015 M 4.7 Vancouver Island Earthquake: Attenuation and Site Response. Bull. Seism. Soc. Am. 2017, 107, 2903–2916. [Google Scholar] [CrossRef]
- Klin, P.; Laurenzano, G.; Barnaba, C.; Priolo, E.; Parolai, S. Site Amplification at Permanent Stations in Northeastern Italy. Bull. Seism. Soc. Am. 2021, 111, 1885–1904. [Google Scholar] [CrossRef]
- Pratt, T.L. Amplification of Seismic Waves by the Seattle Basin, Washington State. Bull. Seism. Soc. Am. 2003, 93, 533–545. [Google Scholar] [CrossRef]
- Assimaki, D. Effects of Local Soil Conditions on the Topographic Aggravation of Seismic Motion: Parametric Investigation and Recorded Field Evidence from the 1999 Athens Earthquake. Bull. Seism. Soc. Am. 2005, 95, 1059–1089. [Google Scholar] [CrossRef]
- Meunier, P.; Hovius, N.; Haines, J.A. Topographic site effects and the location of earthquake induced landslides. Earth Planet. Sci. Lett. 2008, 275, 221–232. [Google Scholar] [CrossRef]
- Bard, P.-Y.; Bouchon, M. The two-dimensional resonance of sediment-filled valleys. Bull. Seism. Soc. Am. 1985, 75, 519–541. [Google Scholar] [CrossRef]
- Shabani, M.J.; Zakerinejad, M. Slope topographic impacts on the nonlinear seismic analysis of soil-foundation-structure interaction for similar MRF buildings. Soil Dyn. Earthq. Eng. 2022, 160, 107365. [Google Scholar] [CrossRef]
- Sitar, N.; Clough, G.W. Seismic Response of Steep Slopes in Cemented Soils. J. Geotech. Eng. 1983, 109, 210–227. [Google Scholar] [CrossRef]
- Bararpour, M.; Janalizade, A.; Tavakoli, H.R. The effect of 2D slope and valley on seismic site response. Arab. J. Geosci. 2016, 9, 93. [Google Scholar] [CrossRef]
- Zhang, Z.; Fleurisson, J.-A.; Pellet, F. The effects of slope topography on acceleration amplification and interaction between slope topography and seismic input motion. Soil Dyn. Earthq. Eng. 2018, 113, 420–431. [Google Scholar] [CrossRef]
- Bard, P.-Y.; Riepl-Thomas, J. Wave Propagation in Complex Geological Structures and Their Effects on Strong Ground Motion. 2000. Available online: https://www.researchgate.net/publication/235623287 (accessed on 17 March 2025).
- Molnar, S.; Cassidy, J.F.; Olsen, K.B.; Dosso, S.E.; He, J. Earthquake Ground Motion and 3D Georgia Basin Amplification in Southwest British Columbia: Deep Juan de Fuca Plate Scenario Earthquakes. Bull. Seism. Soc. Am. 2014, 104, 301–320. [Google Scholar] [CrossRef]
- Molnar, S.; Cassidy, J.F.; Olsen, K.B.; Dosso, S.E.; He, J. Earthquake Ground Motion and 3D Georgia Basin Amplification in Southwest British Columbia: Shallow Blind-Thrust Scenario Earthquakes. Bull. Seism. Soc. Am. 2014, 104, 321–335. [Google Scholar] [CrossRef]
- Marafi, N.A.; Eberhard, M.O.; Berman, J.W.; Wirth, E.A.; Frankel, A.D. Impacts of Simulated M9 Cascadia Subduction Zone Motions on Idealized Systems. Earthq. Spectra 2019, 35, 1261–1287. [Google Scholar] [CrossRef]
- Kakoty, P.; Dyaga, S.M.; Hutt, C.M. Impacts of simulated M9 Cascadia Subduction Zone earthquakes considering amplifications due to the Georgia sedimentary basin on reinforced concrete shear wall buildings. Earthq. Eng. Struct. Dyn. 2021, 50, 237–256. [Google Scholar] [CrossRef]
- Rekoske, J.M.; Moschetti, M.P.; Thompson, E.M. Basin and Site Effects in the U.S. Pacific Northwest Estimated from Small-Magnitude Earthquakes. Bull. Seism. Soc. Am. 2022, 112, 438–456. [Google Scholar] [CrossRef]
- Petersen, M.D.; Shumway, A.M.; Powers, P.M.; Mueller, C.S.; Moschetti, M.P.; Frankel, A.D.; Rezaeian, S.; McNamara, D.E.; Luco, N.; Boyd, O.S.; et al. The 2018 update of the US National Seismic Hazard Model: Overview of model and implications. Earthq. Spectra 2020, 36, 5–41. [Google Scholar] [CrossRef]
- Kakoty, P.; Hutt, C.M.; Ghofrani, H.; Molnar, S. Spectral acceleration basin amplification factors for interface Cascadia Subduction Zone earthquakes in Canada’s 2020 national seismic hazard model. Earthq. Spectra 2023, 39, 1166–1188. [Google Scholar] [CrossRef]
- Hossain, A.S.M.F.; Ansary, M.A. PS Logging for Site Response Analysis in Dhaka City. Aust. J. Sci. Technol. 2017, 6, 83–99. [Google Scholar]
- Kamalb, D.E.H.A.M.; Alama, A.W.U.M.B. Comparison of Shear Wave Velocity Derived from PS Logging and MASW—A Case Study of Mymensingh Pourashava, Bangladesh. Bangladesh J. Geol. 2013, 26, 84–97. [Google Scholar]
- Salsabili, M.; Saeidi, A.; Rouleau, A.; Nastev, M. Development of empirical CPTu-V correlations for post-glacial sediments in Southern Quebec, Canada, in consideration of soil type and geological setting. Soil Dyn. Earthq. Eng. 2022, 154, 107131. [Google Scholar] [CrossRef]
- Nastev, M.; Parent, M.; Benoit, N.; Ross, M.; Howlett, D. Regional VS30model for the St. Lawrence Lowlands, Eastern Canada. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2016, 10, 200–212. [Google Scholar] [CrossRef]
- Mayne, P.W.; Rix, G.J. Correlations Between Shear Wave Velocity and Cone Tip Resistance in Natural Clays. Soils Found. 1995, 35, 107–110. [Google Scholar] [CrossRef]
- Madiai, C.; Simoni, G. Shear wave velocity-penetration resistance correlation for Holocene and Pleistocene soils of an area in central Italy. In ISC-2 on Geotechnical and Geophysical Site Characterization; da Fonseca, V., Mayne, Eds.; Millpress: Rotterdam, The Netherlands, 2004; ISBN 9059660099. [Google Scholar]
- Hegazy, Y.A.; Mayne, P.W. A Global Statistical Correlation between Shear Wave Velocity and Cone Penetration Data. In Proceedings of the Geo Shanghai International Conference 2006, Shanghai, China, 6–8 June 2006; pp. 243–248. [Google Scholar] [CrossRef]
- Andrus, R.D.; Mohanan, N.P.; Piratheepan, P.; Ellis, B.S.; Holzer, T.L. Predicting Shear-Wave Velocity from Cone Penetration Resistance. In Proceedings of the 4th International Conference on Earthquake Geotechnical Engineering, Thessaloniki, Greece, 25–28 June 2007. [Google Scholar]
- Long, M.; Donohue, S. Characterization of Norwegian marine clays with combined shear wave velocity and piezocone cone penetration test (CPTU) data. Can. Geotech. J. 2010, 47, 709–718. [Google Scholar] [CrossRef]
- Tonni, L.; Simonini, P. Shear wave velocity as function of cone penetration test measurements in sand and silt mixtures. Eng. Geol. 2013, 163, 55–67. [Google Scholar] [CrossRef]
- McGann, C.R.; Bradley, B.A.; Taylor, M.L.; Wotherspoon, L.M.; Cubrinovski, M. Development of an empirical correlation for predicting shear wave velocity of Christchurch soils from cone penetration test data. Soil Dyn. Earthq. Eng. 2015, 75, 66–75. [Google Scholar] [CrossRef]
- Perret, D.; Charrois, E.; Bolduc, M. Shear Wave Velocity Estimation from Piezocone Test Data for Eastern Canada Sands (Quebec and Ontario)—Extended Version with Appendices; Natural Resources Canada: Gatineau, QC, Canada, 2016. [Google Scholar] [CrossRef]
- L’Heureux, J.-S.; Long, M. Relationship between Shear-Wave Velocity and Geotechnical Parameters for Norwegian Clays. J. Geotech. Geoenvironmental Eng. 2017, 143, 04017013. [Google Scholar] [CrossRef]
- Karray, M.; Hussien, M.N. Shear wave velocity as function of cone penetration resistance and grain size for Holocene-age uncemented soils: A new perspective. Acta Geotech. 2017, 12, 1129–1158. [Google Scholar] [CrossRef]
- Tong, L.; Che, H.; Zhang, M.; Pan, H. Determination of shear wave velocity of Yangtze Delta sediments using seismic piezocone tests. Transp. Geotech. 2018, 14, 29–40. [Google Scholar] [CrossRef]
- Pelekis, P.; Athanasopoulos, G. An overview of surface wave methods and a reliability study of a simplified inversion technique. Soil Dyn. Earthq. Eng. 2011, 31, 1654–1668. [Google Scholar] [CrossRef]
- Aki, K. Space and Time Spectra of Stationary Stochastic Waves, with Special Reference to Microtremors; Bulletin Earth Research Institute: Tsukuba City, Japan, 1957; pp. 415–456. [Google Scholar]
- Kocaoğlu, A.H.; Fırtana, K. Estimation of shear wave velocity profiles by the inversion of spatial autocorrelation coefficients. J. Seism. 2011, 15, 613–624. [Google Scholar] [CrossRef]
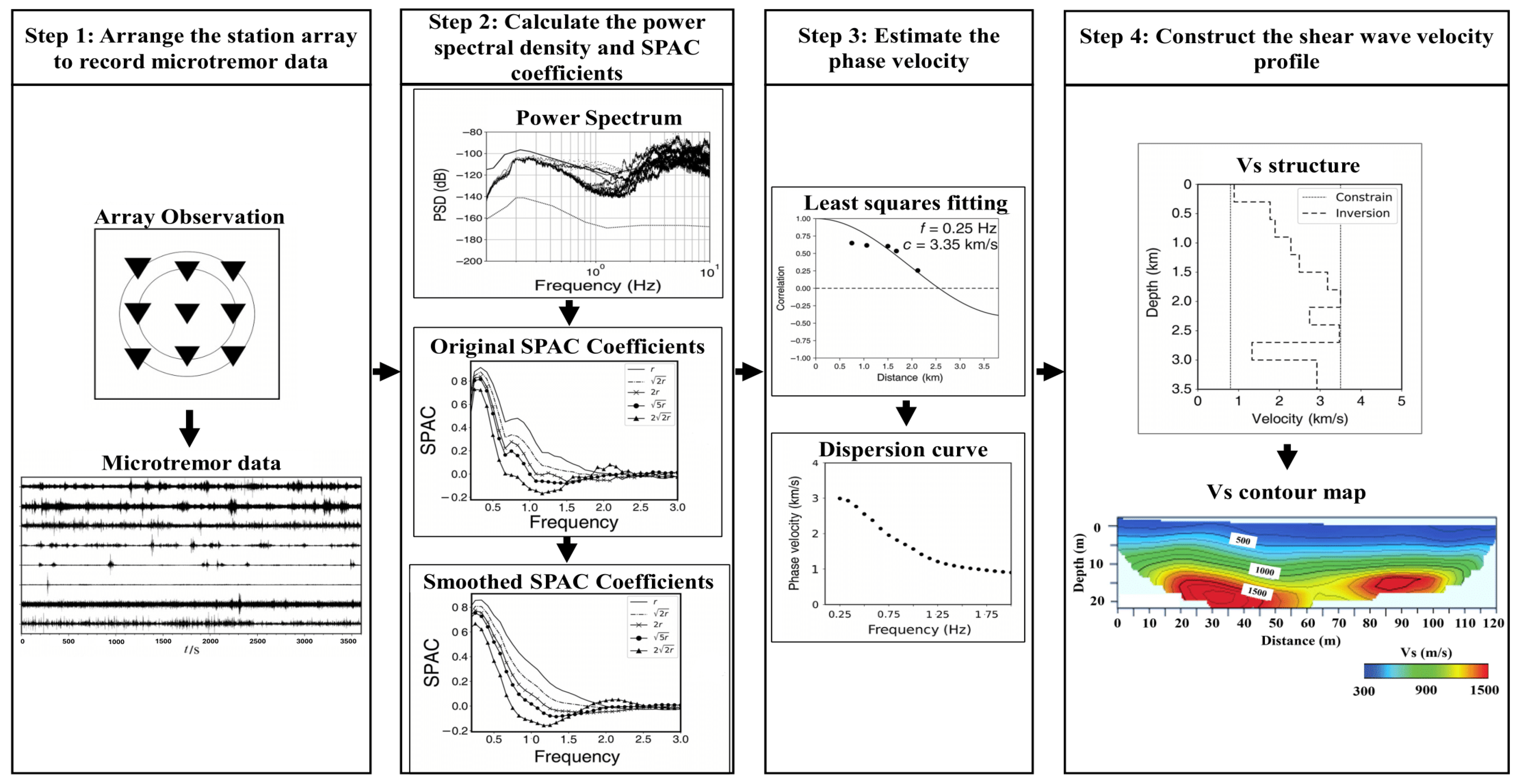
- Asten, M.W.; Hayashi, K. Application of the Spatial Auto-Correlation Method for Shear-Wave Velocity Studies Using Ambient Noise. Surv. Geophys. 2018, 39, 633–659. [Google Scholar] [CrossRef]
- Pan, Q.; Shen, X.; Ye, X.; Wang, L. Fine Shear-Wave Velocity Structures of Subsurface beneath the Guangdong–Hong Kong–Macao Greater Bay Area with Dense Seismic Array and SPAC Method. Seism. Res. Lett. 2024, 95, 2894–2909. [Google Scholar] [CrossRef]
- Ling, S.; Okada, H. An extended use of the spatial autocorre lation method for the estimation of structure using microtremors. In Proceedings of the 89th SEGJ Conference, Nagoya, Japan, 12–14 October 1993; Society of Exploration Geophysicists of Japan: Nagoya, Japan, 1993. [Google Scholar]
- Ohori, M. A Comparison of ESAC and FK Methods of Estimating Phase Velocity Using Arbitrarily Shaped Microtremor Arrays. Bull. Seism. Soc. Am. 2002, 92, 2323–2332. [Google Scholar] [CrossRef]
- Moro, G.D. Effective Active and Passive Seismics for the Characterization of Urban and Remote Areas: Four Channels for Seven Objective Functions. Pure Appl. Geophys. 2019, 176, 1445–1465. [Google Scholar] [CrossRef]
- Mantovani, A.; Abu Zeid, N.; Bignardi, S.; Tarabusi, G.; Santarato, G.; Caputo, R. Seismic Noise-Based Strategies for Emphasizing Recent Tectonic Activity and Local Site Effects: The Ferrara Arc, Northern Italy, Case Study. Pure Appl. Geophys. 2019, 176, 2321–2347. [Google Scholar] [CrossRef]
- Aki, K. A Note on The Use of Microseisms in Determining the Shallow Structures of the Earth’s Crust. Geophysics 1965, 30, 665–666. [Google Scholar] [CrossRef]
- Capon, J. High-resolution frequency-wavenumber spectrum analysis. Proc. IEEE 1969, 57, 1408–1418. [Google Scholar] [CrossRef]
- Lacoss, R.T.; Kelly, E.J.; Toksöz, M.N. S-wave velocity structure and site effect parameters derived from microtremor arrays in the Western Plain of Taiwan. Geophysics 1969, 34, 21–38. [Google Scholar] [CrossRef]
- Kuo, C.-H.; Chen, C.-T.; Lin, C.-M.; Wen, K.-L.; Huang, J.-Y.; Chang, S.-C. S-wave velocity structure and site effect parameters derived from microtremor arrays in the Western Plain of Taiwan. J. Asian Earth Sci. 2016, 128, 27–41. [Google Scholar] [CrossRef]
- Cheng, F.; Xia, J.; Xu, Z.; Hu, Y.; Mi, B. Frequency–Wavenumber (FK)-Based Data Selection in High-Frequency Passive Surface Wave Survey. Surv. Geophys. 2018, 39, 661–682. [Google Scholar] [CrossRef]
- Louie, J.N. Faster, Better: Shear-Wave Velocity to 100 Meters Depth from Refraction Microtremor Arrays. Bull. Seism. Soc. Am. 2001, 91, 347–364. [Google Scholar] [CrossRef]
- Song, Y.Y.; Castagna, J.P.; Black, R.A.; Knapp, R.W. Sensitivity of Near-Surface Shear-Wave Velocity Deter Mination from Rayleigh and Love Waves; Society of Exploration Geophysicists: Houston, TX, USA, 1989. [Google Scholar]
- Xia, J.; Miller, R.D.; Park, C.B. Estimation of near-surface shear-wave velocity by inversion of Rayleigh waves. Geophysics 1999, 64, 691–700. [Google Scholar] [CrossRef]
- Cheng, F.; Xia, J.; Luo, Y.; Xu, Z.; Wang, L.; Shen, C.; Liu, R.; Pan, Y.; Mi, B.; Hu, Y. Multichannel analysis of passive surface waves based on crosscorrelations. Geophysics 2016, 81, EN57–EN66. [Google Scholar] [CrossRef]
- Fernandes, J.B.; Rocha, B.P.; Giacheti, H.L. Maximum shear modulus and modulus degradation curves of an unsaturated tropical soil. Soils Rocks 2023, 46, e2023013122. [Google Scholar] [CrossRef]
- Zayed, M.; Ebeido, A.; Prabhakaran, A.; Kim, K.; Qiu, Z.; Elgamal, A. Shake Table Testing: A High-Resolution Vertical Accelerometer Array for Tracking Shear Wave Velocity. Geotech. Test. J. 2021, 44, 1097–1118. [Google Scholar] [CrossRef]
- Lee, C.-J.; Wang, C.-R.; Wei, Y.-C.; Hung, W.-Y. Evolution of the shear wave velocity during shaking modeled in centrifuge shaking table tests. Bull. Earthq. Eng. 2012, 10, 401–420. [Google Scholar] [CrossRef]
- Likitlersuang, S.; Teachavorasinskun, S.; Surarak, C.; Oh, E.; Balasubramaniam, A. Small strain stiffness and stiffness degradation curve of Bangkok Clays. Soils Found. 2013, 53, 498–509. [Google Scholar] [CrossRef]
- Idriss, I.M.; Seed, H.B. Seismic Response of Horizontal Soil Layers. J. Soil Mech. Found. Div. 1968, 94, 1003–1031. [Google Scholar] [CrossRef]
- Mohammadioun, B. Nonlinear Response of Soils to Horizontal and Vertical Bedrock Earthquake Motion. J. Earthq. Eng. 1997, 1, 93–119. [Google Scholar] [CrossRef]
- Mayne, P.W. Stress-strain-strength-flow parameters from enhanced in-situ tests. In Proceedings of the In-Situ Measurement of Soil Properties & Case Histories, Bali, Indonesia, 21–24 May 2001; pp. 27–47. [Google Scholar]
- Fahey, M.; Carter, J.P. A finite element study of the pressuremeter test in sand using a nonlinear elastic plastic model. Can. Geotech. J. 1993, 30, 348–362. [Google Scholar] [CrossRef]
- Baghbani, A.; Choudhury, T.; Samui, P.; Costa, S. Prediction of secant shear modulus and damping ratio for an extremely dilative silica sand based on machine learning techniques. Soil Dyn. Earthq. Eng. 2023, 165, 107708. [Google Scholar] [CrossRef]
- Saathoff, J.-E.; Achmus, M. Excess pore pressure accumulation in sands—A shear strain threshold concept for optimization of a laboratory testing programme. Soil Dyn. Earthq. Eng. 2023, 165, 107721. [Google Scholar] [CrossRef]
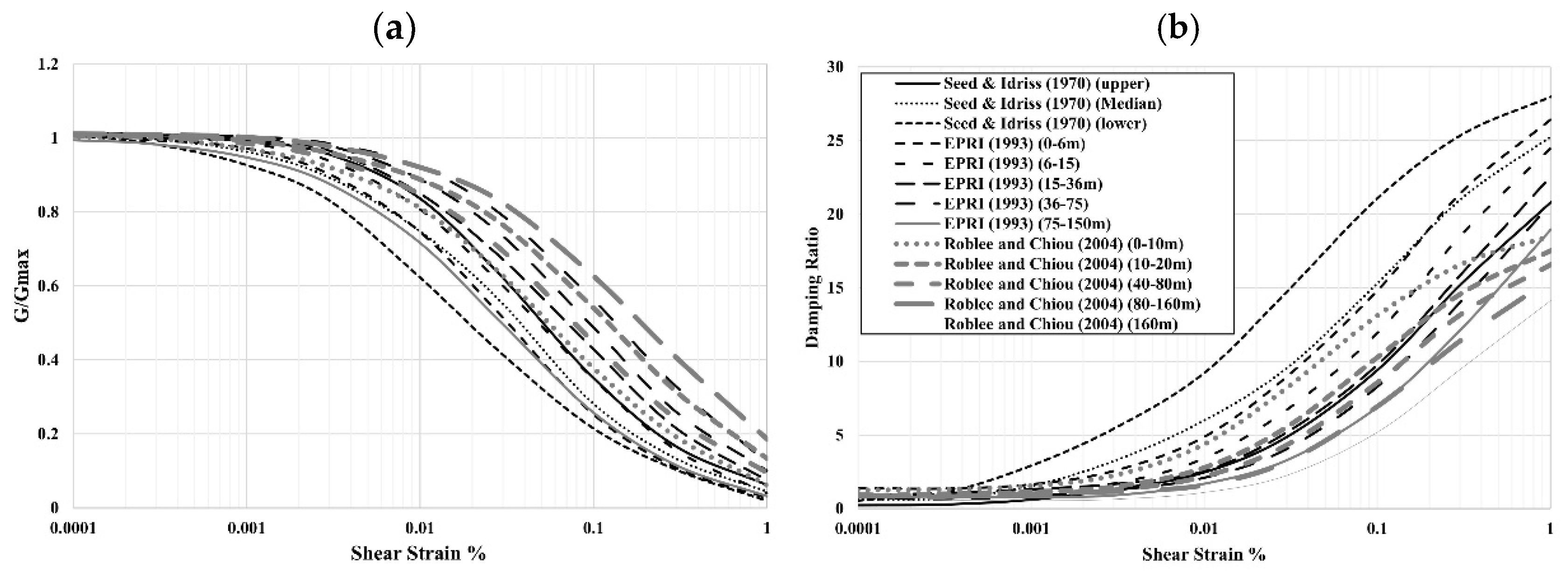
- Seed, H.B.; Wong, R.T.; Idriss, I.M.; Tokimatsu, K. Moduli and Damping Factors for Dynamic Analyses of Cohesionless Soils. J. Geotech. Eng. 1986, 112, 1016–1032. [Google Scholar] [CrossRef]
- Seed, H.B. Soil Moduli and Damping Factors for Dynamic Response Analyses; University of California: Oakland, CA, USA, 1970. [Google Scholar]
- Electric Power Research Institute. Guidelines for Determining Design Basis Ground Motions; EPRI: Palo Alto, CA, USA, 1993; Volume 2, Available online: https://www.ce.memphis.edu/7137/PDFs/EPRI%201993/TR-102293-V2.pdf (accessed on 27 March 2025).
- Assimaki, D.; Kausel, E.; Whittle, A. Model for Dynamic Shear Modulus and Damping for Granular Soils. J. Geotech. Geoenvironmental Eng. 2000, 126, 859–869. [Google Scholar] [CrossRef]
- Rollins, K.M.; Evans, M.D.; Diehl, N.B.; Daily, W.D., III. Shear Modulus and Damping Relationships for Gravels. J. Geotech. Geoenviron. Eng. 1998, 124, 396–405. [Google Scholar] [CrossRef]
- Rohilla, S.; Sebastian, R. Resonant column and cyclic torsional shear tests on Sutlej river sand subjected to the seismicity of Himalayan and Shivalik hill ranges: A case study. Soil Dyn. Earthq. Eng. 2023, 166, 107766. [Google Scholar] [CrossRef]
- Bozyigit, I.; Altun, S. Small-strain behavior and post-cyclic characteristics of low plasticity silts. Bull. Earthq. Eng. 2023, 21, 791–810. [Google Scholar] [CrossRef]
- Bayat, M.; Ghalandarzadeh, A. Stiffness Degradation and Damping Ratio of Sand-Gravel Mixtures Under Saturated State. Int. J. Civ. Eng. 2018, 16, 1261–1277. [Google Scholar] [CrossRef]
- Ishihara, K. Soil Behaviour in Earthquake Geotechnics; Oxford University Press (OUP): Oxford, UK, 1996. [Google Scholar] [CrossRef]
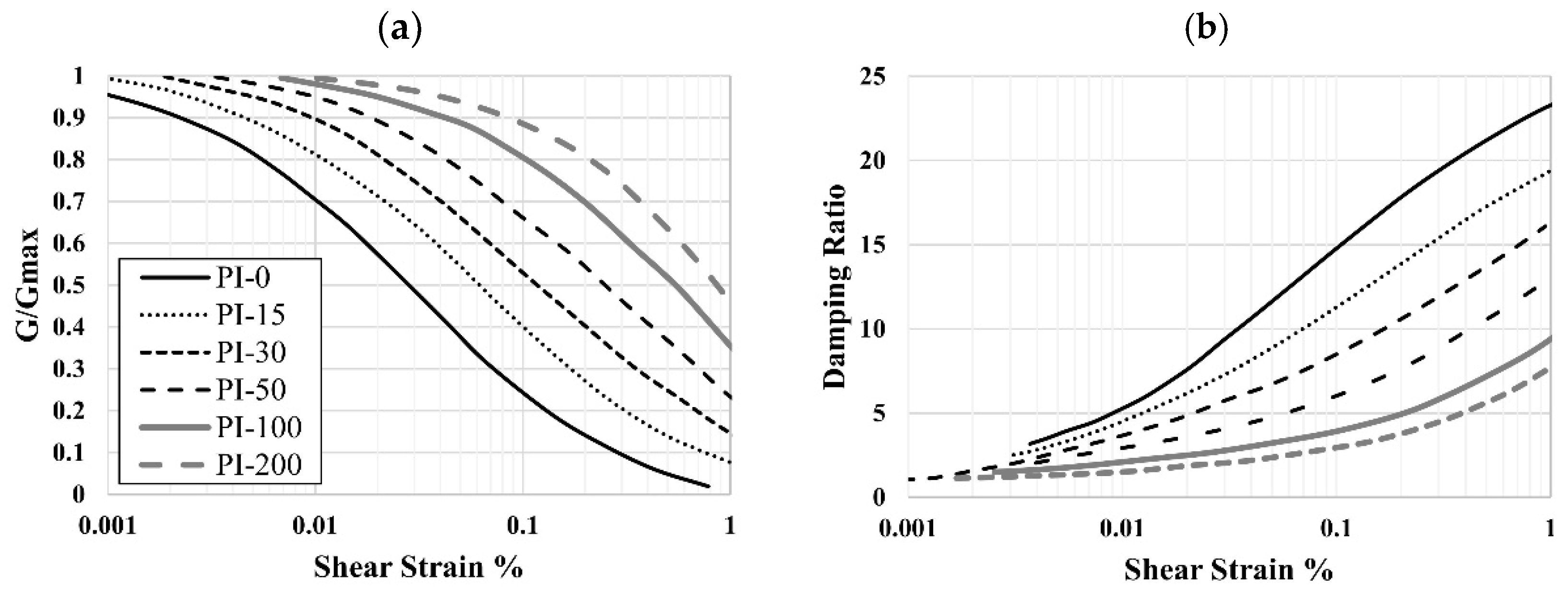
- Vucetic, M.; Dobry, R. Effect of Soil Plasticity on Cyclic Response. J. Geotech. Eng. 1991, 117, 89–107. [Google Scholar] [CrossRef]
- Lanzo, G.; Vucetic, M.; Doroudian, M. Reduction of Shear Modulus at Small Strains in Simple Shear. J. Geotech. Geoenvironmental Eng. 1997, 123, 1035–1042. [Google Scholar] [CrossRef]
- Darendeli, M.B. Development of a New Family of Normalized Modulus Reduction and Material Damping Curves; The University of Texas: Austin, TX, USA, 2001. [Google Scholar]
- Rankka, K.; Andersson-Sköld, Y.; Hultén, C.; Larsson, R.; Leroux, V.; Dahlin, T. Quick Clay in Sweden; Swedish Geotechnical Institute: Linkoping, Sweden, 2004. [Google Scholar]
- Abdellaziz, M.; Karray, M.; Chekired, M.; Delisle, M.-C.; Locat, P.; Ledoux, C.; Mompin, R. Shear modulus and hysteretic damping of sensitive eastern Canada clays. Can. Geotech. J. 2021, 58, 1118–1134. [Google Scholar] [CrossRef]
- Mohammadioun, B.; Pecker, A. Low-frequency transfer of seismic energy by superficial soil deposits and soft rocks. Earthq. Eng. Struct. Dyn. 1984, 12, 537–564. [Google Scholar] [CrossRef]
- Darragh, R.B.; Shakal, A.F. The site response of two rock and soil station pairs to strong and weak ground motion. Bull. Seism. Soc. Am. 1991, 81, 1885–1899. [Google Scholar] [CrossRef]
- Seed, H.B.; Ugas, C.; Lysmer, J. Site-dependent spectra for earthquake-resistant design. Bull. Seism. Soc. Am. 1976, 66, 221–243. [Google Scholar] [CrossRef]
- Atkinson, G.M.; Adams, J. Ground motion prediction equations for application to the 2015 Canadian national seismic hazard maps. Can. J. Civ. Eng. 2013, 40, 988–998. [Google Scholar] [CrossRef]
- Goulet, C.A.; Bozorgnia, Y.; Kuehn, N.; Al Atik, L.; Youngs, R.R.; Graves, R.W.; Atkinson, G.M. PEER 2017/03—NGA-East Ground-Motion Models for the U.S. Geological Survey National Seismic Hazard Maps; University of California: Berkeley, CA, USA, 2017. [Google Scholar]
- Bommer, J.J.; Acevedo, A.B. The Use of Real Earthquake Accelerograms as Input to Dynamic Analysis. J. Earthq. Eng. 2004, 8, 43–91. [Google Scholar] [CrossRef]
- Baker, J.W.; Lee, C. An Improved Algorithm for Selecting Ground Motions to Match a Conditional Spectrum. J. Earthq. Eng. 2018, 22, 708–723. [Google Scholar] [CrossRef]
- Tarbali, K.; Bradley, B.A. The effect of causal parameter bounds in PSHA-based ground motion selection. Earthq. Eng. Struct. Dyn. 2016, 45, 1515–1535. [Google Scholar] [CrossRef]
- Talukder, M.K.; Rosset, P.; Chouinard, L. Reduction of Bias and Uncertainty in Regional Seismic Site Amplification Factors for Seismic Hazard and Risk Analysis. Geohazards 2021, 2, 277–301. [Google Scholar] [CrossRef]
- Atkinson, G.M. Earthquake time histories compatible with the 2005 National building code of Canada uniform hazard spectrum. Can. J. Civ. Eng. 2009, 36, 991–1000. [Google Scholar] [CrossRef]
- Pagliaroli, A.; Lanzo, G. Selection of real accelerograms for the seismic response analysis of the historical town of Nicastro (Southern Italy) during the March 1638 Calabria earthquake. Eng. Struct. 2008, 30, 2211–2222. [Google Scholar] [CrossRef]
- Smerzini, C.; Galasso, C.; Iervolino, I.; Paolucci, R. Ground Motion Record Selection Based on Broadband Spectral Compatibility. Earthq. Spectra 2014, 30, 1427–1448. [Google Scholar] [CrossRef]
- Iervolino, I.; Galasso, C.; Cosenza, E. REXEL: Computer aided record selection for code-based seismic structural analysis. Bull. Earthq. Eng. 2010, 8, 339–362. [Google Scholar] [CrossRef]
- Boore, D.M. Simulation of Ground Motion Using the Stochastic Method. Pure Appl. Geophys. 2003, 160, 635–676. [Google Scholar] [CrossRef]
- Kiani, J.; Khanmohammadi, M. New Approach for Selection of Real Input Ground Motion Records for Incremental Dynamic Analysis (IDA). J. Earthq. Eng. 2015, 19, 592–623. [Google Scholar] [CrossRef]
- Shome, N.; Cornell, C.A.; Bazzurro, P.; Carballo, J.E. Earthquakes, Records, and Nonlinear Responses. Earthq. Spectra 1998, 14, 469–500. [Google Scholar] [CrossRef]
- Vanmarcke, E. State-of-the-Art for Assessing Earthquake Hazards in the United States: Representation of Earthquake Ground Motion: Scaled Accelerograms and Equivalent Response Spectra; US Army Engineer Waterways Experiment Station: Vicksburg, MS, USA, 1979. [Google Scholar]
- Krinitzsky, E.L.; Marcuson, W.F. Principles for Selecting Earthquake Motions in Engineering Design. Environ. Eng. Geosci. 1983, 20, 253–265. [Google Scholar] [CrossRef]
- Baker, J. Vector-Valued Ground Motion Intensity Measures for Probabilistic Seismic Demand Analysis. 2005. Available online: https://stacks.stanford.edu/file/druid:hn186fn6440/TR150_Baker.pdf (accessed on 19 March 2024).
- Baker, J.W.; Cornell, C.A. Spectral shape, epsilon and record selection. Earthq. Eng. Struct. Dyn. 2006, 35, 1077–1095. [Google Scholar] [CrossRef]
- Lin, T. Advancement of Hazard-Consistent Ground Motion Selection Methodology; Stanford University: Stanford, CA, USA, 2012. [Google Scholar]
- Lin, T.; Harmsen, S.C.; Baker, J.W.; Luco, N. Conditional Spectrum Computation Incorporating Multiple Causal Earthquakes and Ground-Motion Prediction Models. Bull. Seism. Soc. Am. 2013, 103, 1103–1116. [Google Scholar] [CrossRef]
- Nastev, M.L.L.; Seismic, N.N. Motions compatible with the NBCC 2005 Uniform Hazard Spectrum for Québec City. In Proceedings of the 36th Annual Conference of the Canadian Society for Civil Engineering, Quebec City, QC, Canada, 10–13 June 2008; p. 8. [Google Scholar]
- Iñarritu, P.G.d.Q.; Šipčić, N.; Alvarez-Sanchez, L.; Kohrangi, M.; Bazzurro, P. A closer look at hazard-consistent ground motion record selection for building-specific risk assessment: Effect of soil characteristics and accelerograms’ scaling. Earthq. Spectra 2023, 39, 1683–1720. [Google Scholar] [CrossRef]
- Gasparini, D.A.; Vanmarcke, E.H. SIMQKE: A Program for Artificial Motion Generation; Department of Civil Engineering, Massachusetts Institute of Technology: Cambridge, MA, USA, 1976. [Google Scholar]
- Silva, W.J.; Lee, K. State-of-the-Art for Assessing Earthquake Hazards in the United States. Report 24. WES RASCAL Code for Synthesizing Earthquake Ground Motions; US Army Corps of Engineers: Vicksburg, MS, USA, 1987. [Google Scholar]
- Naumoski, N. Program SYNTH—Generation of Artificial Accelerograms Compatible with a Target Spectrum; University of Ottawa: Ottawa, ON, Canada, 2001. [Google Scholar]
- Kottke, A.; Rathje, E.M. A Semi-Automated Procedure for Selecting and Scaling Recorded Earthquake Motions for Dynamic Analysis. Earthq. Spectra 2008, 24, 911–932. [Google Scholar] [CrossRef]
- Guorui, H.; Tao, L. Review on Baseline Correction of Strong-Motion Accelerogram. Int. J. Sci. Technol. Soc. 2015, 3, 309. [Google Scholar] [CrossRef]
- Borcherdt, R.D. Estimates of Site-Dependent Response Spectra for Design (Methodology and Justification). Earthq. Spectra 1994, 10, 617–653. [Google Scholar] [CrossRef]
- Harmon, J.; Hashash, Y.M.A.; Stewart, J.P.; Rathje, E.M.; Campbell, K.W.; Silva, W.J.; Xu, B.; Musgrove, M.; Ilhan, O. Site Amplification Functions for Central and Eastern North America—Part I: Simulation Data Set Development. Earthq. Spectra 2019, 35, 787–814. [Google Scholar] [CrossRef]
- Seyhan, E.; Stewart, J.P. Semi-Empirical Nonlinear Site Amplification from NGA-West2 Data and Simulations. Earthq. Spectra 2014, 30, 1241–1256. [Google Scholar] [CrossRef]
- Building Seismic Safety Council. NEHRP Recommended Seismic Provisions for New Buildings and Other Structures; Building Seismic Safety Council: Washington, DC, USA, 2015. [Google Scholar]
- Moon, S.; Hashash, Y.M.A.; Park, D. USGS Hazard Map Compatible Depth-Dependent Seismic Site Coefficients for the Upper Mississippi Embayment. KSCE J. Civ. Eng. 2017, 21, 220–231. [Google Scholar] [CrossRef]
- Kolaj, M.; Allen, T.; Mayfield, R.; Adams, J.; Halchuk, S. Ground-Motion Models for the 6th Generation Seismic Hazard Model of Canada. In Proceedings of the 12th Canadian Conference on Earthquake Engineering, Quebec City, QC, Canada, 17–20 June 2019. [Google Scholar]
- Kobayashi, K. A method for presuming deep ground soil structures by means of longer period microtremors. In Proceedings of the Seventh World Conference on Earthquake Engineering, Istanbul, Turkey, 8–13 September 1980; pp. 237–240. [Google Scholar]
- Borcherdt, R.D. Effects of Local Geology on Ground Motion Near San Francisco Bay. 1970. Available online: http://pubs.geoscienceworld.org/ssa/bssa/article-pdf/60/1/29/5312965/bssa0600010029.pdf (accessed on 17 March 2025).
- Vijayendra, K.V.; Nayak, S.; Prasad, S.K. An Alternative Method to Estimate Fundamental Period of Layered Soil Deposit. Indian Geotech. J. 2015, 45, 192–199. [Google Scholar] [CrossRef]
- Ambraseys, N.N. A note on the response of an elastic overburden of varying rigidity to an arbitrary ground motion. Bull. Seism. Soc. Am. 1959, 49, 211–220. [Google Scholar] [CrossRef]
- Urzua, A. Determinacion del Periodo Fundamental de Vibracion del Suelo; University of Chile: Santiago, Chile, 1974. [Google Scholar]
- Madera, G. Fundamental Period and Amplification of Peak Acceleration in Layered Systems; MIT University: Cambridge, MA, USA, 1970. [Google Scholar]
- Wang, S.; Shi, Y.; Jiang, W.; Yao, E.; Miao, Y. Estimating Site Fundamental Period from Shear-Wave Velocity Profile. Bull. Seism. Soc. Am. 2018, 108, 3431–3445. [Google Scholar] [CrossRef]
- Dobry, R.; Oweis, I.; Urzua, A. Simplified Procedures for Estimating the Fundamental Period of a Soil Profile. Bull. Seismol. Soc. Am. 1976, 66, 1293–1321. [Google Scholar] [CrossRef]
- Building Center of Japan. Building Standard Law; Building Center of Japan: Tokyo, Japan, 2005. [Google Scholar]
- Salsabili, M.; Saeidi, A.; Rouleau, A.; Nastev, M. Seismic microzonation of a region with complex surficial geology based on different site classification approaches. Geoenvironmental Disasters 2021, 8, 27. [Google Scholar] [CrossRef]
- Salsabili, M.; Saeidi, A.; Rouleau, A.; Nastev, M. Probabilistic approach for seismic microzonation integrating 3D geological and geotechnical uncertainty. Earthq. Spectra 2023, 39, 310–334. [Google Scholar] [CrossRef]
- Zhao, J.X. An empirical site-classification method for strong-motion stations in Japan using H/V response spectral ratio. Bull. Seism. Soc. Am. 2006, 96, 914–925. [Google Scholar] [CrossRef]
- Pitilakis, K.; Riga, E.; Anastasiadis, A.; Fotopoulou, S.; Karafagka, S. Towards the revision of EC8: Proposal for an alternative site classification scheme and associated intensity dependent spectral amplification factors. Soil Dyn. Earthq. Eng. 2019, 126, 105137. [Google Scholar] [CrossRef]
- Nakamura, Y. A Method for Dynamic Characteristics Estimation of Subsurface Using Microtremor on the Ground Surface; Railway Technical Research Institute: Tokyo, Japan, 1989. [Google Scholar]
- Costanzo, A.; Caserta, A. Seismic response across the Tronto Valley (at Acquasanta Terme, AP, Marche) based on the geophysical monitoring of the 2016 Central Italy seismic sequence. Bull. Eng. Geol. Environ. 2019, 78, 5599–5616. [Google Scholar] [CrossRef]
- Paolucci, R.; Faccioli, E.; Maggio, F. 3D Response analysis of an instrumented hill at Matsuzaki, Japan, by a spectral method. J. Seism. 1999, 3, 191–209. [Google Scholar] [CrossRef]
- Gallipoli, M.R.; Mucciarelli, M. Comparison of Site Classification from VS30, VS10, and HVSR in Italy. Bull. Seism. Soc. Am. 2009, 99, 340–351. [Google Scholar] [CrossRef]
- Ghofrani, H.; Atkinson, G.M.; Goda, K. Implications of the 2011 M9.0 Tohoku Japan earthquake for the treatment of site effects in large earthquakes. Bull. Earthq. Eng. 2013, 11, 171–203. [Google Scholar] [CrossRef]
- Ghofrani, H.; Atkinson, G.M. Site condition evaluation using horizontal-to-vertical response spectral ratios of earthquakes in the NGA-West 2 and Japanese databases. Soil Dyn. Earthq. Eng. 2014, 67, 30–43. [Google Scholar] [CrossRef]
- Field, E.H.; Zeng, Y.; Johnson, P.A.; Beresnev, I.A. Nonlinear sediment response during the 1994 Northridge earthquake: Observations and finite source simulations. J. Geophys. Res. 1998, 103, 26869–26883. [Google Scholar] [CrossRef]
- Schnabel, P.B.; Lysmer, J.; Seed, H.B. SHAKE: A Computer Program for Earthquake Response Analysis of Horizontally Layered Sites; University of California: Berkeley, CA, USA, 1972. [Google Scholar]
- Idriss, I.M.; Sun, J.I. User’s Manual for SHAKE91: A Computer Program for Conducting Equivalent Linear Seismic Response Analyses of Horizontally Layered Soil Deposits; Center for Geotechnical Modelling, Department of Civil and Environmental Engineering, University of California: Berkeley, CA, USA, 1992. [Google Scholar]
- National Cooperative Highway Research Program; Transportation Research Board; National Academies of Sciences; Engineering. Medicine, Practices and Procedures for Site-Specific Evaluations of Earthquake Ground Motions; The National Academies Press: Washington, DC, USA, 2012. [Google Scholar] [CrossRef]
- Kim, B.; Hashash, Y.M. Site Response Analysis Using Downhole Array Recordings during the March 2011 Tohoku-Oki Earthquake and the Effect of Long-Duration Ground Motions. Earthq. Spectra 2013, 29, 37–54. [Google Scholar] [CrossRef]
- Stewart Jonathan, P. Benchmarking of Nonlinear Geotechnical Ground Response Analysis Procedures; Pacific Earthquake Engineering Research Center: Berkeley, CA, USA, 2008. [Google Scholar]
- Huang, H.-C.; Huang, S.-W.; Chiu, H.-C. Observed Evolution of Linear and Nonlinear Effects at the Dahan Downhole Array, Taiwan: Analysis of the September 21, 1999 M 7.3 Chi-Chi Earthquake Sequence. Pure Appl. Geophys. 2005, 162, 1–20. [Google Scholar] [CrossRef]
- Arslan, H.; Siyahi, B. A comparative study on linear and nonlinear site response analysis. Environ. Geol. 2006, 50, 1193–1200. [Google Scholar] [CrossRef]
- Hosseini, S.M.M.M.; Pajouh, M.A. Comparative study on the equivalent linear and the fully nonlinear site response analysis approaches. Arab. J. Geosci. 2012, 5, 587–597. [Google Scholar] [CrossRef]
- Adampira, M.; Alielahi, H.; Panji, M.; Koohsari, H. Comparison of equivalent linear and nonlinear methods in seismic analysis of liquefiable site response due to near-fault incident waves: A case study. Arab. J. Geosci. 2014, 8, 3103–3118. [Google Scholar] [CrossRef]
- Civelekler, E.; Afacan, K.B.; Okur, D.V. Effect of site specific soil characteristics on the nonlinear ground response analysis and comparison of the results with equivalent linear analysis. J. Appl. Geophys. 2024, 220, 105250. [Google Scholar] [CrossRef]
- Basu, D.; Dey, A. Comparative 1D Ground Response Analysis of Homogeneous Sandy Stratum Using Linear, Equivalent Linear And Nonlinear Masing Approaches. In Indian Geotechnical Society, Kolkata Chapter Geotechnics for Infrastructure Development; Indian Geotechnical Society: Kolkata, India, 2016. [Google Scholar]
- Johari, A.; Heidari, A. Comparison of equivalent linear and nonlinear ground response analysis methods in the time domain. In Proceedings of the 3rd National & 1st International Conference in Applied Research on Civil Engineering, Architecture and Urban Planning, Compiegne, France, 28–30 June 2020; pp. 1–7. [Google Scholar]
- Assimaki, D.; Li, W. Site- and ground motion-dependent nonlinear effects in seismological model predictions. Soil Dyn. Earthq. Eng. 2012, 32, 143–151. [Google Scholar] [CrossRef]
- Kumar, S.S.; Dey, A.; Krishna, M. Equivalent linear and nonlinear ground response analysis of two typical sites at Guwahati city. In Proceedings of the Indian Geotechnical Conference IGC-2014, Kakinada, India, 18–20 December 2014. [Google Scholar]
- Locat, J.; Beauséjour, N. Corrélations entre des propriétés mécaniques dynamiques et statiques de sols argileux intacts et traités à la chaux. Can. Geotech. J. 1987, 24, 327–334. [Google Scholar] [CrossRef]







| Correlation | Soil Type | Reference |
|---|---|---|
| 0.5 | All Soils | [49] |
| Clayey Soil | ||
| Clayey Soil | [50] | |
| Sandy Soil | ||
| Qtne1.786Ic | All Soils | [51] |
| All Soils | [52] | |
| All Soils | ||
| (1 + Bq)1.202 | Marine Clay Soil | [53] |
| Silty Soil | [54] | |
| Sandy Soil | [55] | |
| Sandy Soil | [56] | |
| Marine Clay | [57] | |
| Clayey Soil | [58] | |
| Sandy Soil | ||
| Silt and Sand mixtures | [59] |
| Method | Advantages | Disadvantages |
|---|---|---|
| Seismic Reflection |
|
|
| Seismic Refraction |
|
|
| MASW |
|
|
| SASW |
|
|
| Suspension Logging |
|
|
| Seismic Cone Penetration Test (SCPT) |
|
|
| Code | Site Class and Vs30 (m/s) | ||||
|---|---|---|---|---|---|
| A | B | C | D | E | |
| NBCC (NEHRP) | >1500 (*) | 760–1500 (*) | 360–760 | 180–360 | <180 |
| Eurocode 8 | >800 (**) | 360–800 | 180–360 | <180 | (***) |
| Number | Equation | Velocity Model | Method Name | References |
|---|---|---|---|---|
| 1 | T = 4 | Single Layer | Constant Distribution of Shear-Wave Velocity with Depth | [141,144] |
| 2 | T = 4 | Multiple Layer | ||
| 3 | T = π | Single Layer | π times the VS travel time method (Wang et al., 2018) | [143] |
| 4 | ; μ = T = For μ1 > 1 T = For μ1 ≤ 1 | Single Layer | Linear Distribution of Shear-Wave Velocity with Depth (Deposit with V = a1 + b1z) | [139] |
| 5 | ; T = for 0 ≤ b2 < 0.875 T = for 0.875 ≤ b2 < 0 | Single Layer | Power-Law Distribution of Shear-Wave Velocity with Depth (Deposit with V = a2 zb2) | [82,144] |
| 6 | a3 = ; b3 = μ3 = T = for 0 ≤ μ3 < 1 T = for μ3 > 1 | Single Layer | Linear Distribution of Shear Modulus with Depth (Deposit with V = (a3 + b2z)0.5) | [140,141] |
| 7 | Ta−b = Ta for Tb/Ta > 0.1, ha > hb Ta [1 + β]1/k for Tb/Ta > 0.1, ha ≤ hb Ta [1 + ] for Tb/Ta ≤ 0.1 Here, β = 1 − 0.2 (ha/hb)2 and k = 4 − 1.8 (ha/hb) | Approximate Madera model | [142] | |
| 8 | ; tan() tan() = | Multiple Layer | Successive application of two layers | [142] |
| 9 | Xi = 0; Xi+1 + (H − Hmi) T = π | Multiple Layer | Simplified Rayleigh method | [144] |
| 10 | T = 2π | Multiple Layer | Linear fundamental Mode Shape | [144] |
| 11 | T = | Multiple Layer | Japanese seismic design code (BCJ) method | [145] |
| Site Class | Description | Site Period | NEHRP Site Class |
|---|---|---|---|
| Hard Rock | A | ||
| SC I | Rock | To < 0.2 s | A + B |
| SC II | Hard Soil | 0.2 ≤ To < 0.4 s | C |
| SC III | Medium Soil | 0.4 ≤ To < 0.6 s | D |
| SC IV | Soft Soil | To ≥ 0.6 s | E + F |
| Advantages | Limitations | |
|---|---|---|
| Linear |
|
|
| Equivalent linear |
|
|
| Nonlinear |
|
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hossain, A.S.M.F.; Saeidi, A.; Salsabili, M.; Nastev, M.; Suescun, J.R.; Bayati, Z. A Review of Parameters and Methods for Seismic Site Response. Geosciences 2025, 15, 128. https://doi.org/10.3390/geosciences15040128
Hossain ASMF, Saeidi A, Salsabili M, Nastev M, Suescun JR, Bayati Z. A Review of Parameters and Methods for Seismic Site Response. Geosciences. 2025; 15(4):128. https://doi.org/10.3390/geosciences15040128
Chicago/Turabian StyleHossain, A. S. M. Fahad, Ali Saeidi, Mohammad Salsabili, Miroslav Nastev, Juliana Ruiz Suescun, and Zeinab Bayati. 2025. "A Review of Parameters and Methods for Seismic Site Response" Geosciences 15, no. 4: 128. https://doi.org/10.3390/geosciences15040128
APA StyleHossain, A. S. M. F., Saeidi, A., Salsabili, M., Nastev, M., Suescun, J. R., & Bayati, Z. (2025). A Review of Parameters and Methods for Seismic Site Response. Geosciences, 15(4), 128. https://doi.org/10.3390/geosciences15040128










