Experimental and Numerical Methods for Hydraulic Fracturing at Laboratory Scale: A Review
Abstract
1. Introduction

2. Design Considerations in Hydraulic Fracturing
2.1. Specifications of the Sample
2.2. Stress Regime
2.3. Saturation Conditions
2.4. Fracturing Fluids
3. Scaling Factors in Hydraulic Fracturing Experimentation
4. Nature of Hydraulic Fracturing Instrumentation
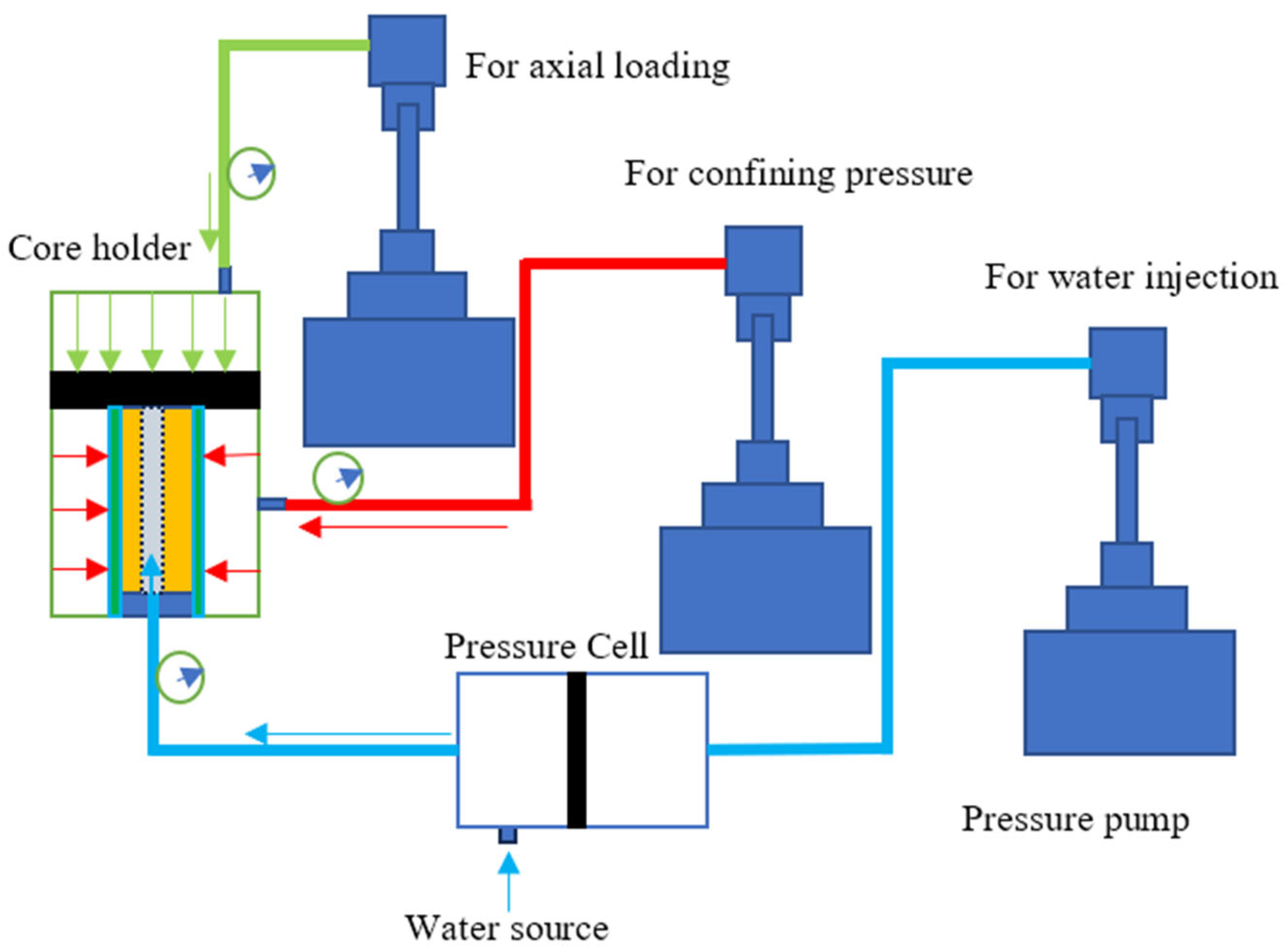
4.1. Uniaxial Testing
4.2. Biaxial Testing
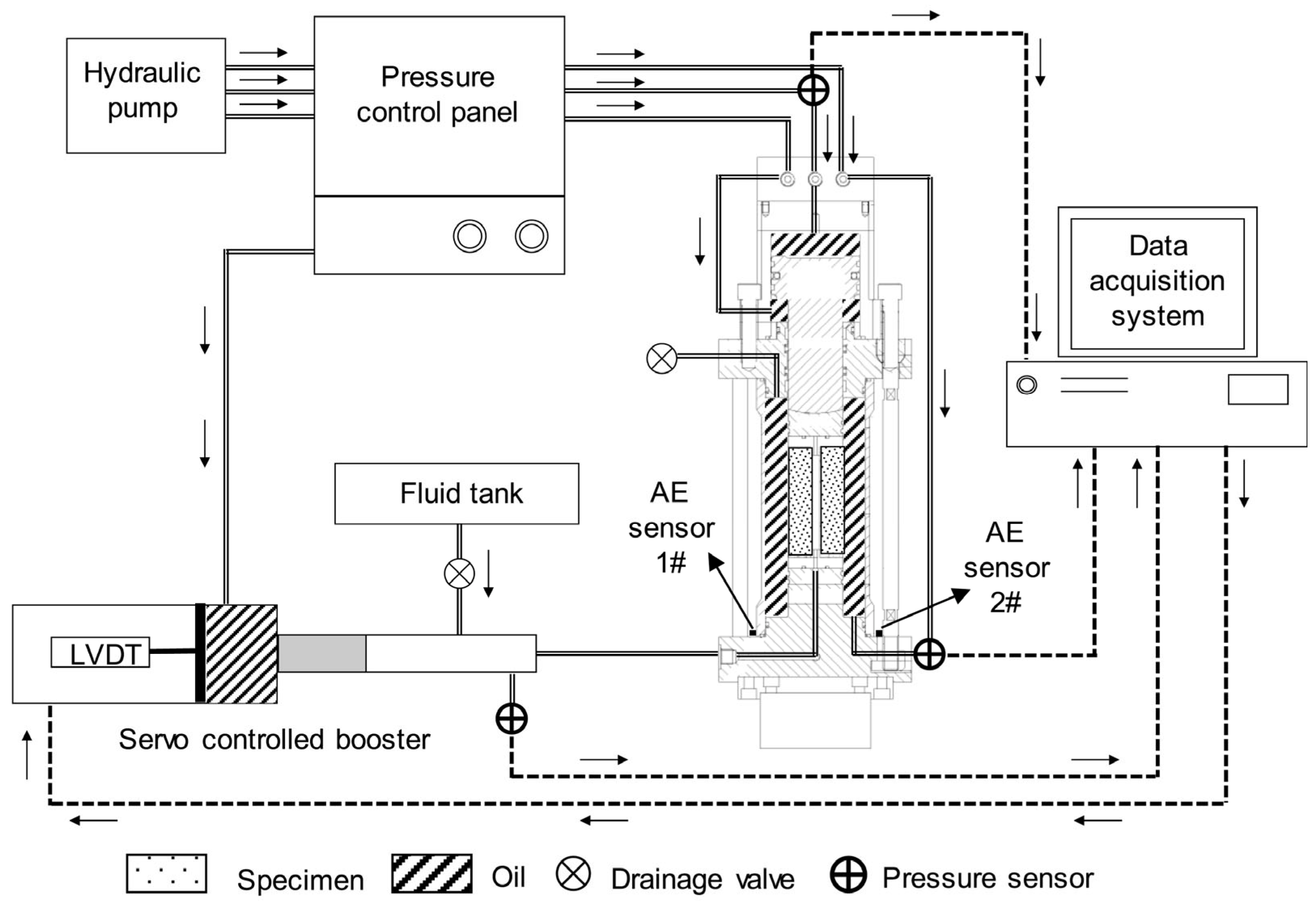
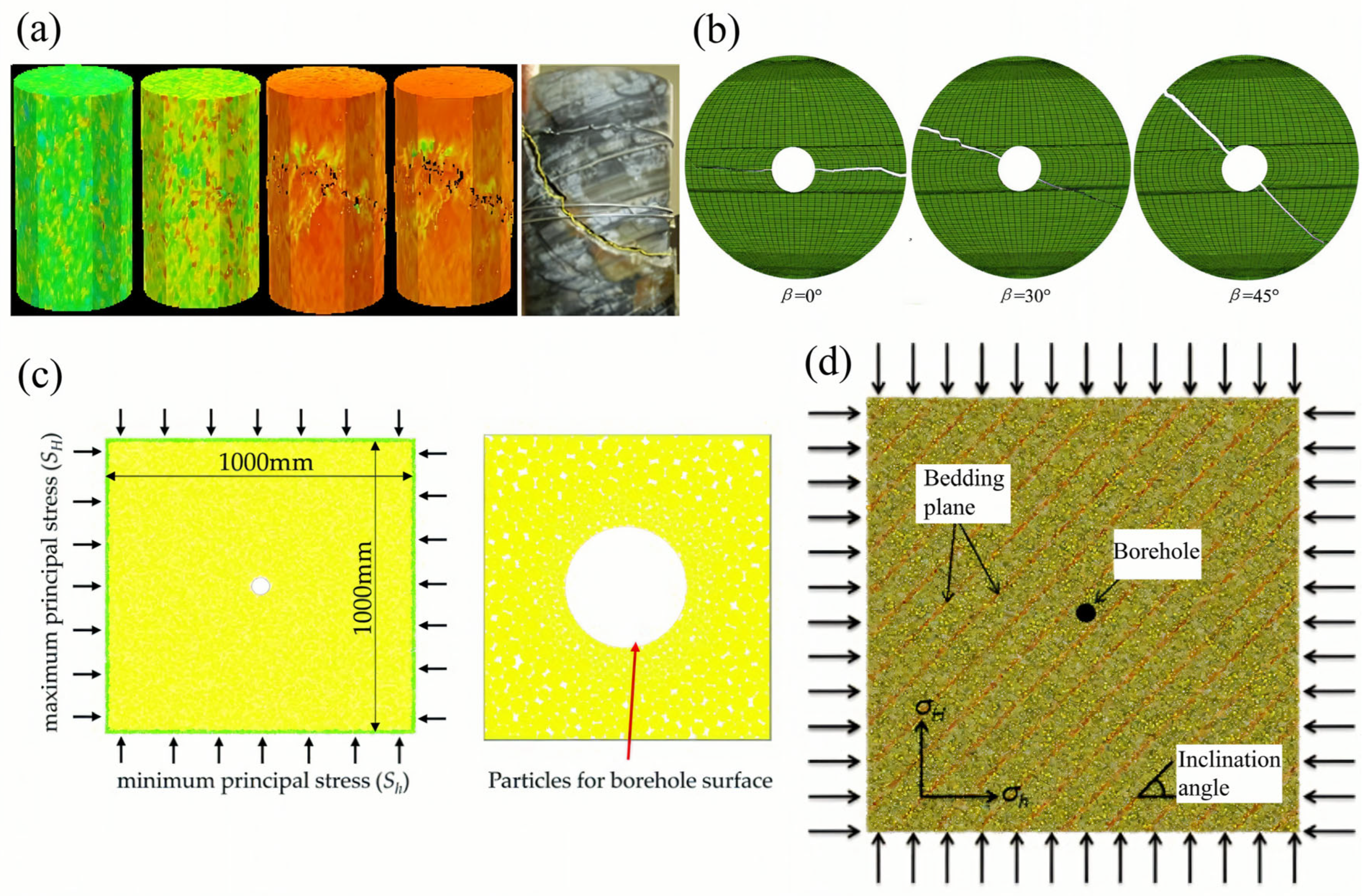
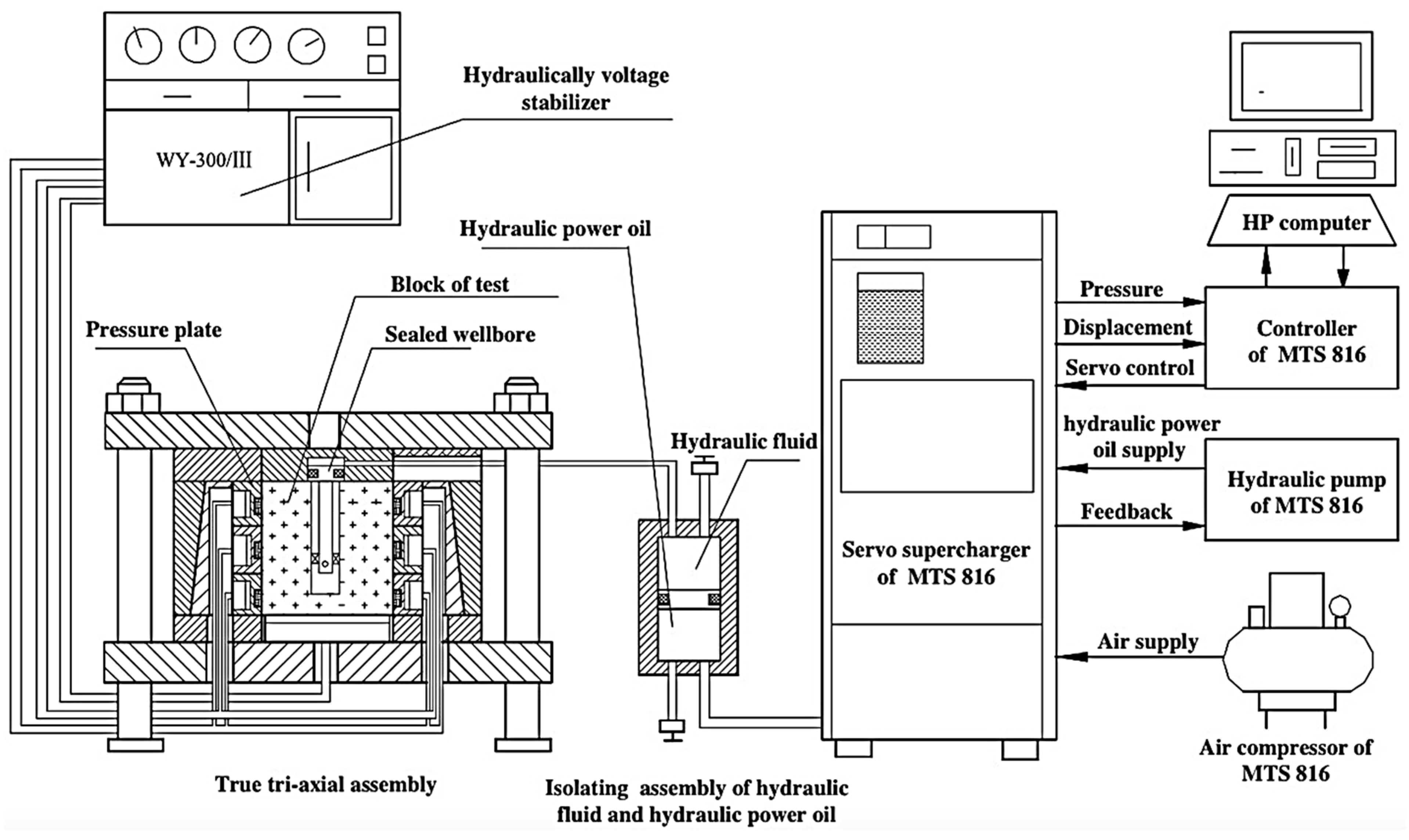
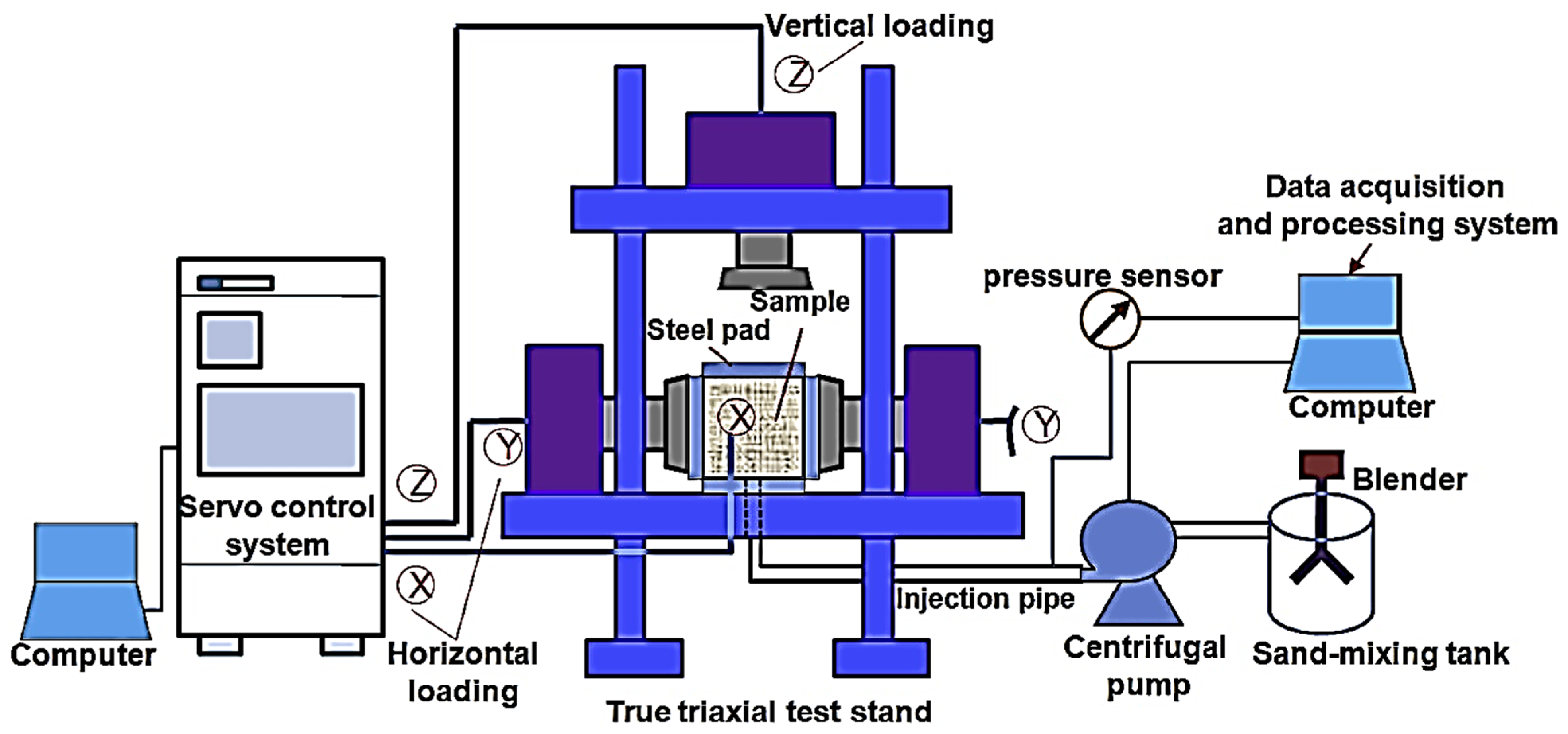
4.3. True Triaxial Testing
5. Numerical Simulation Methods
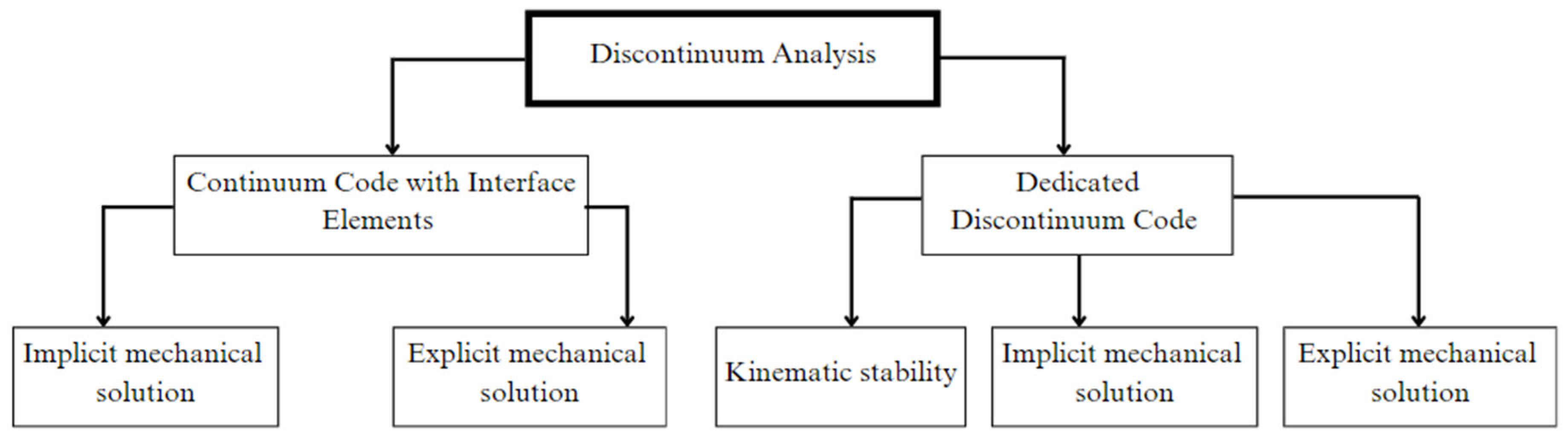
5.1. Discontinuum Modeling
5.1.1. Discrete Elemental Methods
5.1.2. Discontinuous Deformation Analysis
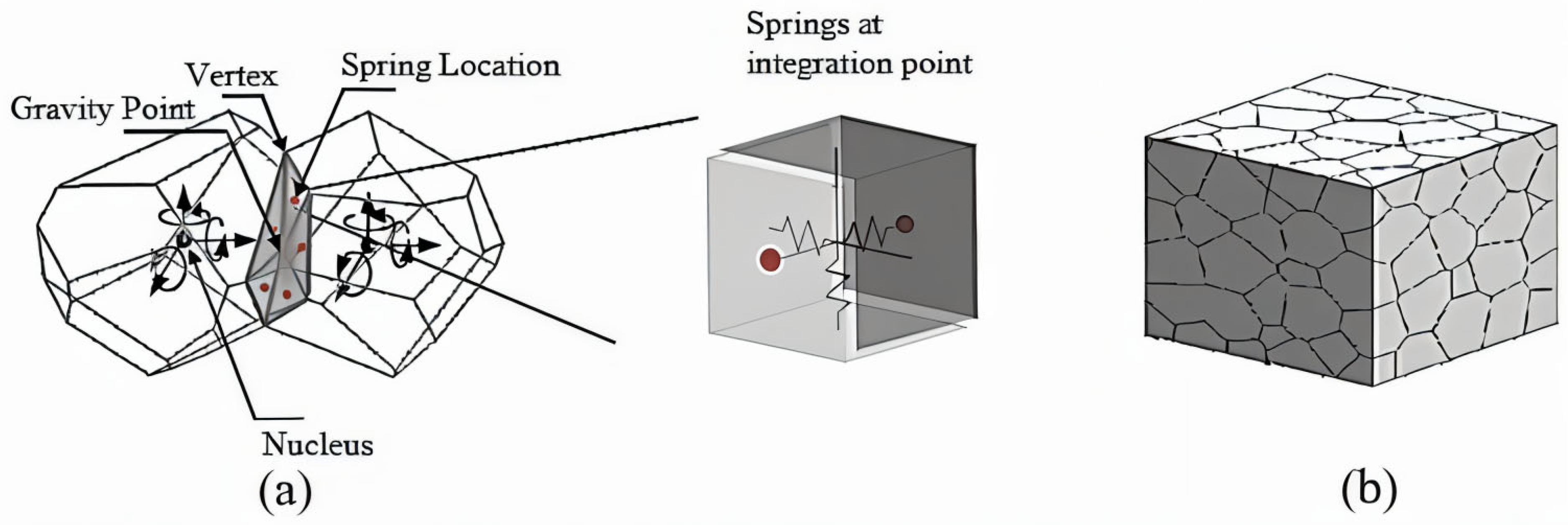
5.1.3. Rigid Body Spring Network
5.1.4. Variants of Virtual Internal Bond
5.2. Integration of Numerical Simulation and Machine Learning Methods
6. Discussion
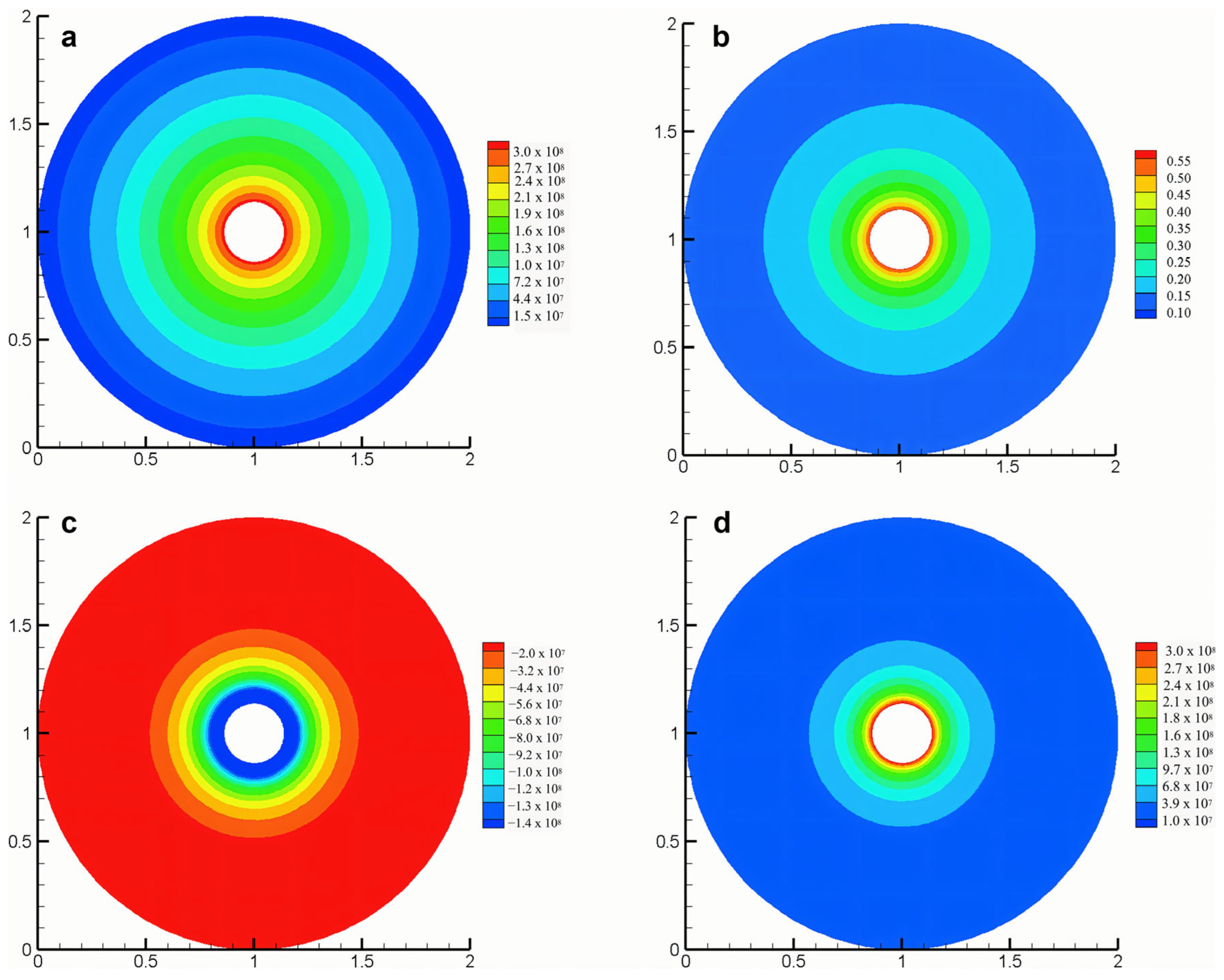
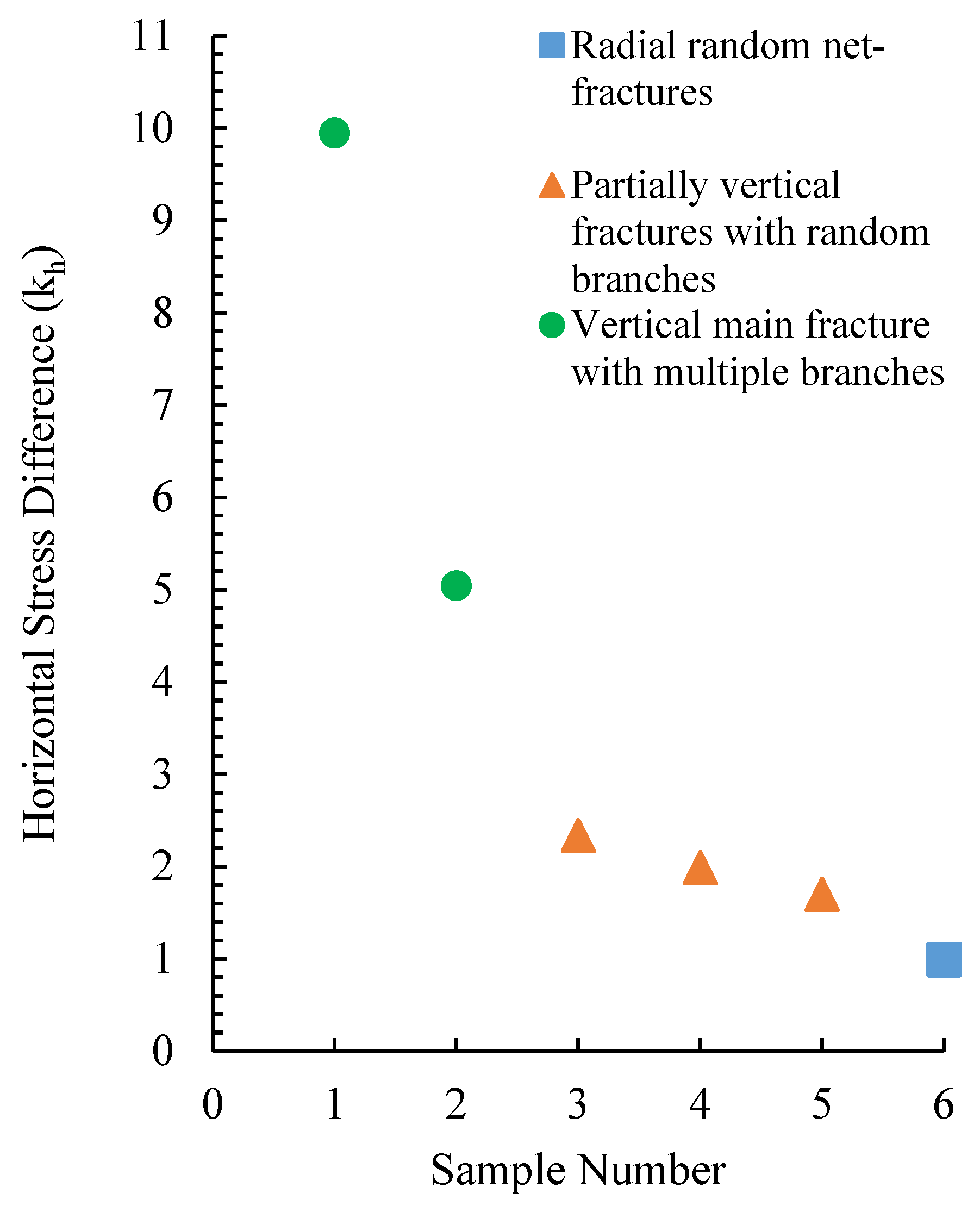
6.1. In Situ Stress Conditions
6.2. Geological Conditions
6.3. Temperature and Pressure Conditions
7. Summary
- Hydraulic fracturing experimentation has advanced with the rise of modern technology, helping to reach more reliable and applicable results for application in the field. This paper summarizes the recent advances in uniaxial, biaxial, and true triaxial testing, and their implications in hydraulic fracturing operations. This review article discusses the basic concepts of fracture models, scaling factors, and the nature of laboratory studies for hydraulic fracturing design. At the end of this article, the shortcomings of the laboratory apparatus regarding the lack of reservoir in situ stresses, geological, temperature, and pressure conditions were discussed.
- The scaling factor is an essential aspect of laboratory testing for the accurate and reliable application of results in field operations. Laboratory-scale performance of the hydraulic fracturing experimentation requires that the testing material has a low fracture toughness and low permeability, and fractured by high-viscosity fracturing fluid. Small research efforts have been made to build a relationship between the laboratory and field operations of hydraulic fracturing through consideration of applicable scaling factors.
- The main components of a basic hydraulic fracturing apparatus include a loading mechanism, fluid injection system, data monitoring, and other advanced sensors, depending on the research objectives. The nature of the loading system differentiates the hydraulic fracturing apparatus into uniaxial, biaxial, and true triaxial experimentation. The varying 3D loading conditions in true triaxial testing have the highest match with the field conditions of hydraulic fracturing. Adding advanced sensors related to the pore pressure, acoustic emission, temperature, stress distribution, and geological discontinuities will increase the adaptability of the results in field conditions. The hydraulic fracturing experimentation on samples from the field environment and the controlled artificial sample experimentation improve the interpretation of the results in more applicable ranges.
- In situ stresses, geological conditions, temperature, and pressure influence the behavior of the hydraulic fracture. Stress differences significantly impact the fracture propagation more than the geomechanical properties, fluid pressures, and geological structures. Continuous stress distribution monitoring in samples needs to be improved in true triaxial apparatus. Simplified laboratory conditions may introduce errors in hydraulic fracturing testing. Natural–hydraulic fracture interaction depends on horizontal stress differences, rock–fluid interactions, and fracturing pressure. Unrealistic representations of natural fractures limit laboratory testing. Temperature effects vary with the reservoir lithology, impacting the fracture complexity and length. The temperature and confining pressure can reduce the fracture aperture and conductivity. A comprehensive understanding of the natural fracture contribution, temperature, and stress distribution requires combined laboratory, numerical, and field methods, including CT scans, microseismic data, pressure analysis, tracer testing, and production logging.
- Laboratory-scale hydraulic fracturing experiments offer critical insights but are constrained by scaling effects, differences in the stress distribution, and reservoir heterogeneity. The limited size of laboratory samples fails to match the field scale, resulting in differences in the anticipated fracture initiation, propagation, and geometry. Discrepancies in factors such as the pore pressure, temperature, and pressure gradients may cause variations in the fluid behavior, leak-off, and rock–fluid interactions between the lab and field scales. Although numerical simulations help to bridge the lab findings to field applications, they often rely on simplified assumptions that overlook real-world geological complexities. Scaling factors may improve and generalize lab findings, but they are ineffective for highly heterogeneous reservoir features. The accuracy of numerical models can be enhanced by integrating machine learning, real-time monitoring, and adaptive fracturing techniques.
- Hydraulic fracturing at the laboratory scale provides valuable insights into fracture initiation, propagation, and interactions with rock heterogeneities, but its limitations necessitate the use of numerical simulations for more comprehensive analyses. Numerical models, such as the DEM, DDA, and RBSN, effectively simulate complex mechanisms, including fracture–fluid interactions, stress redistributions, and the influence of the rock microstructure, thus enhancing our understanding of hydraulic fracturing processes. Advancements in these models, such as integrating nonlinear elasticity in VIB and coupling with finite element analysis or fluid network models, continue to improve the predictive accuracy and efficiency, especially in complex geological settings, offering promising applications for optimizing shale gas production, acid fracturing, and geotechnical engineering.
- Future research should focus on combining microseismic monitoring, well logs, and pressure diagnostics to improve calibration from the nano- and microscale to the megascale. Advancements in high-resolution imaging and ML-driven tools have the potential to further refine predictive capabilities and bridge the gap between lab-scale insights and field-scale applications. More focus is required to design experimentation setups that can observe the fracture initiation and propagation dynamically. Currently, it is of uttermost importance to devise cheaper methods that may provide the capability to exert true triaxial loading. More efforts are required to develop open-access discontinuum simulators with extended flexibility to integrate the lab and field testing data.
Funding
Data Availability Statement
Conflicts of Interest
References
- Holditch, S.A. Tight gas sands. J. Pet. Technol. 2006, 58, 86–93. [Google Scholar] [CrossRef]
- Naik, G. Tight gas reservoirs—An unconventional natural energy source for the future. Accessado em 2003, 1, 2008. [Google Scholar]
- Belyadi, H.; Fathi, E.; Belyadi, F. Introduction to unconventional reservoirs. In Hydraulic Fracturing in Unconventional Reservoirs; Elsevier: Amsterdam, The Netherlands, 2017; pp. 1–12. [Google Scholar]
- Holditch, S.A. Hydraulic fracturing: Overview, trends, issues. Drill. Contract. 2007, 63, 116–118. [Google Scholar]
- Kumar, T.; Shandilya, A. Tight reservoirs: An overview in Indian context. In Proceedings of the 10th Biennial International Exhibition & Conference, Mumbai, India, 4–6 October 2013. [Google Scholar]
- Arthur, M.A.; Cole, D.R. Unconventional hydrocarbon resources: Prospects and problems. Elements 2014, 10, 257–264. [Google Scholar] [CrossRef]
- Gao, Q.; Cheng, Y.; Han, S.; Yan, C.; Jiang, L. Numerical modeling of hydraulic fracture propagation behaviors influenced by pre-existing injection and production wells. J. Pet. Sci. Eng. 2019, 172, 976–987. [Google Scholar] [CrossRef]
- King, G.E. Hydraulic fracturing 101: What every representative, environmentalist, regulator, reporter, investor, university researcher, neighbor and engineer should know about estimating frac risk and improving frac performance in unconventional gas and oil wells. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 6–8 February 2012. [Google Scholar]
- Smith, M.B.; Montgomery, C. Hydraulic Fracturing; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Warpinski, N.R.; Mayerhofer, M.J.; Agarwal, K.; Du, J. Hydraulic fracture geomechanics and microseismic source mechanisms. SPE J. 2013, 18, 766–780. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, X.; Liu, Z. Experimental investigation of hydraulic sand fracturing on fracture propagation under the influence of coal macrolithotypes in Hancheng block. J. Pet. Sci. Eng. 2019, 175, 60–71. [Google Scholar] [CrossRef]
- Cipolla, C.; Wright, C. Diagnostic techniques to understand hydraulic fracturing: What? why? and how? In Proceedings of the SPE/CERI Gas Technology Symposium, Calgary, AB, Canada, 3–5 April 2020.
- Van Der Baan, M.; Eaton, D.; Dusseault, M. Microseismic monitoring developments in hydraulic fracture stimulation. In Proceedings of the ISRM International Conference for Effective and Sustainable Hydraulic Fracturing, Brisbane, Australia, 20–22 May 2013. [Google Scholar]
- Dejam, M. Tracer dispersion in a hydraulic fracture with porous walls. Chem. Eng. Res. Des. 2019, 150, 169–178. [Google Scholar] [CrossRef]
- Dejam, M.; Hassanzadeh, H.; Chen, Z. Semi-analytical solution for pressure transient analysis of a hydraulically fractured vertical well in a bounded dual-porosity reservoir. J. Hydrol. 2018, 565, 289–301. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, H.; Lin, H.; Zhao, Y.; Liu, Y. Fracture behaviour of central-flawed rock plate under uniaxial compression. Theor. Appl. Fract. Mech. 2020, 106, 102503. [Google Scholar] [CrossRef]
- Stanisławek, S.; Kędzierski, P.; Miedzińska, D. Laboratory hydraulic fracturing tests of rock samples with water. Arch. Civ. Eng. 2017, 63, 139–148. [Google Scholar] [CrossRef]
- Sarmadivaleh, M.; Rasouli, V. Test design and sample preparation procedure for experimental investigation of hydraulic fracturing interaction modes. Rock Mech. Rock Eng. 2014, 48, 93–105. [Google Scholar] [CrossRef]
- Mao, R.; Feng, Z.; Liu, Z.; Zhao, Y. Laboratory hydraulic fracturing test on large-scale pre-cracked granite specimens. J. Nat. Gas Sci. Eng. 2017, 44, 278–286. [Google Scholar] [CrossRef]
- Lisjak, A.; Kaifosh, P.; He, L.; Tatone, B.; Mahabadi, O.; Grasselli, G. FDEM formulation for modelling fracturing processes in discontinuous. Comput. Geotech. 2017, 81, 1–18. [Google Scholar] [CrossRef]
- Eshiet, K.I.; Sheng, Y. An overview of principles and designs of hydraulic fracturing experiments and an inquiry into the influence of rock permeability and strength on failure mode. In Advances in Natural Gas Emerging Technologies; IntechOpen: London, UK, 2017. [Google Scholar]
- Huang, M.; Liu, D.; Hong, C.; Du, S.; Luo, Z.; Li, C.; Huang, Y. Representative sample sampling method for size effect experiment of jointed rock mass. Geofluids 2020, 2020, 1–8. [Google Scholar] [CrossRef]
- Cao, W.; Yildirim, B.; Durucan, S.; Wolf, K.-H.; Cai, W.; Agrawal, H.; Korre, A. Fracture behaviour and seismic response of naturally fractured coal subjected to true triaxial stresses and hydraulic fracturing. Fuel 2021, 288, 119618. [Google Scholar] [CrossRef]
- Zhong, Z.; Xu, C.; Zhang, F.; Wang, X.; Hu, Y. Size effect on hydraulic properties of rough-walled fractures upscaled from meter-scale granite fractures. Geomech. Geophys. Geo-Energy Geo-Resour. 2023, 9, 75. [Google Scholar] [CrossRef]
- Kashfi, M.; Shad, S.; Zivar, D. Evaluation of sample scale effect on geomechanical tests. Pet. Res. 2022, 7, 527–535. [Google Scholar] [CrossRef]
- Li, L.; Hu, J.; Li, S.; Qin, C.; Liu, H.; Chen, D.; Wang, J. Development of a novel triaxial rock testing method based on biaxial test apparatus and its application. Rock Mech. Rock Eng. 2021, 54, 1597–1607. [Google Scholar] [CrossRef]
- Shabdirova, A.; Bissekenova, Z.; Minh, N.H.; Kim, J.R. Sample preparation method of clay-rich sandstone analogue of sandstone reservoirs in Kazakhstan. In Proceedings of the ARMA US Rock Mechanics/Geomechanics Symposium, Houston, TX, USA, 26–29 June 2016. [Google Scholar]
- De Pater, C.; Beugelsdijk, L. Experiments and numerical simulation of hydraulic fracturing in naturally fractured rock. In Proceedings of the Alaska Rocks 2005, the 40th US Symposium on Rock Mechanics (USRMS), Anchorage, AK, USA, 25–29 June 2005. [Google Scholar]
- Deng, J.; Lin, C.; Yang, Q.; Liu, Y.; Tao, Z.; Duan, H. Investigation of directional hydraulic fracturing based on true tri-axial experiment and finite element modeling. Comput. Geotech. 2016, 75, 28–47. [Google Scholar] [CrossRef]
- Zhang, X.; Si, G.; Bai, Q.; Xiang, Z.; Li, X.; Oh, J.; Zhang, Z. Numerical simulation of hydraulic fracturing and associated seismicity in lab-scale coal samples: A new insight into the stress and aperture evolution. Comput. Geotech. 2023, 160, 105507. [Google Scholar] [CrossRef]
- Xie, L.; Jin, P.; Su, T.-C.; Li, X.; Liang, Z. Numerical simulation of uniaxial compression tests on layered rock specimens using the discrete element method. Comput. Part. Mech. 2019, 7, 753–762. [Google Scholar] [CrossRef]
- Liu, D.; Shi, X.; Zhang, X.; Wang, B.; Tang, T.; Han, W. Hydraulic fracturing test with prefabricated crack on anisotropic shale: Laboratory testing and numerical simulation. J. Pet. Sci. Eng. 2018, 168, 409–418. [Google Scholar] [CrossRef]
- Li, L.C.; Tang, C.A.; Li, G.; Wang, S.Y.; Liang, Z.Z.; Zhang, Y.B. Numerical simulation of 3D hydraulic fracturing based on an improved flow-stress-damage model and a parallel FEM technique. Rock Mech. Rock Eng. 2012, 45, 801–818. [Google Scholar] [CrossRef]
- Han, Z.; Zhou, J.; Zhang, L. Influence of grain size heterogeneity and in-situ stress on the hydraulic fracturing process by PFC2D modeling. Energies 2018, 11, 1413. [Google Scholar] [CrossRef]
- Qin, X.; Cai, J.; Wang, G. Pore-scale modeling of pore structure properties and wettability effect on permeability of low-rank coal. Int. J. Min. Sci. Technol. 2023, 33, 573–584. [Google Scholar] [CrossRef]
- Wang, Y.; Fu, H.; Liang, T.; Wang, X.; Liu, Y.; Peng, Y.; Yang, L.; Tian, Z. Large-scale physical simulation experiment research for hydraulic fracturing in shale. In Proceedings of the SPE Middle East Oil and Gas Show and Conference, Manama, Bahrain, 8–11 March 2015. [Google Scholar]
- Liberman, M. Hydraulic Fracturing Experiments to Investigate Circulation Losses. Master’s Thesis, Missouri University of Science and Technology, Rolla, MO, USA, 2012. [Google Scholar]
- Brenne, S.; Molena, M.; Stöckert, F.; Alber, M. Hydraulic and sleeve fracturing laboratory experiments on 6 rock types. In Proceedings of the ISRM International Conference for Effective and Sustainable Hydraulic Fracturing, Brisbane, Australia, 20–22 May 2013. [Google Scholar]
- Taherynia, M.H.; Aghda, S.M.F.; Fahimifar, A. In-situ stress state and tectonic regime in different depths of earth crust. Geotech. Geol. Eng. 2016, 34, 679–687. [Google Scholar] [CrossRef]
- Farkas, M.P.; Yoon, J.S.; Zang, A.; Zimmermann, G.; Stephansson, O.; Lemon, M.; Dankó, G. Effect of foliation and fluid viscosity on hydraulic fracturing tests in mica schists investigated using distinct element modeling and field data. Rock Mech. Rock Eng. 2018, 52, 555–574. [Google Scholar] [CrossRef]
- Yan, X.; Yu, H. Numerical simulation of hydraulic fracturing with consideration of the pore pressure distribution based on the unified pipe-interface element model. Eng. Fract. Mech. 2022, 275, 108836. [Google Scholar] [CrossRef]
- Qiu, R.; Zhang, G.; Zheng, X.; Luo, S.; Chen, H.; Zhao, J. Stress transfer law in laboratory hydraulic fracturing experiments. Sci. Rep. 2024, 14, 17287. [Google Scholar] [CrossRef]
- Ye, Z.; Ghassemi, A. Reexamining in-situ stress interpretation using laboratory hydraulic fracturing experiments. In Proceedings of the Unconventional Resources Technology Conference, Denver, CO, USA, 13–15 June 2023. [Google Scholar]
- Fan, P.; Liu, Y.; Lin, Z.; Wang, J.; He, Y.; Zhang, B. Physical Simulation Experiment Research for Hydraulic Fracturing in Tight Sandstone Reservoir Under Different Stress Conditions and Nature Fracture Combinations. In Proceedings of the 58th U.S. Rock Mechanics/Geomechanics Symposium, Golden, CO, USA, 23–26 June 2024. [Google Scholar]
- Jalili, S.; Ahangari, K. Effects of different stress regimes on hydraulic fracture geometry: A particle flow code approach. Innov. Infrastruct. Solut. 2017, 2, 41. [Google Scholar] [CrossRef]
- Shevtsova, A.; Stanchits, S.; Filev, E.; Karamov, T.; Stukachev, V.; Spasennykh, M. Assessment of Saturation Effect on Hydraulic Fracturing in Sandstone and Thermally Treated Granite. Minerals 2023, 13, 777. [Google Scholar] [CrossRef]
- Zhuang, L.; Kim, K.Y.; Diaz, M.; Yeom, S. Evaluation of water saturation effect on mechanical properties and hydraulic fracturing behavior of granite. Int. J. Rock Mech. Min. Sci. 2020, 130, 104321. [Google Scholar] [CrossRef]
- Jian, G.; Sarathi, R.S.; Burghardt, J.; Bonneville, A.; Fernandez, C.A. Effect of initial water saturation on the performance of fracturing fluids with and without polyallylamine under simulated EGS conditions. Geothermics 2023, 111, 102715. [Google Scholar] [CrossRef]
- Cuss, R.; Wiseall, A.C.; Hennissen, J.A.I.; Waters, C.N.; Kemp, S.J.; Ougier-Simonin, A.; Holyoake, S.; Haslam, R.B. Hydraulic Fracturing: A Review of Theory and Field Experience; British Geological Survey: Nottingham, UK, 2015. [Google Scholar]
- Bennour, Z.; Ishida, T.; Nagaya, Y.; Chen, Y.; Nara, Y.; Chen, Q.; Sekine, K.; Nagano, Y. Crack extension in hydraulic fracturing of shale cores using viscous oil. Rock Mech. Rock Eng. 2015, 48, 1463–1473. [Google Scholar] [CrossRef]
- Xing, Y.; Zhang, G.; Luo, T.; Jiang, Y.; Ning, S. Hydraulic fracturing in high-temperature granite characterized by acoustic emission. J. Pet. Sci. Eng. 2019, 178, 475–484. [Google Scholar] [CrossRef]
- AlTammar, M.J.; Gala, D.; Sharma, M.M.; McAndrew, J. Laboratory visualization of fracture initiation and propagation using compressible and incompressible fracturing fluids. J. Nat. Gas Sci. Eng. 2018, 55, 542–560. [Google Scholar] [CrossRef]
- Wanniarachchi, W.; Ranjith, P.; Perera, M.; Rathnaweera, T.; Zhang, C.; Zhang, D. An integrated approach to simulate fracture permeability and flow characteristics using regenerated rock fracture from 3-D scanning: A numerical study. J. Nat. Gas Sci. Eng. 2018, 53, 249–262. [Google Scholar] [CrossRef]
- Ma, W.; Yang, C.; Ahmed, S.F.; Hassan, N.; Cui, H.; Wu, X.; Liu, G. Effects of thermophysical parameters of fracturing fluid on hot dry rock damage in hydraulic fracturing. Geomech. Energy Environ. 2022, 32, 100405. [Google Scholar] [CrossRef]
- Qin, M.; Yang, D.; Chen, W. Numerical investigation of the effects of fracturing fluid parameters on hydraulic fracture propagation in jointed rock mass based on peridynamics. Eng. Anal. Bound. Elem. 2022, 135, 38–51. [Google Scholar] [CrossRef]
- Zhang, K.; Liu, Y.; Sheng, L.; Li, B.; Chen, T.; Liu, X.; Yao, E. Study on the effect of fracturing fluid on the structure and mechanical properties of igneous rock. ACS Omega 2022, 7, 11903–11913. [Google Scholar] [CrossRef]
- Wrobel, M.; Mishuris, G.; Papanastasiou, P. On the influence of fluid rheology on hydraulic fracture. Int. J. Eng. Sci. 2021, 158, 103426. [Google Scholar] [CrossRef]
- Li, X.; Feng, Z.; Han, G.; Elsworth, D.; Marone, C.; Saffer, D. Hydraulic fracturing in shale with H2O, CO2 and N2. In Proceedings of the 49th U.S. Rock Mechanics/Geomechanics Symposium, San Francisco, CA, USA, 1 July–28 June 2015. [Google Scholar]
- Feng, Y.; Haugen, K.; Firoozabadi, A. water and nitrogen in 2D and comparison with laboratory data. J. Geophys. Res. Solid Earth 2021, 126. [Google Scholar] [CrossRef]
- Yang, J.; Lian, H.; Li, L. Fracturing in coals with different fluids: An experimental comparison between water. Sci. Rep. 2020, 10, 18681. [Google Scholar] [CrossRef]
- Hou, B.; Diao, C.; Li, D. An experimental investigation of geomechanical properties of deep tight gas reservoirs. J. Nat. Gas Sci. Eng. 2017, 47, 22–33. [Google Scholar] [CrossRef]
- Gandossi, L.; Von Estorff, U. An Overview of Hydraulic Fracturing and Other Formation Stimulation Technologies for Shale Gas Production; Publications Office of the European Union: Luxembourg, 2015. [Google Scholar]
- Lv, Q.; Li, Z.; Li, B.; Li, S.; Sun, Q. Study of nanoparticle–surfactant-stabilized foam as a fracturing fluid. Ind. Eng. Chem. Res. 2015, 54, 9468–9477. [Google Scholar] [CrossRef]
- Abdelaal, A.; Aljawad, M.S.; Alyousef, Z.; Almajid, M.M. A review of foam-based fracturing fluids applications: From lab studies to field implementations. J. Nat. Gas Sci. Eng. 2021, 95, 104236. [Google Scholar] [CrossRef]
- He, S.; Qin, Q.; Qin, Z.; Zhou, J. Natural fracture development characteristics and their relationship with gas Contents—A case study of Wufeng–Longmaxi formation in Luzhou area, southern Sichuan basin, China. ACS Omega 2022, 7, 34066–34079. [Google Scholar] [CrossRef]
- Khan, J.A.; Padmanabhan, E.; Haq, I.U.; Franchek, M.A. Hydraulic fracturing with low and high viscous injection mediums to investigate net fracture pressure and fracture network in shale of different brittleness index. Geomech. Energy Environ. 2022, 33, 100416. [Google Scholar] [CrossRef]
- de Pater, C.J.; Cleary, M.P.; Quinn, T.S.; Barr, D.T.; Johnson, D.E.; Weijers, L. Experimental verification of dimensional analysis for hydraulic fracturing. SPE Prod. Facil. 1994, 9, 230–238. [Google Scholar] [CrossRef]
- Bunger, A.P.; Jeffrey, R.G.; Detournay, E. Application of scaling laws to laboratory-scale hydraulic fractures. In Proceedings of the Alaska Rocks 2005, The 40th US Symposium on Rock Mechanics (USRMS), Anchorage, AK, USA, 25–29 June 2005. [Google Scholar]
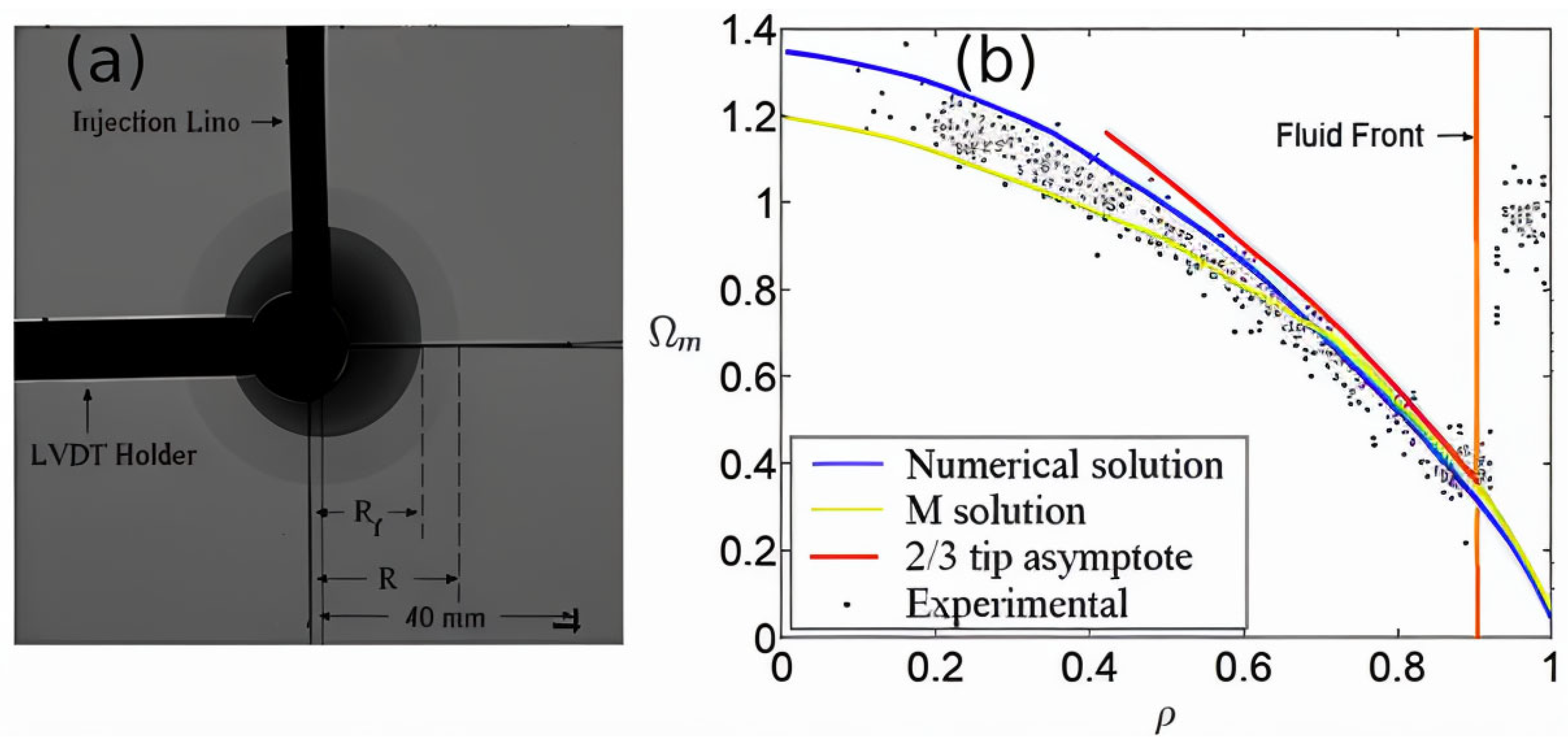
- Savitski, A.; Detournay, E. Propagation of a penny-shaped fluid-driven fracture in an impermeable rock: Asymptotic solutions. Int. J. Solids Struct. 2002, 39, 6311–6337. [Google Scholar] [CrossRef]
- Bunger, A.P.; Detournay, E. Near-surface hydraulic fracture. Eng. Fract. Mech. 2005, 72, 2468–2486. [Google Scholar] [CrossRef]
- Michael, A. Transparent gelatin as a reservoir analogue: Dimensional scaling for hydraulic fracturing laboratory experiments. Int. J. Rock Mech. Min. Sci. 2024, 177, 105732. [Google Scholar] [CrossRef]
- Fu, W.; Morris, J.P.; Fu, P.; Huang, J.; Sherman, C.S.; Settgast, R.R.; Wu, H.; Ryerson, F.J. Developing upscaling approach for swarming hydraulic fractures observed at Hydraulic Fracturing Test Site through multiscale simulations. SPE J. 2021, 26, 2670–2684. [Google Scholar] [CrossRef]
- Zhang, G.; Liu, H.; Zhang, J.; Wu, H.; Wang, X. Three-dimensional finite element simulation and parametric study for horizontal well hydraulic fracture. J. Pet. Sci. Eng. 2010, 72, 310–317. [Google Scholar] [CrossRef]
- Fallahzadeh, S.H.; Rasouli, V.; Sarmadivaleh, M. An investigation of hydraulic fracturing initiation and near-wellbore propagation from perforated boreholes in tight formations. Rock Mech. Rock Eng. 2014, 48, 573–584. [Google Scholar] [CrossRef]
- Detournay, E. Propagation regimes of fluid-driven fractures in impermeable rocks. Int. J. Geomech. 2004, 4, 35–45. [Google Scholar] [CrossRef]
- Wu, K.; Olson, J.E. Numerical investigation of complex hydraulic-fracture development in naturally fractured reservoirs. SPE Prod. Oper. 2016, 31, 300–309. [Google Scholar] [CrossRef]
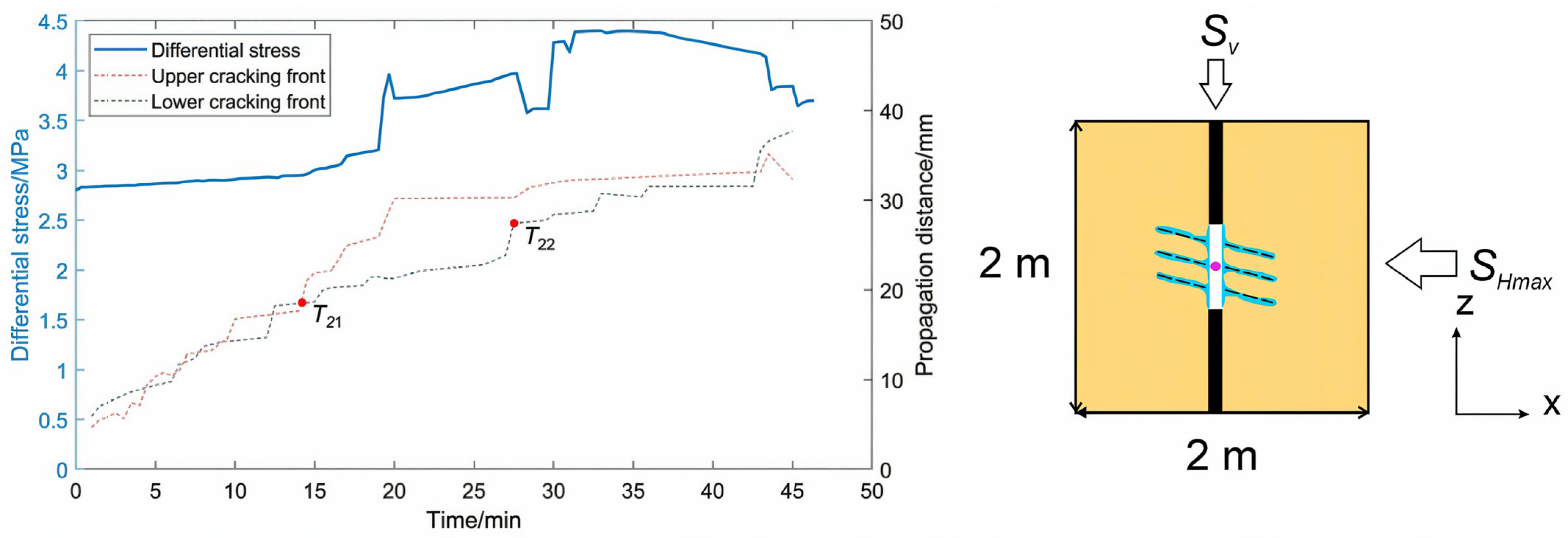
- Lei, B.; Zuo, J.; Coli, M.; Yu, X.; Li, Y.; Liu, H. Investigation on failure behavior and hydraulic fracturing mechanism of Longmaxi shale with different bedding properties. Comput. Geotech. 2024, 167, 106081. [Google Scholar] [CrossRef]
- Liang, D.; Zhang, N.; Rong, H.; Xiang, Z. Experimental and numerical studies on crack initiation and coalescence in sandy mudstone with prefabricated cross-flaws under uniaxial compression. Shock. Vib. 2021, 2021, 6672913. [Google Scholar] [CrossRef]
- Liu, X.; Lei, W.; Huang, J.; Ding, Y.; Liang, L.; Xiong, J. The investigation on initiation and propagation of hydraulic fractures in shale reservoir. Geofluids 2021, 2021, 2366709. [Google Scholar] [CrossRef]
- Naoi, M.; Chen, Y.; Nishihara, K.; Yamamoto, K.; Yano, S.; Watanabe, S.; Morishige, Y.; Kawakata, H.; Akai, T.; Kurosawa, I.; et al. Monitoring hydraulically-induced fractures in the laboratory using acoustic emissions and the fluorescent method. Int. J. Rock Mech. Min. Sci. 2018, 104, 53–63. [Google Scholar] [CrossRef]
- Zhang, X.; Li, X.; Liu, Y.; Liu, W.; Li, Q.; Li, L. Experimental study on crack propagation and failure mode of fissured shale under uniaxial compression. Theor. Appl. Fract. Mech. 2022, 121, 103512. [Google Scholar] [CrossRef]
- Moradian, Z.; Seiphoori, A.; Evans, B. The role of bedding planes on fracture behavior and acoustic emission response of shale under unconfined compression. In Proceedings of the 51st US Rock Mechanics/Geomechanics Symposium, San Francisco, CA, USA, 25–28 June 2017. [Google Scholar]
- Goncalves da Silva, B.; Li, B.Q.; Moradian, Z.; Germaine, J.T.; Einstein, H.H. Development of a test setup capable of producing hydraulic fracturing in the laboratory with image and acoustic emission monitoring. In Proceedings of the 49th US Rock Mechanics/Geomechanics Symposium, San Francisco, CA, USA, 1 July–28 June 2015. [Google Scholar]
- Liu, Q.; Liang, B.; Sun, W.; Zhao, H.; Hao, J.; Hou, M. Experimental study on hydraulic fracturing of bedding shale considering anisotropy effects. ACS Omega 2022, 7, 22698–22713. [Google Scholar] [CrossRef]
- AlDajani, O.; Germaine, J.; Einstein, H. Hydraulic Fracture of opalinus shale under uniaxial stress: Experiment design and preliminary results. In Proceedings of the 52nd US Rock Mechanics/Geomechanics Symposium, Seattle, WA, USA, 17–20 June 2018. [Google Scholar]
- Wang, K.; Zhang, G.; Wang, Y.; Zhang, X.; Li, K.; Guo, W.; Du, F. A numerical investigation of hydraulic fracturing on coal seam permeability based on PFC-COMSOL coupling method. Int. J. Coal Sci. Technol. 2022, 9, 10. [Google Scholar] [CrossRef]
- Su, X.; Li, D.; Zhu, Q.; Ma, J. Experimental study of fatigue load effect on the hydraulic fracturing behavior of granite. Fatigue Fract. Eng. Mater. Struct. 2022, 46, 540–554. [Google Scholar] [CrossRef]
- Wang, S.; Elsworth, D.; Liu, J. Permeability evolution in fractured coal: The roles of fracture geometry and water-content. Int. J. Coal Geol. 2011, 87, 13–25. [Google Scholar] [CrossRef]
- Zhuang, L.; Kim, K.Y.; Jung, S.G.; Diaz, M.; Min, K.-B. injection rate and anisotropy on hydraulic fracturing behavior of granite. Rock Mech. Rock Eng. 2018, 52, 575–589. [Google Scholar] [CrossRef]
- Li, X.; Feng, Z.; Han, G.; Elsworth, D.; Marone, C.; Saffer, D.; Cheon, D.-S. Breakdown pressure and fracture surface morphology of hydraulic fracturing in shale with H2O. Geomech. Geophys. Geo-Energy Geo-Resour. 2016, 2, 63–76. [Google Scholar] [CrossRef]
- Zhang, Y.; Ma, Y.; Hu, Z.; Lei, H.; Bai, L.; Lei, Z.; Zhang, Q. An experimental investigation into the characteristics of hydraulic fracturing and fracture permeability after hydraulic fracturing in granite. Renew. Energy 2019, 140, 615–624. [Google Scholar] [CrossRef]
- Chen, J.; Li, X.; Cao, H. Experimental investigation of coal-like materials for hydraulic fracturing based on fluid-solid interaction. J. Nat. Gas Sci. Eng. 2019, 69, 102928. [Google Scholar] [CrossRef]
- Kumari, W.; Ranjith, P.; Perera, M.; Li, X.; Li, L.; Chen, B.; Isaka, B.A.; De Silva, V. Hydraulic fracturing under high temperature and pressure conditions with micro CT applications: Geothermal energy from hot dry rocks. Fuel 2018, 230, 138–154. [Google Scholar] [CrossRef]
- Han, L.; Li, X.; Liu, Z.; Guo, W.; Cui, Y.; Qian, C.; Huang, Y. Study on rock mechanics characteristics of deep shale in Luzhou block and the influence on reservoir fracturing. Energy Sci. Eng. 2022, 11, 4–21. [Google Scholar] [CrossRef]
- Wang, H.; Gong, W.; Yuan, G.; Wang, X.; Zhao, J.; Su, Y.; Wang, Y. Effect of In-Situ Stress on Hydraulic Fracturing of Tight Sandstone Based on Discrete Element Method. Energies 2022, 15, 5620. [Google Scholar] [CrossRef]
- Zhuang, L.; Kim, K.Y.; Jung, S.G.; Diaz, M.; Min, K.-B.; Zang, A.; Stephansson, O.; Zimmermann, G.; Yoon, J.-S.; Hofmann, H. Cyclic hydraulic fracturing of pocheon granite cores and its impact on breakdown pressure. Int. J. Rock Mech. Min. Sci. 2019, 122, 104065. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, H.; Wang, L.; Zhang, D. Experimental Study on Mechanics and Permeability Properties of Water-Bearing Raw Coal Samples Under In-Situ Stress. Appl. Sci. 2019, 9, 2549. [Google Scholar] [CrossRef]
- Kwasniewski, M.; Li, X.; Takahashi, M. True Triaxial Testing of Rocks; CRC Press: Boca Raton, FL, USA, 2012; Volume 4. [Google Scholar]
- Guo, T.; Rui, Z.; Qu, Z.; Qi, N. Experimental study of directional propagation of hydraulic fracture guided by multi-radial slim holes. J. Pet. Sci. Eng. 2018, 166, 592–601. [Google Scholar] [CrossRef]
- Zhang, R.; Hou, B.; Han, H.; Fan, M.; Chen, M. Experimental investigation on fracture morphology in laminated shale formation by hydraulic fracturing. J. Pet. Sci. Eng. 2019, 177, 442–451. [Google Scholar] [CrossRef]
- Lou, Y.; Zhang, G.; Wang, X. Study on fracture mechanism of hydraulic fracturing in sandstone by acoustic emission parameters. Procedia Eng. 2017, 191, 291–298. [Google Scholar] [CrossRef]
- Heng, S.; Liu, X.; Li, X.; Zhang, X.; Yang, C. Experimental and numerical study on the non-planar propagation of hydraulic fractures in shale. J. Pet. Sci. Eng. 2019, 179, 410–426. [Google Scholar] [CrossRef]
- Jiang, C.; Niu, B.; Yin, G.; Zhang, D.; Yu, T.; Wang, P. CT-based 3D reconstruction of the geometry and propagation of hydraulic fracturing in shale. J. Pet. Sci. Eng. 2019, 179, 899–911. [Google Scholar] [CrossRef]
- Qian, Y.; Guo, P.; Wang, Y.; Zhao, Y.; Lin, H.; Liu, Y. Advances in laboratory-scale hydraulic fracturing experiments. Adv. Civ. Eng. 2020, 2020, 1386581. [Google Scholar] [CrossRef]
- Tan, P.; Jin, Y.; Hou, B.; Zheng, X.; Guo, X.; Gao, J. Experiments and analysis on hydraulic sand fracturing by an improved true tri-axial cell. J. Pet. Sci. Eng. 2017, 158, 766–774. [Google Scholar] [CrossRef]
- Zhou, J.; Jin, Y.; Chen, M. Experimental investigation of hydraulic fracturing in random naturally fractured blocks. Int. J. Rock Mech. Min. Sci. 2010, 47, 1193–1199. [Google Scholar] [CrossRef]
- Zhang, G.-Q.; Fan, T. A high-stress tri-axial cell with pore pressure for measuring rock properties and simulating hydraulic fracturing. Measurement 2014, 49, 236–245. [Google Scholar] [CrossRef]
- Zou, W.; Huang, Z.; Sun, Z.; Wu, X.; Zhang, X.; Xie, Z.; Sun, Y.; Long, T.; Chen, H.; Wang, Z.; et al. Laboratory investigation on fracture initiation and propagation behaviors of hot dry rock by radial borehole fracturing. J. Rock Mech. Geotech. Eng. 2024, 17, 775–794. [Google Scholar] [CrossRef]
- Wu, S.; Li, T.; Ge, H.; Wang, X.; Li, N.; Zou, Y. Shear-tensile fractures in hydraulic fracturing network of layered shale. J. Pet. Sci. Eng. 2019, 183, 106428. [Google Scholar] [CrossRef]
- Zhou, Z.-L.; Hou, Z.-K.; Guo, Y.-T.; Zhao, H.; Wang, D.; Qiu, G.-Z.; Guo, W.-H. Experimental study of hydraulic fracturing for deep shale reservoir. Eng. Fract. Mech. 2024, 307, 110259. [Google Scholar] [CrossRef]
- Zhang, Y.; Long, A.; Zhao, Y.; Zang, A.; Wang, C. borehole orientation and bedding inclination on laboratory hydraulic fracturing of Lushan shale. J. Rock Mech. Geotech. Eng. 2023, 15, 3131–3147. [Google Scholar] [CrossRef]
- Hart, R. An Overview of Methods for Discontinuum Analysis; Itasca Consulting Group Inc.: Minneapolis, MN, USA, 1988. [Google Scholar]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Pine, R.; Cundall, P. Applications of the fluid-rock interaction program (FRIP) to the modelling of hot dry rock geothermal enery systems. In Proceedings of the International Symposium on Fundamentals of Rock Joints, Lapland, Sweden, 15–20 September 1985. [Google Scholar]
- Chang, S.-H.; Yun, K.-J.; Lee, C.-I. Modeling of fracture and damage in rock by the bonded-particle model. Geosyst. Eng. 2002, 5, 113–120. [Google Scholar] [CrossRef]
- Al-Busaidi, A.; Hazzard, J.F.; Young, R.P. Distinct element modeling of hydraulically fractured Lac du Bonnet granite. J. Geophys. Res. 2005, 110. [Google Scholar] [CrossRef]
- Zhao, X.P.; Young, R. Numerical simulation of seismicity induced by hydraulic fracturing in naturally fractured reservoirs. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 4–7 October 2009. [Google Scholar]
- Bona Park, B.P.; Min, K.-B. Discrete element modelling of shale as a transversely isotropic rock. In Proceedings of the ISRM International Symposium-Asian Rock Mechanics Symposium, Seoul, Republic of Korea, 15–19 October 2012. [Google Scholar]
- Damjanac, B.; Gil, I.; Pierce, M.; Sanchez, M.; Van As, A.; McLennan, J. A new approach to hydraulic fracturing modeling in naturally fractured reservoirs. In Proceedings of the 44th U.S. Rock Mechanics Symposium and 5th U.S.-Canada Rock Mechanics Symposium, Salt Lake City, UT, USA, 27–30 June 2010. [Google Scholar]
- Han, Y.; Damjanac, B.; Nagel, N. A microscopic numerical system for modeling interaction between natural fractures and hydraulic fracturing. In Proceedings of the ARMA US Rock Mechanics/Geomechanics Symposium, Chicago, IL, USA, 24–27 June 2012. [Google Scholar]
- Nasehi, M.J.; Mortazavi, A. Effects of in-situ stress regime and intact rock strength parameters on the hydraulic fracturing. J. Pet. Sci. Eng. 2013, 108, 211–221. [Google Scholar] [CrossRef]
- Deng, S.; Li, H.; Ma, G.; Huang, H.; Li, X. Simulation of shale–proppant interaction in hydraulic fracturing by the discrete element method. Int. J. Rock Mech. Min. Sci. 2014, 70, 219–228. [Google Scholar] [CrossRef]
- Marina, S.; Derek, I.; Mohamed, P.; Yong, S.; Imo-Imo, E.K. Simulation of the hydraulic fracturing process of fractured rocks by the discrete element method. Environ. Earth Sci. 2015, 73, 8451–8469. [Google Scholar] [CrossRef]
- Zhang, L.; Zhou, J.; Han, Z. Hydraulic fracturing process by using a modified two-dimensional particle flow code-case study. Prog. Comput. Fluid Dyn. Int. J. 2017, 17, 13–26. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, L.; Han, Z. Hydraulic fracturing process by using a modified two-dimensional particle flow code-method and validation. Prog. Comput. Fluid Dyn. Int. J. 2017, 17, 52–62. [Google Scholar] [CrossRef]
- Liu, S.; Ma, F.; Zhao, H.; Guo, J.; Lu, R.; Feng, X. Numerical analysis on the mechanism of hydraulic fracture behavior in heterogeneous reservoir under the stress perturbation. J. Nat. Gas Sci. Eng. 2020, 78, 103277. [Google Scholar] [CrossRef]
- He, Q.; Zhu, L.; Li, Y.; Li, D.; Zhang, B. Simulating hydraulic fracture re-orientation in heterogeneous rocks with an improved discrete element method. Rock Mech. Rock Eng. 2021, 54, 2859–2879. [Google Scholar] [CrossRef]
- Zhang, F.; Damjanac, B.; Furtney, J. Hydraulic Stimulation of Naturally Fractured Reservoirs. In Coupled Thermo-Hydro-Mechanical Processes in Fractured Rock Masses: Discrete Element Modeling and Engineering Applications; Springer: Berlin/Heidelberg, Germany, 2023; pp. 161–180. [Google Scholar]
- Yazdani, M.; Fatehi Marji, M.; Najafi, M.; Sanei, M. Simulating the Hydraulic Fracturing Mechanism Around the Hydrocarbon Wellbores with Emphasizing its Effects on the Sand Production. J. Min. Environ. 2025, 16, 241–258. [Google Scholar]
- Shi, G.H.; Goodman, R.E. Two dimensional discontinuous deformation analysis. Int. J. Numer. Anal. Methods Geomech. 1985, 9, 541–556. [Google Scholar] [CrossRef]
- Shi, G.; Goodman, R.E. Generalization of two-dimensional discontinuous deformation analysis for forward modelling. Int. J. Numer. Anal. Methods Geomech. 1989, 13, 359–380. [Google Scholar] [CrossRef]
- Tang, C.; Tang, S.; Gong, B.; Bai, H. Discontinuous deformation and displacement analysis: From continuous to discontinuous. Sci. China Technol. Sci. 2015, 58, 1567–1574. [Google Scholar] [CrossRef]
- Shahami, M.H.; Bafghi, A.Y.; Marji, M.F. Investigating the effect of external forces on the displacement accuracy of discontinuous deformation analysis (DDA) method. Comput. Geotech. 2019, 111, 313–323. [Google Scholar] [CrossRef]
- Kim, Y.-I.; Amadei, B.; Pan, E. excavation sequence and rock reinforcement with discontinuous deformation analysis. Int. J. Rock Mech. Min. Sci. 1999, 36, 949–970. [Google Scholar] [CrossRef]
- Grayeli, R.; Mortazavi, A. Discontinuous deformation analysis with second-order finite element meshed block. Int. J. Numer. Anal. Methods Geomech. 2006, 30, 1545–1561. [Google Scholar] [CrossRef]
- Bao, H.; Zhao, Z.; Tian, Q. On the Implementation of augmented Lagrangian method in the two-dimensional discontinuous deformation Analysis. Int. J. Numer. Anal. Methods Geomech. 2013, 38, 551–571. [Google Scholar] [CrossRef]
- Li, X.; Zheng, H. Condensed form of complementarity formulation for discontinuous deformation analysis. Sci. China Technol. Sci. 2015, 58, 1509–1519. [Google Scholar] [CrossRef]
- Fu, G.; Ma, G.; Qu, X. Boundary element based discontinuous deformation analysis. Int. J. Numer. Anal. Methods Geomech. 2017, 41, 994–1015. [Google Scholar] [CrossRef]
- Jiao, Y.-Y.; Wu, Z.; Zheng, F.; Zhao, Q.; Wang, L.; Huang, G.-H.; Tan, F. Parallelization of spherical discontinuous deformation analysis (SDDA) for geotechnical problems based on cloud computing environment. Sci. China Technol. Sci. 2021, 64, 1971–1980. [Google Scholar] [CrossRef]
- Ben, Y.; Xue, J.; Miao, Q.; Wang, Y.; Shi, G.H. Simulating hydraulic fracturing with discontinuous deformation analysis. In Proceedings of the 46th U.S. Rock Mechanics/Geomechanics Symposium, Chicago, IL, USA, 24–27 June 2012. [Google Scholar]
- Morgan, W.E.; Aral, M.M. An implicitly coupled hydro-geomechanical model for hydraulic fracture simulation with the discontinuous deformation analysis. Int. J. Rock Mech. Min. Sci. 2015, 73, 82–94. [Google Scholar] [CrossRef]
- Choo, L.Q.; Zhao, Z.; Chen, H.; Tian, Q. Hydraulic fracturing modeling using the discontinuous deformation analysis (DDA) method. Comput. Geotech. 2016, 76, 12–22. [Google Scholar] [CrossRef]
- Hu, Y.; Li, X.; Zhang, Z.; He, J.; Li, G. Numerical investigation on the hydraulic stimulation of naturally fractured Longmaxi shale reservoirs using an extended discontinuous deformation analysis (DDA) method. Geomech. Geophys. Geo-Energy Geo-Resour. 2020, 6, 73. [Google Scholar] [CrossRef]
- Hu, Y.; Li, X.; Zhang, Z.; He, J.; Li, G. Numerical modeling of complex hydraulic fracture networks based on the discontinuous deformation analysis (DDA) method. Energy Explor. Exploit. 2021, 39, 1640–1665. [Google Scholar] [CrossRef]
- Gao, J.; Chen, G.; Mitani, Y. Hydro-Mechano-Chemical analysis of the reactive transportation process using the extended DDA method. In Proceedings of the 57th U.S. Rock Mechanics/Geomechanics Symposium, Atlanta, GA, USA, 25–28 June 2023. [Google Scholar]
- Hu, Y.; Li, X.; Li, S.; Zhang, Z.; He, J.; Li, G.; Zhang, M. A Fully Coupled Discontinuous Deformation Analysis Model for Simulating Hydromechanical Processes in Fractured Porous Media. Water 2024, 16, 3014. [Google Scholar] [CrossRef]
- Kawai, T. New discrete models and their application to seismic response analysis of structures. Nucl. Eng. Des. 1978, 48, 207–229. [Google Scholar] [CrossRef]
- Bolander, J.; Yoshitake, K.; Thomure, J. Stress analysis using elastically homogeneous rigid-body-spring networks. Doboku Gakkai Ronbunshu 1999, 1999, 25–32. [Google Scholar] [CrossRef] [PubMed]
- Gedik, Y.H.; Nakamura, H.; Yamamoto, Y.; Ueda, N.; Kunieda, M. Effect of stirrups on the shear failure mechanism of deep beams. J. Adv. Concr. Technol. 2012, 10, 14–30. [Google Scholar] [CrossRef]
- Asahina, D.; Houseworth, J.; Birkholzer, J. Thermalhydrological-mechanical model for fracture propagation, fluid flow, and transport in porous rock. In Proceedings of the TOUGH Symposium 2012, Berkeley, CA, USA, 17–19 September 2012. [Google Scholar]
- Rutqvist, J. TOUGH-based hydraulic fracturing models. In Modelling Rock Fracturing Processes: Theories, Methods, and Applications; Springer International Publishing: Cham, Switzerland, 2020; pp. 203–226. [Google Scholar]
- Asahina, D.; Houseworth, J.; Birkholzer, J.; Rutqvist, J.; Bolander, J. Hydro-mechanical model for wetting/drying and fracture development in geomaterials. Comput. Geosci. 2014, 65, 13–23. [Google Scholar] [CrossRef]
- Kim, K.; Rutqvist, J.; Nakagawa, S.; Birkholzer, J. TOUGH–RBSN simulator for hydraulic fracture propagation within fractured media: Model validations against laboratory experiments. Comput. Geosci. 2017, 108, 72–85. [Google Scholar] [CrossRef]
- Rasmussen, L.L.; de Farias, M.M.; de Assis, A.P. Extended Rigid Body Spring Network method for the simulation of brittle rocks. Comput. Geotech. 2018, 99, 31–41. [Google Scholar] [CrossRef]
- Rasmussen, L.L.; Min, K.-B. Developments to the Bonded Block Modeling technique for Discrete Element simulation of transversely isotropic rocks. Int. J. Rock Mech. Min. Sci. 2023, 170, 105518. [Google Scholar] [CrossRef]
- Potyondy, D.O.; Fu, W. A 3D Subspring Network Breakable Voronoi Model for Rock: Laboratory-Scale Behavior. In Proceedings of the 58th U.S. Rock Mechanics/Geomechanics Symposium, Golden, CO, USA, 23–26 June 2024. [Google Scholar]
- Klein, P.; Gao, H. Crack nucleation and growth as strain localization in a virtual-bond continuum. Eng. Fract. Mech. 1998, 61, 21–48. [Google Scholar] [CrossRef]
- Gao, H.; Klein, P. Numerical simulation of crack growth in an isotropic solid with randomized internal cohesive bonds. J. Mech. Phys. Solids 1998, 46, 187–218. [Google Scholar] [CrossRef]
- Zhennan, Z.; Xiurun, G. Micromechanical modelling of elastic continuum with virtual multi-dimensional internal bonds. Int. J. Numer. Methods Eng. 2005, 65, 135–146. [Google Scholar] [CrossRef]
- Patil, S.R.; Jalwadi, S. Implementation of Modified Virtual Internal Bond Method to Investigate Fracture Simulations in Brittle Materials. JournalNX 2018, 330–335. [Google Scholar]
- Zhang, Z. Multiscale simulation of fracture propagation in heterogeneous materials using virtual multidimensional internal bonds. Theor. Appl. Fract. Mech. 2008, 49, 233–241. [Google Scholar] [CrossRef]
- Zhang, Z.; Ghassemi, A. Three-dimensional fracture simulation using the virtual multidimensional internal bond. In Proceedings of the 44th U.S. Rock Mechanics Symposium and 5th U.S.-Canada Rock Mechanics Symposium, Salt Lake City, UT, USA, 27–30 June 2010. [Google Scholar]
- Peng, S.; Zhang, Z.; Mou, J.; Zhao, B.; Liu, Z.; Ghassemi, A. Hydraulic fracture simulation with hydro-mechanical coupled discretized virtual internal bond. J. Pet. Sci. Eng. 2018, 169, 504–517. [Google Scholar] [CrossRef]
- Zhu, T.; Zhang, Z. Modeling of thermal–hydraulic–mechanical–chemical acid fracturing with discretized virtual internal bond. Geomech. Energy Environ. 2023, 35, 100477. [Google Scholar] [CrossRef]
- Zhu, T.; Zhao, B.; Zhang, Z. Quasi-3D fracture acidizing simulation based on discrete virtual internal bond method. Comput. Geotech. 2024, 173, 106537. [Google Scholar] [CrossRef]
- Antony, S. Link between single-particle properties and macroscopic properties in particulate assemblies: Role of structures within structures. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2007, 365, 2879–2891. [Google Scholar] [CrossRef] [PubMed]
- Antony, S.J.; Chapman, D.; Sujatha, S.J.; Barakat, T. Interplay between the inclusions of different sizes and their proximity to the wall boundaries on the nature of their stress distribution within the inclusions inside particulate packing. Powder Technol. 2015, 286, 98–106. [Google Scholar] [CrossRef]
- He, Y.; Bayly, A.E.; Hassanpour, A.; Muller, F.; Wu, K.; Yang, D. A GPU-based coupled SPH-DEM method for particle-fluid flow with free surfaces. Powder Technol. 2018, 338, 548–562. [Google Scholar] [CrossRef]
- Ma, K.; Liu, G.; Guo, L.; Zhuang, D.; Collins, D. Deformation and stability of a discontinuity-controlled rock slope at Dagangshan hydropower station using three-dimensional discontinuous deformation analysis. Int. J. Rock Mech. Min. Sci. 2020, 130, 104313. [Google Scholar] [CrossRef]
- Mohaghegh, S.D.; Gaskari, R.; Maysami, M. Shale analytics: Making production and operational decisions based on facts: A case study in marcellus shale. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, The Woodlands, TX, USA, 24–26 January 2017. [Google Scholar]
- Wang, S.; Wang, X.; Bao, L.; Feng, Q.; Wang, X.; Xu, S. Characterization of hydraulic fracture propagation in tight formations: A fractal perspective. J. Pet. Sci. Eng. 2020, 195, 107871. [Google Scholar] [CrossRef]
- Silveira, B.; Mejia, E.; Roehl, D. Artificial Neural Network to Predict the Interaction Between Natural and Hydraulic Fracture. In Proceedings of the ARMA US Rock Mechanics/Geomechanics Symposium, New York, NY, USA, 23–26 June 2019. [Google Scholar]
- Ben, Y.; Perrotte, M.; Ezzatabadipour, M.; Ali, I.; Sankaran, S.; Harlin, C.; Cao, D. Real-time hydraulic fracturing pressure prediction with machine learning. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, The Woodlands, TX, USA, 4–6 February 2020. [Google Scholar]
- Ismail, A.; Azadbakht, S.; Rashid, H.M.A.; Yasin, Q.; Liu, B.; Ijaz, W. Statistical and machine learning hybridization for predicting shear wave velocity in tight sand reservoirs: A case study. Geoenergy Sci. Eng. 2023, 231, 212420. [Google Scholar] [CrossRef]
- Ismail, A.; Yasin, Q.; Du, Q. Application of hydraulic flow unit for pore size distribution analysis in highly heterogeneous sandstone reservoir: A case study. J. Jpn. Pet. Inst. 2018, 61, 246–255. [Google Scholar] [CrossRef]
- Ismail, A.; Yasin, Q.; Du, Q.; Bhatti, A.A. statistical and virtual analysis for the estimation of pore network permeability. J. Nat. Gas Sci. Eng. 2017, 45, 825–839. [Google Scholar] [CrossRef]
- Gong, Y.; Mehana, M.; Xiong, F.; Xu, F.; El-Monier, I. Towards better estimations of rock mechanical properties integrating machine learning techniques for application to hydraulic fracturing. In Proceedings of the SPE Annual Technical Conference and Exhibition, Calgary, AB, Canada, 30 September–2 October 2019. [Google Scholar]
- Lizhe, L.; Fujian, Z.; You, Z.; Zhuolin, C.; Bo, W.; Yingying, Z.; Yutian, L. The prediction and optimization of Hydraulic fracturing by integrating the numerical simulation and the machine learning methods. Energy Rep. 2022, 8, 15338–15349. [Google Scholar] [CrossRef]
- Yan, B.; Zhong, Z. Deep reinforcement learning for optimal hydraulic fracturing design in real-time production optimization. Geoenergy Sci. Eng. 2025, 250, 213815. [Google Scholar] [CrossRef]
- Santoso, R.; He, X.; Hoteit, H. Application of machine-learning to construct simulation models from high-resolution fractured formation. In Proceedings of the Abu Dhabi International Petroleum Exhibition & Conference, Abu Dhabi, United Arab Emirates, 11–14 November 2019. [Google Scholar]
- Khan, A.M.; Luo, Y.; Ugarte, E.; Bannikov, D. Physics-Informed Machine Learning for Hydraulic Fracturing—Part I: The Backbone Model. In Proceedings of the SPE Conference at Oman Petroleum & Energy Show, Muscat, Oman, 22–24 April 2024. [Google Scholar]
- Ma, Y.; Ye, M. Application of Machine Learning in Hydraulic Fracturing: A Review. ACS Omega 2025, 10, 10769–10785. [Google Scholar] [CrossRef] [PubMed]
- Sobhaniaragh, B.; Mansur, W.; Peters, F. The role of stress interference in hydraulic fracturing of horizontal wells. Int. J. Rock Mech. Min. Sci. 2018, 106, 153–164. [Google Scholar] [CrossRef]
- Fatahi, H.; Hossain, M.; Fallahzadeh, S.H.; Mostofi, M. Numerical simulation for the determination of hydraulic fracture initiation and breakdown pressure using distinct element method. J. Nat. Gas Sci. Eng. 2016, 33, 1219–1232. [Google Scholar] [CrossRef]
- Ismail, A.; Raza, A.; Gholami, R.; Rezaee, R. Reservoir characterization for sweet spot detection using color transformation overlay scheme. J. Pet. Explor. Prod. Technol. 2020, 10, 2313–2334. [Google Scholar] [CrossRef]
- Daneshy, A.A. Factors controlling the vertical growth of hydraulic fractures. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TA, USA, 19–21 January 2009. [Google Scholar]
- Yasin, Q.; Du, Q.; Sohail, G.M.; Ismail, A. Impact of organic contents and brittleness indices to differentiate the brittle-ductile transitional zone in shale gas reservoir. Geosci. J. 2017, 21, 779–789. [Google Scholar] [CrossRef]
- Wu, J.; Li, X.; Wang, Y. Insight into the Effect of Natural Fracture Density in a Shale Reservoir on Hydraulic Fracture Propagation: Physical Model Testing. Energies 2023, 16, 612. [Google Scholar] [CrossRef]
- Asahina, D.; Pan, P.; Tsusaka, K.; Takeda, M.; Bolander, J.E. Simulating hydraulic fracturing processes in laboratory-scale geological media using three-dimensional TOUGH-RBSN. J. Rock Mech. Geotech. Eng. 2018, 10, 1102–1111. [Google Scholar] [CrossRef]
- Ismail, A.; Torabi, F.; Azadbakht, S.; Yasin, Q. Identification of natural fractures in shale gas reservoirs using fracture signature function and machine learning models. Unconv. Resour. 2024, 4, 100069. [Google Scholar] [CrossRef]
- Yasin, Q.; Du, Q.; Ismail, A.; Ding, Y. Identification and characterization of natural fractures in gas shale reservoir using conventional and specialized logging tools. In Proceedings of the SEG International Exposition and Annual Meeting, Anaheim, CA, USA, 14–19 October 2024. [Google Scholar]
- Wang, W.; Wu, K.; Olson, J. Characterization of hydraulic fracture geometry in shale rocks through physical modeling. Int. J. Fract. 2019, 216, 71–85. [Google Scholar] [CrossRef]
- Fu, H.; Huang, L.; Hou, B.; Weng, D.; Guan, B.; Zhong, T.; Zhao, Y. Experimental and numerical investigation on interaction mechanism between hydraulic fracture and natural fracture. Rock Mech. Rock Eng. 2024, 57, 10571–10582. [Google Scholar] [CrossRef]
- Yin, T.; Zhuang, D.; Li, Q.; Tan, X.; Wu, Y. Temperature-dependent factors on hydraulic fracturing of hot dry rock (HDR): An experimental investigation. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2020. [Google Scholar]
- Yang, Y.; Xie, L.; He, B.; Zhao, P. Numerical Study on the Use of Alternating Injection Hydraulic Fracturing Technology to Optimize the Interaction Between Hydraulic Fracture and Natural Fracture. Front. Earth Sci. 2022, 10, 873715. [Google Scholar] [CrossRef]
- Taron, J.; Elsworth, D.; Min, K.-B. Numerical simulation of thermal-hydrologic-mechanical-chemical processes in deformable. Int. J. Rock Mech. Min. Sci. 2009, 46, 842–854. [Google Scholar] [CrossRef]
- Shu, B.; Zhu, R.; Elsworth, D.; Dick, J.; Liu, S.; Tan, J.; Zhang, S. Effect of temperature and confining pressure on the evolution of hydraulic and heat transfer properties of geothermal fracture in granite. Appl. Energy 2020, 272, 115290. [Google Scholar] [CrossRef]
- Ismail, A.; Azadbakht, S. A comprehensive review of numerical simulation methods for hydraulic fracturing. Int. J. Numer. Anal. Methods Geomech. 2024, 48, 1433–1459. [Google Scholar] [CrossRef]
- Fitzgerald, T. Frackonomics: Some economics of hydraulic fracturing. Case West. Res. Law Rev. 2012, 63, 1337. [Google Scholar]






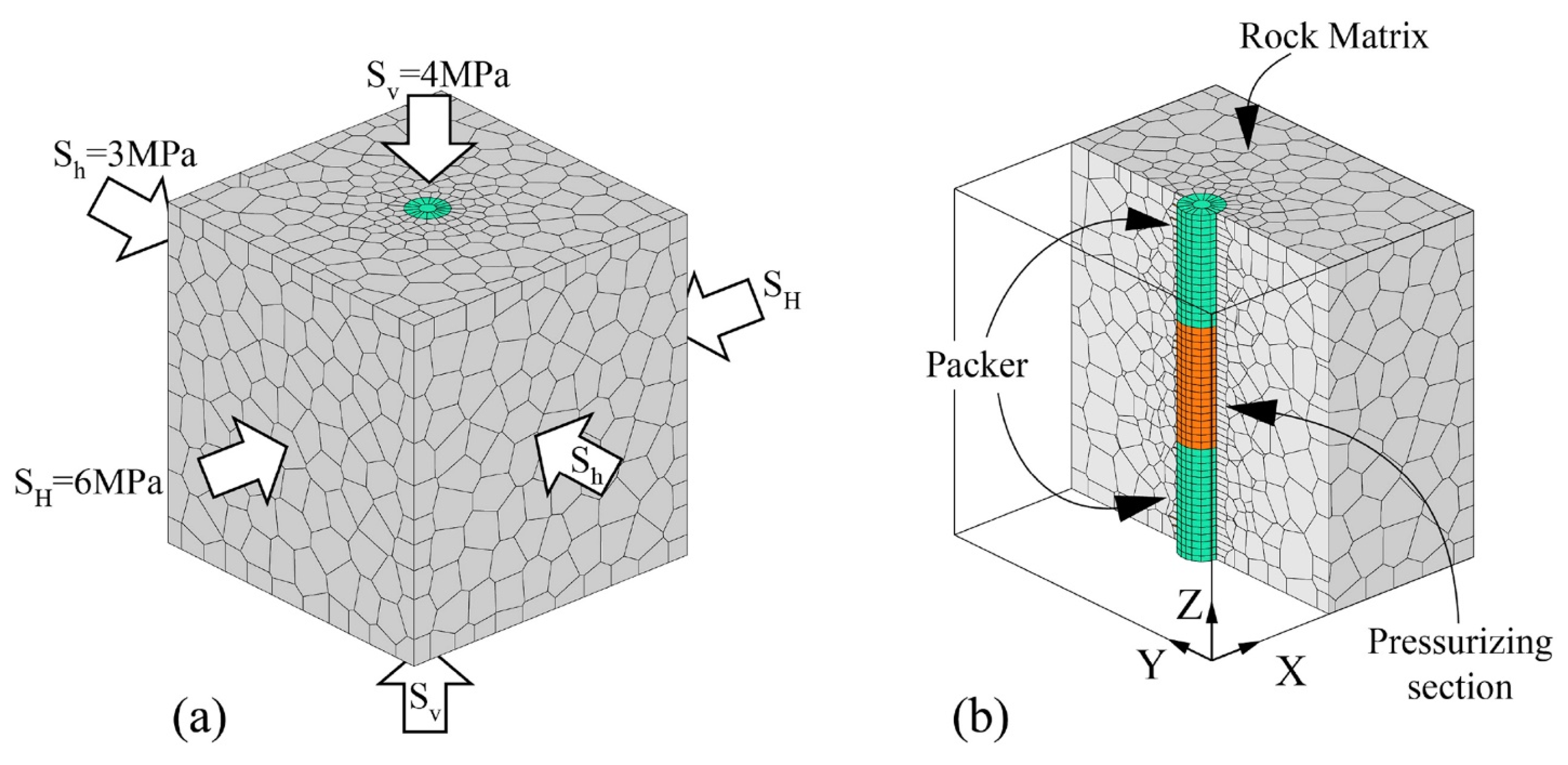

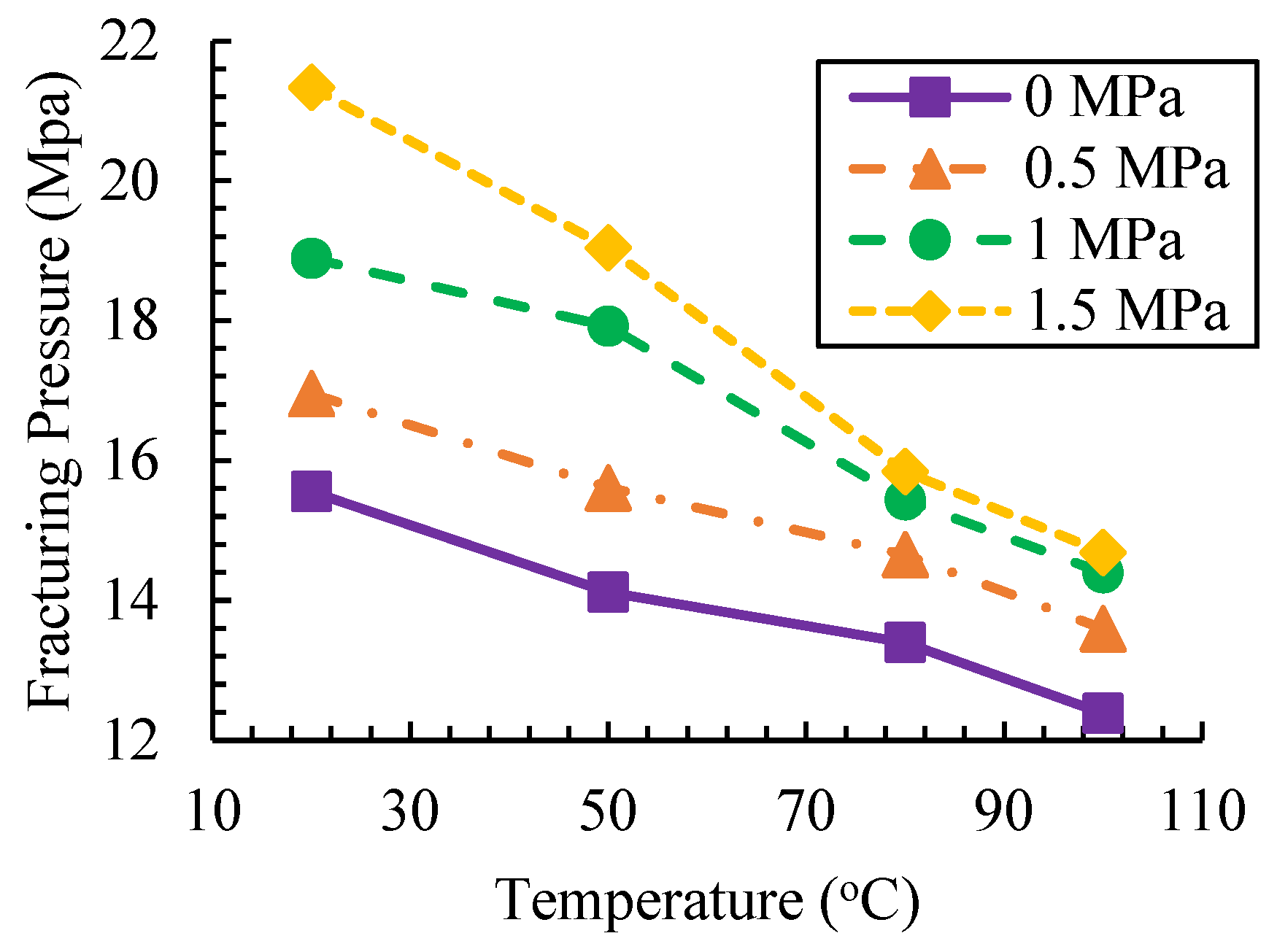
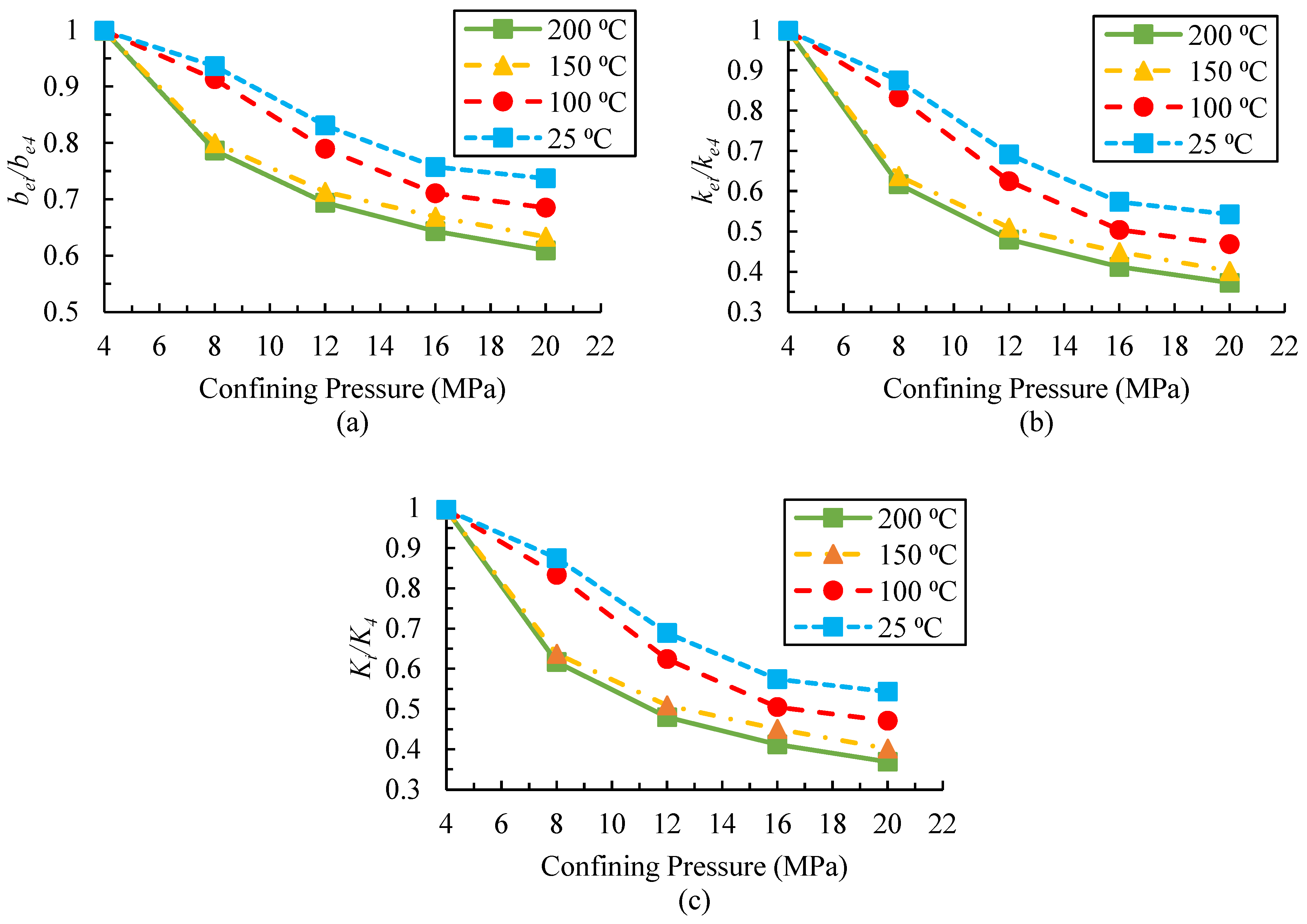
| Parameter | Lab Scale | Field Scale | Scaling Factor |
|---|---|---|---|
| Fracture length | 0.1 m | 10 m | 100 |
| Grain size | 0.1 mm | 10 mm | 100 |
| Viscosity | 100 cp | 500,000 cp | 5000 |
| Well diameter | 2 cm | 20 cm | 10 |
| Fracture propagation time | 1000 s | 0.1 s | 0.0001 |
| Sample Type | Material | Sample Dimension (mm) | Fracturing Fluid | Viscosity (cp) | UCS (MPa) | Flow Rate (mL/min) | Reference |
|---|---|---|---|---|---|---|---|
| Cylindrical | Granite | 60 × 100 | Dry | - | 210 | - | [87] |
| Rectangular | Shale | 100 × 50 × 25 | Dry | - | 174.32 | - | [81] |
| Cylindrical | Tight Sandstone | 25 × 50 | Dry | - | NA | - | [86] |
| Cylindrical | Shale | NA | Dry | - | 101.6 | - | [79] |
| Rectangular | Sandy Mudstone | 70 × 35 × 140 | Dry | - | 28.12 | - | [78] |
| Rectangular | Plaster | 152.4 × 152.4 × 5.08 | Glycerin, Nitrogen | 942, 0.018 | * 414–630 | 15 | [52] |
| Rectangular | Granite, Shale | 85 × 85 × 170 | Methyl Methacrylate | 800 | * 10.39–18.64 | 2 | [80] |
| Cylindrical | Shale | 25.4 × 50.8 | Dry | - | ≈13–53 | - | [82] |
| Cylindrical | Shale | 85 × 170 | L-CO2 | 100 | * 5.24–16.44 | 1 | [50] |
| Sample Type | Material | Sample Dimension (mm) | Confining Pressure (MPa) | Axial Stress (MPa) | Reference |
|---|---|---|---|---|---|
| Cylindrical | Shale | 50 × 100 | NA | NA | [77] |
| Cylindrical | Shale | 25 × 50 | 10 | NA | [94] |
| Cylindrical | Tight Sandstone | 25 × 50 | 5, 10, 20 | NA | [95] |
| Cylindrical | Coal | 25 × (25–50) | 6–12 | 35 | [88] |
| Cylindrical | Granite | 50 × 100 | up to 20 | 20 * | [96] |
| Cylindrical | Shale | 25.4 × 50.8 | 10–15 | 0–35 | [90] |
| Cylindrical | Granite | 25 × 50 | 8–12 | 15 | [91] |
| Cylindrical | Granite | 50 × 100 | 25 | 35 * | [89] |
| Cylindrical | Coal | 100 × 200 | 3 | 3.5 | [92] |
| Cylindrical | Coal | 50 × 100 | 10 | 18.6–25.85 | [97] |
| Cylindrical | Granite | 22.5 × 45 | 0–60 | NA | [93] |
| Sample Type | Material | Sample Dimension (mm) | Fracturing Fluids | Viscosity (cp) | Flow Rate (mL/min) | Reference |
|---|---|---|---|---|---|---|
| Block | Granite | 2003 | Water | 1 | 30 | [108] |
| Block | Shale | 3003 | Water, CO2, N2 | 3 | 3 | [110] |
| Block | Shale | 2003 | NA | NA | 20 | [111] |
| Block | Coal | 3003 | Slick water | NA | 0.1–100 | [23] |
| Block | Shale | 3003 | Guar fluid | 30–60 | 15–20 | [100] |
| Block | Granite | 3003 | CaCl2 solution | 1 | 2 | [51] |
| Block | Shale | 3003 | Water | NA | 0.5, 1, 1.5 | [102] |
| Block | Shale | 1003 | Water | NA | NA | [103] |
| Block | Coal | 3003 | NA | 8 | NA | [11] |
| Block | Artificial Sandstone | 3003 | Slick water | 2.5 | NA | [99] |
| Block and Rectangular | Sandstone | 3003, 600 × 3002 | Guanidine gum | NA | 20 | [101] |
| Discontinuum Methods | Software | Advantages | Disadvantages |
|---|---|---|---|
| Discrete elemental methods | PFC, PFC3, UDEC, 3DEC, YadeDEM, ESys Particle | Realistically simulates the granular flow and rock mechanics at the micro-level. Allows for the simulation of the micro-dynamics of the particle flow. Force transmitting contacts match well with experimentation [166,167]. | Computation power controls the simulation time and number of particles. Grain crushing is seen in simulation [168]. |
| Discontinuous deformation analysis | DDA, Y-flow, UDEC, PFC | Good performance in discontinuous rock; higher accuracy for solid–fluid interaction and coupling dynamics [169]. | High computation, difficulties in fracture propagation, and challenges in calibration. |
| Rigid body spring network | PFC, TOUGH-RBSN, Y-Flow. | Reduced computation and complexity of assumptions [147] Flexible enough to couple with TOUGH2 for hydromechanical simulation [155,156]. | Addition of minor heterogeneity in the elastic response. Loading rate differences with laboratory settings for the computing performance [154]. |
| Virtual internal bond | Customized code coupled with finite element model | No dedicated criteria are required for fracture initiation and propagation, and the easy implementation of elastoplasticity [161]. | Difficult to analyze the bond size and relevant parameters. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ismail, A.; Azadbakht, S. Experimental and Numerical Methods for Hydraulic Fracturing at Laboratory Scale: A Review. Geosciences 2025, 15, 142. https://doi.org/10.3390/geosciences15040142
Ismail A, Azadbakht S. Experimental and Numerical Methods for Hydraulic Fracturing at Laboratory Scale: A Review. Geosciences. 2025; 15(4):142. https://doi.org/10.3390/geosciences15040142
Chicago/Turabian StyleIsmail, Atif, and Saman Azadbakht. 2025. "Experimental and Numerical Methods for Hydraulic Fracturing at Laboratory Scale: A Review" Geosciences 15, no. 4: 142. https://doi.org/10.3390/geosciences15040142
APA StyleIsmail, A., & Azadbakht, S. (2025). Experimental and Numerical Methods for Hydraulic Fracturing at Laboratory Scale: A Review. Geosciences, 15(4), 142. https://doi.org/10.3390/geosciences15040142






