Abstract
Unfavorable land cover leads to excessive damage from landslides and other natural hazards, whereas the presence of vegetation is expected to mitigate rainfall-induced landslide potential. Hence, unexpected and rapid changes in land cover due to deforestation would be detrimental in landslide-prone areas. Also, vegetation cover is subject to phenological variations and therefore, timely classification of land cover is an essential step in effective evaluation of landslide hazard potential. The work presented here investigates methods that can be used for land cover classification based on the Normalized Difference Vegetation Index (NDVI), derived from up-to-date satellite images, and the feasibility of application in landslide risk prediction. A major benefit of this method would be the eventual ability to employ NDVI as a stand-alone parameter for accurate assessment of the impact of land cover in landslide hazard evaluation. An added benefit would be the timely detection of undesirable practices such as deforestation using satellite imagery. A landslide-prone region in Oregon, USA is used as a model for the application of the classification method. Five selected classification techniques—k-nearest neighbor, Gaussian support vector machine (GSVM), artificial neural network, decision tree and quadratic discriminant analysis support the viability of the NDVI-based land cover classification. Finally, its application in landslide risk evaluation is demonstrated.
1. Introduction
Thick vegetation cover improves the shear strength of soil by increasing cohesion and suction through evapotranspiration []. Thus, the presence of vegetation indicates conditions that are unfavorable for landsliding. Conversely, the lack of vegetation cover would create favorable conditions for erosion and slope failure. Moreover, the destruction of vegetation cover due to deforestation, construction and urbanization invariably enhances the potential for erosion and landsliding []. Hence, timely identification of changes in land cover, particularly the reduction of forest cover due to deforestation, is vital to landslide risk mitigation.
In landslide hazard evaluation, it is important to first identify the factors which contribute to landslide occurrence. There are two types of factors that can affect the potential for landslide occurrence at a given location: (1) factors that can be attributed to that location and (2) factors that trigger mass soil movement []. Location-dependent causative factors consist of land cover, slope angle, soil type, rock type, land form, hydrological factors, etc. []. If the conditions of the above attributes are favorable for landsliding, such as low vegetation cover, landslides can be triggered by rainfall, earthquakes, volcanic activity, wildfire, human activity, etc. []. Rainfall-triggered landslides are mostly caused by conditions that promote sudden increases in pore water pressures and the soil overburden.
In addition to increasing shear strength, the presence of vegetation affects the development of pore pressures and overburden []. Thus, research efforts have been focused on understanding the negative relationship between vegetation density and landsliding [,,]. Furthermore, visible signs of occurrence of a past landslide at a given location indicate a higher probability of reccurrence of landslides at the same location []. Phenological changes, human activity and landslides themselves can vastly change the land cover pattern, hence regular monitoring of land cover patterns can be useful in identifying the risk of landsliding at a given location [].
1.1. Land Cover Classification Techniques
Of the numerous techniques that have been employed for land cover classification in landslide studies, the most widely used method is the image-based land cover classification. Image based classification utilizes differences in spectral signatures between different land cover classes. This classification can be performed as a supervised classification or as an unsupervised classification []. In supervised classification, prior knowledge regarding the locations of land cover classes is necessary. Conventional matching techniques are applied to classify unknown areas into pre-defined classes. Supervised classification techniques include nearest neighbor classification, maximum likelihood classification, use of artificial neural networks, etc. On the other hand, unsupervised classification identifies natural groupings in spectral properties with the use of clustering algorithms. Both of the above techniques have been employed by various authors to derive land cover classifications in the study of landslides [,,,].
On the other hand, several landslide studies have used normalized difference vegetation index (NDVI) along with land cover class as parameters in landslide risk assessment [,]. NDVI can be derived from satellite imagery using the following relationship:
where NIR represents the near infra-red band’s reflectance and R represents the red band’s reflectance in a satellite image. For example, chlorophyll in green vegetation absorbs R for photosynthesis while NIR is mostly reflected. Therefore for vegetation, NIR reflectance is high while R reflectance is low. Thus, NDVI provides an indication of the vegetation density and has the potential to be used as a parameter for land cover classification. As mentioned earlier, rapid changes in forest cover is a major contributing factor for landslide occurrence. In this regard, NDVI’s ability to detect changes in vegetation density would be crucial in identifying locations at increased risk for landslding due to human activities such as deforestation. Furthermore, this would combine the two parameters used for landslide risk assessment mentioned above, namely land cover class and NDVI into a single parameter. Thus, the use of NDVI as a stand-alone parameter has the potential to eliminate the redundancy associated with the existing method of landslide risk assessment.
NDVI has been used as a tool in effective land cover classification in the past [,,]. Supervised techniques such as decision tree classification and maximum likelihood classification have been successfully employed in developing land cover classification criteria from NDVI [,]. DeFries et al. (1994) developed a land cover classification at the global level using NDVI obtained from Advanced Very High Resolution Radiometer (AVHRR) imagery with the maximum likelihood classification applied to derive eleven land cover types. However, the derived land cover classes only represent vegetation or barren lands. Thus, this method is unable to classify areas with water bodies or urban development. Furthermore, Friedl et al. (1997) developed a land cover classification using both NDVI and land surface temperature as parameters, with imagery derived from Landsat Thematic Mapper (TM) and AVHRR sensors []. The above classification was performed based on a decision tree analysis. The results were compared with the results from linear discriminant analysis and a maximum likelihood classification. However, the above researchers have not considered the seasonal behavior of vegetation in selecting Landsat imagery for the analysis. Moreover, the developed land cover classes from Landsat imagery were limited to either distinct vegetation classes or barren land.
This research aims to investigate the use of NDVI as a reliable stand-alone parameter in deriving land cover classification in a timely manner, as required for the evaluation of landslide hazard potential. The investigation is based on a case study in the landslide prone west coast of Oregon, USA. Five supervised classification techniques were employed to determine the most accurate classification. In the next section, the five supervised classification techniques employed in this research are introduced.
1.2. k-Nearest Neighbor Classification (kNN)
kNN is a non-parametric classification technique where no assumption is made regarding the frequency distribution of the input parameters. Although it is one of the oldest classification techniques available, it provides reasonably accurate estimations []. Furthermore, the nearest neighbor classification technique is used widely in land cover classification from satellite imagery. Classification is performed by establishing the distance to every point to be classified from all the training data points. The k-number of points which are nearest to the above point in terms of the distance is selected and the appropriate class of the point is assigned based on the majority rule, i.e., the class with a majority within the set of “k” is selected. Thus, the criteria for establishing the distance is crucial for the accuracy [].
Euclidean distance is the most common metric used for distance measuring, although for optimal results, the distance metric should be adopted according to the problem being solved. Other widely used distance metrics are cosine distance metric, cubic distance metric, etc. The fineness of the model is based on the number of training data points which are considered to be “near”, i.e., the value of “k”, with models which contain a k-value of 1 being considered the finest. In this study, use of different distance metrics and “k” values were attempted and finally, a Euclidian distance metric with a “k” value of 10 was used since it resulted in the best overall classification accuracy.
1.3. Support Vector Machine Classification (SVM)
SVM is a non-parametric machine learning technique. This technique can be used in problems which are linearly separable or non-separable. A set of machine learning algorithms are employed to estimate optimal boundaries between classes []. In this classification technique, only the points which are closest to the decision boundary, named “support vectors”, are employed in developing the optimal decision boundary. The optimal boundary is selected such that the distance between support vectors and the boundary is maximized. Commonly used SVM kernels include linear, quadratic, cubic and Gaussian kernels. Linear classification is used for linearly separable problems, where an optimal hyperplane is selected based on support vectors. In problems which are not linearly separable, the original map is transformed to a new space. A Gaussian SVM (GSVM) with a kernel scale of 2.4 was selected for the current study as it presented better overall classification accuracies compared to other SVM kernels and kernel scales.
1.4. Sclaed Conjugate Gradient Backpropagation Neural Network (SCGB)
The objective of an artificial neural network (ANN) is to unveil any complex relationship between an input and the output, with the aid of a number of hidden layers (Figure 1). A neural network can be trained with a set of input and the corresponding output parameter values, to derive the relationship which exists between inputs and outputs. Training data are first fed to the input layer of a neural network. The output of any hidden layer is calculated from the input, weights associated with the connections, bias term and activation function associated with that layer []. Then, the output of that hidden layer is considered as the input to the next hidden layer and so on. The output of the last layer is considered as the model output. The error is calculated by comparing the model output to the corresponding actual output of training data which was initially fed to the network.
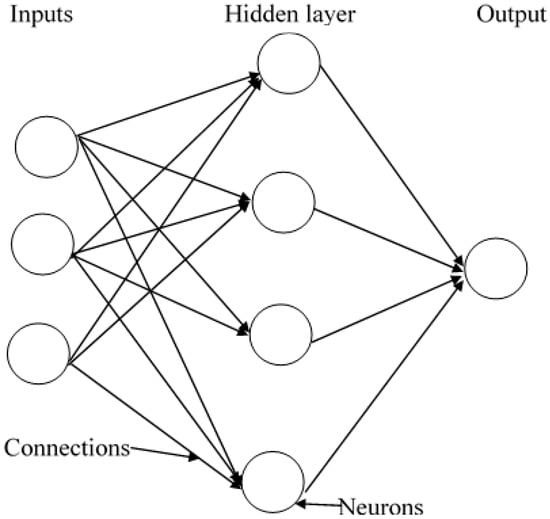
Figure 1.
Architecture of a neural network with a single hidden layer.
For this problem, ANN can be used to determine land cover classes from the NDVI value and the location. In the neural network selected for this study, backpropagation is used to distribute the error computed in the training process between connections. The gradient of the error function is computed in conjugate directions and weights and biases are adjusted in order to minimize this error []. Once the network is trained, validation is performed to prevent overfitting and identify when the optimum level of training is achieved. A trained and validated neural network can be used in testing new data and eventually, for prediction purposes. In this study, the number of neurons in the hidden layer was varied until the result is optimized. It was observed that 30 neurons in the hidden layer provided the best overall classification accuracy.
1.5. Decision Trees (DT)
Decision tree-based classification is a non-parametric classification method which is composed of the continuous partitioning and classification of data based on a decision rule []. A decision tree consists of a root node, split nodes and terminal nodes. The root node consists of input data while split nodes consist of results of the intermediate partitioning of input data based on the decision rule. Terminal nodes, also known as leaves, consist of final classifications assigned to the partitioned data. Splitting is performed such that the classification error at each node is minimized. Three popular splitting criteria, namely Gini index, twoing rule and cross-entropy were attempted, and the Gini index was selected for classification since it resulted in the best overall classification accuracy. The “Gini index” defined as,
where stands for the proportion of observations that are in the mth region belonging to kth class and K represents the number of classes in the classification
1.6. Quadratic Discriminant Analysis (QDA)
Discriminant analysis, also known as the maximum likelihood classification [] is a probabilistic classification technique. This is a parametric classification method which assumes each class to be normally distributed. With this assumption, the means and covariance matrices of each class can be obtained from training data. Thus, the probability of a given data point belonging to each class can be computed using the probabilities of occurrence of each class, the mean and the standard deviation of each class and the Bayes’ theorem. Finally, the considered data point is assigned to the class with the highest probability of belonging.
2. Methodology
2.1. Site Selection
A region located along the west coast of Oregon, USA was selected for this study (Figure 2). The study area has been continuously affected by landslides, with the February 1996 and November 1996’s ones being the major rainfall triggered landslide events []. The study area is subject to seasonality in weather conditions with spring, summer, autumn and winter seasons occurring from March to May, June to August, September to October and November to February respectively. Thus, seasonal behavior patterns can be observed in vegetation. The study area was sub-divided into 1 km × 1 km sections and the center point of each section was considered as a single data point in the ensuing classification.
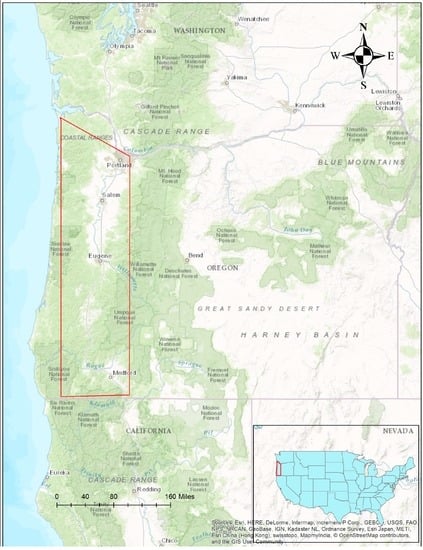
Figure 2.
Geographical location of the selected site in the state of Oregon.
2.2. Development of the Database
Two distinct types of data were used for development of the database which was used in formulating the model. First data type was the land cover data relevant to the points selected for classification obtained from the National Land Cover Dataset (NLCD) 2011 []. NLCD 2011 consists of sixteen land cover classes as shown in Table 1. Land cover classes in Table 1 were further condensed to seven basic land cover classes, namely: (1) water (2) crop land (3) forests (4) impervious (5) bare land (6) grass land and (7) herbaceous/wetlands as shown in Table 2. A similar classification excluding the herbaceous/wetlands class has been used successfully by Jia et al. (2014) [] in performing land cover classification.

Table 1.
Land cover classes according to National Land Cover Dataset (NLCD) 2011.

Table 2.
Developed land cover classes.
The second data type consists of NDVI values derived for the site locations (Section 2.1). NDVI was obtained from surface reflectance derived using atmospherically corrected Landsat TM imagery at a spatial resolution of 30 m × 30 m. The data points were selected randomly from the above 1 km × 1 km grid. Phenological changes in plant life occur throughout the year. Thus, in order to capture these changes, several NDVI images from the same locations, obtained during different seasons of the year have to be employed in the analysis. Hence, four Landsat derived NDVI images of the study area, each representing one of the four seasons, were used for this study. The dates and the observed cloud cover condition in the NDVI images on above dates are given by Table 3. In addition to NDVI and land cover class, the database includes information regarding the location of the data points.

Table 3.
Dates and percentage of cloud cover of NDVI images used in the study.
2.3. Classification Procedure
The above developed database, which consists of NDVI, location of each of the selected points from the study area and land cover class was classified according to the five classification techniques described and parameterized in Section 1.2, Section 1.3, Section 1.4, Section 1.5 and Section 1.6, and the performance of each of the above techniques was evaluated. The validation set approach was selected to validate the results with 70% of the dataset been assigned for training while the remaining 30% of the data was used for testing of models developed by kNN, GSVM, DT and QDA classifications. In SCGB neural network classification, 70% of the data was used for training, 15% of the data was used for validation while the remaining 15% was used for testing.
Furthermore, the land cover classification performed using NDVI was compared with a land cover classification performed using surface reflectance Red, NIR and SWIR (Short Wave Infrared) bands. The results of this analysis are demonstrated in Section 3.4.
3. Results of the Study
3.1. Frequency Distribution of Classes
The frequency distribution of NDVI values belonging to each class in Table 2 was derived and modeled with a normal distribution to obtain the mean and the standard deviation of that class. The results of this analysis is listed in Table 4. Since R radiation is absorbed while NIR radiation is reflected by green vegetation, the NDVI increases with the increase of vegetation density. Thus, highest mean NDVI values were obtained for the “forest” class (class 3). However, NIR and R reflection from water is generally low, thus reducing the NDVI values for water. The other land cover classes assume NDVI values in-between water and forest cover. It is seen in Table 4 that mean NDVI increased for water, barren land, crop, grass land, herbaceous/wetlands, impervious and forest classes in the mentioned order.

Table 4.
Frequency distribution of NDVI values of individual land cover classes.
Phenological changes which occur in vegetation throughout the year can be observed in NDVI values with low mean values in winter and high mean values, especially in the forest class, observed during summer and autumn.
3.2. Overall Accuracy of Classification
The overall classification accuracy was defined as the percentage of points accurately classified w.r.t. the total number of points classified. The results obtained by applying each of the classification techniques is shown in Table 5. While most classification techniques yielded similar results, it can be observed that GSVM classification demonstrates the highest overall classification accuracy, closely followed by SCGB, kNN and DT, while the QDA method produced the least accurate results. It was noted that of all the supervised classification techniques employed, QDA is the only parametric classification technique which assumes data to be normally distributed, while the other classification techniques are not based on assumptions regarding the frequency distribution of data. Thus, this assumption can be attributed to the relatively low classification accuracy observed using QDA.

Table 5.
Overall accuracies of NDVI based land cover classification.
3.3. Accuracies of Individual Classes
Table 6 demonstrates the classification accuracies of testing data observed for individual land cover classes under the alternative classification techniques, while Table 7 demonstrates the confusion matrices for true comparison of known (true) class vs. class predicted by NDVI w.r.t. each classification method. The classification accuracy listed in Table 6 is the percentage that was classified correctly in each class w.r.t the number of points which were assigned to that class. It can be observed that irrespective of the classification technique, classes 1 and 3 consistently demonstrate higher levels of accuracy compared to other classes. Generally, the other classes demonstrate similar levels of accuracy with all classification techniques. Furthermore, QDA, which displayed the lowest overall classification accuracy (Table 5), demonstrates lowest class accuracies in most cases as well. It must be noted that confusion matrices in Table 7 are derived from model testing data introduced in Section 2.3.

Table 6.
Individual class accuracies of NDVI-based land cover classification.

Table 7.
Confusion matrices for the results obtained for the five classification techniques.
3.4. Comparison of Results with Classification Accuracies Obtained Using Raw Spectral Information
The classification accuracies obtained by performing the land cover classification with Landsat-derived NDVI were compared with a land cover classification performed using the corresponding Red, NIR and SWIR (Short Wave Infrared) surface reflectance images. The Landsat images used in this analysis were obtained on the same dates as the Landsat-derived NDVI images. Four Landsat images, with one image from each season, were used in the analysis. The results of this analysis are shown in Table 8. By comparing the results obtained using NDVI (Table 5) and Red-NIR-SWIR surface reflectance (Table 8), it can be observed that the two methods yield similar overall classification accuracies, indicating that changes in spectral signatures do, in fact, translate well into changes in NDVI.

Table 8.
Overall accuracies of Red-NIR-SWIR-based land cover classification.
4. Application to Landsliding
The NDVI-based land cover classification method developed above was applied in a landslide study performed for a site in Western Oregon, USA. The authors have developed a landslide database consisting of information regarding past landslides as part of an ongoing research. This database consists of location of past landsides as well as extensive information on landslide attribute and triggering factors (Section 1) at the above locations. The attributing factors include slope angle, soil type, rock type as well as land cover classification derived using both NLCD and NDVI. The slope angle was obtained from the digital elevation models while soil type information was obtained from Natural Resources Conservation Service (NRCS) of United States []. The observed soil types were aggregated into 9 broader categories based on the ‘soil order’. Soil orders are differentiated from each other based on soil formation, horizon characteristics, etc. The soil orders identified at these locations were, alfisols, andisols, mollisols, inceptisols, ultisols, urban and complex soil formations including inceptisols-rock outcrop, inceptisols-urban, mollisols-rock outcrop.
Information regarding the type of bedrock was obtained from United States Geological Survey (USGS) []. 11 different rock types were observed at the above locations, which include basalt, andesite, clay or mud, gravel, sandstone, mudstone, greywacke, pelitic schist, sand, siltstone and theolite. The landslide attributing factor freshly included in this database is the land cover class, derived with NDVI (Section 2 and Section 3).
In addition, information on one major landslide triggering factor, rainfall, was included in the database since all the selected landslides in the database are rainfall triggered landslides. A relationship between remotely sensed soil moisture and landsliding events have been observed in the past [,]. Thus, remotely sensed soil moisture obtained from the Climate Change Initiative (CCI) project of European Space Agency (ESA) was used in this study to represent the impact of the landslide trigger []. The database consisted of 696 landsliding locations from 1996–2010. Apart from landsliding locations, the database includes information regarding non-landsliding locations as well. A randomly selected equal (696) set of non-landsliding locations from the same study area was also included in the database to provide a control set of data.
Statistical classification techniques can be employed to formulate a landslide prediction model based on the above attributes and the triggering factor (moisture) using such a database. Logistic regression modeling is a promising technique that can be employed in this regard since landslide occurrence or non-occurrence is a binary outcome and hence it cannot be modeled with ordinary least squares regression. Thus the natural logarithm of the odds of landslide occurrence, i.e., the natural logarithm of probability of landslide occurrence over the probability of non-occurrence, or the “logit”, was employed for the model development. The probability of landslide occurrence using logistic regression can be expressed as shown in Equation (3) [].
Logistic regression was applied to the above developed dataset to identify landsliding locations from non-landsliding locations based on above attributes. In order to validate the model results and improve its accuracy, a “10 fold cross validation” technique was employed. A cross validation approach is better suited for this dataset compared to a validation set approach due to its small size []. Two different logistic regression models were developed with the above dataset (1) land cover classification derived from NDVI (2) land cover classification derived from NLCD. The parameter estimates of the two logistic regression models are given in Table 9. It should be noted that no data points were observed under ‘bare land’ category with the NDVI based method while no data points were observed under ‘water’ category with the NLCD based method. The land cover class ‘Grass land’ demonstrated a high parameter estimate of 100.55 with NLCD method. However, the p-value of the mentioned parameter was high (0.99), indicating that the parameter is not statistically significant. This class demonstrated a relatively high p-value in NDVI based classification as well. Furthermore all the parameter estimates with a p-value greater than 0.05 were considered statistically insignificant. Hence, slope, basalt, sandstones, gravel, andisols, urban and mollisols-rock outcrop under both classification methods were determined to be statistically insignificant. Herbaceous/wetlands, theolite and mollisols demonstrated a high p-value under NLCD based classification, while water class and Inceptisol-rock outcrop demonstrated a high p-value with NDVI based classification, indicating their statistical insignificance for prediction of landslide events.

Table 9.
Parameter estimates and p-values of developed logistic regression models.
An overall classification accuracy of 81.2% was observed with the NDVI-based land cover classification, as opposed to classification accuracy of 80.6% observed with the NLCD-based land cover classification. Hence, NDVI based land cover classification exhibits the potential to replace the NLCD-based land cover classification in landslide risk assessment.
5. Discussion and Conclusions
Risks due to natural disasters faced by humankind such as landslides can be escalated by unfavorable variations in land cover conditions and unplanned construction. This is particularly an issue with landslides induced by human activities such as deforestation. Absence of vegetation is a major promoting factor for landslide occurrence in mountainous areas, since the presence of vegetation reduces the erodibility of a slope. Thus, effective land cover classification methods that can be updated regularly such as those based on imagery have been employed in landslide risk assessment. In developing a reliable land cover classification for landslide risk assessment, facility for updated assessment of the vegetation density should be an important requirement. The NDVI derived from satellite imagery provides a convenient method for quantifying the vegetation density in a timely manner. Furthermore, the NDVI’s ability to distinguish between vegetation densities would provide the ability for timely detection of sudden changes in land cover due to deforestation and construction. Of the existing methods of landslide risk assessment, several methods consider NDVI and land cover class as two separate parameters [,]. However, this study employed the NDVI itself as the land cover classification parameter, thereby combining the above mentioned two parameters into a stand-alone parameter. Therefore, the NDVI-based land cover classification method would also eliminate the redundancy in some current landslide risk assessment methods.
Five supervised classification techniques were selected for this study and applied in an Oregon, USA-based database to determine the method which would result in the best overall classification accuracy. For effective classification, sixteen land cover classes defined in NLCD 2011 were condensed to seven classes which include two non-vegetative classes, water and impervious land. All classification techniques yielded similar classification accuracies with GSVM classification yielding the best accuracy. The results from the NDVI-based analysis were compared with classification accuracies obtained using Landsat Red, NIR and SWIR surface reflectance values and it was seen that the classification accuracies were similar for both methods. Furthermore, one NDVI image per season was used in developing the model so that the effect of phenological changes that occur over the year would be captured by the model. It was noted that the NDVI images obtained during spring and winter seasons were obstructed by greater cloud cover compared to images obtained during summer and autumn, thereby impacting the overall accuracy.
The developed NDVI-based land cover classification method was applied in a landslide risk prediction model formulated for a site in western Oregon, USA. The model results were compared with those obtained using the NLCD derived land cover classification on the same dataset. The NDVI-based method was observed to provide a similar classification accuracy as the NLCD-based method. Thus, the NDVI has the potential to be used in land cover classification as part of landslide risk assessment.
In the study, development of NDVI-based land cover classification was performed using freely available Landsat images. The surface reflectance NDVI product can be obtained free of charge at the Landsat spatial resolution of 30 m × 30 m. Moreover, Landsat imagery covering the entire globe can be obtained at a temporal resolution of 16 days. Once the model is developed with training data from a given geographic region, predictions can be performed conveniently for that region. In this study, the analysis was performed with Matlab software with an academic license; however, a similar analysis can be performed with freely available statistical tools as well. Hence, land cover classification with the proposed method can be performed at a relatively low cost in terms of time and funds. On the other hand, obtaining Landsat images with low cloud cover can be a challenging task, especially during the winter and spring seasons.
Of the land cover classes employed by the authors, water and forest classes consistently demonstrated better classification accuracies compared to other classes which can possibly be attributed to the forest cover predominance in the selected study area. On the other hand, the above two classes represent the two extreme values on the NDVI spectrum with significantly different NDVI values. In spite of being a biomass indicator, NDVI’s ability to detect forest cover would be vital for landslide risk assessment since it can be used effectively in the identification of sudden loss of forest cover due to deforestation, and construction that promote landslides.
The results of this study demonstrates that NDVI can in fact be used in landslide studies for land cover classification in a timely manner with a reasonable prediction accuracy. Therefore, the new classification method is expected to advance the state of the art in assessing the impact of land cover in landslide risk assessment.
Author Contributions
Thilanki Dahigamuwa and Manjriker Gunaratne conceived the idea; Thilanki Dahigamuwa performed the analysis; Thilanki Dahigamuwa, Qiuyan Yu and Manjriker Gunaratne participated in writing the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gomez, H.; Kavzoglu, T. Assessment of shallow landslide susceptibility using artificial neural networks in Jabonosa River Basin, Venezuela. Eng. Geol. 2005, 78, 11–27. [Google Scholar] [CrossRef]
- Weerasinghe, K.M.; Gunaratne, M.; Ratnaweera, P.; Arambepola, N.M.S.I. Upgrading of the subjective landslide hazard evaluation scheme in Sri Lanka. Civ. Eng. Environ. Syst. 2011, 28, 99–121. [Google Scholar] [CrossRef]
- Sithamparapillai, P.M.; Senanayake, K.S.; de Silva, G.P.R. Some recent landslides in the hills of Sri Lanka. In Landslides in Sri Lanka; National Building Research Organization, Publications: Colombo, Sri Lanka, 1994; pp. 37–44. [Google Scholar]
- Karsli, F.; Atasoy, M.; Yalcin, A.; Reis, S.; Demir, O.; Gokceoglu, C. Effects of land-use changes on landslides in a landslide-prone area (Ardesen, Rize, NE Turkey). Environ. Monit. Assess. 2009, 156, 241–255. [Google Scholar] [CrossRef] [PubMed]
- Beguería, S. Changes in land cover and shallow landslide activity: A case study in the Spanish Pyrenees. Geomorphology 2006, 74, 196–206. [Google Scholar] [CrossRef]
- Jakob, M. The impacts of logging on landslide activity at Clayoquot Sound, British Columbia. Catena 2000, 38, 279–300. [Google Scholar] [CrossRef]
- Weerasinghe, K.M. Application of Fuzzy Seys and Other Statistical Techniques in Landslide Hazard Zonation Mapping. Master’s Thesis, University of Moratuwa, Moratuwa, Sri Lanka, 2001. [Google Scholar]
- Friedl, M.A.; Brodley, C.E. Decision tree classification of land cover from remotely sensed data. Remote Sens. Environ. 1997, 61, 399–409. [Google Scholar] [CrossRef]
- Reichenbach, P.; Busca, C.; Mondini, A.C.; Rossi, M. The Influence of Land Use Change on Landslide Susceptibility Zonation: The Briga Catchment Test Site (Messina, Italy). Environ. Manag. 2014, 54, 1372–1384. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.; Talib, J.A. Probabilistic landslide susceptibility and factor effect analysis. Environ. Geol. 2005, 47, 982–990. [Google Scholar] [CrossRef]
- Pradhan, B.; Lee, S. Landslide risk analysis using artificial neural network model focussing on different training sites. Int. J. Phys. Sci. 2009, 4, 1–15. [Google Scholar]
- Lenney, M.P.; Woodcock, C.E.; Collins, J.B.; Hamdi, H. The status of agricultural lands in Egypt: The use of multitemporal NDVI features derived from landsat TM. Remote Sens. Environ. 1996, 56, 8–20. [Google Scholar] [CrossRef]
- Defries, R.S.; Townshend, J.R.G. NDVI-derived land cover classifications at a global scale. Int. J. Remote Sens. 1994, 15, 3567–3586. [Google Scholar] [CrossRef]
- Weinberger, K.Q.; Blitzer, J.; Saul, L.K. Distance Metric Learning for Large Margin Nearest Neighbor Classification. Adv. Neural Inf. Process. Syst. 2005, 18, 1473–1480. [Google Scholar]
- Huang, J.R.G.; Davis, C.; Townshed, L.S.; Huang, C.; Davis, L.S.; Townshend, J.R.G. An assessment of support vector machines for land cover classification. Int. J. Remote Sens. 2002, 23, 725–749. [Google Scholar] [CrossRef]
- Yang, J.; Lu, J.; Gunaratne, M.; Dietrich, B. Modeling Crack Deterioration of Flexible Pavements: Comparison of Recurrent Markov Chains and Artificial Neural Networks. Transp. Res. Rec. 2006, 1974, 18–25. [Google Scholar] [CrossRef]
- Nielsen, M.A. Neural Networks and Deep Learning; Determination Press, 2015; Avaliable online: http://neuralnetworksanddeeplearning.com/ (accessed on 19 October 2016).
- Hogland, J.; Billor, N.; Anderson, N. Comparison of standard maximum likelihood classification and polytomous logistic regression used in remote sensing. Eur. J. Remote Sens. 2013, 46, 623–640. [Google Scholar] [CrossRef]
- Robison, E.G.; Mills, K.A.; Paul, J.; Dent, L.; Skaugset, A. Oregon Department of Forestry Storm Impacts and Landslides of 1996. Available online: http://www.waterboards.ca.gov/water_issues/programs/tmdl/records/region_1/2003/ref1785.pdf (accessed on 19 October 2016).
- Homer, C.G.; Dewitz, J.A.; Yang, L.; Jin, S.; Danielson, P.; Xian, G.; Coulston, J.; Herold, N.D.; Wickham, J.D.; Megown, K. Completion of the 2011 National Land Cover Database for the conterminous United States-Representing a decade of land cover change information. Photogramm. Eng. Remote Sens. 2015, 81, 345–354. [Google Scholar]
- Jia, K.; Liang, S.; Wei, X.; Yao, Y.; Su, Y.; Jiang, B.; Wang, X. Land cover classification of landsat data with phenological features extracted from time series MODIS NDVI data. Remote Sens. 2014, 6, 11518–11532. [Google Scholar] [CrossRef]
- Soil Survey Staff; Natural Resources Conservation Service, United States Department of Agriculture. Web Soil Survey. Available online: http://websoilsurvey.nrcs.usda.gov/ (accessed on 3 January 2016).
- Walker, N.S.; MacLeod, G.W. Geologic Map of Oregon: U.S. Geological Survey, Scale 1:500,000; U.S. Geological Survey: Reston, VA, USA, 1991.
- Ray, R.L.; Jacobs, J.M. Relationships among remotely sensed soil moisture, precipitation and landslide events. Nat. Hazards 2007, 43, 211–222. [Google Scholar] [CrossRef]
- Ray, R.L.; Jacobs, J.M.; Cosh, M.H. Landslide susceptibility mapping using downscaled AMSR-E soil moisture: A case study from Cleveland Corral, California, US. Remote Sens. Environ. 2010, 114, 2624–2636. [Google Scholar] [CrossRef]
- Dorigo, W.A.; Gruber, A.; de Jeu, R.A.M.; Wagner, W.; Stacke, T.; Loew, A.; Albergel, C.; Brocca, L.; Chung, D.; Parinussa, R.M.; et al. Evaluation of the ESA CCI soil moisture product using ground-based observations. Remote Sens. Environ. 2015, 162, 380–395. [Google Scholar] [CrossRef]
- Ohlmacher, G.C.; Davis, J.C. Using multiple logistic regression and GIS technology to predict landslide hazard in northeast Kansas, USA. Eng. Geol. 2003, 69, 331–343. [Google Scholar] [CrossRef]
- James, G.; Daniela, W.; Trevor, H.; Robert, T. An Introduction to Statistical Learning; Springer: New York, NY, USA, 2007; Volume 64, pp. 9–12. [Google Scholar]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).