Kriging Method Optimization for the Process of DTM Creation Based on Huge Data Sets Obtained from MBESs

Abstract

The paper presents an optimized method of digital terrain model (DTM) estimation based on modified kriging interpolation. Many methods are used for digital terrain model creation; the most popular methods are: inverse distance weighing, nearest neighbour, moving average, and kriging. The latter is often considered to be one of the best methods for interpolation of non-uniform spatial data, but the good results with respect to model’s accuracy come at the price of very long computational time. In this study, the optimization of the kriging method was performed for the purpose of seabed DTM creation based on millions of measurement points obtained from a multibeam echosounder device (MBES). The purpose of the optimization was to significantly decrease computation time, while maintaining the highest possible accuracy of created model. Several variants of kriging method were analysed (depending on search radius, minimum of required points, fixed number of points, and used smoothing method). The analysis resulted in a proposed optimization of the kriging method, utilizing a new technique of neighbouring points selection throughout the interpolation process (named “growing radius”). Experimental results proved the new kriging method to have significant advantages when applied to DTM estimation.

1. Introduction

Digital terrain model (DTM) models are commonly used in geographic information system (GIS) as a method of describing continuous spatial data. Their most common application is the shape description of the land surface or seabed surface. It constitutes one of the most important information layers in GIS systems; hence, the accuracy of such a model is very important [1].

GIS users have high requirements, prioritizing data quality (accuracy, reliability, up-to-dateness), processing speed, and the possibilities for analyses in real time.

In case of a sea environment, the most commonly performed kind of measurements are sea surveys. Utilizing modern measurement devices such as multibeam echosounder devices (MBESs), we have possibility to gather a huge amount of measurement data which densely cover the surface being measured. Each of such measurements contains information about the spatial location (x,y) and the depth at a given point. Those data are spaced irregularly, which makes it more difficult to directly analyse or visualise them. That is why the first stage after having gathered the data is the creation of a regular grid-based model. Various interpolation methods are commonly used to that effect; other methods, such as artificial intelligence, are less common.

There are many research reports related to the processing of large datasets, including data coming from MBESs. Most of them describe algorithms of data reduction and organization. For example, in the paper [2] a multiple-angle subarray beamforming is employed to reduce the requirements in terms of the signal-to-noise ratio, number of snapshots, and computational effort for provide better fine-structure resolution. In one study [3], the estimates of uncertainty for a surface model generated from the archive MBES data are constructed, taking into account measurement, interpolation, and hydrographic uncertainty. The authors of [4] present different processing procedures employed to extract useful information from MBES backscatter data and the various intentions for which the user community collect the data.

Advantages and disadvantages of several familiar fast gridding methods based on MBES data are compared in [5]. In another paper [6], a new Optimum Dataset method in the processing of Light Detection and Ranging (LiDAR) point clouds was proposed. This algorithm can reduce the dataset in terms of the number of measuring points for a given optimization criterion. In [7], the authors describe the generalization methodology for data contained in a digital terrain model (DTM) for the purpose of relief presentation on new topographic maps. In [8], the authors described an adaptive generalization approach to provide optimized representation of 3D digital terrain models with minimum loss of information, serving specific applications. The tests were performed on land data and the resulting errors coming from generalization were rather high (1–6 m). In another study [9], the authors present possibilities of geostatistical interpolation kriging method used in the process of generating digital terrain models (DTMs). The source of this data were direct measurements realized with a precise Global Navigation Satellite System (GNSS) positioning kinematic measurement technique—Real Time Network (RTN).

The processing of large such amounts of data (millions of measurement points) requires the application of specially prepared methods and properly selected processing algorithms [10,11]. There are numerous methods of determining grid based on huge datasets, the ones most frequently applied being minimum nearest neighbour, inverse distance to a power, curvature, natural neighbour, modified Shepard’s method, radial basis function, triangulation with linear interpolation, moving average, kriging, and methods based on artificial intelligence [12,13,14,15,16]. These methods make use of a series of differentiated algorithms to calculate the values of interpolated parameters at node points (the depth). In the case of measurement data with irregular distribution, selecting the interpolation method should be based on a number of characteristics of the data set: the level of data dispersion homogeneity, data density (number of points per unit), degree of data variability (variance), and the type of surface described by the data.

In the paper, the author focused on the optimization of the kriging method employed for DTM creation. The main goal of this optimization was to decrease the computation time while maintaining the accuracy of created model. Significant reductions in data volume and the simplification of created grid were not the aims of the study (yet they may represent the subsequent stages of the DTM creation algorithm).

Kriging is a geostatistical gridding method that has proven useful and popular in many fields. This method produces visually appealing models from irregularly spaced data (like source MBES data). The kriging defaults can be accepted to produce an accurate grid of data, or kriging can be custom-fit to a data set by specifying the appropriate variogram model [17].

The main disadvantage of the kriging method for huge dataset processing is the long computation time. Compared to other methods, DTM creation time can require as much as eight times longer as compared to the Inverse Distance to a Power method, or 20 times longer than the moving average method [18]. Therefore, kriging is commonly used for smaller datasets (hundreds of thousands of measurement points), but for larger datasets other methods are used that are significantly faster and only slightly less accurate (resulting in an error increase by approximately 0.1%) [15]. A viable question arises as to whether it is possible to optimize the generic kriging method for the purpose of processing large bathymetric datasets in the process of DTM creation. The goal of the optimization would be to increase computation speed while preserving the high model accuracy.

2. The Basis of Kriging Method

Kriging is an alternative to many other point interpolation techniques. The basic idea of kriging is to predict the value of a function at a given point by computing a weighted average of the known values of the function in the neighbourhood of the point [18]. The kriging method is more accurate whenever the unobserved value is closer to the calculated values [19]. A couple variants of kriging interpolation exist, but the most commonly used for large spatial datasets is the ordinary kriging method.

Kriging allows for determination of the best linear unbiased estimator, which is given by the formula:

$$\widehat{Z}\left(x_o\right)=\sum _{i=1}^n{\omega }_{i}Z\left(x_0\right)Z\left(x_i\right)$$

The estimator obtained using the above formula is a sum of products of the known points’ heights Z(x_i) and their weights. The rules of stochastic methods require the weights to meet the condition of minimizing the mean square estimation error.

$$\begin{array}{c}{\sigma }_k^2\left(x_0\right):=\mathrm{Var}(\widehat{Z}\left(x_0\right)-Z\left(x_0\right)\hfill \\ ={\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^n}{w}_i\left(x_o\right)w_j\left(x_0\right)c\left(x_i,x_j\right)+\mathrm{Var}\left(Z\left(x_0\right)\right)\hfill \\ -2{\displaystyle \sum _{i=1}^n}{w}_i\left(x_o\right)c\left(x_i,x_0\right)\hfill \end{array}$$

where c(x_i, x_o) is the covariance between the location of the known point and interpolated point. Both the above equations allow to meet the condition $\mu \left(x\right)=E[Z\left(x\right)]$:

$$E[\widehat{Z}\left(x\right)-Z\left(x\right)]=\sum _{i=1}^n{w}_i\left(x_o\right)\mu \left(x_i\right)-\mu \left(x_0\right)=0$$

In the ordinary kriging method it is assumed that: $\mu \left(x\right)=\mu$.

All the above conditions allow to determine optimal weights values, in order to minimize the estimation error. All the mathematical details of the kriging method can be found in [20,21].

Most GIS systems implement the kriging method in such way that a value is assigned to a point by averaging the points inside a certain lookup area (pre-set by a user and fixed). There is also possibility of defining a minimum number of points inside the search area that allows to calculate a new point value. Otherwise, the point node is set as a blank.

3. Research

3.1. Test Surfaces

The tests were done using three real surfaces prepared from actual survey data collected by Maritime Office Szczecin. This surfaces differ significantly in their shapes and roughness (see Figure 1):

• ‘gate’—rough surface with many holes and slopes,
• ‘swinging’—varying surface, partly flat, partly rough,
• ‘wrecks’—flat surface with five car wrecks.

For each of the surfaces listed above, a grid model was built. Their sizes are presented in

Table 1. Sizes of tested surfaces.

Name	Rows	Columns	Maximum Depth (m)	Minimum Depth (m)	Number of Measured Points (mln)	Number of Grid Nodes (mln)	Grid Size (m)
‘gate’	2000	2000	21.78	3.95	17.80	4.00	0.1 × 0.1
‘swinging’	2000	2000	13.89	8.14	16.34	4.00	0.1 × 0.1
‘wrecks’	3536	1263	7.88	4.32	23.25	4.47	0.02 × 0.02

.

3.2. Preparation of Test Data

An important issue when researching interpolation methods using real measurement data is the impossibility of comparing the obtained test models and the real surface (as the latter is described using a set of XYZ points instead of a grid). In order to solve that problem, the original virtual survey software was used (developed by authors) [22], allowing for the generation of measurement XYZ datasets based on a high-resolution grid and a virtual survey. The simulator takes into consideration such parameters as: the speed of a boat, MBES parameters, random MBES measurement error (device error), and the arranged profile layout. As an outcome of the simulation, a new test XYZ dataset is obtained. Testing of interpolation methods consists in using such a dataset to create subsequent models, with varying interpolation parameters. Both the models (the base model and the test model) are described using the grid structure of the same size, so they are directly comparable, and the resulting interpolation errors can be calculated (including the mean error) [22,23]. The workflow is depicted in Figure 2.

When preparing the test data obtained using the virtual survey, the following simulation parameters were set:

• boat speed: 5 knots,
• angle of beams: 110°,
• number of beams: 127,
• impulse frequency: 10 Hz,
• profile layout: parallel, overlapping: 20%,
• surface coverage: 100%,
• MBES error (measurement noise)—5 cm for ‘gate’ surface and 2 cm for ‘swinging’ and ‘wrecks’ surfaces.

3.3. Testing Procedure

The purpose of this experiment was primarily to use kriging interpolation method, facilitated by the SURFER v8.0 software (GoldenSoftware, Golden-Colorado, USA), to create a DTM of all surfaces. The first research stage consisted in searching for the optimal number of points and their distance from the newly calculated points in the course of kriging-based interpolation. The influence of two factors was examined: the minimum number of points and the search radius were taken into consideration while calculating new node values. Proposed search radius experimental values were: 0.2–4 m. The default value of minimum number of surrounding points inside the search area was set to 4. Moreover, the influence of minimum number of points was also tested (especially with respect to the number of outcoming blank nodes). A linear variogram was used.

During subsequent experiments, the influence of the number of points used for interpolation on the accuracy of created models was examined. Finally, it was tested how utilising additional surface smoothing methods affected the accuracy of created model.

All the resulting test surfaces were compared to the base surface and the 95% confidence level of error was determined (in centimetres), as well as the computation time (in seconds).

All the calculations were performed on a personal computer equipped with Intel Core i7 processor (model 870, 2.93 GHz), 4 GB RAM, HDD 2TB (ST32000641AS), and 64-bit Windows 7. The performance index for the above configuration, calculated in Cinebench R15 (the CPU Test), is equal to 478 points.

3.4. Research

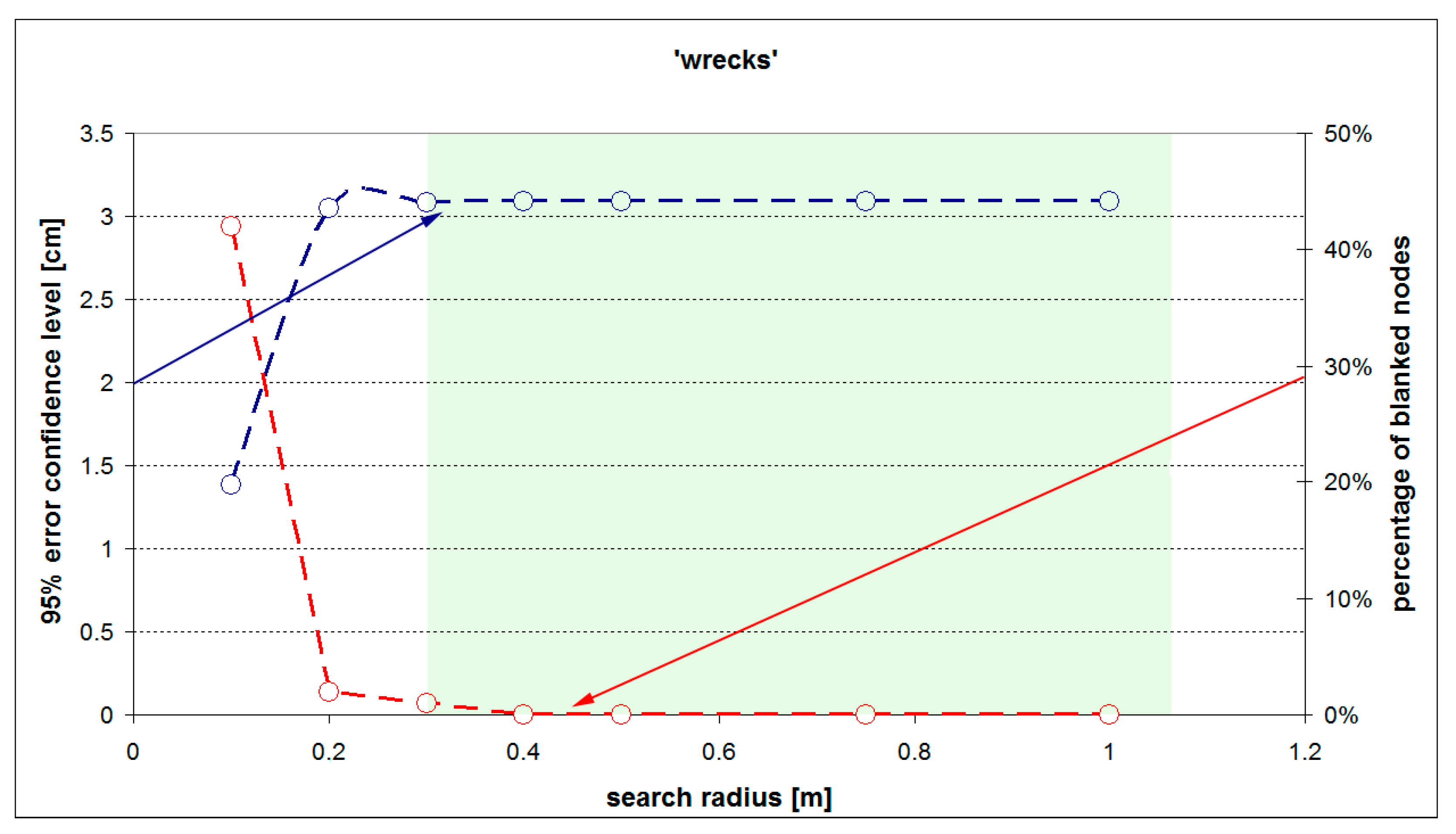
The first research stage consisted in looking for the optimal search radius size. The tests were performed for search radius equal to 0.2, 0.4, 0.6, 0.8, 1.0, 2.0, and 4.0 m for the ‘gate’ and ‘swinging’ surfaces. Because of the high density of measurement points, the search radius values used for the ‘wrecks’ surface were 0.1, 0.2, 0.3, 0.4, 0.5, 0.75, and 1.0 m. The value of minimum required points inside the search radius was set to 4. The results for the three test surfaces are presented in Figure 3, Figure 4 and Figure 5.

Figure 3 (surface ‘gate’) shows that the 95% confidence level of error rate increases from 5.1 cm to 6.6 cm. The percentage of blank nodes drops rapidly from 25% to 0%. Because of the fact that our goal was the minimal value of the 95% confidence level, the chosen value of search radius was 0.6 m. The bright green highlight in the charts denotes the values for which satisfactory results were obtained.

Figure 4 (surface ‘swinging’) shows that the 95% confidence level of error rate increase from the value 2.3 cm to 2.6 cm. The percentage of blank nodes falls rapidly to between 0.2 and 0.4 m. Because of the fact that our goal was the minimal value of a 95% confidence level, a optimal search radius for this surface equal to 0.4 m was chosen.

Figure 5 (surface ‘wrecks’) presents that the 95% confidence level of error rate increase from the value 1.4 cm to 3.1 cm. The percentage of blank nodes falls from 43% at 0.1 m and it stabilised at 0% (for radius = 0.4 m and more). Consequently, the value of optimal search radius for this surface equal to 0.2 m was chosen.

Given all the obtained results for all three surfaces it is easy to notice, that the smaller radius was used, the better the accuracy of created model is. On the other hand, for the smallest values of radius, the number of blank nodes was too high for that model to be acceptable. It can be assumed that optimal results were obtained for the radius of 0.6–1.0 m.

The computation time strongly depends on the search radius and initially increases rapidly (almost exponentially) with the increase of the search radius. Further increase in the computation time (for larger values of search radius) is slower, as the number of points during interpolation is constrained from above to 64. The total time required to create the test models is shown in Figure 6.

As can be seen, only for the small values of the search radius is the computation time short (under 3 min); in all the other cases creating of the model took much more time, up to 16 min. Hence, determining the appropriate value of search radius turns out to be crucial for speeding up the kriging method.

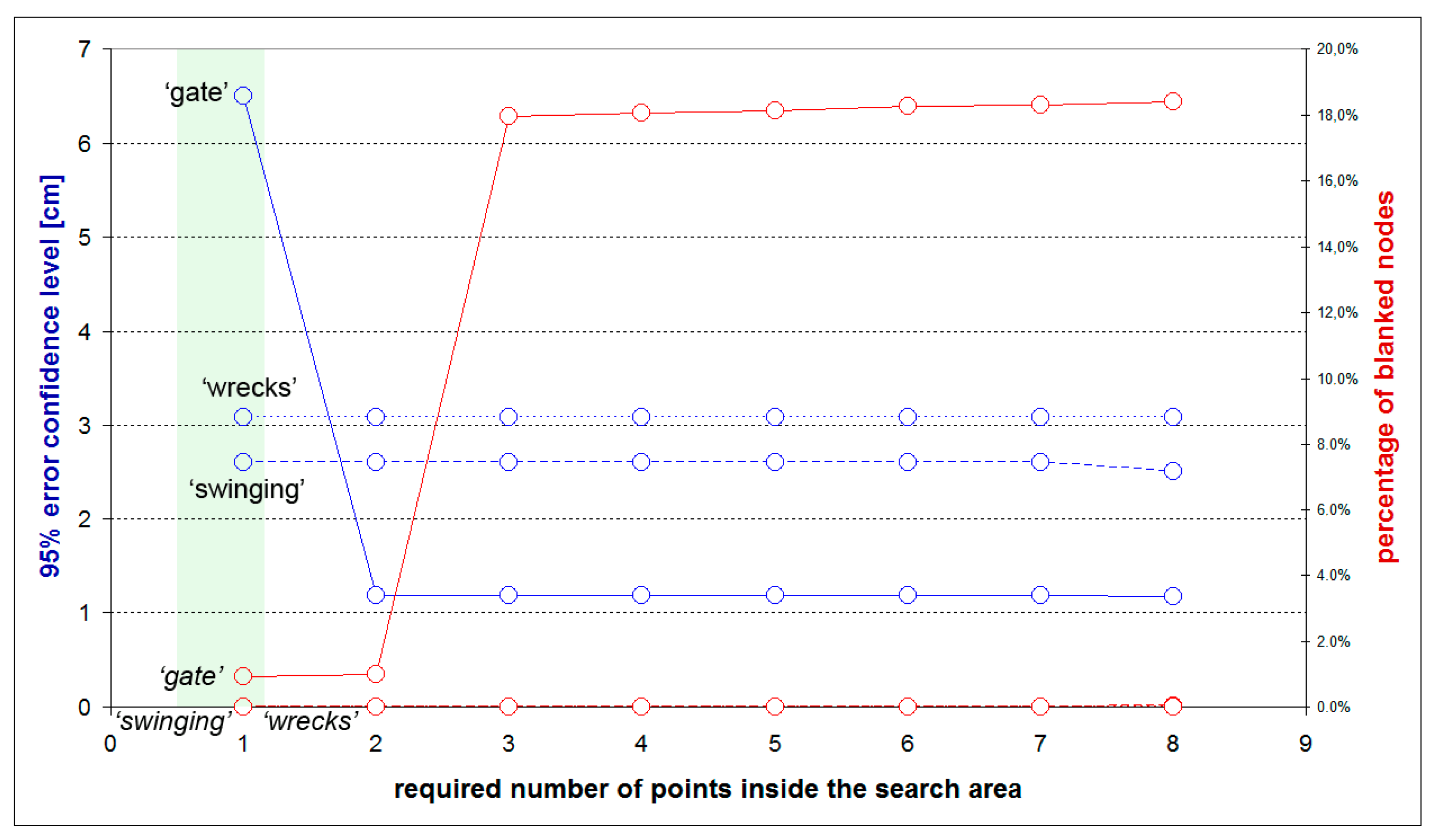
In the next stage of the research, the influence of minimum required number of points that were needed to compute the node value was analysed (the maximum amount of points was set to 64). The best performing search radius size (based on all surfaces) was used for further research (0.8 m). The results are presented in Figure 7.

As can be seen in the Figure 7, the value of blank nodes only slightly depends on search radius. For the ‘swinging’ and ‘wrecks’ surfaces there were always at least eight measurement points within the tested 0.8 m radius, therefore there were no blank nodes in the created model. Only for the ‘gate’ surface, when the required number of points was set to three or higher, did the model created contain 19% of blank nodes. In such cases, a possible solution could consist in slightly increasing the search radius or performing interpolation using just two available measurement points.

When analysing the accuracy of created models it becomes clear, that the accuracy does not depend on the minimum number of points taken for the kriging process, except for one case, when it was set to one for the ‘gate’ surface. It should be noted though, that in that particular case what was tested was not the influence of the exact number of points used during the interpolation, but only the influence of the minimum number of points on the number of created blank nodes. To sum up, for two of the surfaces that influence was not found, and for the third one (‘gate’), the radius of 0.8 m turned out to be too small, which resulted in the significant increase of the number of blank nodes. It could be generally stated that it is relatively difficult to set an optimal search radius for interpolation, as it highly depends on the density of measurement points.

During the next stage of research, the influence of the exact numbers of points used during the interpolation on the accuracy of created model and the number of blank nodes was thoroughly examined. For the experiments the search radius was set to 1.0 m and the tests were performed for the number of points equal to 1, 2, 3, 5, 7, 10, 20, 30, and 50. The obtained results are presented in Figure 8.

Based on the obtained results it can be concluded that the accuracy of the model is lowest when only one point is used for interpolation (in such case the averaging occurs), and for the number of points equal to three or higher, the accuracy increases very slowly (‘gate’) or remains constant (‘wrecks’) or even slightly decreases (‘swinging’). At the same time, along with the increase of the number of measurement points, the computation time increases significantly (an almost linear correlation). It could be assumed that for five points or less the time is sufficiently short. Considering the above, it can be concluded that the optimal number of points used for interpolation is between 3 and 8, which allows to speed up computation significantly while maintaining a high quality of the model.

3.5. Proposal of Improved Variant of Kriging—‘Growing Radius’

Based on the research performed so far, several important conclusions can be drawn:

• the value of search radius has no significant influence on the accuracy of the model;
• a too small search radius results in many blank nodes being created, which prevents creating a correct model;
• increasing the value of search radius results in a considerably longer computation time;
• the number of measurement points used for the interpolation only slightly influences the accuracy of created model, except for the case when the number is too small (between 1 and 3);
• the value of search radius, combined with the number of measurement points used for interpolation, has the biggest impact on the computation time.

Considering the above, a new approach to interpolation method has been proposed, consisting in replacing a constant search radius with an adaptive, growing radius. In the proposed approach, the size of interpolation window grows, starting from the size of 3 × 3 points up until it encloses enough measurement points or until it reaches the pre-set upper bound. Only certain number P of points (set by the user) located inside such a frame and placed the closest to the point of interest will be considered during the interpolation. If there are still not enough points, a blank node will be inserted.

The algorithm of adaptive kriging variant begins with declaration of:

• minimum number of points used for calculations P,
• start radius size R_MIN,
• maximum radius size R_MAX,

In the next step, points that fall within the search area are ordered according to the squared radius (see Figure 9a). Then, P points are chosen, that are the closest inside the search area denoted by radius R (Figure 9b). If the number of points within the search area is greater or equal P, kriging interpolation is performed using P nearest points. Otherwise, the R is enlarged by R_STEP; as long as R <= R_MAX or the required number of points is greater or equal P, kriging interpolation is done using these points (Figure 9c), otherwise the blank node is set.

Simplified scheme of the proposed method is shown in Figure 10.

3.6. The Tests of Presented Method

The empirical verification of the proposed approach consisted in creating several test models using the modified kriging method, and calculating the accuracy by comparing the results to the ones obtained using conventional methods. A series of modified interpolation tests was performed with the following parameters: P = 1 to 5 points, R_MIN = 3 × 3 points, R_MAX = 10 × 10 points (corresponding search radius = 1 m), and R_STEP = 1 point. The obtained results are presented in

Table 2. The comparison of the modified kriging and ordinary kriging results (95% confidence level error and time).

Number	Parameters		95% Confidence Level Error and Calculation Time
	Search Radius	Points Required	Gate (cm, (s))	Swinging (cm, (s))	Wrecks (cm, (s))
1	1	2	6.83 (10.56)	2.32 (9.92)	5.20 (11.68)
2	1	5	6.52 (21.92)	2.31 (21.92)	3.35 (21.28)
3	0.6	2	6.91 (10.20)	2.32 (9.4)	5.20 (11.20)
4	0.6	5	6.54 (19.82)	2.31 (20.65)	3.35 (20.96)
5	improved kriging	1	7.44 (6.51)	3.32 (7.5)	5.20 (8.3)
6	adaptive kriging	2	6.83 (6.90)	2.31 (7.6)	3.35 (8.6)
7	adaptive kriging	3	6.62 (7.06)	2.31 (7.9)	3.06 (9.0)
8	adaptive kriging	4	6.49 (7.22)	2.30 (8.2)	3.06 (10.21)
9	adaptive kriging	5	6.52 (7.26)	2.31 (8.5)	3.09 (10.55)

(bold denotes the best results).

Based on the results, the following conclusions can be drawn:

• the best results (the smallest error) were obtained when the closest 3–4 points were taken for interpolation,
• dimensions of the window (growing radius) for which the best results were obtained were approximately 0.3–0.6 m,
• the depth accuracy in created models (using improved variant of kriging) is higher by approximately 1–2 cm,
• calculation time for optimal results when using the improved variant of kriging is 2–3 times shorter,
• the more points are used for interpolation, the slower the algorithm; however, the time increase is rapid when using a fixed search radius, and slow for a growing radius variant.

It should be pointed out that using the proposed interpolation method speeds up the interpolation process to some extent as compared with conventional methods of interpolation (with constant search radius). The size of the frame adapts to measurement point density, which can vary even for data coming from one survey, not to mention data obtained for various surfaces within separate surveys. The proposed approach allows the operator to decide how many points should be taken into consideration when calculating a new node and to define the conditions for creating a blank node (R_MAX).

3.7. Surface Smoothing

As the source data (obtained from MBES) are affected with a certain small random error (about 2–5 cm at a 10 m depth), complementing the interpolation with an additional surface smoothing method can increase the accuracy of created model (while only slightly increasing computational time). That is why in the last part of research using a smoothing filter was considered. Three smoothing methods were analysed:

• Gaussian with mask 3 × 3,
• 5-Node + Averaging 3 × 3,
• Median filter 3 × 3.

The tests were performed using the ‘growing radius’ method, with the optimal number of points required for interpolation. The results are presented in

Table 3. The comparison of the modified kriging results with and without smoothing (95% confidence level error and time).

No	Parameters			95% Confidence Level Error and Calculation Time
	Smoothing Method	Search Radius	Point Required	Gate (cm, (s))	Swinging (cm, (s))	Wrecks (cm, (s))
1	Gaussian (3 × 3)	growing	4	6.15 (8.81)	2.17 (10.90)	2.91 (13.6)
2	5-NODE (3 × 3)	growing	4	6.23 (8.40)	2.22 (10.99)	2.94 (12.8)
3	Median (3 × 3)	growing	4	6.13 (8.96)	2.17 (10.08)	2.90 (12.9)
4	None	growing	4	6.49 (7.22)	2.30 (8.2)	3.06 (10.21)

(bold denotes the best results).

Utilizing an additional smoothing filter results in the increase in model’s accuracy by approximately 0.5 cm, wherein the computation time increases by approximately 20–30%. The best results were obtained using Gaussian and median filters. Since the quality gain is quite small (relative accuracy increase of just 0.05%), with an accompanying significant increase in computation time using the additional smoothing filter could be an option left to end-user choice.

4. Conclusions

The paper presents a research on kriging method variants in case of digital terrain model creation using bathymetric data obtained from MBES. The method was verified using surfaces of varying shapes, hence the experiments proved the proposed method variants to be valid. Furthermore, the performance of kriging method for tested surfaces was very good, with satisfying 95% confidence level of error (respectively, less than 7 cm, 3 cm, and 3 cm for the ‘gate’, ‘swinging’ and ‘wrecks’ surfaces, respectively). According norms set by International Hydrographic Organization (IHO) [24], the error rate of interpolated grid must be less than about 20 cm, for tested surfaces. The error rate resulting for each of tested surfaces was much below that constraint, which means that kriging can be used for the kind of interpolation in question.

Kriging with proposed ‘growing radius’ method and optimal number of points required as well as with median smoothing applied was chosen as the best kriging variant.

Considering the results of the extensive research carried out by the author (part of which is outside the scope of this paper), the following conclusions can be drawn:

• Increasing the search radius beyond 1 m results in a slightly larger errors and very long computation time; the reason for that is the high density of measurement data coming from MBES, reaching as high as 40 points per square meter;
• Too many measurement points considered during interpolation also result in a larger error, accompanied by a significant increase in computation time (10 times or more);
• The best results are obtained for approximately 3–5 measurement points lying in the closest proximity (radius about 0.3–0.6 m);
• Using the modified kriging method (with ‘growing radius’) results in only minor increase in model’s accuracy, but more importantly, it reduces the computation time considerably (long computation time being the main disadvantage of the kriging method with typical settings).

Based on the above the hypothesis has been proposed, that the kriging method can be optimized by eliminating fixed size of search radius and focusing instead on several closest measurement points (the operator specifies the number of measurement points required and their maximum distance from the node being calculated).

The proposed approach is aimed at improving the kriging method resulting from the observations of conventional kriging method’s behaviour. As the experiments have proven, the application of proposed modification results in a slightly higher accuracy of obtained grid, which fits to the real seabed surface better (comparing to results without kriging optimization), together with almost 3 times lower calculation time.

A comparison with other author’s research (based on exactly the same measurement data and the same hardware platform) [11], it should be emphasized that optimized kriging method is still 2–4 times slower than other, widely used interpolation methods (moving average, Inverse Distance to a Power). On the other hand, we obtain more accurate DTM (10–20% more precise). It seems that it is justified claim, that in cases when we expect the most accurate results, the application of optimized kriging method gives the satisfying results.

A comparison of the proposed method with other approaches described in the literature is extremely complicated. The experiments should, in this case, be based on the same test data (of just the data collected in the similar areas). Created models should also have the same properties (in terms of resolution and size of the created model).

The proposed adaptive kriging method (called “growing radius”) can be implemented in GIS systems for modelling surfaces based on large amounts of measurement data.