Influence of Load Frequency on Cohesive Soil Respond
Abstract
:1. Introduction
2. Material Characterization
3. Triaxial Test Procedure
4. The Results and Discussion
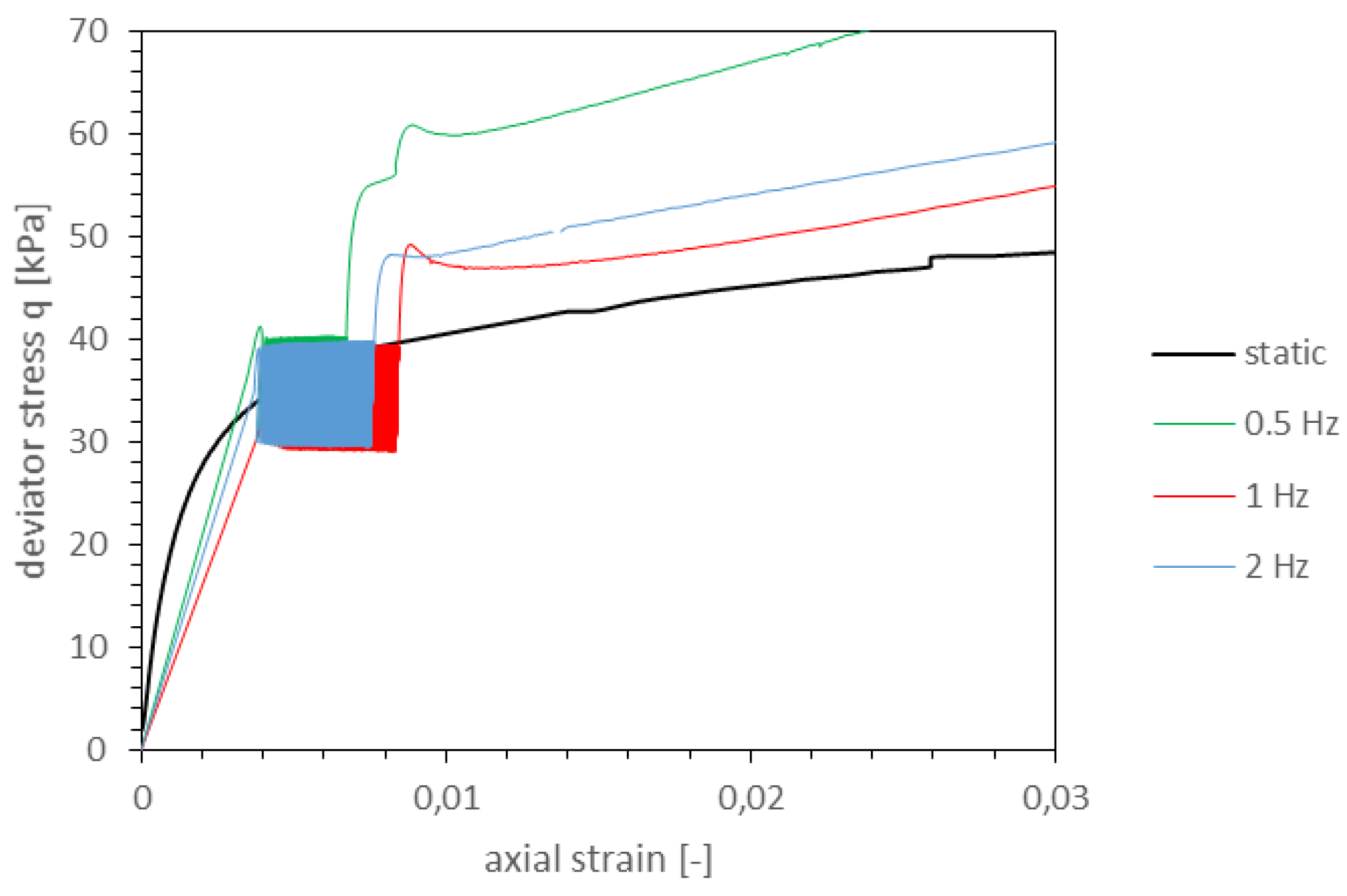
4.1. Cyclic Triaxial Loading Test Results
4.2. Static Triaxial Loading Test Results
5. Conclusions
- The stress-strain observed during cyclic loading triaxial test, indicates the pattern of soil behaviour. Three phases were identified which refers to different rate of plastic strain accumulation. The plastic strain accumulation characteristics was logarithmic, which means that, with increasing number of cycles the accumulated plastic strain will decrease per one cycle. This type of behaviour was reported before by Goldscheider and Gudehus [36].
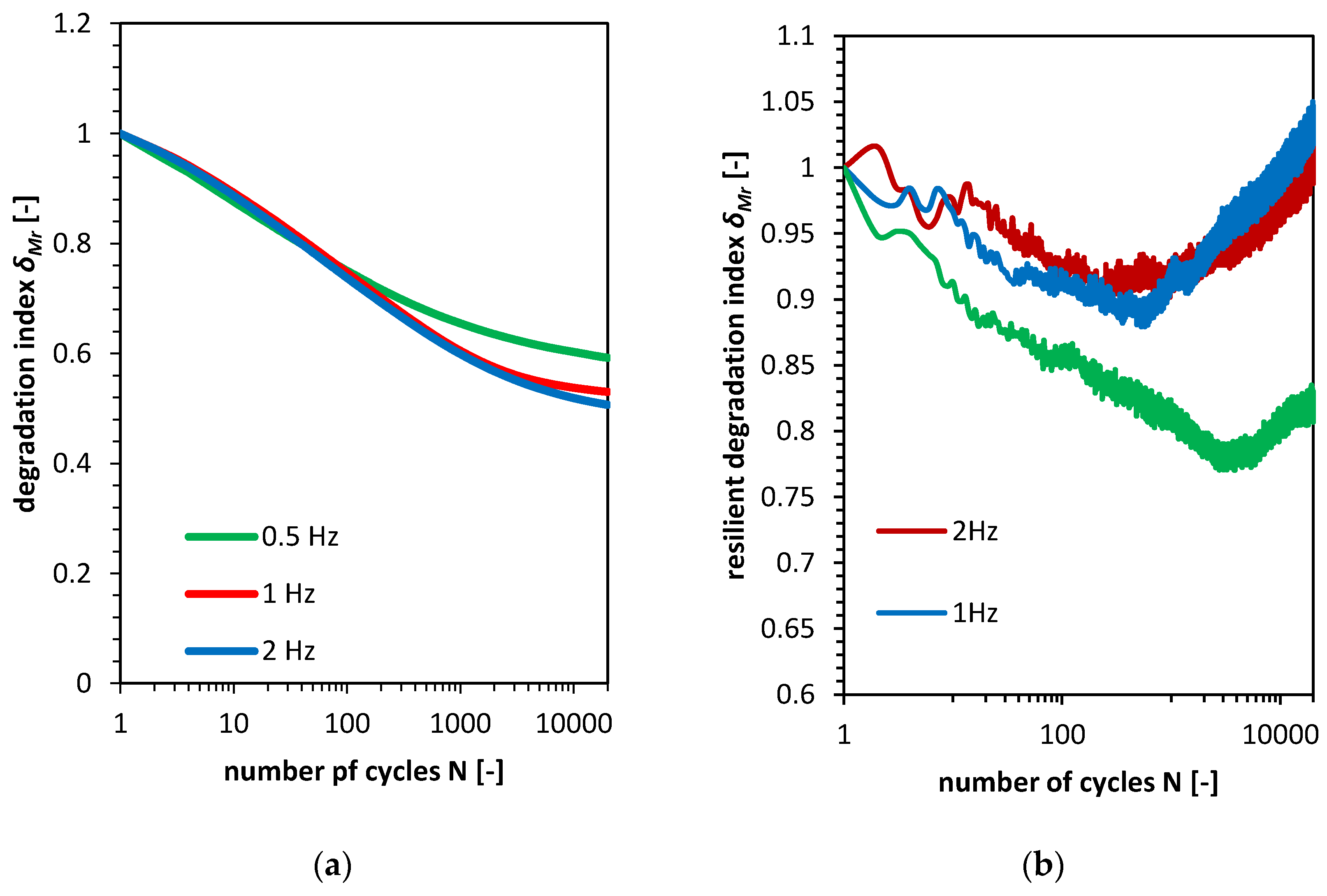
- The degradation index and the resilient degradation index were employed in order to study the plastic strain accumulation and change in stiffness more precisely.
- The degradation characteristics in all cases of frequency loading were similar for first 120 cycles. The long term cyclic loading caused grater degradation in case of sample tested in f equal to 1 Hz and 2 Hz.
- The stiffness change analysis was conducted by application of resilient modulus Mr which for first cycles of loading was between 70.7 MPa and 79.0 MPa. The resilient degradation index proposed in this article refers to quotient of resilient modulus in N-th cycle to Mr in first cycle.
- The resilient degradation analysis have shown that, despite the greater amount of accumulated plastic strains the samples tested in 1 Hz and 2 Hz will recover its stiffness in long term cyclic loading process. The recovery process was also observed in case of 0.5 Hz frequency loading sample but the process started later and the sample did not recovered its initial stiffness.
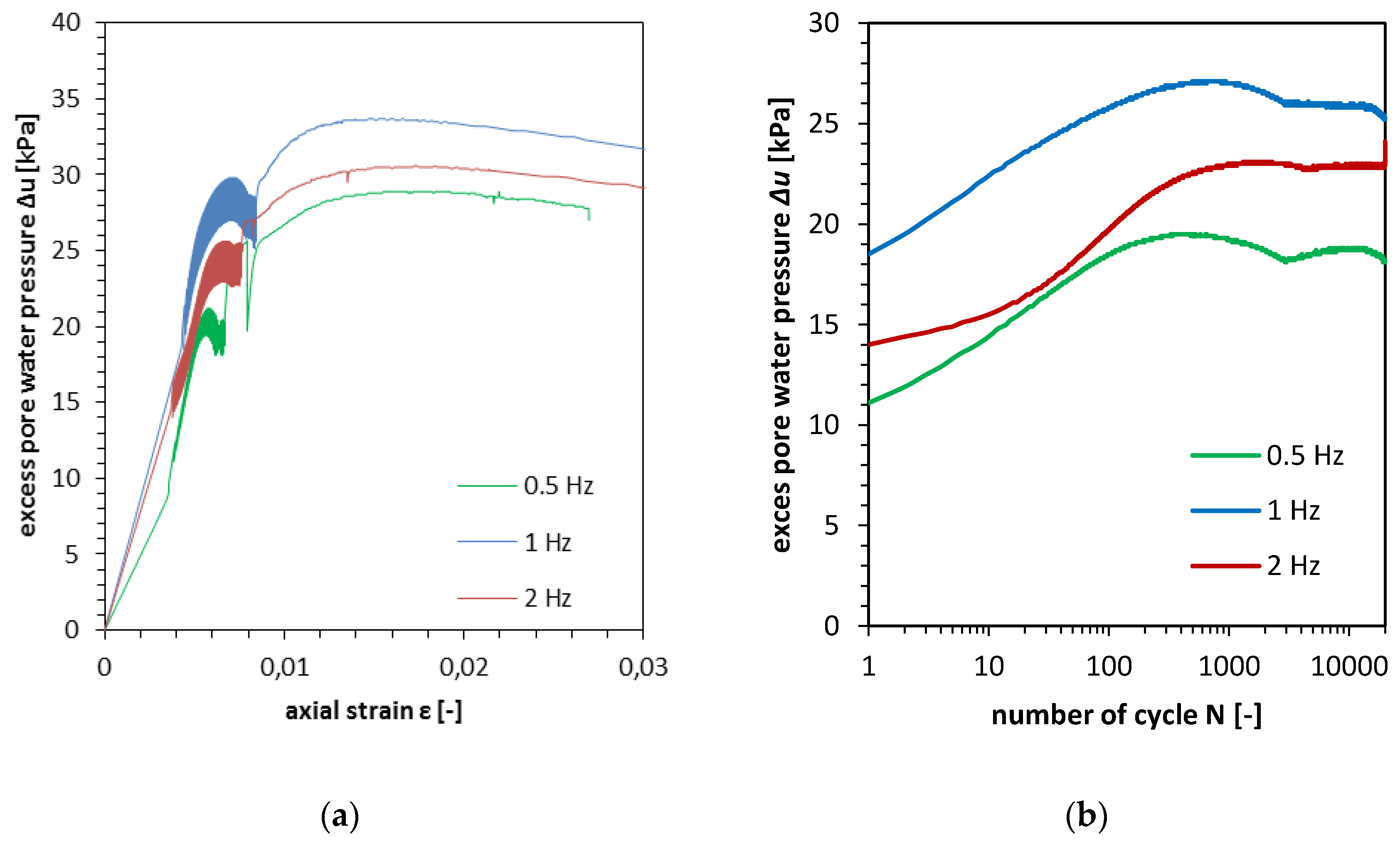
- The excess pore water pressure analysis have shown that the degradation index is connected to the pore pressure generation. The steady value of excess pore which occurs in long term cyclic loading indicates reverse of the soil respond to cyclic loading and after the phase of softening, the hardening occurs. Pore pressure generation in long term cyclic loading of soft soil was studied by Tang et al. [37], the test results have shown, that the excess pore water pressure generation is different than for compacted cohesive soils. The cyclic loading with qa equal to 10 kPa and with σ’3 equal to 95 kPa lead to generation of Δu equal to 28 kPa after 2000 repetitions. The frequency in this test was equal to 0.5 Hz. The tests in the same stress conditions and with frequency equal to 2.5 Hz has led to generation of Δu equal to 19 kPa.
- The characteristics of accumulated plastic strain versus number of cycles and the characteristics of excess pore water pressure development were found to be similar. The conclusion can be drown, the excess pore water pressure characteristics impact on the accumulation of the plastic strains. Such phenomena can also explain why in lower frequencies lower accumulated vertical plastic strains are observed. The results of Tang et al. [37] studies for cohesive soft soil shows different picture. The lower frequency causes higher accumulated plastic strains (0.7% and 0.96% respectively for 0.5 Hz and 2.5 Hz). This indicates that there exists the difference between compacted and soft soil response to cyclic loading of cohesive soils.
- The soil behaviour during undrained shear process after the cyclic loading shows the increase of pore pressure is the cause of preconsolidated behaviour of clay samples during shearing. This type of behaviour differs from this observed during static triaxial test where normally consolidated soil respond was observed.
Author Contributions
Funding
Conflicts of Interest
References
- Pecker, A.; Prevost, J.H.; Dormieux, L. Analysis of pore pressure generation and dissipation in cohesionless materials during seismic loading. J. Earthq. Eng. 2001, 5, 441–464. [Google Scholar] [CrossRef]
- Paolucci, R.; Pecker, A. Seismic bearing capacity of shallow strip foundations on dry soils. Soils Found. 1997, 37, 95–105. [Google Scholar] [CrossRef]
- Newmark, N. Effects of earthquakes on dams and embankments. Geotechnique 1965, 15, 139–160. [Google Scholar] [CrossRef]
- Pecker, A.; Salençon, J. Seismic bearing capacity of shallow strip foundations on clay soils. In Proceedings of the International Workshop on Seismology and Earthquake Engineering, Mexico City, Mexico, 22–26 April 1991; pp. 287–304. [Google Scholar]
- Paolucci, R.; Shirato, M.; Yilmaz, M.T. Seismic behaviour of shallow foundations: Shaking table experiments vs numerical modelling. Earthq. Eng. Struct. Dyn. 2008, 37, 577–595. [Google Scholar] [CrossRef]
- Baralis, M.; Barla, M.; Bogusz, W.; Donna, A.D.; Ryzynski, G.; Żeruri, M. Geothermal Potential of the NE Extension Warsaw Metro Tunnels. Environ. Geotech. 2018, 1–37. [Google Scholar] [CrossRef]
- Crawford, C.B.; Morrison, K.I. Case histories illustrate the importance of secondary-type consolidation settlements in the Fraser River Delta. Can. Geotech. J. 1996, 33, 866–878. [Google Scholar] [CrossRef]
- Yin, Z.Y.; Zhu, Q.Y.; Yin, J.H.; Ni, Q. Stress relaxation coefficient and formulation for soft soils. Géotech. Lett. 2014, 4, 45–51. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.; Tang, Y.; Yan, X.; Zhou, J. Experimental and theoretical methods on determination of stress-dependent natural frequency of marine sedimentary clay. Mar. Georesour. Geotechnol. 2017, 35, 1168–1180. [Google Scholar] [CrossRef]
- Wichtmann, T.; Triantafyllidis, T. Strain accumulation due to packages of cycles with varying amplitude and/or average stress–On the bundling of cycles and the loss of the cyclic preloading memory. Soil Dyn. Earthq. Eng. 2017, 101, 250–263. [Google Scholar] [CrossRef]
- Boulbibane, M.; Ponter, A.R.S. The linear matching method for the shakedown analysis of geotechnical problems. Int. J. Numer. Anal. Methods Geomech. 2006, 30, 157–179. [Google Scholar] [CrossRef]
- Nieto Leal, A.; Kaliakin, V.N. General response observed in cyclically loaded cohesive soils. Ciencia e Ingeniería Neogranadina 2016, 26, 21–39. [Google Scholar] [CrossRef]
- Kumar, S.S.; Krishna, A.M.; Dey, A. Dynamic properties and liquefaction behaviour of cohesive soil in northeast India under staged cyclic loading. J. Rock Mech. Geotech. Eng. 2018, 10, 958–967. [Google Scholar] [CrossRef]
- Martínez, E.; Patiño, H.; Galindo, R. Evaluation of the risk of sudden failure of a cohesive soil subjected to cyclic loading. Soil Dyn. Earthq. Eng. 2017, 92, 419–432. [Google Scholar] [CrossRef]
- Ajmera, B.; Tiwari, B.; Pandey, P. Use of pore pressure response to determine shear strength degradation from cyclic loading. In Proceedings of the Geotechnical Frontiers 2017, Orlando, FL, USA, 12–15 March 2017; pp. 19–26. [Google Scholar]
- Brunarski, L.; Dohojda, M. An approach to in-situ compressive strength of concrete. Bull. Pol. Acad. Sci. Tech. Sci. 2016, 64, 687–695. [Google Scholar] [CrossRef] [Green Version]
- Kalinowska, M.; Jastrzębska, M. Behaviour of cohesive soil subjected to low-frequency cyclic loading in strain-controlled tests. Stud. Geotech. Mech. 2014, 36, 21–35. [Google Scholar] [CrossRef]
- Sas, W.; Głuchowski, A.; Gabryś, K.; Soból, E.; Szymański, A. Resilient modulus characterization of compacted cohesive subgrade soil. Appl. Sci. 2017, 7, 370. [Google Scholar] [CrossRef]
- Mortezaie, A.; Vucetic, M. Threshold shear strains for cyclic degradation and cyclic pore water pressure generation in two clays. J. Geotech. Geoenviron. Eng. 2016, 142, 04016007. [Google Scholar] [CrossRef]
- Lei, H.; Li, B.; Lu, H.; Ren, Q. Dynamic deformation behavior and cyclic degradation of ultrasoft soil under cyclic loading. J. Mater. Civ. Eng. 2016, 28, 04016135. [Google Scholar] [CrossRef]
- Yang, G.; Ye, J. Wave & current-induced progressive liquefaction in loosely deposited seabed. Ocean Eng. 2017, 142, 303–314. [Google Scholar]
- Borowiec, A.; Stanuszek, M. Liquefaction mechanism induced by dynamic excitation modeled in Plaxis AE with the use of UBC and MOHR–coulomb constitutive relationships. Stud. Geotech. Mech. 2016, 38, 123–133. [Google Scholar] [CrossRef] [Green Version]
- Ichii, K.; Mikami, T. Cyclic threshold shear strain in pore water pressure generation in clay in situ samples. Soils Found. 2018, 58, 756–765. [Google Scholar] [CrossRef]
- Leng, J.; Ye, G.L.; Ye, B.; Jeng, D.S. Laboratory test and empirical model for shear modulus degradation of soft marine clays. Ocean Eng. 2017, 146, 101–114. [Google Scholar] [CrossRef]
- Wang, Y.; Lei, J.; Gong, X.; Wang, Y.; Yang, P. Post-cyclic undrained shear behavior of marine silty clay under various loading conditions. Ocean Eng. 2018, 158, 152–161. [Google Scholar] [CrossRef]
- Idriss, I.M.; Dobry, R.; Singh, R. Nonlinear behavior of soft clays during cyclic loading. J. Geotech. Eng. Div. 1978, 104, 1427–1448. [Google Scholar]
- Yamanouchi, T.; Yasuhara, K. Settlement of clay sub grades after opening to traffic. In Proceedings of the 2nd Australia and New Zealand Conference on Geomechanics, Brisbane, Australia, 21–25 July 1975; Volume 1, pp. 115–118. [Google Scholar]
- Hardin, B.O.; Drnevich, V.P. Shear modulus and damping in soils: Measurement and parameter effects. J. Soil Mech. Found. Div. 1972, 98, 603–624. [Google Scholar]
- Konrad, J.M.; Wagg, B.T. Undrained cyclic loading of anisotropically consolidated clayey silts. J. Geotech. Eng. 1993, 119, 929–949. [Google Scholar] [CrossRef]
- Matsui, T.; Ohara, H.; Ito, T. Cyclic stress strain history and shear characteristics of clay. J. Geotech. Eng. Div. 1980, 106, 1101–1120. [Google Scholar]
- Lebebvre, G.; LeBoeuf, D. Rate effects and cyclic loading of sensitive clays. J. Geotech. Eng. 1987, 113, 476–489. [Google Scholar] [CrossRef]
- Procter, D.C.; Khaffaf, J.H. Cyclic triaxial tests on remoulded clays. J. Geotech. Eng. 1984, 110, 1431–1445. [Google Scholar] [CrossRef]
- Vucetic, M.; Dobry, R. Degradation of marine clays under cyclic loading. J. Geotech. Eng. 1988, 114, 133–149. [Google Scholar] [CrossRef]
- Aksnes, J. A Study of Load Responses Towards the Pavement Edge. Ph.D. Thesis, Department of Road End Railway Engineering, Norwegian University of Science and Technology, Trondheim, Norway, 2002. [Google Scholar]
- Jiang, M.; Cai, Z. Stiffness degradation of soft marine clay under uniaxial cyclic loading. Electron. J. Geotech. Eng. 2012, 17, 3889–3895. [Google Scholar]
- Goldscheider, M.; Gudehus, G. Einige Bodenmechanische Probleme bei Küsten-und Offshore-Bauwerken. In Vorträge der Baugrundtagung; Deutsche Gesellschaft für Erd- und Grundbau: Nurnberg, Germany, 1976; pp. 507–522. [Google Scholar]
- Tang, Y.Q.; Zhou, J.; Liu, S.; Yang, P.; Wang, J.X. Test on cyclic creep behavior of mucky clay in Shanghai under step cyclic loading. Environ. Earth Sci. 2011, 63, 321–327. [Google Scholar] [CrossRef]


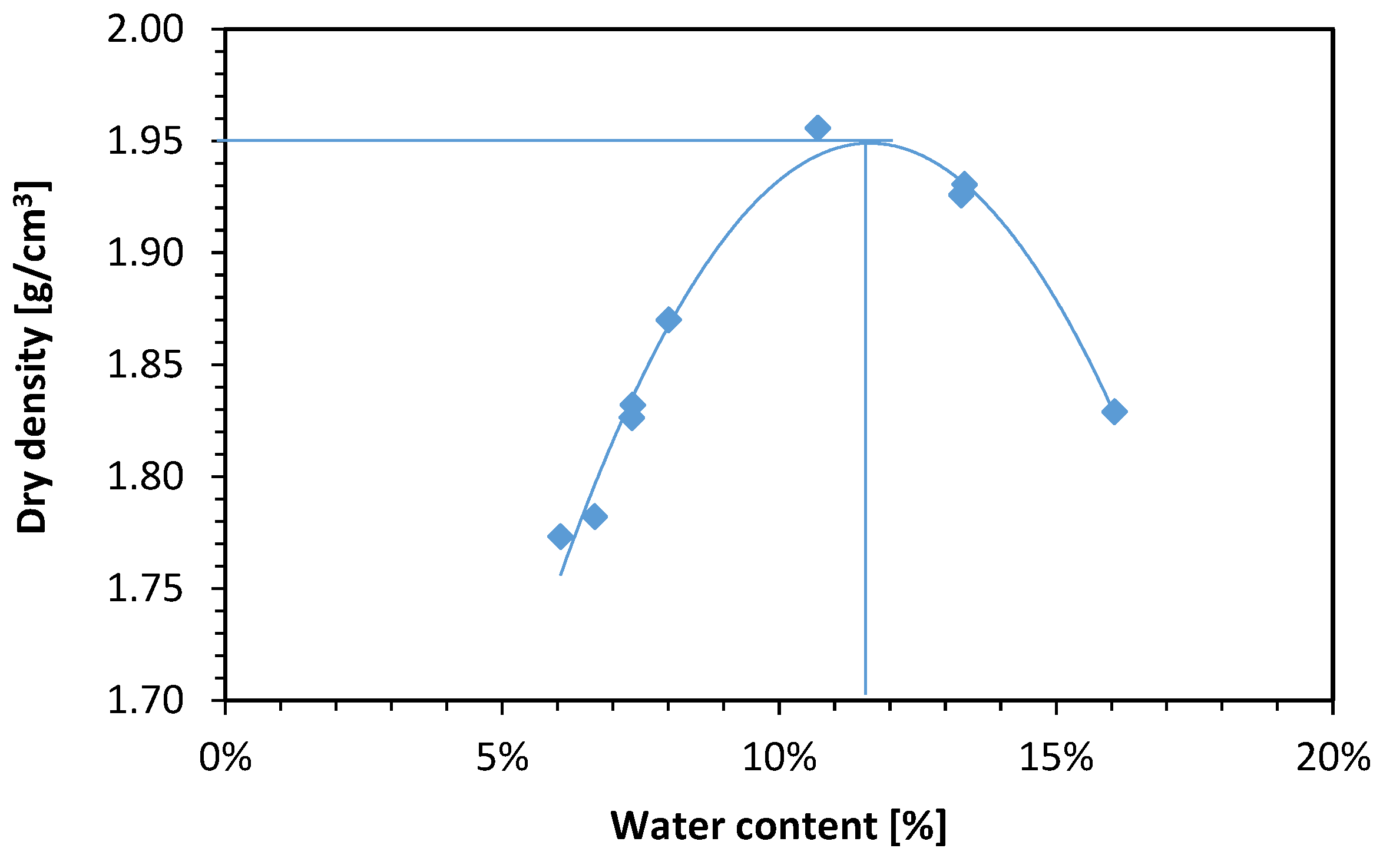
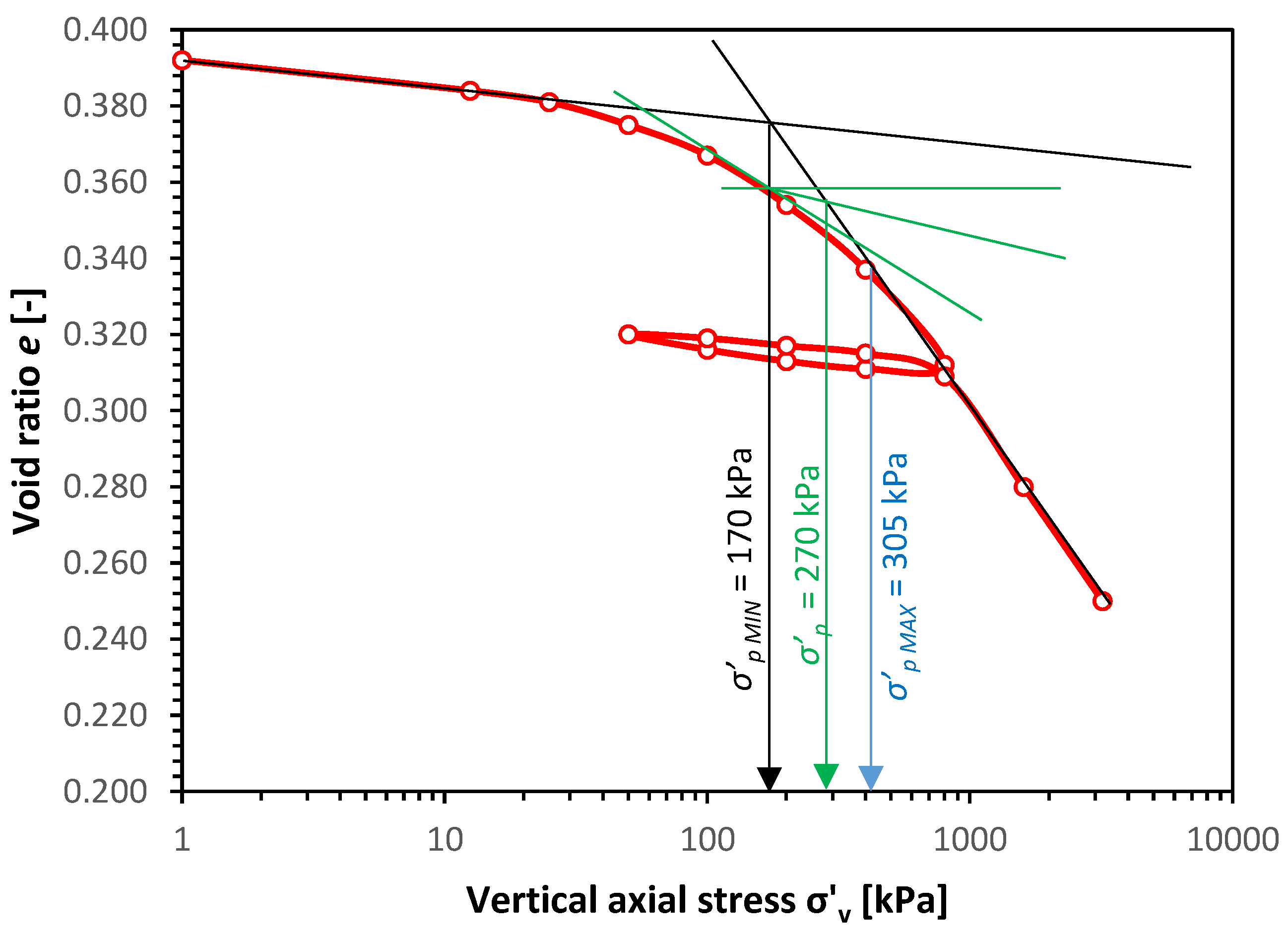


| Property | Sample 1 (f = 0.5 Hz) | Sample 1 (f = 1.0 Hz) | Sample 1 (f = 2.0 Hz) |
|---|---|---|---|
| dry density (g/cm3) | 1.97 | 1.88 | 1.92 |
| initial void ratio e0 (–) | 0.352 | 0.442 | 0.39 |
| natural moisture content (%) | 11.87 | 11.74 | 11.54 |
| liquidity index LI (%) | 0.0 | 0.0 | 0.0 |
| consistency index CI (%) | 1.0 | 1.0 | 1.0 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kucharczyk, K.; Głuchowski, A.; Miturski, M.; Sas, W. Influence of Load Frequency on Cohesive Soil Respond. Geosciences 2018, 8, 468. https://doi.org/10.3390/geosciences8120468
Kucharczyk K, Głuchowski A, Miturski M, Sas W. Influence of Load Frequency on Cohesive Soil Respond. Geosciences. 2018; 8(12):468. https://doi.org/10.3390/geosciences8120468
Chicago/Turabian StyleKucharczyk, Krystian, Andrzej Głuchowski, Maciej Miturski, and Wojciech Sas. 2018. "Influence of Load Frequency on Cohesive Soil Respond" Geosciences 8, no. 12: 468. https://doi.org/10.3390/geosciences8120468
APA StyleKucharczyk, K., Głuchowski, A., Miturski, M., & Sas, W. (2018). Influence of Load Frequency on Cohesive Soil Respond. Geosciences, 8(12), 468. https://doi.org/10.3390/geosciences8120468







