2. Inversion Algorithm
The inversion algorithm is based on the solution presented in [
1,
5]. Here, only the main work-flow (schematically represented in
Figure 1), which is essentially required to understand the numerical investigations presented later on, is summarized, leaving the interested reader to consult the above literature for more details.
The first step of the procedure is the classification of the study area into geological provinces, i.e., the definition of regions where the crustal mass density can be considered homogeneous. This information can be retrieved from external sources e.g., geological provinces maps, or it can be directly inferred from the gravity field itself [
5]. Each single geological province (
i) is then associated with a function describing an a priori relation between the depth
D and the crystalline crust mass density (
), thus creating an a priori crust density model.
Once the geological provinces map and the crystalline crust density model are generated, the gravity field observations can be reduced for the effects of the topography, bathymetry, and sediments (from a priori information) as well as for the effects of the density variations inside the crust (up to the mean Moho depth,
) and in the upper mantle (from
up to a certain given depth, e.g., fixed to the expected maximum depth of the Moho obtained for instance from seismic refraction data or from global Moho models). A comment is required here: within the data reduction in fact, all the masses above the sea level are removed, while the densities from the sea level down to the maximum depth of the model are brought to a constant reference density fixed to 2670 kg/m
for details on the data reduction, and, of the possible problematic related to this operation, the interested reader can refer to [
1].
At this point, it is possible to define the density contrast at the Moho and apply the inversion operator I. Here, I is thought as an operator that inverts the gravitational field in order to retrieve , with the unknown Moho undulation with respect to .
The inversion operator
I can be derived in different ways: it can be obtained from the well-known Oldenburg–Parker solution of the two-layer problem [
6,
7], or from a least squares collocation solution [
8] as well as from a Wiener filter [
9]. In the present study, this last technique has been exploited. With the application of the
I operator,
is retrieved and
can be adjusted (e.g., for a scale factor for each geological province) in such a way that the
is close, in a least squares sense, to the available local seismic derived information. Thereupon,
and
are updated and the data reduction is applied again in order to be coherent with the new model. This procedure is iterated until convergence is met.
Basically, the presented processing scheme allows the user to estimate a final crustal model, which, on one hand, generates the expected gravitational field and, on the other hand, is as close as possible to the available seismic-derived Moho depths.
3. The Levantine Area
The study area, namely the Levantine area, is located in the Eastern region of the Mediterranean Sea and extends from
E to
E and from
N to
N. It is mainly characterized by the presence of the Levantine Basin, a small basin surrounded by continental masses in the Easternmost part of the Mediterranean Sea and the Herodotus Basin in the Western part (see
Figure 2).
The Levant Basin evolved through long and complicated processes, which started in the Late Palaeozoic, when the Eastern Mediterranean Sea was characterized by the presence of Palaeotethys, a wide Ocean separating the Africa and Eurasia tectonic plates. During the Late Palaeozoic and Early Mesozoic, deep-water basins were formed by rifting along the northern margin of the African plate [
10,
11,
12,
13]. The nature and formation of the Levant Basin have been the subject of many studies since the beginning of the century [
14]. Extensive reviews of previous works and models are given, for instance, by [
11,
15,
16].
The deep crustal structure of the Eastern Mediterranean Sea has been a matter of debate for a long time. In spite of the numerous geophysical works done in this region, e.g., [
17,
18,
19,
20,
21,
22], there is still no agreement on the nature of the crust nor on its age. One of the main problems in obtaining information about the deep structure in this region is the existence of a thick sedimentary sequence, which, in some areas, reaches a thickness of more than 10 km [
23]. A prominent unit within the sedimentary sequence was deposited during the Messinian age, at the end of Miocene, when a desiccation of the Mediterranean Sea occurred. Although this event lasted less than 1 Ma, it led to a major erosional phase on the margins of the Mediterranean Sea and to a deposition of layers of salts and evaporites in the basinal areas [
24]. In the recent years, several commercial surveys have acquired numerous multichannel seismic profiles (e.g., [
19]), thus providing detailed information about most of the sedimentary sequence. However, the lower part of this sequence was not penetrated by the seismic reflection data; therefore, information about the basement and Moho depths and about the nature of the crystalline crust are still scarce. In 1983, a long-range seismic refraction acquisition was conducted with the aim to address some of the aforementioned questions [
25]. The results indicated a 35 km thick continental crust, under Cyprus, and an oceanic crust of 8 km thickness, within the Levant Basin between the continental margin of southern Israel and the Eratosthenes Sea-mount. However, other aspects, such as, for example, the nature of the crust under the Eratosthenes Sea-mount and in the surrounding area still remains a matter of study [
26,
27].
4. The Levant Case Study: Data Reduction
As presented in
Section 2, before applying the gravity inversion procedure, it is necessary to reduce the gravitational field for the effects of topography, bathymetry and sediments. In this section, the results of this reduction are presented. The gravity field data have been synthesized from the GECO (GOCE and EGM2008 COmbined) model [
28], which is basically a combination of GOCE and EGM2008 [
29] data. In detail, the spherical harmonics of the GECO model have been synthesized in terms of gravity anomalies, on a grid of a constant altitude of 3500 m with a spatial resolution of 1 arc-min, which coincides to about
km in the West–East direction and
km in the South–North one. Within the data reduction and the inversion phases, an extension of
with respect to the actual extension of the study area has been considered, in order to mitigate any expected errors related to border effects [
30]. The altitude of 3500 m has been selected in such a way to be as close as possible to the Earth surface, but always outside the topographic masses.
In order to assess the Global Gravity field Model (GGM) accuracy on the considered area, its synthesized signal has been compared with a set of marine gravity observations provided by the International Gravimetric Bureau (BGI) [
31]. Starting from the differences and assuming that the terrestrial observations have a 1 mGal white error, an empirical localized GECO error power spectrum has been computed, thus fully representing (at least from the stochastic point of view) the main characteristics of the GGM error itself.
In
Figure 3, this empirical error power spectrum is compared to the one of the gravitational signal due to the Moho undulation. The latter has been simply obtained by computing the gravitational effects of the European Moho model [
32] by means of GTE software [
33,
34].
As it can be seen, for wavelengths smaller than about 20 km, the observation error (blue line) is larger than the Moho signal (red line), which implies that useful information is not retrievable, from GECO, below such a threshold.
To remove the gravitational effects of the topographic layers, namely the bathymetry and topography, the ETOPO1 model [
35] has been used. In detail, a complete Bouguer anomaly (see
Figure 4a) has been computed by estimating the gravitational effects of topography and bathymetry with the GTE package (a FFT-based software for the computation of the terrain effect) [
33,
34], using a reference density value of 2670 kg/m
. Note that the used gravitational field has a formal resolution of about 10 km. A simple test (i.e., a residual terrain correction computed as the difference of a high-resolution terrain model and a smoothed terrain model with a smoothing average size of 10 km) show that the expected magnitude of the omission error in the area is of the order of 2 mGal (std), which drops to only
mGal if the offshore area only is considered. As a consequence, the possible error due to the different spatial resolutions of the used gravitational field and of the field generated by the data reduction is smaller than the expected observation error and therefore negligible.
Regardless that the sedimentary layer, which is known to have a drastic effects on this specific area, has not been considered yet, it can be noticed that the Bouguer anomaly map already reflects the main geological characteristics of the region. In particular, the highly positive regions (reddish area in
Figure 4a) well delineate the Oceanic crust of the Herodotus Basin, crossed by the Mediterranean Ridge (an accretionary wedge caused by the African Plate that subducts under the Eurasian and Anatolian plates), as well as of the Cyprus arc. Moreover, the gravitational effects of the structures lying beneath the Eratosthenes Sea-mount and the boundaries of the Levantine Basin can be identified too. The maximum value of the signal is found in correspondence of the Cyprus arc and on the boundary between the Levantine and the Herodotus basins. The former signal is due to the presence of a crustal plate subducting beneath Cyprus [
36], while the latter can be attributed to the presence of localize ophiolites structures [
27,
37].
In order to reduce the subduction plate effects, a simple model of the plate itself was built up. Both the geometry up to a depth of 40 km and the density contrast, fixed at 380 kg/m
, of such a model are taken from [
36], and the corresponding gravitational effect has been obtained by means of a point mass approximation, i.e., by discretizing the plate with a set of about 6000 point masses, and summing up the effect of each point mass. The reduced signal is shown in
Figure 4b. It can be seen that the applied reduction leads to a much more homogeneous signal, in which the effects of the subduction plate basically disappeared, thus proving the adequacy of the, even simple, considered model.
About the others’ localized maxima, they have been removed by exploiting the stochastic characteristics of the gravitational field itself with a Kriging procedure [
38]. Basically, the effects of these local anomalies are disentangled by considering a proper mask in correspondence with the anomalies, then by estimating an empirical and theoretical variogram from the data located outside the mask, and finally by interpolating on the whole study area (applying a Kriging technique using only the data outside the mask). This procedure gives a new field in which the over-mentioned localized maxima anomalies are removed. Analyzing the difference between the new field and the original one (see
Figure 5a), some information on the causative bodies can be derived. Using a brute-force method, it is possible, for instance, to estimate the parameters (depth and size in the
x-,
y-, and
z-directions) of a prism centered in correspondence of the maximum value of the anomalous field. A constant density contrast of 650 kg/m
(corresponding to the difference between ophiolites and sediments density, 2850 kg/m
and 2200 kg/m
, respectively) was considered here. Once the best prism parameters have been estimated, one can reduce the observed signal for the effect of the prism itself and iterate the procedure. In
Figure 5c, the inversion-based estimated thickness, positions and size are presented. It can be noticed from
Figure 5b that this simple modeling allows for reducing the signal standard deviation from 10 mGal to about 2 mGal. A more detailed modeling of these anomalies, at this point, seems to therefore not be required, since the residual effects are smaller than the global gravity observation error. In any case, the results are highly-consistent with previous studies [
27], with local thickness of the ophiolites up to 10 km.
Once such local anomalies have been explained, a further data reduction was performed to remove the gravitational effects of the sedimentary layer. For this purpose, the geometry and depth of the basement have been retrieved from [
23]. About the density distribution, the full sedimentary succession has been divided into three parts of equal thickness, in which a constant density value was assigned to each part, specifically 2000 kg/m
, 2300 kg/m
and 2600 kg/m
, respectively, according to [
39]. The reduced gravity field is shown in
Figure 4c. It can be observed that the positive regions, reflecting the effects of the superposition of the heavy oceanic crust and the light sedimentary layers, are locally emphasized giving, after the reduction, a more demarcated field over the Herodotus Basin.
The following step is the definition of the main geological provinces. We have to recall that this step is basically required to identify areas, inside the studied region, that can be considered homogeneous (from the mass density distribution point of view). For this reason, the conceptual model developed in [
39,
40] was analyzed, attempting to identify the boundaries of the different regions from the reduced gravitational field plotted in
Figure 4b. This objective has been fulfilled by searching for the different domain boundaries by means of the tilt angle, theta angle, and their correlation angle. Briefly, the tilt angle is defined in terms of the arctangent of the ratio of the first vertical derivative to the horizontal gradient of the potential field [
41], the theta angle is the arccosine of the ratio between total horizontal derivative and the analytical signal of the gravity potential field [
42], and the correlation angle is computed exploiting the amplitude and gradients of both angles [
43]. For more details on these angles, the interested reader can consult, for instance, [
44,
45].
From the results reported in
Figure 6, it can be noticed how all three of the methods are suitable to detect the edges between different geological provinces, i.e., the Herodotus oceanic crust and the Mediterranean Ridge, as well as the Cyprus Arc. Moreover, the tilt angle and theta angle maps can clearly delineate the boundaries of the Levantine Basin. The correlation angle, however, seems to suggest the presence of an Oceanic crust in correspondence with the Eratosthenes Sea-mount and the Levantine Basin (values of the correlation angle close to −180 are typical of oceanic crust, while values close to 0 are found in correspondence with the continental crust [
45]); these two areas will be in any case thoroughly discussed in the following section. From the analysis of these results, in order to define the geological provinces, we updated the boundaries of the model done by [
40] in accordance with the observed offshore gravity field, thus obtaining the map shown in
Figure 7. With respect to the densities, the initial value of 2850 kg/m
is assumed for the Oceanic crust [
46], while values starting from 2670 kg/m
with a linear gradient of 9 kg/m
km
up to 40 km in the continental domain are adopted [
47]. In case of larger depths, the density of the continental crust is fixed to 3030 kg/m
, according to [
47]. A note must be taken that the continental domain, in yellow color located to the South of Cyprus, coincides to the Eratosthenes Sea-mount.
Before applying the inversion procedure, the lateral density variation inside the mantle should also be considered. In this study, it has been taken from a global model [
48] directly.
Note that the proposed data reduction scheme implies having precise information on the shape and density of topography, bathymetry, and sediments as well as the mantle. While this is well-justified for the topography and bathymetry, which are the most exterior layers of the crust and therefore probably the best known, the situation is completely different for the involved sedimentary successions and the mantle mass densities. Starting from the former, namely the sedimentary layer, the one should underline that, in the study area, its gravitational effects cannot be properly disentangled from the one of the Moho. In fact, the forward computed signal of the sediments, due to the large extension and thickness of the sedimentary layer of the Nile Basin, has a complete overlap (in terms of wavelengths) with the Moho one. Therefore, it should be retrieved from external sources. In addition, the situation of the mantle density is so similar. For this reason, in the current research, we prefer to evaluate their errors and to propagate the uncertainty in terms of accuracy in the final results.
5. The Levant Crustal Structure from Gravity Inversion
In this section, the main results obtained by applying the proposed inversion algorithm on the Levant case-study are presented.
Apart from the gravitational field observations and the geological information on the possible densities of homogeneous regions, other information can be exploited in order to apply the inversion algorithm. A set of available seismic profiles (see red lines in
Figure 2) has been exploited to constrain the model. In detail, seismic profiles from [
39,
49] bounded by the information retrieved from the receiver functions [
50,
51] have been used.
The numerical assessment starts by attempting to understand the actual amount of information as well as the accuracy retrievable from solely exploiting the available seismic acquisitions. In order to achieve that a simple Moho depths map was estimated by applying the Kriging procedure to the seismic-derived dataset. The results of the Kriging interpolation and its corresponding estimation errors are reported in
Figure 8.
The estimation error clearly shows that the Moho is well constrained with estimates characterized by a standard deviation (STD) smaller than 2 km, in the whole Levantine Basin with important uncertainties whose STD reaches 6 km, only in correspondence to the Cyprus Arc and the Mediterranean Ridge. The above maps will be considered as a useful benchmark to validate the inversion result. The expected Moho depth in fact should be consistent with the results of the Kriging interpolation. From the statistical point of view, we can test the hypothesis
(with
and
the Moho depth from seismic and from gravity inversion, respectively) for each pixel, supposing a confidence level of 95% and properly considering the respective predicted accuracy
and
[
52].
As pointed out in
Section 3, among the interesting features of the study area still not completely understood is whether the Eratosthenes block and the Levantine Basin crust belong to the oceanic domain or not. For this reason, the experiment described in the following was conducted. It consisted of performing several inversions assuming different crustal density functions for the two zones and then comparing the obtained results with the information provided by the available seismic profiles. In particular, for each of the two regions, a density of 2670 kg/m
with a linear gradient of 9 kg/m
/km (typical of the continental crust [
47]), a density of 2850 kg/m
(typical of the Oceanic crust [
46]), and a constant density of 2780 kg/m
(i.e., of a heavy continental crust [
47]) have been tested. The results are reported in
Table 1 together with the statistics of the differences of the seismic-based Moho depths and those obtained from the gravity inversion for the two zones. The results of this simplified test, due to the low number of the seismic profiles and the small size of the two regions, have a low significance level from the statistical point of view. In any case, they seem to suggest the presence of a continental crust in correspondence with both the Eratosthenes Block and the Levantine Basin with a constant density value of about 2780 kg/m
for the former and of 2670 kg/m
with a density gradient of 9 kg/m
per km for the latter.
As for the Eratosthenes Block, the above conclusion seems to be coherent with the result obtained by [
26], which reveals a complex velocity structure for Eratosthenes made by a thicker middle crust and a thinner lower crust.
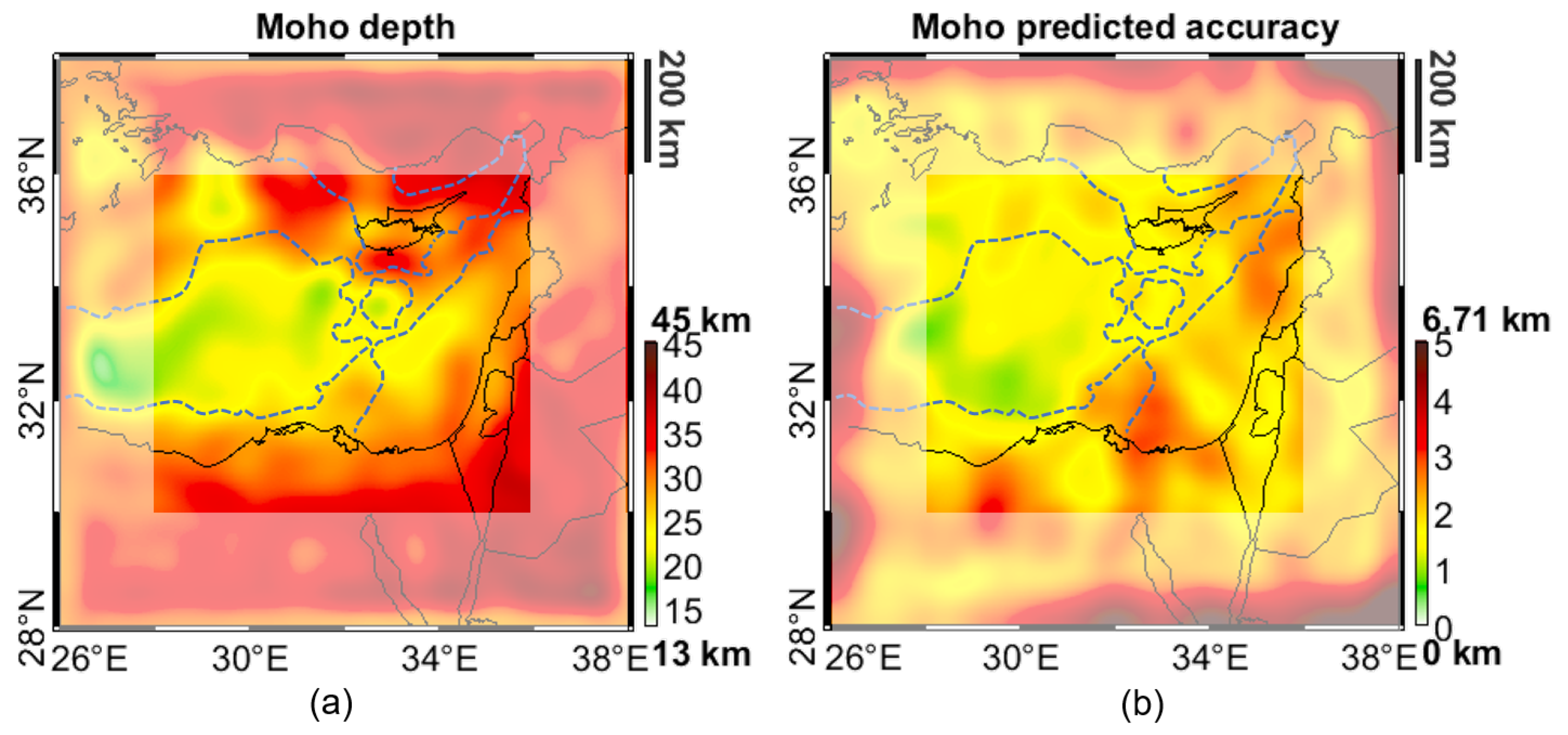
Once the initial density models of these two regions are fixed, it has been possible to perform the inversion of the gravitational field data. The Moho depth estimates are presented in
Figure 9, where the presence of a shallower Moho beneath the Oceanic crust of the Herodotus Basin as well as in correspondence to the Cyprus Arc are evident. As for the Levantine Basin, it presents a Moho depth ranging between 20 km in the Northernmost area to about 30 km close to the Sinai coastline. The Eratosthenes Block instead shows a general crust thickening with a Moho depth reaching a value of 28 km.
Considering now the density distribution, the inversion basically decreases the density of the Eratosthenes Block with a factor of while leaving unchanged all the others’ density functions (variations are smaller than %).
Comparing the obtained Moho model with the seismic-derived information,
Figure 8a, a good consistency between the two models where seismic profiles are available can be seen. Considering the statistics presented above, it turns out that 99% of the two maps are consistent with a confidence level of 95%.
In
Figure 10, the European Moho model [
51] and the GEMMA1.0 global model [
1] are chosen for comparison purposes. Neglecting the different spatial resolution of the models, it can be observed that the GEMMA1.0 model is able to retrieve the major Moho variation in the considered area, even if different long-wavelengths can be easily observed. This is probably due to the fact that, in the GEMMA1.0 global model, the Mediterranean Sea region of the study area has been modeled with a unique geological province, therefore simplifying the real geological setting. Moreover, the GEMMA1.0 model does not incorporate a detailed local sediment thickness model. As for the Moho depth of the European plate,
Figure 10b, it shows a completely different shape. It should be observed that this model, which has a good consistency with the CRUST1.0 model [
53], in the considered area is not properly constrained with seismic profiles. This is confirmed also by the predicted map of the Moho depth uncertainty, which ranges between 4 and more than 8 km (STD), in the study area [
51].
In order to evaluate the accuracy of the obtained results, three factors should at least be considered: namely the accuracy of the inversion algorithm, the accuracy of the gravitational field data, and the accuracy of the different models used within the data reduction step. The first factor, namely the accuracy of the inversion operator, can be evaluated by means of a simple closed-loop test, where a realistic Moho model in the region of interest, e.g., obtained from the European Moho, is considered. By means of the GTE software [
33], the effects, in terms of gravity disturbances, of a synthetic model made of only two layers (i.e., crust and upper Mantle) were computed considering constant densities equivalent to 2850 kg/m
and 3250 kg/m
, respectively, and separated by the Moho interface. Consequently, the inversion algorithm on the synthetic field is executed. It turns out, from this synthetic experiment, that the error related to the inversion operator is of the order of
km in terms of STD, which drops to solely
km if a
border (where the boundary effects are expected) is considered.
As for the gravitational field related error, it can be simply propagated by means of the inversion operator I. Assuming an observation error of 5 mGal (STD), an accuracy of km is retrievable, in terms of Moho depth.
Considering now the last factor, namely the accuracy related to the data reduction, the effects of each component is evaluated by means of a Monte Carlo analysis, in which, for each component, a certain error variance and a correlation length are assumed. Therefore, a set of Monte Carlo samples are randomly generated. The inversion algorithm is then applied to each sample and the final accuracy is evaluated in terms of the Moho depth. The statistics are reported in
Table 2, where it can be seen that the effect of the lateral variation of the Mantle density is quite small with a STD of
km, while those related to the crystalline crust are more considerable with a STD of
km.
The total accuracy of the estimated Moho depth is displayed in
Figure 9b and it is evaluated to be
km.