Framework for Offline Flood Inundation Forecasts for Two-Dimensional Hydrodynamic Models
Abstract
:1. Introduction
2. Methodology
2.1. Framework for Offline Flood Inundation Forecast
2.2. Evaluation Metrics
3. Study Area, Data and Models
3.1. Study Area
3.2. Case Study Data
3.3. Pre-Calibration and Validation of the 2D Flood Inundation Model
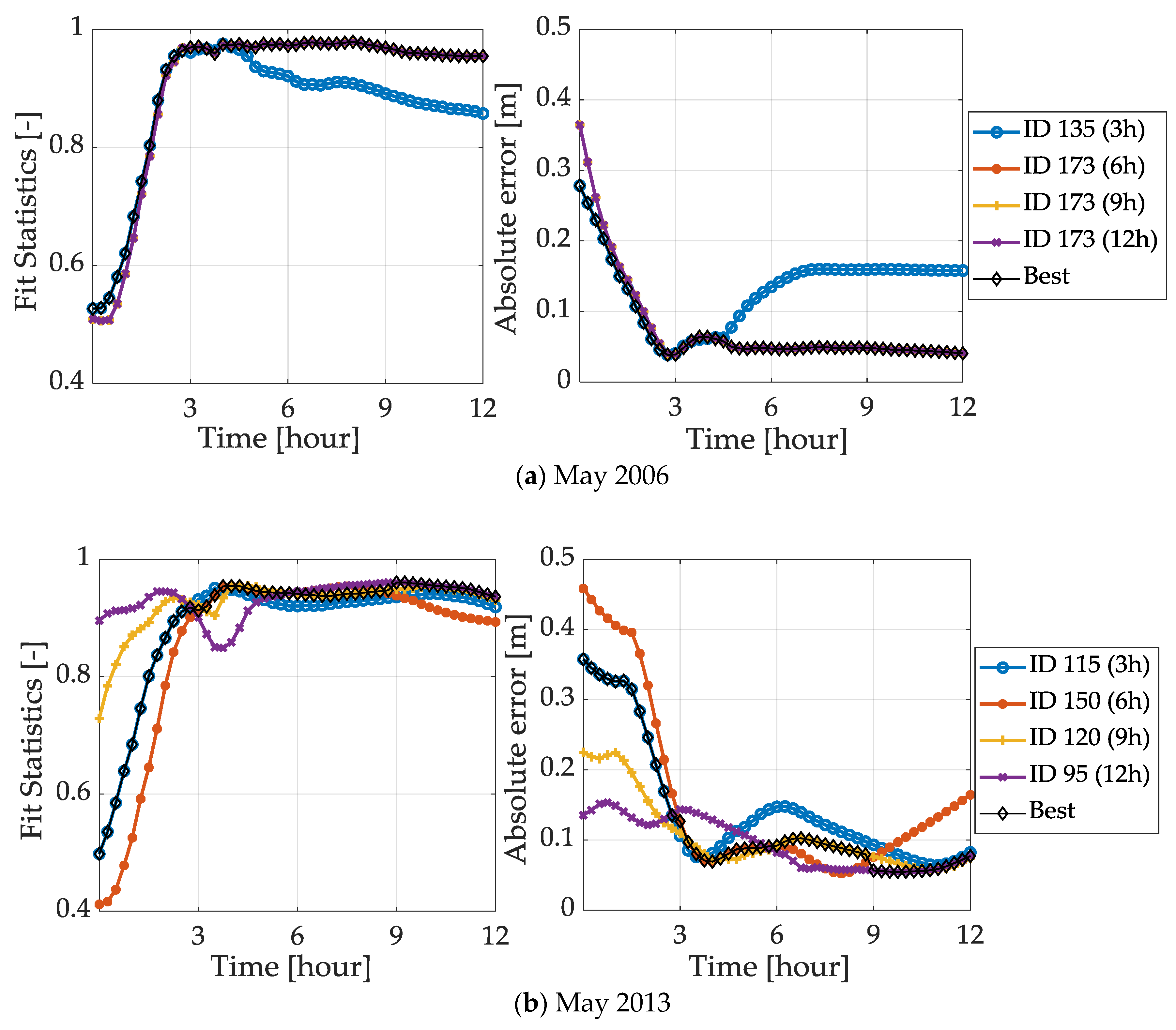
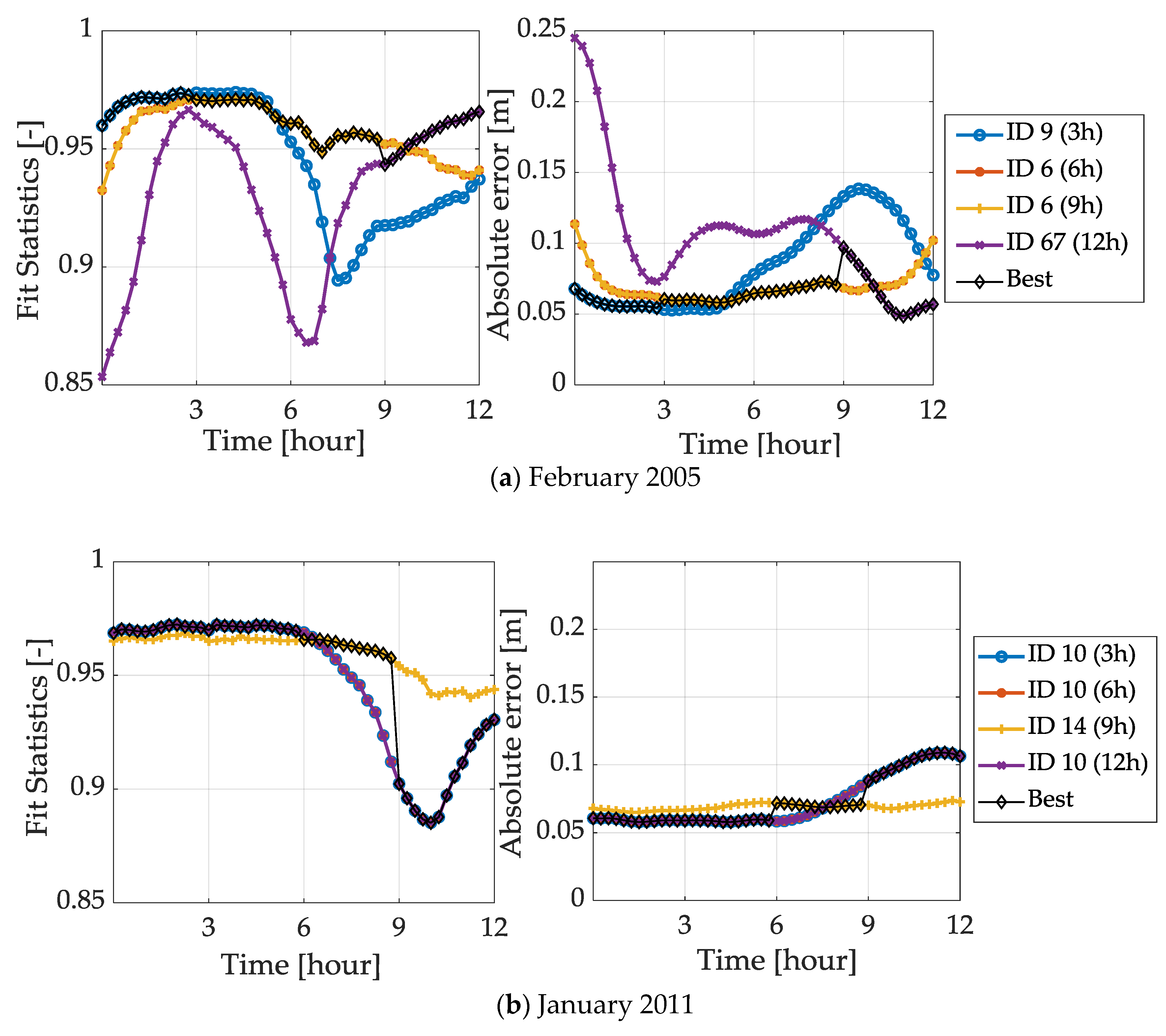
4. Results and Discussion
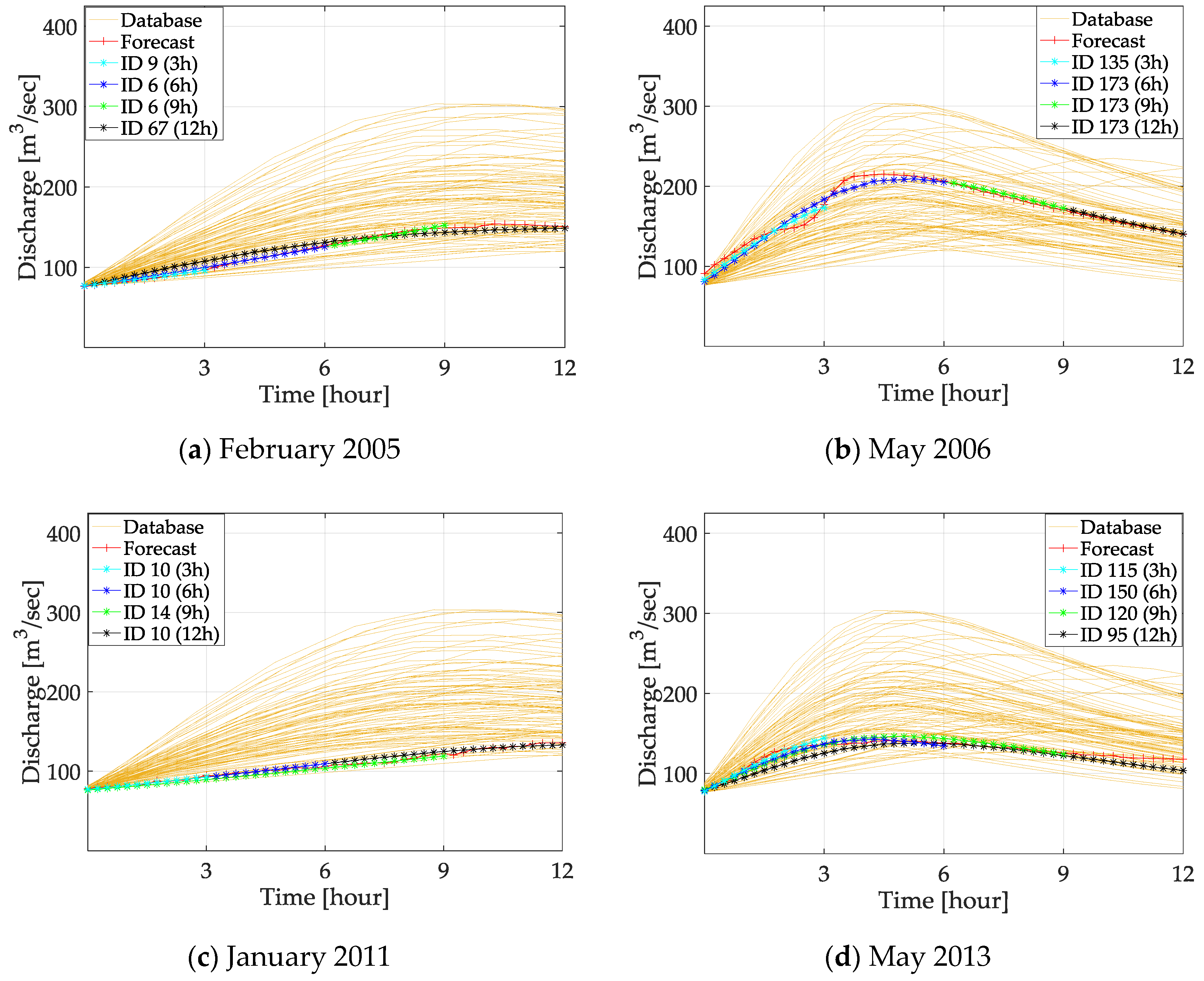
4.1. Discharge Comparison
4.2. Inundation Forecast Comparison
4.2.1. Convective Events
4.2.2. Advective Events
4.3. Update Map Selection
5. Framework Performance
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- European Commission. Directive 2007/60/EC of the European Parliament and of the Council of 23 October 2007 on the Assessment and Management of Flood Risks. 2007. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/PDF/?uri=CELEX:32007L0060&from=EN (accessed on 23 March 2018).
- Munich Re. Topics GEO Natural Catastrophes 2016—Analyses, Assessments, Positions; Münchener Rückversicherung-Gesellschaft (Munich Re): Munich, Germany, 2017. [Google Scholar]
- Thieken, A.H.; Kienzler, S.; Kreibich, H.; Kuhlicke, C.; Kunz, M.; Mühr, B.; Müller, M.; Otto, A.; Petrow, T.; Pisi, S.; et al. Review of the Flood Risk Management System in Germany after the Major Flood in 2013. Ecol. Soc. 2016, 21, 1–12. [Google Scholar] [CrossRef]
- Laurent, S.; Hangen-Brodersen, C.; Ehret, U.; Meyer, I.; Moritz, K.; Vogelbacher, A.; Holle, F.K. Forecast Uncertainties in the Operational Flood Forecasting of the Bavarian Danube Catchment. In Hydrological Processes of the Danube River Basin—Perspectives from the Danubian Countries; Brilly, M., Ed.; Springer: Dordrecht, The Netherlands, 2010; pp. 367–387. [Google Scholar]
- Bates, P.D.; Pappenberger, F.; Romanowicz, R.J. Uncertainty in Flood Inundation Modelling. In Applied Uncertainty Analysis for Flood Risk Management; Beven, K., Hall, J., Eds.; Imperial College Press: London, UK, 2014; pp. 232–269. [Google Scholar]
- Hu, X.; Song, L. Hydrodynamic Modeling of Flash Flood in Mountain Watersheds Based on High-performance GPU Computing. Nat. Haz. 2018, 91, 567–586. [Google Scholar] [CrossRef]
- Zhang, S.; Yuan, R.; Wu, Y.; Yi, Y. Parallel Computation of a Dam-break Flow Model Using Openacc Applications. J. Hydraul. Eng. 2017, 143, 04016070. [Google Scholar] [CrossRef]
- Henonin, J.; Russo, B.; Mark, O.; Gourbesville, P. Real-time Urban Flood Forecasting and Modelling—A State of the Art. J. Hydroinform. 2013, 15, 717–736. [Google Scholar] [CrossRef]
- Bhatt, C.M.; Rao, G.S.; Diwakar, P.G.; Dadhwal, V.K. Development of Flood Inundation Extent Libraries Over a Range of Potential Flood Levels: A Practical Framework for Quick Flood Response. Geomat. Nat. Haz. Risk 2017, 8, 384–401. [Google Scholar] [CrossRef]
- Voigt, S.; Kemper, T.; Riedlinger, T.; Kiefl, R.; Scholte, K.; Mehl, H. Satellite Image Analysis for Disaster and Crisis-management Support. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1520–1528. [Google Scholar] [CrossRef]
- Bates, P.D. Integrating Remote Sensing Data with Flood Inundation Models: How Far Have We Got? Hydrol. Process 2012, 26, 2515–2521. [Google Scholar] [CrossRef]
- Bales, J.D.; Wagner, C.R. Sources of Uncertainty in Flood Inundation Maps. J. Flood Risk Manag. 2009, 2, 139–147. [Google Scholar] [CrossRef]
- René, J.-R.; Djordjević, S.; Butler, D.; Madsen, H.; Mark, O. Assessing the Potential for Real-time Urban Flood Forecasting Based on a Worldwide Survey on Data Availability. Urban Water J. 2014, 11, 573–583. [Google Scholar] [CrossRef]
- Chen, A.S.; Hsu, M.-H.; Teng, W.-H.; Huang, C.-J.; Yeh, S.-H.; Lien, W.-Y. Establishing the Database of Inundation Potential in Taiwan. Nat. Haz. 2006, 37, 107–132. [Google Scholar] [CrossRef] [Green Version]
- Schulz, A.; Kiesel, J.; Kling, H.; Preishuber, M.; Petersen, G. An Online System for Rapid and Simultaneous Flood Mapping Scenario Simulations—The Zambezi FloodDSS. Presented at the EGU General Assembly Conference, Vienna, Austria, 12–17 April 2015. [Google Scholar]
- Raymond, M.; Peyron, N.; Bahl, M.; Martin, A.; Alfonsi, F. ESPADA: Un Outil Innovant Pour la Gestion en Temps Réel Descrues Rrbaines. In Proceedings of the Novatech 6th Conference of Sustainable Techniques and Strategies in Urban Water Management, Lyon, France, 25–27 June 2007; pp. 793–800. [Google Scholar]
- Dottori, F.; Kalas, M.; Salamon, P.; Bianchi, A.; Alfieri, L.; Feyen, L. An Operational Procedure for Rapid Flood Risk Assessment in Europe. Nat. Haz. Earth Syst. Sci. 2017, 17, 1111–1126. [Google Scholar] [CrossRef]
- Alfieri, L.; Salamon, P.; Bianchi, A.; Neal, J.; Bates, P.; Feyen, L. Advances in Pan-European Flood Hazard Mapping. Hydrol. Proc. 2014, 28, 4067–4077. [Google Scholar] [CrossRef]
- Ludwig, K.; Bremicker, M. The Water Balance Model LARSIM: Design, Content and Applications; Institut für Hydrologie der Universität: Freiberg, Germany, 2006. [Google Scholar]
- Disse, M.; Konnerth, I.; Bhola, P.K.; Leandro, J. Unsicherheitsabschätzung für die Berechnung von Dynamischen Überschwemmungskarten—Fallstudie Kulmbach. Wasserwirtsch. Springer Prof. 2017, 11, 47–51. [Google Scholar] [CrossRef]
- Leandro, J.; Konnerth, I.; Bhola, P.; Amin, K.; Köck, F.; Disse, M. Floodevac Interface zur Hochwassersimulation mit Integrierten Unsicherheitsabschätzungen. In Tag der Hydrologie, Fachgemeinschaft Hydrologische; Reinhardt-Imjela, C., Ed.; Wissenschaften in der DWA Geschäftsstelle: Trier, Germany, 2017; pp. 185–192. [Google Scholar]
- Krause, P.B.; Boyle, D.P.; Bäse, F. Comparison of Different Efficiency Criteria for Hydrological Model Assessment. Adv. Geosci. 2005, 5, 89–97. [Google Scholar] [CrossRef]
- Moriasi, D.; Arnold, J.; Van Liew, M.; Bingner, R.; Harmel, R.D.; Veith, T. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Leandro, J.; Djordjević, S.; Chen, A.S.; Savić, D.A.; Stanić, M. Calibration of a 1D/1D Urban Flood Model Using 1D/2D Model Results in the Absence of Field Data. J. Water Sci. Technol. 2011, 64, 1016–1024. [Google Scholar] [CrossRef]
- Moya Quiroga, V.; Kure, S.; Udo, K.; Mano, A. Application of 2D Numerical Simulation for the Analysis of the February 2014 Bolivian Amazonia Flood: Application of the New HEC-RAS Version 5. RIBAGUA Rev. Iberoam. Agua 2016, 3, 25–33. [Google Scholar] [CrossRef]
- Verworn, H.R. Praxisrelevante Extremwerte des Niederschlags; Institut für Wasserwirtschaft, Hydrologie und Landwirtschaftlichen Wasserbau: Magdenburg, Germany, 2016; pp. 173–185. [Google Scholar]
- Maniak, U. Niederschlag-abfluss-modelle für Hochwasserabläufe. In Hydrologie und Wasserwirtschaft: Eine Einführung für Ingenieure; Springer: Berlin, Germany, 2010; pp. 261–360. [Google Scholar]
- Brunner, G.W. HEC-RAS River Analysis System Hydraulic Reference Manual; Report for US Army Corps of Engineers; Hydrologic Engineering Center (HEC): Davis, CA, USA, 2010. [Google Scholar]
- Leandro, J.; Chen, A.S.; Schumann, A. A 2D Parallel Diffusive Wave Model for Floodplain Inundation with Variable Time Step (P-D Wave). J. Hydrol. 2014, 517, 250–259. [Google Scholar] [CrossRef]
- Hof, W. Flood Events of January 2011 in Main. Available online: www.wwa-ho.bayern.de/hochwasser/hochwasserereignisse/januar2011/main/index.htm (accessed on 20 March 2018).
- Wolf, L. Hochwassergroßeinsatz in Kulmbach. Available online: https://fotothurnau.wordpress.com/2011/01/15/hochwasser-groseinsatz-in-kulmbach/ (accessed on 20 March 2018).
- Leandro, J.; Schumann, A.; Pfister, A. A Step Towards Considering the Spatial Heterogeneity of Urban Key Features in Urban Hydrology Flood Modelling. J. Hydrol. 2016, 535, 356–365. [Google Scholar] [CrossRef]
- Molinari, D.; Ballio, F.; Handmer, J.; Menoni, S. On the Modeling of Significance for Flood Damage Assessment. Int. J. Disaster Risk Reduct. 2014, 10, 381–391. [Google Scholar] [CrossRef]









| Evaluation Metrics | Equation | Terms |
|---|---|---|
| Nash-Sutcliffe efficiency (NSE) | —the number of samples —the forecasted discharge —the discharge of the database —the gradient of the regression line | |
| Weighted coefficient of determination (wr2) | ||
| Fit Statistic (F) | —the overlap of flooded cells in the online () and offline () maps —the number of flooded cells and —the water depth in the offline and online maps | |
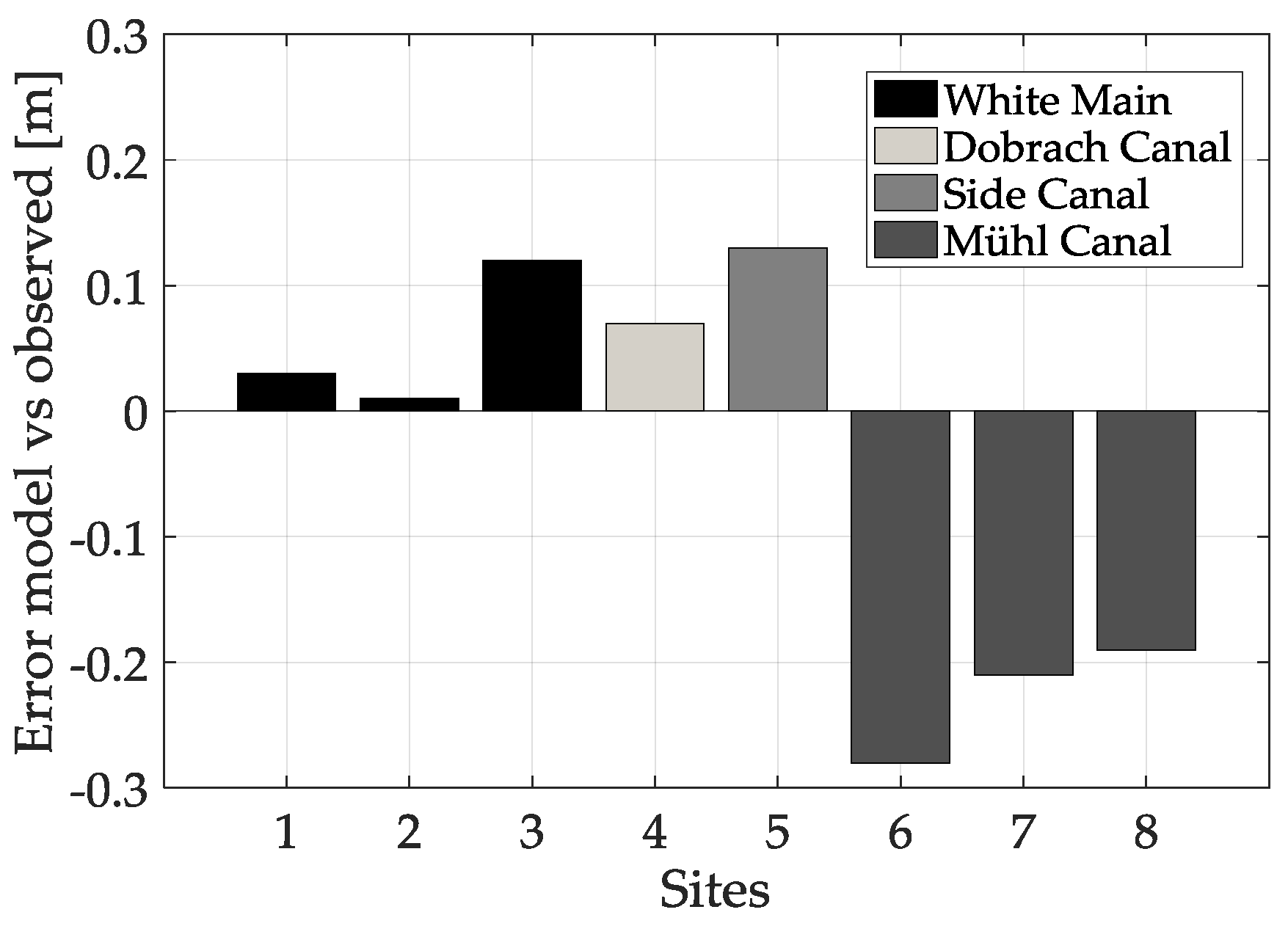
| Absolute Error (e) |
| Data | Value |
|---|---|
| Model area | 11.5 km2 |
| Total number of cells | 430,485 |
| Number of cells in results domain | 193,161 |
| Δt | 20 s |
| Minimum cell area | 6.8 m2 |
| Maximum cell area | 59.8 m2 |
| Average cell area | 24.8 m2 |
| Land Use | Calibrated Manning’s n [s/m(1/3)] | Ranges of Manning’s n [s/m(1/3)] |
|---|---|---|
| Water bodies | 0.022 | 0.015–0.149 |
| Agriculture | 0.043 | 0.025–0.110 |
| Forest | 0.189 | 0.110–0.200 |
| Transportation | 0.014 | 0.012–0.020 |
| Urban | 0.074 | 0.040–0.080 |
| Duration | No. of Data Samples | Goodness of Fit [-] | |||
|---|---|---|---|---|---|
| February 2005 | May 2006 | January 2011 | May 2013 | ||
| 0–3 h | 13 | 0.98 (NSE) | 0.91 (NSE) | 0.96 (NSE) | 0.97 (NSE) |
| 0–6 h | 25 | 0.99 (NSE) | 0.95 (NSE) | 0.97 (NSE) | 0.96 (NSE) |
| 0–9 h | 37 | 0.99 (NSE) | 0.95 (NSE) | 0.95 (NSE) | 0.91 (NSE) |
| 0–12 h | 49 | 0.94 (NSE) | 0.95 (NSE) | 0.97 (NSE) | 0.87 (wr2) |
| Duration | Average Fit Statistics [-] | Average Absolute Error [m] | ||||||
|---|---|---|---|---|---|---|---|---|
| February 2005 | May 2006 | January 2011 | May 2013 | February 2005 | May 2006 | January 2011 | May 2013 | |
| 0–3 h | 0.97 | 0.75 | 0.97 | 0.76 | 0.06 | 0.14 | 0.06 | 0.27 |
| 0–6 h | 0.96 | 0.84 | 0.97 | 0.80 | 0.07 | 0.11 | 0.06 | 0.22 |
| 0–9 h | 0.96 | 0.89 | 0.97 | 0.92 | 0.07 | 0.09 | 0.07 | 0.12 |
| 0–12 h | 0.93 | 0.90 | 0.95 | 0.93 | 0.11 | 0.08 | 0.07 | 0.11 |
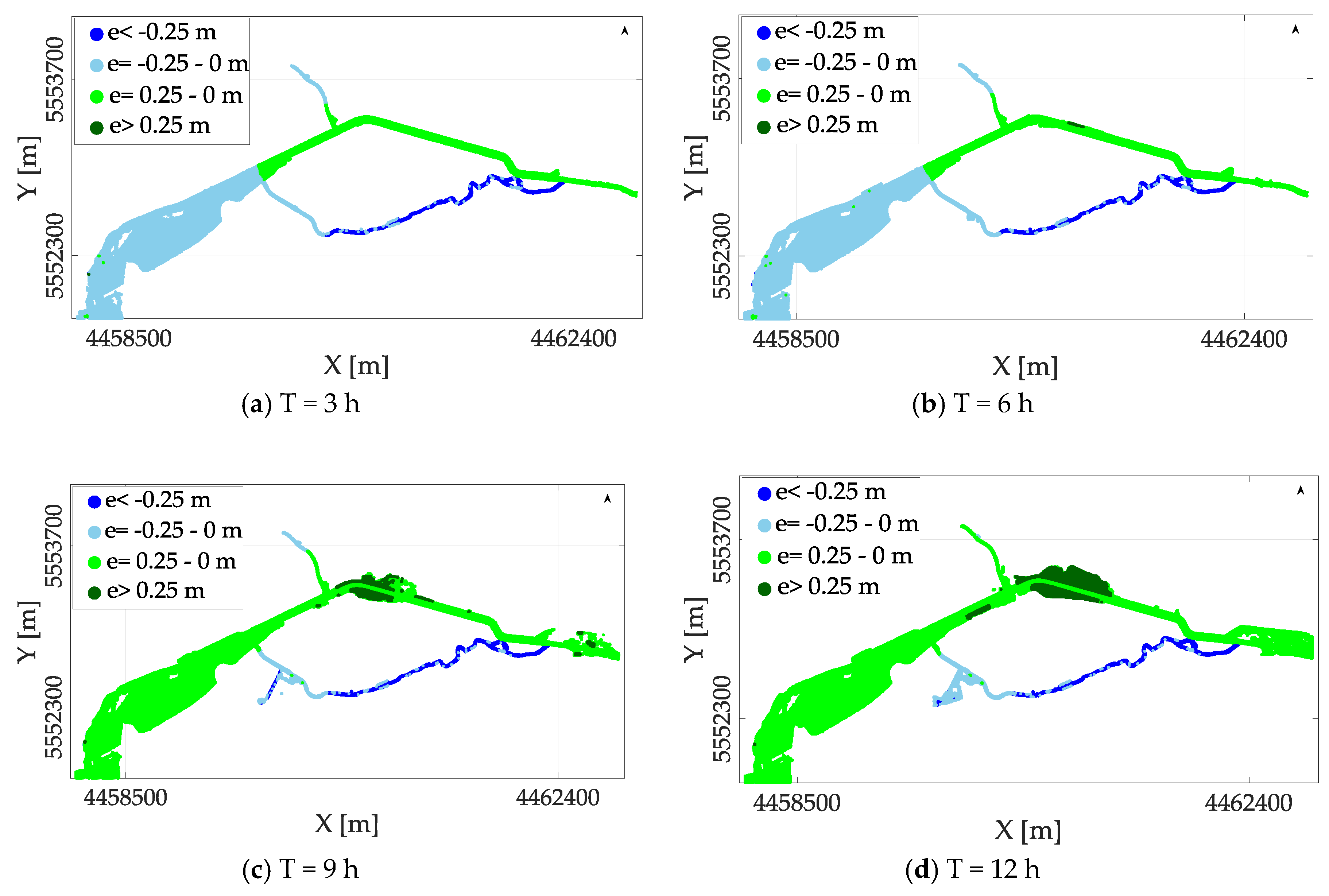
| Time | Flooded Cells | May 2006 [%] | |||
|---|---|---|---|---|---|
| <−0.25 m | −0.25–0 m | 0.25–0 m | >0.25 m | ||
| T = 3 h | 36,865 | 3 | 48 | 49 | 0 |
| T = 6 h | 55,550 | 3 | 96 | 1 | 0 |
| T = 9 h | 60,012 | 3 | 11 | 86 | 0 |
| T = 12 h | 60,418 | 3 | 13 | 84 | 0 |
| Time | Flooded Cells | May 2013 [%] | |||
|---|---|---|---|---|---|
| <−0.25 m | −0.25–0 m | 0.25–0 m | >0.25 m | ||
| T = 3 h | 34,493 | 8 | 92 | 0 | 0 |
| T = 6 h | 44,553 | 5 | 4 | 84 | 7 |
| T = 9 h | 45,864 | 4 | 6 | 89 | 1 |
| T = 12 h | 44,204 | 8 | 88 | 3 | 1 |
| Time | Flooded Cells | February 2005 [%] | |||
|---|---|---|---|---|---|
| <−0.25 m | −0.25–0 m | 0.25–0 m | >0.25 m | ||
| T = 3 h | 30,915 | 6 | 7 | 87 | 0 |
| T = 6 h | 37,426 | 5 | 2 | 87 | 5 |
| T = 9 h | 43,691 | 5 | 12 | 76 | 7 |
| T = 12 h | 46,790 | 7 | 91 | 2 | 0 |
| Time | Flooded Cells | January 2011 [%] | |||
|---|---|---|---|---|---|
| <−0.25 m | −0.25–0 m | 0.25–0 m | >0.25 m | ||
| T = 3 h | 30,825 | 6 | 70 | 24 | 0 |
| T = 6 h | 32,348 | 6 | 69 | 25 | 0 |
| T = 9 h | 37,097 | 6 | 3 | 87 | 4 |
| T = 12 h | 42,603 | 5 | 4 | 81 | 10 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhola, P.K.; Leandro, J.; Disse, M. Framework for Offline Flood Inundation Forecasts for Two-Dimensional Hydrodynamic Models. Geosciences 2018, 8, 346. https://doi.org/10.3390/geosciences8090346
Bhola PK, Leandro J, Disse M. Framework for Offline Flood Inundation Forecasts for Two-Dimensional Hydrodynamic Models. Geosciences. 2018; 8(9):346. https://doi.org/10.3390/geosciences8090346
Chicago/Turabian StyleBhola, Punit Kumar, Jorge Leandro, and Markus Disse. 2018. "Framework for Offline Flood Inundation Forecasts for Two-Dimensional Hydrodynamic Models" Geosciences 8, no. 9: 346. https://doi.org/10.3390/geosciences8090346
APA StyleBhola, P. K., Leandro, J., & Disse, M. (2018). Framework for Offline Flood Inundation Forecasts for Two-Dimensional Hydrodynamic Models. Geosciences, 8(9), 346. https://doi.org/10.3390/geosciences8090346






