Pressure Dependence of Magnesite Creep
Abstract
1. Introduction
2. Materials and Methods
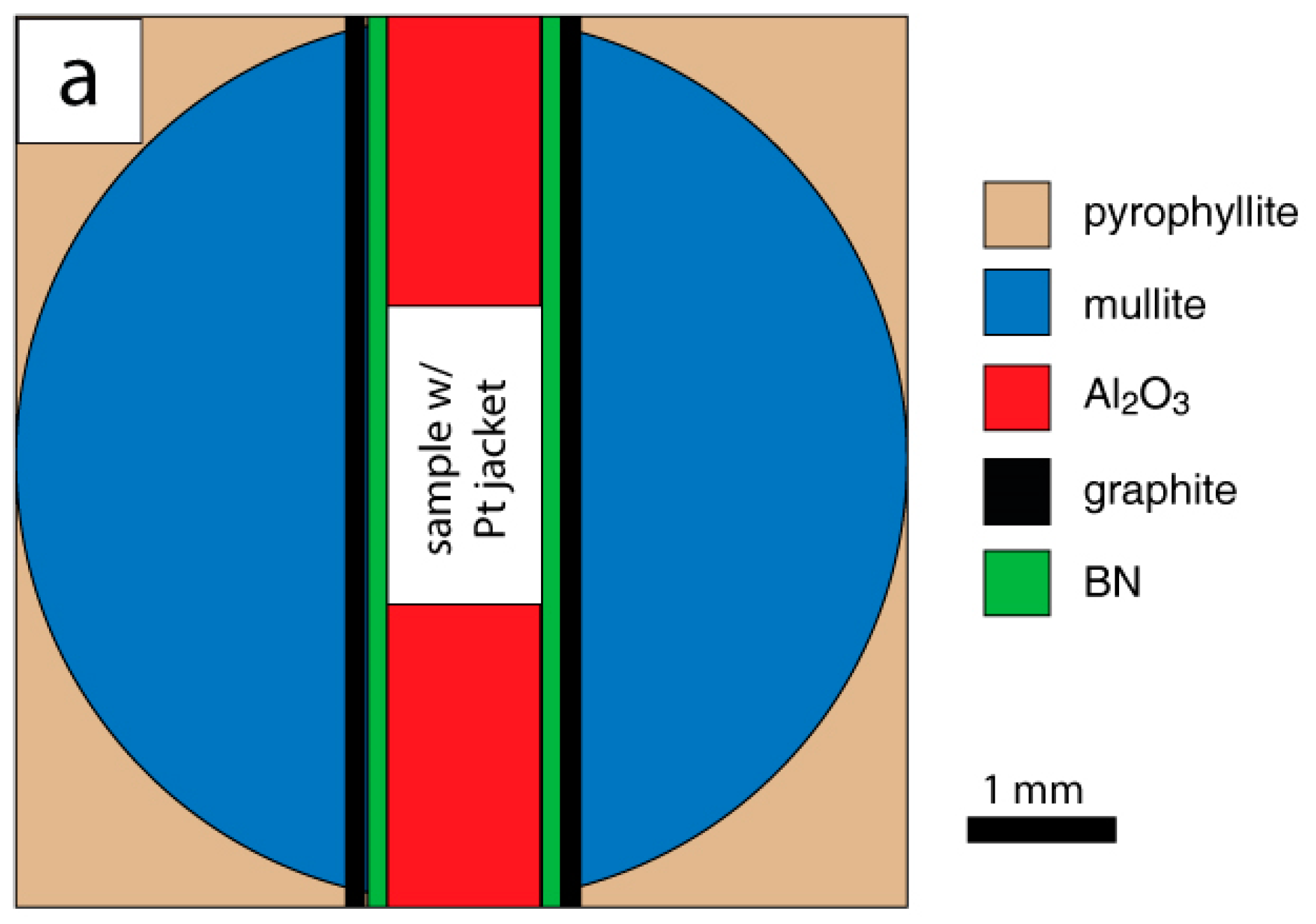
2.1. Starting Materials and Preparation
2.2. Experimental Techniques
2.2.1. D-DIA Apparatus
2.2.2. D-DIA Strain, Strain Rate and Stress Calculation
2.2.3. Griggs Apparatus
2.3. Microstructure and Texture Analyses
3. Results
3.1. 500 °C Fine-Grained Magnesite Deformation
3.2. 750 °C Fine-Grained Magnesite Deformation
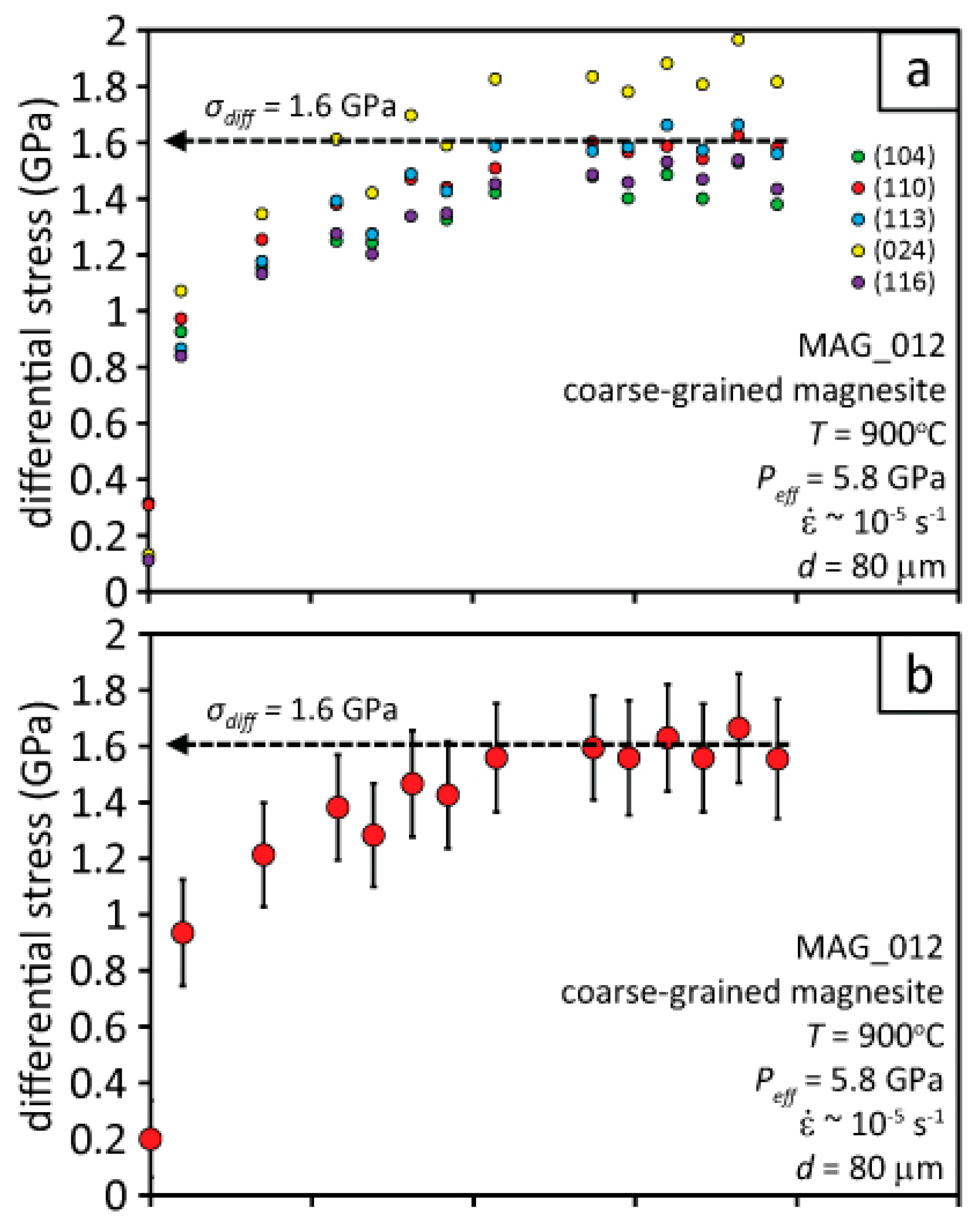
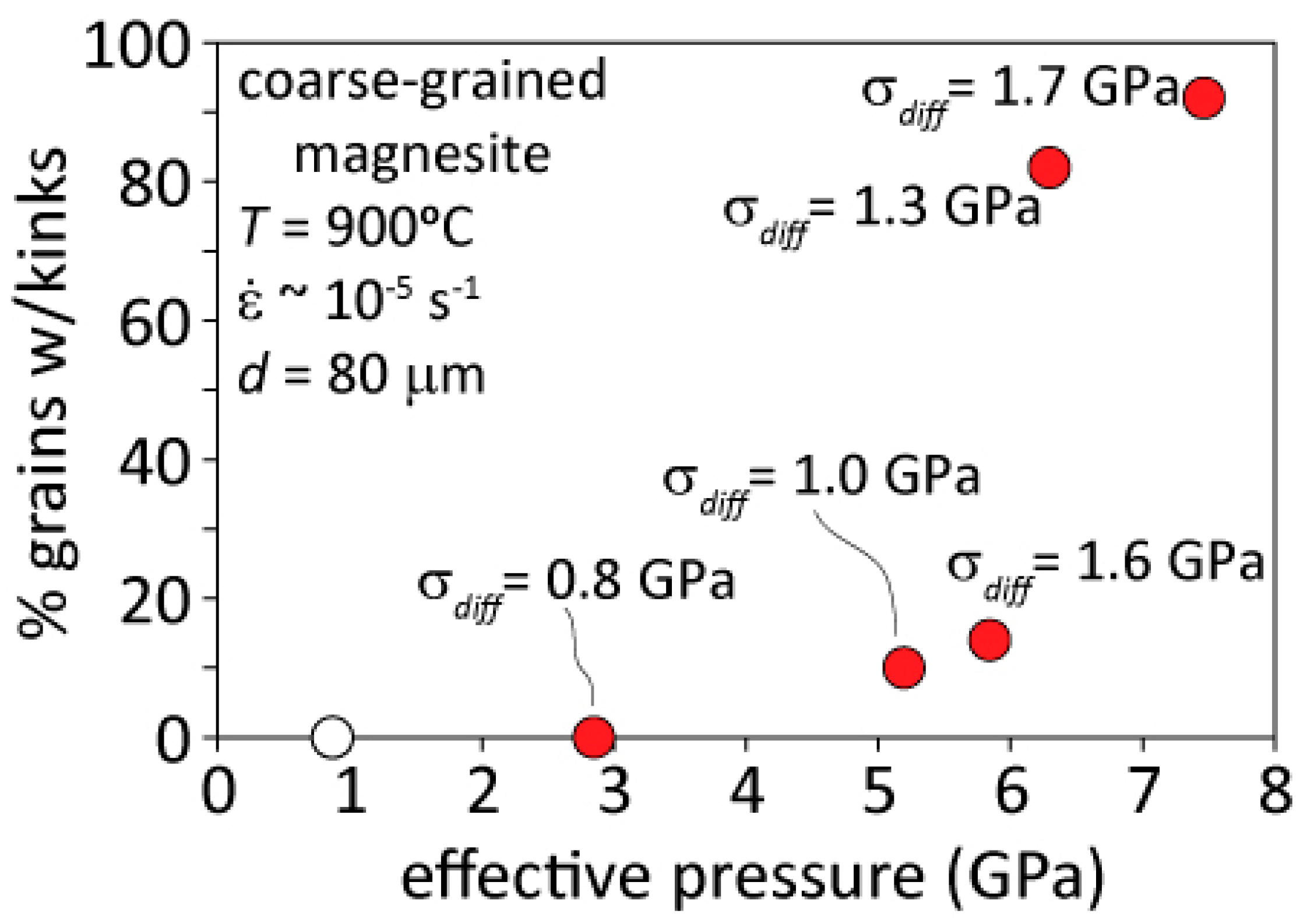
3.3. 900 °C Coarse-Grained Magnesite Deformation
4. Discussion
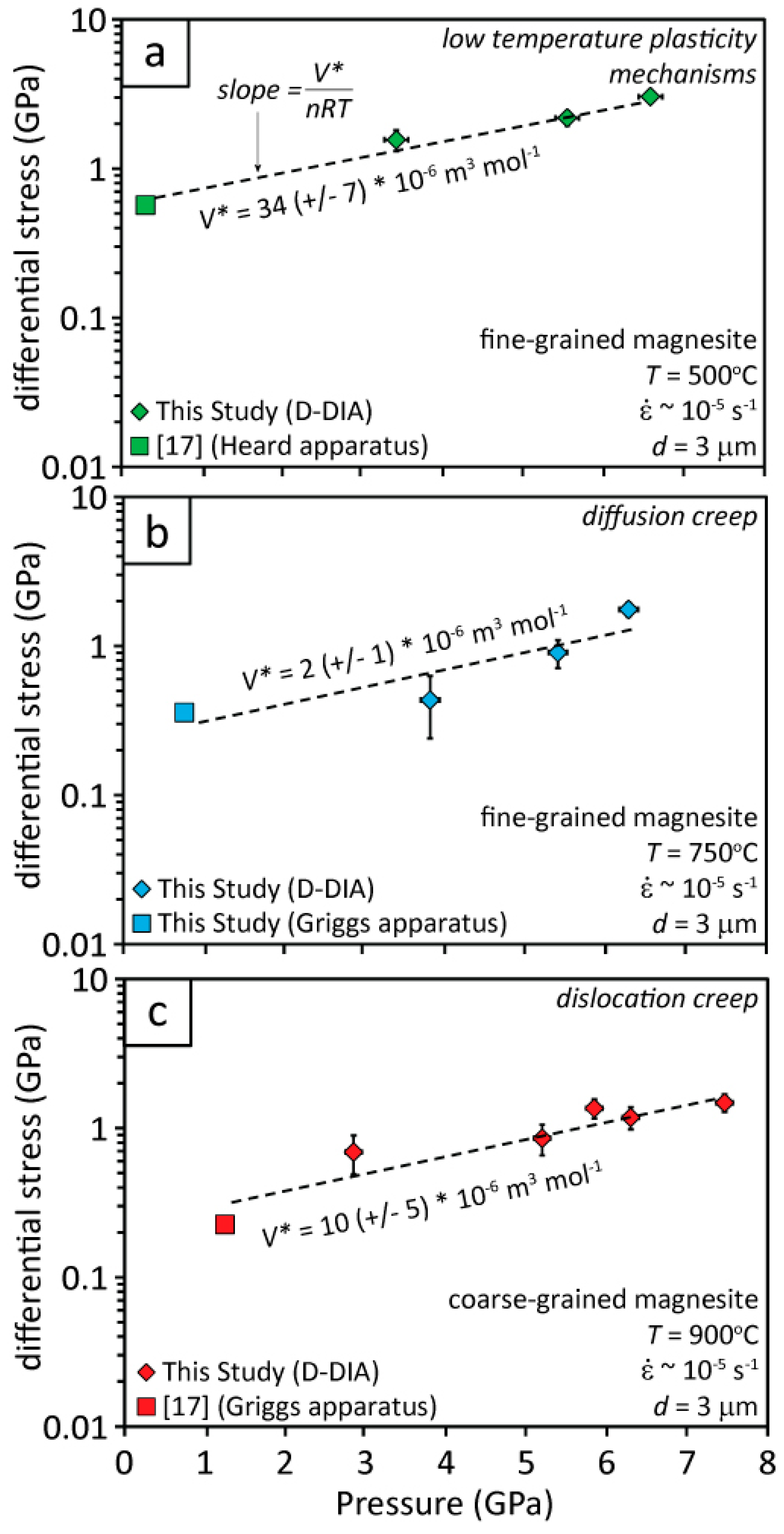
4.1. Deformation of Fine-Grained Magnesite at 500 °C
4.2. Deformation of Fine-Grained Magnesite at 750 °C
4.3. Deformation of Coarse-grained Magnesite at 900 °C
4.4. The effect of Pressure on Magnesite Deformation Mechanisms
4.5. Physical Interpretations of V*
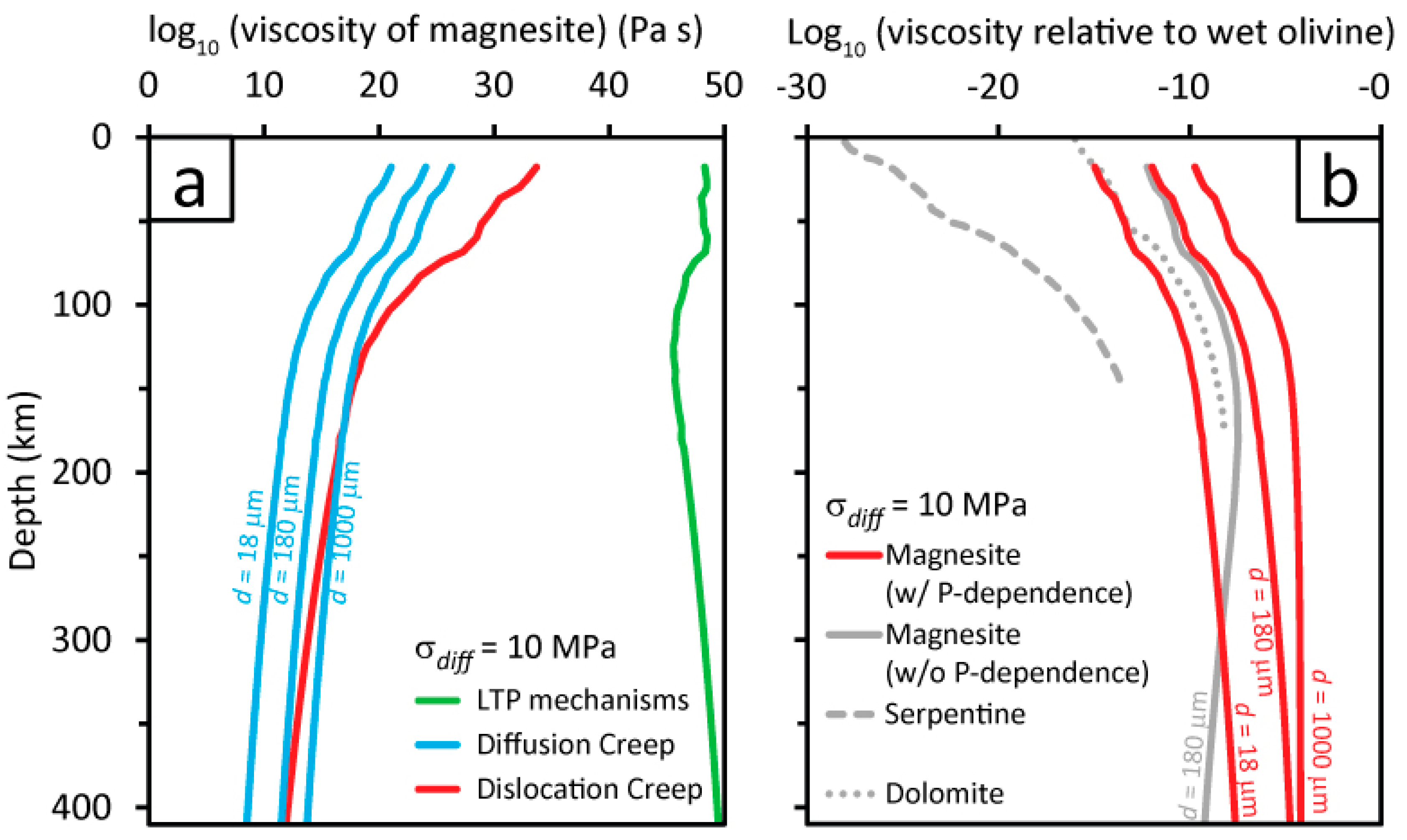
4.6. Application to Nature
5. Conclusions
- The activation volumes calculated for LTP, diffusion creep, and dislocation creep of magnesite are V* = 34 (±7), 2 (±1), and 10 (±5) × 10−6·m−3·mol−1, respectively.
- The effective viscosity of magnesite is 5–6 orders of magnitude lower than that of wet olivine in subducting slabs, when the pressure dependence is considered.
- Strain may localize within magnesite horizons in subducting slabs resulting in intermediate depth deep focus earthquakes.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Green, H.W.; Houston, H. The mechanics of deep earthquakes. Annu. Rev. Earth Plant. Sci. 1995, 23, 169–213. [Google Scholar] [CrossRef]
- Bilek, S.L.; Lay, T. Subduction Zone Megathrust Earthquakes. Geosphere 2018, 14, 1468–1500. [Google Scholar] [CrossRef]
- Wadati, K. Shallow and deep earthquakes. Geophys. Mag. 1928, 1, 162–202. [Google Scholar]
- Hacker, B.R.; Peacock, S.M.; Abers, G.A.; Holloway, S.D. Subduction factory-2. Are intermediate-depth earthquakes in subducting slabs linked to metamorphic dehydration reactions? J. Geophys. Res. Sol. Earth 2003, 108. [Google Scholar] [CrossRef]
- Hilairet, N.; Reynard, B.; Wang, Y.B.; Daniel, I.; Merkel, S.; Nishiyama, N.; Petitgirard, S. High-pressure creep of serpentine, interseismic deformation, and initiation of subduction. Science 2007, 318, 1910–1913. [Google Scholar] [CrossRef] [PubMed]
- Peacock, S.M. Are the lower planes of double seismic zones caused by serpentine dehydration in subducting oceanic mantle? Geology 2001, 29, 299–302. [Google Scholar] [CrossRef]
- Raleigh, C.B.; Paterson, M.S. Experimental deformation of serpentinite and its tectonic implications. J. Geophys. Res. 1965, 70, 3965–3985. [Google Scholar] [CrossRef]
- Ulmer, P.; Trommsdorff, V. Serpentine stability to mantle depths and subduction-related magmatism. Science 1995, 268, 858–861. [Google Scholar] [CrossRef]
- Burnley, P.; Green, D.H.; Prior, D. Faulting associated with the olivine to spinel transformation in Mg2GeO4 and its implications for deep-focus earthquake. J. Geophys. Res. 1991, 96, 425–443. [Google Scholar] [CrossRef]
- Kirby, S.H.; Stein, S.; Okal, E.A.; Rubie, D.C. Metastable mantle phase transformations and deep earthquakes in subducting oceanic lithosphere. Rev. Geophys. 1996, 34, 261–306. [Google Scholar] [CrossRef]
- Schubnel, A.; Brunet, F.; Hilairet, N.; Gasc, J.; Wang, Y.B.; Green, H.W. Deep-focus earthquake analogs recorded at high pressure and temperature in the laboratory. Science 2013, 341, 1377–1380. [Google Scholar] [CrossRef] [PubMed]
- Flinn, E.A.; Engdahl, E.R. A proposed basis for geographical and seismic regionalization. Rev. Geophys. 1965, 3, 123–149. [Google Scholar] [CrossRef]
- Frohlich, C. Deep Earthquakes; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Karato, S.; Riedel, M.R.; Yuen, D.A. Rheological structure and deformation of subducted slabs in the mantle transition zone: Implications for mantle circulation and deep earthquakes. Phys. Earth Planet. Inter. 2001, 127, 83–108. [Google Scholar] [CrossRef]
- Griggs, D.T.; Baker, D.W. The origin of deep-focus earthquakes. In Properties of Matter under Unusual Conditionss (in Honor of Edward Teller’s 60th Birthday); Mark, H., Fernbach, S., Eds.; Interscience Publishers: New York, NY, USA; London, UK, 1969; pp. 23–42. [Google Scholar]
- Kelemen, P.B.; Hirth, G. A periodic shear-heating mechanism for intermediate-depth earthquakes in the mantle. Nature 2007, 446, 787–790. [Google Scholar] [CrossRef] [PubMed]
- Holyoke, C.W.I.; Kronenberg, A.K.; Newman, J.; Ulrich, C. Rheology of magnesite. J. Geophys. Res. 2014, 119, 1–24. [Google Scholar] [CrossRef]
- Li, J.; Zheng, Y.; Thomsen, T.; Lapen, T.; Fang, X. Deep earthquakes in subducting slabs hosted in highly anisotropic rock fabric. Nat. Geosci. 2018, 11, 696–700. [Google Scholar] [CrossRef]
- Dasgupta, R.; Hirschmann, M.M. The deep carbon cycle and melting in Earth’s interior. Earth Planet. Sci. Lett. 2010, 298, 1–13. [Google Scholar] [CrossRef]
- Ducea, M.N.; Saleeby, J.; Morrison, J.; Valencia, V.A. Subducted carbonates, metasomatism of mantle wedges, and possible connections to diamond formation: An example from California. Am. Mineral. 2005, 90, 864–870. [Google Scholar] [CrossRef]
- Goto, A.; Kunugiza, K.; Omori, S. Evolving fluid composition during prograde metamorphism in subduction zones: A new approach using carbonate-bearing assemblages in the pelitic system. Gondwana Res. 2007, 11, 166–179. [Google Scholar] [CrossRef]
- Isshiki, M.; Irifune, T.; Hirose, K.; Ono, S.; Ohishi, Y.; Watanuki, T.; Nishibori, E.; Takata, M.; Sakata, M. Stability of magnesite and its high-pressure form in the lowermost mantle. Nature 2004, 427, 60–63. [Google Scholar] [CrossRef]
- Kerrick, D.M.; Connolly, J.A.D. Metamorphic devolatilization of subducted oceanic metabasalts: Implications for seismicity, arc magmatism and volatile recycling. Earth Planet. Sci. Lett. 2001, 189, 19–29. [Google Scholar] [CrossRef]
- Kilian, R.; Behrmann, J.H. Geochemical constraints on the sources of Southern Chile Trench sediments and their recycling in arc magmas of the Southern Andes. J. Geol. Soc. Lond. 2003, 160, 57–70. [Google Scholar] [CrossRef]
- Plank, T.; Langmuir, C.H. The chemical composition of subducting sediment and its consequences for the crust and mantle. Chem. Geol. 1998, 145, 325–394. [Google Scholar] [CrossRef]
- Rea, D.K.; Ruff, L.J. Composition and mass flux of sediment entering the world’s subduction zones: Implications for global sediment budgets, great earthquakes, and volcanism. Earth Planet. Sci. Lett. 1996, 140, 1–12. [Google Scholar] [CrossRef]
- Sleep, N.H.; Zahnle, K. Carbon dioxide cycling and implications for climate on ancient Earth. J. Geophys. Res. 2001, 106, 1373–1399. [Google Scholar] [CrossRef]
- Snyder, G.; Poreda, R.; Hunt, A.; Fehn, U. Regional variations in volatile composition: Isotopic evidence for carbonate recycling in the Central American volcanic arc. Geochem. Geophys. Geosyst. 2001, 2. [Google Scholar] [CrossRef]
- Zhang, L.; Ellis, D.J.; Arculus, R.J.; Jiang, W.; Wei, C. ‘Forbidden zone’ subduction of sediments to 150 km depth—The reaction of dolomite to magnesite plus aragonite in the UHPM metapelites from western Tianshan, China. J. Metamorph. Geol. 2003, 21, 523–529. [Google Scholar] [CrossRef]
- Kelemen, P.B.; Matter, J.; Streit, E.E.; Rudge, J.F.; Curry, W.B.; Blusztajn, J. Rates and mechanisms of mineral carbonation in peridotite: Natural processes and recipes for enhanced, in situ CO2 capture and storage. Annu. Rev. Earth Plant. Sci. 2011, 39, 545–576. [Google Scholar] [CrossRef]
- Quesnel, B.; Gautier, P.; Boulvais, P.; Cathelineau, M.; Maurizot, P.; Cluzel, D.; Ulrich, M.; Guillot, S.; Lesimple, S.; Couteau, C. Syn-tectonic, meteoric water-derived carbonation of the New Caledonia peridotite nappe. Geology 2013, 41, 1063–1066. [Google Scholar] [CrossRef]
- Saldi, G.D.; Jordan, G.; Schott, J.; Oelkers, E.H. Magnesite growth rates as a function of temperature and saturation state. Geochim. Cosmochim. Acta 2009, 73, 5646–5657. [Google Scholar] [CrossRef]
- Seto, Y.; Hamane, D.; Nagai, T.; Fujino, K. Fate of carbonates within oceanic plates subducted to the lower mantle, and a possible mechanism of diamond formation. Phys. Chem. Miner. 2008, 35, 223–229. [Google Scholar] [CrossRef]
- Kelemen, P.B.; Hirth, G. Reaction-driven cracking during retrograde metamorphism: Olivine hydration and carbonation. Earth Planet. Sci. Lett. 2012, 345, 81–89. [Google Scholar] [CrossRef]
- Biellmann, C.; Gillet, P.; Guyot, F.; Peyronneau, J.; Reynard, B. Experimental-evidence for carbonate stability in the Earths lower mantle. Earth Planet. Sci. Lett. 1993, 118, 31–41. [Google Scholar] [CrossRef]
- Brey, G.; Brice, W.R.; Ellis, D.J.; Green, D.H.; Harris, K.L.; Ryabchikov, I.D. Pyroxene-carbonate reactions in the upper mantle. Earth Planet. Sci. Lett. 1983, 62, 63–74. [Google Scholar] [CrossRef]
- Canil, D.; Scarfe, C.M. Phase-relations in peridotite + CO2 systems to 12 GPa-Implications for the origin of kimberlite and carbonate stability in the Earths upper mantle. J. Geophys. Res. 1990, 95, 15805–15816. [Google Scholar] [CrossRef]
- Katsura, T.; Ito, E. Melting and subsolidus phase-relations in the MgSiO3-MgCO3 system at high-pressures - Implications to evolution of the Earths atmosphere. Earth Planet. Sci. Lett. 1990, 99, 110–117. [Google Scholar] [CrossRef]
- Newton, R.C.; Sharp, W.E. Stability of forsterite + CO2 and its bearing on role of CO2 in mantle. Earth Planet. Sci. Lett. 1975, 26, 239–244. [Google Scholar] [CrossRef]
- Durham, W.B.; Mei, S.; Kohlstedt, D.L.; Wang, L.; Dixon, N.A. New measurements of activation volume in olivine under anhydrous conditions. Phys. Earth Planet. Inter. 2009, 172, 67–73. [Google Scholar] [CrossRef]
- Raterron, P.; Amiguet, E.; Chen, J.H.; Li, L.; Cordier, P. Experimental deformation of olivine single crystals at mantle pressures and temperatures. Phys. Earth Planet. Inter. 2009, 172, 74–83. [Google Scholar] [CrossRef]
- Wang, Y.; Durham, W.B.; Getting, I.C.; Weidner, D.J. The deformation-DIA: A new apparatus for high-temperature triaxial deformation to pressures up to 15 GPa. Rev. Sci. Instrum. 2003, 74, 3002–3011. [Google Scholar] [CrossRef]
- Goldsmith, J.R.; Heard, H.C. Subsolidus phase relations in the system CaCO3-MgCO3. J. Geol. 1961, 69, 45–74. [Google Scholar] [CrossRef]
- Harker, R.I.; Tuttle, O.F. Studies in the system CaO-MgO-CO2; Part 2, Limits of solid solution along the binary join CaCO3-MgCO3. Am. J. Sci. 1955, 253, 274–282. [Google Scholar] [CrossRef]
- Irving, A.J.; Wyllie, P.J. Subsolidus and Melting Relationships for Calcite, Magnesite and Join Caco3-Mgco3 to 36 Kb. Geochim. Cosmochim. Acta 1975, 39, 35–53. [Google Scholar] [CrossRef]
- Blasko, C. Pressure Dependence of Polycrystalline Magnesite and Dolomite; University of Akron: Akron, OH, USA, 2017. [Google Scholar]
- Raterron, P.; Holyoke, C.W.; Merkel, S. Temperature gradients and stress measurements in the deformation-DIA cell using alumina pistons. Rev. Sci. Instrum. 2013, 84, 043906. [Google Scholar] [CrossRef] [PubMed]
- Girard, J.; Chen, J.H.; Raterron, P.; Holyoke, C. Deformation of single crystal sample using D-DIA apparatus coupled with synchrotron X-rays: In situ stress and strain measurements at high pressure and temperature. J. Phys. Chem. Solids 2010, 71, 1053–1058. [Google Scholar] [CrossRef]
- Merkel, S.; Hilairet, N. Multifit/Polydefix: A framework for the analysis of polycrystal deformation using X-rays. J. Appl. Crystallogr. 2015, 48, 1307–1313. [Google Scholar] [CrossRef]
- Griggs, D.T. Hydrolytic weakening of quartz and other silicates. Geophys. J. R. Astron. Soc. 1967, 14, 19–31. [Google Scholar] [CrossRef]
- Holyoke, C.W.; Kronenberg, A.K. Accurate differential stress measurement using the molten salt cell and solid salt assemblies in the Griggs apparatus with applications to strength, piezometers and rheology. Tectonophysics 2010, 494, 17–31. [Google Scholar] [CrossRef]
- Tullis, T.E.; Tullis, J. Experimental rock deformation techniques. In Mineral and Rock Deformation; Laboratory Studies; the Paterson Volume; American Geophysical Union: Washington, DC, USA, 1986; Volume 36, pp. 297–324. [Google Scholar]
- Barbery, A. The Effect of Water Content on the Strength of Quartzite. Master’s Thesis, University of Akron, Akron, OH, USA, 2017. [Google Scholar]
- Holyoke, C.W.; Newman, J.; Kronenberg, A.K. Dislocation creep of polycrystalline dolomite. Tectonophysics 2013, 590, 72–82. [Google Scholar] [CrossRef]
- Kido, M.; Muto, J.; Nagahama, H. Method for correction of differential stress calculations from experiments using the solid salt assembly in a Griggs-type deformation apparatus. Tectonophysics 2016, 672, 170–176. [Google Scholar] [CrossRef]
- Liu, J.; Walter, J.; Weber, K. Fluid-enhanced low-temperature plasticity of calcite marble: Microstructures and mechanisms. Geology 2002, 30, 787–790. [Google Scholar] [CrossRef]
- Rutter, E.H. Influence of temperature, strain rate and interstitial water in experimental deformation of calcite rocks. Tectonophysics 1974, 22, 311–334. [Google Scholar] [CrossRef]
- Davis, N.E.; Kronenberg, A.K.; Newman, J. Plasticity and diffusion creep of dolomite. Tectonophysics 2008, 456, 127–146. [Google Scholar] [CrossRef]
- Delle Piane, C.; Burlini, L.; Kunze, K.; Brack, P.; Burg, J.P. Rheology of dolomite: Large strain torsion experiments and natural examples. J. Struct. Geol. 2008, 30, 767–776. [Google Scholar] [CrossRef]
- Schmid, S.M.; Boland, J.N.; Paterson, M.S. Superplastic flow in finegrained limestone. Tectonophysics 1977, 43, 257–291. [Google Scholar] [CrossRef]
- Schmid, S.M.; Paterson, M.S.; Boland, J.N. High temperature flow and dynamic recrystallization in Carrara marble. Tectonophysics 1980, 65, 245–280. [Google Scholar] [CrossRef]
- De Bresser, J.H.P. On the mechanism of dislocation creep of calcite at high temperature: Inferences from experimentally measured pressure sensitivity and strain rate sensitivity of flow stress. J. Geophys. Res. 2002, 107. [Google Scholar] [CrossRef]
- Wenk, H.R.; Barber, D.J.; Reeder, R.J. Microstructures in carbonates. In Carbonates; Mineralogy and Chemistry; Mineralogical Society of America: Washington, DC, USA, 1983; Volume 11, pp. 301–367. [Google Scholar]
- Panero, W.R.; Kabbes, J.E. Mantle-wide sequestration of carbon in silicates and the structure of magnesite II. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Peacock, S.M.; van Keken, P.E.; Holloway, S.D.; Hacker, B.R.; Abers, G.A.; Fergason, R.L. Thermal structure of the Costa Rica-Nicaragua subduction zone. Phys. Earth Planet. Inter. 2005, 149, 187–200. [Google Scholar] [CrossRef]
- Twiss, R.J. Theory and Applicability of a Recrystallized Grain-Size Paleopiezometer. Pure Appl. Geophys. 1977, 115, 227–244. [Google Scholar] [CrossRef]
- Hirth, G.; Kohlstedt, D. Rheology of the upper mantle and mantle wedge; a view from the experimentalists. In Inside the Subduction Factory; American Geophysical Union: Washington, DC, USA, 2003; Volume 138, pp. 83–105. [Google Scholar]










| Magnesite | Grain Size | Porosity | Mg 1 | Ca | Mn | Fe | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (µm) | +\− | n | % | |||||||||
| Nevada Coarse | 80 | 16 | 324 | <1 | 0.994 | +/−0.005 | 0.004 | +/−0.003 | ND | +/−0.000 | 0.002 | +/−0.002 |
| Nevada Fine | 2 | 0.6 | 216 | <1 | 0.996 | +/−0.001 | 0.004 | +/−0.001 | ND | +/−0.000 | ND | +/−0.000 |
| Experiment | Temperature | Pressure | Effective Pressure | Initial Strain Rate | Final Strain Rate | Strain | Peak Strength | Final Strength | Grain Size | Porosity | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| (°C) | (GPa) | (GPa) | (×10−5 s−1) | (×10−5 s−1) | (%) | (GPa) | (GPa) | (µm) | n | % | |
| MAG_005 ad | 500 | 3.4 ± 0.1 | 3.4 ± 0.1 | 0.7 | 2.7 | 27 | 1.6 ± 0.3 | 1.6 ± 0.3 | 2.1 ± 1.5 | 194 | <1 |
| MAG_006 ad | 500 | 5.6 ± 0.3 | 5.6 ± 0.3 | 1.3 | 2.8 | 28 | 2.2 ± 0.3 | 2.2 ± 0.3 | 2.2 ± 0.9 | 167 | <1 |
| MAG_004 ad | 500 | 6.6 ± 0.2 | 6.6 ± 0.2 | 0.9 | 2.5 | 27 | 3.1 ± 0.3 | 3.1 ± 0.3 | 2.2 ± 1.1 | 196 | <1 |
| MAG_020 acd | 750 | 6.4 ± 0.1 | 6.3 ± 0.1 | 0.6 | 1.3 | 5 | 1.2 ± 0.2 | 1.2 ± 0.2 | - | - | |
| 5.5 ± 0.1 | 5.4 ± 0.1 | 0.4 | 2.1 | 6 | 0.9 ± 0.2 | 0.9 ± 0.2 | - | - | |||
| 3.9 ± 0.1 | 3.8 ± 0.1 | 1.9 | 3.0 | 6 | 0.6 ± 0.2 | 0.6 ± 0.2 | 1.9 ± 1.5 | 144 | 5 | ||
| Z-100 b | 750 | 0.85 ± 0.02 | 0.76 ± 0.02 | 1.5 | 2.1 | 15 | 0.50 ± 0.02 | 0.38 ± 0.02 | 3.8 ± 2.4 | 212 | 5 |
| Experiment | Temperature | Pressure | Effective Pressure | Initial Strain Rate | Final Strain Rate | Strain | Peak Strength | Final Strength | Porphyroclast Grain Size | Recrystallized Grain Size | Grains w/ Kinks | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (°C) | (GPa) | (GPa) | (×10−5 s−1) | (×10−5 s−1) | (%) | (GPa) | (GPa) | (µm) | n | (µm) | n | (%) | |
| MAG_008 | 900 | 5.6 ± 0.1 | 5.2 ± 0.1 | 1.5 | 2.9 | 30 | 1.1 ± 0.2 | 1.0 ± 0.2 | 63 ± 23 | 245 | 2.0 ± 1.3 | 438 | 10 |
| MAG_010 | 900 | 7.9 ± 0.1 | 7.5 ± 0.1 | 1.2 | 2.9 | 36 | 1.7 ± 0.2 | 1.7 ± 0.2 | 59 ± 19 | 202 | 1.8 ± 1.1 | 388 | 92 |
| MAG_012 | 900 | 6.2 ± 0.1 | 5.8 ± 0.1 | 1.8 | 3.3 | 30 | 1.6 ± 0.2 | 1.6 ± 0.2 | 75 ± 24 | 118 | 1.9 ± 1.1 | 442 | 14 |
| MAG_014 | 900 | 3.2 ± 0.1 | 2.9 ± 0.1 | 1.5 | 3.5 | 36 | 0.9 ± 0.2 | 0.8 ± 0.2 | 65 ± 20 | 211 | 2.2 ± 0.9 | 536 | 0 |
| MAG_016 | 900 | 6.7 ± 0.1 | 6.3 ± 0.1 | 1.1 | 2.9 | 27 | 1.3 ± 0.2 | 1.3 ± 0.2 | 74 ± 18 | 192 | 1.8 ± 1.2 | 334 | 82 |
| Deformation Mechanism | A | n a | m | E* a | V* | ||
|---|---|---|---|---|---|---|---|
| (±) | Units | KJ mol−1 | *10−6 m3/mol | ||||
| LTP | 7.44 × 10−41 | 3.57 × 10−40 | MPa−n s | 19.7 | - | 233 ± 16 | 34 ± 7 |
| Diffusion Creep | 9.75 × 104 | 5.87 × 104 | MPa−n s | 1.1 | 3 | 209 ± 10 | 2 ± 1 |
| Dislocation Creep | 3.81 × 108 | 7.66 × 108 | MPa−n µmm s | 3 | - | 410 ± 20 | 10 ± 5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Millard, J.W.; Holyoke, C.W., III; Wells, R.K.; Blasko, C.; Kronenberg, A.K.; Raterron, P.; Braccia, C.; Jackson, N.; McDaniel, C.A.; Tokle, L. Pressure Dependence of Magnesite Creep. Geosciences 2019, 9, 420. https://doi.org/10.3390/geosciences9100420
Millard JW, Holyoke CW III, Wells RK, Blasko C, Kronenberg AK, Raterron P, Braccia C, Jackson N, McDaniel CA, Tokle L. Pressure Dependence of Magnesite Creep. Geosciences. 2019; 9(10):420. https://doi.org/10.3390/geosciences9100420
Chicago/Turabian StyleMillard, Joseph W., Caleb W. Holyoke, III, Rachel K. Wells, Cole Blasko, Andreas K. Kronenberg, Paul Raterron, Casey Braccia, Nicholas Jackson, Caleb A. McDaniel, and Leif Tokle. 2019. "Pressure Dependence of Magnesite Creep" Geosciences 9, no. 10: 420. https://doi.org/10.3390/geosciences9100420
APA StyleMillard, J. W., Holyoke, C. W., III, Wells, R. K., Blasko, C., Kronenberg, A. K., Raterron, P., Braccia, C., Jackson, N., McDaniel, C. A., & Tokle, L. (2019). Pressure Dependence of Magnesite Creep. Geosciences, 9(10), 420. https://doi.org/10.3390/geosciences9100420





