Deformation Modeling of Flexible Pavement in Expansive Subgrade in Texas
Abstract
:1. Introduction
2. Materials and Methods
2.1. Site Selection
2.2. Subsurface Exploration
2.3. Deformation Monitoring
2.4. Moisture Monitoring by Field Instrumentation
2.5. Seasonal Moisture Variation by Resistivity
3. Results
3.1. Subsurface Results
3.2. Moisture Variation in Center Borehole of FM 2757
3.3. Moisture Variation in Edge Borehole of SH 342
3.4. Moisture Variation in Subgrade by Resistivity
3.5. Moisture Intrusion from Edge of the Pavement
3.6. Influence of Trees
3.7. Deformation Behavior of FM 2757 Site
3.8. Deformation Behavior of SH 342 Site
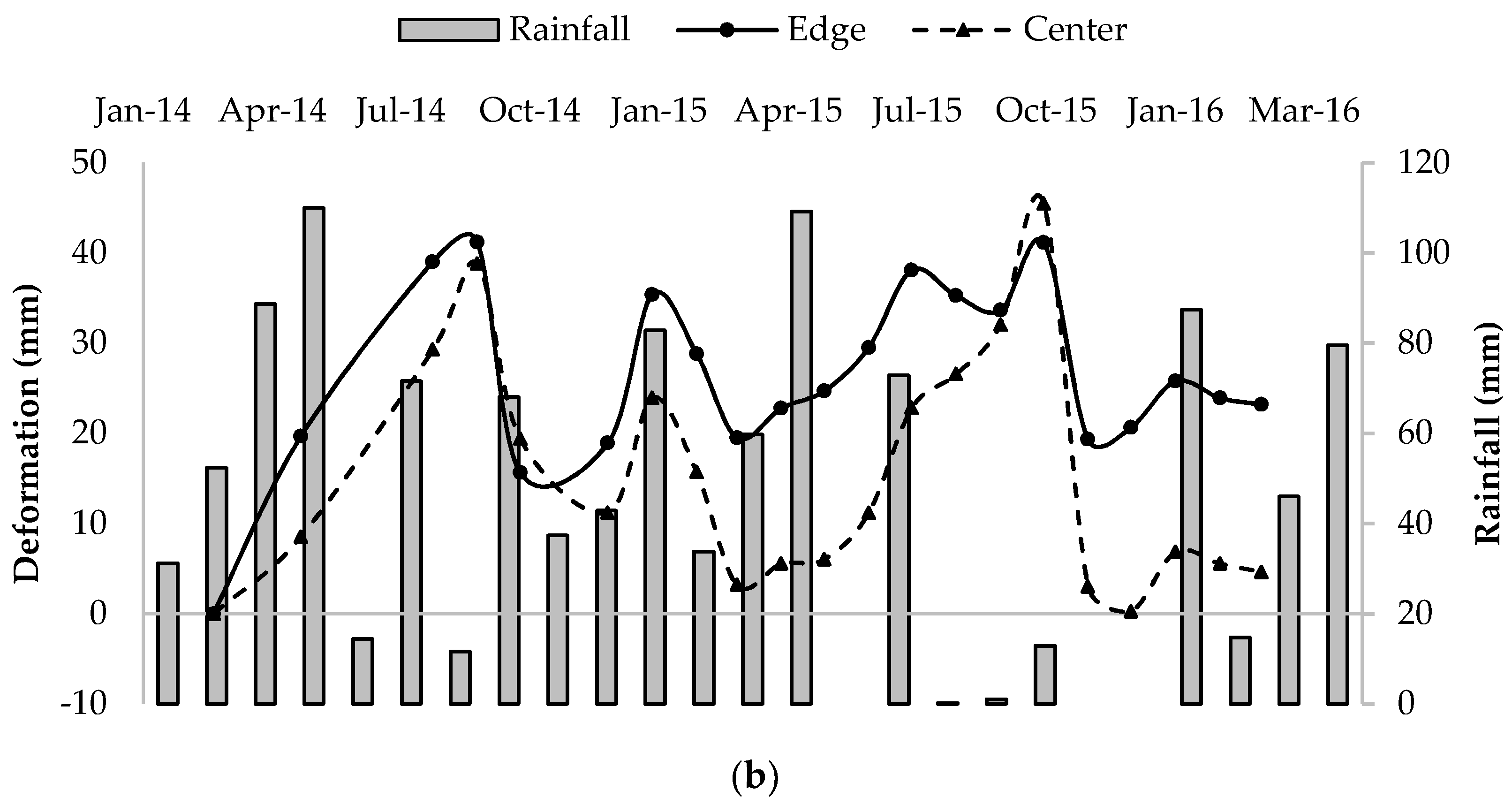
3.9. Deformation with Rainfall at Both Sites
4. Development of Deformation Model
4.1. Development of Initial Model
4.2. Modification of the Model
- figy (deformation factor) = 0.3169 × (rainfall factor) + 1.4849
- y (deformation factor) = 0.7464 × (rainfall factor) − 2.221
4.3. Statistical Validation of the Deformation Model
- mean of the actual field deformation
- mean of the model predicted deformation
4.4. Limitations of the Deformation Model
4.5. Discussion on the Resilient Modulus
5. Conclusions and Discussions
- Previous studies focused on deformation behavior of expansive subgrade based on laboratory testing and numerical model; this study attempts to develop deformation model based on real-time deformation data collected over three consecutive years.
- As rainfall and change of moisture content are correlated, only rainfall amount was included in the model to avoid multicollinearity. Temperature and suction were also eliminated from the model development as a significant correlation was not attained.
- The influence of trees was discussed in a qualitative manner, and it was excluded from model development.
- Moisture variation data from field instrumentation and resistivity imaging indicated that the edge of the pavement is more vulnerable; as such, the edge deformation model was considered.
- Both seasonal variation and temporal variation due to rainfall were included for the deformation model.
- The initial model can capture the seasonal trend but modification is required to include the rainfall effect in the deformation model.
- Rainfall factor was determined to be included in the final deformation model, which satisfied the validation statistically.
- The model was limited to the assumption of single soil layer/homogeneous stratigraphy. The inclusion of different soil layer and evaporation consideration will further improve the model.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Day | Rain | Deformation | |
| 14 March | 0 | 1.23 | 0 |
| 14 May | 60 | 3.49 | 0.7746 |
| 14 August | 150 | 2.82 | 1.5354 |
| 14 September | 180 | 0.46 | 1.623 |
| 14 October | 210 | 2.68 | 0.6156 |
| 14 December | 270 | 1.69 | 0.7446 |
| 15 Jane | 300 | 3.26 | 1.3932 |
| 15 February | 330 | 1.33 | 1.1352 |
| 15 March | 360 | 2.35 | 0.768 |
| 15 April | 390 | 4.3 | 0.8976 |
| 15 May | 420 | 9.44 | 0.9726 |
| 15 June | 450 | 2.87 | 1.1622 |
| 15 July | 480 | 0.01 | 1.5 |
| 15 August | 510 | 0.04 | 1.3878 |
| 15 September | 540 | 0.51 | 1.3254 |
| 15 October | 570 | 9.29 | 1.62 |
| 15 November | 600 | 6.84 | 0.7608 |
| 15 December | 630 | 3.44 | 0.8136 |
| 16 Jane | 660 | 0.58 | 1.0158 |
| 16 February | 690 | 1.81 | 0.942 |
| 16 March | 720 | 3.13 | 0.9132 |
References
- Djellali, A.; Ounis, A.; Saghafi, B. Behavior of flexible pavements on expansive soils. Int. J. Transp. Eng. 2013, 1, 1–16. [Google Scholar]
- Steinberg, M.L. Further Monitoring of Twelve Geomembrane Sites in Texas; Texas State Department of Highways & Public Transp: Austin, TX, USA, 1990.
- Nelson, J.; Miller, D.J. Expansive Soils: Problems and Practice in Foundation and Pavement Engineering; John Wiley & Sons: Hoboken, NJ, USA, 1997. [Google Scholar]
- Jones, L.D.; Jefferson, I. Expansive soils. In ICE Manual of Geotechnical Engineering; ICE Publishing: London, UK, 2012; pp. 413–441. [Google Scholar]
- Das, B.M. Advanced Soil Mechanics; Crc Press: Boca Raton, FL, USA, 2013; ISBN 978-1-4822-3483-1. [Google Scholar]
- Khan, M.S.; Hossain, S.; Ahmed, A.; Faysal, M. Investigation of a shallow slope failure on expansive clay in Texas. Eng. Geol. 2017, 219, 118–129. [Google Scholar] [CrossRef]
- Chabrillat, S.; Goetz, A.F.; Krosley, L.; Olsen, H.W. Use of hyperspectral images in the identification and mapping of expansive clay soils and the role of spatial resolution. Remote Sens. Environ. 2002, 82, 431–445. [Google Scholar] [CrossRef]
- Punthutaecha, K.; Puppala, A.J.; Vanapalli, S.K.; Inyang, H. Volume change behaviors of expansive soils stabilized with recycled ashes and fibers. J. Mater. Civ. Eng. 2006, 18, 295–306. [Google Scholar] [CrossRef]
- Manosuthikij, T.; Chittoori, B.C. Swell and shrinkage characterizations of unsaturated expansive clays from Texas. Eng. Geol. 2013, 164, 187–194. [Google Scholar] [Green Version]
- Sebesta, S. Investigation of Maintenance Base Repairs over Expansive Soils: Year 1 Report; Texas Transportation Institute, Texas A & M University System: Austin, TX, USA, 2002. [Google Scholar]
- Hedayati, M. Rainfall induced distress in low volume pavements. Ph.D. Thesis, The University of Texas at Arlington, Arlington, TX, USA, 2014. [Google Scholar]
- Ahmed, A.; Hossain, M.S.; Khan, M.S.; Greenwood, K.; Shishani, A. Moisture Variation in Expansive Subgrade Through Field Instrumentation and Geophysical Testing. In Proceedings of the International Congress and Exhibition “Sustainable Civil Infrastructures: Innovative Infrastructure Geotechnology”, Sharm El Sheikh, Egypt, 15–19 July 2017; pp. 45–58. [Google Scholar]
- Sapkota, A.; Ahmed, A.; Pandey, P.; Hossain, M.; Lozano, N. Stabilization of Rainfall-Induced Slope Failure and Pavement Distresses Using Recycled Plastic Pins and Modified Moisture Barrier. In Proceedings of the Eighth International Conference on Case Histories in Geotechnical Engineering (Geo-Congress 2019), Philadelphia, PA, USA, March 24–27 2019. [Google Scholar]
- Hashem, M.D.; Abu-Baker, A.M.; Hashem, M.D. Numerical Modeling of Flexible Pavement Constructed On Expansive Soils. Eur Int J Sci Tech. 2013, 2, 19–34. [Google Scholar]
- Inclinometer: Casing and Portable Measurement Systems. DGSI. 2018. Available online: https://durhamgeo.com/inclinometers/ (accessed on 17 October 2019).
- Bae, A.; Stoffels, S.M.; Antle, C.E.; Lee, S.W. Observed evidence of subgrade moisture influence on pavement longitudinal profile. Can. J. Civ. Eng. 2008, 35, 1050–1063. [Google Scholar] [CrossRef]
- Manzur, S.R.; Hossain, M.S.; Kemler, V.; Khan, M.S. Monitoring extent of moisture variations due to leachate recirculation in an ELR/bioreactor landfill using resistivity imaging. Waste Manag. 2016, 55, 38–48. [Google Scholar] [CrossRef] [PubMed]
- Advanced Geosciences, Inc. Instruction Manual for EarthImager 2D, Version 2.1. 7, Resistivity and IP Inversion Software; Advanced Geosciences, Inc.: Saint Antonio, TX, USA, 2004. [Google Scholar]
- Hossain, S.; Ahmed, A.; Khan, M.S.; Aramoon, A.; Thian, B. Expansive subgrade behavior on a state highway in North Texas. In Proceedings of the Geotechnical and Structural Engineering Congress 2016 Structural Engineering Institute, Phoenix, AZ, USA, 14–17 February 2016. [Google Scholar]
- Hsu, S.-C.; Nelson, P.P. Characterization of eagle ford shale. Eng. Geol. 2002, 67, 169–183. [Google Scholar] [CrossRef]
- Abrams, T.G.; Wright, S.G. A Survey of Earth Slope Failures and Remedial Measures in Texas; Texas State Department of Highways & Public Transp: Austin, TX, USA, 1972.
- Li, M.; Fang, C.; Kawasaki, S.; Achal, V. Fly ash incorporated with biocement to improve strength of expansive soil. Sci. Rep. 2018, 8, 2565. [Google Scholar] [CrossRef] [PubMed]
- Goodarzi, A.R.; Akbari, H.R.; Salimi, M. Enhanced stabilization of highly expansive clays by mixing cement and silica fume. Appl. Clay Sci. 2016, 132, 675–684. [Google Scholar] [CrossRef]
- Pandey, P.; Ahmed, A.; Sapkota, A.; Hossain, M.S.; Thian, B. Performance Evaluation of Pavement Subgrade by In Situ Moisture and Matric Suction Measurements. In Proceedings of the Eighth International Conference on Case Histories in Geotechnical Engineering (Geo-Congress 2019) American Society of Civil Engineers, Philadelphia, PA, USA, 24–27 March 2019. [Google Scholar]
- Ward, W.H. Soil Movements and Weather. In Proceedings of the Third International Conference On Soil Mechanics And Foundation Engineering, Zurich, Switzerland, 16–27 August 1953; Volume 2, pp. 477–481. [Google Scholar]
- Manosuthikij, T. Studies on volume change movements in high PI clays for better design of low volume pavements. Ph.D. Thesis, The University of Texas at Arlington, Arlington, TX, USA, 2008. [Google Scholar]
- Manosuthkij, T.; Nazarian, S.; Hoyos, L.R.; Chittoori, B. In situ matric suction and moisture content measurements in expansive clay during seasonal fluctuations. Geotech. Test. J. 2011, 35, 74–82. [Google Scholar]
- Wagner, J.-F. Mechanical properties of clays and clay minerals. In Developments in Clay Science; Elsevier: London, UK, 2013; Volume 5, pp. 347–381. [Google Scholar]
- Luo, R.; Prozzi, J.A. Development of longitudinal cracks on pavement over shrinking expansive subgrade. Road Mater. Pavement Des. 2010, 11, 807–832. [Google Scholar] [CrossRef]
- Kutner, M.H.; Nachtsheim, C.J.; Neter, J.; Li, W. Applied Linear Statistical Models; McGraw-Hill Irwin Boston: Boston, MA, USA, 2005; Volume 5. [Google Scholar]
- WP4C Dew Point PotentiaMeter. 2017. Available online: http://daskumars.com/ProductDetail.aspx?ProductName=WP4%20-%20Water%20Potential%20Meter%20(Dew%20Point%20Potentiometer) (accessed on 17 October 2019).
- Fredlund, D.G.; Rahardjo, H.; Rahardjo, H. Soil Mechanics for Unsaturated Soils; John Wiley & Sons: Hoboken, NJ, USA, 1993. [Google Scholar]
- Fityus, S.G. A soil moisture-based method of estimating ys. In Proceedings 8th Australia New Zealand Conference on Geomechanics: Consolidating Knowledge; Australian Geomechanics Society: Sydney, Australia, 1999; p. 809. [Google Scholar]
- Kodikara, J.; Rajeev, P.; Chan, D.; Gallage, C. Soil moisture monitoring at the field scale using neutron probe. Can. Geotech. J. 2013, 51, 332–345. [Google Scholar] [CrossRef]
- Sastry, S.S. Introductory Methods of Numerical Analysis; PHI Learning Pvt. Ltd.: New Delhi, India, 2012. [Google Scholar]
- Ng, C.W.W.; Zhou, C. Cyclic behaviour of an unsaturated silt at various suctions and temperatures. Géotechnique 2014, 64, 709–720. [Google Scholar] [CrossRef]
- Naji, K. Resilient modulus-moisture content relationships for pavement engineering applications. Int. J. Pavement Eng. 2018, 19, 651–660. [Google Scholar] [CrossRef]

















| Mean | Std. Dev. | SE Mean | t-Value | Value | |
|---|---|---|---|---|---|
| Actual | 24.56 | 3.79 | 1.1 | −1.0 | 0.332 |
| Predicted | 26.79 | 6.73 | 1.9 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, A.; Hossain, M.S.; Pandey, P.; Sapkota, A.; Thian, B. Deformation Modeling of Flexible Pavement in Expansive Subgrade in Texas. Geosciences 2019, 9, 446. https://doi.org/10.3390/geosciences9100446
Ahmed A, Hossain MS, Pandey P, Sapkota A, Thian B. Deformation Modeling of Flexible Pavement in Expansive Subgrade in Texas. Geosciences. 2019; 9(10):446. https://doi.org/10.3390/geosciences9100446
Chicago/Turabian StyleAhmed, Asif, MD Sahadat Hossain, Pratibha Pandey, Anuja Sapkota, and Boon Thian. 2019. "Deformation Modeling of Flexible Pavement in Expansive Subgrade in Texas" Geosciences 9, no. 10: 446. https://doi.org/10.3390/geosciences9100446
APA StyleAhmed, A., Hossain, M. S., Pandey, P., Sapkota, A., & Thian, B. (2019). Deformation Modeling of Flexible Pavement in Expansive Subgrade in Texas. Geosciences, 9(10), 446. https://doi.org/10.3390/geosciences9100446





